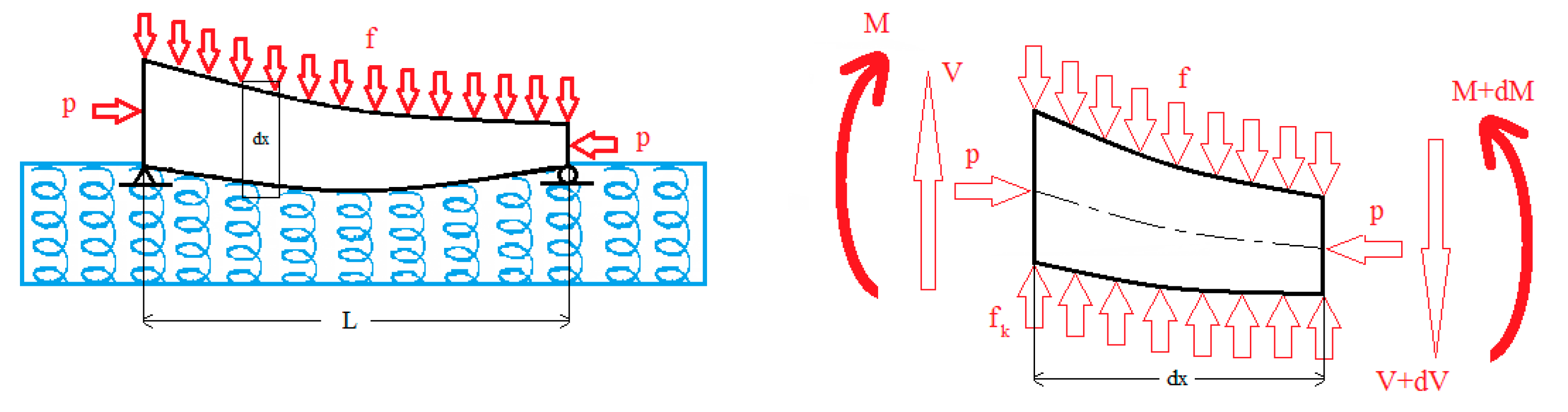
4.2. Results and Discussion
In this section, our calculation results are provided for the mid-section deflection of the possible different cases for a symmetrical and asymmetrical nanobeam under the influence of an axial force and a transverse distributed force , resting on a two-layered elastic foundation and Winkler and Pasternak elastic foundations, under three types of boundary condition- (SS, CS, and CC) supported beams. The effect of the different geometric properties of the nanobeam is given according to the polynomial of by taking two general cases of the varying cross-sectional area of the nanobeam: the first case is that the cross-sectional area changes linearly; the second case is that the cross-sectional area changes parabolically.
The first case entails that the cross-sectional area of the nanobeam changes linearly according to the polynomial
, where
and
are the steepness of the linear polynomial. In this case, we examined the leverage of the steepness of the linear polynomial on the mid-section deflection of the nanobeam by taking four specific situations of the linear nonuniformity distributions according to the steepness of the linear polynomial: the first situation
, i.e.,
; the second situation
, i.e.,
; the third situation
, i.e.,
; and the fourth situation
, i.e., the uniform beam
, as shown in
Figure 5.
The non-dimensional coefficient of the Winkler elastic foundation
, the non-dimensional coefficient of the Pasternak elastic foundation
, the non-dimensional distributed force
, and the non-dimensional axial force
are added one by one for beams with different values of the scaling effect parameter
in the next subsections to show how every parameter affects the midpoint deflection and the final results after adding all of them together, under three sets of boundary conditions, shown in
Table 3,
Table 4,
Table 5,
Table 6,
Table 7,
Table 8,
Table 9,
Table 10,
Table 11,
Table 12,
Table 13 and
Table 14.
To provide quick conclusions from
Table 3,
Table 4,
Table 5,
Table 6,
Table 7,
Table 8,
Table 9,
Table 10,
Table 11,
Table 12,
Table 13 and
Table 14, the following can be noted. First, the nondimensional midpoint deflection of the non-uniform nanobeam decreases in comparison with the uniform nanobeam. Second, the steepness
of the linear polynomial
has a devastating effect on nondimensional midpoint deflection, i.e., the nondimensional midpoint deflection of the non-uniform nanobeam decreases with the increasing steepness
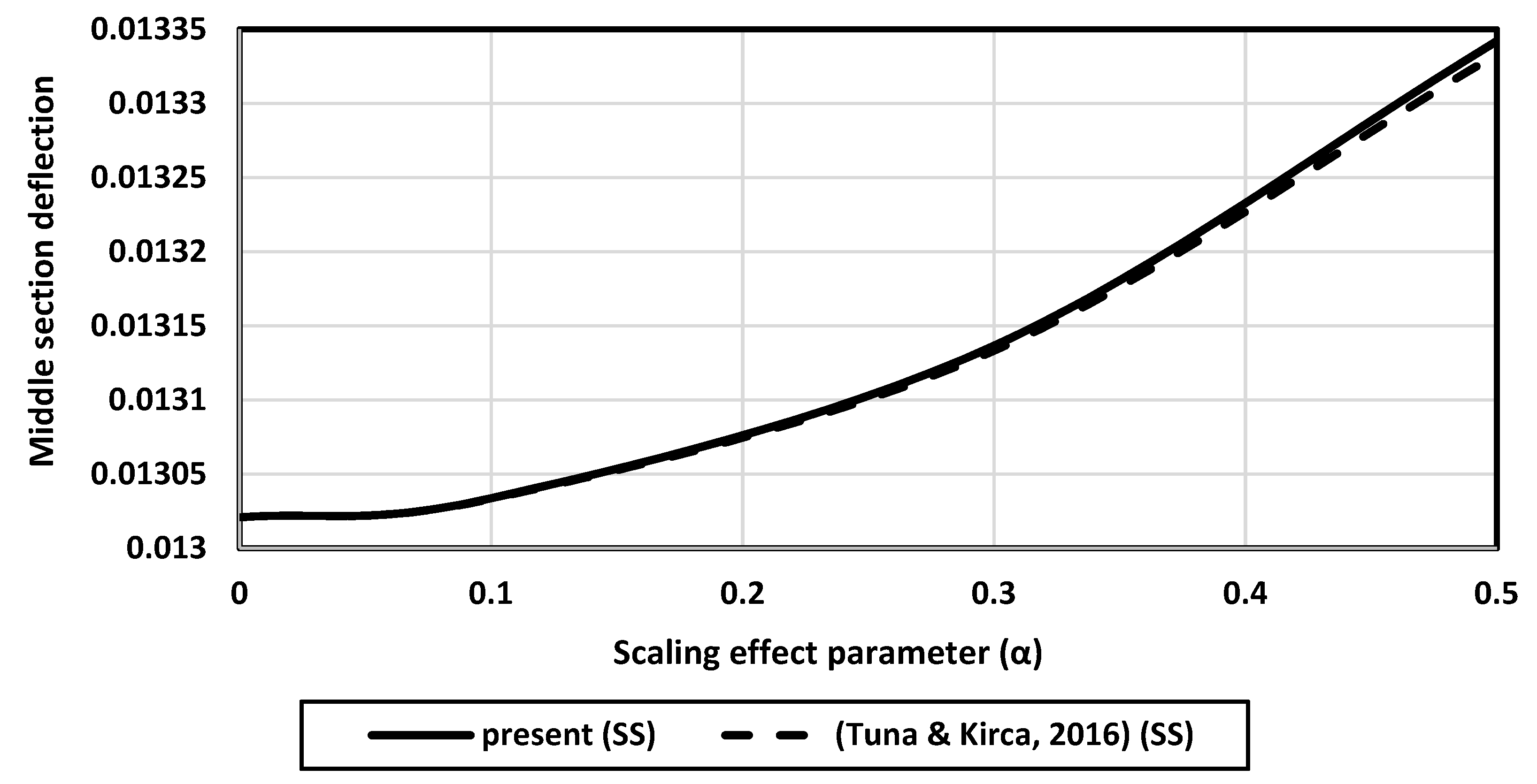
of the linear polynomial. Third, the nondimensional midpoint deflection of the nanobeam decreases in the presence of a Winkler elastic foundation under the beam. This decrease in deflection increases by adding the Pasternak elastic foundation under the beam. Fourth, the nondimensional midpoint deflection of the nanobeam increases in the presence of the axial compressive force. Fifth, in the case where the beam is not resting on any foundations, the midpoint deflection of the nanobeam increases with the increasing scaling effect parameter
. Conversely, when the beam is resting on a Winkler elastic foundation, the midpoint deflection of the beam decreases with the increasing scaling effect parameter
. In addition, when the Pasternak elastic foundation is added under the beam, the midpoint deflection is further decreased with the increase in the scaling effect parameter
.
Table 3.
The midpoint deflection for the non-uniform nanobeam with various scaling parameters and the nonuniformity distribution .
Table 3.
The midpoint deflection for the non-uniform nanobeam with various scaling parameters and the nonuniformity distribution .
| Scaling Effect Parameters () | Middle Section Deflection |
|---|
| | | | | | | | | | | | | | | |
|---|
| 1 | 0 | 0 | 0 | 1 | 30 | 0 | 0 | 1 | 30 | 30 | 0 | 1 | 30 | 30 | 1 |
|---|
| 0 | 0.0088005 | 0.0072758 | 0.0026753 | 0.0027331 |
| 0.1 | 0.0088092 | 0.0071602 | 0.0025083 | 0.0025639 |
| 0.2 | 0.0088352 | 0.0068357 | 0.0021133 | 0.0021631 |
| 0.3 | 0.0088787 | 0.0063590 | 0.0016762 | 0.0017183 |
| 0.4 | 0.0089395 | 0.0057992 | 0.0013031 | 0.0013376 |
| 0.5 | 0.0090176 | 0.0052174 | 0.0010166 | 0.0010446 |
Table 4.
The midpoint deflection for the non-uniform nanobeam with various scaling parameters and the nonuniformity distribution .
Table 4.
The midpoint deflection for the non-uniform nanobeam with various scaling parameters and the nonuniformity distribution .
| Scaling Effect Parameters () | Middle Section Deflection |
|---|
| | | | | | | | | | | | | | | |
|---|
| 1 | 0 | 0 | 0 | 1 | 30 | 0 | 0 | 1 | 30 | 30 | 0 | 1 | 30 | 30 | 1 |
|---|
| 0 | 0.0104673 | 0.0083809 | 0.0028135 | 0.0028775 |
| 0.1 | 0.0104776 | 0.0082272 | 0.0026301 | 0.0026913 |
| 0.2 | 0.0105086 | 0.0077995 | 0.0021998 | 0.0022538 |
| 0.3 | 0.0105603 | 0.0071818 | 0.0017304 | 0.0017753 |
| 0.4 | 0.0106326 | 0.0064721 | 0.0013356 | 0.0013719 |
| 0.5 | 0.0107256 | 0.0057518 | 0.0010362 | 0.0010653 |
Table 5.
The midpoint deflection for the non-uniform nanobeam with various scaling parameters and the nonuniformity distribution .
Table 5.
The midpoint deflection for the non-uniform nanobeam with various scaling parameters and the nonuniformity distribution .
| Scaling Effect Parameters () | Middle Section Deflection |
|---|
| | | | | | | | | | | | | | | | | |
|---|
| | 1 | 0 | 0 | 0 | 1 | 30 | 0 | 0 | 1 | 30 | 30 | 0 | 1 | 30 | 30 | 1 |
|---|
| 0 | 0.0115913 | 0.0090872 | 0.0028891 | 0.0029566 |
| 0.1 | 0.0116027 | 0.0089062 | 0.0026964 | 0.0027607 |
| 0.2 | 0.0116370 | 0.0084056 | 0.0022463 | 0.0023026 |
| 0.3 | 0.0116942 | 0.0076904 | 0.0017591 | 0.0018055 |
| 0.4 | 0.0117743 | 0.0068797 | 0.0013525 | 0.0013897 |
| 0.5 | 0.0118773 | 0.0060690 | 0.0010463 | 0.0010759 |
Table 6.
The midpoint deflection for the uniform nanobeam , with various scaling parameters .
Table 6.
The midpoint deflection for the uniform nanobeam , with various scaling parameters .
| Scaling Effect Parameters () | Middle Section Deflection |
|---|
| | | | | | | | | | | | | | | | | |
|---|
| | 1 | 0 | 0 | 0 | 1 | 30 | 0 | 0 | 1 | 30 | 30 | 0 | 1 | 30 | 30 | 1 |
|---|
| 0 | 0.0130208 | 0.0099433 | 0.0029695 | 0.0030410 |
| 0.1 | 0.0130337 | 0.0097261 | 0.0027667 | 0.0028344 |
| 0.2 | 0.0130722 | 0.0091300 | 0.0022951 | 0.0023539 |
| 0.3 | 0.0131365 | 0.0082892 | 0.0017888 | 0.0018369 |
| 0.4 | 0.0132265 | 0.0073516 | 0.0013700 | 0.0014082 |
| 0.5 | 0.0133421 | 0.0064298 | 0.0010566 | 0.0010869 |
Table 7.
The midpoint deflection for the non-uniform nanobeam with various scaling parameters and the nonuniformity distribution .
Table 7.
The midpoint deflection for the non-uniform nanobeam with various scaling parameters and the nonuniformity distribution .
| Scaling Effect Parameters () | Middle Section Deflection |
|---|
| | | | | | | | | | | | | | | |
|---|
| 1 | 0 | 0 | 0 | 1 | 30 | 0 | 0 | 1 | 30 | 30 | 0 | 1 | 30 | 30 | 1 |
|---|
| 0 | 0.0037978 | 0.0034813 | 0.0018206 | 0.0018498 |
| 0.1 | 0.0038015 | 0.0034530 | 0.0016346 | 0.0016638 |
| 0.2 | 0.0038127 | 0.0033711 | 0.0012577 | 0.0012846 |
| 0.3 | 0.0038315 | 0.0032440 | 0.0009141 | 0.0009365 |
| 0.4 | 0.0038577 | 0.0030834 | 0.0006645 | 0.0006824 |
| 0.5 | 0.0038915 | 0.0029018 | 0.0004942 | 0.0005083 |
Table 8.
The midpoint deflection for the non-uniform nanobeam with various scaling parameters and the nonuniformity distribution .
Table 8.
The midpoint deflection for the non-uniform nanobeam with various scaling parameters and the nonuniformity distribution .
| Scaling Effect Parameters () | Middle Section Deflection |
|---|
| | | | | | | | | | | | | | | |
|---|
| 1 | 0 | 0 | 0 | 1 | 30 | 0 | 0 | 1 | 30 | 30 | 0 | 1 | 30 | 30 | 1 |
|---|
| 0 | 0.0043704 | 0.0039543 | 0.0019298 | 0.0019630 |
| 0.1 | 0.0043747 | 0.0039166 | 0.0017247 | 0.0017574 |
| 0.2 | 0.0043877 | 0.0038082 | 0.0013131 | 0.0013424 |
| 0.3 | 0.0044092 | 0.0036418 | 0.0009441 | 0.0009680 |
| 0.4 | 0.0044394 | 0.0034345 | 0.0006806 | 0.0006992 |
| 0.5 | 0.0044783 | 0.0032042 | 0.0005031 | 0.0005176 |
Table 9.
The midpoint deflection for the non-uniform nanobeam with various scaling parameters and the nonuniformity distribution .
Table 9.
The midpoint deflection for the non-uniform nanobeam with various scaling parameters and the nonuniformity distribution .
| Scaling Effect Parameters () | Middle Section Deflection |
|---|
| | | | | | | | | | | | | | | |
|---|
| 1 | 0 | 0 | 0 | 1 | 30 | 0 | 0 | 1 | 30 | 30 | 0 | 1 | 30 | 30 | 1 |
|---|
| 0 | 0.0047446 | 0.0042562 | 0.0019906 | 0.0020261 |
| 0.1 | 0.0047493 | 0.0042117 | 0.0017745 | 0.0018092 |
| 0.2 | 0.0047633 | 0.0040842 | 0.0013431 | 0.0013738 |
| 0.3 | 0.0047867 | 0.0038899 | 0.0009600 | 0.0009847 |
| 0.4 | 0.0048195 | 0.0036502 | 0.0006889 | 0.0007081 |
| 0.5 | 0.0048617 | 0.0033869 | 0.0005077 | 0.0005225 |
Table 10.
The midpoint deflection for the uniform nanobeam , with various scaling parameters .
Table 10.
The midpoint deflection for the uniform nanobeam , with various scaling parameters .
| Scaling Effect Parameters () | Middle Section Deflection |
|---|
| | | | | | | | | | | | | | | |
|---|
| 1 | 0 | 0 | 0 | 1 | 30 | 0 | 0 | 1 | 30 | 30 | 0 | 1 | 30 | 30 | 1 |
|---|
| 0 | 0.0052083 | 0.0046225 | 0.0020561 | 0.0020943 |
| 0.1 | 0.0052135 | 0.0045688 | 0.0018279 | 0.0018649 |
| 0.2 | 0.0052289 | 0.0044158 | 0.0013749 | 0.0014071 |
| 0.3 | 0.0052546 | 0.0041847 | 0.0009766 | 0.0010022 |
| 0.4 | 0.0052906 | 0.0039030 | 0.0006976 | 0.0007172 |
| 0.5 | 0.0053368 | 0.0035977 | 0.0005124 | 0.0005275 |
Table 11.
The midpoint deflection for the non-uniform nanobeam with various scaling parameters and the nonuniformity distribution .
Table 11.
The midpoint deflection for the non-uniform nanobeam with various scaling parameters and the nonuniformity distribution .
| Scaling Effect Parameters () | Middle Section Deflection |
|---|
| | | | | | | | | | | | | | | |
|---|
| 1 | 0 | 0 | 0 | 1 | 30 | 0 | 0 | 1 | 30 | 30 | 0 | 1 | 30 | 30 | 1 |
|---|
| 0 | 0.0017769 | 0.0017059 | 0.0011447 | 0.0011573 |
| 0.1 | 0.0017786 | 0.0016992 | 0.0010071 | 0.0010209 |
| 0.2 | 0.0017839 | 0.0016795 | 0.0007426 | 0.0007566 |
| 0.3 | 0.0017926 | 0.0016479 | 0.0005187 | 0.0005308 |
| 0.4 | 0.0018049 | 0.0016061 | 0.0003663 | 0.0003759 |
| 0.5 | 0.0018207 | 0.0015563 | 0.0002671 | 0.0002746 |
Table 12.
The midpoint deflection for the non-uniform nanobeam with various scaling parameters and the nonuniformity distribution .
Table 12.
The midpoint deflection for the non-uniform nanobeam with various scaling parameters and the nonuniformity distribution .
| Scaling Effect Parameters () | Middle Section Deflection |
|---|
| | | | | | | | | | | | | | | |
|---|
| 1 | 0 | 0 | 0 | 1 | 30 | 0 | 0 | 1 | 30 | 30 | 0 | 1 | 30 | 30 | 1 |
|---|
| 0 | 0.0021003 | 0.0020022 | 0.0012722 | 0.0012877 |
| 0.1 | 0.0021024 | 0.0019926 | 0.0011059 | 0.0011225 |
| 0.2 | 0.0021086 | 0.0019647 | 0.0007963 | 0.0008123 |
| 0.3 | 0.0021190 | 0.0019201 | 0.0005447 | 0.0005580 |
| 0.4 | 0.0021335 | 0.0018618 | 0.0003791 | 0.0003895 |
| 0.5 | 0.0021521 | 0.0017930 | 0.0002738 | 0.0002818 |
Table 13.
The midpoint deflection for the non-uniform nanobeam with various scaling parameters and the nonuniformity distribution .
Table 13.
The midpoint deflection for the non-uniform nanobeam with various scaling parameters and the nonuniformity distribution .
| Scaling Effect Parameters () | Middle Section Deflection |
|---|
| | | | | | | | | | | | | | | |
|---|
| 1 | 0 | 0 | 0 | 1 | 30 | 0 | 0 | 1 | 30 | 30 | 0 | 1 | 30 | 30 | 1 |
|---|
| 0 | 0.0023206 | 0.0022015 | 0.0013504 | 0.0013679 |
| 0.1 | 0.0023229 | 0.0021897 | 0.0011651 | 0.0011835 |
| 0.2 | 0.0023297 | 0.0021554 | 0.0008269 | 0.0008442 |
| 0.3 | 0.0023412 | 0.0021010 | 0.0005589 | 0.0005729 |
| 0.4 | 0.0023572 | 0.0020302 | 0.0003860 | 0.0003967 |
| 0.5 | 0.0023778 | 0.0019472 | 0.0002773 | 0.0002855 |
Table 14.
The midpoint deflection for the uniform nanobeam , with various scaling parameters .
Table 14.
The midpoint deflection for the uniform nanobeam , with various scaling parameters .
| Scaling Effect Parameters () | Middle Section Deflection |
|---|
| | | | | | | | | | | | | | | |
|---|
| 1 | 0 | 0 | 0 | 1 | 30 | 0 | 0 | 1 | 30 | 30 | 0 | 1 | 30 | 30 | 1 |
|---|
| 0 | 0.0026042 | 0.0024552 | 0.0014421 | 0.0014624 |
| 0.1 | 0.0026067 | 0.0024403 | 0.0012331 | 0.0012537 |
| 0.2 | 0.0026144 | 0.0023970 | 0.0008606 | 0.0008794 |
| 0.3 | 0.0026273 | 0.0023287 | 0.0005741 | 0.0005889 |
| 0.4 | 0.0026453 | 0.0022405 | 0.0003931 | 0.0004042 |
| 0.5 | 0.0026684 | 0.0021381 | 0.0002810 | 0.0002894 |
The second case in this study is that the cross-sectional area of the nanobeam changes parabolically according to the polynomial .
In this case, we examined the leverage of the polynomial equation of a second degree on the deflection of the nanobeam by taking three specific situations of the asymmetricity distributions; the first situation
, i.e.,
; the second situation
, i.e.,
; and the third situation
, i.e.,
, as shown in
Figure 6.
For quick conclusions from
Table 15,
Table 16,
Table 17,
Table 18,
Table 19,
Table 20,
Table 21,
Table 22 and
Table 23, the following can be noted. First, the constant
of the polynomial
has a devastating effect on nondimensional midpoint deflection, i.e., the nondimensional midpoint deflection of the asymmetric nanobeam decreases with the increasing constant
of the polynomial. Second, the nondimensional midpoint deflection of nanobeam decreases in the presence of a Winkler elastic foundation under the beam. This decrease in deflection increases by adding the Pasternak elastic foundation under the beam. Third, the nondimensional midpoint deflection of the nanobeam increases in the presence of an axial compressive force. Fourth, in the case where the beam is not resting on any foundations, the midpoint deflection of the nanobeam increases when increasing the scaling effect parameter
; conversely, when the beam is resting on a Winkler elastic foundation, the midpoint deflection of the beam decreases when increasing the scaling effect parameter
. Fifth, when the Pasternak elastic foundation is added under the beam, the midpoint deflection is further decreased with the increase in the scaling effect parameter
.
Table 15.
The midpoint deflection for the non-uniform nanobeam with various scaling parameters and the nonuniformity distribution .
Table 15.
The midpoint deflection for the non-uniform nanobeam with various scaling parameters and the nonuniformity distribution .
| Scaling Effect Parameters () | Middle Section Deflection |
|---|
| | | | | | | | | | | | | | | |
|---|
| 1 | 0 | 0 | 0 | 1 | 30 | 0 | 0 | 1 | 30 | 30 | 0 | 1 | 30 | 30 | 1 |
|---|
| 0 | 0.0060328 | 0.0052717 | 0.0023373 | 0.0023814 |
| 0.1 | 0.0060387 | 0.0052114 | 0.0022065 | 0.0022496 |
| 0.2 | 0.0060566 | 0.0050391 | 0.0018915 | 0.0019315 |
| 0.3 | 0.0060863 | 0.0047780 | 0.0015317 | 0.0015670 |
| 0.4 | 0.0061280 | 0.0044584 | 0.0012135 | 0.0012434 |
| 0.5 | 0.0061816 | 0.0041105 | 0.0009611 | 0.0009862 |
Table 16.
The midpoint deflection for the non-uniform nanobeam with various scaling parameters and the nonuniformity distribution .
Table 16.
The midpoint deflection for the non-uniform nanobeam with various scaling parameters and the nonuniformity distribution .
| Scaling Effect Parameters () | Middle Section Deflection |
|---|
| | | | | | | | | | | | | | | |
|---|
| 1 | 0 | 0 | 0 | 1 | 30 | 0 | 0 | 1 | 30 | 30 | 0 | 1 | 30 | 30 | 1 |
|---|
| 0 | 0.0084559 | 0.0070382 | 0.0026414 | 0.0026977 |
| 0.1 | 0.0084642 | 0.0069300 | 0.0024781 | 0.0025324 |
| 0.2 | 0.0084893 | 0.0066258 | 0.0020914 | 0.0021401 |
| 0.3 | 0.0085310 | 0.0061773 | 0.0016621 | 0.0017036 |
| 0.4 | 0.0085894 | 0.0056481 | 0.0012945 | 0.0013286 |
| 0.5 | 0.0086645 | 0.0050953 | 0.0010114 | 0.0010391 |
Table 17.
The midpoint deflection for the non-uniform nanobeam with various scaling parameters and the nonuniformity distribution .
Table 17.
The midpoint deflection for the non-uniform nanobeam with various scaling parameters and the nonuniformity distribution .
| Scaling Effect Parameters () | Middle Section Deflection |
|---|
| | | | | | | | | | | | | | | |
|---|
| 1 | 0 | 0 | 0 | 1 | 30 | 0 | 0 | 1 | 30 | 30 | 0 | 1 | 30 | 30 | 1 |
|---|
| 0 | 0.0103341 | 0.0082953 | 0.0028038 | 0.0028673 |
| 0.1 | 0.0103443 | 0.0081447 | 0.0026215 | 0.0026822 |
| 0.2 | 0.0103749 | 0.0077254 | 0.0021937 | 0.0022473 |
| 0.3 | 0.0104259 | 0.0071192 | 0.0017266 | 0.0017713 |
| 0.4 | 0.0104973 | 0.0064214 | 0.0013333 | 0.0013694 |
| 0.5 | 0.0105891 | 0.0057121 | 0.0010348 | 0.0010638 |
Table 18.
The midpoint deflection for the non-uniform nanobeam with various scaling parameters and the nonuniformity distribution .
Table 18.
The midpoint deflection for the non-uniform nanobeam with various scaling parameters and the nonuniformity distribution .
| Scaling Effect Parameters () | Middle Section Deflection |
|---|
| | | | | | | | | | | | | | | |
|---|
| 1 | 0 | 0 | 0 | 1 | 30 | 0 | 0 | 1 | 30 | 30 | 0 | 1 | 30 | 30 | 1 |
|---|
| 0 | 0.0027714 | 0.0026007 | 0.0015625 | 0.0015835 |
| 0.1 | 0.0027741 | 0.0025860 | 0.0014172 | 0.0014389 |
| 0.2 | 0.0027824 | 0.0025432 | 0.0011174 | 0.0011386 |
| 0.3 | 0.0027960 | 0.0024755 | 0.0008340 | 0.0008527 |
| 0.4 | 0.0028152 | 0.0023875 | 0.0006199 | 0.0006354 |
| 0.5 | 0.0028398 | 0.0022848 | 0.0004687 | 0.0004813 |
Table 19.
The midpoint deflection for the non-uniform nanobeam with various scaling parameters and the nonuniformity distribution .
Table 19.
The midpoint deflection for the non-uniform nanobeam with various scaling parameters and the nonuniformity distribution .
| Scaling Effect Parameters () | Middle Section Deflection |
|---|
| | | | | | | | | | | | | | | |
|---|
| 1 | 0 | 0 | 0 | 1 | 30 | 0 | 0 | 1 | 30 | 30 | 0 | 1 | 30 | 30 | 1 |
|---|
| 0 | 0.0036685 | 0.0033731 | 0.0017939 | 0.0018222 |
| 0.1 | 0.0036721 | 0.0033467 | 0.0016122 | 0.0016405 |
| 0.2 | 0.0036830 | 0.0032705 | 0.0012433 | 0.0012696 |
| 0.3 | 0.0037011 | 0.0031518 | 0.0009060 | 0.0009280 |
| 0.4 | 0.0037264 | 0.0030013 | 0.0006601 | 0.0006777 |
| 0.5 | 0.0037590 | 0.0028305 | 0.0004917 | 0.0005056 |
Table 20.
The midpoint deflection for the non-uniform nanobeam with various scaling parameters and the nonuniformity distribution .
Table 20.
The midpoint deflection for the non-uniform nanobeam with various scaling parameters and the nonuniformity distribution .
| Scaling Effect Parameters () | Middle Section Deflection |
|---|
| | | | | | | | | | | | | | | |
|---|
| 1 | 0 | 0 | 0 | 1 | 30 | 0 | 0 | 1 | 30 | 30 | 0 | 1 | 30 | 30 | 1 |
|---|
| 0 | 0.0043226 | 0.0039155 | 0.0019220 | 0.0019548 |
| 0.1 | 0.0043269 | 0.0038787 | 0.0017182 | 0.0017506 |
| 0.2 | 0.0043397 | 0.0037727 | 0.0013090 | 0.0013381 |
| 0.3 | 0.0043610 | 0.0036097 | 0.0009418 | 0.0009656 |
| 0.4 | 0.0043909 | 0.0034066 | 0.0006794 | 0.0006980 |
| 0.5 | 0.0044293 | 0.0031806 | 0.0005025 | 0.0005169 |
Table 21.
The midpoint deflection for the non-uniform nanobeam with various scaling parameters and the nonuniformity distribution .
Table 21.
The midpoint deflection for the non-uniform nanobeam with various scaling parameters and the nonuniformity distribution .
| Scaling Effect Parameters () | Middle Section Deflection |
|---|
| | | | | | | | | | | | | | | |
|---|
| 1 | 0 | 0 | 0 | 1 | 30 | 0 | 0 | 1 | 30 | 30 | 0 | 1 | 30 | 30 | 1 |
|---|
| 0 | 0.0012030 | 0.0011696 | 0.0008711 | 0.0008785 |
| 0.1 | 0.0012042 | 0.0011667 | 0.0007851 | 0.0007936 |
| 0.2 | 0.0012077 | 0.0011582 | 0.0006100 | 0.0006196 |
| 0.3 | 0.0012137 | 0.0011445 | 0.0004484 | 0.0004575 |
| 0.4 | 0.0012220 | 0.0011260 | 0.0003291 | 0.0003370 |
| 0.5 | 0.0012327 | 0.0011034 | 0.0002466 | 0.0002531 |
Table 22.
The midpoint deflection for the non-uniform nanobeam with various scaling parameters and the nonuniformity distribution .
Table 22.
The midpoint deflection for the non-uniform nanobeam with various scaling parameters and the nonuniformity distribution .
| Scaling Effect Parameters () | Middle Section Deflection |
|---|
| | | | | | | | | | | | | | | |
|---|
| 1 | 0 | 0 | 0 | 1 | 30 | 0 | 0 | 1 | 30 | 30 | 0 | 1 | 30 | 30 | 1 |
|---|
| 0 | 0.0016894 | 0.0016250 | 0.0011062 | 0.0011181 |
| 0.1 | 0.0016910 | 0.0016190 | 0.0009766 | 0.0009896 |
| 0.2 | 0.0016960 | 0.0016012 | 0.0007253 | 0.0007387 |
| 0.3 | 0.0017044 | 0.0015726 | 0.0005100 | 0.0005217 |
| 0.4 | 0.0017161 | 0.0015348 | 0.0003619 | 0.0003713 |
| 0.5 | 0.0017311 | 0.0014895 | 0.0002647 | 0.0002721 |
Table 23.
The midpoint deflection for the non-uniform nanobeam with various scaling parameters and the nonuniformity distribution .
Table 23.
The midpoint deflection for the non-uniform nanobeam with various scaling parameters and the nonuniformity distribution .
| Scaling Effect Parameters () | Middle Section Deflection |
|---|
| | | | | | | | | | | | | | | |
|---|
| 1 | 0 | 0 | 0 | 1 | 30 | 0 | 0 | 1 | 30 | 30 | 0 | 1 | 30 | 30 | 1 |
|---|
| 0 | 0.0020661 | 0.0019711 | 0.0012590 | 0.0012743 |
| 0.1 | 0.0020682 | 0.0019618 | 0.0010959 | 0.0011122 |
| 0.2 | 0.0020743 | 0.0019348 | 0.0007910 | 0.0008068 |
| 0.3 | 0.0020845 | 0.0018916 | 0.0005422 | 0.0005554 |
| 0.4 | 0.0020988 | 0.0018351 | 0.0003779 | 0.0003882 |
| 0.5 | 0.0021171 | 0.0017683 | 0.0002732 | 0.0002811 |
The general form of the beam equation is ; this means that the values of and control the deflection of the beam.
Table 24 and
Table 25, show the effect of the values of
and
on the deflection of the nonuniform nanobeam, whose cross-sectional area changes linearly and parabolically for the three sets of boundary conditions. It is assumed for the nanobeam that, at foundation parameters
, the non-dimensional distributed force
, the non-dimensional axial force
, and the scaling effect parameter
.
Table 24 describes the first case, where the cross-sectional area of the nanobeam changes linearly according to the polynomial
, where
. This means that, in this case, we are studying the influence of changing the nonuniformity parameter
on the deflection of the beam. In addition,
Table 24 presents a comparison of the deflection of the beam between the uniform and nonuniform changes linearly for the three sets of boundary conditions.
Table 25 describes the second case, where the cross-sectional area of the nanobeam changes parabolically according to the polynomial
. This means that we are studying the effect of changing the nonuniformity parameters
and
on the deflection of the beam. In addition,
Table 25 presents a comparison of the deflection of the nonuniform beam changes linearly and parabolically, for the three sets of boundary conditions.
Table 24 and
Table 25 briefly show the effect of changing the nonuniformity parameters
and
of the nanobeam on midpoint deflection.
From
Table 24 and
Table 25, the midpoint deflection decreases with the increase in
or the increase in
.
Figure 12,
Figure 13 and
Figure 14 present a comparison between the uniform and nonuniform parameters (whose cross-sectional area changes linearly and parabolically) of the nanobeam on the midpoint deflection for the three sets of boundary conditions.
From
Figure 13,
Figure 14 and
Figure 15, the following can be noted. First, the midpoint deflection of the non-uniform nanobeam decreases in comparison with the uniform nanobeam. Second, the midpoint deflection decreases with the increase in
or the increase in
.