Analytical Attitude Guidance Planner for Multiple Ground Targets Acquisitions
Abstract
1. Introduction
2. Problem Description and Proposed Solution
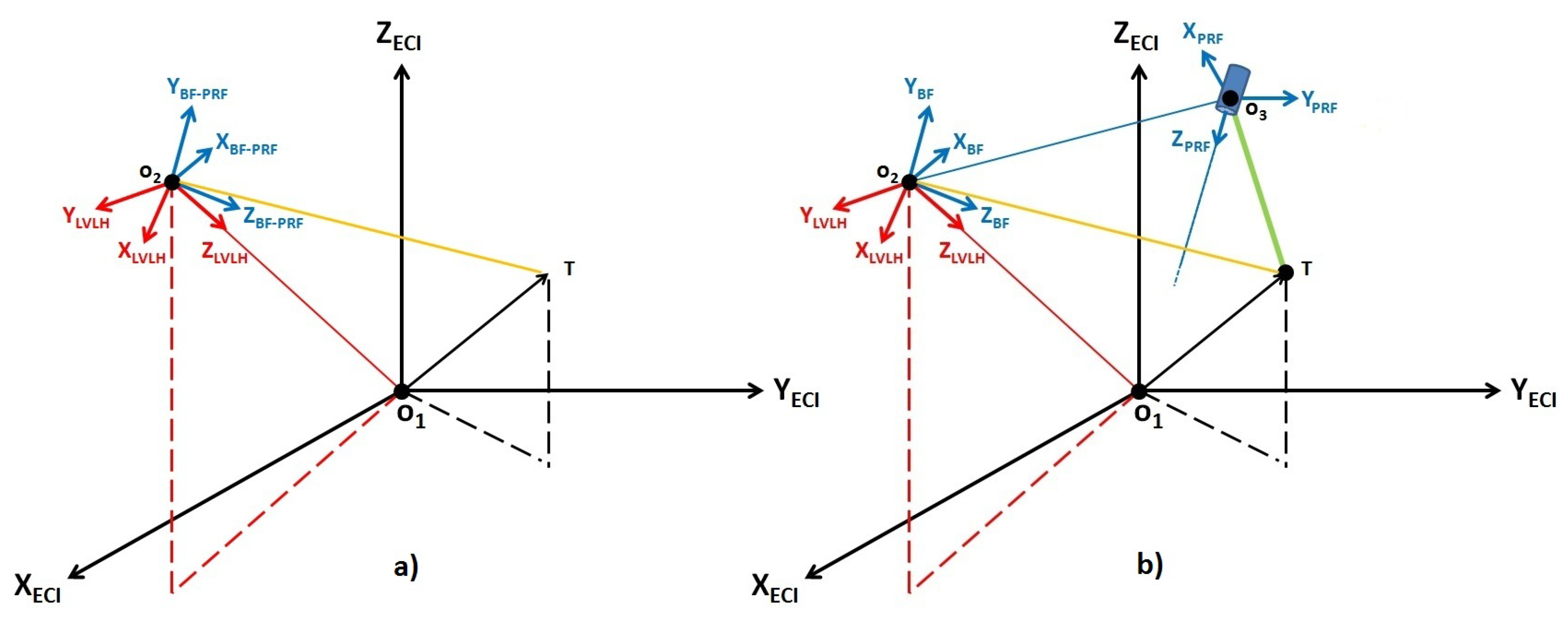
2.1. Reference Frames Review
- Earth-Centered Inertial (ECI) The coordinate system has its origin in the Earth’s center of mass and it is fixed with respect to the stars. The axis is aligned with the Earth’s rotational axis and points to the north, the axis points in the direction of the vernal equinox, and the axis completes the right-handed orthogonal reference system.
- Earth-Centered Earth-Fixed (ECEF) This reference frame has the same origin and the same Z axis () as the frame but rotates with the Earth. The is in the equatorial plane and points to the Greenwich meridian, while the is taken in order to have a right-handed orthogonal reference system.
- Local-Vertical Local-Horizontal (LVLH) It has the origin in the satellite’s center of mass, points to the center of the Earth, and is parallel to the local horizontal plane (which is the plane normal to the radial position vector connecting the center of the Earth and the satellite), its orientation is such that the satellite’s velocity vector is contained in the plane, and its positive direction is taken to be concordant with the satellite velocity vector direction. The axis is taken to form a right-handed orthogonal reference system.
- Body-Fixed (BF) This frame corresponds to the satellite’s principal inertia axes reference frame centered on its center of mass. The frame is useful to describe the attitude of the satellite. Indeed, the nominal reference attitude of the satellite is often given when the BF frame is aligned with the LVLH frame, and the attitude is described as the displacement of the BF frame with respect to the frame.
- Payload Reference Frame (PRF) In this work, the payload consists of a camera mounted with a displacement with respect to the origin, as shown in Figure 1. Point identifies the center of the charge-coupled device (), which is the camera detector. The frame has axis aligned with the optical axis and the other two axes () are taken to be a right triad. This reference frame is fixed with respect to the BF reference frame, so its rotational matrix is constant and is the payload mounting matrix.
2.2. Dynamical Model
2.3. Physical Constraints
2.3.1. Angular Velocity Constraint
2.3.2. Mapping the Control Constraint to a Kinematic Constraint
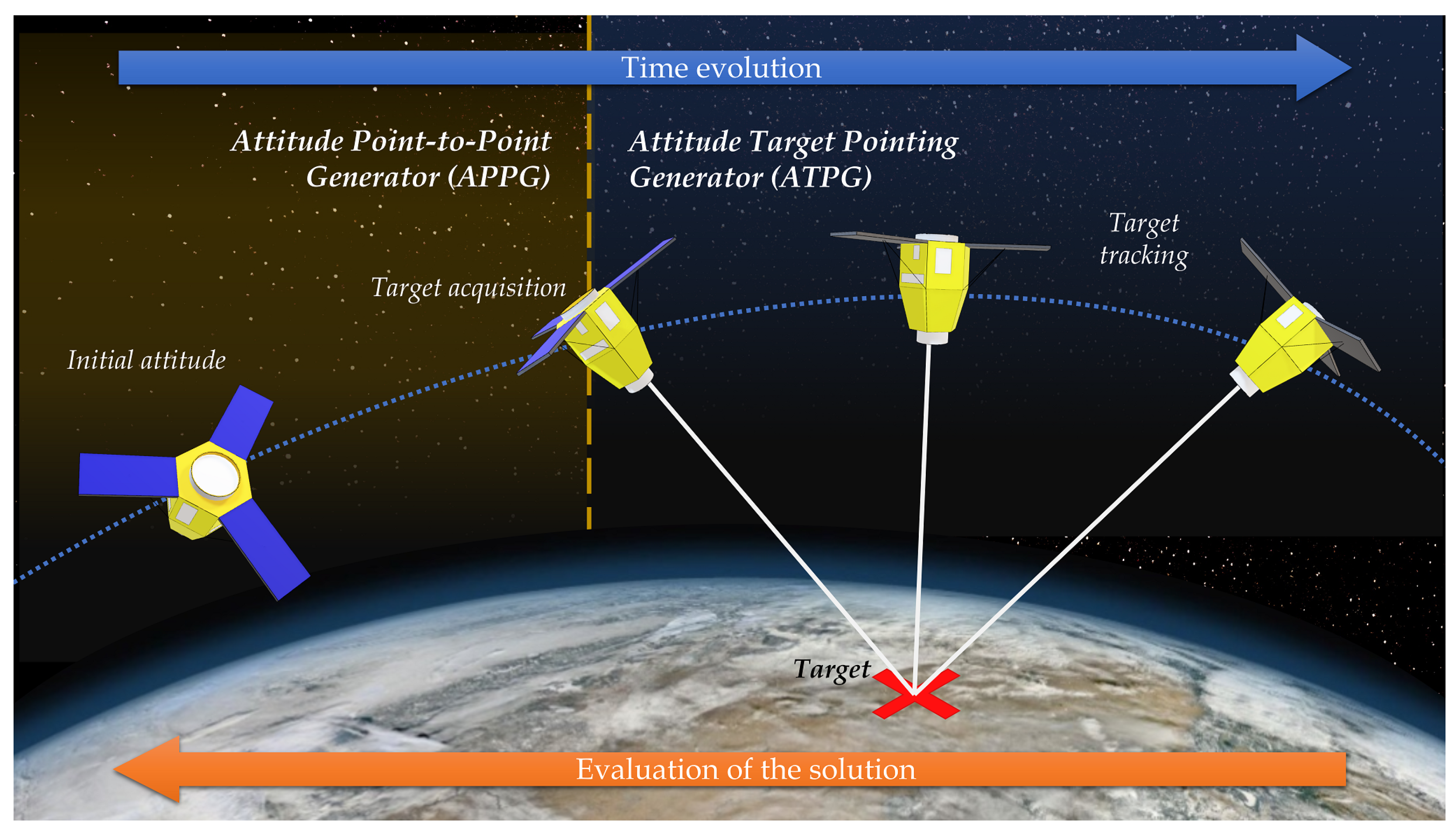
2.4. Solution Setup
- First phase: the problem is to modify the attitude from any initial condition to the required initial condition to start image acquisition. This is translated into a boundary value problem that can be solved with a point-to-point solution. From now on we refer to this part as the attitude point-to-point generator ().
- Second phase: the problem focuses on the generation of the reference guidance path ensuring that the camera view axis constantly remains pointed towards the ground target. This phase starts at and lasts the time of image acquisition, . We will refer to this phase as the attitude target pointing generator ().
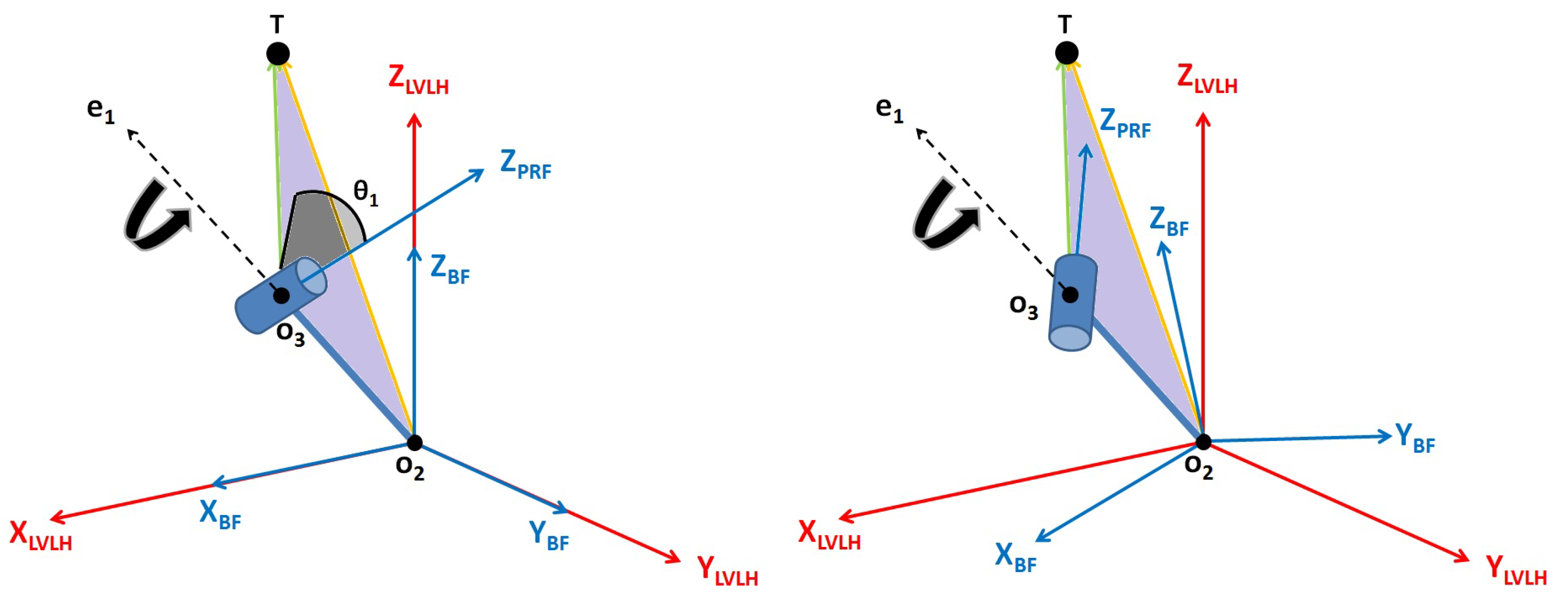
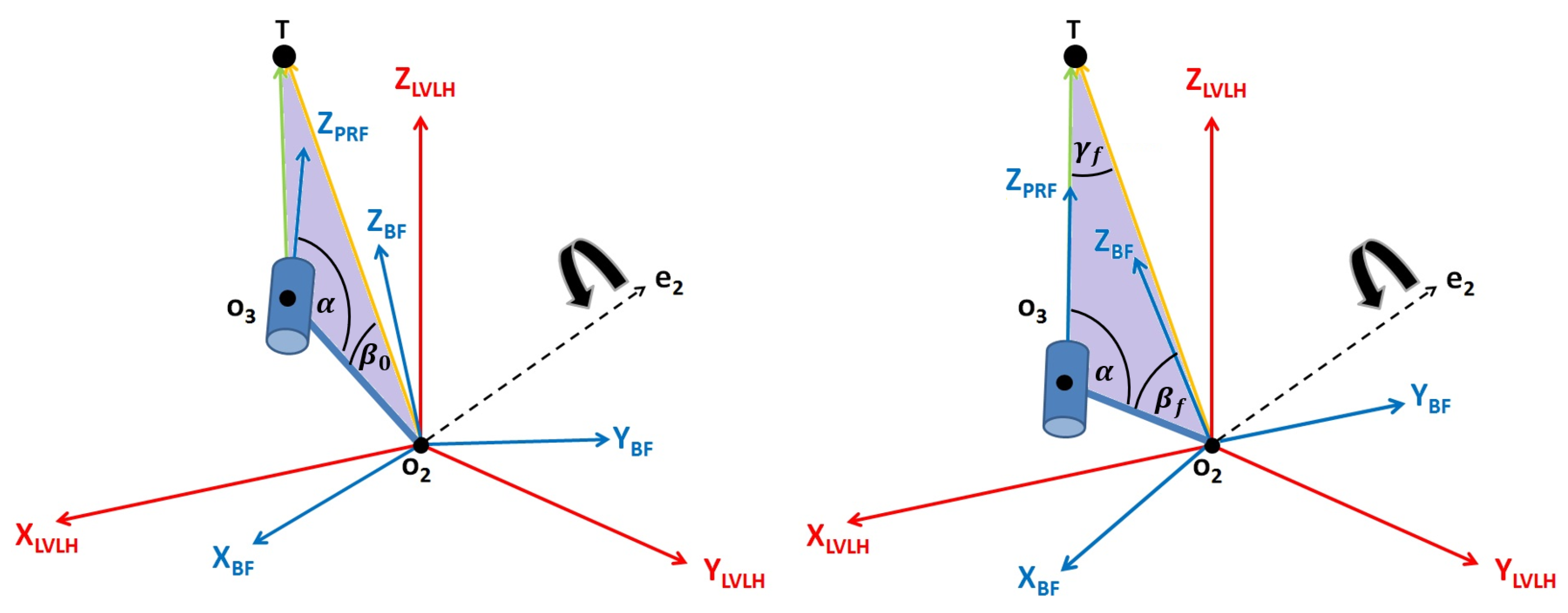
3. Attitude Target Pointing Generator
- 1.
- The first rotation occurs around the unit vector and it has the purpose of bringing the axis to lay on the plane identified by , without modifying either the direction or the magnitude of (as shown in Figure 3):where , and
- 2.
- The second rotation brings the view axis of the camera to coincide with the direction by means of an Euler’s rotation around a principal axis, such thatwhere, with respect to Figure 4, , , and is equal to the angle between and .
4. Attitude Point-to-Point Generator
- Step 1.
- The satellite arrests its motion and reaches its final attitude .
- Step 2.
- A rest-to-rest maneuver from to a proper switching attitude is performed.
- Step 3.
- The satellite motion is accelerated from until it reaches the final attitude , the final angular velocity and final acceleration.
- APPG-Step 1.
- APPG-Step 2.
- APPG-Step 3.
- APPG-Summary.
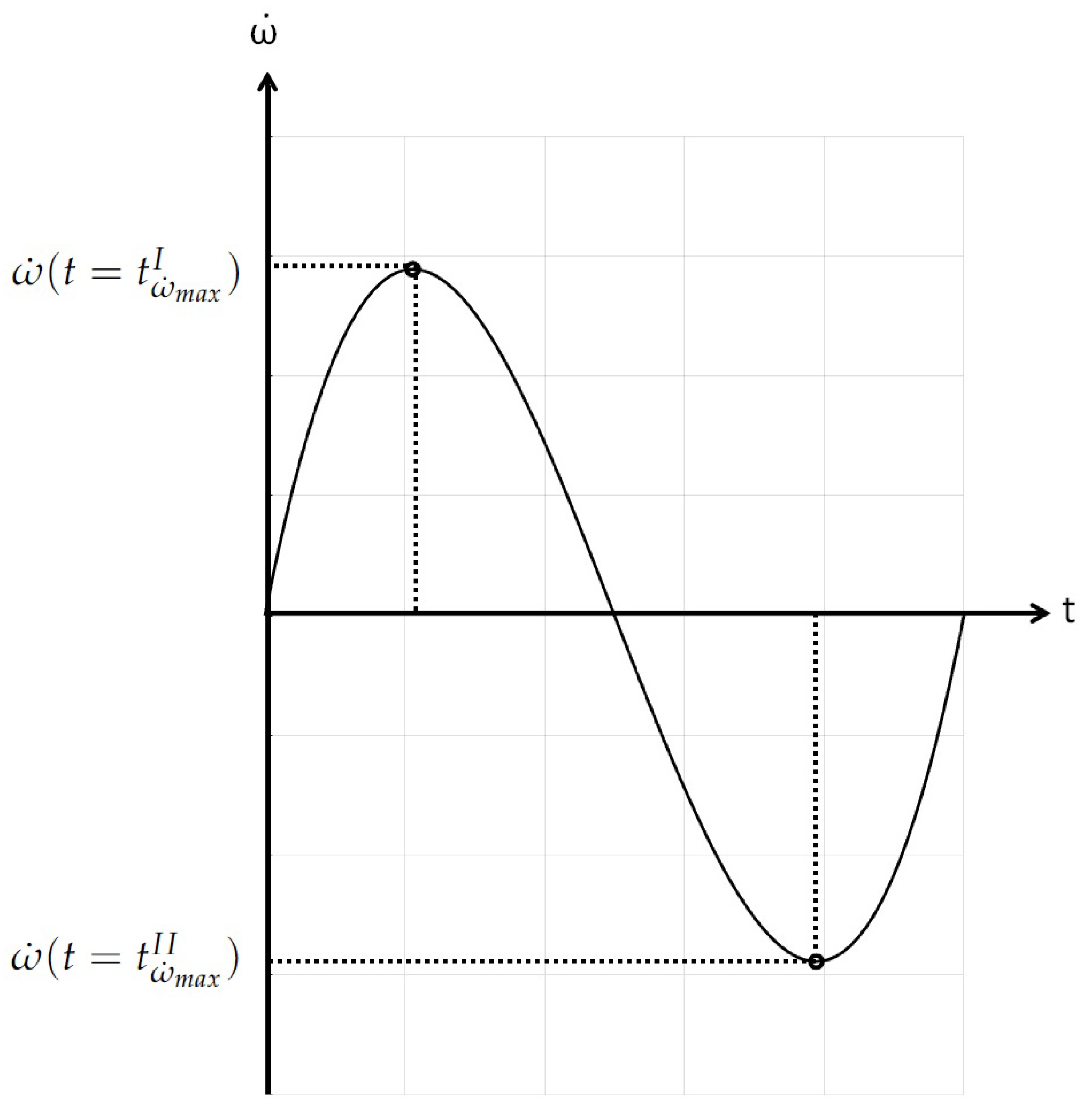
4.1. Near Optimal Time
4.1.1. Maneuver Time for Step 1
4.1.2. Maneuver Time for Step 2
- 1.
- 2.
- The conditions and are respectively substituted in the first and in the second expression of Equation (46). Thus, their final expressions as functions of are obtained.
- 3.
- After several simplifications, Equation (47), can be written as followsThe rest-to-rest guidance law gives two different solutions. and are the final times which allow to verify and respectively.
4.1.3. Maneuver Time for Step 3
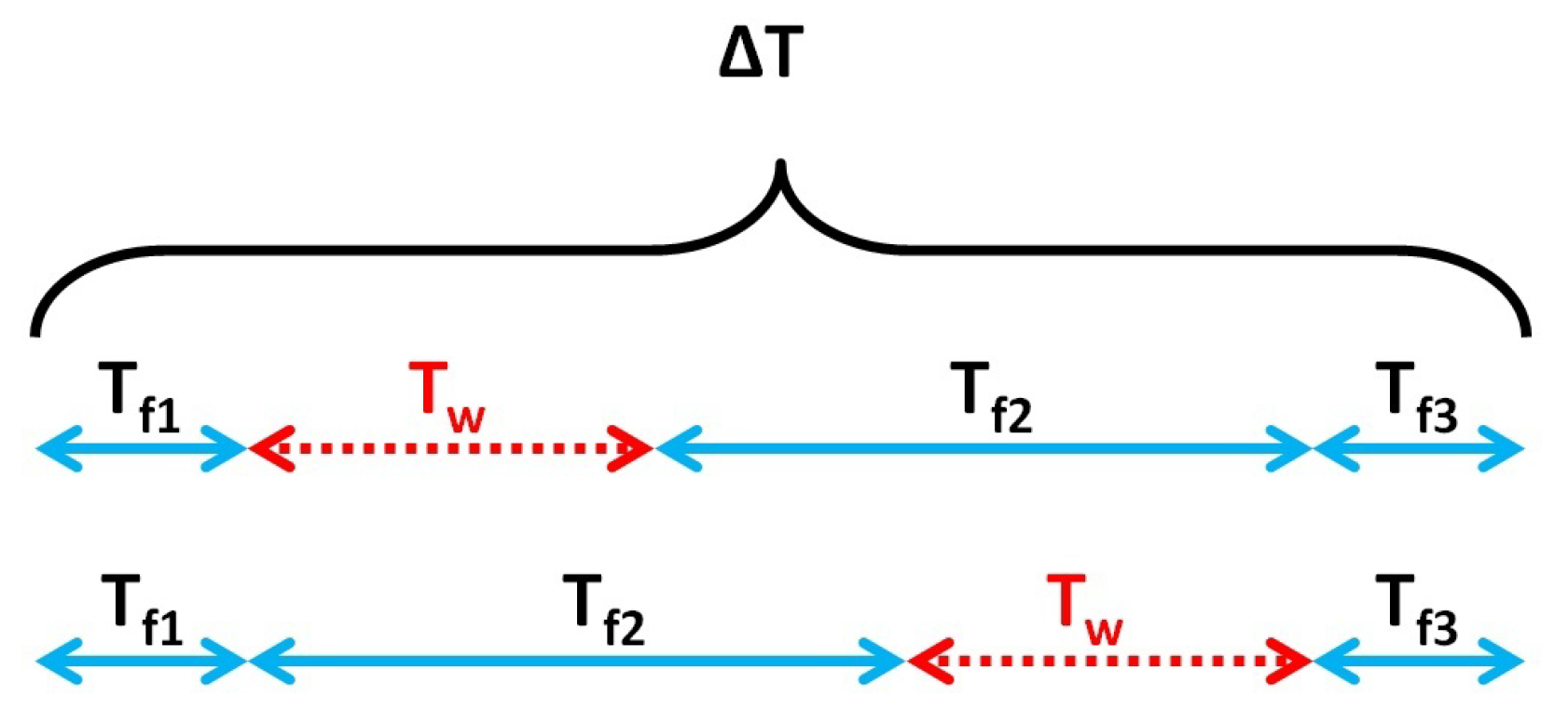
4.2. Final Strategy
4.2.1. Selection of the Minimum Maneuver Times
4.2.2. Combining the Manoeuvres
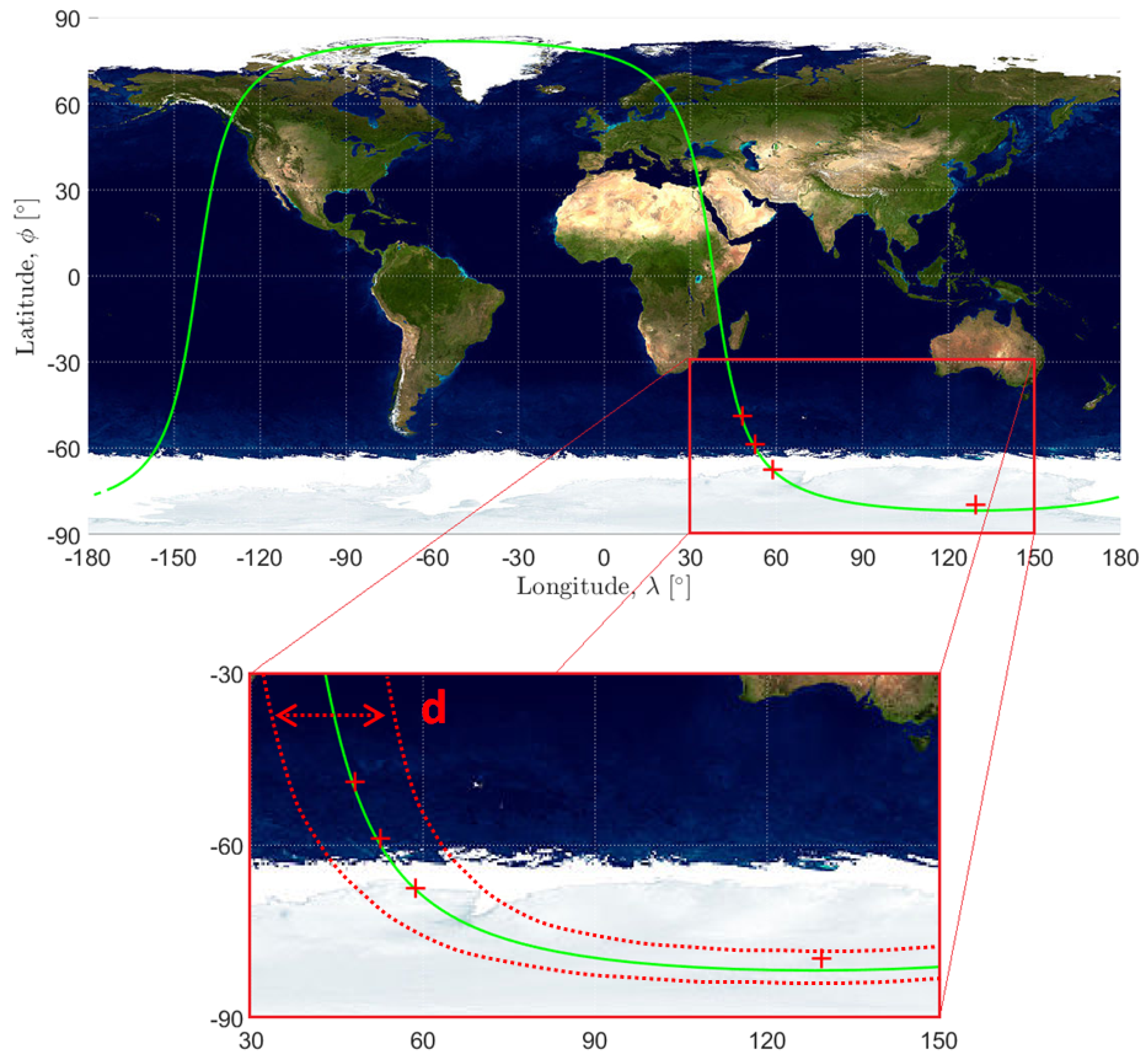
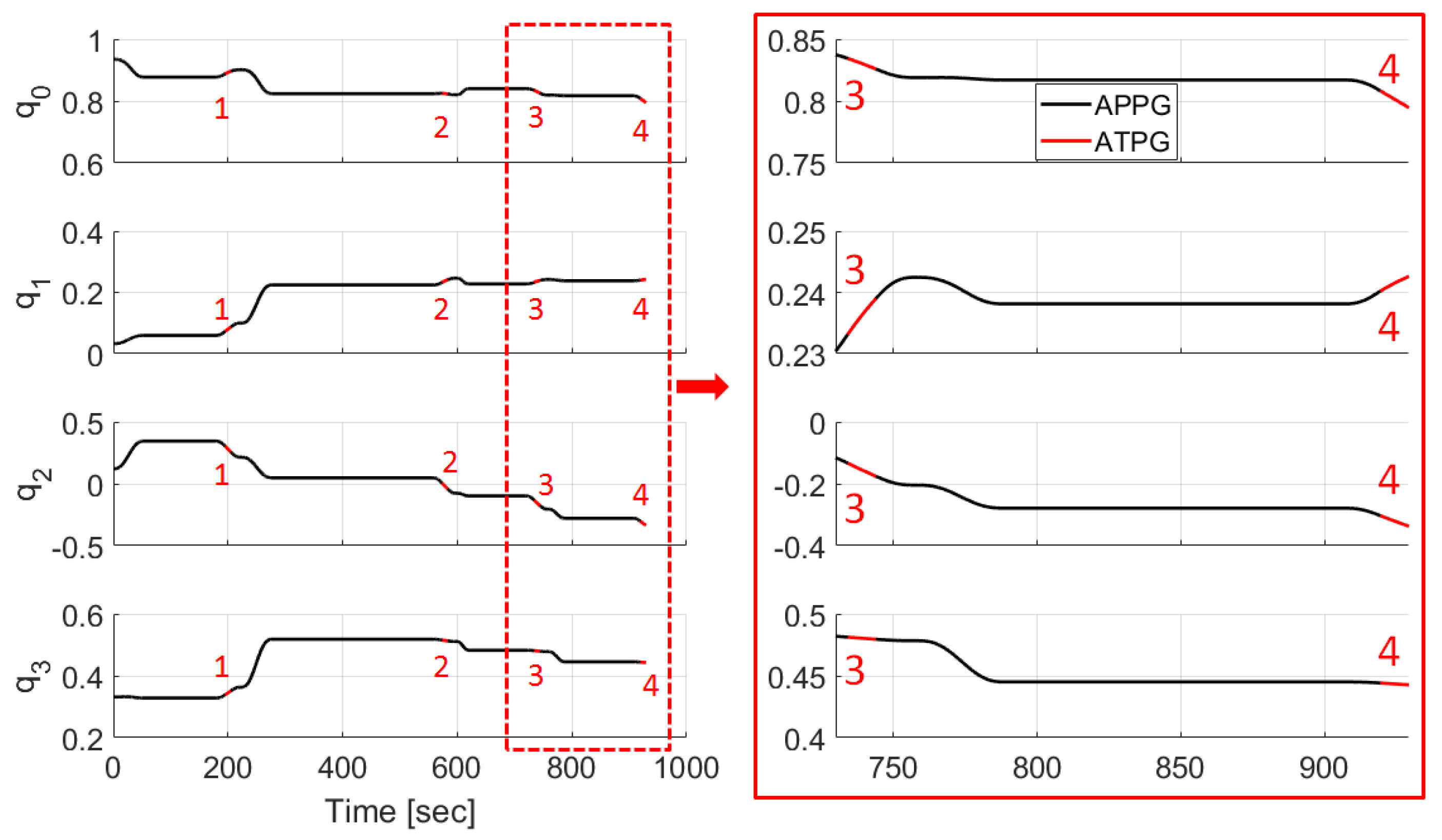
5. Simulation and Results
5.1. Simulation Environment
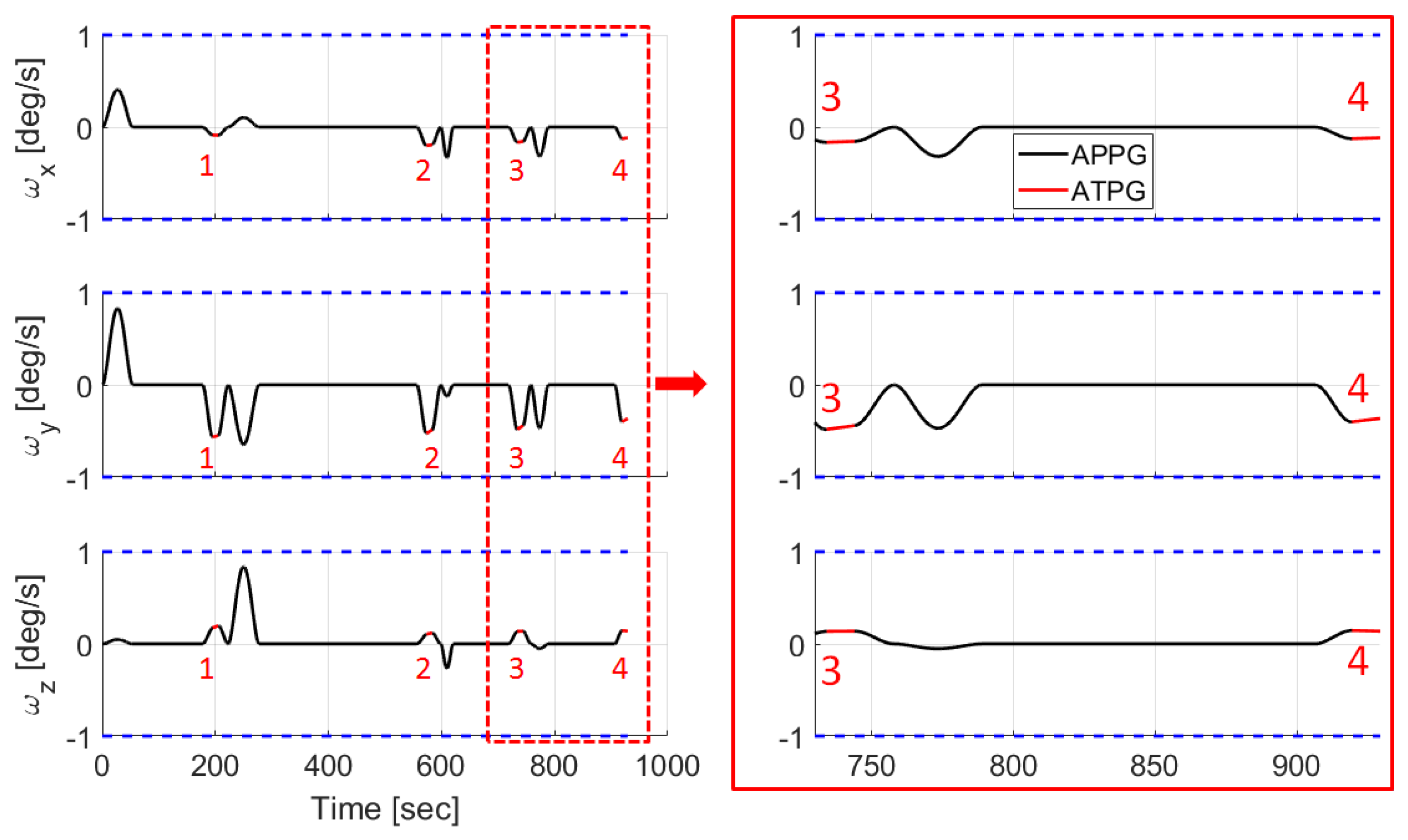
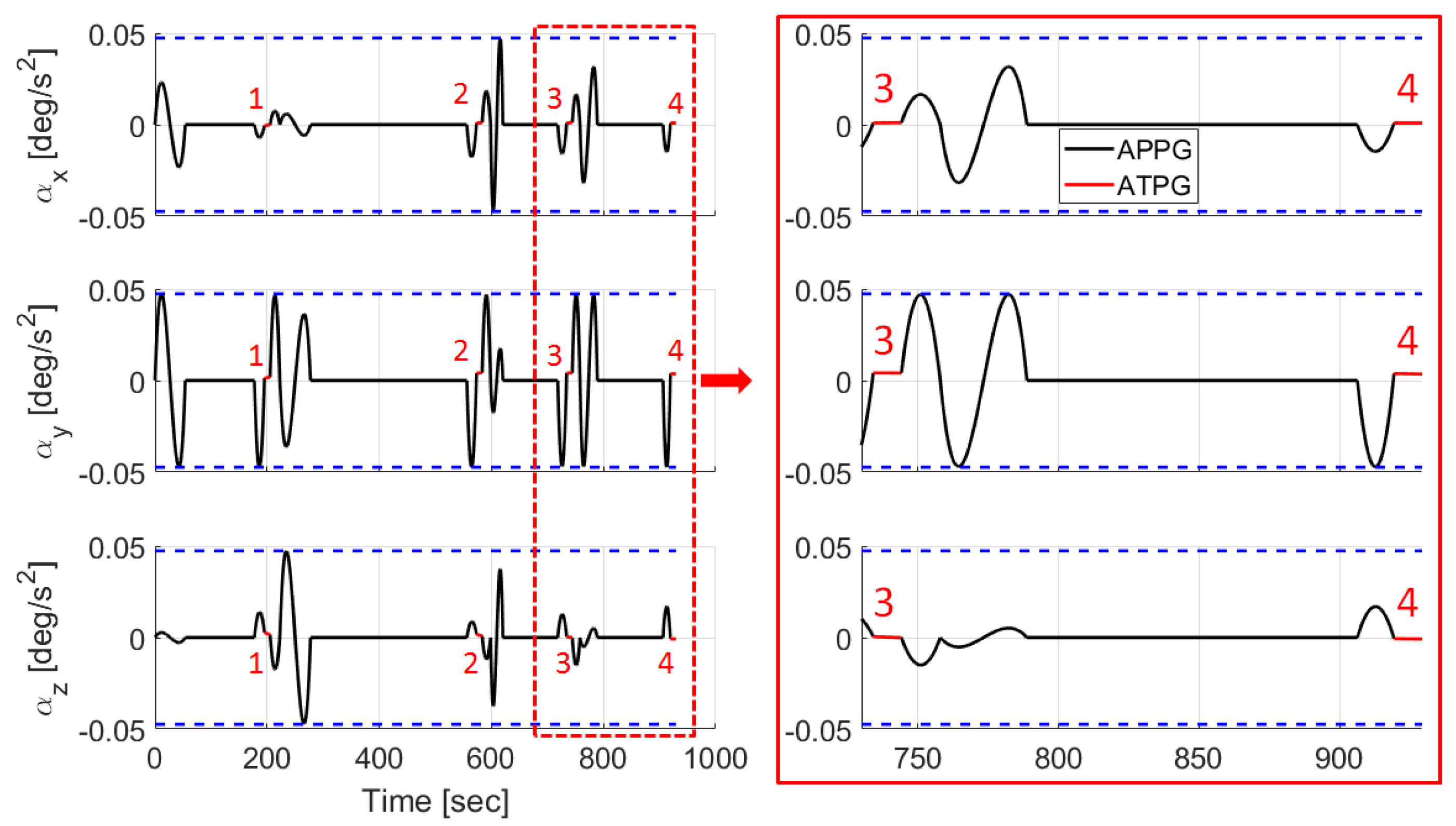
5.2. Simulation Results
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Campbell, J.B. Introduction to remote sensing. In Introduction to Remote Sensing; Guilford Press: New York, NY, USA, 1987. [Google Scholar]
- Press, N.A. Earth Observations from Space: The First 50 Years of Scientific Achievements; National Academies Press: Washington, DC, USA, 2008; pp. 1–130. [Google Scholar] [CrossRef]
- Chuvieco, E. Earth Observation of Global Change: The Role of Satellite Remote Sensing in Monitoring the Global Environment; Springer: Berlin, Germany, 2008; pp. 1–223. [Google Scholar] [CrossRef]
- Li, Z.; Tomás, R. Earth Observations for Geohazards; MDPI: Basel, Switzerland, 2017. [Google Scholar] [CrossRef]
- D’Errico, M. Distributed Space Missions for Earth System Monitoring; Springer: New York, NY, USA, 2013; pp. 1–675. [Google Scholar] [CrossRef]
- Kornfeld, R. On-board autonomous attitude maneuver planning for planetary spacecraft using genetic algorithms. In Proceedings of the AIAA Guidance, Navigation, and Control Conference and Exhibit, Austin, TX, USA, 11–14 August 2003; p. 5784. [Google Scholar]
- Wu, C.; Xu, R.; Zhu, S.; Cui, P. Time-optimal spacecraft attitude maneuver path planning under boundary and pointing constraints. Acta Astronaut. 2017, 137, 128–137. [Google Scholar] [CrossRef]
- Wu, C.; Han, X. Energy-optimal spacecraft attitude maneuver path-planning under complex constraints. Acta Astronaut. 2019, 157, 415–424. [Google Scholar] [CrossRef]
- Melton, R.G. Hybrid methods for determining time-optimal, constrained spacecraft reorientation maneuvers. Acta Astronaut. 2014, 94, 294–301. [Google Scholar] [CrossRef]
- Spiller, D.; Melton, R.G.; Curti, F. Inverse dynamics particle swarm optimization applied to constrained minimum-time maneuvers using reaction wheels. Aerosp. Sci. Technol. 2018, 75, 1–12. [Google Scholar] [CrossRef]
- Spiller, D.; Ansalone, L.; Curti, F. Particle swarm optimization for time-optimal spacecraft reorientation with keep-out cones. J. Guid. Control. Dyn. 2016, 39, 312–325. [Google Scholar] [CrossRef]
- Zhang, G.; Li, X.; Hu, G.; Zhang, Z.; An, J.; Man, W. Mission Planning Issues of Imaging Satellites: Summary, Discussion, and Prospects. Int. J. Aerosp. Eng. 2021, 2021, 7819105. [Google Scholar] [CrossRef]
- Florio, S.; Zehetbauer, T.; Neff, T. Optimal operations planning for SAR satellite constellations. In Proceedings of the Low Earth Orbit. 6th International Symposium on Reducing the Costs of Spacecraft Ground Systems and Operations, ESOC, Darmstadt, Germany, 14–17 June 2005. [Google Scholar]
- Stock, G.; Fraire, J.; Hermanns, H.; Cruz, E.; Isaacs, A.; Imbrosh, Z. On the Automation, Optimization, and In-Orbit Validation of Intelligent Satellite Constellation Operations. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 2021, 39, 3762–3773. [Google Scholar] [CrossRef]
- Song, Y.; Huang, D.; Zhou, Z.; Chen, Y. An emergency task autonomous planning method of agile imaging satellite. EURASIP J. Image Video Process. 2018, 2018, 1–11. [Google Scholar] [CrossRef]
- Liu, S.; Yang, J. A satellite task planning algorithm based on a symmetric recurrent neural network. Symmetry 2019, 11, 1373. [Google Scholar] [CrossRef]
- Lai, L.C.; Yang, C.C.; Wu, C.J. Time-optimal maneuvering control of a rigid spacecraft. Acta Astronaut. 2007, 60, 791–800. [Google Scholar] [CrossRef]
- Weiguo, Z.; Pingyuan, C.; Hutao, C. Autonomous Attitude Maneuver Planning for Spacecraft under Complex Constraints (TN). Acta Aeronaut. Astronaut. Sin.-Ser. A B 2007, 28, 1091. [Google Scholar]
- Wie, B.; Bailey, D.; Heiberg, C. Rapid multitarget acquisition and pointing control of agile spacecraft. J. Guid. Control. Dyn. 2002, 25, 96–104. [Google Scholar] [CrossRef]
- Zhou, H.; Wang, D.; Wu, B.; Poh, E.K. Time-optimal reorientation for rigid satellite with reaction wheels. Int. J. Control. 2012, 85, 1452–1463. [Google Scholar] [CrossRef]
- Xu, R.; Wu, C.; Zhu, S.; Fang, B.; Wang, W.; Xu, L.; He, W. A rapid maneuver path planning method with complex sensor pointing constraints in the attitude space. Inf. Syst. Front. 2017, 19, 945–953. [Google Scholar] [CrossRef]
- Calaon, R.; Schaub, H. Constrained Attitude Maneuvering via Modified-Rodrigues-Parameter-Based Motion Planning Algorithms. J. Spacecr. Rocket. 2022, 59, 1–15. [Google Scholar] [CrossRef]
- Dearing, T.L.; Hauser, J.; Chen, X.; Nicotra, M.M.; Petersen, C. Efficient Trajectory Optimization for Constrained Spacecraft Attitude Maneuvers. J. Guid. Control. Dyn. 2022, 45, 638–650. [Google Scholar] [CrossRef]
- Li, Z.; Zhao, L.; Liu, Y.; Chen, X.; Chen, H.; Zheng, F.; Zhang, Y.; Wang, D.; Li, J.; Liu, J.; et al. Autonomous Mission Planning Method for Optical Imaging Satellites Based on Real-Time Cloud Cover Information. Remote Sens. 2022, 14, 2635. [Google Scholar] [CrossRef]
- He, Y.; Wang, Y.; Chen, Y.; Xing, L. Auto mission planning system design for imaging satellites and its applications in environmental field. Pol. Marit. Res. 2016, 23, 59–70. [Google Scholar] [CrossRef][Green Version]
- Sandau, R.; Röser, H.P.; Valenzuela, A. Small Satellites for Earth Observation; Springer: Berlin, Germany, 2008; pp. 1–406. [Google Scholar] [CrossRef]
- Rosso, M.P.D.; Ullo, S.L.; Sebastianelli, A.; Spiller, D.; Puglisi, E.; Martire, D.D.; Aparício, S.; Addabbo, P. Artificial intelligence, machine learning and deep learning. In Artificial Intelligence Applied to Satellite-Based Remote Sensing Data for Earth Observation; IET Digital Library: London, UK, 2021; pp. 39–61. [Google Scholar] [CrossRef]
- Rosso, M.P.D.; Ullo, S.L.; Sebastianelli, A.; Spiller, D.; Puglisi, E.; Biondi, F.; Orlando, D. Artificial neural network. In Artificial Intelligence Applied to Satellite-Based Remote Sensing Data for Earth Observation; IET Digital Library: London, UK, 2021; pp. 63–90. [Google Scholar] [CrossRef]
- Ullo, S.L.; Sebastianelli, A.; Rosso, M.P.D.; Spiller, D.; Puglisi, E.; Nowakowski, A.; Bernardi, M.L.; Cimitile, M. Convolutional neural networks. In Artificial Intelligence Applied to Satellite-Based Remote Sensing Data for Earth Observation; IET Digital Library: London, UK, 2021; pp. 91–111. [Google Scholar] [CrossRef]
- Sebastianelli, A.; Rosso, M.P.D.; Zarro, C.; Martire, D.D.; Napoli, M.D.; Spiller, D.; Nowakowski, A.; Bonifacio, R.; Kim, D.H.; Garcia-Herranz, M. A classification problem. In Artificial Intelligence Applied to Satellite-Based Remote Sensing Data for Earth Observation; IET Digital Library: London, UK, 2021; pp. 159–206. [Google Scholar] [CrossRef]
- Rosso, M.P.D.; Sebastianelli, A.; Spiller, D.; Mathieu, P.P.; Ullo, S.L. On-Board Volcanic Eruption Detection through CNNs and Satellite Multispectral Imagery. Remote Sens. 2021, 13, 3479. [Google Scholar] [CrossRef]
- Giuffrida, G.; Fanucci, L.; Meoni, G.; Batic, M.; Buckley, L.; Dunne, A.; Dijk, C.V.; Esposito, M.; Hefele, J.; Vercruyssen, N.; et al. The Φ-Sat-1 Mission: The First On-Board Deep Neural Network Demonstrator for Satellite Earth Observation. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5517414. [Google Scholar] [CrossRef]
- Spiller, D.; Ansalone, L.; Carotenuto, F.; Mathieu, P.P. Crop Type Mapping Using Prisma Hyperspectral Images and One-Dimensional Convolutional Neural Network. In Proceedings of the 2021 IEEE International Geoscience and Remote Sensing Symposium IGARSS, Brussels, Belgium, 11–16 July 2021. [Google Scholar] [CrossRef]
- Spiller, D.; Ansalone, L.; Amici, S.; Piscini, A.; Mathieu, P.P. Analysis and detection of wildfires by using prisma hyperspectral imagery. Int. Arch. Photogramm. Remote. Sens. Spat. Inf. Sci. 2021, 43, 215–222. [Google Scholar] [CrossRef]
- Spiller, D.; Ansalone, L.; Longépé, N.; Wheeler, J.; Mathieu, P.P. Wildfire detection and monitoring by using PRISMA hyperspectral data and convolutional neural networks. In Proceedings of the EGU General Assembly 2021, Online, 19–30 April 2021. EGU21-12330. [Google Scholar] [CrossRef]
- Wertz, J.R. Spacecraft Attitude Determination and Control; Springer Science & Business Media: Berlin, Germany, 2012; Volume 73. [Google Scholar]
- Yang, Y. Spacecraft Modeling, Attitude Determination, and Control: Quaternion-Based Approach; CRC Press: Boca Raton, FL, USA, 2019. [Google Scholar] [CrossRef]
- Vallado, D.A. Fundamentals of Astrodynamics and Applications; Springer Science & Business Media: Berlin, Germany, 2001; Volume 12. [Google Scholar]
- Markley, F.L.; Crassidis, J.L. Fundamentals of Spacecraft Attitude Determination and Control; Springer: Berlin/Heidelberg, Germany, 2014; Volume 33. [Google Scholar]
- Neumark, S. Solution of Cubic and Quartic Equations; Elsevier: Amsterdam, The Netherlands, 2014. [Google Scholar]




| Step 1 | Step 2 | Step 3 |
|---|---|---|
| Constraints on each component | Constraints on the magnitude only | Constraints on each component |
|
from Equation (15), from Equation (22). | by differentiating Equation (29), from Equation (38). | as in Equation (15), as in Equation (22). |
| Inertia along | 603.896 (kg/m2) | |
| Inertia along | 565.396 (kg/m2) | |
| Inertia along | 318.792 (kg/m2) | |
| Maximum torque | 0.5 (Nm) | |
| Maximum angular acceleration | 0.0474 (deg/s2) | |
| Maximum angular velocity | 1 (deg/s) | |
| a | Semi-major axis | 7075.945 (km) |
| e | Eccentricity | 1.251 × 10 |
| e-04 i | Inclination | 98.165 (deg) |
| Right ascension of the ascending node | 38.184 (deg) | |
| Argument of periapsis | 102.289 (deg) | |
| True anomaly | 155.692 (deg) |
| (min) | LAT (deg) | LON (deg) | HEIGHT (m) | |
|---|---|---|---|---|
| 1 | 3.253 | −79.783 | 129.459 | 91.452 |
| 2 | 9.557 | −67.536 | 58.597 | 167.932 |
| 3 | 12.237 | −58.779 | 52.500 | 942.248 |
| 4 | 15.320 | −48.961 | 48.114 | 849.432 |
| Symbol | Description | Value |
|---|---|---|
| displacement with respect to | [1 0.5 1] | |
| rotation with respect to | −30 | |
| rotation with respect to | −30 | |
| rotation with respect to | 0 | |
| Acquisition time | 10 (s) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Carbone, A.; Spiller , D.; Curti , F. Analytical Attitude Guidance Planner for Multiple Ground Targets Acquisitions. Symmetry 2022, 14, 2341. https://doi.org/10.3390/sym14112341
Carbone A, Spiller D, Curti F. Analytical Attitude Guidance Planner for Multiple Ground Targets Acquisitions. Symmetry. 2022; 14(11):2341. https://doi.org/10.3390/sym14112341
Chicago/Turabian StyleCarbone, Andrea, Dario Spiller , and Fabio Curti . 2022. "Analytical Attitude Guidance Planner for Multiple Ground Targets Acquisitions" Symmetry 14, no. 11: 2341. https://doi.org/10.3390/sym14112341
APA StyleCarbone, A., Spiller , D., & Curti , F. (2022). Analytical Attitude Guidance Planner for Multiple Ground Targets Acquisitions. Symmetry, 14(11), 2341. https://doi.org/10.3390/sym14112341








