Abstract
The propagation dynamics of two-dimensional (2D) ring-Airy beams is studied in the framework of the fractional Schrödinger equation, which includes saturable or cubic self-focusing or defocusing nonlinearity and Lévy index ((LI) alias for the fractionality) taking values . The model applies to light propagation in a chain of optical cavities emulating fractional diffraction. Management is included by making the diffraction and/or nonlinearity coefficients periodic functions of the propagation distance, . The management format with the nonlinearity coefficient decaying as is considered too. These management schemes maintain stable propagation of the ring-Airy beams, which maintain their axial symmetry, in contrast to the symmetry-breaking splitting instability of ring-shaped patterns in 2D Kerr media. The instability driven by supercritical collapse at all values in the presence of the self-focusing cubic term is eliminated, too, by the means of management.
1. Introduction
The nonspreading solution of the Schrödinger equation in the form of the Airy function was found by Berry and Balazs in the context of quantum mechanics in 1979 [1]. This solution follows a curved parabolic trajectory, similar to a projectile moving under the action of gravity. The prediction has been realized experimentally in the form of Airy-shaped electron beams [2]. Following the commonly known principle that the propagation of classical optical beams in linear media and the dynamics of a quantum particle are governed by essentially the same Schrödinger equation, nonspreading/nondiffracting packets, including Airy waves, have been investigated in detail in linear optics [3] and plasmonics [4]. Bessel beams are also commonly known examples of diffraction-free waves, and were predicted and experimentally demonstrated by Durnin et al. in 1987 [5,6]. Other classes of nondiffracting wave modes, including Mathieu and parabolic beams, have also been investigated [7,8]; see, also, review [9].
Airy beams have been created in optics by dint of inputs with properly shaped intensity and phase [10,11]. Those works demonstrated, in particular, self-healing of perturbed beams. Cylindrically symmetric ring-Airy beams are able to abruptly autofocus in the linear regime, thus delivering high-energy pulses into transparent samples, as predicted theoretically [12] and demonstrated experimentally [13,14]. By engineering the phase profile in the Fourier space, classes of abruptly autofocusing Airy beams that follow different trajectories have also been proposed [15,16]. Propagation dynamics of ring-Airy beams with embedded optical vorticity (angular momentum) have also been investigated theoretically and experimentally [17,18,19]. Applications of Airy beams range from optical filamentation [20,21,22], imaging [23,24,25], transportation and manipulation of particles [26,27,28], and to driving surface plasmon polaritons [29,30,31].
The propagation of self-interacting high-power Airy beams has been studied in the framework of Schrödinger equations with various nonlinearities. Accelerating self-trapped beams were thus predicted in Kerr, saturable, and nonlocal nonlinear media [32,33]. For strong Kerr nonlinearity, soliton shedding by Airy beams was analyzed in [34]. The latter phenomenon was also predicted in nonlocal nonlinear media [35]. Trajectories of Airy beams and pulses have been studied experimentally in nonlinear photorefractive and Kerr media [36,37]. Comparison of self-accelerating linear Airy beams and solitons, which may feature similar dynamics in specific two-component systems, was presented in a recent review [38].
The propagation of two-component Airy waves in second-harmonic-generating media with quadratic nonlinearities was observed in [39]. In this setting, it was further predicted that linear Airy beams launched in the one- or two-dimensional (1D or 2D) second-harmonic component generate sets of solitons through parametric instability [40,41]. An extension of the analysis was also developed for 1D and 2D three-wave systems [42,43].
A non-Hermitian parity–time symmetric potential can modify the trajectory of an Airy beam without affecting its ability for diffraction-free propagation [44]. Specifically, Airy beams in a parity–time symmetric Gaussian potential feature diffraction-free propagation over long parabolic trajectories [45].
Kinetic equations with fractional partial derivatives have been used to describe anomalous diffusion and relaxation phenomena, including Hamiltonian chaos, disordered media, underground water pollution, reactions in complex systems, and fractional diffusion in inhomogeneous media [46,47,48]. The concept of fractional derivatives also appears in diverse areas of physical phenomenology, such as the quantum Hall effect and the fractional Josephson effect [49,50]. Further, the fractional Schrödinger equation (FSE) generalizes the classical Schrödinger equation, which is a canonical model for various physical phenomena, such as nonlinear optics, hydrodynamics, and the Bose–Einstein condensates [51,52,53].
A vast research area in optics and related areas deals with the FSE. It was introduced by Laskin [54,55,56], who considered, by means of the Feynman-integral technique, the evolution of the wave function of quantum particles moving by Lévy flights (random jumps). The aforementioned similarity between the quantum–mechanical linear Schrödinger equation and the equation for the paraxial diffraction of light beams suggests schemes for the realization of FSE in optics, as first proposed by Longhi [57]. That work elaborated a scheme based on the so-called 4f configuration in an optical cavity. The beam is transformed by a lens from the coordinate space into the Fourier domain, in which a phase-shift emulating the fractional diffraction is introduced by means of an appropriate phase plate. Then, the second lens casts the optical field back into the spatial form, which carries the phase structure corresponding to the fractional diffraction. Experimentally, this scheme was recently realized in the temporal domain [58].
The propagation of beams with various shapes under the action of fractional paraxial diffraction has been addressed in the framework of FSE. In particular, Airy beams have been studied in this context [59,60,61,62,63]. Furthermore, the self-interaction and propagation dynamics of Airy beams have been investigated in the framework of the fractional nonlinear Schrödinger equation (NLSE), which adds the Kerr term to the optical FSE [64,65]; see, also, review [66].
The above-mentioned possibility to implement fractional diffraction implies that it is possible to build a system with an array of 4f setups with different parameters. This option, in turn, suggests one to consider an FSE including a management scheme [67] that makes the effective diffraction coefficient a function of the propagation distance, z. Moreover, the fact that the diffraction-emulating phase shifts are introduced by the phase plates inserted into the optical cavities makes it possible to emulate not only positive but also negative diffraction. The latter possibility allows one to define management patterns in the form of periodic alternation of artificial diffraction between positive and negative strengths; see Equation (8) below. Such diffraction management schemes are akin to ones that have been previously realized for normal (non-fractional) diffraction by beam propagation in waveguiding arrays with periodically varying orientation of the guiding cores [68].
The subject of the present work is the dynamics of axially symmetric ring-Airy beams governed by the 2D fractional NLSE with the aforementioned z-dependent local diffraction and/or nonlinearity coefficients. The paper is organized as follows. The model is introduced in Section 2, which is followed by a detailed analysis of the dynamics of ring-Airy beams in Section 3. In particular, it is found that a saturable self-focusing nonlinearity does not break the axial symmetry of the ring-shaped beams through azimuthal instability. This is an essential result, as similarly shaped modes are often vulnerable to that instability [69,70]. The paper is concluded in Section 4.
A more sophisticated management scheme may apply to the fractionality degree (i.e., the Lévy index (LI))in linear or nonlinear FSE, making LI a function of z; cf. [71]. Such a scheme will be considered elsewhere.
2. The Model
As outlined above, we consider beam propagation along the z-axis in a 2D nonlinear isotropic medium with saturable nonlinear correction to the refractive index, which can be described by the fractional NLSE:
where is the amplitude of the optical field, and is the wavenumber corresponding to carrier wavelength and linear refractive index . The fractional-diffraction operator in Equation (1), with LI, , belonging to interval and variable diffraction coefficient , is defined as the 2D version of the Riesz derivative [72,73]:
where and are 2D operators of the direct and inverse Fourier transform, and are wavenumbers conjugate to transverse coordinates . The nonlinear correction to the refractive index is represented by the term
which features saturation with strength . The saturable nonlinearity is well-known to occur, in particular, in semiconductor-doped glasses and photorefractive media [74,75]. The saturation in this model is a crucially important factor because, as is well known, cubic (unsaturated) self-focusing in the 2D fractional NLSE leads to the supercritical collapse at all values [66] (and to the usual critical collapse in the case of non-fractional diffraction, ); hence, the solitons are unstable in the absence of the saturation. Note that, in the absence of the saturation and management (, ), the collapse is driven by the symmetry (invariance) of Equation (1) with respect to the scaling transform:
The saturation stabilizes the model against collapse by breaking the scaling symmetry.
Following the pattern of Equation (4) but in the presence of the saturation and diffraction management, the variables in Equation (1) can be normalized by means of rescaling:
where is the characteristic width of the input beam, and is the respective diffraction (Rayleigh) length corresponding to a characteristic value of the diffraction coefficient. The accordingly scaled form of Equation (1) is
where is the normalized diffraction-modulation coefficient, and
with positive or negative values corresponds, respectively, to the self-focusing or defocusing nonlinearity.
In particular, it is relevant to consider the case of the periodic management corresponding to
in Equation (6). As suggested by previous works on dispersion and diffraction management [67], a more general form of this format may be taken as , including the path-average term, , which may be negative or positive. Actually, simulations demonstrate that the latter term readily becomes a dominant one in the ensuing evolution, making it similar to the standard model, with ; therefore, here we concentrate on the format (8), which produces most interesting findings. By means of additional rescaling admitted by Equation (6), we fix the modulation amplitude in Equation (8) as .
To investigate the propagation characteristics of beams under the action of different management formats, we also address decaying diffraction-coefficient modulation:
A similar modulation format has been considered in the case of dispersion management in nonlinear fiber optics [76].
Note that the substitution of
transforms Equation (6) into a fractional NLSE with nonlinearity management:
where is a function inverse to . In particular, it is seen that the management is eliminated by substitution (10) in the linear version of Equation (6), with . The model with nonlinearity management is considered below too, neglecting the saturation (dropping the denominator in the nonlinear term) in Equation (11). The aim is to check the possibility of stabilization of the 2D solitons by means of nonlinearity management against the above-mentioned supercritical collapse driven by the unsaturated nonlinearity. This possibility is suggested by the previously discovered mechanism of the stabilization of fundamental solitons (rather than Airy beams) by nonlinearity management against the onset of the critical collapse in the case of (the usual non-fractional diffraction) [77,78,79,80].
As mentioned above, another version of the management, which is specific to the fractional setting, can be introduced by periodic modulation of LI: . Unlike what is considered above, this form of the management (that will be addressed elsewhere) cannot be eliminated from the linearized equation.
3. Numerical Results
3.1. The Model with Diffraction Management
In this section, we address the propagation of the ring-Airy beam governed by Equation (6) with input
where Ai is the Airy function, is the input’s amplitude, is the radial coordinate, and determine the initial radius and width, respectively, of the ring-Airy beam, and is the exponential truncation factor that is necessary to secure convergence of the integral power,
cf. [11].
Characteristic results can be presented using input (13) with
They are displayed in Figure 1 and Figure 2 for the self-focusing and self-defocusing nonlinearity, respectively.
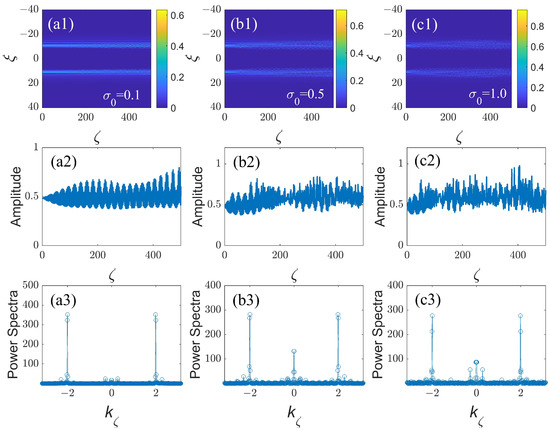
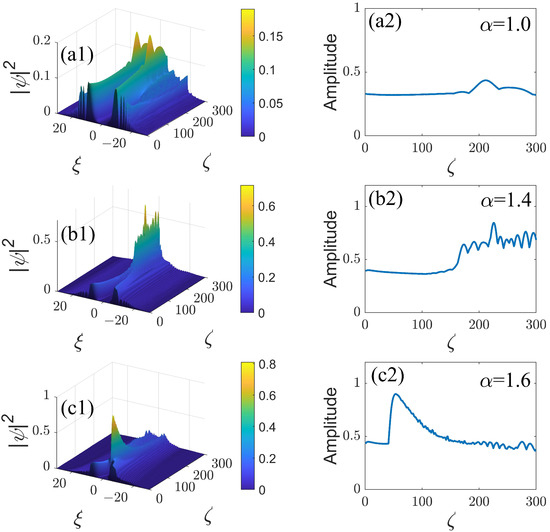
Figure 1.
The propagation dynamics of the ring-Airy beams under the combined action of the self-focusing saturable nonlinearity, defined by Equation (3) with values of indicated in the top panels, and the periodic modulation of the diffraction coefficient, defined by Equation (8) with and , in the framework of Equation (6) with . The propagation is initiated by input (13) with parameters (15). (a1,b1,c1): Side views (i.e., the cross-section drawn through ) of the propagating ring-Airy beams for different values of nonlinearity parameter as indicated in the panels. Panels (a2,b2,c2) show the amplitude of the optical field as the function of the propagation distance. Panels (a3,b3,c3) present power spectra of the amplitude from (a2,b2,c2): is the respective wavenumber of the Fourier transform applied to the functions of .
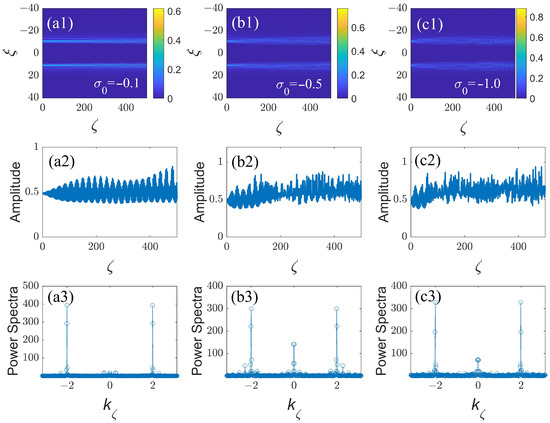
Figure 2.
The same as Figure 1 but for the case of self-defocusing saturable nonlinearity defined by Equation (6) with negative values indicated in the panels.(a1,b1,c1): Side views (i.e., the cross-section drawn through ) of the propagating ring-Airy beams for different values of nonlinearity parameter as indicated in the panels. Panels (a2,b2,c2) show the amplitude of the optical field as the function of the propagation distance. Panels (a3,b3,c3) present power spectra of the amplitude from (a2,b2,c2): is the respective wavenumber of the Fourier transform applied to the functions of .
Figure 1(a1,b1,c1) present the propagation dynamics with different values of the self-focusing nonlinearity strength in Equation (3) and a fixed value of the modulation frequency, in Equation (8) (recall is fixed by rescaling). In Figure 1(a1), the main lobe of the ring-Airy beam exhibits nearly periodic oscillations in the presence of the weak nonlinearity. It is seen in Figure 1(b1,c1) that the oscillations gradually extend to side lobes of the beam as the strength of the self-focusing nonlinearity increases. The oscillation amplitude also gradually grows and exhibits a trend towards chaotization with the increase of ; see Figure 1(a2,b2,c2). The respective power spectra of the variable amplitude of the beam are displayed in Figure 1(a3,b3,c3). It is seen that the dominant spectral components, located at , are obviously determined by the aforementioned management frequency (), while the apparent chaotization is produced, with the growth of the nonlinearity strength, by the appearance of long-wave spectral components around .
The results for the self-defocusing nonlinearity, which are displayed in Figure 2, are generally similar. However, at stronger nonlinearity, , the long-wave component of the spectrum, which accounts for the chaotization, is, quite naturally, broader (hence, more conspicuous) for the self-focusing sign; cf. Figure 1(c3) and Figure 2(c3).
Next, we address the propagation dynamics of the nonlinear beams under the action of the decaying modulation format, defined as per Equation (9). Figure 3(a1,b1,c1) show that, in this case, the ring-Airy beams naturally shrink, while their amplitude increases under the action of self-focusing, following the decay of the diffraction strength. In the cases of and (Figure 3(a2,b2)), the increase in the amplitude is arrested and then it falls to a somewhat lower, nearly constant value, which is conspicuously larger than the initial one, due to the saturable character of the nonlinearity in Equation (11). The situation is different in the case of , shown in Figure 3(c2), where the amplitude initially attains a higher value in the course of the shrinkage, but then, due to a stronger effect of the saturation, it falls back to a quasi-constant level, which is close to the initial value.
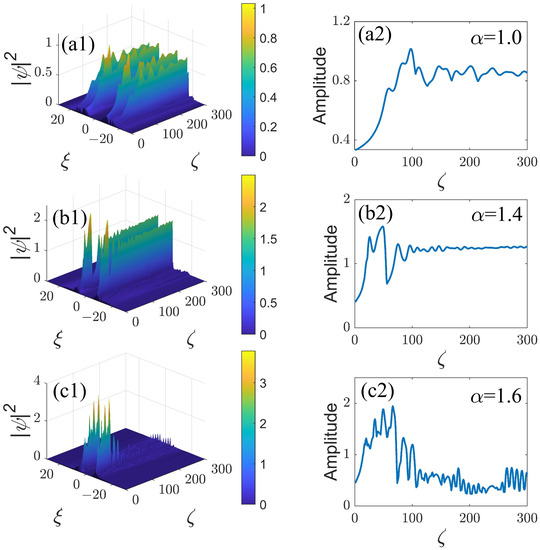
Figure 3.
The propagation dynamics of ring-Airy beams under the action of the modulation format (9), as produced by simulations of Equation (6). Panels (a1,b1,c1) display, in the cross-section , the evolution of the propagating beams with the self-focusing nonlinearity, , and LI values , , and , as indicated in the panels. The respective evolution of the amplitude of the optical field is displayed in panels (a2,b2,c2).
In the case of the combination of the modulation format (9) and self-defocusing, corresponding to in Equation (6), Figure 4(a1,b1,c1) show that the main lobe of the ring-Airy beams tends to autofocus at a certain point, while the sidelobes do not significantly shrink. In the cases of , relatively weak autofocusing occurs at , as seen in Figure 4(a1,a2). As the Lévy index increases, stronger autofocusing occurs at shorter transmission distances in the cases of and (Figure 3(b1,c1), respectively).
3.2. The Model with Nonlinearity Management
Next, we consider the possibility of stabilization of ring-Airy beams by means of nonlinearity management, modeled by the following fractional NLSE:
cf. Equation (11). Here, following [77,78,79,80], the spatially periodic management format is considered, with wavenumber k, viz.:
cf. Equation (8), where the coefficient in front of is set equal so that by means of rescaling.
The propagation dynamics of the ring-Airy beams is summarized in Figure 5 for a fixed modulation wavenumber under the combined action of the periodic diffraction management, defined as per Equation (8), with , and nonlinearity management. In Figure 5(a,b1,c1,a2,b2,c2), the ring-Airy beams with are stabilized as the absolute value of constant term in Equation (17) decreases in the cases of the self-focusing () and defocusing () nonlinearity. It is seen that stabilization of the beam against the above-mentioned supercritical collapse can be achieved when the average value in the modulation profile (17) is smaller than the modulation amplitude (which is equal to 1 in Equation (17)). Because the supercritical collapse is driven by the constant term , while the effective stabilization is provided by the oscillatory one, the stabilization is clearly seen to be most efficient at for different values of in Figure 5(a3,b3,c3), carrying over into an apparently chaotic regime (but still not a collapsing one) with the increase of . Fully clean stabilization at and different values of LI is clearly observed in Figure 5(a3,b3,c3).
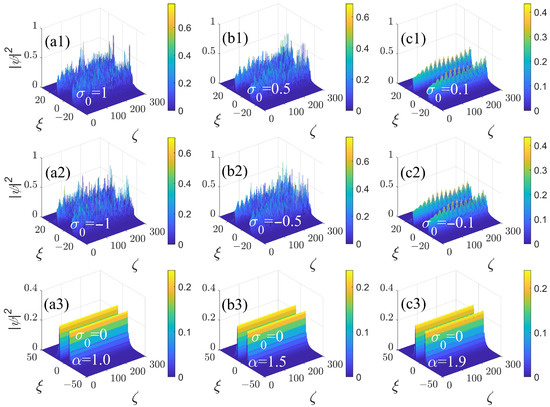
Figure 5.
The simulated propagation of the ring-Airy beams under the action of diffraction management with modulation format (8), where is set again in combination with nonlinearity management (17) with , as produced by simulations of Equation (16). Panels (a1,b1,c1) and (a2,b2,c2) display, in the cross-section , the propagation dynamics of the propagating beams with a fixed value of for different values of the self-focusing and defocusing nonlinearity parameter , as indicated in the panels. Panels (a3,b3,c3) display the results for fixed and different values of the LI: , , and , respectively.
As an additional test of the stabilization of the ring-Airy beams by the nonlinearity management, the transmission of the beams was tested under the combined effect of the fast management with and or , as shown with multiple examples in Figure 6 and Figure 7. It is observed that for different values of LI, the ring-Airy beams autofocus after passing a certain distance, which is followed by quasi-stabilization, with the amplitude converging to nearly constant values.
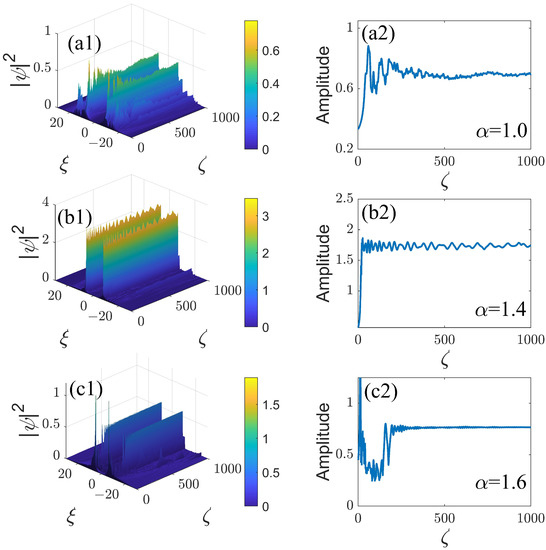
Figure 6.
The propagation dynamics of the ring-Airy beams under the combined action of the decaying diffraction-modulation format (9) and nonlinearity management (17) with and , as produced by simulations of Equation (16). Panels (a1,b1,c1) display, in cross-section , the evolution of the beams with fixed values of , as indicated in the panels. Panels (a2,b2,c2) show the corresponding evolution of the amplitude of the optical field.
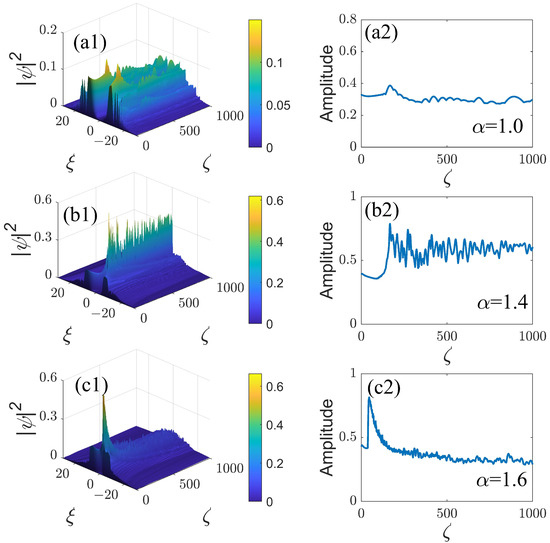
Figure 7.
The same as in Figure 6, but for .
4. Conclusions
We have numerically investigated the propagation dynamics of 2D ring-Airy beams with axial symmetry, governed by the fractional NLSE with the saturable or cubic nonlinear term and variable diffraction and nonlinearity coefficients. These equations, which belong to the general class of management systems, model optical waveguides composed as an array of elements emulating the fractional diffraction and carrying the Kerr (saturable or non-saturable) nonlinearity. Adjusting the LI (Lévy index) and the modulation format of the fractional-diffraction coefficient provides efficient means to maintain stable propagation of the ring-Airy beams, keeping their symmetry unbroken. These findings are essential, as normally 2D ring-shaped patterns in Kerr media are unstable against symmetry-breaking azimuthal perturbations that split the ring, and, moreover, all localized states are destroyed by the supercritical or critical collapse at or , respectively (the latter value corresponds to the usual non-fractal diffraction). We have considered the spatially periodic modulation profiles of the diffraction and nonlinearity coefficients, as well as the diffraction-management profile decaying inversely proportional to the propagation distance, in the case of the saturable nonlinearity. The main lobe of the ring-Airy beam exhibits nearly periodic oscillations under the action of periodic modulation of the diffraction in the presence of the weak nonlinearity. The oscillation amplitude gradually grows and exhibits a trend towards chaotization with the growth of the nonlinearity strength. The ring-Airy beams naturally shrink, while their amplitude increases under the action of the decaying modulation format and self-focusing nonlinearity; then their amplitudes fall to a somewhat lower, nearly quasi-constant value. In the case of the combination of the decaying modulation and self-defocusing, the main lobe of the ring-Airy beams tends to autofocus at a certain point, while the sidelobes do not significantly shrink. Generally, the ring-Airy beams are stabilized by means of nonlinearity management both for the periodic and decaying modulation formats of diffraction. The management schemes introduced in this work offer new possibilities for manipulating and controlling the ring-shaped optical beams that would be unstable otherwise. As an extension of the work, it is relevant to address the propagation of the ring beams carrying angular momentum (vorticity).
Author Contributions
Conceptualization, P.L. and Y.W.; methodology, P.L.; software, Y.W.; validation, Y.W.; formal analysis, B.A.M.; investigation, P.L. and W.Y; writing—original draft preparation, P.L. and B.A.M.; writing—review and editing, B.A.M. and D.M.; visualization, P.L. and Y.W.; supervision, P.L.; project administration, P.L.; funding acquisition, P.L. and B.A.M. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the National Natural Science Foundation of China (NSFC) (No. 11805141), the Applied Basic Research Program of Shanxi Province (No. 201901D211424), and the Scientific and Technological Innovation Programs of Higher Education Institutions in Shanxi (STIP) (2021L401). The work of BAM was partly supported by the Israel Science Foundation through grant No. 1695/22.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| 2D | Two-dimensional |
| LI | Lévy index |
| FSE | Fractional Schrödinger equation |
| NLSE | Nonlinear Schrödinger equation |
References
- Berry, M.V.; Balazs, N.L. Diffraction-free beams. Am. J. Phys. 1979, 47, 264–267. [Google Scholar] [CrossRef]
- Voloch-Bloch, N.; Lereah, Y.; Lilach, Y.; Gover, A.; Arie, A. Generation of electron Airy beams. Nature 2013, 494, 331–335. [Google Scholar] [CrossRef] [PubMed]
- Efremidis, N.K.; Chen, Z.G.; Segev, M.; Christodoulides, D.N. Airy beams and accelerating waves: An overview of recent advances. Optica 2019, 6, 686–701. [Google Scholar] [CrossRef]
- Minovich, A.E.; Klein, A.E.; Neshev, D.N.; Pertsch, T.; Kivshar, Y.S.; Christodoulides, D.N. Airy plasmons: Non-diffracting optical surface waves. Laser. Phot. Res. 2014, 8, 221–232. [Google Scholar] [CrossRef]
- Durnin, J. Exact solutions for nondiffracting beams. I. The scalar theory. J. Opt. Soc. Am. A 1987, 4, 651–654. [Google Scholar] [CrossRef]
- Durnin, J.; Miceli, J.J.; Eberly, J.H. Diffraction-free beams. Phys. Rev. Lett. 1987, 58, 1499–1501. [Google Scholar] [CrossRef]
- Gutiérrez-Vega, J.C.; Iturbe-Castillo, M.D.; Chávez-Cerda, S. Alternative formulation for invariant optical fields: Mathieu beams. Opt. Lett. 2000, 25, 1493–1495. [Google Scholar] [CrossRef]
- Bandres, M.A.; Gutiérrez-Vega, J.C.; Chávez-Cerda, S. Parabolic nondiffracting optical wave fields. Opt. Lett. 2004, 29, 44–46. [Google Scholar] [CrossRef]
- Recami, E.; Zamboni-Rached, M. Localized waves: A review. Adv. Imaging Electron. Phys. 2009, 56, 235–353. [Google Scholar]
- Siviloglou, G.A.; Broky, J.; Dogariu, A.; Christodoulides, D.N. Observation of accelerating Airy beams. Phys. Rev. Lett. 2007, 99, 213901. [Google Scholar] [CrossRef]
- Siviloglou, G.A.; Christodoulides, D.N. Accelerating finite energy Airy beams. Opt. Lett. 2007, 32, 979–981. [Google Scholar] [CrossRef]
- Efremidis, N.K.; Christodoulides, D.N. Abruptly autofocusing waves. Opt. Lett. 2010, 35, 4045–4047. [Google Scholar] [CrossRef]
- Papazoglou, D.G.; Efremidis, N.K.; Christodoulides, D.N.; Tzortzakis, S. Observation of abruptly autofocusing waves. Opt. Lett. 2011, 36, 1842–1844. [Google Scholar] [CrossRef]
- Zhang, P.; Prakash, J.; Zhang, Z.; Mills, M.S.; Efremidis, N.K.; Christodoulides, D.N.; Chen, Z.G. Trapping and guiding microparticles with morphing autofocusing Airy beams. Opt. Lett. 2011, 36, 2883–2885. [Google Scholar] [CrossRef] [PubMed]
- Chremmos, I.; Zhang, P.; Prakash, J.; Efremidis, N.K.; Christodoulides, D.N.; Chen, Z.G. Fourier-space generation of abruptly autofocusing beams and optical bottle beams. Opt. Lett. 2011, 36, 3675–3677. [Google Scholar] [CrossRef]
- Liu, S.; Wang, M.R.; Li, P.; Zhang, P.; Zhao, J.L. Abrupt polarization transition of vector autofocusing Airy beams. Opt. Lett. 2013, 38, 2416–2418. [Google Scholar] [CrossRef]
- Jiang, Y.F.; Huang, K.K.; Lu, X.H. Propagation dynamics of abruptly autofocusing Airy beams with optical vortices. Opt. Express 2012, 20, 18579–18584. [Google Scholar] [CrossRef] [PubMed]
- Chen, B.; Chen, C.D.; Peng, X.; Peng, Y.L.; Zhou, M.L.; Deng, D.M. Propagation of sharply autofocused ring Airy Gaussian vortex beams. Opt. Express 2015, 23, 19288–19298. [Google Scholar] [CrossRef] [PubMed]
- Li, P.; Liu, S.; Peng, T.; Xie, G.F.; Gan, X.T.; Zhao, J.L. Spiral autofocusing Airy beams carrying power-exponent-phase vortices. Opt. Express 2014, 22, 7598–7606. [Google Scholar] [CrossRef]
- Polynkin, P.; Kolesik, M.; Moloney, J.V.; Siviloglou, G.A.; Christodoulides, D.N. Curved plasma channel generation using ultraintense Airy beams. Science 2009, 324, 229–232. [Google Scholar] [CrossRef]
- Polynkin, P.; Kolesik, M.; Moloney, J.V. Filamentation of femtosecond laser Airy beams in water. Phys. Rev. Lett. 2009, 103, 123902. [Google Scholar] [CrossRef] [PubMed]
- Clerici, M.; Hu, Y.; Lassonde, P.; Milián, C.; Couairon, A.; Christodoulides, D.N.; Chen, Z.G.; Razzari, L.; Vidal, F.; Légaré, F.; et al. Laser-assisted guiding of electric discharges around objects. Sci. Adv. 2015, 1, e1400111. [Google Scholar] [CrossRef]
- Vettenburg, T.; Dalgarno, H.I.C.; Nylk, J.; Coll-Lladó, C.; Ferrier, D.E.K.; Cizmar, T.; Gunn-Moore, F.J.; Dholakia, K. Light-sheet microscopy using an Airy beam. Nat. Methods 2014, 11, 541–544. [Google Scholar] [CrossRef] [PubMed]
- Nylk, J.; McCluskey, K.; Preciado, M.A.; Mazilu, M.; Yang, Z.; Gunn-Moore, F.J.; Aggarwal, S.; Tello, J.A.; Ferrier, D.E.; Dholakia, K. Light sheet microscopy with attenuation-compensated propagation-invariant beams. Sci. Adv. 2018, 4, eaar4817. [Google Scholar] [CrossRef]
- Preciado, M.A.; Dholakia, K.; Mazilu, M. Generation of attenuation compensating Airy beams. Opt. Lett. 2014, 39, 4950–4953. [Google Scholar] [CrossRef] [PubMed]
- Baumgartl, J.; Mazilu, M.; Dholakia, K. Optically mediated particle clearing using Airy wavepackets. Nat. Photonics 2008, 2, 675–678. [Google Scholar] [CrossRef]
- Cheng, H.; Zang, W.P.; Zhou, W.Y.; Tian, J.G. Analysis of optical trapping and propulsion of Rayleigh particles using Airy beam. Opt. Express 2010, 18, 20384–20394. [Google Scholar] [CrossRef]
- Zheng, Z.; Zhang, B.F.; Chen, H.; Ding, J.P.; Wang, H.T. Optical trapping with focused Airy beams. Appl. Opt. 2011, 50, 43–49. [Google Scholar] [CrossRef]
- Salandrino, A.; Christodoulides, D.N. Airy plasmon: A nondiffracting surface wave. Opt. Lett. 2010, 35, 2082–2084. [Google Scholar] [CrossRef]
- Minovich, A.; Klein, A.E.; Janunts, N.; Pertsch, T.; Neshev, D.N.; Kivshar, Y.S. Generation and near-field imaging of Airy surface plasmons. Phys. Rev. Lett. 2011, 107, 116802. [Google Scholar] [CrossRef]
- Li, L.; Li, T.; Wang, S.M.; Zhang, C.; Zhu, S.N. Plasmonic Airy beam generated by in-plane diffraction. Phys. Rev. Lett. 2011, 107, 126804. [Google Scholar] [CrossRef] [PubMed]
- Kaminer, I.; Segev, M.; Christodoulides, D.N. Self-accelerating self-trapped optical beams. Phys. Rev. Lett. 2011, 106, 213903. [Google Scholar] [CrossRef] [PubMed]
- Bekenstein, R.; Segev, M. Self-accelerating optical beams in highly nonlocal nonlinear media. Opt. Express 2011, 19, 23706–23715. [Google Scholar] [CrossRef] [PubMed]
- Fattal, Y.; Rudnick, A.; Marom, D.M. Soliton shedding from Airy pulses in Kerr media. Opt. Express 2011, 19, 17298–17307. [Google Scholar] [CrossRef] [PubMed]
- Shen, M.; Gao, J.S.; Ge, L.J. Solitons shedding from Airy beams and bound states of breathing Airy solitons in nonlocal nonlinear media. Sci. Rep. 2015, 5, 9814. [Google Scholar] [CrossRef]
- Hu, Y.; Sun, Z.; Bongiovanni, D.; Song, D.H.; Lou, C.B.; Xu, J.J.; Chen, Z.G.; Morandotti, R. Reshaping the trajectory and spectrum of nonlinear Airy beams. Opt. Lett. 2012, 37, 3201–3203. [Google Scholar] [CrossRef]
- Hu, Y.; Li, M.; Bongiovanni, D.; Clerici, M.; Yao, J.P.; Chen, Z.G.; Azaña, J.; Morandotti, R. Spectrum to distance mapping via nonlinear Airy pulses. Opt. Lett. 2013, 38, 380–382. [Google Scholar] [CrossRef]
- Malomed, B.A. Self-accelerating solitons. EPL 2022, 140, 22001. [Google Scholar] [CrossRef]
- Dolev, I.; Kaminer, I.; Shapira, A.; Segev, M.; Arie, A. Experimental observation of self-accelerating beams in quadratic nonlinear media. Phys. Rev. Lett. 2012, 108, 113903. [Google Scholar] [CrossRef]
- Mayteevarunyoo, T.; Malomed, B.A. Generation of χ2 solitons from the Airy wave through the parametric instability. Opt. Lett. 2015, 40, 4947–4950. [Google Scholar] [CrossRef]
- Mayteevarunyoo, T.; Malomed, B.A. Two-dimensional χ2 solitons generated by the downconversion of Airy waves. Opt. Lett. 2016, 41, 2919–2922. [Google Scholar] [CrossRef]
- Mayteevarunyoo, T.; Malomed, B.A. The interaction of Airy waves and solitons in the three-wave system. J. Optics. 2017, 19, 085501. [Google Scholar] [CrossRef]
- Prasatsap, U.; Mayteevarunyoo, T.; Malomed, B.A. Two-dimensional Airy waves and three-wave solitons in quadratic media. J. Optics. 2022, 24, 055501. [Google Scholar] [CrossRef]
- Liu, J.F.; Zhang, Y.Q.; Zhong, H.; Zhang, J.W.; Wang, R.; Belić, M.R.; Zhang, Y.P. Optical Bloch oscillations of a dual Airy beam. Ann. Phys. 2017, 530, 1700307. [Google Scholar] [CrossRef]
- Wang, X.N.; Fu, X.Q.; Huang, X.W.; Yang, Y.J.; Bai, Y.F. The robustness of truncated Airy beam in PT Gaussian potentials media. Opt. Commun 2018, 410, 717–722. [Google Scholar] [CrossRef]
- Metzler, R.; Klafter, J. The random walk’s guide to anomalous diffusion: A fractional dynamics approach. Phys. Rep. 2020, 339, 1–77. [Google Scholar] [CrossRef]
- Zaslavsky, G.M. Chaos, fractional kinetics, and anomalous transport. Phys. Rep. 2002, 371, 461–580. [Google Scholar] [CrossRef]
- Chechkin, A.C.; Gorenflo, R.; Sokolov, I.M. Fractional diffusion in inhomogeneous media. J. Phys. A Math. Gen. 2005, 38, L679–L684. [Google Scholar] [CrossRef]
- Laughlin, R.B. Anomalous quantum hall efect: An incompressible quantum fuid with fractionally charged excitations. Phys. Rev. Lett. 1983, 50, 1395–1398. [Google Scholar] [CrossRef]
- Rokhinson, L.P.; Liu, X.Y.; Furdyna, J.K. The fractional A.C. Josephson efect in a semiconductor-superconductor nanowire as a signature of Majorana particles. Nat. Phys. 2012, 8, 795–799. [Google Scholar] [CrossRef]
- Momani, S.; Arqub, O.A.; Maayah, B.; Yousef, F.; Alsaedi, A. A reliable algorithm for solving linear and nonlinear Schrödinger equations. Appl. Comput. Math. 2018, 17, 151–160. [Google Scholar]
- Sulem, C.; Sulem, P. The Nonlinear Schrödinger Equation: Self-Focusing and Wave Collapse; Springer Series in Mathematical Sciences; Springer: Berlin, Germany, 1999. [Google Scholar]
- Bao, W.; Cai, Y. Mathematical theory and numerical methods for Bose-Einstein condensation. Kinet. Relat. Models 2013, 6, 1–135. [Google Scholar] [CrossRef]
- Laskin, N. Fractional quantum mechanics. Phys. Rev. E 2000, 62, 3135–3145. [Google Scholar] [CrossRef] [PubMed]
- Laskin, N. Fractional quantum mechanics and Lévy path integrals. Phys. Lett. A 2000, 268, 298–305. [Google Scholar] [CrossRef]
- Laskin, N. Fractional Schrödinger equation. Phys. Rev. E 2002, 66, 056108. [Google Scholar] [CrossRef]
- Longhi, S. Fractional Schrödinger equation in optics. Opt. Lett. 2015, 40, 1117–1120. [Google Scholar] [CrossRef] [PubMed]
- Liu, S.; Zhang, Y.; Malomed, B.A.; Karimi, E. Experimental realisations of the fractional Schrödinger equation in the temporal domain. arXiv 2022, arXiv:2208.01128. [Google Scholar]
- Huang, X.W.; Deng, Z.X.; Fu, X.Q. Dynamics of finite energy Airy beams modeled by the fractional Schrödinger equation with a linear potential. J. Opt. Soc. Am. B 2017, 34, 976–982. [Google Scholar] [CrossRef]
- Huang, X.W.; Deng, Z.X.; Shi, X.H.; Fu, X.Q. Propagation characteristics of ring Airy beams modeled by fractional Schrödinger equation. J. Opt. Soc. Am. B 2017, 34, 2190–2197. [Google Scholar] [CrossRef]
- Huang, X.W.; Shi, X.H.; Deng, Z.X.; Bai, Y.F.; Fu, X.Q. Potential barrier-induced dynamics of finite energy Airy beams in fractional Schrödinger equation. Opt. Express 2017, 25, 32560–32569. [Google Scholar] [CrossRef]
- He, S.L.; Malomed, B.A.; Mihalache, D.; Peng, X.; Yu, X.; He, Y.J.; Deng, D.M. Propagation dynamics of abruptly autofocusing circular Airy Gaussianvortex beams in the fractional Schrödinger equation. Chaos Solitons Fractals 2021, 142, 110470. [Google Scholar] [CrossRef]
- He, S.L.; Malomed, B.A.; Mihalache, D.; Peng, X.; He, Y.J. Propagation dynamics of radially polarized symmetric Airy beams in the fractional Schrödinger equation. Phys. Lett. A 2021, 404, 127403. [Google Scholar] [CrossRef]
- Zhang, L.F.; Zhang, X.; Wu, H.Z.; Li, C.X.; Pierangeli, D.; Gao, Y.X.; Fan, D.Y. Anomalous interaction of Airy beams in the fractional nonlinear Schrödinger equation. Opt. Express 2019, 27, 27936–27945. [Google Scholar] [CrossRef] [PubMed]
- He, S.L.; Zhou, K.Z.; Malomed, B.A.; Mihalache, D.; Zhang, L.P.; Tu, J.L.; Wu, Y.; Zhao, J.J.; Peng, X.; He, Y.J.; et al. Airy-Gaussian vortex beams in the fractional nonlinear Schrödinger medium. J. Opt. Soc. Am. B 2021, 38, 3230–3236. [Google Scholar] [CrossRef]
- Malomed, B.A. Optical solitons and vortices in fractional media: A mini-review of recent results. Photonics 2021, 8, 353. [Google Scholar] [CrossRef]
- Malomed, B.A. Soliton Management in Periodic Systems; Springer: New York, NY, USA, 2006. [Google Scholar]
- Eisenberg, H.S.; Silberberg, Y.; Morandotti, R.; Aitchinson, J.S. Diffraction management. Phys. Rev. Lett. 2000, 85, 1863–1866. [Google Scholar] [CrossRef]
- Firth, W.J.; Skryabin, D.V. Optical solitons carrying orbital angular momentum. Phys. Rev. Lett. 1997, 79, 2450–2453. [Google Scholar] [CrossRef]
- Malomed, B.A. Multidimensional Solitons; AIP Publishing: Melville, NY, USA, 2022. [Google Scholar]
- Wang, Q.; Zhang, L.; Malomed, B.A.; Mihalache, D.; Zeng, L. Transformation of multipole and vortex solitons in the nonlocal nonlinear fractional Schrödinger equation by means of Lévy-index management. Chaos Solitons Fractals 2022, 157, 111995. [Google Scholar] [CrossRef]
- Samko, G.; Kilbas, A.A.; Marichev, O.I. Fractional Integrals and Derivatives: Theory and Applications; Gordon and Breach: New York, NY, USA, 1993. [Google Scholar]
- Duo, S.W.; Zhang, Y.Z. Mass-conservative Fourier spectral methods for solving the fractional nonlinear Schrödinger equation. Comput. Math. Appl. 2016, 71, 2257–2271. [Google Scholar] [CrossRef]
- Coutaz, J.L.; Kull, M. Saturation of the nonlinear index of refraction in semiconductor-doped glass. J. Opt. Soc. Am. B 1991, 8, 95–98. [Google Scholar] [CrossRef]
- Tikhonenko, V.; Christou, J.; Luther-Davies, B. Three dimensional bright spatial soliton collision and fusion in a saturable nonlinear medium. Phys. Rev. Lett. 1996, 76, 2698–2701. [Google Scholar] [CrossRef] [PubMed]
- Malomed, B.A.; Matera, F.; Settembre, M. Reduction of the jitter for return-to-zero signals. Opt. Commun. 1997, 143, 193–198. [Google Scholar] [CrossRef]
- Towers, I.; Malomed, B.A. Stable (2+1)-dimensional solitons in a layered medium with sign-alternating Kerr nonlinearity. J. Opt. Soc. Am. B 2002, 19, 537–543. [Google Scholar] [CrossRef]
- Abdullaev, F.K.; Caputo, J.G.; Kraenkel, R.A.; Malomed, B.A. Controlling collapse in Bose-Einstein condensation by temporal modulation of the scattering length. Phys. Rev. A 2003, 67, 013605. [Google Scholar] [CrossRef]
- Saito, H.; Ueda, M. Dynamically stabilized bright solitons in a two-dimensional Bose-Einstein condensate. Phys. Rev. Lett. 2003, 90, 040403. [Google Scholar] [CrossRef]
- Itin, A.; Morishita, T.; Watanabe, S. Reexamination of dynamical stabilization of matter-wave solitons. Phys. Rev. A 2006, 74, 033613. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).