Fully Nonlinear Small Amplitude Dynamical Waves for Multicomponent Complex Plasma with Kappa Distributed Electrons and Ions

Abstract

Multicomponent plasmas are ubiquitous in astrophysics and space plasma environments. In the present manuscript, we assumed a dusty plasma system consisting of negative and positive dust species and kappa-distributed electrons and ions. The analysis is based on the fluid model of plasmas, and the reductive perturbation method was used to study the behavior of propagating waves. New arbitrary parameters were obtained to measure the strength of nonlinearity, dispersion, and dissipation in the plasma system. We investigated the effects of the arbitrary parameters on the appearance of the different nonlinear waves as soliton, shock, and solitary waves. Furthermore, we studied the effects of the kappa parameter, the viscosity of dust species, and the ratio between the temperature of positive and negative dust species in the type of wave, i.e., compressive or rarefactive.

1. Introduction

Dust-acoustic waves (DAWs) have many industrial applications such as laboratory plasma devices, semiconductor chips, and fusion reactors [1,2,3,4]. They are also commonly observed in various space environments such as asteroid zones, the lower and upper mesosphere and ionosphere of the Earth, cometary tails, interplanetary spaces, and interstellar media [5,6,7,8,9]. The numerous applications of DAWs have motivated researchers to study these waves for different plasma conditions. For instance, Angelis et al. [10] studied dusty ion acoustic waves (DIAW), and their results were compared with observations of Halley’s Comet. Rao et al. [11] showed, theoretically, that the propagation of low energetic acoustic waves in both linear and nonlinear modes is due to the existence of dusty particles. Piel et al. [12,13] studied low energetic acoustic waves under microgravity conditions. Looking for a different way of propagating acoustic waves in dusty plasma was continued by many researchers [14,15,16,17,18,19].

The propagation of nonlinear dust-acoustic (DA) solitary waves in unmagnetized dusty plasma composed of Maxwellian electrons, vortex-like (trapped) ions, and cold mobile dust grain was studied by Rahman et al. [20]. The Korteweg–de Vries (KdV) equation, which emits the solitary wave solution and was derived using the standard reductive perturbation method for positively and negatively charged warm dust species and ions, was found to have nonthermal distribution by Abdel Mannan and Mamun [21]. The reductive perturbation method, used to study shock waves that may exist in a dusty plasma system, is composed of four components via the derivation of Burgers’ equation under the effect of viscosity, which causes the dissipation of energy in the system under consideration [22]. The possibility of observing shock waves related to the dust-charging process was studied for three components of dusty plasma [23]. The reductive perturbation method was used to derive the KdV–Burgers’ equation to study the effects of dust size distribution on the propagation of shock waves that propagate in a dusty plasma system composed of negatively dust species, two types of ions that differ in temperature, and electrons [24]. Mahmoud et al. studied the propagation of dust-acoustic solitary waves and double-layer waves for four-component dusty plasma system containing nonextensive distributed electrons and ions via Sagdeev pseudopotential and using the traditional reductive perturbation method to derive KdV and modified KdV equations [25,26,27].

Suprathermal populations are ubiquitous in space plasmas. The observed particle velocity distributions from space show superthermal, high-energy tails, which take the formula as a power law. As such, the so-called kappa distributions fit very well into the observed populations of plasma species [28]. In the mid-1960s, the formulas of kappa distributions were firstly introduced by Binsack, Olbert, and Vasyliũnas [29,30,31]. The effects of kappa distribution parameters and viscosity on the polarity of shock waves propagated in four-component dusty plasma composed of positive and negative cold dust species and kappa distributed electrons and ions were studied by L. Akpabio and S. Akpabio [32].

In this paper, the effects of both thermal motion and viscosity on the inertial species in a four-component, collision-less, unmagnetized dusty plasma system were investigated, while the effects of kappa parameters for inertialess species were introduced. Thus, a plasma system under consideration contains negative and positive dust species as well as kappa-distributed electrons and ions, and this system can be found in both space environments and laboratories [33,34,35]. This paper is arranged as follows: Section 2 presents the governing equations that account for the four-component dusty plasma system. The momentum equation contains the effect of the viscosity on both the positive and negative dust species. In Section 3, the generalized reductive perturbation method is used to derive some nonlinear partial differential equations, which propagate some interesting waves, such as soliton, shock, solitary, and double layers waves. The results and a discussion are presented in Section 4.

2. Governing Equations

In our multicomponent complex plasma system, the negative and positive dust species are taken as two fluids, while the light species, i.e., electrons and ions, are assumed to be kappa distributed. The following normalized continuity and momentum equations were used to study the motion of the two fluids [25,26] after adding the effect of viscosity and taking the distribution of inertialess species via kappa distribution:

$$\frac{\partial }{\partial t}{N}_1+\frac{\partial }{\partial x}[N_1{V}_1]=0,$$

(1a)

$$\frac{\partial }{\partial t}{V}_1+V_1\frac{\partial }{\partial x}{V}_1-\frac{\partial }{\partial x}\varphi +{\eta }_1\frac{{\partial }^2}{\partial x^2}{V}_1=0,$$

(1b)

$$\frac{\partial }{\partial t}{N}_2+\frac{\partial }{\partial x}[N_2{V}_2]=0,$$

(2a)

$$\frac{\partial }{\partial t}P+V_2\frac{\partial }{\partial x}P+3P\frac{\partial }{\partial x}{V}_2=0,$$

(2b)

$$\mu \left[\frac{\partial }{\partial t}{V}_2+V_2\frac{\partial }{\partial x}{V}_2\right]+\frac{\partial }{\partial x}\varphi +\frac{\sigma }{N_2}\frac{\partial }{\partial x}P+{\eta }_2\frac{{\partial }^2}{\partial x^2}{V}_2=0.$$

(2c)

In order to make a self-consistent system, the following Poisson’s equation is used:

$$\frac{{\partial }^2}{\partial x^2}\varphi -N_1+{\mu }_{+}{N}_2+{\mu }_i{N}_i-{\mu }_e{N}_e=0$$

(3)

where $N_i(x,t)$ and $N_e(x,t)$ are the number densities of ions and electrons, respectively. In this paper, the normalized densities of ions and electrons are provided in kappa distribution forms as

$$N_i={\left(1+\frac{\varphi }{k_i-3/2}\right)}^{-(k_i-1/2)},$$

(4a)

$$N_e={\left(1-{\sigma }_e\frac{\varphi }{k_e-3/2}\right)}^{-(k_e-1/2)}$$

(4b)

In Equations (1)–(3), $N_1\left(x,t\right)(N_2\left(x,t\right))$ and $V_1\left(x,t\right)(V_2\left(x,t\right))$ are, respectively, the negative (positive) normalized densities by their equilibrium values, $N_{10}(N_{20})$, and the negative (positive) normalized velocity by the dust-acoustic speed, $C_d=\sqrt{\mu }{v}_T$; $\mu =Z_1{m}_2/(Z_2{m}_1)$, $v_T={(k_B{T}_i{Z}_2/m_2)}^{1/2}$ is the thermal velocity, $m_2$($m_1$) and $Z_2$($Z_1$) are the rest mass of positive (negative) dust fluid and the number of charges on the positive (negative) dust grain surface, $T_i$ is the ion temperature, and $k_B$ is the Boltzmann constant. $P(x,t)$ and $\varphi (x,t)$ are the normalized pressure and electrostatic potential by $N_{20}{k}_{B}T$ and ($k_B{T}_i/e$), respectively. Space and time are normalized by the dusty Debye length (${\lambda }_D={[k_B{T}_i/(4\pi e^2{N}_{10}{Z}_1)]}^{1/2}$) and the inverse of the dusty plasma frequency ${\omega }_{-}^{-1}={[m_1/(4\pi N_{10}{e}^2{Z}_1^2)]}^{1/2}$, respectively. ${\sigma }_e=T_i/T_e$ and $\sigma =T_2/(Z_2{T}_i)$ is the temperature ratio between the positive dust and ions, where $T_e$ is the electron temperature. ${\mu }_{+}=N_{20}{Z}_2/(N_{10}{Z}_1)$, ${\mu }_e=N_{e0}/(N_{10}{Z}_1)$, and ${\mu }_i=N_{i0}/(N_{10}{Z}_1)$, which satisfy the neutrality condition, and ${\mu }_{+}-{\mu }_e+{\mu }_i=1$, $N_{e0}$, and $N_{i0}$ are the densities of electrons and ions at equilibrium, respectively. ${\eta }_1$(${\eta }_2$) is the normalized viscosity of negative (positive) massive species. ${\kappa }_i$(${\kappa }_e$) is the kappa parameter of ions (electrons).

Equations (1)–(4) are complex, nonlinear, partial differential equations of six unknown functions: $N_1$, $V_1$, $N_2$, $P$, $V_2$, and $\varphi$. Therefore, in the next section, we perform a small amplitude wave analysis by using the reductive perturbation method (RPM) [36,37].

3. Small Amplitude Wave Approximation

To study the properties of propagating DAW by deriving nonlinear partial differential equations, that is emit the most important waves that may appear in the plasma system under consideration, the following stretching is introduced [36,37]:

$$\tau ={\epsilon }^{\alpha +\beta }t, \xi ={\epsilon }^{\alpha }(x-\lambda t), {\eta }_{1,2}={\epsilon }^{\gamma }{\eta }_{1.2}$$

(5)

where the strength of the nonlinearity is measured by using the small parameter, $\epsilon$. $\alpha$, $\beta$, and $\gamma$ are positive arbitrary parameters that are greater than or equal to zero. $\lambda$ is the phase velocity of the dust fluid. All the unknown quantities manifest in Equations (1)–(4) can be expanded around their equilibrium values as:

$$N_1(\xi ,\tau )=1+\epsilon N_{11}+{\epsilon }^2{N}_{12}+{\epsilon }^3{N}_{13}+\dots$$

(6a)

$$V_1(\xi ,\tau )=0+\epsilon V_{11}+{\epsilon }^2{V}_{12}+{\epsilon }^3{V}_{13}+\dots ,$$

(6b)

$$N_2(\xi ,\tau )=1+\epsilon N_{21}+{\epsilon }^2{N}_{22}+{\epsilon }^3{N}_{23}+\dots$$

(6c)

$$V_2(\xi ,\tau )=0+\epsilon V_{21}+{\epsilon }^2{V}_{22}+{\epsilon }^3{V}_{23}+\dots$$

(6d)

$$P(\xi ,\tau )=1+\epsilon P_1+{\epsilon }^2{P}_2+{\epsilon }^3{P}_3+\dots ,$$

(6e)

$$\varphi (\xi ,\tau )=0+\epsilon {\varphi }_1+{\epsilon }^2{\varphi }_2+{\epsilon }^3{\varphi }_3+\dots$$

(6f)

By substituting (5) and (6) into the system of Equations (1)–(4) and collecting the like-power of $\epsilon$, the least order of $\epsilon$ yields:

$$V_{11}=-\frac{{\varphi }_1}{\lambda }, N_{11}=-\frac{{\varphi }_1}{{\lambda }^2},$$

(7a)

$$N_{21}=\frac{1}{\left({\lambda }^2\mu -3\sigma \right)}{\varphi }_1, V_{21}=\frac{\lambda }{\left({\lambda }^2\mu -3\sigma \right)}{\varphi }_1,$$

(7b)

$$P_1=\frac{3}{\left({\lambda }^2\mu -3\sigma \right)}{\varphi }_1,$$

(7c)

The following complementary equation can be obtained due to the substitution of Equation (7) into the Poisson equation, yielding:

$$\frac{1}{{\lambda }^2}+\frac{{\mu }_{+}}{\left({\lambda }^2\mu -3\sigma \right)}+{\alpha }_1=0,$$

(8a)

where

$${\alpha }_1=-\left[\frac{{\mu }_i\left(2k_i-1\right)}{\left(2k_i-3\right)}+{\mu }_e{\sigma }_e\frac{\left(2k_e-1\right)}{\left(2k_e-3\right)}\right]$$

(8b)

The next order of $\epsilon$ yields a set of equations that are dependent mainly on the values of the introduced arbitrary constants, $\alpha$, $\beta$ and $\gamma$; thus, for the sake of simplicity, different cases are studied.

3.1. Case 1 ($\beta =1$)

The next order of $\epsilon$ provides a set of equations that gathers between the first and second perturbed quantity, and by eliminating the second perturbed quantities, we obtain the following evolution equation:

$$\frac{\partial }{\partial \tau }{\varphi }_1+A{\varphi }_1\frac{\partial }{\partial \xi }{\varphi }_1+B{\epsilon }^{2\alpha +1}\frac{{\partial }^3}{\partial {\xi }^3}{\varphi }_1+C{\epsilon }^{\alpha +\gamma +1}\frac{{\partial }^2}{\partial {\xi }^2}{\varphi }_1=0$$

(9)

where

$$A=\frac{1}{A_0}\left[2{\alpha }_2-\frac{3}{{\lambda }^4}+\frac{3{\mu }_{+}\left({\lambda }^2\mu +\sigma \right)}{{\left({\lambda }^2\mu -3\sigma \right)}^3}\right],$$

(10a)

$$B=\frac{1}{A_0},$$

(10b)

$$C=\frac{1}{A_0}\left[\frac{{\eta }_1}{{\lambda }^3}+\frac{{\mu }_{+}{\eta }_2\lambda }{{\left({\lambda }^2\mu -3\sigma \right)}^2}\right],$$

(10c)

$$A_0=\left[\frac{2}{{\lambda }^3}+\frac{2{\mu }_{+}\lambda \mu }{{\left({\lambda }^2\mu -3\sigma \right)}^2}\right],$$

(10d)

$${\alpha }_2=\frac{1}{2}\left[{\mu }_i\frac{4k_i^2-1}{{\left(2k_i-3\right)}^2}-{\mu }_e{\sigma }_e^2\frac{4k_e^2-1}{{\left(2k_e-3\right)}^2}\right]$$

(10e)

Equation (9) represents the Kortweg–de Vreis Burger equation, where the second term describes the nonlinearity, while the third and fourth terms represent the dispersion and dissipation, respectively. Equation (9) shows that the dispersion and dissipation terms are mainly dependent on the two arbitrary parameters, $\alpha$ and $\gamma$. At $\alpha =\frac{1}{2},\hspace{0.17em}\gamma >\frac{1}{2}$, Equation (9) tends to the so-called KdV evaluation equation. This means that at $\hspace{0.17em}\gamma >\frac{1}{2}$ the effect of the dissipation term can be neglected in comparison with the dispersion term. Consequently, the KdV equation has a soliton solution at the balance between nonlinear and dispersion terms as

$${\varphi }_{KdV}\left(\xi ,\tau \right)={\varphi }_{0KdV}\sec h^2\left(\frac{\xi -v\tau }{\Delta }\right), {\varphi }_{0KdV}=3v/A,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\Delta =v/4B,$$

(10f)

However, at $\alpha =1,\hspace{0.17em}\gamma =0$, Equation (9) converts to Burgers’ equation, and the effect of dispersion can be neglected in comparison with the effect of the dissipation term. In this case, Equation (9) has a shock wave solution:

$${\varphi }_B\left(\xi ,\tau \right)={\varphi }_{0B}\left(1+\tanh \left(\frac{\xi -v\tau }{\Delta }\right)\right),\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{\varphi }_{0B}=v/A,\hspace{0.17em}\Delta =2C/v$$

(10g)

Conversely, the effects of both dispersion and dissipation exist, and a solitary wave appears from the interaction between nonlinearity with dispersion and dissipation at $\alpha =\frac{1}{2},\hspace{0.17em}\gamma =\frac{1}{2}$. At $\beta =1$, as is clear from (10f) and (10g), there is a possibility of two types of propagating wave (compressive and rarefactive), depending mainly on the sign of the nonlinear coefficient, but when the nonlinear coefficient equals zero, the propagated waves are undefined, so the nonlinear term must have more strength.

3.2. Case 2 ($\beta =2$)

In this case, the least order of $\epsilon$ provides relations (7) and (8), while the next order of $\epsilon$ leads to the following relations:

$$V_{12}=-\frac{1}{\lambda }{\varphi }_2+\frac{1}{2{\lambda }^3}{\varphi }_1^2,$$

(11a)

$$N_{12}=-\frac{1}{{\lambda }^2}{\varphi }_2+\frac{3}{2{\lambda }^4}{\varphi }_1^2,$$

(11b)

$$V_{22}=\frac{\lambda }{\left({\lambda }^2\mu -3\sigma \right)}{\varphi }_2+\frac{\lambda \left({\lambda }^2\mu +9\sigma \right)}{2{\left({\lambda }^2\mu -3\sigma \right)}^3}{\varphi }_1^2,$$

(11c)

$$N_{22}=\frac{1}{\left({\lambda }^2\mu -3\sigma \right)}{\varphi }_2+\frac{3\left({\lambda }^2\mu +\sigma \right)}{2{\left({\lambda }^2\mu -3\sigma \right)}^3}{\varphi }_1^2,$$

(11d)

$$P_2=\frac{3}{\left({\lambda }^2\mu -3\sigma \right)}{\varphi }_2+\frac{9\left({\lambda }^2\mu +\sigma \right)}{2{\left({\lambda }^2\mu -3\sigma \right)}^3}{\varphi }_1^2,$$

(11e)

By substituting Equation (11) into the Poisson Equation (3), the following relationship can be obtained

$$\left(\frac{1}{{\lambda }^2}+\frac{{\mu }_{+}}{\left({\lambda }^2\mu -3\sigma \right)}+{\alpha }_1\right){\varphi }_2+\left(-\frac{3}{2{\lambda }^4}+\frac{3{\mu }_{+}\left({\lambda }^2\mu +\sigma \right)}{\left({\lambda }^2\mu -3\sigma \right)}+{\alpha }_2\right){\varphi }_1^2=0$$

(12)

In Equation (12), the coefficient of ${\varphi }_2\left(\xi ,\tau \right)$ is complementary (Equation (8a)) is equal to zero and ${\varphi }_1(\xi ,\tau )\ne 0$; therefore, the coefficient of ${\varphi }_1^2(\xi ,\tau )$ can be considered equal to zero, and in this case, the following relation can be obtained:

$$\left(-\frac{3}{2{\lambda }^4}+\frac{3{\mu }_{+}\left({\lambda }^2\mu +\sigma \right)}{\left({\lambda }^2\mu -3\sigma \right)}+{\alpha }_2\right)=0,$$

(13)

The third order of $\epsilon$ represents the following evolution equation:

$$\frac{\partial }{\partial \tau }{\varphi }_1\left(\xi ,\tau \right)+A^{\prime }{\varphi }_1^2\left(\xi ,\tau \right)\frac{\partial }{\partial \xi }{\varphi }_1\left(\xi ,\tau \right)+B{\epsilon }^{2\alpha +1}\frac{{\partial }^3}{\partial {\xi }^3}{\varphi }_1\left(\xi ,\tau \right)+C{\epsilon }^{\alpha +\gamma +1}\frac{{\partial }^2}{\partial {\xi }^2}{\varphi }_1\left(\xi ,\tau \right)=0$$

(14)

where

$$A^{\prime }=\frac{1}{A_0}\left[3{\alpha }_3+\frac{15}{2{\lambda }^6}+\frac{3{\mu }_{+}\left(5{\lambda }^4{\mu }^2+30{\lambda }^2\mu \sigma +9{\sigma }^2\right)}{2{\left({\lambda }^2\mu -3\sigma \right)}^5}\right],$$

(15a)

$${\alpha }_3=-\frac{1}{6}\left[{\mu }_i\frac{\left(4k_{{}_i}^2+8k_i+3\right)\left(2k_i-1\right)}{{\left(2k_i-3\right)}^3}+{\mu }_e{\sigma }_e^3\frac{\left(4k_e^2+8k_e+3\right)\left(2k_e-1\right)}{{\left(2k_e-3\right)}^3}\right]$$

(15b)

Equation (14) represents the modified Kortweg–de Vreis –Burger equation, with dispersion and dissipation terms depending mainly on the arbitrary parameters $\alpha ,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\mathrm{and}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\gamma$. At $\alpha =1,\hspace{0.17em}\gamma >1$, Equation (14) tends to the modified KdV equation, but at $\alpha =2,\hspace{0.17em}\gamma =0$, Equation (14) converts into the modified Burgers’ equation, while at $\alpha =1,\hspace{0.17em}\gamma =1$, the modified KdV–Burgers’ equation appears. In Equation (12) the coefficient of ${\varphi }_1^2(\xi ,\tau )$ can be considered of the order of $\epsilon$ and not equal to zero, so $\left(-\frac{3}{2{\lambda }^4}+\frac{3{\mu }_{+}\left({\lambda }^2\mu +\sigma \right)}{\left({\lambda }^2\mu -3\sigma \right)}+{\alpha }_2\right){\varphi }_1^2\left(\xi ,\tau \right)$ becomes an order of ${\epsilon }^3$, and it must appear in the higher order of Poisson’s equation. Therefore, in this case, the higher order of $\epsilon$, it yields the Further–Burgers equation as:

$$\frac{\partial }{\partial \tau }{\varphi }_1+\left(A^{\prime }{\varphi }_1^2+A{\varphi }_1\right)\frac{\partial }{\partial \xi }{\varphi }_1+B{\epsilon }^{2\alpha +1}\frac{{\partial }^3}{\partial {\xi }^3}{\varphi }_1+C{\epsilon }^{\alpha +\gamma +1}\frac{{\partial }^2}{\partial {\xi }^2}{\varphi }_1=0$$

(16)

At $\alpha =1,\hspace{0.17em}\gamma >1$, Equation (16) tends toward the so-called Further equation, but at $\alpha =2,\hspace{0.17em}\gamma =0,\hspace{0.17em}\hspace{0.17em}\mathrm{and}\hspace{0.17em}\hspace{0.17em}A=0$, Equation (16) converts into the modified Burgers’ equation, while at $\alpha =1,\hspace{0.17em}\gamma =1$, the Further–Burgers equation appears as:

$$\frac{\partial }{\partial \tau }{\varphi }_1+\left(A^{\prime }{\varphi }_1^2+A{\varphi }_1\right)\frac{\partial }{\partial \xi }{\varphi }_1+B\frac{{\partial }^3}{\partial {\xi }^3}{\varphi }_1+C\frac{{\partial }^2}{\partial {\xi }^2}{\varphi }_1=0$$

(17)

4. Results and Discussion

In this paper, the reductive perturbation method in its generalized form (5) was used to derive some important nonlinear partial differential evolution equations (the KdV–Burgers family) to theoretically study some important waves, such as soliton, shock, and solitary waves, for unmagnetized, collisionless four-component dusty plasma, as taken from [25,26], after adding the effect of viscosity and taking the distribution of inertialess particles as a kappa distribution. Some arbitrary parameters were presented in a reductive perturbation method to control the strength of nonlinearity, dispersion, and dissipation in the system under consideration.

As shown in the theoretical analysis for the system under consideration, the existence of three arbitrary parameters is very important: $\alpha$, which controls the strength of dispersion; $\beta$, which controls the strength of nonlinearity; and $\gamma$, which controls the strength of dissipation in our system. The nonlinear KdV–Burgers equation (9) can be obtained at $\beta =1$, and this equation is a very important in plasma physics because it is a combination of two important equations, that is, the KdV and Burgers equations. This equation combines the nonlinear, dispersion, and dissipation terms in one equation with their coefficients depending on the arbitrary parameters $\alpha$ and $\gamma$. At $\alpha =\frac{1}{2},\hspace{0.17em}\gamma >\frac{1}{2}$, i.e., the dissipation effect can be neglected in comparison with the dispersion, and the resultant equation is called the KdV evaluation equation, which balances between nonlinearity and disperses a soliton solution given by (10f), while at $\alpha =1,\hspace{0.17em}\gamma =0$ (in this case, the effect of dissipation is larger than that of dispersion), in Equation (9) it can be converted to the so-called Burgers’ equation, which emits a shock wave solution given in (10g).

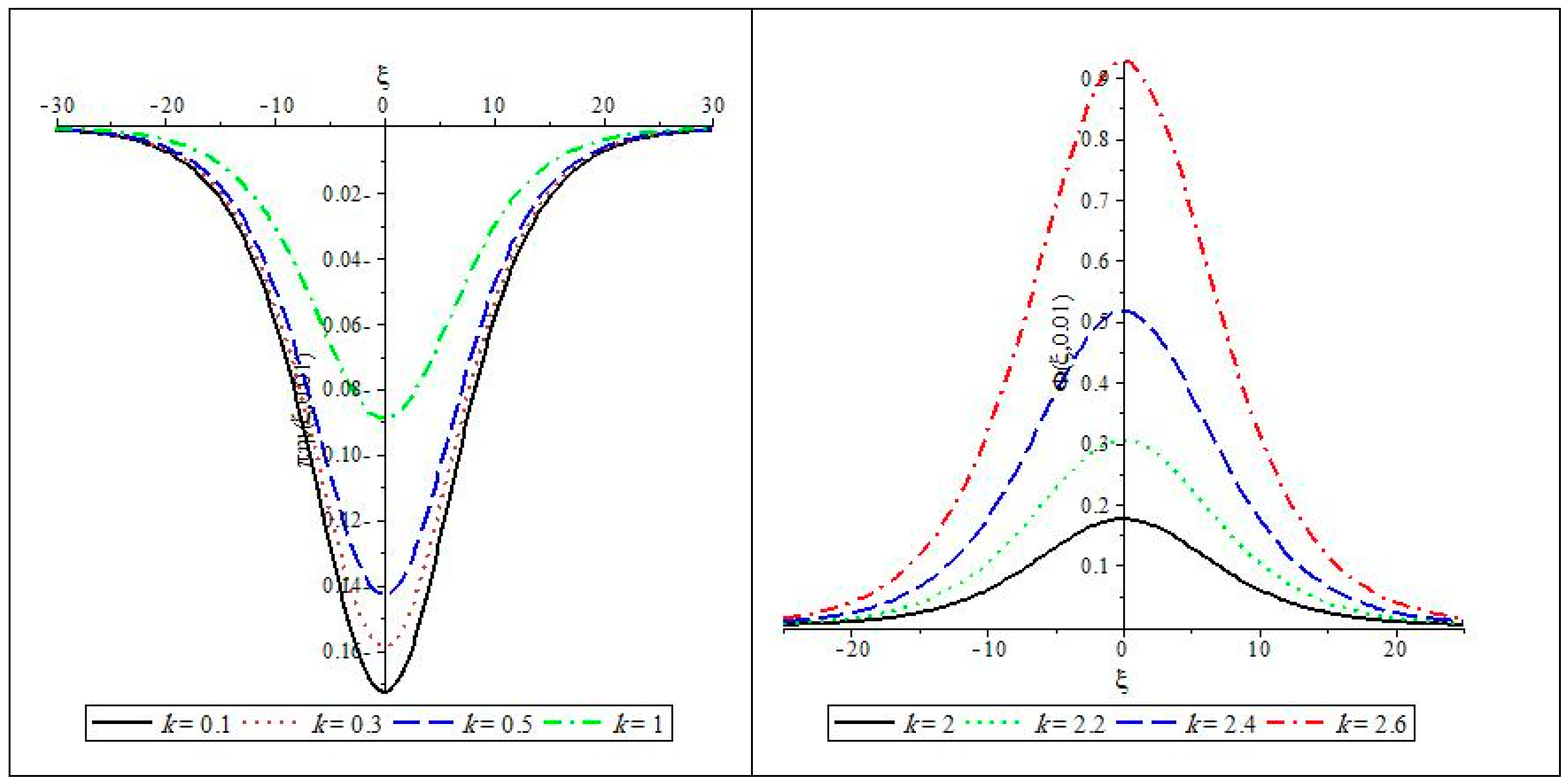
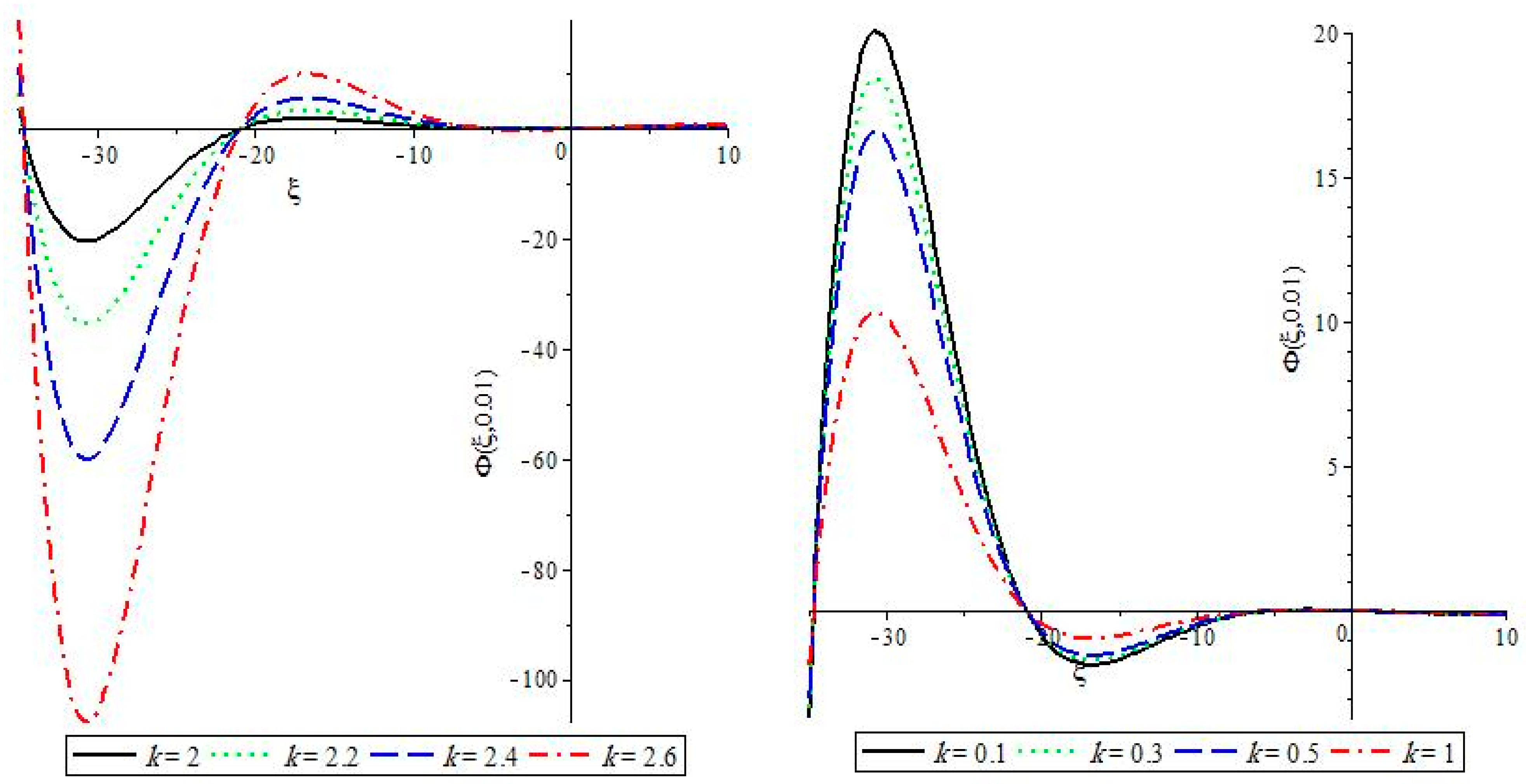
As shown from the soliton solution of the KdV Equation (10f) and the shock wave solution for Burgers’ Equation (10g), the sign of the amplitudes of the propagated waves depends on the sign of the nonlinear coefficient, $A$, as given in (10a), which depends mainly on the configurationally plasma parameters. The plotting of electrostatic potential, ${\varphi }_{KdV}\left(\xi ,\tau \right)$, given by (10f) at $\sigma =0.\hspace{0.17em}{\sigma }_e=0.5,\hspace{0.17em}\hspace{0.17em}{\mu }_e=0.2,\hspace{0.17em}{\mu }_2=0.5,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\mu =2,\hspace{0.17em}\hspace{0.17em}\tau =0.01,\hspace{0.17em}\hspace{0.17em}v=0.04$ and at different values of the kappa parameter, $k$, shows the propagation of negative (rarefactive) solitons at $k<1.5$ and positive (compressible) solitons at $k>1.5$ in Figure 1. 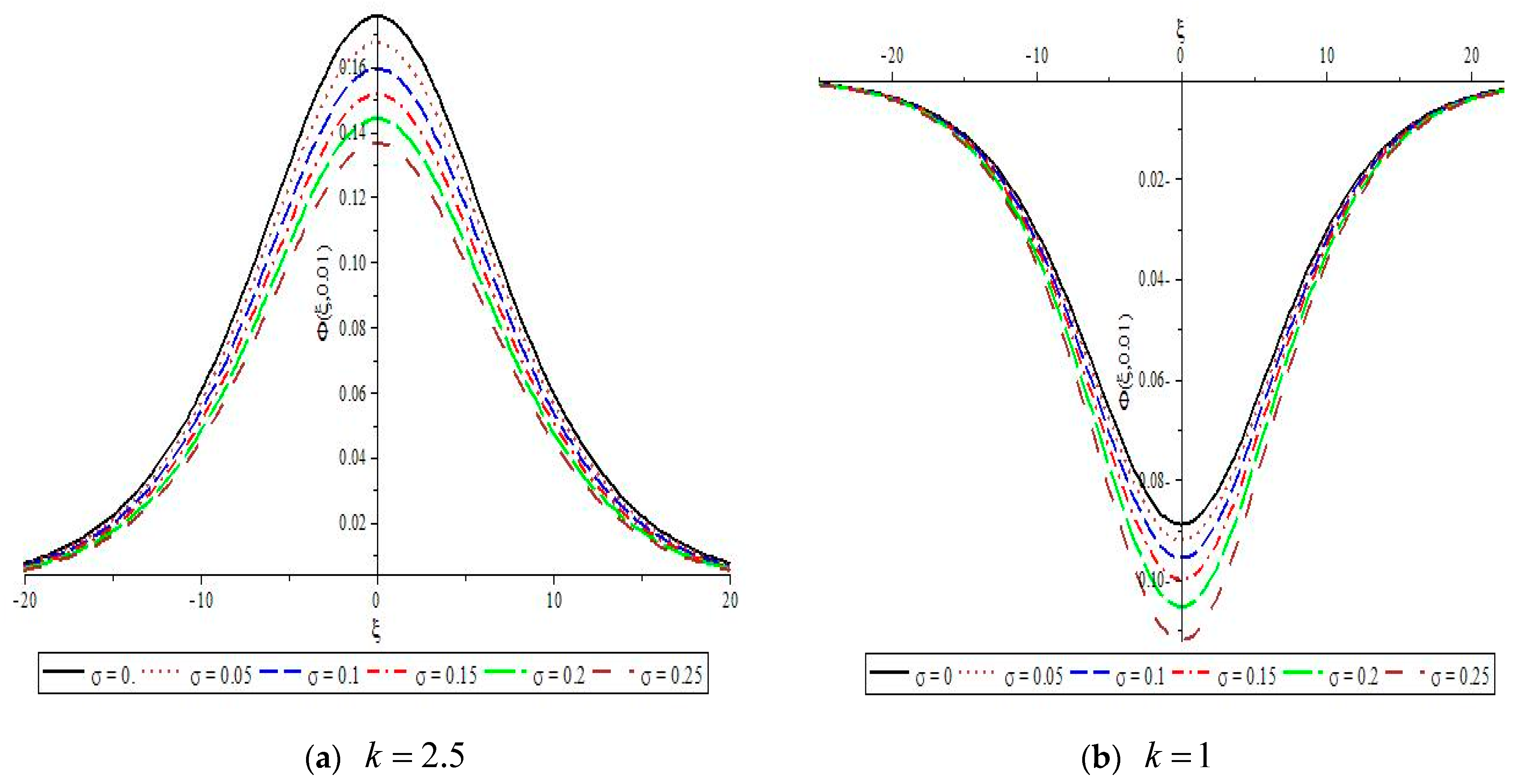The effects of the kappa parameter, $k$, are obvious in Figure 1 in the shape (width and amplitude); that is, at $k>1.5$, the change in both width and amplitude for the compressive soliton is very sensitive to the change in the kappa parameter, while the shape of the rarefactive soliton is slightly changed by the kappa parameter in comparison with that of the compressive soliton. The effects of the thermal motion of the positive dust fluid on the propagation of the compressive parameter at $k=2.5$ and the rarefactive solitons at $k=1$ are shown in Figure 2. It is clear from the graph that as the thermal parameter, $\sigma$, increases, both the width and amplitude decrease, but the compressive soliton is affected by the thermal parameter, which is higher than that of the rarefactive parameter.

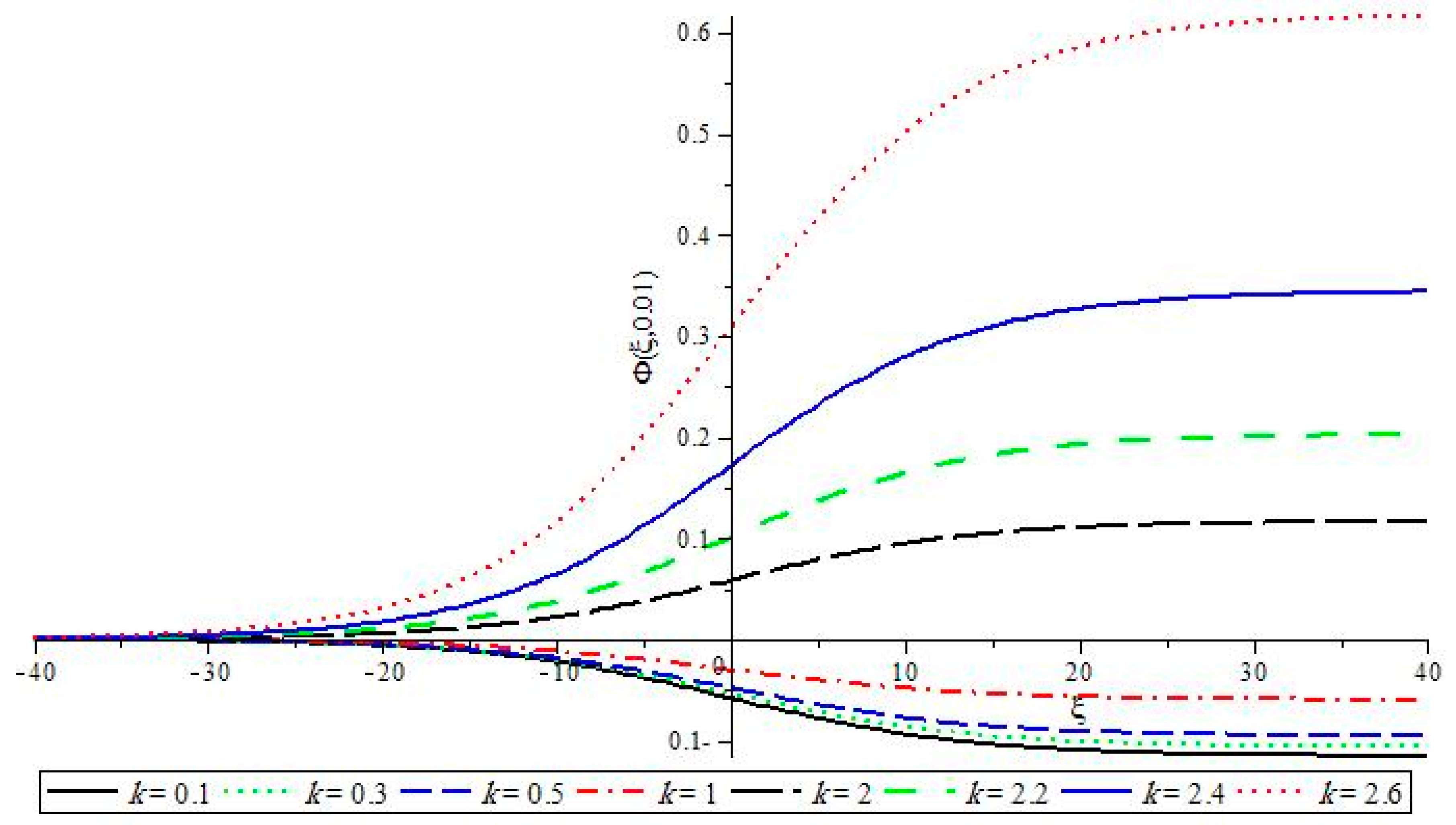
At $\alpha =1,\hspace{0.17em}\gamma =0$, the effect of dispersion can be neglected in comparison with the dissipation effect in this case, and absent the effect of thermal motion, the system under consideration is converted to that of [32]. 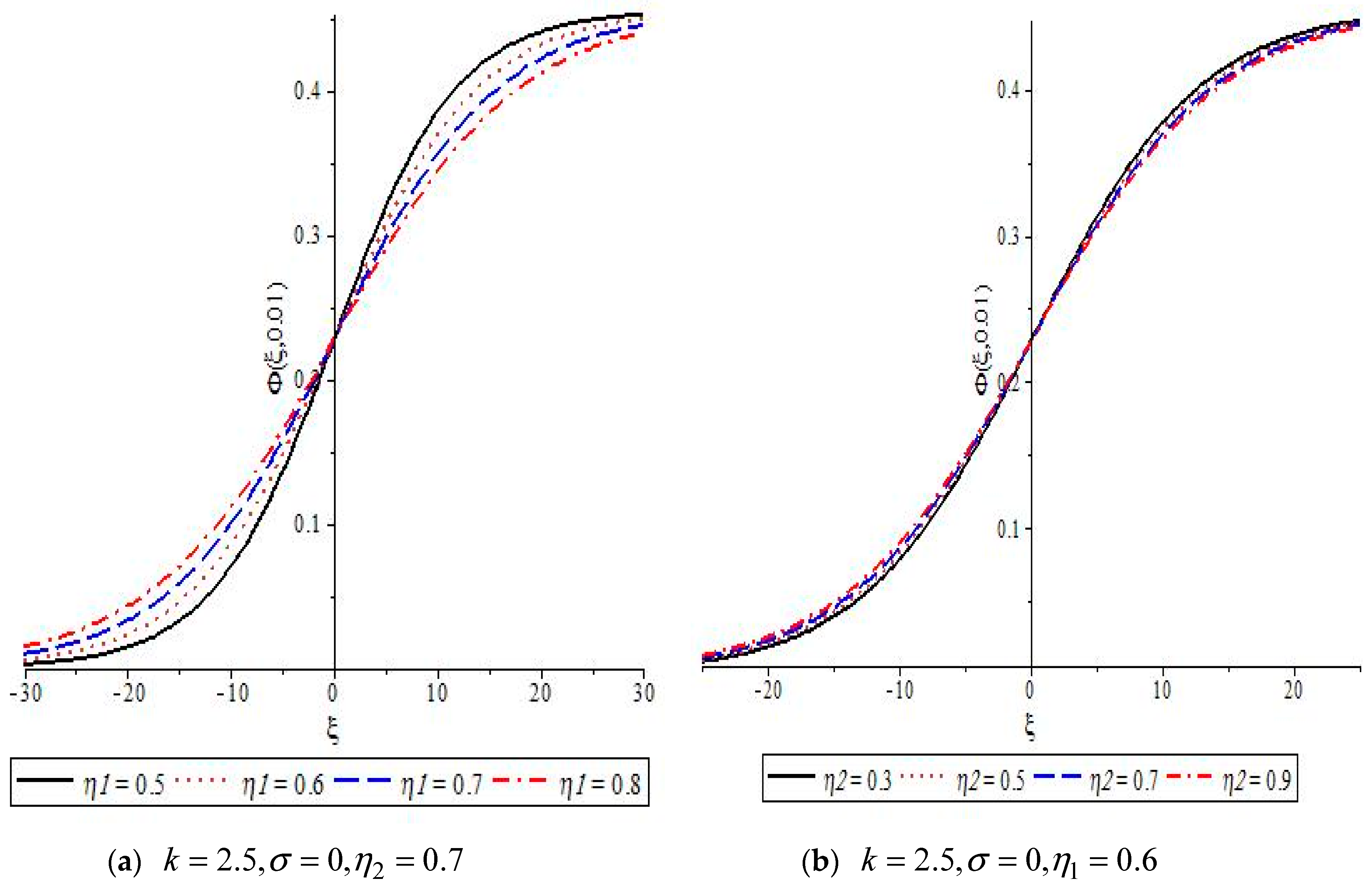The appearance of both positive and negative shock waves, which are provided by the graph of the electrostatic potential, ${\varphi }_B\left(\xi ,\tau \right)$, via the space parameter, $\xi$, for different values of the kappa parameter, $k$, and the other parameters taken from Figure 1 and Figure 2 are shown in Figure 3. The effects of viscosity for both positive and negative dust components are shown to be able to plot the positive electrostatic potential, ${\varphi }_B\left(\xi ,\tau \right)$ (at $k=2.5,\hspace{0.17em}\hspace{0.17em}\mathrm{and}\hspace{0.17em}\hspace{0.17em}\sigma =0$) in Figure 4. The graphs in Figure 4 show that the shapes of the positive shock waves are changed due to varying the viscosity values of the positive and negative dust fluids, but the variations in both the amplitude and steepness of the propagated shock wave are more sensitive to variations in the viscosity of the negative dust than that of positive dust.

Figure 5 shows that positive and negative solitary waves are propagated by the interaction between a nonlinear term with dispersion and dissipation, taking the introduced arbitrary parameters as $\alpha =\frac{1}{2},\hspace{0.17em}\gamma =\frac{1}{2}$. In this case, Equation (9) has a solitary wave solution:

$$\begin{array}{l}{\varphi }_B\left(\xi ,\tau \right)={\varphi }_{0KdV-B}\left(1-e^{C_1(\xi -v\tau )}\cos \left(C_2\left(\xi -v\tau \right)\right)\right),\hspace{0.17em}\\ \hspace{0.17em}{\varphi }_{0KdV-B}=2v/A,\hspace{0.17em}{C}_1=-C/2B,\hspace{0.17em}\hspace{0.17em}and\hspace{0.17em}\hspace{0.17em}{C}_2=\sqrt{\frac{v}{B}}.\end{array}$$

(18)

From the solutions of the KdV Equation (10f), Burgers’ Equation (10g), and the KdV–Burgers Equation (18), we can say that the types (compressive or rarefactive) of propagated waves are controlled by the values of nonlinear term coefficient A. Compressive waves (soliton, shock, and solitary) are propagated at $A>0$, while rarefactive waves are propagated at $A<0$. At $A=0$, the propagated wave cannot be defined. Thus, the strength of the nonlinear term must be increased. The so-called modified KdV–Burgers and Further–Burgers equations are derived at $\beta =2$, with the dispersion and dissipation coefficient depending mainly on the arbitrary parameters $\alpha$ and $\gamma$.

Finally, as shown from the introduced stretching and derived equations, there are three parameters that can directly affect the strength of nonlinearity and the appearance of the effects of both dispersion and dissipation in the medium, in addition to the propagation of compressive and rarefactive waves, which depend mainly on the kappa parameter values, as shown in Figure 1, Figure 2, Figure 3, Figure 4 and Figure 5. As it appears from the form of the dissipation coefficient, the dissipation of energy depends mainly on the dust fluid viscosity. This analysis may be useful in predicting the types of propagated dust-acoustic waves in the auroral zone of the ionosphere, for laser-produced plasma, and for interstellar dust plasma where non-Maxwellian distributions are considered. The chosen plasma parameters are relevant to different areas of space science, such as Jupiter’s magnetosphere, Earth’s mesosphere, and cometary tails [33,34,35].