The Black Hole Universe, Part I
Abstract
:1. Introduction
- Section 2: A FLRW cloud (FLRW*) is also a GR solution. The FLRW metric with a finite spherical volume of proper radius is also a GR solution. When FLRW* is inside its Schwarzschild radius and the space outside can be approximated as empty, this is a BHU. This solution for a BH interior is different from the SBH solution.
- Section 3: A BHU without DE has the same observable background as ΛCDM. The observed cosmic acceleration can be understood as resulting from a BHU without DE, where GM acts like as an effective term, with . A co-moving observer, anywhere within R in a BHU, sees the same background as an observer in the CDM with the same density.
2. The FLRW Cloud (FLRW*)
2.1. Classical Solutions
2.2. Junction Conditions for FLRW*
2.2.1. Timelike Junction
2.2.2. The GHY Boundary Term
2.2.3. Null Junction
2.2.4. The GHY Null Boundary Term
3. The Observable Universe
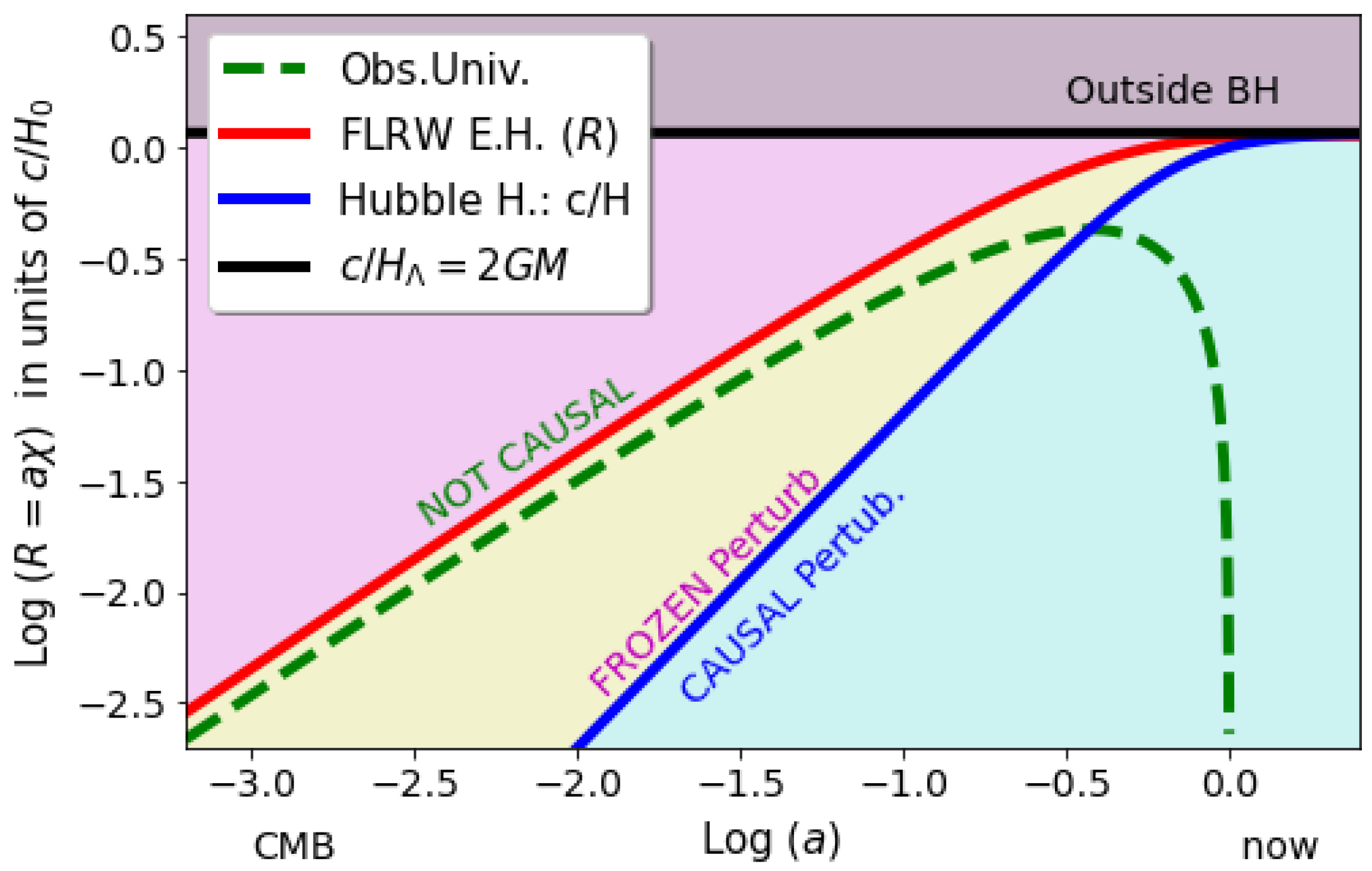
3.1. The Black Hole Universe
3.2. Off-Centred Co-Moving Observer
4. Discussion and Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Some Simple Solutions
Spherical Symmetry in Physical Coordinates
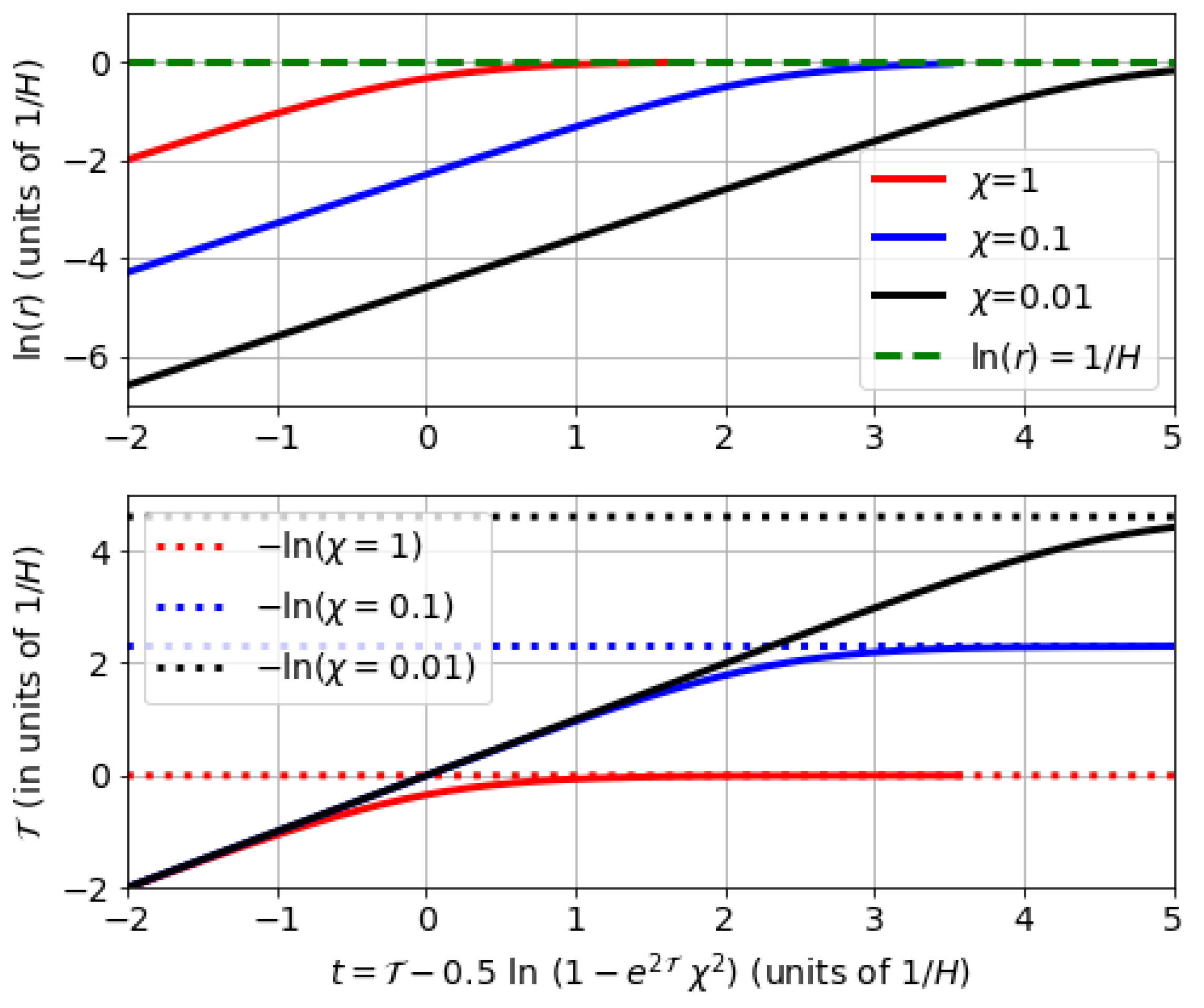
Appendix B. Frame Duality
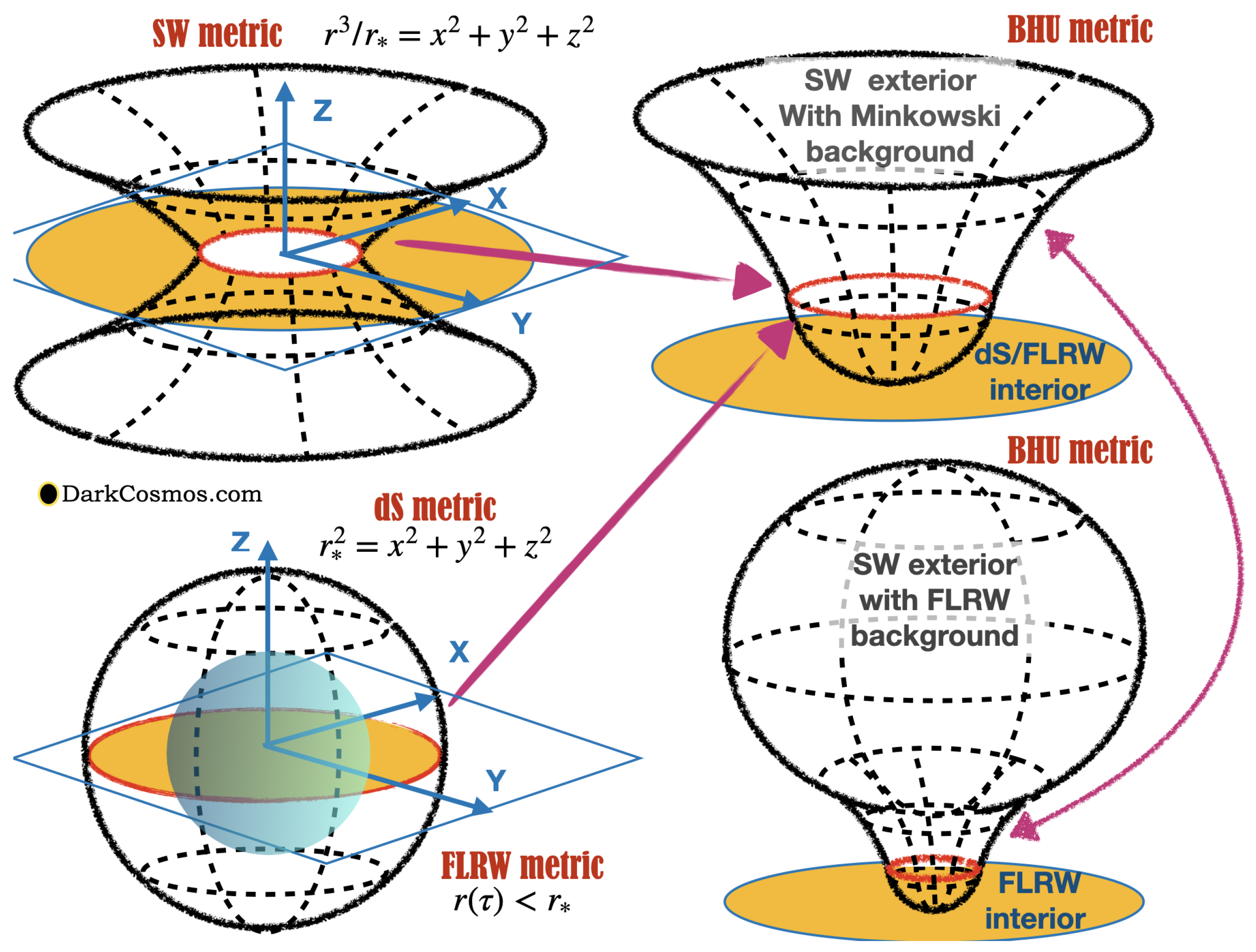
Appendix C. Geometrical Representations
Appendix D. The FLRM* Mass
References
- Ellis, G. Opposing the multiverse. Astron. Geophys. 2008, 49, 2.33–2.35. [Google Scholar] [CrossRef]
- Kormendy, J.; Ho, L.C. Coevolution (Or Not) of Supermassive Black Holes and Host Galaxies. ARAA 2013, 51, 511–653. [Google Scholar]
- Kusenko, A.E. Exploring Primordial Black Holes from the Multiverse with Optical Telescopes. PRL 2020, 125, 181304. [Google Scholar] [CrossRef] [PubMed]
- Buchdahl, H.A. General Relativistic Fluid Spheres. Phys. Rev. 1959, 116, 1027–1034. [Google Scholar] [CrossRef]
- Brustein, R.; Medved, A.J.M. Resisting collapse. PRD 2019, 99, 064019. [Google Scholar] [CrossRef]
- Mazur, P.O.; Mottola, E. Surface tension and negative pressure interior of a non-singular ‘black hole’. Class. Quantum Gravity 2015, 32, 215024. [Google Scholar] [CrossRef]
- Lemaître, G. Un Univers homogène de masse constante et de rayon croissant rendant compte de la vitesse radiale des nébuleuses extra-galactiques. Ann. Société Sci. Brux. 1927, 47, 49–59. [Google Scholar]
- Elizalde, E. The True Story of Modern Cosmology: Origins, Main Actors and Breakthroughs; Springer: Berlin/Heidelberg, Germany, 2021. [Google Scholar]
- Padmanabhan, T. Gravitation; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Misner, C.W.; Sharp, D.H. Relativistic Equations for Adiabatic, Spherically Symmetric Gravitational Collapse. Phys. Rev. 1964, 136, 571. [Google Scholar] [CrossRef]
- Lemaître, G. Expansion of the universe, A homogeneous universe of constant mass and increasing radius accounting for the radial velocity of extra-galactic nebulae. MNRAS 1931, 91, 483–490. [Google Scholar] [CrossRef]
- Friedmann, A. Über die Krümmung des Raumes. Z. Phys. 1922, 10, 377–386. [Google Scholar]
- Friedmann, A. On the Curvature of Space. Gen. Relativ. Gravit. 1999, 31, 1991. [Google Scholar] [CrossRef]
- Tolman, R.C. Effect of Inhomogeneity on Cosmological Models. Proc. Natl. Acad. Sci. USA 1934, 20, 169–176. [Google Scholar] [PubMed]
- Oppenheimer, J.R.; Snyder, H. On Continued Gravitational Contraction. Phys. Rev. 1939, 56, 455–459. [Google Scholar] [CrossRef] [Green Version]
- Faraoni, V.; Atieh, F. Turning a Newtonian analogy for FLRW cosmology into a relativistic problem. PRD 2020, 102, 044020. [Google Scholar] [CrossRef]
- Johansen, N.; Ravndal, F. On the discovery of Birkhoff’s theorem. Gen. Relativ. Gravit. 2006, 38, 537–540. [Google Scholar]
- Vaidya, P.C. Nonstatic Analogs of Schwarzschild’s Interior Solution in General Relativity. Phys. Rev. 1968, 174, 1615–1619. [Google Scholar] [CrossRef]
- Hayward, S.A. Gravitational energy in spherical symmetry. Phys. Rev. D 1996, 53, 1938–1949. [Google Scholar]
- Faraoni, V.; Giusti, A.; Bean, T.F. Asymptotic flatness and Hawking quasilocal mass. PRD 2021, 103, 044026. [Google Scholar]
- Israel, W. Singular hypersurfaces and thin shells in general relativity. Nuovo Cimento B Ser. 1967, 48, 463. [Google Scholar]
- Barrabès, C.; Israel, W. Thin shells in general relativity and cosmology: The lightlike limit. PRD 1991, 43, 1129–1142. [Google Scholar] [CrossRef]
- Crisostomo, J.; Olea, R. Hamiltonian treatment of the gravitational collapse of thin shells. Phys. Rev. D 2004, 69, 104023. [Google Scholar] [CrossRef]
- Dodelson, S. Modern Cosmology; Academic Press: New York, NY, USA, 2003. [Google Scholar]
- Gaztañaga, E. The size of our causal Universe. MNRAS 2020, 494, 2766–2772. [Google Scholar] [CrossRef]
- Gaztañaga, E. The cosmological constant as a zero action boundary. MNRAS 2021, 502, 436–444. [Google Scholar]
- Parattu, K.; Chakraborty, S.; Majhi, B.R.; Padmanabhan, T. A boundary term for the gravitational action with null boundaries. Gen. Relativ. Gravit. 2016, 48, 94. [Google Scholar] [CrossRef]
- Ellis, G.F.R.; Rothman, T. Lost horizons. Am. J. Phys. 1993, 61, 883–893. [Google Scholar] [CrossRef]
- Melia, F. The apparent (gravitational) horizon in cosmology. Am. J. Phys. 2018, 86, 585–593. [Google Scholar]
- Kaloper, N.; Kleban, M.; Martin, D. McVittie’s legacy: Black holes in an expanding universe. PRD 2010, 81, 104044. [Google Scholar] [CrossRef]
- Pathria, R.K. The Universe as a Black Hole. Nature 1972, 240, 298–299. [Google Scholar] [CrossRef]
- Zhang, T.X. The Principles and Laws of Black Hole Universe. J. Mod. Phys. 2018, 9, 1838–1865. [Google Scholar] [CrossRef] [Green Version]
- Smolin, L. The Life of the Cosmos; Oxford University Press: Oxford, UK, 1997. [Google Scholar]
- Easson, D.A.; Brandenberger, R.H. Universe generation from black hole interiors. J. High Energy Phy. 2001, 2001, 024. [Google Scholar] [CrossRef]
- Daghigh, R.G.; Kapusta, J.I.; Hosotani, Y. False Vacuum Black Holes and Universes. arXiv 2000, arXiv:gr-qc/0008006. [Google Scholar]
- Firouzjahi, H. Primordial Universe Inside the Black Hole and Inflation. arXiv 2016, arXiv:1610.03767. [Google Scholar]
- Oshita, N.; Yokoyama, J. Creation of an inflationary universe out of a black hole. Phys. Lett. B 2018, 785, 197–200. [Google Scholar] [CrossRef]
- Dymnikova, I. Universes Inside a Black Hole with the de Sitter Interior. Universe 2019, 5, 111. [Google Scholar] [CrossRef]
- Grøn, Ø.; Soleng, H.H. Dynamical instability of the González-Díaz black hole model. Phys. Lett. A 1989, 138, 89–94. [Google Scholar] [CrossRef]
- Blau, S.K.; Guendelman, E.I.; Guth, A.H. Dynamics of false-vacuum bubbles. PRD 1987, 35, 1747–1766. [Google Scholar] [CrossRef]
- Frolov, V.P.; Markov, M.A.; Mukhanov, V.F. Through a black hole into a new universe? Phys Lett. B 1989, 216, 272–276. [Google Scholar] [CrossRef]
- Aguirre, A.; Johnson, M.C. Dynamics and instability of false vacuum bubbles. PRD 2005, 72, 103525. [Google Scholar] [CrossRef]
- Garriga, J.; Vilenkin, A.; Zhang, J. Black holes and the multiverse. JCAP 2016, 2016, 064. [Google Scholar] [CrossRef]
- Gonzalez-Diaz, P.F. The space-time metric inside a black hole. Nuovo Cimento Lett. 1981, 32, 161–163. [Google Scholar] [CrossRef]
- Shen, W.; Zhu, S.T. Junction conditions on null hypersurface. Phys. Lett. A 1988, 126, 229–232. [Google Scholar]
- Poisson, E.; Israel, W. Structure of the black hole nucleus. Class. Quantum Gravity 1988, 5, L201–L205. [Google Scholar] [CrossRef]
- Penrose, R. Gravitational Collapse and Space-Time Singularities. Phys. Rev. Lett. 1965, 14, 57–59. [Google Scholar] [CrossRef]
- Dadhich, N. Singularity: Raychaudhuri equation once again. Pramana 2007, 69, 23. [Google Scholar] [CrossRef]
- Good, I.J. Chinese universes. Phys. Today 1972, 25, 15. [Google Scholar] [CrossRef]
- Knutsen, H. The idea of the universe as a black hole revisited. Gravit. Cosmol. 2009, 15, 273–277. [Google Scholar] [CrossRef]
- Stuckey, W.M. The observable universe inside a black hole. Am. J. Phys. 1994, 62, 788–795. [Google Scholar] [CrossRef]
- Popławski, N. Universe in a Black Hole in Einstein-Cartan Gravity. ApJ 2016, 832, 96. [Google Scholar] [CrossRef]
- Secrest, N.J.; von Hausegger, S.; Rameez, M.; Mohayaee, R.; Sarkar, S.; Colin, J. A Test of the Cosmological Principle with Quasars. ApJL 2021, 908, L51. [Google Scholar] [CrossRef]
- Moss, A.; Zibin, J.P.; Scott, D. Precision cosmology defeats void models for acceleration. Phys. Rev. D 2011, 83, 103515. [Google Scholar] [CrossRef]
- Fosalba, P.; Gaztañaga, E. Explaining cosmological anisotropy: Evidence for causal horizons from CMB data. MNRAS 2021, 504, 5840–5862. [Google Scholar] [CrossRef]
- Gaztañaga, E.; Fosalba, P. A peek outside our Universe. Symmetry 2022, 14, 285. [Google Scholar] [CrossRef]
- Yeung, S.; Chu, M.C. Directional Variations of Cosmological Parameters from the Planck CMB Data. arXiv 2022, arXiv:2201.03799. [Google Scholar] [CrossRef]
- Camacho, B.; Gaztañaga, E. A measurement of the scale of homogeneity in the Early Universe. arXiv 2021, arXiv:2106.14303. [Google Scholar]
- Gaztañaga, E. How the Big Bang Ends up Inside a Black Hole. Universe 2022, 8, 257. [Google Scholar] [CrossRef]
- Gaztanaga, E.; Camacho-Quevedo, B. Super-Horizon modes and cosmic expansion. arXiv 2022, arXiv:astro-ph.CO/2204.10728. [Google Scholar]
- Abdalla, E.; Abellán, G.F.; Aboubrahim, A.; Agnello, A.; Akarsu, Ö.; Akrami, Y.; Pettorino, V. Cosmology Intertwined: A Review of the Particle Physics, Astrophysics, and Cosmology Associated with the Cosmological Tensions and Anomalies. arXiv 2022, arXiv:2203.06142. [Google Scholar]
- O’Raifeartaigh, C.; Mitton, S. A new perspective on steady-state cosmology. arXiv 2015, arXiv:1506.01651. [Google Scholar]
- Bondi, H.; Gold, T. The Steady-State Theory of the Expanding Universe. MNRAS 1948, 108, 252. [Google Scholar] [CrossRef]
- Hoyle, F. A New Model for the Expanding Universe. MNRAS 1948, 108, 372. [Google Scholar] [CrossRef]
- Gaztañaga, E. Inside a Black Hole: The Illusion of a Big Bang. 2020. Available online: https://hal.archives-ouvertes.fr/hal-03106344 (accessed on 11 January 2021).
- Gaztañaga, E. The Black Hole Universe (BHU) from a FLRW Cloud. 2021. Available online: https://hal.archives-ouvertes.fr/hal-03344159 (accessed on 14 September 2021).
- Gaztañaga, E. The Cosmological Constant as Event Horizon. Symmetry 2022, 14, 300. [Google Scholar]
- Hilbert, D. Die Grundlage der Physick. Konigl. Gesell. D. Wiss. Göttingen Math-Phys K 1915, 3, 395–407. [Google Scholar]
- Weinberg, S. Gravitation and Cosmology; John Wiley & Sons: Hoboken, NJ, USA, 1972. [Google Scholar]
- Weinberg, S. Cosmology; Oxford University Press: Oxford, UK, 2008. [Google Scholar]
- Einstein, A. Die Grundlage der allgemeinen Relativitätstheorie. Ann. Der Phys. 1916, 354, 769–822. [Google Scholar]
- Landau, L.D.; Lifshitz, E.M. The Classical Theory of Fields; Elsevier: Amsterdam, The Netherlands, 1971. [Google Scholar]
- Carroll, S.M. Spacetime and Geometry; Addison-Wesley: Boston, MA, USA, 2004. [Google Scholar]
- York, J.W. Role of Conformal Three-Geometry in the Dynamics of Gravitation. PRL 1972, 28, 1082–1085. [Google Scholar]
- Gibbons, G.W.; Hawking, S.W. Cosmological event horizons, thermodynamics, and particle creation. PRD 1977, 15, 2738–2751. [Google Scholar]
- Hawking, S.W.; Horowitz, G.T. The gravitational Hamiltonian, action, entropy and surface terms. Cl. Quantum Gravity 1996, 13, 1487. [Google Scholar] [CrossRef]
- Tolman, R.C. Relativity, Thermodynamics, and Cosmology; Dover Publications: New York, NY, USA, 1934. [Google Scholar]
- Diez-Tejedor, A.; Feinstein, A. Homogeneous scalar field the wet dark sides of the universe. PRD 2006, 74, 023530. [Google Scholar] [CrossRef]
- Lanczos, K. Bemerkung zur de Sitterschen Welt. Phys. Z. 1922, 23, 539–543. [Google Scholar]
- Mitra, A. Interpretational conflicts between the static and non-static forms of the de Sitter metric. Nat. Sci. Rep. 2012, 2, 923. [Google Scholar] [CrossRef] [Green Version]
- Lanczos, K.; Hoenselaers, C. On a Stationary Cosmology in the Sense of Einstein’s Theory of Gravitation [1923]. GR Gravit. 1997, 29, 361–399. [Google Scholar]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gaztanaga, E. The Black Hole Universe, Part I. Symmetry 2022, 14, 1849. https://doi.org/10.3390/sym14091849
Gaztanaga E. The Black Hole Universe, Part I. Symmetry. 2022; 14(9):1849. https://doi.org/10.3390/sym14091849
Chicago/Turabian StyleGaztanaga, Enrique. 2022. "The Black Hole Universe, Part I" Symmetry 14, no. 9: 1849. https://doi.org/10.3390/sym14091849






