Gas-Solid Heat Transfer Computation from Particle-Resolved Direct Numerical Simulations
Abstract
:1. Introduction
2. Numerical Methodology
2.1. Viscous Penalty Method
| Algorithm 1: Augmented Lagrangian (AL) method [27] |
|
2.2. Heat Transfer Rate Computation
3. Convective Heat Transfer Forced by a Uniform Flow around a Stationary Sphere
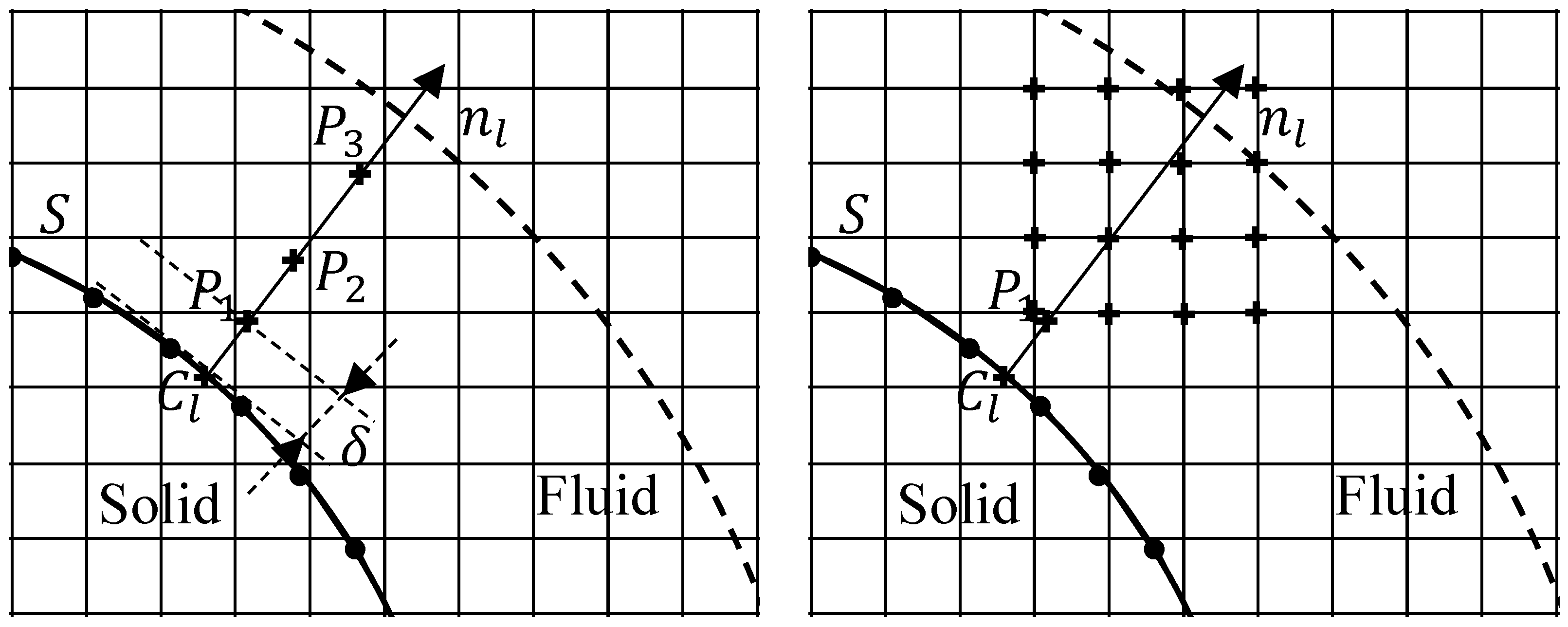
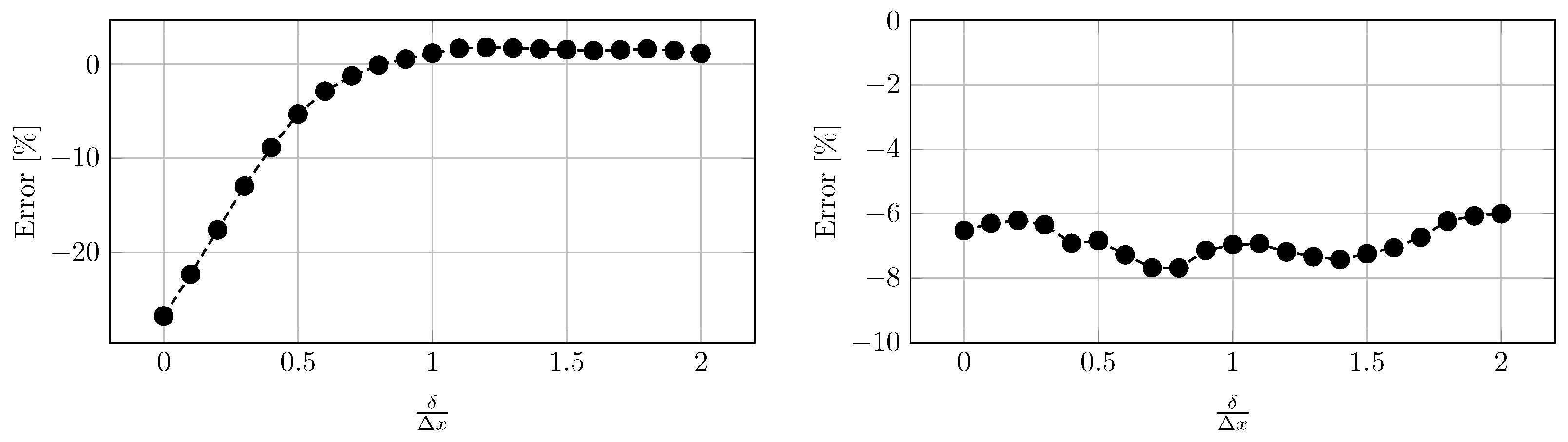
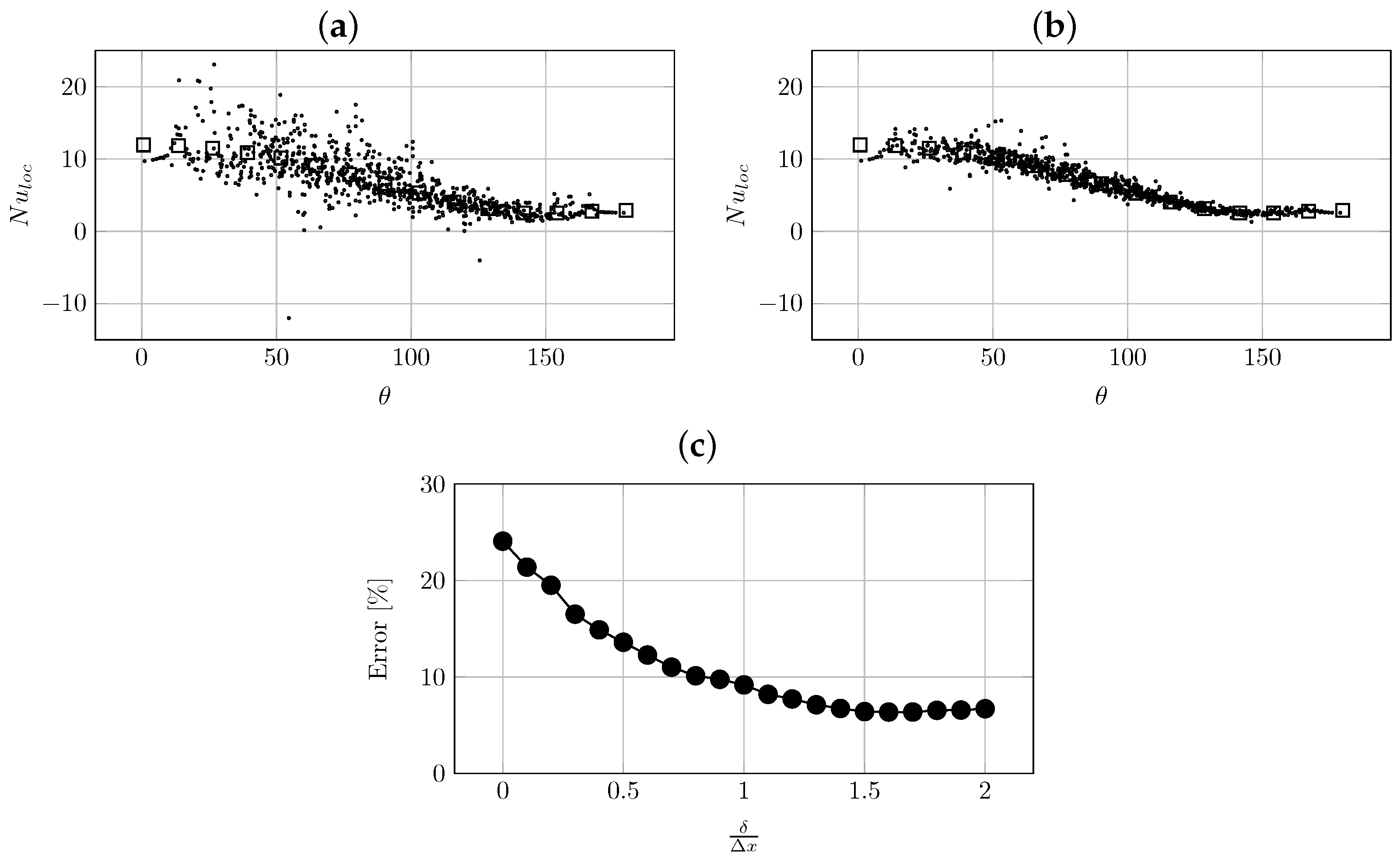
3.1. Effect of the Extrapolation Distance
3.2. Result on the Nusselt Coefficient
4. Face-Centered Cubic Periodic Arrangement of Spheres
4.1. Flow Analysis
4.1.1. Attached Flows
4.1.2. Separated Flows Downstream of the Spheres
4.2. Global Nusselt Coefficient
5. Finite Size Random Arrangement of Spheres
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Bagheri, G.; Bonadonna, C.; Manzella, I.; Vonlanthen, P. On the characterization of size and shape of irregular particles. Powder Technol. 2015, 270, 141–153. [Google Scholar] [CrossRef]
- Dartevelle, S. From Model Conception to Verification and Validation, a Global Approach to Multiphase Navier-Stoke Models with an Emphasis on Volcanic Explosive Phenomenology. Technical Report LA-14346, 948564; 2007. Available online: https://permalink.lanl.gov/object/tr?what=info:lanl-repo/lareport/LA-14346 (accessed on 9 September 2021).
- Adanez, J.; Abad, A.; Garcia-Labiano, F.; Gayan, P.; de Diego, L.F. Progress in Chemical-Looping Combustion and Reforming technologies. Prog. Energy Combust. Sci. 2012, 38, 215–282. [Google Scholar] [CrossRef] [Green Version]
- Lyngfelt, A.; Leckner, B.; Mattisson, T. A fuidized-bed combustion process with inherent CO2 separation; application of chemical-looping combustion. Chem. Eng. Sci. 2001, 56, 3101–3113. [Google Scholar] [CrossRef]
- Mattisson, T.; Keller, M.; Linderholm, C.; Moldenhauer, P.; Rydan, M.; Leion, H.; Lyngfelt, A. Chemical-looping technologies using circulating fluidized bed systems: Status of development. Fuel Process. Technol. 2018, 172, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Acrivos, A.; Hinch, E.J.; Jeffrey, D.J. Heat transfer to a slowly moving fluid from a dilute fixed bed of heated spheres. J. Fluid Mech. 1980, 101, 403–421. [Google Scholar] [CrossRef] [Green Version]
- Pfeffer, R.; Happel, J. An analytical study of heat and mass transfer in multiparticle systems at low Reynolds numbers. AIChE J. 1964, 10, 605–611. [Google Scholar] [CrossRef]
- Wakao, N.; Kaguei, S. Heat and Mass Transfer in Packed Beds Volume 1; Gordon and Breach Science Publishers Inc.: New York, NY, USA, 1983. [Google Scholar]
- Vincent, S.; de Motta, J.C.B.; Sarthou, A.; Estivalezes, J.L.; Simonin, O.; Climent, E. A Lagrangian VOF tensorial penalty method for the DNS of resolved particle-laden flows. J. Compuat. Phys. 2014, 256, 582–614. [Google Scholar] [CrossRef] [Green Version]
- Massol, A. Simulations Numériques d’écoulements à Travers des réseaux Fixes de Spheres Monodisperses et Bidisperses, Pour des Nombres de Reynolds Modérés. Ph.D. Thesis, Institut National Polytechnique de Toulouse, Toulouse, France, 2004. Available online: https://www.researchgate.net/publication/242075914_Adaptive_Augmented_Lagrangian_techniques_for_simulating_unsteady_multiphase_flows (accessed on 9 September 2021).
- Schönfeld, T.; Rudgyard, M. Steady and Unsteady Flow Simulations Using the Hybrid Flow Solver AVBP. AIAA J. 1999, 37, 1378–1385. [Google Scholar] [CrossRef]
- Deen, N.G.; Kriebitzsch, S.H.; van der Hoef, M.A.; Kuipers, J. Direct numerical simulation of flow and heat transfer in dense fluid–particle systems. Chem. Eng. Sci. 2012, 81, 329–344. [Google Scholar] [CrossRef]
- Tavassoli, H.; Kriebitzsch, S.; van der Hoef, M.; Peters, E.; Kuipers, J. Direct numerical simulation of particulate flow with heat transfer. Int. J. Multiph. Flow 2013, 57, 29–37. [Google Scholar] [CrossRef]
- Gunn, D. Transfer of heat or mass to particles in fixed and fluidized beds. Int. J. Heat Mass Transf. 1978, 21, 467–476. [Google Scholar] [CrossRef]
- Tenneti, S.; Sun, B.; Garg, R.; Subramaniam, S. Role of fluid heating in dense gas-solid flow as revealed by particle-resolved direct numerical simulation. Int. J. Heat Mass Transf. 2013, 58, 471–479. [Google Scholar] [CrossRef]
- Deen, N.G.; Peters, E.A.J.F.; Padding, J.T.; Kuipers, J.A.M. Review of direct numerical simulation of fluid-particle mass, momentum and heat transfer in dense gas-solid flows. Chem. Eng. Sci. 2014, 116, 710–724. [Google Scholar] [CrossRef]
- Sun, B.; Tenneti, S.; Subramaniam, S. Modeling average gas–solid heat transfer using particle-resolved direct numerical simulation. Int. J. Heat Mass Transf. 2015, 86, 898–913. [Google Scholar] [CrossRef] [Green Version]
- Thiam, E.I.; Masi, E.; Climent, E.; Simonin, O.; Vincent, S. Particle-resolved numerical simulations of the gas–solid heat transfer in arrays of random motionless particles. Acta Mech. 2019, 230, 541–567. [Google Scholar] [CrossRef] [Green Version]
- Chadil, M.A.; Vincent, S.; Estivalèzes, J.L. Accurate estimate of drag forces using particle-resolved direct numerical simulations. Acta Mech. 2018, 230, 569–595. [Google Scholar] [CrossRef] [Green Version]
- Kataoka, I. Local instant formulation of two-phase flow. Int. J. Multiph. Flow 1986, 12, 745–758. [Google Scholar] [CrossRef]
- Kataoka, I.; Ishii, M.; Serizawa, A. Local formulation and measurements of interfacial area concentration in two-phase flow. Int. J. Multiph. Flow 1986, 12, 505–529. [Google Scholar] [CrossRef]
- Chadil, M.A.; Vincent, S.; Estivalezes, J.L. Improvement of the Viscous Penalty Method for Particle-Resolved Simulations. Open J. Fluid Dyn. 2019, 09, 168–192. [Google Scholar] [CrossRef] [Green Version]
- Glowinski, R.; Pan, T.W.; Hesla, T.I.; Joseph, D.; Périaux, J. A fictitious domain approach to the direct numerical simulation of incompressible viscous flow past moving rigid bodies: application to particulate flow. J. Comput. Phys. 2001, 169, 363–426. [Google Scholar] [CrossRef] [Green Version]
- Khadra, K.; Angot, P.; Parneix, S.; Caltagirone, J. Fictitious domain approach for numerical modelling of Navier-Stokes equations. Int. J. Numer. Methods Fluids 2000, 34, 651–684. [Google Scholar] [CrossRef]
- Hirt, C.W.; Nichols, B.D. Volume of fluid (VOF) method for the dynamics of free boundaries. J. Comput. Phys. 1981, 39, 201–225. [Google Scholar] [CrossRef]
- Caltagirone, J.P.; Vincent, S. Tensorial penalisation method for solving Navier–Stokes equations. Comptes Rendus De L’académie Des Sci. Paris Série IIb 2001, 329, 607–613. [Google Scholar]
- Vincent, S.; Larocque, J.; Lubin, P.; Caltagirone, J.P.; Pianet, G.; Climent, E. Adaptive Augmented Lagrangian Techniques for Simulating Unsteady Multiphase Flows. In Proceedings of the 6th International Conference on Multiphase Flow, ICMF 2007, Leipzig, Germany, 9–13 July 2007. [Google Scholar]
- Gustafsson, I. On First- and Second-Order Symmetric Factorisation Methods for the Solution of Elliptic Difference Equations; Chalmers University of Technology: Gothenburg, Sweden, 1978. [Google Scholar]
- der Vost, H.V. Bi-CGSTAB: A fast and smoothly converging variant of Bi-CG for the solution of non-symmetric systems. SIAM J. Sci. Comput. 1992, 33, 631–644. [Google Scholar] [CrossRef]
- Schiller, L.; Naumann, A.Z. Über die grundlegenden Berechnungen bei der Schwerkraftaufbereitung. Ver. Deut. Ing. 1933, 77, 318–320. [Google Scholar]
- Ranz, W.E.; Marshall, W.R. Evaporation from drops. Parts I & II. Chem. Eng. Progr. 1952, 48, 141–146. [Google Scholar]
- Feng, Z.G.; Michaelides, E.E. A numerical study on the transient heat transfer from a sphere at high Reynolds and Peclet numbers. Int. J. Heat Mass Transf. 2000, 43, 219–229. [Google Scholar] [CrossRef]
- Whitaker, S. Forced convection heat transfer correlations for flow in pipes, past flat plates, single cylinders, single spheres, and for flow in packed beds and tube bundles. AIChE J. 1972, 18, 361–371. [Google Scholar] [CrossRef]



 ) Ranz and Marshall [31], (
) Ranz and Marshall [31], (  ) Feng and Michaelides [32], (
) Feng and Michaelides [32], (  ) Whitaker [33], (•) present work.
) Whitaker [33], (•) present work.


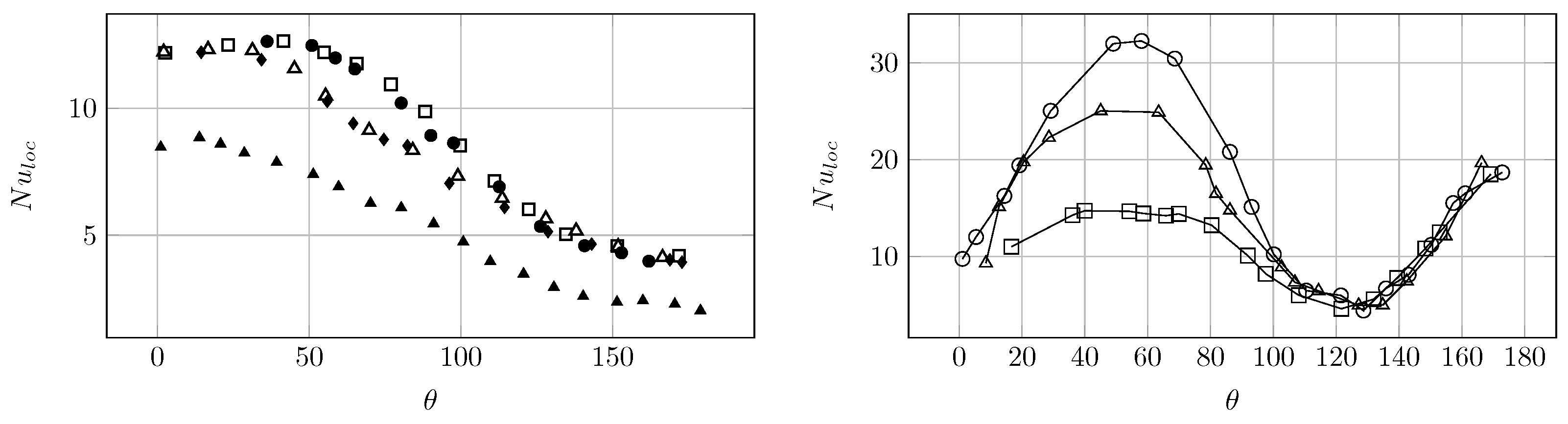
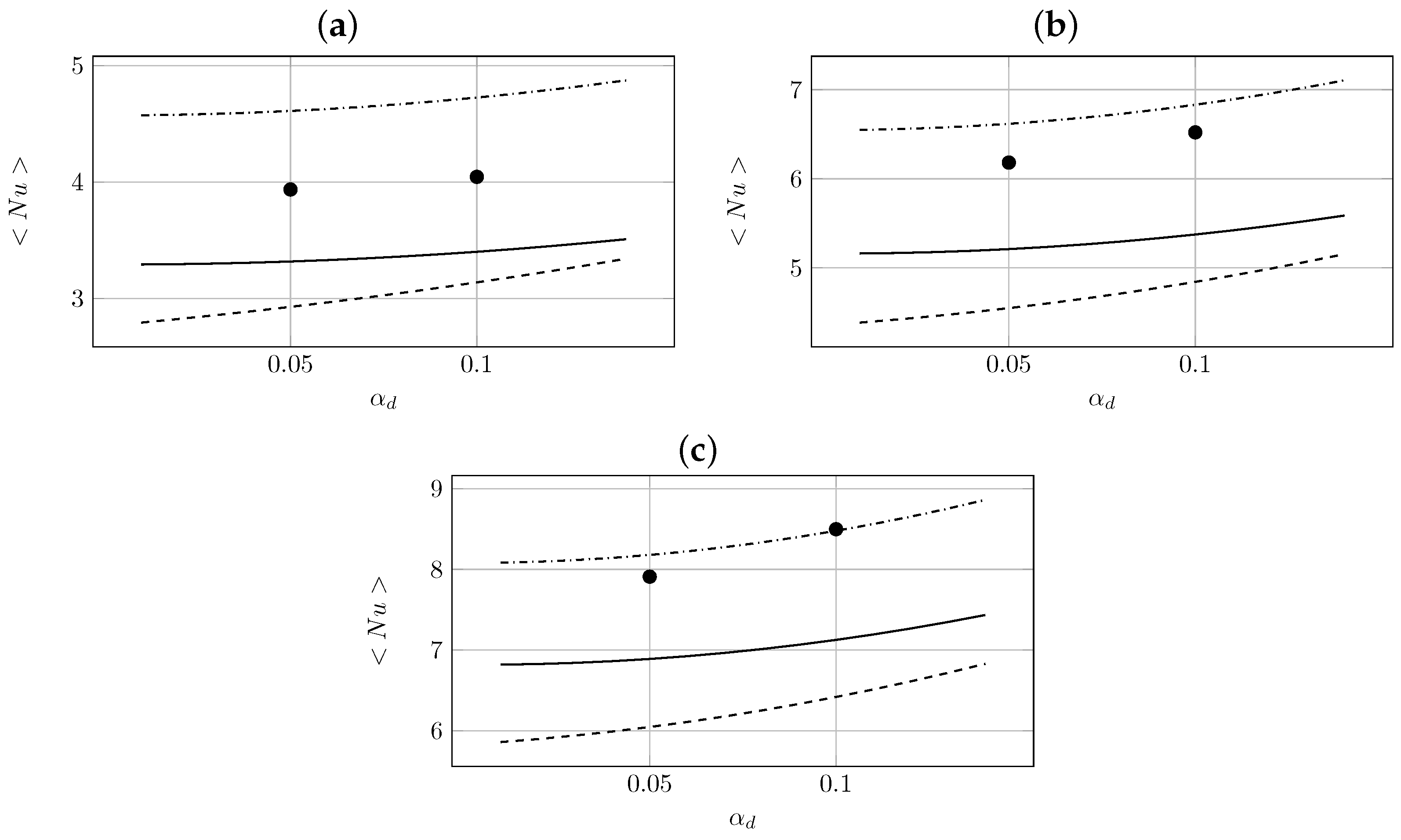
 ) Gunn [14], (□) Massol [10], (•) present work.
) Gunn [14], (□) Massol [10], (•) present work.

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chadil, M.-A.; Vincent, S.; Estivalèzes, J.-L. Gas-Solid Heat Transfer Computation from Particle-Resolved Direct Numerical Simulations. Fluids 2022, 7, 15. https://doi.org/10.3390/fluids7010015
Chadil M-A, Vincent S, Estivalèzes J-L. Gas-Solid Heat Transfer Computation from Particle-Resolved Direct Numerical Simulations. Fluids. 2022; 7(1):15. https://doi.org/10.3390/fluids7010015
Chicago/Turabian StyleChadil, Mohamed-Amine, Stéphane Vincent, and Jean-Luc Estivalèzes. 2022. "Gas-Solid Heat Transfer Computation from Particle-Resolved Direct Numerical Simulations" Fluids 7, no. 1: 15. https://doi.org/10.3390/fluids7010015