Numerical Study of Bamboo Breakwater for Wave Reduction
Abstract
:1. Introduction
1.1. Permeable Structures
1.2. Introduction of the SPH Method
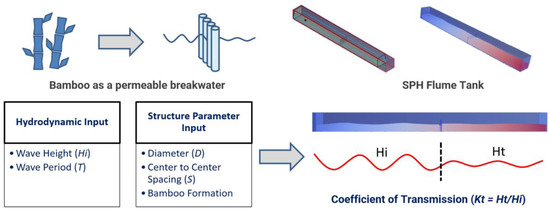
2. Material and Methods
2.1. Experimental Setup
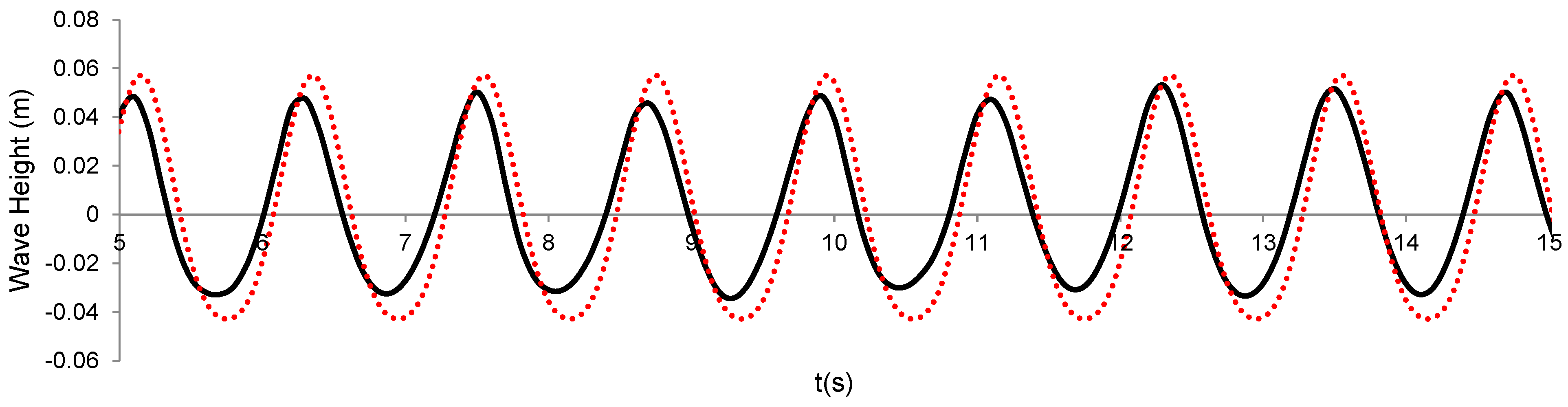
2.2. Validation
3. Result and Discussion
3.1. Wave Steepness
3.2. Wave Height
3.3. Wave Period
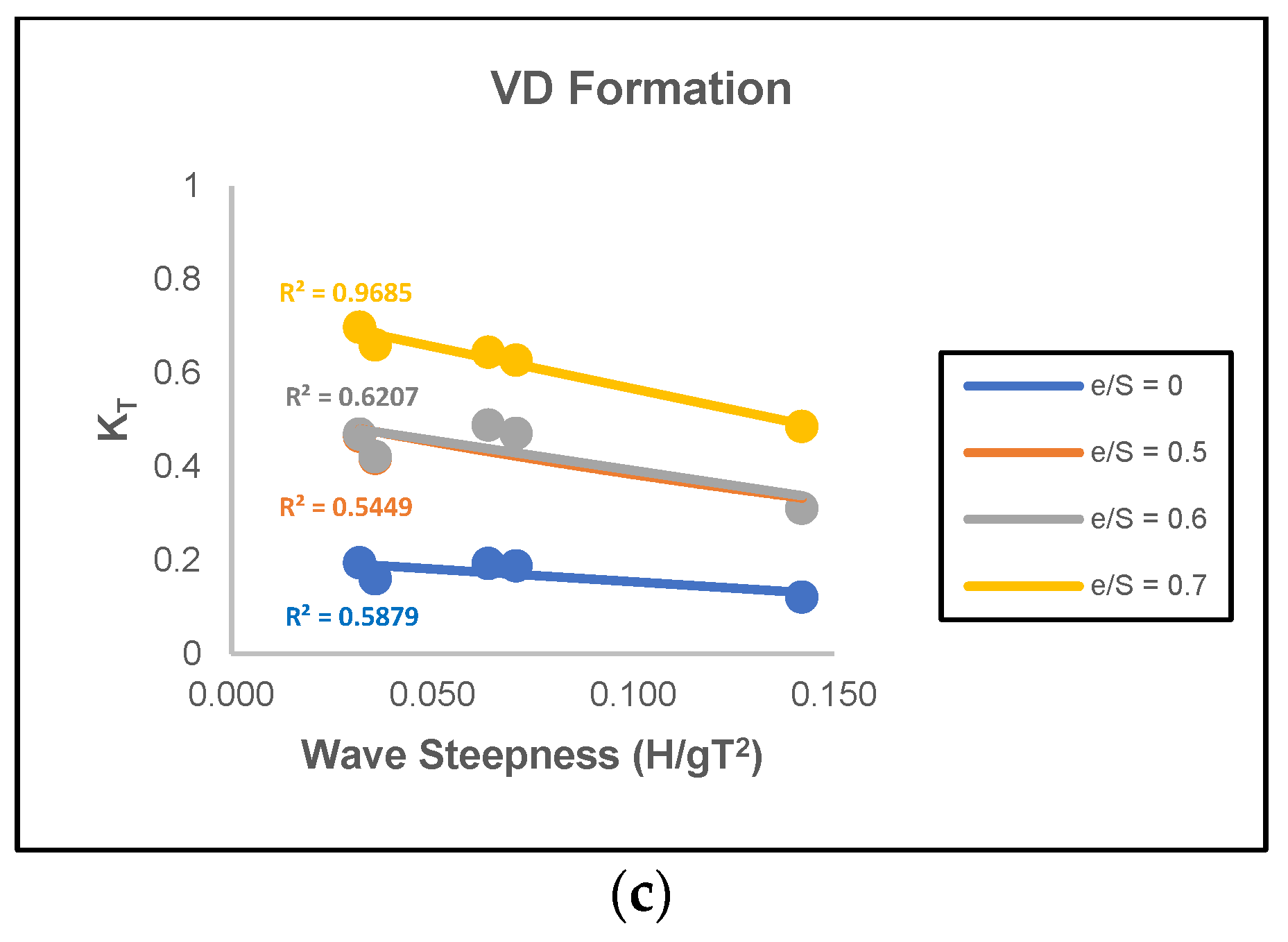
3.4. Ratio of e/S
3.5. Bamboo Diameter (D)
3.6. Center-to-Center Spacing (S)
3.7. Formation of Bamboo Poles
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Buchori, I.; Sugiri, A.; Mussadun, M.; Wadley, D.; Liu, Y.; Pramitassari, A.; Pamungkas, I.T.D. A predictive model to assess spatial planning in addressing hydro-meteorological hazards: A case study of Semarang City, Indonesia. Int. J. Disaster Risk Reduct. 2017, 27, 415–426. [Google Scholar] [CrossRef]
- Bilskie, M.V.; Hagen, S.C.; Medeiros, S.C.; and Passeri, D.L. Dynamics of sea level rise and coastal flooding on a changing landscape. Geophys. Res. Lett. 2014, 41, 927–934. [Google Scholar] [CrossRef]
- Intergovernmental Panel on Climate Change. Sea Level Change. In Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2013; pp. 1137–1216. [Google Scholar] [CrossRef]
- Djalante, R. Key assessments from the IPCC special report on global warming of 1.5 °C and the implications for the Sendai framework for disaster risk reduction. Prog. Disaster Sci. 2019, 1, 100001. [Google Scholar] [CrossRef]
- Muskananfola, M.R.; Supriharyono, S.; Febrianto, S. Spatio-temporal analysis of shoreline change along the coast of Sayung Demak, Indonesia using Digital Shoreline Analysis System. Reg. Stud. Mar. Sci. 2020, 34, 1–9. [Google Scholar] [CrossRef]
- Winterwerp, J.C.; Erftemeijer, P.L.A.; Suryadiputra, N.; van Eijk, P.; Zhang, L. Defining Eco-Morphodynamic Requirements for Rehabilitating Eroding Mangrove-Mud Coasts. Wetlands 2013, 33, 515–526. [Google Scholar] [CrossRef]
- Schmitt, K.; Albers, Y. Area Coastal Protection and the Use of Bamboo Breakwaters in the Mekong Delta. In Coastal Disasters and Climate Change in Vietnam: Engineering and Planning Perspectives; Thao, N.D., Takagi, H., Esteban, M., Eds.; Elsevier Inc.: London, UK, 2014; pp. 107–132. [Google Scholar]
- van Loon-Steensma, J.M.; Schelfhout, H.A. Wide Green Dikes: A sustainable adaptation option with benefits for both nature and landscape values? Land Use Policy 2017, 63, 528–538. [Google Scholar] [CrossRef]
- Temmerman, S.; Meire, P.; Bouma, T.J.; Herman, P.M.J.; Ysebaert, T.; De Vriend, H.J. Ecosystem-based coastal defence in the face of global change. Nature 2013, 504, 79–83. [Google Scholar] [CrossRef]
- Salem, M.E.; Mercer, D.E. The Economic Value of Mangroves: A Meta-Analysis. Sustainability 2012, 4, 359–383. [Google Scholar] [CrossRef] [Green Version]
- Johnson, M. Coastline Stability Restoration: Bamboo Poles and Fences’ Wave Attenuation Efficiency Analysis. Bachelor’s Thesis, Civil Engineering, HZ University, Vlissingen, The Netherlands, 2018. [Google Scholar]
- Sollitt, C.K.; Cross, R.H. Wave Transmission through Permeable Breakwaters. In Proceedings of the 13th Coastal Engineering Conference, Vancouver, Canada, 10–14 July 1972; Morrough, P.O., Ed.; ASCE: Reston, VA, USA, 1973; Volume 103, pp. 1827–1846. [Google Scholar] [CrossRef]
- Karim, M.F.; Tanimoto, K.; Hieu, P.D. Simulation of wave transformation in vertical permeable structure. Int. J. Offshore Polar Eng. 2004, 14, 89–96. [Google Scholar]
- Dao, T.; Stive, M.J.F.; Hofland, B.; Mai, T. Wave Damping due to Wooden Fences along Mangrove Coasts. J. Coast. Res. 2018, 34, 1317–1327. [Google Scholar] [CrossRef]
- Quang, T.T.; Trong, L.M. Monsoon wave transmission at bamboo fences protecting mangroves in the lower mekong delta. Appl. Ocean Res. 2020, 101, 102259. [Google Scholar] [CrossRef]
- Rao, S.; Rao, N.B.S.; Sathyanarayana, V.S. Laboratory investigation on wave transmission through two rows of perforated hollow piles. Ocean Eng. 1999, 26, 675–699. [Google Scholar] [CrossRef]
- Gingold, R.A.; Monaghan, J.J. Smoothed particle hydrodynamics: Theory and application to non-spherical stars. Mon. Not. R. Astron. Soc. 1977, 181, 375–389. [Google Scholar] [CrossRef]
- Lucy, L.B. A numerical approach to the testing of the fission hypothesis. Astron. J. 1977, 82, 1013–1024. [Google Scholar] [CrossRef]
- Lind, S.J.; Rogers, B.D.; Stansby, P.K. Review of smoothed particle hydrodynamics: Towards converged Lagrangian flow modelling. Proc. R. Soc. A Math. Phys. Eng. Sci. 2020, 476, 20190801. [Google Scholar] [CrossRef] [PubMed]
- Ni, X.; Feng, W.; Huang, S.; Zhang, Y.; Feng, X. A SPH numerical wave flume with non-reflective open boundary conditions. Ocean Eng. 2018, 163, 483–501. [Google Scholar] [CrossRef]
- Crespo, A.J.C.; Domínguez, J.M.; Rogers, B.D.; Gómez-Gesteira, M.; Longshaw, S.; Canelas, R.; Vacondio, R.; Barreiro, A.; García-Feal, O. DualSPHysics: Open-source parallel CFD solver based on Smoothed Particle Hydrodynamics (SPH). Comput. Phys. Commun. 2015, 187, 204–216. [Google Scholar] [CrossRef]
- Gomez-Gesteira, M.; Rogers, B.D.; Dalrymple, R.A.; Crespo, A.J.C. State-of-the-art of classical SPH for free-surface flows. J. Hydraul. Res. 2010, 48 (Suppl. S1), 6–27. [Google Scholar] [CrossRef]
- Neves, D.R.C.B.; Pires-Silva, A.A.; Fortes, C.J.E.M.; Matos, J.J.G. A comparison of wave breaking with RANS and SPH numerical models. In Proceedings of the 26th International Ocean and Polar Engineering Conference, Rhodes, Greece, 26 June–2 July 2016; pp. 1182–1189. [Google Scholar]
- Altomare, C.; Domínguez, J.M.; Crespo, A.J.C.; González-Cao, J.; Suzuki, T.; Gómez-Gesteira, M.; Troch, P. Long-crested wave generation and absorption for SPH-based DualSPHysics model”. Coast. Eng. 2017, 127, 37–54. [Google Scholar] [CrossRef]
- Monaghan, J.J. Smoothed Particle Hydrodynamics. Rep. Progess Phys. 2005, 68, 1703–1759. [Google Scholar] [CrossRef]
- Altomare, C.; Crespo, A.J.C.; Rogers, B.D.; Domínguez, J.M.; Gironella, X.; Gómez-Gesteira, M. Numerical modelling of armour block sea breakwater with smoothed particle hydrodynamics. Comput. Struct. 2014, 130, 34–45. [Google Scholar] [CrossRef]
- Domínguez, J.M.; Crespo, A.J.C.; Gómez-Gesteira, M. Optimization strategies for CPU and GPU implementations of a smoothed particle hydrodynamics method. Comput. Phys. Commun. 2013, 184, 617–627. [Google Scholar] [CrossRef]
- Dalrymple, R.A.; Rogers, B.D. Numerical modeling of water waves with the SPH method. Coast. Eng. 2006, 53, 141–147. [Google Scholar] [CrossRef]
- Crespo, A.J.; Gómez-Gesteira, M.; Dalrymple, R.A. Modeling Dam Break Behavior over a Wet Bed by a SPH Technique. J. Waterw. Port Coast. Ocean Eng. 2008, 134, 313–320. [Google Scholar] [CrossRef]
- Gómez-Gesteira, M.; Dalrymple, R.A. Using a Three-Dimensional Smoothed Particle Hydrodynamics Method for Wave Impact on a Tall Structure. J. Waterw. Port Coast. Ocean Eng. 2004, 130, 63–69. [Google Scholar] [CrossRef]
- Rogers, B.D.; Dalrymple, R.A.; Stansby, P.K. Simulation of caisson breakwater movement using 2-D SPH. J. Hydraul. Res. 2009, 48, 135–141. [Google Scholar] [CrossRef]
- Kamphuis, J.W. Introduction to Coastal Engineering and Management, 2nd ed.; World Scientific: Singapore, 2010; p. 67. [Google Scholar] [CrossRef]
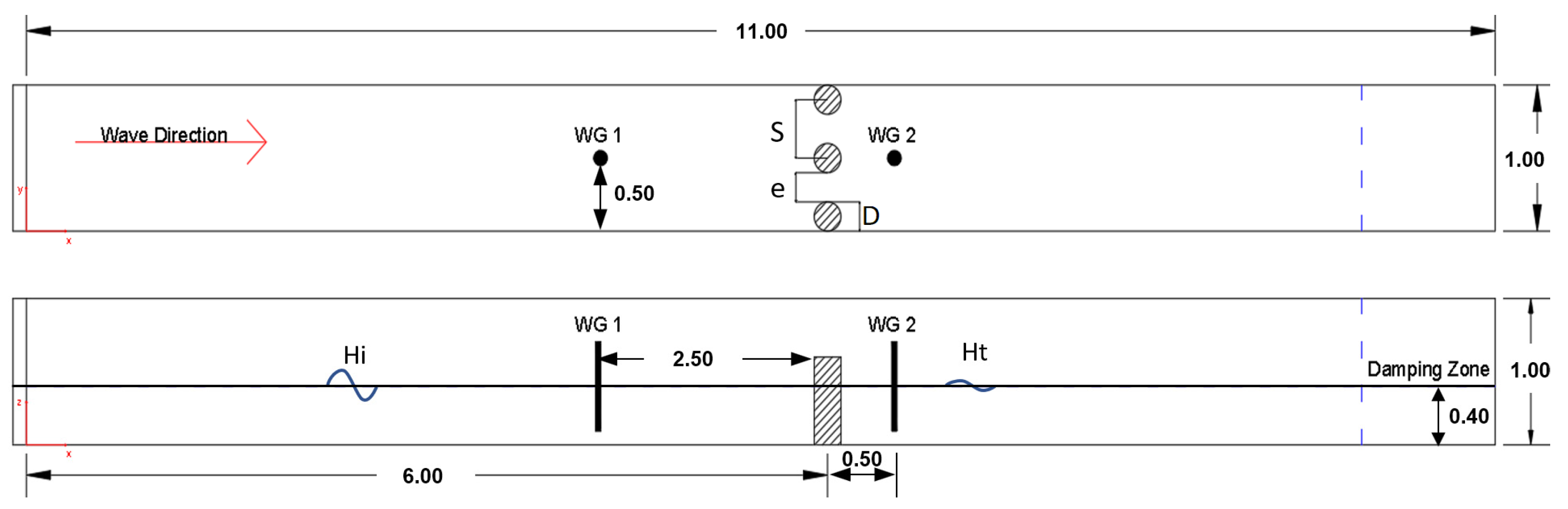





| Diameter D (m) | Wave Height Hi (m) | ||||
| 0.048 | 0.060 | 0.08 | 0.09 | 0.1 | 0.2 |
| Center to Center Spacing S (m) | Wave Period T (m) | ||||
| 0.12 | 0.16 | 1.2 | 1.6 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Armono, H.D.; Bromo, B.H.; Sholihin; Sujantoko. Numerical Study of Bamboo Breakwater for Wave Reduction. Fluids 2022, 7, 14. https://doi.org/10.3390/fluids7010014
Armono HD, Bromo BH, Sholihin, Sujantoko. Numerical Study of Bamboo Breakwater for Wave Reduction. Fluids. 2022; 7(1):14. https://doi.org/10.3390/fluids7010014
Chicago/Turabian StyleArmono, Haryo Dwito, Briangga Herswastio Bromo, Sholihin, and Sujantoko. 2022. "Numerical Study of Bamboo Breakwater for Wave Reduction" Fluids 7, no. 1: 14. https://doi.org/10.3390/fluids7010014
APA StyleArmono, H. D., Bromo, B. H., Sholihin, & Sujantoko. (2022). Numerical Study of Bamboo Breakwater for Wave Reduction. Fluids, 7(1), 14. https://doi.org/10.3390/fluids7010014