1. Introduction
Three common methods for radiolabeling monoclonal antibodies or proteins involve the direct radioiodination of tyrosine residues, the reaction of maleimide with cysteine and the conjugation of activated ester-or isothiocyanate-bearing chelators with lysine. In these cases, it is typically not possible to achieve selective labeling of a specific reaction site (e.g., tyrosine, cysteine or lysine) in the primary structure. This lack of selectivity results in complex heterogeneous mixtures of radiolabeled macromolecules. Often, a site in the complementarity-determining regions (CDRs) of antibodies is radiolabeled, leading to the disruption of the binding affinity. In addition, oxidative damage may occur in the primary structure owing to the reaction conditions or to radiolysis. Since structural similarities make separation impossible by chromatography, the resulting non-immunoreactive impurities are present in the final product. Therefore, quantification of the percentage of immunoreactive radioactive compound relative to the total radioactive mixture is required. This test is an immunoreactivity assay, which is currently a mandatory step in the development of new radiolabeled monoclonal antibodies [
1,
2,
3,
4].
There is no established method for determining the immunoreactive fraction (
r). Ideally,
r is equal to the maximum value of the specifically bindable radioactive antibody, divided by the total radioactivity. Over the years, several methods have been proposed to give an estimate of
r: one-point determination [
5,
6,
7], multi-points assays with concentration variation in antibody [
8], antigen [
9], or both antibody and antigen [
10], saturation assays with excess antigen [
11], or kinetic assays [
12]. Several physical supports for antigens have been used: live or fixed cells in tubes [
6,
11], coated microplates [
13], coated beads [
7,
14], cell membranes on filter plates [
10], and immunoaffinity columns [
15]. Experimentally,
r can be defined as the maximal bound fraction attained [
5,
6,
15]; alternatively, the data points are mathematically processed by extrapolation of the binding isotherm: (i) as a function of antigen [
8,
16], (ii) as a function of radiolabeled antibody [
8,
16], or (iii) by multi-variables iterative computation [
10,
17]. By far, the most commonly used method for the determination of
r is that proposed by Lindmo et al. in 1984, which involves a saturation assay with an excess of antigen followed by data linearization and extrapolation of
r to infinite antigen excess [
11].
To our knowledge, whilst the intricacies of radioimmunoassays describing the pharmacological properties of drugs (i.e.,
KD, IC
50,
koff, etc.) have been extensively discussed [
10,
18,
19,
20,
21], the critical aspects specifically concerning the immunoreactive fraction assay (IRFA) have not been systematically analysed. For example, achieving the necessary dynamic equilibrium is generally taken for granted in IRFA and their low reproducibility is attributed to a lack of sufficient antigen excess [
8,
9,
11,
22]. Furthermore, the poor error management—especially at low bound fractions—resulting from the linear transformation used by Lindmo et al., has not been discussed [
11].
In this paper, we systematically analysed the theoretical basis of an IRFA. After examining the binding curves, the main assumptions, the experimental context, the error propagation, and the kinetics, randomness was introduced to simulate an experimental setting. Our simulation compares two approximate equations for the extrapolation of r and KD, namely the conventional saturation binding curve (rectangular hyperbola) and the Lindmo plot (linear transformation). Examples are given with radiolabeled antibodies displaying slow kinetics. It will become evident that the method of Lindmo et al. leads to chaotic behaviour because of errors amplification at low binding. Instead, we propose a more precise and robust method based on the Langmuir isotherm to obtain the immunoreactive fraction of radioimmunoconjugates from complete binding data. This method will prove more useful for future evaluation of new imaging and theranostic radiopharmaceuticals.
2. Methods
2.1. General Equation from the Law of Mass Action
The simplest model for the binding of an antibody (
Ab) to an antigen (
Ag) postulates monovalent binding [
19]. Then, the antigen-antibody complex 1:1 (
Ag•Ab, also called
B) is the product of the association reaction:
The association reaction follows a rate of second order proportional to the free concentration of antigen and antibody—[
Ag] and [
Ab]—with the association rate constant
kon:
The dissociation of the antigen-antibody complex into starting components is the reverse reaction:
The first order rate for the dissociation of the
B complex depends on the concentration of
B by the dissociation rate constant
koff:
When the dissociation rate of the complex is equal to its association rate, the system is in dynamic equilibrium:
The law of mass action defines the equilibrium dissociation constant (
KD) of the system as follows:
The concentration of the antigen-antibody complex at equilibrium is
If the total applied antibody (
T) contains a non-reactive damaged antibody, only a fraction of
T is immunoreactive. Let
r be the immunoreactive fraction. The concentration of free antibody [
Ab] is the concentration of the total reactive antibody
minus the bound antibody [
B], and
The equation, which is a modification of the Langmuir isotherm, is reorganized as follows:
2.2. Approximate Equations for the Immunoreactive Fraction Assay
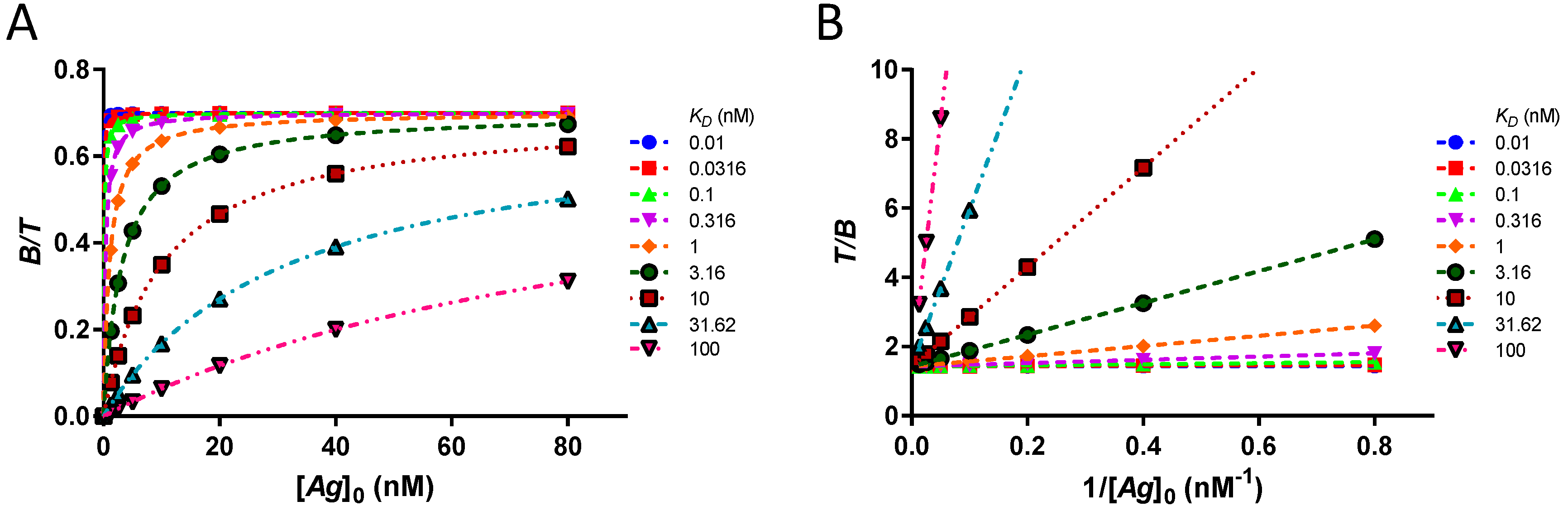
In this assay, the bound fraction of the labeled antibody is a function of the concentration of free antigen [Ag], the immunoreactive fraction r and the dissociation constant KD. For [Ag] ≫ KD, the bound fraction at equilibrium approaches the immunoreactive fraction r.
During the assay, [
Ag] is unknown, however, in the presence of a large excess of antigen, the [
Ag] concentration can be approximated with the total concentration of antigen [
Ag]
Total. At the beginning of the experiment (
t0), [
Ag]
0 = [
Ag]
Total and at equilibrium:
A single-point experiment with [
Ag]
0 ≫ [
T] and [
Ag]
0 ≫
KD will give a minimal value of
r from the bound fraction
. For greater accuracy, a conventional saturation assay may be performed with several increasing concentrations of antigen until
reaches a maximum. The series of data points can be fitted with
KD and
r as parameters in a rectangular hyperbolic binding curve [
23]. This isotherm of the bound fraction
as a function of [
Ag]
0, extrapolated to an infinite concentration of antigen, provides the most accurate value for the immunoreactive fraction
r. In addition, the dissociation constant
KD can be extracted from the fit using any modern software.
Often, a transformation of the data points is done by a double inversion (Equation (11)). The data thus analysed is known as the Lindmo plot [
11].
A linear extrapolation of the double inverse plot of as a function of gives the reciprocal of the immunoreactive fraction at y-intercept and the slope is equal to .
2.3. Exact Expression of the Bound Fraction as a Second-Order Equation
In the previous section, Equation (9) was modified to use [Ag]0 instead of [Ag] because, by reason of antigen depletion, the concentration of free antigen is unknown except at t0. Equations (10) and (11) thus obtained are useful approximations for the assay. The correct equation linking [Ag]0, B, T, r and KD is developed below.
From the equalities
and
, Equation (9) is expressed as follows:
By artificially multiplying the numerator and the denominator on the right-hand side by
:
By rearranging the terms,
The quadratic equation is solved with respect to
and two solutions are found:
One solution (+) is discarded because it is not equal to the origin when
is equal to zero and does not converge to
r at infinite
. The second solution (−) is kept in order to generate datasets with the theoretical binding curve. Similar equations have been described in the literature [
8,
10,
20].
2.4. Goodness of Fit
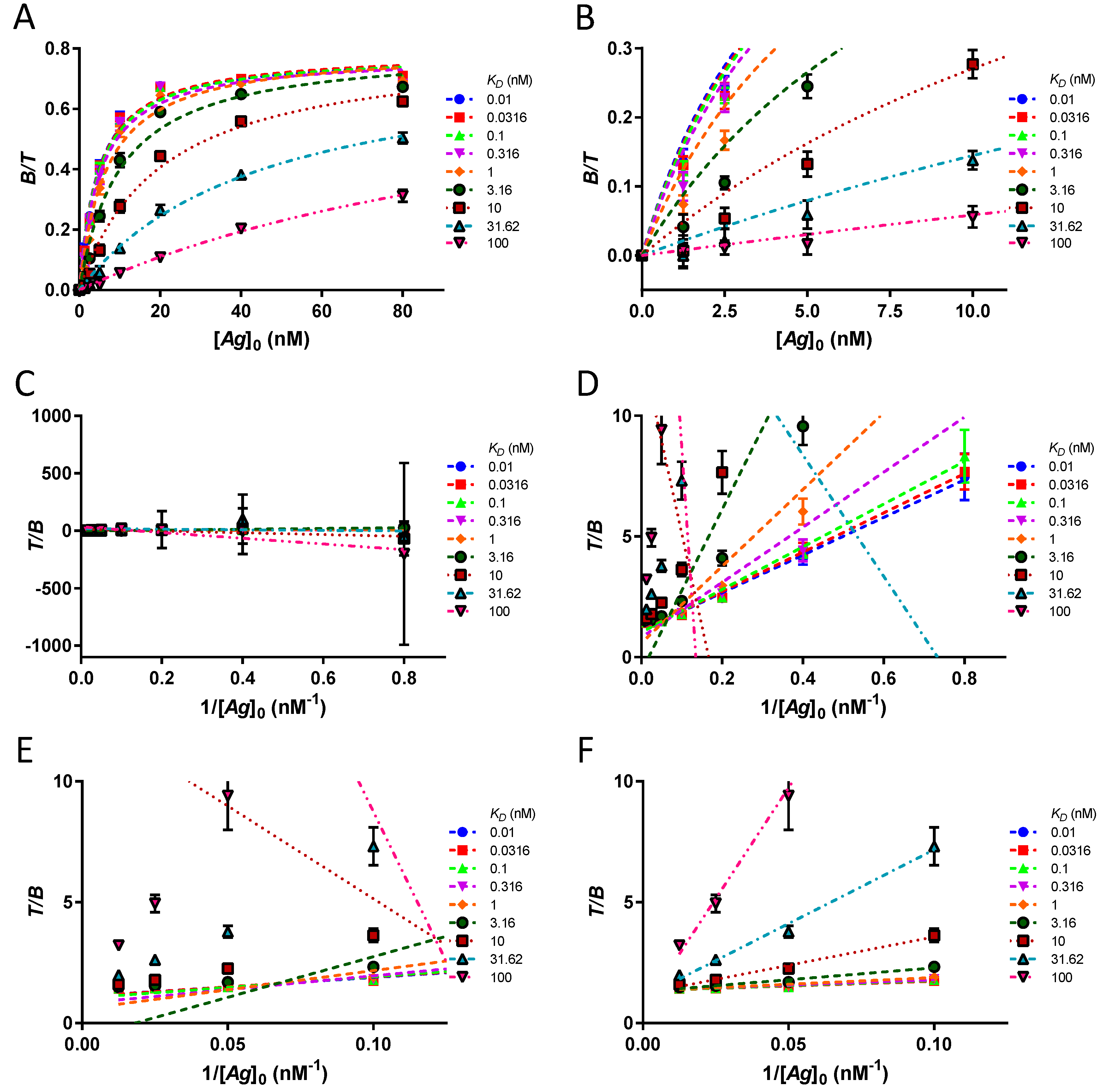
A dataset of the theoretical bound fractions as a function of [Ag]0 is generated with Equation (16) (Matlab R2017a, RRID:SCR_001622). The two approximate models are fitted (GraphPad Prism 8, RRID:SCR_002798) to the obtained values. The rectangular hyperbola (Equation (10)) provides the immunoreactive fraction r at infinite antigen excess and KD. The Lindmo plot (Equation (11)) by least squares linear regression gives at the y-intercept and the slope multiplied by r gives KD. The extrapolated results are compared to the original values. The goodness of fit for the immunoreactive fraction r and the dissociation constant KD is reflected in the lack of discrepancy for a wide range of KD and [T] parameters. The [Ag]0 used are and r = 70% in all cases. In doing so, the monovalent binding, the total adsorption of applied antigen on the surface of the plate, the total loss of affinity for a damaged antibody, the reversibility of complex formation and the attainment of equilibrium are assumed to be true. The tested assumptions are (i) [Ag]0 ≫ KD, (ii) [Ag]0 ≫ [T], (iii) [T] ≪ KD.
2.5. Study of the Assumption [Ag]0 ≫ KD
A common statement postulates that in IRFA, a maximum plateau of the bound fraction must be reached [
22]. Let [
Ag]
0 ≫ [
T]. Consider the following equation, obtained from the division of the numerator and the denominator of Equation (10) by [
Ag]
0:
In a single point experiment, a threshold of 91% of the value of r is obtained from the bound fraction if [Ag]0 ≥ 10 · KD. However, in the case of an experiment using several data points, such an excess of [Ag]0 over KD is not required for a good estimate of the value of r. By definition, the equation of a rectangular hyperbola is completely determined by two points and the origin. Therefore, any two values as a function of [Ag]0 (even those of the steep part of the curve if the KD is high) will provide a correct estimate of r at infinite [Ag]0. In the same way, using the Lindmo plot, any two values as a function of will give at the y-intercept and from the slope. Consequently, in theory, it is not necessary to have KD ≪ [Ag]0, nor to reach a plateau of the bound fraction. Computational verification involves a dataset of original values as a function of [Ag]0, for a set of KD, at a fixed [T] = 0.1 nM. Values for KD cover four orders and are .
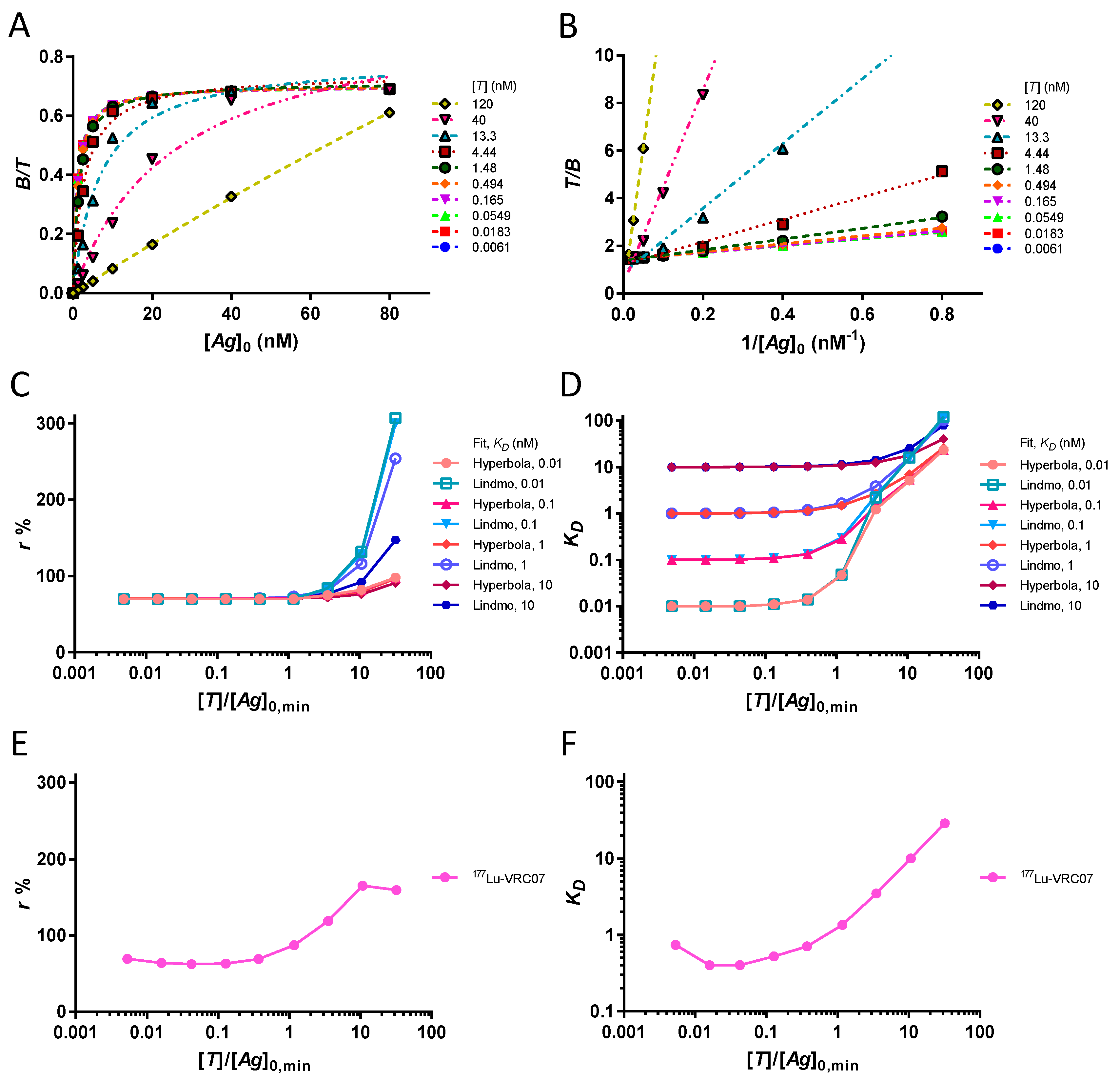
2.6. Study of the Assumptions [Ag]0 ≫ [T] and [T] ≪ KD
The assumption of [
T] ≪
KD is described as important in the literature [
16]. The assumption [
Ag]
0 ≫ [
T] is required to approximate [
Ag] with [
Ag]
0. Mathematical verification is performed from a set of original
values as a function of [
Ag]
0, for several [
T], at a fixed
KD (1 nM). Ten total antibody concentrations
are tested. Graphs are provided to visually assess goodness of fit for the individual data points.
Graphs analysing in parallel the assumptions [T] ≪ KD and [Ag]0 ≫ [T] on the extrapolation of r and KD are useful for studying the effect of antigen depletion with various KD values. In this way, the estimated r and KD are shown for the four as a function of . The concentration [Ag]0,min, is the minimum concentration of total antigen from the vector of [Ag]0 (i.e., 1.25 nM).
A laboratory experiment using the CD4bs anti-gp120 177Lu-PCTA-VRC07 antibody bound to the 426c core gp120 heptamer provides a comparison for the extrapolation of r and KD at increasing [T].
2.7. Antigen, Antibodies and Radiolabeling
The recombinant protein 426c core gp120 heptamer is a modified envelope (Env) glycoprotein derived from a primary clade C virus (426c) isolated from an HIV-1 infected subject. The variable regions 1, 2 and 3 were deleted and three
N-linked glycosylation sites in loop D and in variable region 5 of 426c gp120 were removed to allow binding to germline B cell receptors [
24]. Heptamerisation was achieved by adding a 55 amino acids peptide from the multimerisation domain of the human C4b-binding protein to the carboxy terminus of 426c Core. This antigen of molecular weight 315 kDa binds to the VRC01-class antibodies directed against the CD4-binding site (CD4bs) of the HIV-1 Env gp120 including VRC01, VRC07, 3BNC117.
The human (IgG1) monoclonal antibody 3BNC117 belongs to a recently discovered family of broadly neutralising monoclonal antibodies (bnMAbs) directed to the CD4bs of the HIV-1 Env protein gp120. The 3BNC117 antibody was isolated from a HIV-1 positive donor and has been produced in a Chinese Hamster Ovary (CHO) cell line CHOK1.SV. The 3BNC117 antibody has been shown to block about 90% of HIV isolates [
25]. The human (IgG1) monoclonal antibody VRC07 is a variant of the bnMAb VRC01. VRC07 is also directed to the CD4bs of gp120 and neutralizes 96% of HIV isolates [
26].
These two antibodies binding to gp120 were used to provide illustrative examples of two different radiolabeling methods, namely a direct radioiodination and a conjugation-chelation process. Radioiodination involves short oxidative stress due to the presence of the iodogen chlorinating agent and target tyrosine. Conjugation involves a long basic stress (pH 9.5) and target lysine. The conjugated antibody can be chelated later with different metal radioisotopes.
Radioiodination of 3BNC117 was done in a glass vial coated with 50 μg iodogen by the addition of a phosphate buffer solution (PO43−, 0.2 M, pH 8.0, 125 μL), 3BNC117 (100 μg, 100 μL) and 5 MBq of sodium 125I-iodide (Perkin Elmer, specific activity of 629 GBq/mg, 30 μL). After 5 min, the reaction was recovered by aspiration and quenched with 300 μL of a 2% ascorbate in PO43− buffer. The unreacted 125I-iodide was removed by ultrafiltration with PO43− buffer. 125I-3BNC117 was obtained with a purity of >95% (iTLC, citrate buffer pH 5; HPLC, XBridge Protein BEH SEC 200Å, PO43− buffer 0.1 M with 2% NaCl, pH 6.5).
The conjugation of VRC07 (334 µg) was realized after buffer exchange using ultrafiltration (Amicon Ultra, 0.5 mL, 50 kD) with four successive additions of carbonate/bicarbonate buffer (CBC, 0.4 M, pH 9.5). A 14.2 µL volume (20 eq.) of a freshly made solution of p-SCN-Bn-PCTA (Macrocyclics, 1.0 mg) in DMSO (50 µL) and CBC (0.4 M, pH 9.5, 0.450 mL) was added to the concentrated VRC07 solution and stirred at RT for 16 h. The excess chelator was removed by ultrafiltration with four NaCl 0.9% additions. The 40 µL solution was stored at the approximate concentration of 8 mg/mL. PCTA-VRC07 was homogeneous in HPLC (XBridge Protein BEH SEC 200Å, 3.5 μm, 7.8 × 300 mm Waters, PO43− buffer 0.1 M with 2% NaCl, pH 6.5) and had preserved binding to gp120-expressing tumour cell line HeLa 243 (flow cytometry). Radiolabeling was realized with 177LuCl3 (EndolucinBeta, specific activity of 3500 GBq/mg). To 150 µL of NH4OAc/AcOH buffer (pH 5.4, 0.4 M), 12.5 µL of PCTA-VRC07 (8 mg/mL, 100 µg) and 20 MBq of diluted 177Lu (10 µL) were added. After 1 h of incubation at 37 °C, 177Lu-PCTA-VRC07 was obtained without further purification with a purity of 98% (iTLC, citrate buffer pH 5).
2.8. Immunoreactive Fraction Assay on Microplate
The assay uses an antigen coated on a high-binding microplate in polystyrene (PS) (Corning 96 Well EIA/RIA Clear Flat Bottom Polystyrene High Bind Microplate, 360 µL). In this mathematical model, we assume a 100 kDa univalent antigen that is completely adsorbed on the plate and has fully accessible binding sites. A triplicate of 100 µL of antigen in PBS at concentrations
(antigen molecular weight e.g., 100 kDa) was coated for 16 h at 5 °C. The uncoated antigen was decanted by flicking the plate; the wells were rinsed and blocked with 2% BSA for 2 h. Three empty wells were also blocked for nonspecific binding determination. The wells were rinsed with 2% BSA and 100 µL of a 0.1 nM solution (0.015 µg/mL for an antibody molecular weight of e.g., 150 kDa) of freshly labeled antibody in 2% BSA were added. The concentration of this solution is known from HPLC measurement post-labeling and standard dilution techniques. The same quantity was also placed in three γ-counter tubes for the measurement of the total activity
T (internal control). The incubation time and temperature depend on the previous kinetic experiments, the stability of the radioimmunoconjugate and the half-life of the radioisotope, for example, 20 h of incubation at 5 °C. The unbound antibody (
U) present in the supernatants of each well was pipetted into γ-counter tubes, the wells were rinsed once with cold PBS and the pooled fractions were counted (in case of high
koff, this rinse is cancelled). The specifically bound antibody (
BSpec) was calculated by the following equation, which takes into account nonspecific binding (
BNS):
The bound fraction in the blank wells (wells blocked but not coated with antigen) is nonspecific and corresponds to
Nonspecific binding is invariant in this assay because the coated PS surface area is invariant, its value is
It follows logically that
In the
Supplementary Information, a step by step protocol for the immunoreactive fraction assay of radiolabeled antibodies using coated antigens on microplate is presented.
2.9. Kinetic Assay on Microplate
For kinetic experiments, two plates were run in parallel as above but with six rows each and each row contains three copies of blank wells. All manipulations were performed on ice and incubation at 5 °C. After the application of the labeled antibody, a counter was started. A row (without replicates) with the corresponding triplicate of blank wells were pipetted into γ-counter tubes exactly at times . From the second plate, duplicate wells were pipetted into tubes at times with the respective blank triplicate. Wells were not rinsed.
2.10. Error Propagation for Experimental Variations
To test the influence of stochastic errors on the goodness of fit, the original
dataset for several
KD, with [
T] = 0.1 nM,
r = 70% and
obtained with the theoretical binding curve (Equation (16)) was modified by simulated variations as would be obtained in an experimental setting. Stochastic variations were modelled as a quadratic sum of four errors (on
, on
T, on
and on γ-count). For each error, a standard deviation (SD) matrix was calculated. To calculate each SD, all other errors were assumed to be zero. Notwithstanding variations, it is always assumed for error propagation that all unbound antibodies are correctly accounted for (
U is exactly quantified). The relevant certainties for each considered error are summarized in
Table 1. The systematic errors of incomplete achievement of equilibrium and saturation of the PS plate are detailed later on.
For reading purposes, in the following sections, all variables (B, T, U) are expressed as representative of a quantitative radioactivity value, without unit.
2.11. Stochastic Variations in the Amount of Antigen
The standard deviation matrix for variations on coated
was computed by first generating three matrices of theoretical
data at different concentrations of total antigen. It was assumed that the whole antigen present in the applied solution was coated on the plate, within the limits of the stochastic variations. The original dataset, a set with a 10% negative difference on the antigen (
), and another with a 10% positive difference on the antigen (
) were constructed. This percentage was chosen to approximate serial dilution errors and variations in binding uniformity for a microplate [
27]. Assuming a normal distribution, the three matrices were used to calculate the SD matrix from triplets of
values.
2.12. Stochastic Variations in the Amount of Antibody
The SD matrix for T variations represents uncertainties in the volume of labeled antibody pipetted into the blocked wells. A systematic error in the concentration of radiolabeled antibody solution is possible but irrelevant. The difference in volume of T will be reflected in the radioactivity measured in the supernatant (U).
In the absence of nonspecific binding, Equation (19) gives:
Within the assay, the
value will be equated with
T and used for all well computations. The value of
T is assumed to be constant; however, this is not the case. Consider that for a certain well, there is a difference between the
T′ actually added and
T equal to
The bound fraction
is invariant to the change in
T, as long as [
Ag]
0 is in large excess. Hence,
Moreover, in the absence of nonspecific binding
and
, so
For that well, there is a difference
between the measured supernatant
U′ and the supernatant
U obtained if the constant
T had been applied. From Equation (25),
In the assay,
T′ is not measured; instead,
is substituted for
T′. The resulting apparent unbound fraction
is equal to
The apparent bound fraction can be expressed as follows:
Finally, from Equation (25):
To evaluate the error introduced by changes in
T, three matrices of theoretical
data are constructed, one with the original
values and the other two with
transformed by the Equation (30) for an error
of ± 1%. This error percentage is chosen to approximate the imprecision of a micropipette with a viscous liquid [
28]. Assuming a normal distribution, the three matrices are used to calculate the SD matrix from triplets of
values.
2.13. Stochastic Variations in the Nonspecific Binding
Variations in nonspecific binding account for the nonspecific binding difference between blanks and coated wells. In case of nonspecific affinity of the radiolabeled antibody with the PS surface of a well, this nonspecific binding must be subtracted from the bound fraction. In each well, the bound antibody is
Total antibody
T is the sum of unbound, specific binding and nonspecific binding, so that
By definition, for the blanks, there is only nonspecific binding:
Since
T is constant (
Table 1) and
U is exactly quantified, in case of uncertainty in the nonspecific binding such that
, the difference
is reflected on
and
More generally, in the absence of error on
, the difference in the nonspecific binding gives an equal difference on
U:
Since the amount of antibody
T is constant, Equations (32) and (33) can be equated:
Because the coated PS surface area is the same for all the wells, the mean value of the nonspecific binding
is constant and the nonspecific binding can be simplified:
Equation (21) is obtained.
However, although
can be simplified from Equation (36), the differences
have to be accounted for. According to Equations (21), (34) and (35), the error that will be propagated to
is equal to
The SD of the bound antibody imputable to nonspecific binding changes is estimated at . The value is determined as a SD value from a set of laboratory experiments.
2.14. Gamma Counter Errors
The measurement of the radioactivity of the wells relies on a γ-counter, a source of experimental errors. Various causes for errors in the counting step have been discussed in the literature, e.g., geometric errors and random noise [
29]. Geometric errors can be minimized by using the same tubes for all samples and the same volume of liquid. The error introduced by the random noise is important for the low activities (<1000 cpm) often used in IRFA. These come from a low specific activity of radiolabeled antibodies and the need for [
T] ≪ [
Ag]
0. The error can be minimized by using a higher specific activity or a higher [
T] value. The signal-to-noise ratio (SNR) can also be improved by averaging the measurements over a longer period due to the SNR dependence on the square root of the acquisition time. In our simulation, the standard deviation of the bound antibody attributable to the error of the γ-counter is constant and estimated at
.
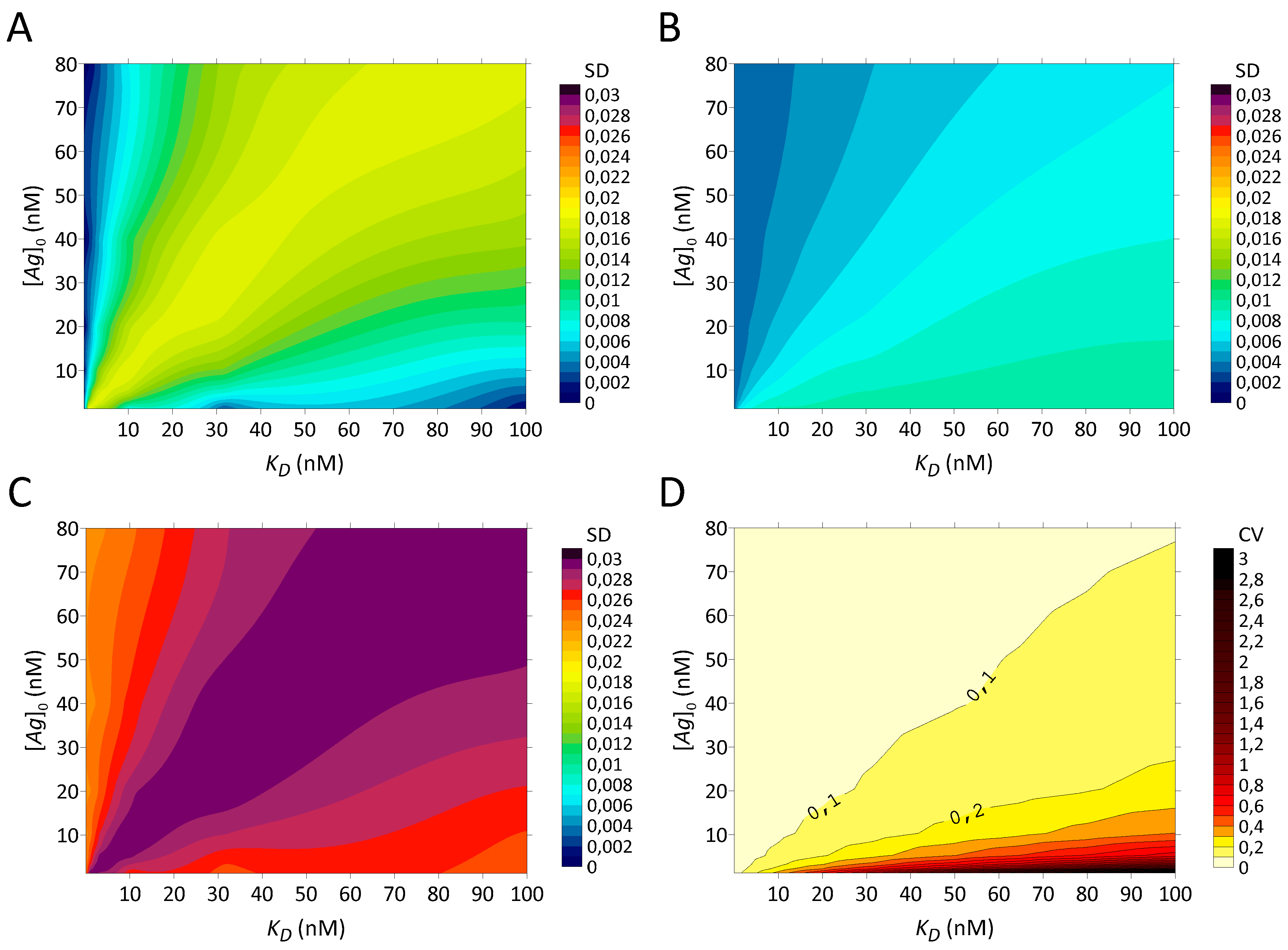
2.15. Overall Stochastic Errors
Assuming a normal distribution, the previously developed SD matrices for stochastic errors on antigen quantity and amount of antibody are summed with the constant SD values for nonspecific binding changes and for γ-counter error to obtain a matrix of overall SD. The quadratic sum of the four standard deviations is equal to
The resulting coefficients of variation (CV) are also calculated by dividing the matrix of overall standard deviations by the matrix of original data (Equation (16)). To provide more accurate interpolation of the CV, additional points were calculated at . Contour plots are used for visualisation based on KD and [Ag]0 (Surfer version 16, Golden Software, Golden, CO, USA).
2.16. Influence of Kinetics
Failure to achieve equilibrium is known to alter the results of binding assays [
20]. Indeed, the equations of the binding curve (Equations (9) and (16)) and its approximations (Equations (10) and (11)) all postulate equilibrium at all data points. A thorough simulation should examine the nonattainment of equilibrium as an effect of slow binding kinetics.
For simplicity, let the complex B formation be irreversible in this discussion owing to negligible dissociation. Recalling the second-order association rate of the antigen-antibody complex 1:1 (Equation (2)).
Let [
Ag]
0 ≫ [
T], in this case the second-order reaction
can be considered as a pseudo-first order reaction because
is invariant in the whole process. A new pseudo-first order rate constant including the starting antigen
can be formulated. The new rate for the association reaction is as follows:
By integrating the differential form of the rate law
, we obtain the following equation:
At the beginning of the reaction,
is equal to the total concentration of immunoreactive antibody
. At any time, the free immunoreactive antibody
is equal to the total immunoreactive antibody minus the already bound antibody in the
B complex:
Dividing by [
T] and after rearrangement, the bound fraction at any time is as follows:
Equation (43) describes the irreversible conversion of the total immunoreactive antibody with a rate constant
dependent on
. At start time
t0,
is equal to zero. Then, [
B] increases as the free immunoreactive antibody [
Ab] decreases with a constant half-life. In an excess of antigen, the half-time
of complex formation does not depend on the total concentration of antibody [
T] but only on the total concentration of antigen
as
The above irreversible model reaching total conversion is an approximation. In a real context, complex formation is reversible, so the equilibrium value of the fraction bound to each particular
will eventually be obtained. In this way, to estimate the kinetic error for each
KD, the matrix of original
values at [
T] = 0.1 nM is multiplied by the integrated rate function (
) at time
t = 1200 min [
20]. From this modified dataset, the
r and
KD values are estimated using hyperbola and Lindmo plots with and without exclusion of the bound fractions at [
Ag]
0 ≤ 5 nM.
A representative value of the
kon rate constant was determined from a kinetic assay in the laboratory using the CD4bs anti-gp120
125I-3BNC117 antibody bound to 426c core gp120 heptamer. For simplicity, the effective rate constant in this assay is assumed to be
and the
koff contribution in the integrated rate constant is omitted. The dataset modified for kinetics gives qualitative results only. The interested reader will be able to find reversible models for kinetics in the literature [
10,
20].
2.17. Computation of the Maximum [Ag]0
A standard 96-well high-binding PS microplate binds proteins by hydrophobic interactions and π–π stacking [
30]. The binding capacity of a high-binding plate is approximately 500 ng mouse IgG/cm² and the diameter of the well is 6.4 mm [
27]. The geometric computation of a cylinder with a base gives 94.7 mm
2 of PS area for a volume of 100 µL. Therefore, about 500 ng of protein can be bound using 100 µL of solution. For a representative antigen molecular weight of 100 kDa, the maximum value of [
Ag]
0 is 50 nM. However, in this work, a maximum level of coated [
Ag]
0 = 30 nM was used to account for higher molecular weight antigens or low PS binding efficiency.
2.18. Using Kinetics to Study PS Saturation and B Desorption
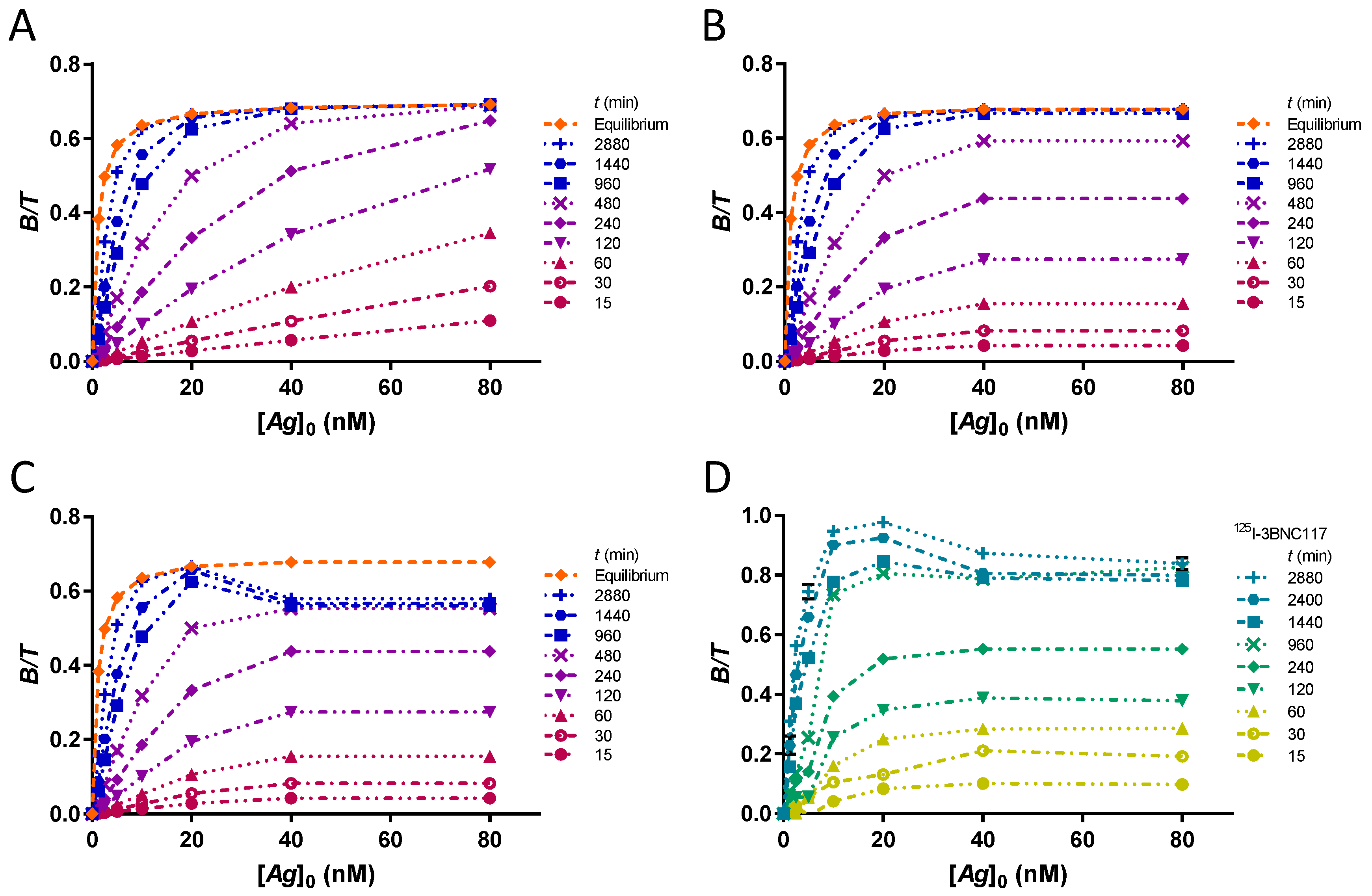
Owing to the limited amount of antigen that can be attached to the PS surface, it is necessary to recognize when the maximum amount of [Ag]0 is coated. For this, a kinetic assay is adequate. The time-course of complex formation is illustrated using the original values for a single KD = 1 nM, at [T] = 0.1 nM, multiplied for each [Ag]0 by the corresponding integrated rate function (), at different times .
The cases of an unsaturated PS plate, a plate saturated at [Ag]0 = 30 nM and a saturated plate subject to desorption of the complex B are presented. The time-course of complex formation in the laboratory kinetic assay of the CD4bs anti-gp120 125I-3BNC117 antibody bound to 426c core gp120 heptamer is presented for comparison.
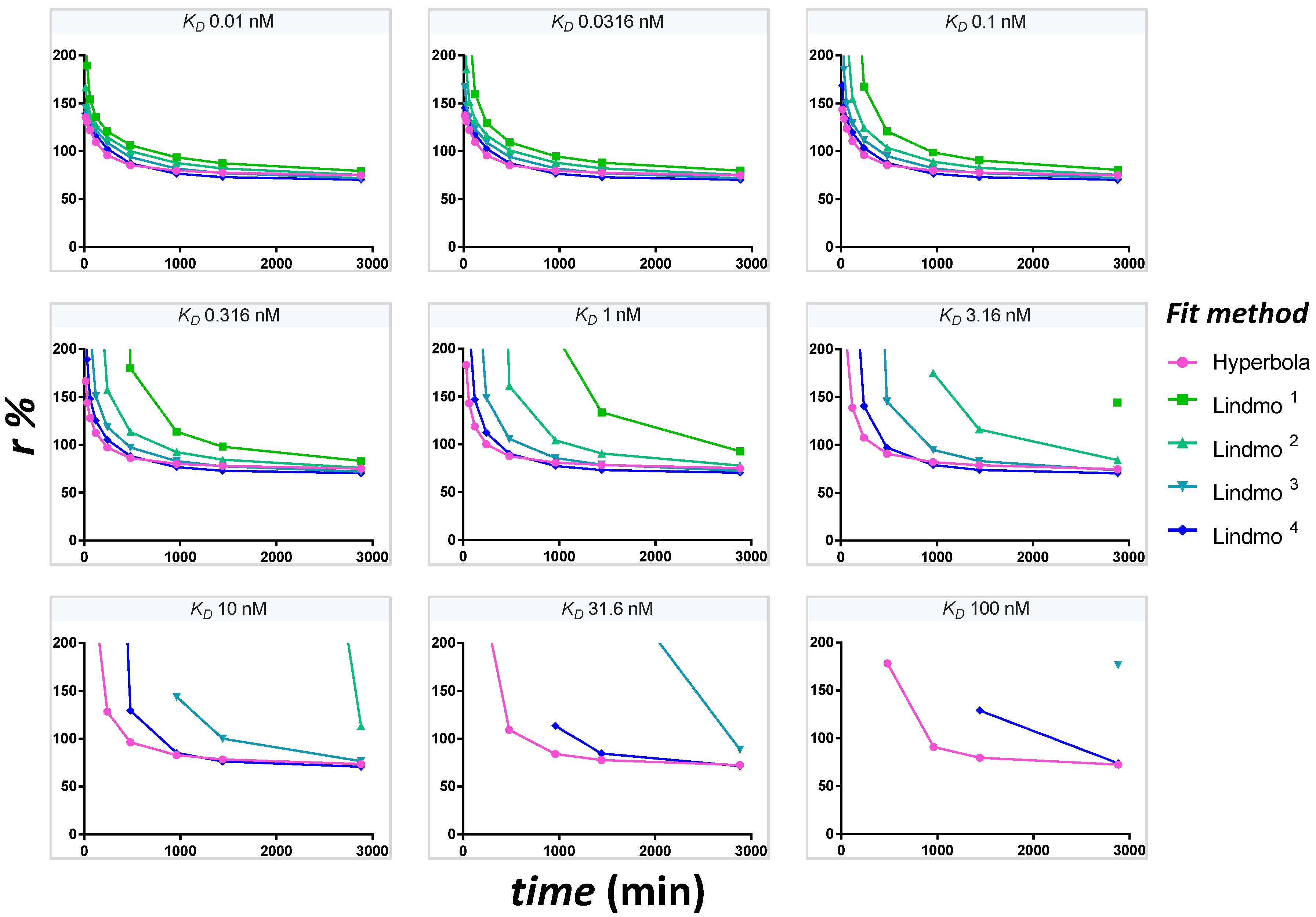
2.19. Time-Dependence of the Estimation of r
The evolution of extrapolated r values at time points min reflects the time-dependence of the estimate of r in case of unreached equilibrium. To provide the dataset for different times, the theoretical fraction bound at each [Ag]0 is multiplied by the integrated rate function at that time with the appropriate (kon = 0.0001444 nM−1min−1). A graph of r as a function of time is plotted for each KD at [T] = 0.1 nM. To show the influence of the extrapolation method on the resulting r estimate, five different fits are compared simultaneously for accuracy and robustness. These are hyperbola, Lindmo plot, Lindmo plots with exclusion of [Ag]0 = 1.25 nM, [Ag]0 ≤ 2.5 nM, [Ag]0 ≤ 5 nM. The graphs are shown for an unsaturated PS plate.
In
Figure S1 and S2, the graphs of
r as a function of time for a plate saturated at [
Ag]
0 = 30 nM and for a saturated plate subject to desorption of 10% of the complex
B are represented. The vector of
is used, [
T] = 0.1 nM and
r = 70%. In this desorption model, the same multiplier of 0.9 is used for
values at 30 nM, regardless of the time. In
Figure S3, a graph of
r as a function of time is also presented for the kinetic assay with the anti-gp120
125I-3BNC117 antibody. To illustrate the variation of the fits with time, the data at each time point are extrapolated with a Lindmo plot (excluding [
Ag]
0 ≤ 5 nM) and a hyperbola (
Figure S4).
2.20. Comparing Extrapolation Methods with Simulated Data
The original
dataset as a function of [
Ag]
0 is calculated for
r = 70%, [
T] = 0.1 nM and a series of nine
(Equation (16)). The
values are corrected for kinetics at each [
Ag]
0 by multiplication with the integrated rate function (
) at time
t = 1200 min with a representative rate constant
kon. Then, the standard deviations
and
are adjusted to account for the systematic variations resulting of kinetics and are summed with the other two SD (Equation (39)). Finally,
n = 25 matrices of normally distributed random
data points are generated with a mean equal to each
value and the respective standard deviation of the quadratic sum, using the Mersenne Twister pseudo-random function (Microsoft Excel 2016, RRID:SCR_016137). In this way, 95% of the simulated
data points are within the following confidence interval for a triplicate of experiments:
Each curve of as a function of [Ag]0, corresponding to a single KD, is fitted with hyperbola (Equation (10)) and Lindmo plot (Equation (11)). The process is repeated n times for each KD. The mean and SD of the r and KD estimates are calculated and compared to the actual input values in the original dataset. The r and KD estimates after exclusion of low bound fractions are also compared: the stepwise deletion of the values associated with the lowest [Ag]0 levels is followed by computation of the fit with both equations.
In the
Supplementary Information, two tables of estimated
r values for
n = 25 matrices of normally distributed random
data points for a saturated PS plate and for a saturated plate showing desorption of
B are shown. The influence of PS saturation on the fit results is studied by substituting
values at [
Ag]
0 = 30 nM for values at [
Ag]
0 = 40 nM and [
Ag]
0 = 80 nM (
Table S1). Desorption of complex
B is studied in the same way, but in addition by multiplying the corresponding
values (for [
Ag]
0 = 30 nM) by 0.9 to simulate a 10% desorption of
B (
Table S2). The influence on the estimate of
r of the exclusion of the duplicate bound fraction at the highest, saturated [
Ag]
0 is quantified.
2.21. Graphical Analysis of Simulated Data
Graphical analyses are displayed for n = 10 matrices of simulated data points. The mean bound fractions for the ten experiments are drawn with error bars corresponding to the SD. The fits with hyperbola and Lindmo plot are compared graphically. The resulting change in goodness of fit for the Lindmo plot after exclusion of data points corresponding to [Ag]0 ≤ 5 nM is revealed.
4. Discussion
Despite the importance of the immunoreactive fraction assay (IRFA) for determining the purity of radioimmunoconjugates, there is no established method or guideline for quantifying functional quality. The true value of the immunoreactive fraction
r, defined in dynamic equilibrium with an infinite excess of antigen, can only be approached by mathematical extrapolation. The most appropriate data analysis involves the direct representation of the bound fraction as a function of [
Ag]
0 in a conventional saturation binding curve shaped as a rectangular hyperbola (Langmuir isotherm) [
23]. Historically, because of the difficulty for the human eye to correctly estimate a curve that extends to infinity, manual extrapolation of
r with this method has hardly ever been used. In fact, in 1984, Lindmo et al. introduced a mathematical transformation to linearize the data through a double inversion, making the Lindmo plot the most common extrapolation method of
r for its apparent simplicity [
11].
In the past, some authors have recognized that the use of Lindmo plot may be problematic [
8,
9,
12,
16,
22]. However, a systematic analysis of the individual problems and their effects on the extrapolation of
r and
KD was lacking. In the absence of consensus, the subject is made more difficult by the inability to compare extrapolated
r values with a benchmark
r value. Therefore, without a clear demonstration of its lack of accuracy, precision, and robustness, the Lindmo plot continues to be widely used.
Mathematically, the Lindmo plot is sound as it is easily derived from the hyperbola. With ideal data points at equilibrium, in the absence of antigen depletion, there is excellent goodness of fit of both approximate equations with the theoretical data. The extrapolated values of r and KD are correctly determined.
At first glance, the range is wide for the values of [Ag]0 and KD, the only assumption required for the ideal dataset being the antigen always in excess of the antibody. For instance, [Ag]0 ≫ KD is not necessary because the hyperbola and the linear fit of Lindmo plot are entirely determined by knowing only the exact bound fractions, regardless of their size. Moreover, the assumption [T] ≪ KD is not relevant if [Ag]0 ≫ [T]. If [Ag]0 ≫ [T] is not true for at least one [Ag]0, the adverse case of antigen depletion is encountered. Then, errors are observed and become significant if the antigen is exhausted for several [Ag]0. A comparison of the Lindmo plot with hyperbola establishes that the Lindmo plot always provides worse estimates of r and KD than the hyperbola in the case of antigen depletion. However, this can be avoided simply by using a lower [T], if necessary, with a higher specific activity.
Unlike ideal data points, experimental data points are generally subject to uncertainties and incomplete equilibration. Since the two approximate equations give excellent estimates for the ideal dataset, but not in an experimental setting, we deduce that the problems attributed to the Lindmo plot result from mismanagement of the discrepancies between the ideal points and the experimental data. It is also interesting to know whether the mathematical transformation of Lindmo plot exacerbates these errors or whether hyperbola is also subject to them. To challenge the accuracy, precision, and robustness of the Lindmo plot and hyperbola, an in silico simulation was performed. In this way, the estimates of r and KD obtained with the two approximate equations from the simulated datasets can be directly compared to the original input values.
Three types of errors were examined: stochastic, kinetic and PS saturation. To model the stochastic variations in the pseudo-experimental data, standard deviations matrices were computed. The two dominant elements of the quadratic sum of SD are the uncertainties on [
Ag]
0 and on the nonspecific binding. SD are relatively constant over the entire range of
KD and [
Ag]
0. Nevertheless, CV show a wide range (3–300%). This contrasts with Lindmo et al. which assumes a constant CV value [
11]. Owing to the minimized CV at [
Ag]
0 >
KD, the assumption of [
Ag]
0 ≫
KD is now gaining importance with the use of a disturbed dataset in order to avoid errors in the estimates of
r and
KD.
The error of kinetics was investigated using a mono-exponential rate law reaching the equilibrium values at each [
Ag]
0. In IRFA, the kinetics depend on [
Ag]
0 and not on the radioligand concentration. Indeed, when [
Ag]
0 ≫ [
T] the association reaction follows a pseudo-first order rate which includes [
Ag]
0 in the rate constant. With decreasing [
Ag]
0, at some point, the rate constant is small enough that the equilibrium is not reached within a reasonable time, despite resembling a steady state because of slow association kinetics. This leads to a systematic depression of the bound fractions at the low [
Ag]
0. A dataset including points that are not in equilibrium leads to extrapolation errors of
r and
KD. With hyperbola, a stable overestimation of
r of about 10% is obtained. The
KD values are overestimated. The same dataset extrapolated with the Lindmo plot give estimates of
r > 100%, even negative. Thus, the Lindmo plot, but not the hyperbola, requires the exclusion of data points at low [
Ag]
0 in case of incomplete equilibration. Similar results were obtained by Hulme in saturation assays of antigen (Scatchard) [
20]. However, in IRFA (saturation assays of antibody), this kinetic effect is more problematic. In Scatchard, the kinetics depend on the excess concentration of radioligand in solution and not on coated [
Ag]
0 as in IRFA. A lower [
Ag]
0 can be coated on a solid surface than the radioligand concentration available in Scatchard, thus slowing kinetics. Complexes with low
kon aggravate this slowdown. In this study, the complex has a low
kon value (
). However, we used a long incubation period of 20 h. High affinity or avidity and the low temperature of 5 °C used in our laboratory experiments may explain the measurement of a low
kon [
20,
31]. Complexes with such a low
kon have been reported [
12,
32]. With the trend of developing long residence time and potent ligands, the problem of slow kinetics in IRFA will probably remain [
33,
34]. The influence of incomplete equilibration is scarcely recognized because discrepancies revealed in the data are imputed in place to insufficient antigen excess and antigen depletion [
8,
9,
11,
22].
The saturation of the PS is another source of systematic error. The time-course of complex formation is useful for establishing the equilibrium time at different [Ag]0. Owing to the presence of [Ag]0 in the rate constant, the equilibration time for each [Ag]0 can be compared. By observing equal equilibration times for different [Ag]0, one can deduce the saturation of the PS plate in antigen. Thus, crucial information for understanding the IRFA is obtained from kinetic assays.
Using several equilibration times, the time-dependence of the estimation of r was investigated. We showed that a fit using a hyperbola always provides a more accurate extrapolation of r at an earlier time, with greater precision and robustness than a Lindmo plot. The Lindmo plot requires the exclusion of the low bound fractions to provide better estimates of r.
By combining the ideal dataset, the kinetic function and the standard deviations matrix, the final simulation was performed. The pseudo-random dataset provides disturbed bound fractions and unattained equilibrium that model an experimental setting. The estimation of r using the hyperbola is precise and robust, but slightly inaccurate because of kinetics. The Lindmo plot is fragile and chaotic owing to the artificial amplification of fluctuations at the low bound fractions. The causal factors affecting the Lindmo plot were disclosed in a graphical analysis. Depending on the binding isotherm, the bound fractions at low [Ag]0 are low. At these low [Ag]0 values, additional depression occurs because of slower kinetics. SD being relatively constant, significant CV appear. Inversion of the ordinate with the Lindmo plot creates mathematical distortions resulting from poor error management. This changes the scale of stochastic variations from small absolute values to extremely large random fluctuations. A linear fit with the complete dataset generates nonsensical r values, unless the low bound fractions are excluded.