A Quasi-Distributed Crack Sensor Based on Weakly Coupled Vertical U-Shaped Ring Array
Abstract
1. Introduction
2. Sensor Design
2.1. Sensor Structure
2.2. Sensing Mechanism
2.3. Sensing Performance
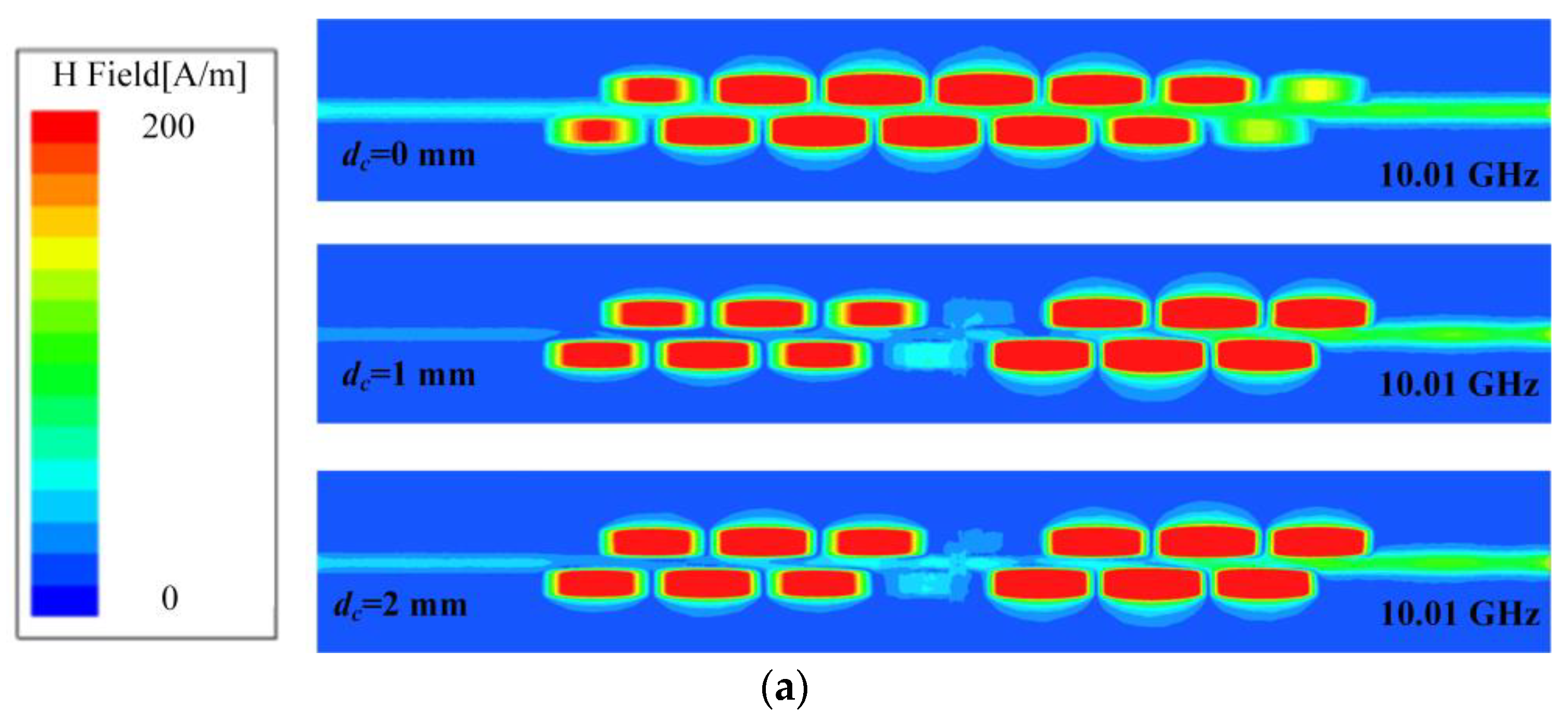
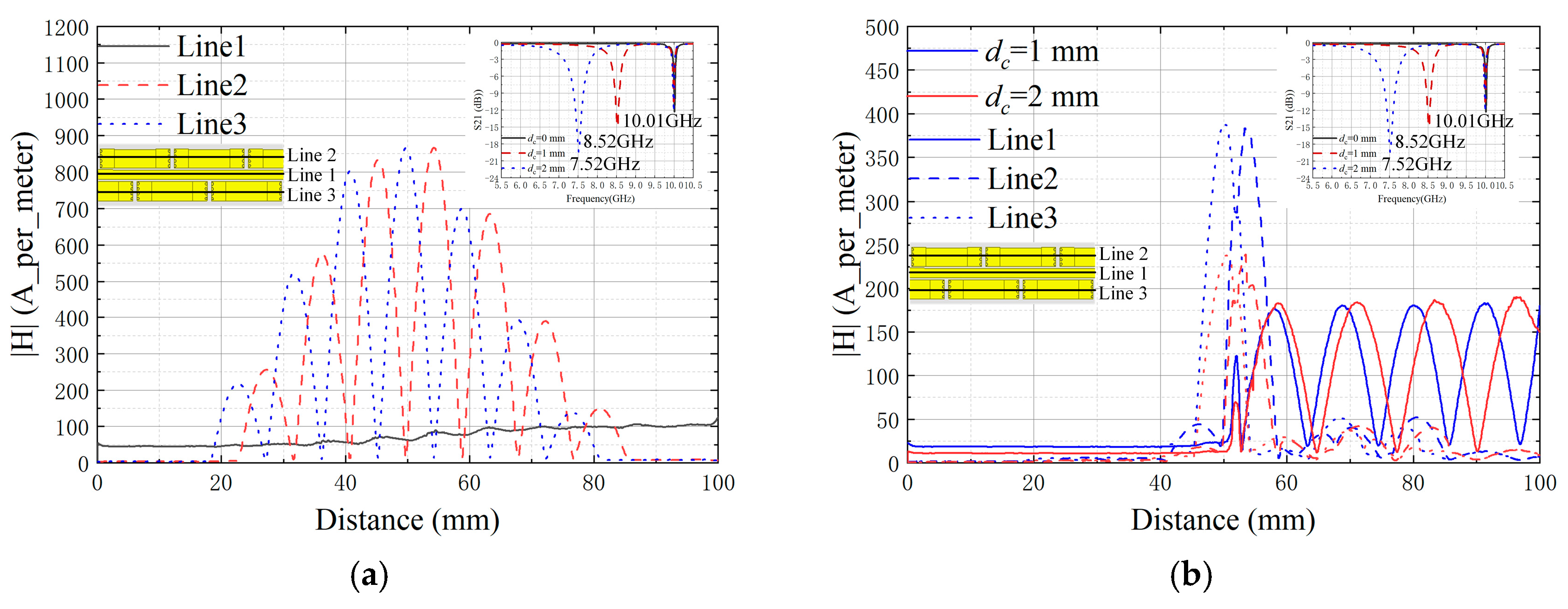
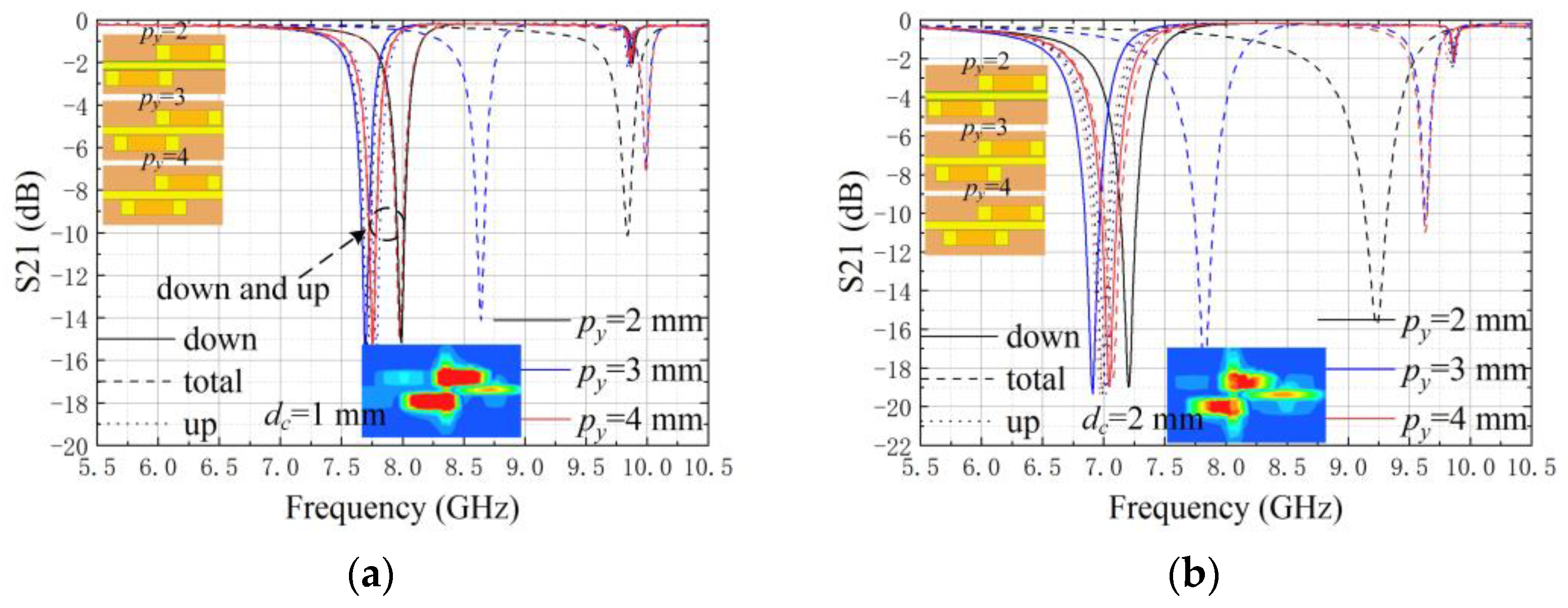
3. Measurements and Results
3.1. Test Setup
3.2. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| SHM | Structural health monitoring |
| VUR | Vertical U-shaped ring |
| BIC | Bound states in the continuum |
| ORWG | Open rectangular waveguide |
References
- Hu, S.; Wang, Y.; Wang, C.; Pu, W.; Qiu, L. Realization Method of Sensing-Integrated Fishbone with Deformation Monitoring Based on Screen Printing Technology. IEEE Sens. J. 2024, 24, 2079–2088. [Google Scholar] [CrossRef]
- Abou-Khousa, M.A.; Rahman, M.S.U.; Donnell, K.M.; Qaseer, M.T.A. Detection of Surface Cracks in Metals Using Microwave and Millimeter-Wave Nondestructive Testing Techniques—A Review. IEEE Trans. Instrum. Meas. 2023, 72, 8000918. [Google Scholar] [CrossRef]
- Xie, C.; Liu, T.; Pei, C.; Chen, Z. A Flexible Thin-Film Magnetostrictive Patch Guided-Wave Transducer for Structural Health Monitoring. IEEE Sens. J. 2022, 22, 12237–12244. [Google Scholar] [CrossRef]
- Bao, Y.Q.; Chen, Z.C.; Wei, S.Y.; Xu, Y.; Tang, Z.Y.; Li, H. The State of the Art of Data Science and Engineering in Structural Health Monitoring. Engineering 2019, 5, 234–242. [Google Scholar] [CrossRef]
- Prasetyo, A.; Yuniarto, E.M.; Suprobo, P.; Tambusay, A. Application of Edge Detection Technique for Concrete Surface Crack Detection. In Proceedings of the 2022 International Seminar on Intelligent Technology and Its Applications (ISITIA), Virtual, 20–21 July 2022; pp. 209–213. [Google Scholar]
- Bado, M.F.; Casas, J.R. A Review of Recent Distributed Optical Fiber Sensors Applications for Civil Engineering Structural Health Monitoring. Sensors 2021, 21, 1818. [Google Scholar] [CrossRef]
- Min, R.; Liu, Z.; Pereira, L.; Yang, C.; Sui, Q.; Marques, C. Optical fiber sensing for marine environment and marine structural health monitoring: A review. Opt. Laser Technol. 2021, 140, 107082. [Google Scholar] [CrossRef]
- Broda, D.; Staszewski, W.J.; Martowicz, A.; Uhl, T.; Silberschmidt, V.V. Modelling of nonlinear crack-wave interactions for damage detection based on ultrasound—A review. J. Sound Vib. 2014, 333, 1097–1118. [Google Scholar] [CrossRef]
- Feng, K.; Ji, J.C.; Ni, Q.; Beer, M. A review of vibration-based gear wear monitoring and prediction techniques. Mech. Syst. Signal Process. 2023, 182, 109605. [Google Scholar] [CrossRef]
- Goyal, D.; Pabla, B.S. The Vibration Monitoring Methods and Signal Processing Techniques for Structural Health Monitoring: A Review. Arch. Comput. Methods Eng. 2016, 23, 585–594. [Google Scholar] [CrossRef]
- Ju, M.; Dou, Z.; Li, J.-W.; Qiu, X.; Shen, B.; Zhang, D.; Yao, F.-Z.; Gong, W.; Wang, K. Piezoelectric Materials and Sensors for Structural Health Monitoring: Fundamental Aspects, Current Status, and Future Perspectives. Sensors 2023, 23, 543. [Google Scholar] [CrossRef] [PubMed]
- Qing, X.; Li, W.; Wang, Y.; Sun, H. Piezoelectric Transducer-Based Structural Health Monitoring for Aircraft Applications. Sensors 2019, 19, 545. [Google Scholar] [CrossRef] [PubMed]
- Kim, Y.; Park, E.; Salim, A.; Kim, J.; Lim, S. Microwave Dual-Crack Sensor with a High Q-Factor Using the TE20 Resonance of a Complementary Split-Ring Resonator on a Substrate-Integrated Waveguide. Micromachines 2023, 14, 578. [Google Scholar] [CrossRef] [PubMed]
- Pang, Q.; Dong, G.; Yang, X. Metal Crack Detection Sensor Based on Microstrip Antenna. IEEE Sens. J. 2023, 23, 8375–8384. [Google Scholar] [CrossRef]
- Deif, S.; Daneshmand, M. Multiresonant Chipless RFID Array System for Coating Defect Detection and Corrosion Prediction. IEEE Trans. Ind. Electron. 2020, 67, 8868–8877. [Google Scholar] [CrossRef]
- Zhou, X.; Yang, X.; Su, P.; Wang, J.; Wang, Z.; Peng, H.; Gu, D. Detection and Location of Defects in Non-Metallic Composites Pipeline Based on Multi-Resonant Spoof Surface Plasmon Polaritons. IEEE Sens. J. 2022, 22, 2091–2098. [Google Scholar] [CrossRef]
- Liang, Y.; Tsai, D.P.; Kivshar, Y. From Local to Nonlocal High-Q Plasmonic Metasurfaces. Phys. Rev. Lett. 2024, 133, 053801. [Google Scholar] [CrossRef]
- Bin-Alam, M.S.; Reshef, O.; Mamchur, Y.; Alam, M.Z.; Carlow, G.; Upham, J.; Sullivan, B.T.; Ménard, J.M.; Huttunen, M.J.; Boyd, R.W.; et al. Ultra-high-Q resonances in plasmonic metasurfaces. Nat. Commun. 2021, 12, 974. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Cao, J.; Li, Y.; Huang, C.; Wang, K. A Quantitative Study of Crack Monitoring for Electromagnetic Resonators by Perturbation Method. In Proceedings of the 2020 IEEE 3rd International Conference on Electronic Information and Communication Technology (ICEICT), Shenzhen, China, 13–15 November 2020; pp. 755–757. [Google Scholar]
- Wang, Q.; Bi, K.; Hao, Y.; Guo, L.; Dong, G.; Wu, H.; Lei, M. High-Sensitivity Dielectric Resonator-Based Waveguide Sensor for Crack Detection on Metallic Surfaces. IEEE Sens. J. 2019, 19, 5470–5474. [Google Scholar] [CrossRef]
- Albishi, A.M.; Boybay, M.S.; Ramahi, O.M. Complementary Split-Ring Resonator for Crack Detection in Metallic Surfaces. IEEE Microw. Wirel. Compon. Lett. 2012, 22, 330–332. [Google Scholar] [CrossRef]
- Marindra, A.M.J.; Tian, G.Y. Chipless RFID Sensor Tag for Metal Crack Detection and Characterization. IEEE Trans. Microw. Theory Tech. 2018, 66, 2452–2462. [Google Scholar] [CrossRef]
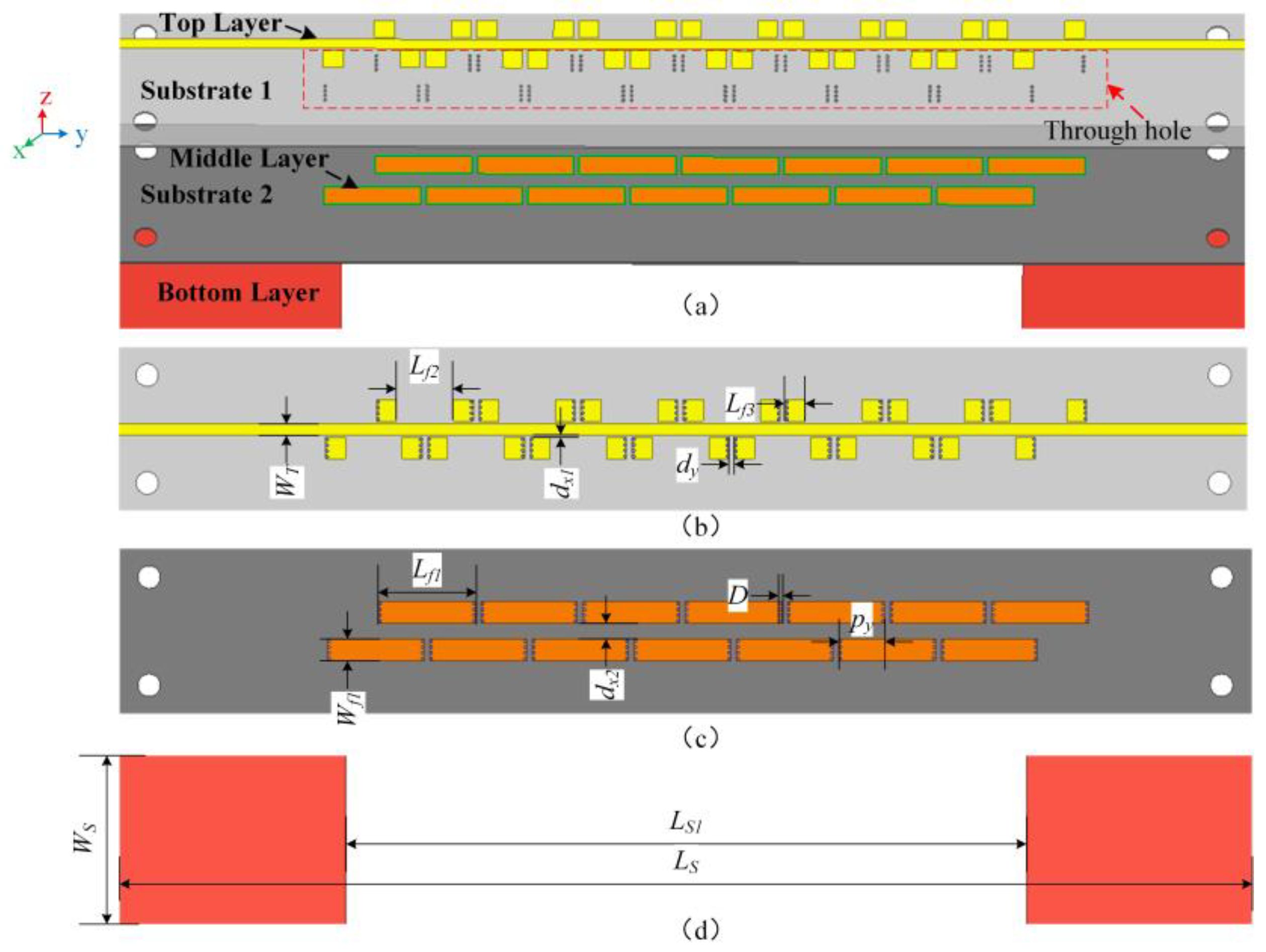






| WS | LS | LS1 | Lf1 | Lf2 |
| 15 | 100 | 60 | 8.5 | 5 |
| Wf1 | dy | dx1 | dx2 | WT |
| 1.9 | 0.5 | 0.2 | 1.4 | 1 |
| py | Lf3 | D | ||
| interweaving distance | 1.75 | 0.25 |
| Ref. | Structure (Feed + Resonator) | Frequency f0 (GHz) | Sensitivity (GHz/mm2) | RS | Resolution | Long Coverage |
|---|---|---|---|---|---|---|
| [20] | ORWG + Dielectric resonator | 16.8 | depth: 0.71 width: 1.24 | 0.042 0.074 | 1 mm × 1 mm | N |
| [21] | CSRR + TL | 5.05 | 1.25 | 0.247 | 0.2 mm × 1 mm | N |
| [22] | Chipless + Patch | 4.7 | 0.1343 | 0.029 | 0.1 mm × 1 mm | N |
| This work | VUR + TL | 9.08 | depth: 0.95 width: 0.685 | 0.104 0.075 | 1 mm × 0.5 mm | Y |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chu, C.; Huang, J.; Xie, X.; Zhang, J. A Quasi-Distributed Crack Sensor Based on Weakly Coupled Vertical U-Shaped Ring Array. Sensors 2025, 25, 2852. https://doi.org/10.3390/s25092852
Chu C, Huang J, Xie X, Zhang J. A Quasi-Distributed Crack Sensor Based on Weakly Coupled Vertical U-Shaped Ring Array. Sensors. 2025; 25(9):2852. https://doi.org/10.3390/s25092852
Chicago/Turabian StyleChu, Chenjie, Jiayi Huang, Xuan Xie, and Jun Zhang. 2025. "A Quasi-Distributed Crack Sensor Based on Weakly Coupled Vertical U-Shaped Ring Array" Sensors 25, no. 9: 2852. https://doi.org/10.3390/s25092852
APA StyleChu, C., Huang, J., Xie, X., & Zhang, J. (2025). A Quasi-Distributed Crack Sensor Based on Weakly Coupled Vertical U-Shaped Ring Array. Sensors, 25(9), 2852. https://doi.org/10.3390/s25092852







