A Hierarchical PSMC–LQR Control Framework for Accurate Quadrotor Trajectory Tracking
Abstract
1. Introduction
- A hierarchical control architecture is developed, in which a model predictive controller is coupled with a PSO-based compensator in the outer loop, and an enhanced LQR with gain scheduling and rate relaxation is employed in the inner loop. This structure decouples position and attitude control while improving adaptability to time-varying disturbances.
- A PSO-compensated MPC (PSMC) scheme is designed to correct prediction mismatches and suppress external perturbations. By iteratively optimizing compensation terms based on tracking error feedback, the outer-loop control improves robustness without increasing the MPC horizon or computational load.
- An inner-loop LQR is augmented with gain scheduling and control-rate relaxation to enhance attitude convergence and reduce actuator fluctuation. The former adapts feedback gains online according to the system state, while the latter smooths control updates to avoid excessive rate changes. This combination accelerates tracking response and improves stability under uncertain conditions.
2. System Modeling and Problem
2.1. Quadrotor Dynamics
- The quadrotor is modeled as a rigid body with constant mass and moment of inertia.
- The center of mass of the UAV remains fixed and coincides with the geometric center of the frame.
- The UAV is subjected only to gravitational force and thrust generated by the propellers, while aerodynamic drag is neglected.
2.2. Problem Formulation
- The tracking error asymptotically or remains bounded within a small neighborhood.
- State and input constraints are satisfied: and .
- The controller is suitable for real-time embedded implementation.
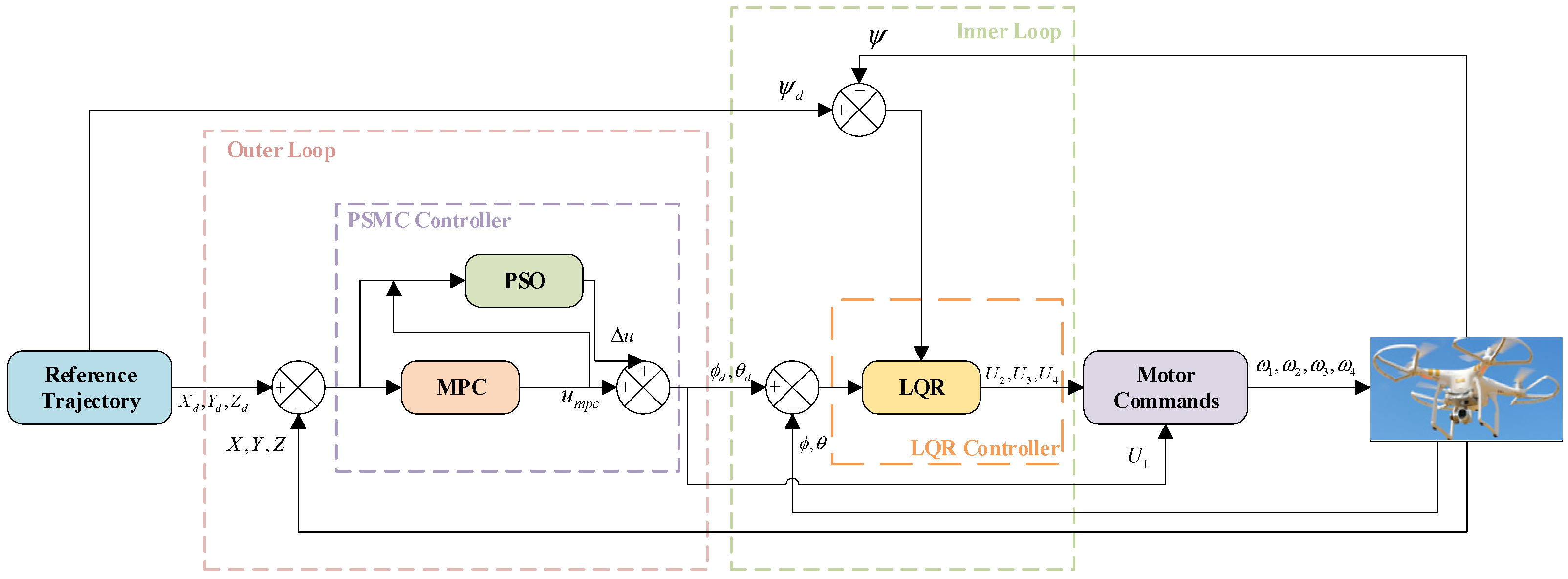
3. Hierarchical Control Architecture and Controller Design
3.1. Hierarchical Control Architecture
- The outer loop focuses on trajectory planning, constraint handling, and robustness enhancement through adaptive optimization.
- The inner loop guarantees high-bandwidth attitude stabilization and torque control.
3.2. Outer-Loop Controller
3.2.1. Particle Swarm Optimization
| Algorithm 1. Particle Swarm Optimization Procedure |
| Input: Objective function , number of particles , dimension , inertia weight , acceleration coefficients , , max iterations Initialize particle positions and velocities for = 1 to Initialize personal bests , evaluate Set For to DO For to DO Update velocity Update position Evaluate fitness If then If then END IF END IF END FOR END FOR return , Output: Global best position and value |
3.2.2. PSMC Outer-Loop Controller
- If , then update
- If , then update
| Algorithm 2. Execution Procedure of the PSMC Position Controller |
| Input: Current UAV state Desired reference , System matrices MPC horizons: prediction horizon , control horizon Weighting matrices Input and state constraints PSO parameters Compute tracking error: Linearize nonlinear UAV dynamics at operating point : Obtain linear system: Construct standard MPC cost function: Formulate MPC constraints: State limits: Input limits: Terminal condition: optional Solve convex MPC optimization problem to obtain Initialize PSO search around : Define particle positions as perturbations around Define PSO objective function: Run PSO optimizer (see Algorithm 1) to minimize Obtain best particle Compute final control input: Apply to UAV system Wait for next sampling interval and repeat Output: Optimized control input |
3.3. LQR Inner-Loop Controller
4. Lyapunov-Based Stability Analysis
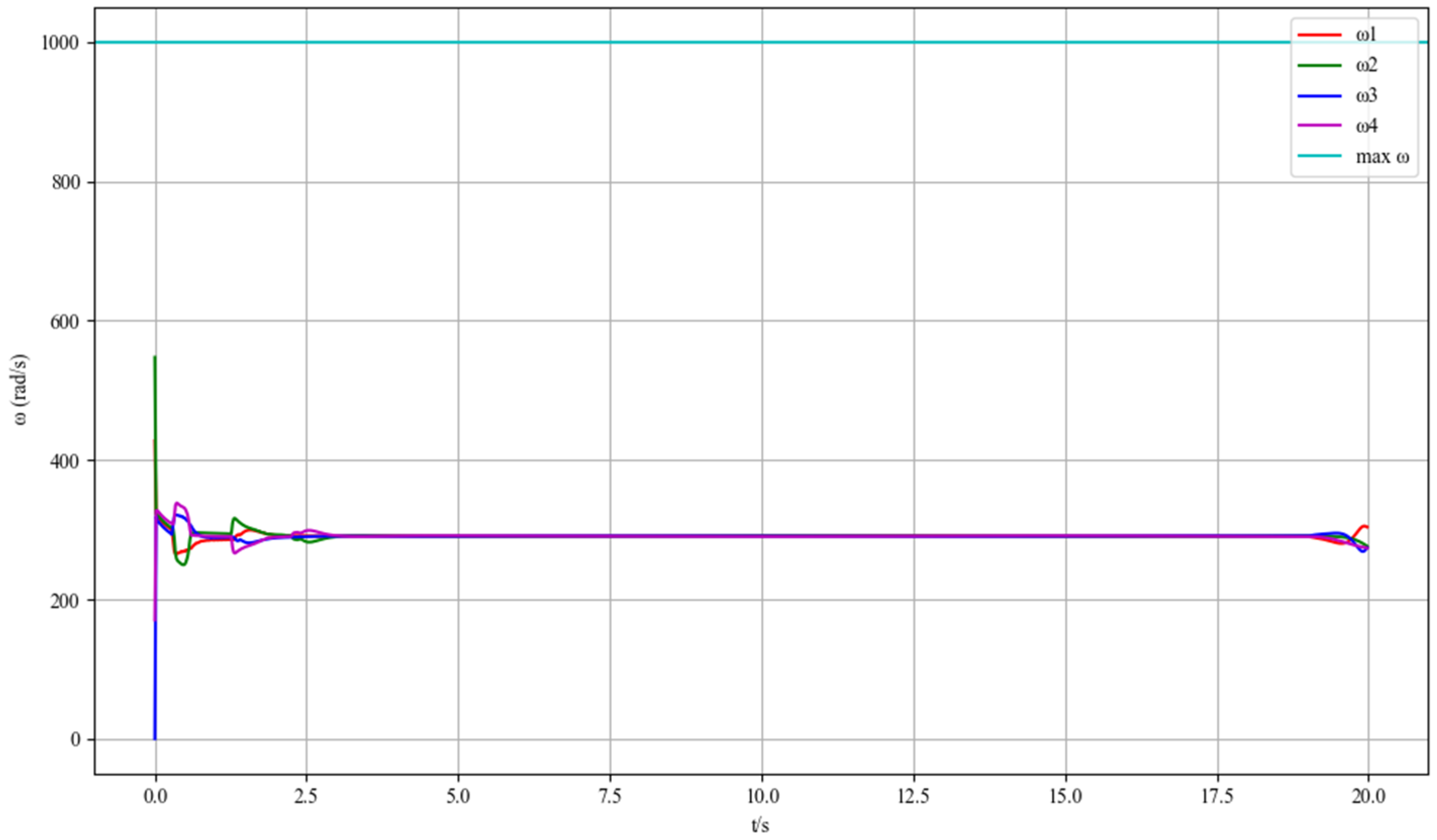
5. Simulation and Discussion
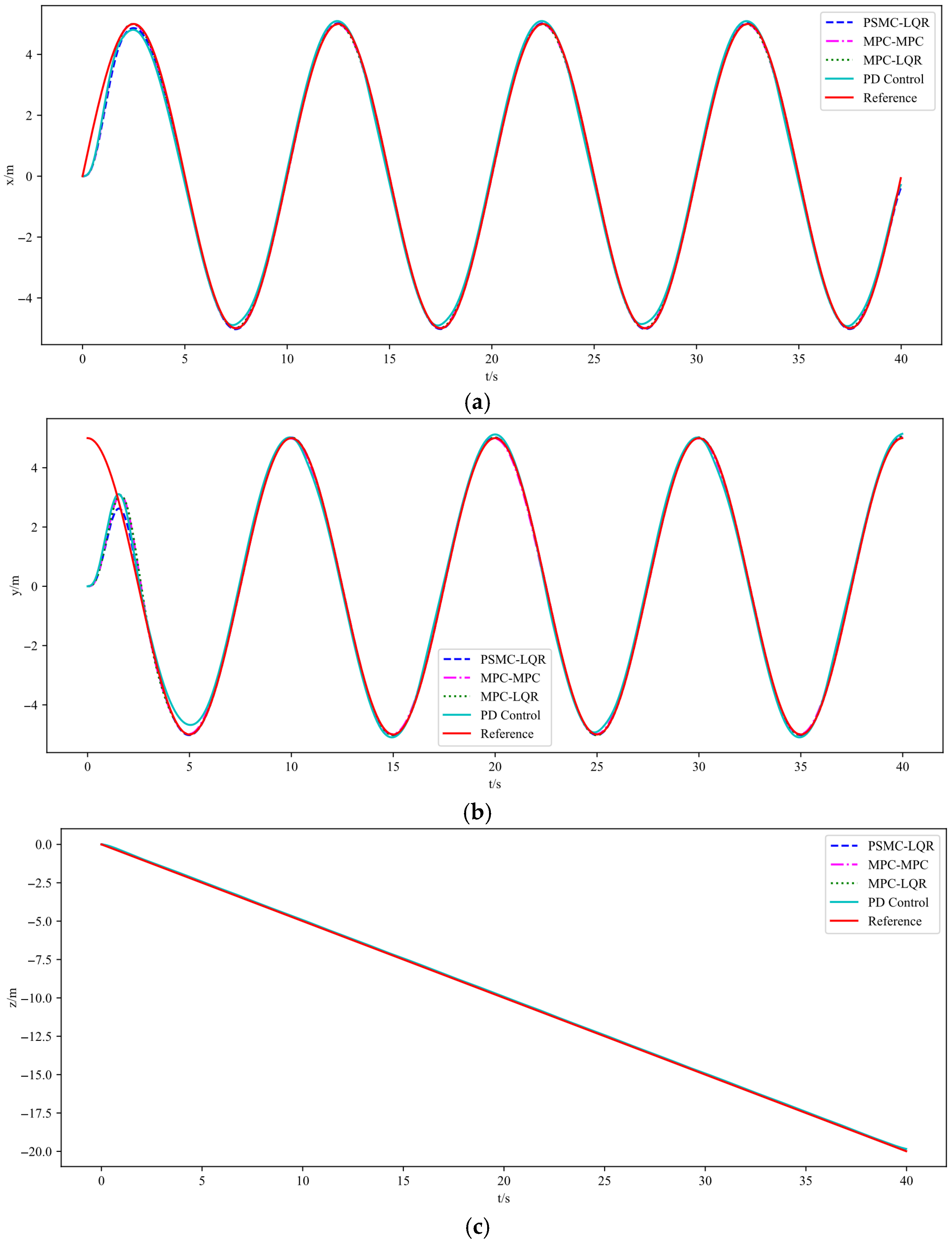
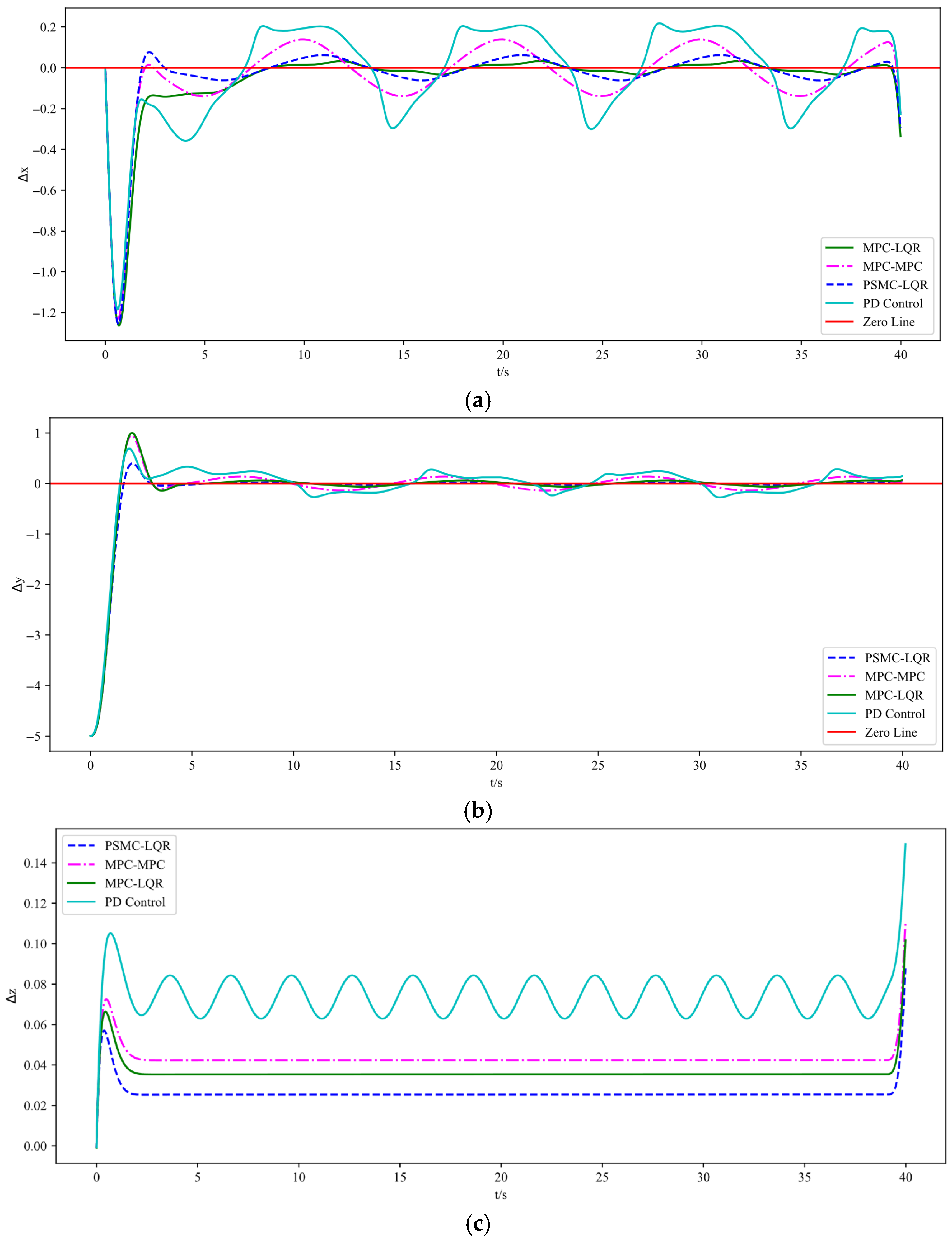
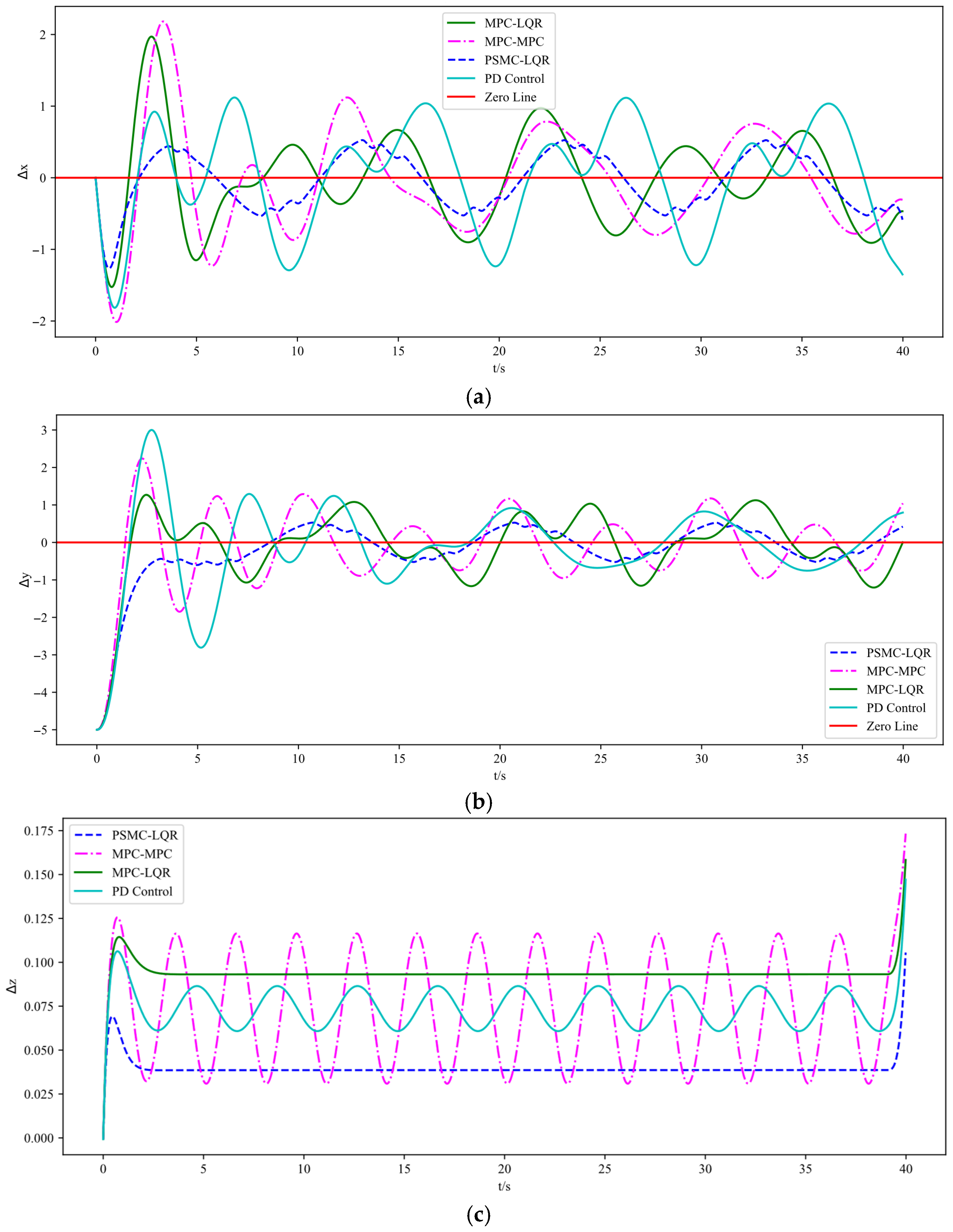
5.1. Trajectory Tracking Performance Evaluation in Calm Air Conditions
5.2. Trajectory Tracking Performance Evaluation in Wind Disturbance Conditions
5.3. Ablation Analysis of Component Contributions
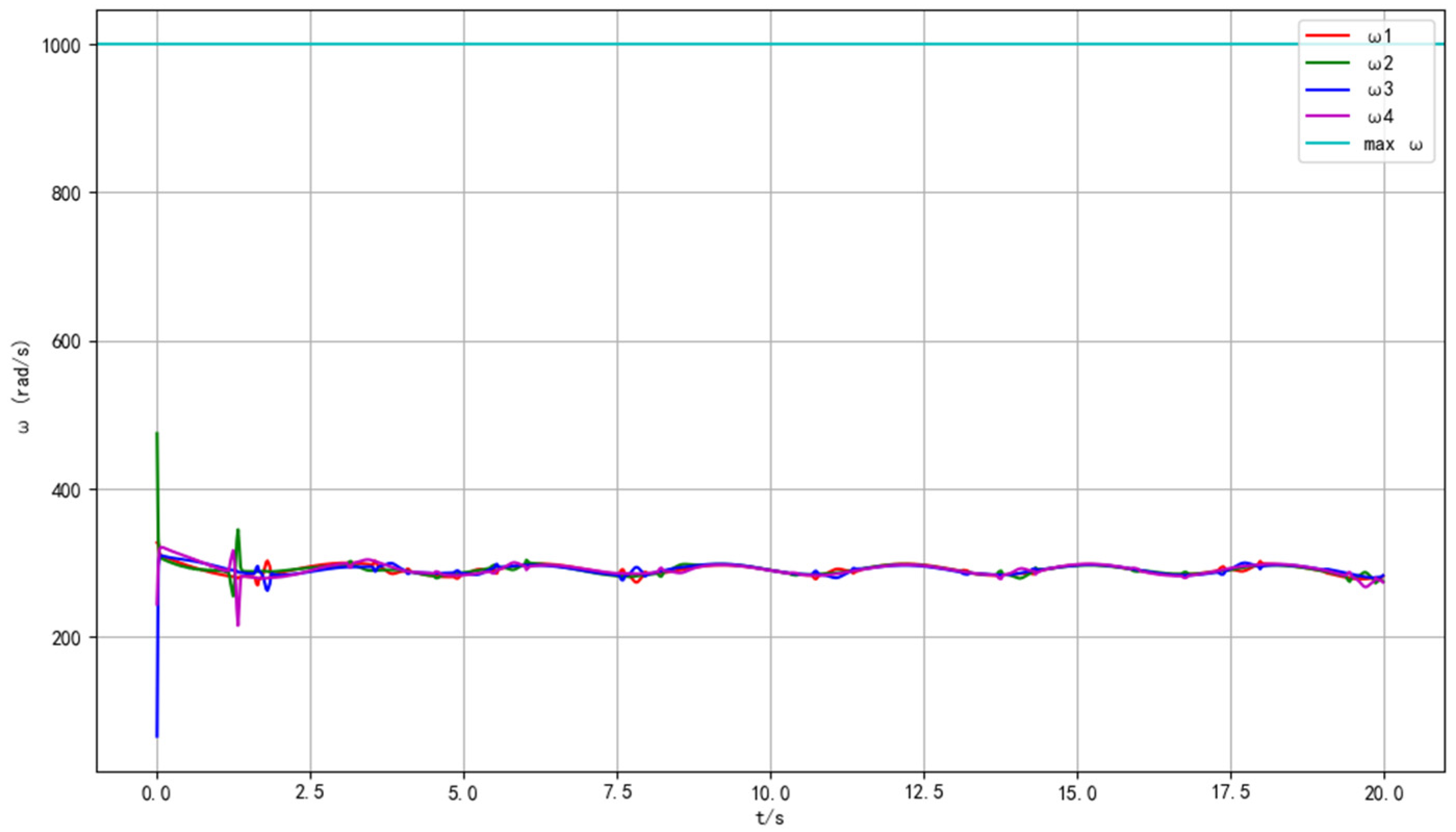
5.4. Computational Complexity Analysis
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Wang, H.; Li, Z.; Xiong, H.; Nian, X. Robust H∞ attitude tracking control of a quadrotor UAV on SO(3) via variation-based linearization and interval matrix approach. ISA Trans. 2019, 87, 10–16. [Google Scholar] [CrossRef]
- Wang, K.; Hua, C.; Chen, J.; Cai, M. Dual-loop integral sliding mode control for robust trajectory tracking of a quadrotor. Int. J. Syst. Sci. 2020, 51, 203–216. [Google Scholar] [CrossRef]
- Hoffmann, G.; Huang, H.; Waslander, S.; Tomlin, C. Quadrotor helicopter flight dynamics and control: Theory and experiment. In Proceedings of the AIAA Guidance, Navigation and Control Conference and Exhibit, Hilton Head, SC, USA, 20–23 August 2007; p. 6461. [Google Scholar]
- Cao, N.; Lynch, A.F. Inner–outer loop control for quadrotor UAVs with input and state constraints. IEEE Trans. Control Syst. Technol. 2015, 24, 1797–1804. [Google Scholar] [CrossRef]
- Liu, H.; Li, D.; Xi, J.; Zhong, Y. Robust attitude controller design for miniature quadrotors. Int. J. Robust Nonlinear Control 2016, 26, 681–696. [Google Scholar] [CrossRef]
- Cui, L.; Zhang, R.; Yang, H.; Zuo, Z. Adaptive super-twisting trajectory tracking control for an unmanned aerial vehicle under gust winds. Aerosp. Sci. Technol. 2021, 115, 106833. [Google Scholar] [CrossRef]
- Hou, Z.; Lu, P.; Tu, Z. Nonsingular terminal sliding mode control for a quadrotor UAV with a total rotor failure. Aerosp. Sci. Technol. 2020, 98, 105716. [Google Scholar] [CrossRef]
- Ma, R.; Han, J.; Ding, L. Finite-time trajectory tracking control of quadrotor UAV via adaptive RBF neural network with lumped uncertainties. Math. Biosci. Eng. 2023, 20, 1841–1855. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Alattas, K.A.; Bouteraa, Y.; Mofid, O.; Mobayen, S. Adaptive finite-time backstepping control tracker for quadrotor UAV with model uncertainty and external disturbance. Aerosp. Sci. Technol. 2023, 133, 108088. [Google Scholar] [CrossRef]
- Li, J.; Wan, L.; Li, J.; Hou, K. Adaptive backstepping control of quadrotor UAVs with output constraints and input saturation. Appl. Sci. 2023, 13, 8710. [Google Scholar] [CrossRef]
- Shao, S.; Chen, M.; Hou, J.; Zhao, Q. Event-triggered-based discrete-time neural control for a quadrotor UAV using disturbance observer. IEEE/ASME Trans. Mechatron. 2021, 26, 689–699. [Google Scholar] [CrossRef]
- Chen, M.; Shao, S.Y.; Jiang, B. Adaptive neural control of uncertain nonlinear systems using disturbance observer. IEEE Trans. Cybern. 2017, 47, 3110–3123. [Google Scholar] [CrossRef]
- Kuang, J.; Chen, M. Adaptive Sliding Mode Control for Trajectory Tracking of Quadrotor Unmanned Aerial Vehicles Under Input Saturation and Disturbances. Drones 2024, 8, 614. [Google Scholar] [CrossRef]
- Sun, Z.; Xiao, M.; Li, D.; Chu, J. Tracking controller design for quadrotor UAVs under external disturbances using a high-order sliding mode-assisted disturbance observer. Meas. Control 2025, 58, 155–167. [Google Scholar] [CrossRef]
- Kim, K.; Ahn, J.M.; Kim, S.K.; Kim, D.M.; Suk, J.; Lim, H.; Hur, G.; Kim, N.; Kim, B. Flight test of a flying-wing type UAV with partial wing loss using neural network controller. In Proceedings of the AIAA Guidance, Navigation, and Control (GNC) Conference, Boston, MA, USA, 19–22 August 2013; p. 5169. [Google Scholar]
- Garcia-Aunon, P.; Peñas, M.S.; de la Cruz García, J.M. Parameter selection based on fuzzy logic to improve UAV path-following algorithms. J. Appl. Log. 2017, 24, 62–75. [Google Scholar] [CrossRef]
- Nakamura-Zimmerer, T.; Gong, Q.; Kang, W. Neural network optimal feedback control with guaranteed local stability. IEEE Open J. Control Syst. 2022, 1, 210–222. [Google Scholar] [CrossRef]
- Gong, B.; Li, Y.; Zhang, L.; Ai, J. Adaptive Factor Fuzzy Controller for Keeping Multi-UAV Formation While Avoiding Dynamic Obstacles. Drones 2024, 8, 344. [Google Scholar] [CrossRef]
- Chipofya, M.; Lee, D.J.; Chong, K.T. Trajectory tracking and stabilization of a quadrotor using model predictive control of Laguerre functions. In Abstract and Applied Analysis; Hindawi Publishing Corporation: London, UK, 2015; Volume 2015, p. 916864. [Google Scholar]
- Khan, M.; Zafar, M.; Chatterjee, A. Barrier functions in cascaded controller: Safe quadrotor control. In Proceedings of the 2020 American Control Conference (ACC), Denver, CO, USA, 1–3 July 2020; IEEE: New York, NY, USA, 2020; pp. 1737–1742. [Google Scholar]
- Kooijman, D.; Schoellig, A.P.; Antunes, D.J. Trajectory Tracking for Quadrotors with Attitude Control on S2×S1. In Proceedings of the 2019 18th European Control Conference (ECC), Naples, Italy, 25–28 June 2019; IEEE: New York, NY, USA, 2019; pp. 4002–4009. [Google Scholar]
- Wang, D.; Pan, Q.; Shi, Y.; Hu, J.; Zhao, C. Efficient nonlinear model predictive control for quadrotor trajectory tracking: Algorithms and experiment. IEEE Trans. Cybern. 2021, 51, 5057–5068. [Google Scholar] [CrossRef] [PubMed]
- Pereira, J.C.; Leite, V.J.; Raffo, G.V. Nonlinear model predictive control on SE (3) for quadrotor aggressive maneuvers. J. Intell. Robot. Syst. 2021, 101, 62. [Google Scholar] [CrossRef]
- Sun, S.; Romero, A.; Foehn, P.; Kaufmann, E.; Scaramuzza, D. A comparative study of nonlinear mpc and differential-flatness-based control for quadrotor agile flight. IEEE Trans. Robot. 2022, 38, 3357–3373. [Google Scholar] [CrossRef]
- Tian, J.; Zeng, Q.; Wang, P.; Wang, X. Active steering control based on preview theory for articulated heavy vehicles. PLoS ONE 2021, 16, e0252098. [Google Scholar] [CrossRef] [PubMed]
- Elkhatem, A.S.; Engin, S.N. Robust LQR and LQR-PI control strategies based on adaptive weighting matrix selection for a UAV position and attitude tracking control. Alex. Eng. J. 2022, 61, 6275–6292. [Google Scholar] [CrossRef]
- Tahir, Z.; Jamil, M.; Liaqat, S.A.; Mubarak, L.; Tahir, W.; Gilani, S.O. Design and development of optimal control system for quad copter UAV. Indian J. Sci. Technol. 2016, 9, 10–17485. [Google Scholar] [CrossRef]
- Okyere, E.; Bousbaine, A.; Poyi, G.T.; Joseph, A.K.; Andrade, J.M. LQR controller design for quad-rotor helicopters. J. Eng. 2019, 2019, 4003–4007. [Google Scholar] [CrossRef]
- Abbas, N.; Abbas, Z.; Zafar, S.; Ahmad, N.; Liu, X.; Khan, S.S.; Foster, E.D.; Larkin, S. Survey of advanced nonlinear control strategies for UAVs: Integration of sensors and hybrid techniques. Sensors 2024, 24, 3286. [Google Scholar] [CrossRef] [PubMed]
- Li, R.; Yang, Z.; Yan, G.; Jian, L.; Li, G.; Li, Z. Robust approximate optimal trajectory tracking control for quadrotors. Aerospace 2024, 11, 149. [Google Scholar] [CrossRef]
- Madeiras, J.; Cardeira, C.; Oliveira, P. Position and attitude tracking controllers using Lyapunov transformations for quadrotors. J. Intell. Robot. Syst. 2024, 110, 9. [Google Scholar] [CrossRef]
- Wang, Z.; Zhang, Y. Research on Prediction-PID Compound Control of Quadrotor UAV. Control Eng. China 2021, 28, 1390–1397. [Google Scholar]
- Zhang, K.; Chen, J.; Chang, Y.; Shi, Y. EKF-based LQR tracking control of a quadrotor helicopter subject to uncertainties. In Proceedings of the IECON 2016-42nd Annual Conference of the IEEE Industrial Electronics Society, Florence, Italy, 23–26 October 2016; IEEE: New York, NY, USA, 2016; pp. 5426–5431. [Google Scholar]
- Marini, F.; Walczak, B. Particle swarm optimization (PSO). A tutorial. Chemom. Intell. Lab. Syst. 2015, 149, 153–165. [Google Scholar] [CrossRef]




| Parameter | Value |
|---|---|
| Mass | |
| Gravitational acceleration | |
| Moment of inertia about the X-axis | |
| Moment of inertia about the Y-axis | |
| Moment of inertia about the Z-axis |
| Metric | MPC-MPC | MPC-LQR | PSMC-LQR | PD Control |
|---|---|---|---|---|
| X-Error Variance | 0.03586 | 0.03400 | 0.03067 | 0.05741 |
| Y-Error Variance | 0.47491 | 0.46824 | 0.46974 | 0.47777 |
| Z-Error Variance | 0.000031 | 0.000028 | 0.000025 | 0.000104 |
| X-Mean Error | 0.1117 | 0.0775 | 0.0673 | 0.1852 |
| Y-Mean Error | 0.2150 | 0.1746 | 0.1447 | 0.2719 |
| Z-Mean Error | 0.04334 | 0.03638 | 0.02621 | 0.7455 |
| Disturbance | (m) | (Hz) | (rad) |
|---|---|---|---|
| 5 | 0 | ||
| 4 | 0.5 | ||
| 2 | 0.2 | 0.5 |
| Metric | MPC-MPC | MPC-LQR | PSMC-LQR | PD Control |
|---|---|---|---|---|
| X-Error Variance | 0.55657 | 0.53966 | 0.14670 | 0.55657 |
| Y-Error Variance | 1.02599 | 0.90950 | 0.64590 | 1.35781 |
| Z-Error Variance | 0.00984 | 0.000045 | 0.000030 | 0.000126 |
| X-Mean Error | 0.6063 | 0.5109 | 0.3370 | 0.6103 |
| Y-Mean Error | 0.7352 | 0.6464 | 0.4768 | 0.7970 |
| Z-Mean Error | 0.0748 | 0.0938 | 0.0395 | 0.0743 |
| Method | Control Effort | |||||
|---|---|---|---|---|---|---|
| MPC–LQR (baseline) | 12.48 | 14.67 | 21.80 | 39.86 | 85.19 | 43.52 |
| MPC–LQR + PSO | 12.52 | 14.63 | 21.88 | 39.96 | 85.32 | 43.61 |
| MPC–LQR + Scheduling only | 12.40 | 14.72 | 22.32 | 40.17 | 84.89 | 43.81 |
| MPC–LQR + Relaxation only | 12.10 | 12.82 | 5.93 | 28.31 | 70.70 | 22.14 |
| MPC–LQR (inner-only) | 12.10 | 12.81 | 5.94 | 28.31 | 70.68 | 22.14 |
| PSMC–LQR (full) | 12.06 | 12.78 | 5.91 | 28.25 | 70.51 | 22.12 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, S.; Zhu, X.; Fang, Y.; Zhan, Y.; Han, D.; Qiu, Y.; Sun, Y. A Hierarchical PSMC–LQR Control Framework for Accurate Quadrotor Trajectory Tracking. Sensors 2025, 25, 7032. https://doi.org/10.3390/s25227032
Chen S, Zhu X, Fang Y, Zhan Y, Han D, Qiu Y, Sun Y. A Hierarchical PSMC–LQR Control Framework for Accurate Quadrotor Trajectory Tracking. Sensors. 2025; 25(22):7032. https://doi.org/10.3390/s25227032
Chicago/Turabian StyleChen, Shiliang, Xinyu Zhu, Yichao Fang, Yucheng Zhan, Dan Han, Yun Qiu, and Yaru Sun. 2025. "A Hierarchical PSMC–LQR Control Framework for Accurate Quadrotor Trajectory Tracking" Sensors 25, no. 22: 7032. https://doi.org/10.3390/s25227032
APA StyleChen, S., Zhu, X., Fang, Y., Zhan, Y., Han, D., Qiu, Y., & Sun, Y. (2025). A Hierarchical PSMC–LQR Control Framework for Accurate Quadrotor Trajectory Tracking. Sensors, 25(22), 7032. https://doi.org/10.3390/s25227032





