Optimizing Fuel Consumption Prediction Model Without an On-Board Diagnostic System in Deep Learning Frameworks
Abstract
1. Introduction
- We propose a method that combines Bayesian optimization with the LSTM network to optimize probabilistically the hyperparameters of the network, i.e., the learning rate, learning rate decay, batch size, the number of hidden layers, and the number of nodes in each hidden layer. The method models the outcome of each hyperparameter combination as a probabilistic function.
- The method presents an FCR prediction model trained using the MC-Dropout method to quantify epistemic uncertainty, improving robustness to distribution shift.
- The method requires only the vehicle translational speed, longitudinal acceleration, and throttle position at inference time.
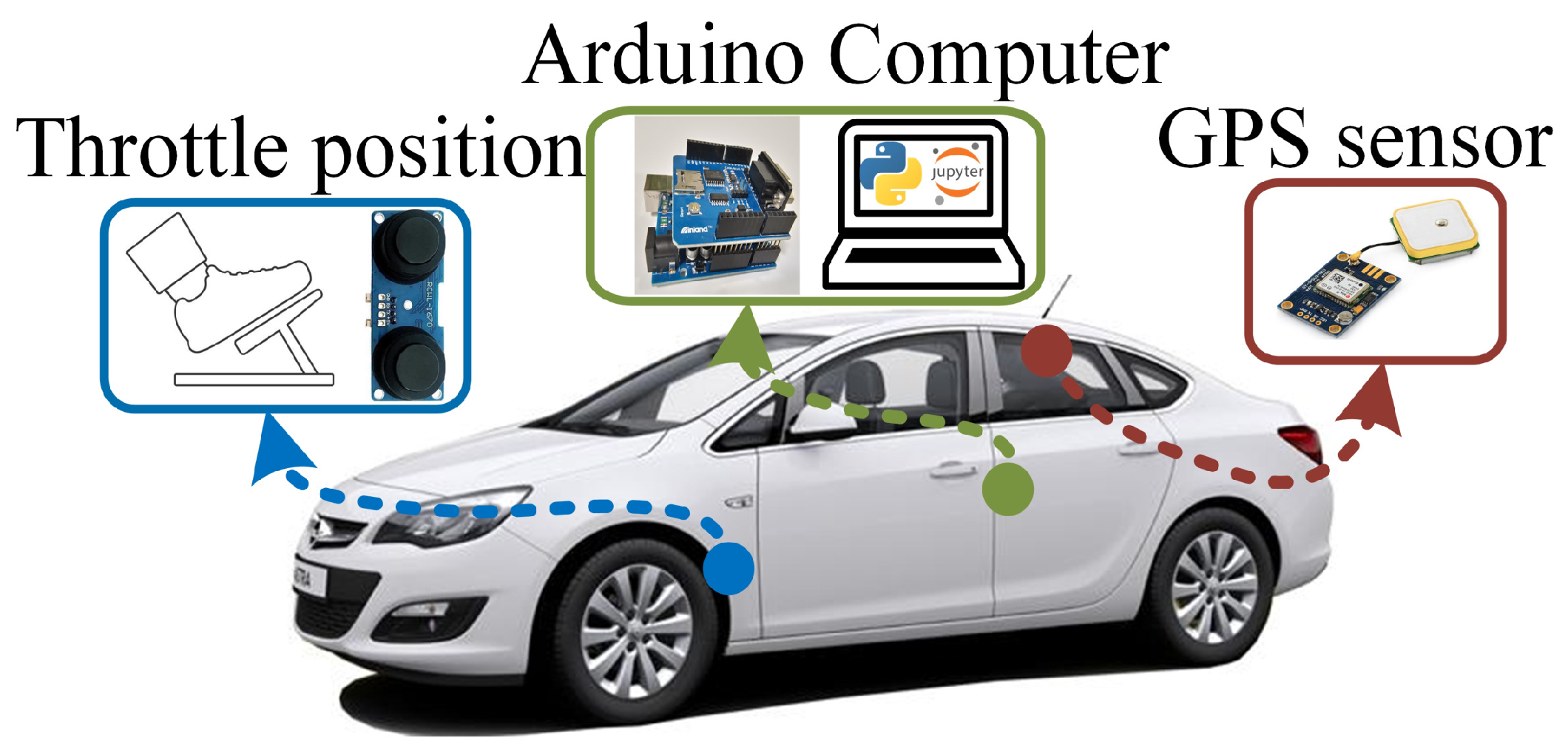
2. System Description and Problem Formulation
3. Deep Learning-Based Prediction Model
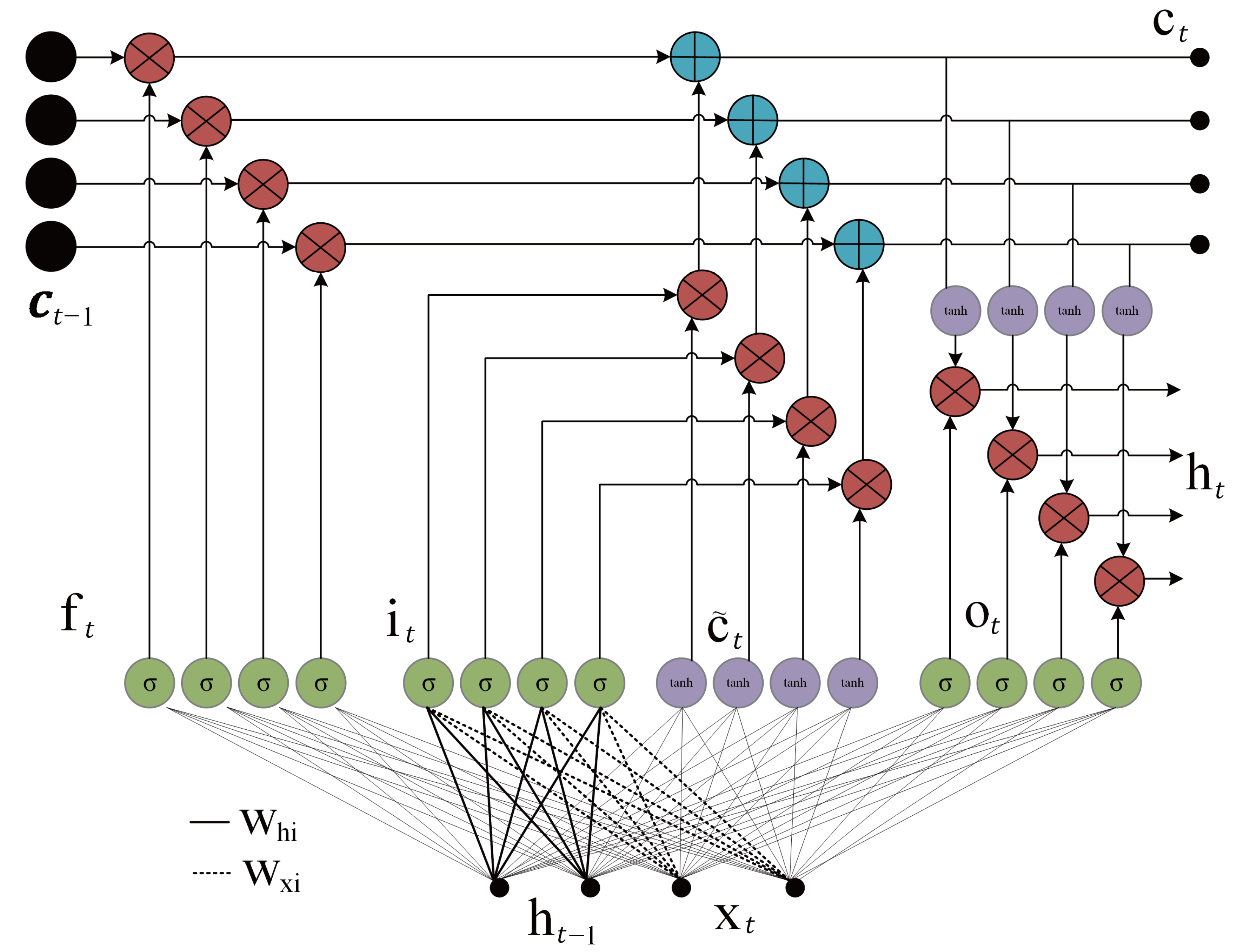
3.1. Long Short-Term Memory
3.2. Bidirectional LSTM
3.3. Bayesian Method-Based Hyperparameter Optimization
3.4. Ridge-Regularized Polynomial Model
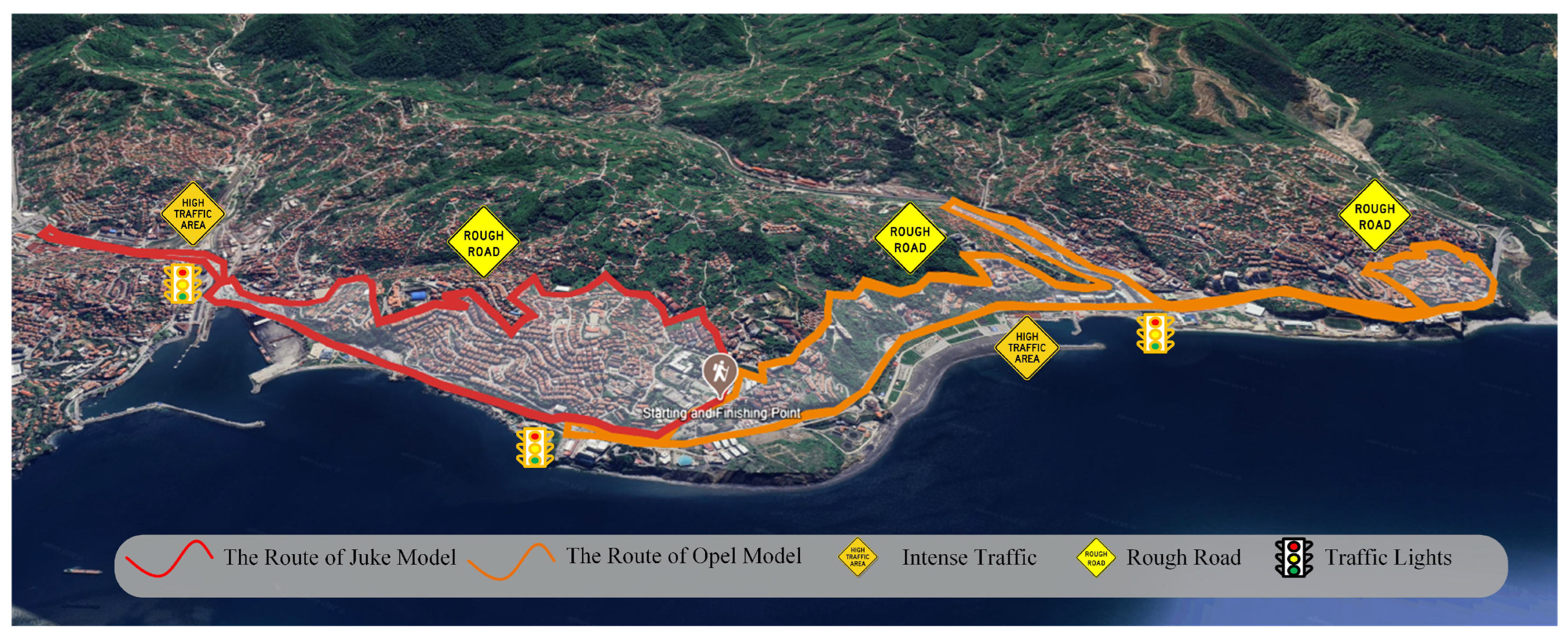
4. Data Collection
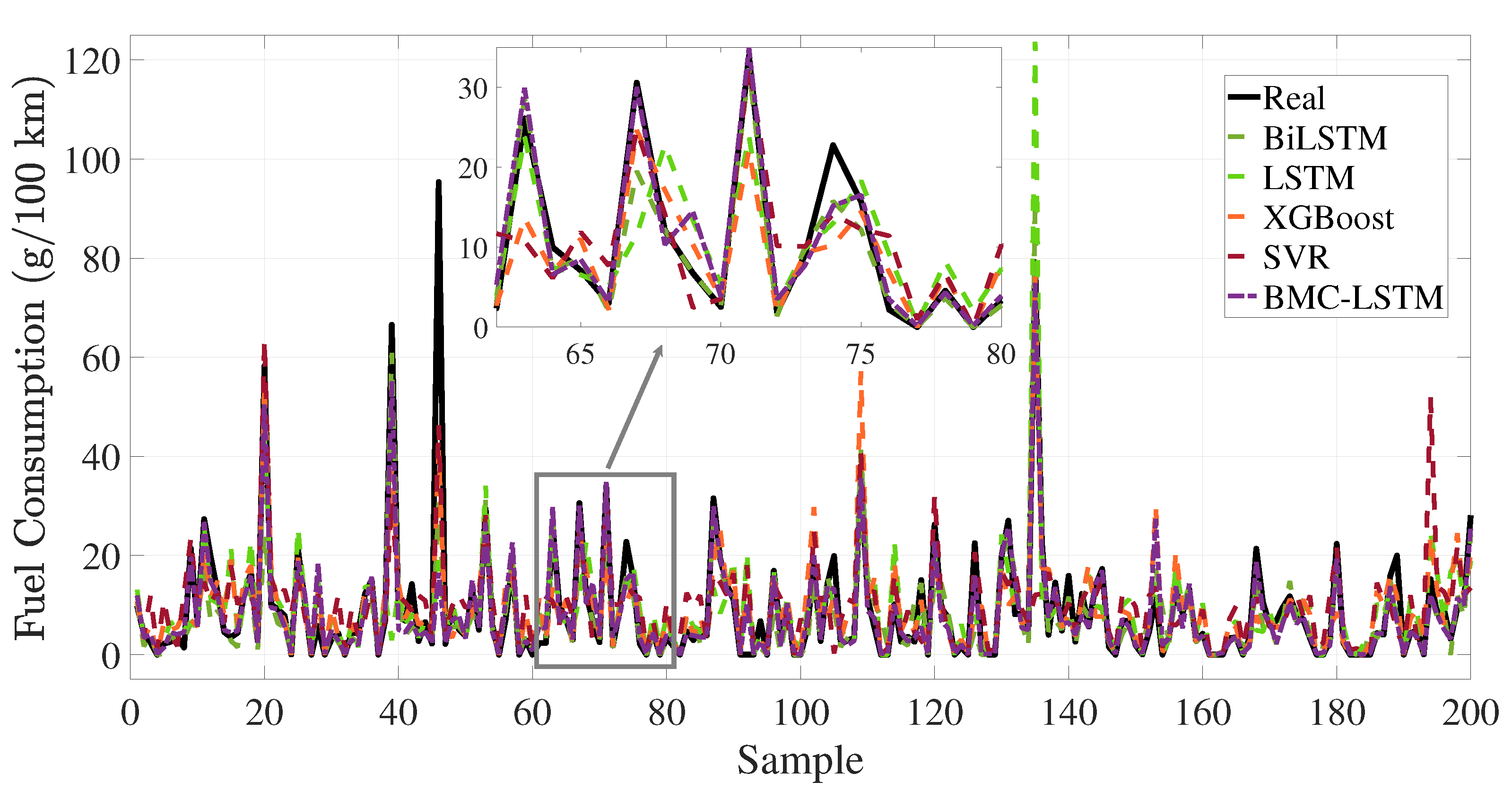
5. Performance Results of the Data-Driven Prediction Model
6. Conclusions
7. Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kabir, R.; Remias, S.M.; Waddell, J.; Zhu, D. Time-Series fuel consumption prediction assessing delay impacts on energy using vehicular trajectory. Transp. Res. Part D Transp. Environ. 2023, 117, 103678. [Google Scholar]
- Öztürk, A.T.; Kasliwal, A.; Fitzmaurice, H.; Kavvada, O.; Calvez, P.; Cohen, R.C.; González, M.C. A mesoscopic model of vehicular emissions informed by direct measurements and mobility science. Sustain. Cities Soc. 2025, 129, 106421. [Google Scholar] [CrossRef]
- Singh, M.; Dubey, R.K. Deep learning model based CO2 emissions prediction using vehicle telematics sensors data. IEEE Trans. Intell. Veh. 2021, 8, 768–777. [Google Scholar] [CrossRef]
- Ammar, M.; Janjua, H.; Thangarajan, A.S.; Crispo, B.; Hughes, D. Securing the on-board diagnostics port (obd-ii) in vehicles. SAE Int. J. Transp. Cybersecur. Priv. 2020, 2, 83–106. [Google Scholar]
- Jiansen, Y.; Konghui, G.; Haitao, D.; Jianwei, Z.; Bin, X. The application of sae j1939 protocol in automobile smart and integrated control system. In Proceedings of the 2010 International Conference on Computer, Mechatronics, Control and Electronic Engineering, Changchun, China, 24–26 August 2010; IEEE: New York, NY, USA, 2010; Volume 3, pp. 412–415. [Google Scholar]
- Wang, J.; Wang, R.; Yin, H.; Wang, Y.; Wang, H.; He, C.; Liang, J.; He, D.; Yin, H.; He, K. Assessing heavy-duty vehicles (HDVs) on-road NOx emission in China from on-board diagnostics (OBD) remote report data. Sci. Total Environ. 2022, 846, 157209. [Google Scholar] [CrossRef]
- Zhao, D.; Li, H.; Hou, J.; Gong, P.; Zhong, Y.; He, W.; Fu, Z. A review of the data-driven prediction method of vehicle fuel consumption. Energies 2023, 16, 5258. [Google Scholar] [CrossRef]
- Campos-Ferreira, A.E.; Lozoya-Santos, J.d.J.; Tudon-Martinez, J.C.; Mendoza, R.A.R.; Vargas-Martínez, A.; Morales-Menendez, R.; Lozano, D. Vehicle and driver monitoring system using on-board and remote sensors. Sensors 2023, 23, 814. [Google Scholar] [CrossRef]
- Li, S.; Li, G.; He, L.; Wang, H.; Ji, L.; Wang, J.; Chen, W.; Kang, Y.; Yin, H. Heavy-duty diesel vehicle NOX emissions and fuel consumption: Remote on-board monitoring analysis. Transp. Res. Part D Transp. Environ. 2025, 146, 104875. [Google Scholar] [CrossRef]
- Qu, L.; Wang, W.; Li, M.; Xu, X.; Shi, Z.; Mao, H.; Jin, T. Dependence of pollutant emission factors and fuel consumption on driving conditions and gasoline vehicle types. Atmos. Pollut. Res. 2021, 12, 137–146. [Google Scholar] [CrossRef]
- Molina-Campoverde, J.J.; Zurita-Jara, J.; Molina-Campoverde, P. Driving Pattern Analysis, Gear Shift Classification, and Fuel Efficiency in Light-Duty Vehicles: A Machine Learning Approach Using GPS and OBD II PID Signals. Sensors 2025, 25, 4043. [Google Scholar] [CrossRef]
- Udoh, J.; Lu, J.; Xu, Q. Application of Machine Learning to Predict CO2 Emissions in Light-Duty Vehicles. Sensors 2024, 24, 8219. [Google Scholar] [CrossRef]
- Jimenez-Palacios, J.L. Understanding and Quantifying Motor Vehicle Emissions with Vehicle Specific Power and TILDAS Remote Sensing. Ph.D.Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 1998. [Google Scholar]
- Frey, H.C.; Unal, A.; Chen, J.; Li, S. Modeling mobile source emissions based upon in-use and second-by-second data: Development of conceptual approaches for EPA’s new moves model. In Proceedings of the Proceedings, Annual Meeting of the Air and Waste Management Association, Pittsburgh, PA, USA, 26 June 2003. [Google Scholar]
- Wang, H.; Chen, C.; Huang, C.; Fu, L. On-road vehicle emission inventory and its uncertainty analysis for Shanghai, China. Sci. Total Environ. 2008, 398, 60–67. [Google Scholar]
- Lindhjem, C.E.; Pollack, A.K.; Slott, R.S.; Sawyer, R.F. Analysis of EPA’s Draft Plan for Emissions Modeling in MOVES and MOVES GHG; Research Report# CRC Project E-68; ENVIRON International Corporation: Novato, CA, USA, 2004. [Google Scholar]
- Mendes, M.; Duarte, G.; Baptista, P. Introducing specific power to bicycles and motorcycles: Application to electric mobility. Transp. Res. Part C Emerg. Technol. 2015, 51, 120–135. [Google Scholar] [CrossRef]
- Topić, J.; Škugor, B.; Deur, J. Neural network-based prediction of vehicle fuel consumption based on driving cycle data. Sustainability 2022, 14, 744. [Google Scholar] [CrossRef]
- Oehlerking, A.L. StreetSmart: Modeling Vehicle Fuel Consumption with Mobile Phone Sensor Data Through a Participatory Sensing Framework. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 2011. [Google Scholar]
- Varga, B.; Lulić, Z.; Tettamanti, T. Systematic Error Correction of SUMO Traffic Simulator’s HBEFA Vehicle Emission Model. In Proceedings of the 2024 IEEE International Conference on Electrical Systems for Aircraft, Railway, Ship Propulsion and Road Vehicles & International Transportation Electrification Conference (ESARS-ITEC), Naples, Italy, 26–29 November 2024; IEEE: New York, NY, USA, 2024; pp. 1–6. [Google Scholar]
- Stokić, M.; Momčilović, V.; Dimitrijević, B. A bilinear interpolation model for estimating commercial vehicles’ fuel consumption and exhaust emissions. Sustain. Futur. 2023, 5, 100105. [Google Scholar] [CrossRef]
- Zeng, X.; Jiang, X.; Song, D.; Bi, D.; Xiang, R. High-precision vehicle engine fuel consumption model based on data augmentation. Energy 2025, 333, 137400. [Google Scholar] [CrossRef]
- Ansari, A.; Abediasl, H.; Patel, P.R.; Hosseini, V.; Koch, C.R.; Shahbakhti, M. Estimating instantaneous fuel consumption of vehicles by using machine learning and real-time on-board diagnostics (OBD) data. In Proceedings of the Canadian Society for Mechanical Engineering International Congress 2022, Edmonton, AB, Canada, 5–8 June 2022. [Google Scholar]
- Moradi, E.; Miranda-Moreno, L. Vehicular fuel consumption estimation using real-world measures through cascaded machine learning modeling. Transp. Res. Part D Transp. Environ. 2020, 88, 102576. [Google Scholar]
- Abediasl, H.; Ansari, A.; Hosseini, V.; Koch, C.R.; Shahbakhti, M. Real-time vehicular fuel consumption estimation using machine learning and on-board diagnostics data. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2024, 238, 3779–3793. [Google Scholar] [CrossRef]
- Kanarachos, S.; Mathew, J.; Fitzpatrick, M.E. Instantaneous vehicle fuel consumption estimation using smartphones and recurrent neural networks. Expert Syst. Appl. 2019, 120, 436–447. [Google Scholar] [CrossRef]
- Yoo, S.r.; Shin, J.w.; Choi, S.H. Machine learning vehicle fuel efficiency prediction. Sci. Rep. 2025, 15, 14815. [Google Scholar] [CrossRef]
- Zhu, X.; Shen, X.; Chen, K.; Zhang, Z. Research on the prediction and influencing factors of heavy duty truck fuel consumption based on LightGBM. Energy 2024, 296, 131221. [Google Scholar] [CrossRef]
- Gong, J.; Shang, J.; Li, L.; Zhang, C.; He, J.; Ma, J. A comparative study on fuel consumption prediction methods of heavy-duty diesel trucks considering 21 influencing factors. Energies 2021, 14, 8106. [Google Scholar] [CrossRef]
- Liu, A.; Fan, P.; He, X.; Lu, H.; Yu, L.; Song, G. CatBoost-based fuel consumption modeling and explainable analysis for heavy-duty diesel trucks: Impact of engine, driving behavior, and vehicle weight. Energy 2025, 333, 137485. [Google Scholar] [CrossRef]
- Zhao, J.; Liang, K.; Guan, W.; Sang, H.; Zhou, S.; Deng, L.; Pan, M. Energy management strategy for diesel vehicles based on fuel consumption prediction. Transp. Res. Part D Transp. Environ. 2025, 146, 104896. [Google Scholar] [CrossRef]
- Gülmez, B. Stock price prediction with optimized deep LSTM network with artificial rabbits optimization algorithm. Expert Syst. Appl. 2023, 227, 120346. [Google Scholar] [CrossRef]
- Ewees, A.A.; Al-qaness, M.A.; Abualigah, L.; Abd Elaziz, M. HBO-LSTM: Optimized long short term memory with heap-based optimizer for wind power forecasting. Energy Convers. Manag. 2022, 268, 116022. [Google Scholar] [CrossRef]
- Liu, L.; Li, Y. Research on a photovoltaic power prediction model based on an IAO-LSTM optimization algorithm. Processes 2023, 11, 1957. [Google Scholar] [CrossRef]
- Bergstra, J.; Bengio, Y. Random search for hyper-parameter optimization. J. Mach. Learn. Res. 2012, 13, 281–305. [Google Scholar]
- Waqas, M.; Humphries, U.W. A critical review of RNN and LSTM variants in hydrological time series predictions. MethodsX 2024, 13, 102946. [Google Scholar] [CrossRef]
- awryńczuk, M.; Zarzycki, K. LSTM and GRU type recurrent neural networks in model predictive control: A Review. Neurocomputing 2025, 632, 129712. [Google Scholar] [CrossRef]
- Martínez-Ramón, M.; Ajith, M.; Kurup, A.R. Deep Learning: A Practical Introduction; John Wiley & Sons: Hoboken, NJ, USA, 2024. [Google Scholar]
- Singla, P.; Duhan, M.; Saroha, S. An ensemble method to forecast 24-h ahead solar irradiance using wavelet decomposition and BiLSTM deep learning network. Earth Sci. Inform. 2022, 15, 291–306. [Google Scholar] [CrossRef]
- Peng, S.; Zhu, J.; Wu, T.; Yuan, C.; Cang, J.; Zhang, K.; Pecht, M. Prediction of wind and PV power by fusing the multi-stage feature extraction and a PSO-BiLSTM model. Energy 2024, 298, 131345. [Google Scholar] [CrossRef]
- Michael, N.E.; Hasan, S.; Al-Durra, A.; Mishra, M. Short-term solar irradiance forecasting based on a novel Bayesian optimized deep Long Short-Term Memory neural network. Appl. Energy 2022, 324, 119727. [Google Scholar] [CrossRef]
- Gal, Y.; Ghahramani, Z. Dropout as a bayesian approximation: Representing model uncertainty in deep learning. In Proceedings of the International Conference on Machine Learning, New York, NY, USA, 19–24 June 2016; PMLR: Cambridge, MA, USA, 2016; pp. 1050–1059. [Google Scholar]
- Seoh, R. Qualitative analysis of monte carlo dropout. arXiv 2020, arXiv:2007.01720. [Google Scholar] [CrossRef]
- Folgoc, L.L.; Baltatzis, V.; Desai, S.; Devaraj, A.; Ellis, S.; Manzanera, O.E.M.; Nair, A.; Qiu, H.; Schnabel, J.; Glocker, B. Is MC dropout bayesian? arXiv 2021, arXiv:2110.04286. [Google Scholar] [CrossRef]
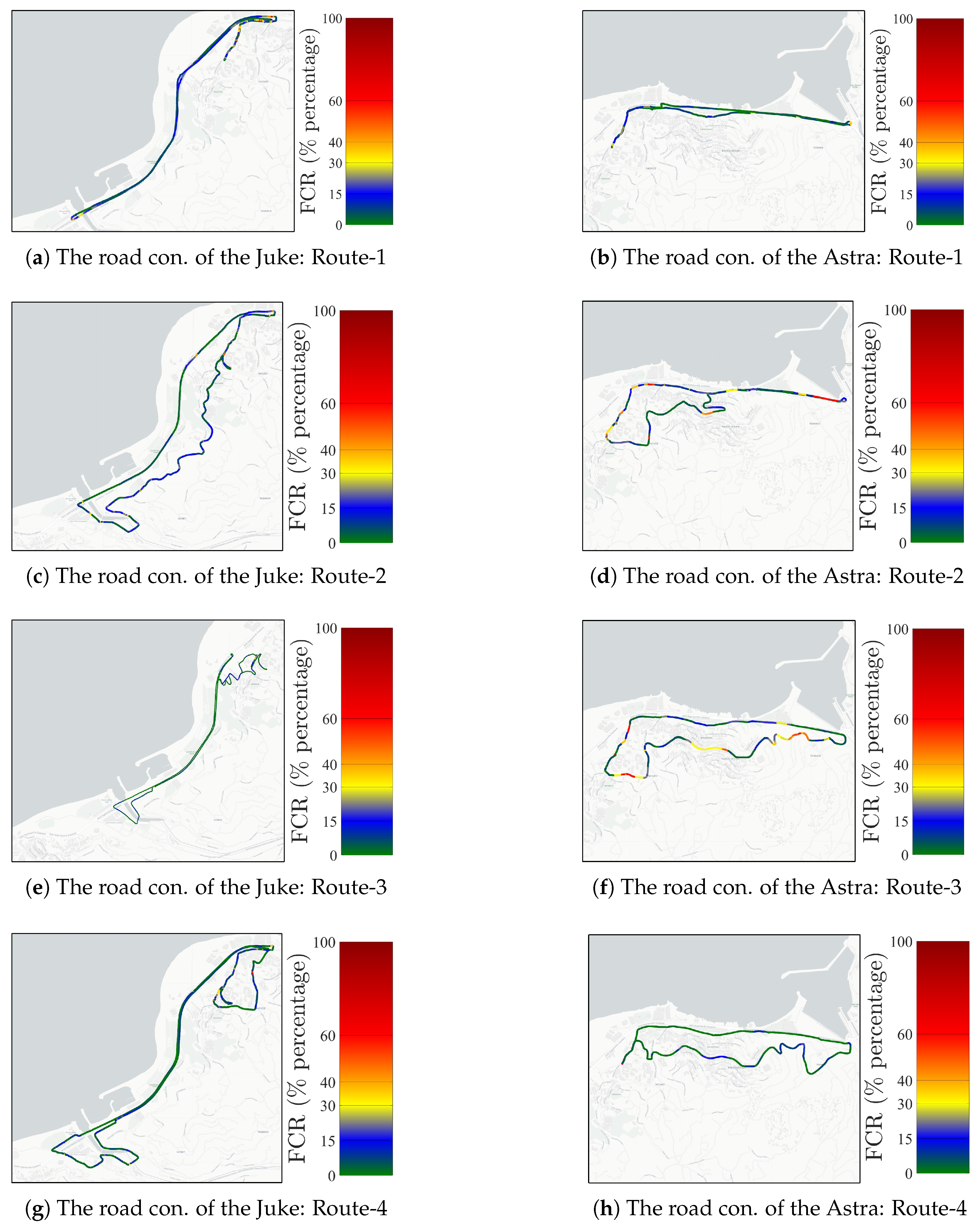
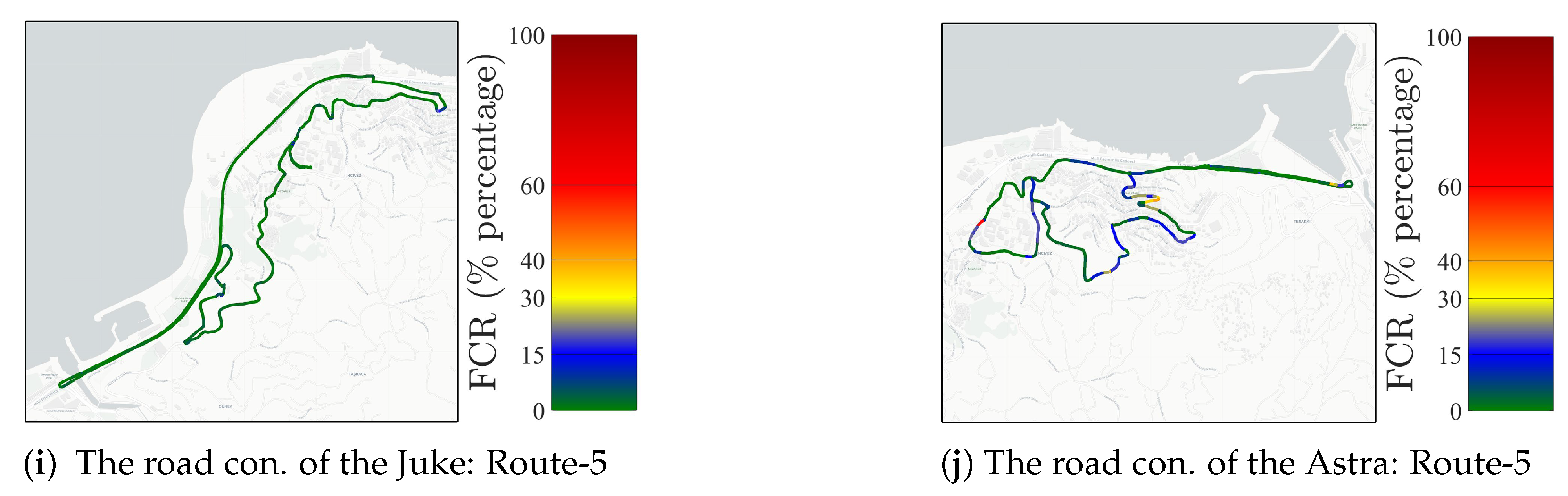
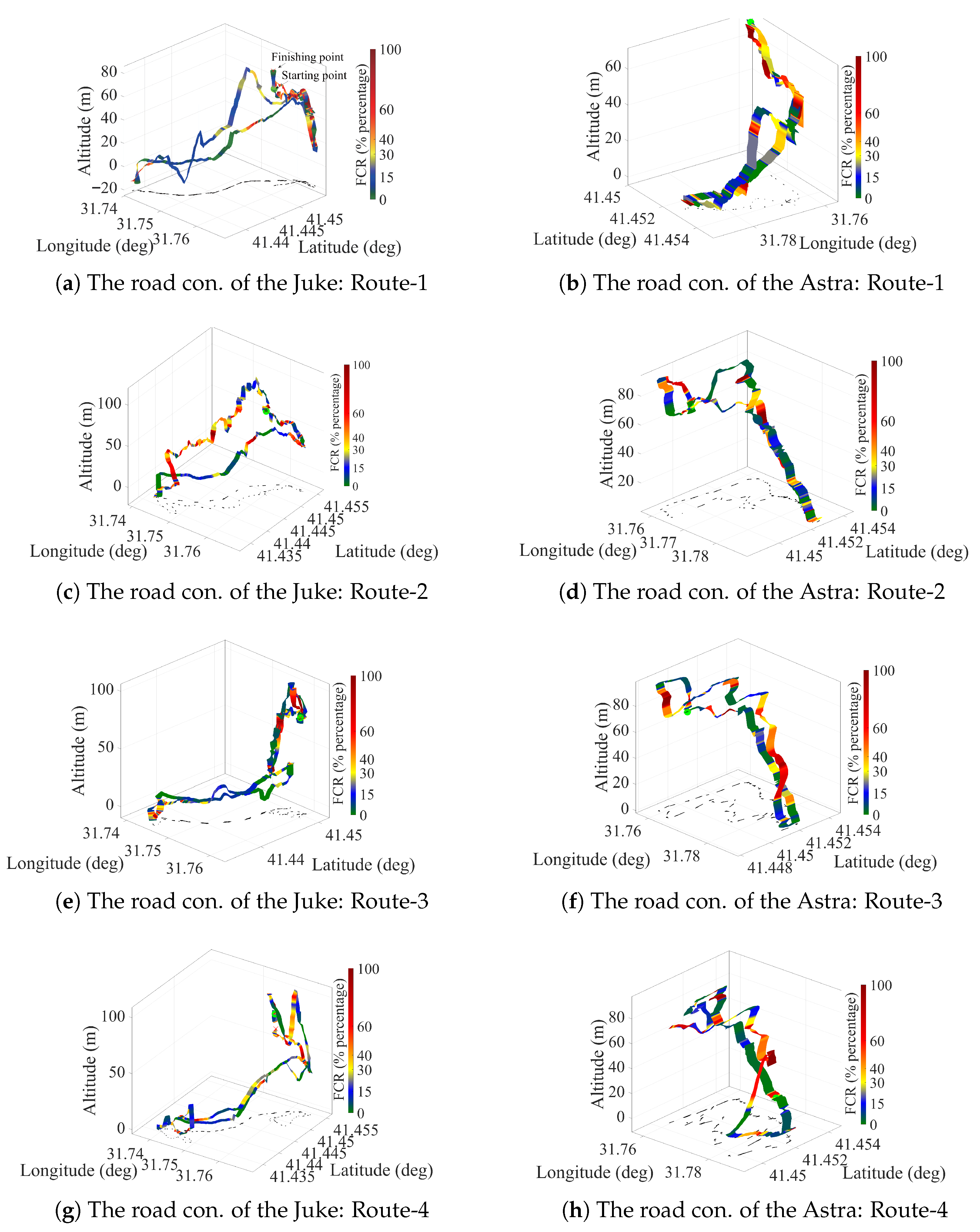
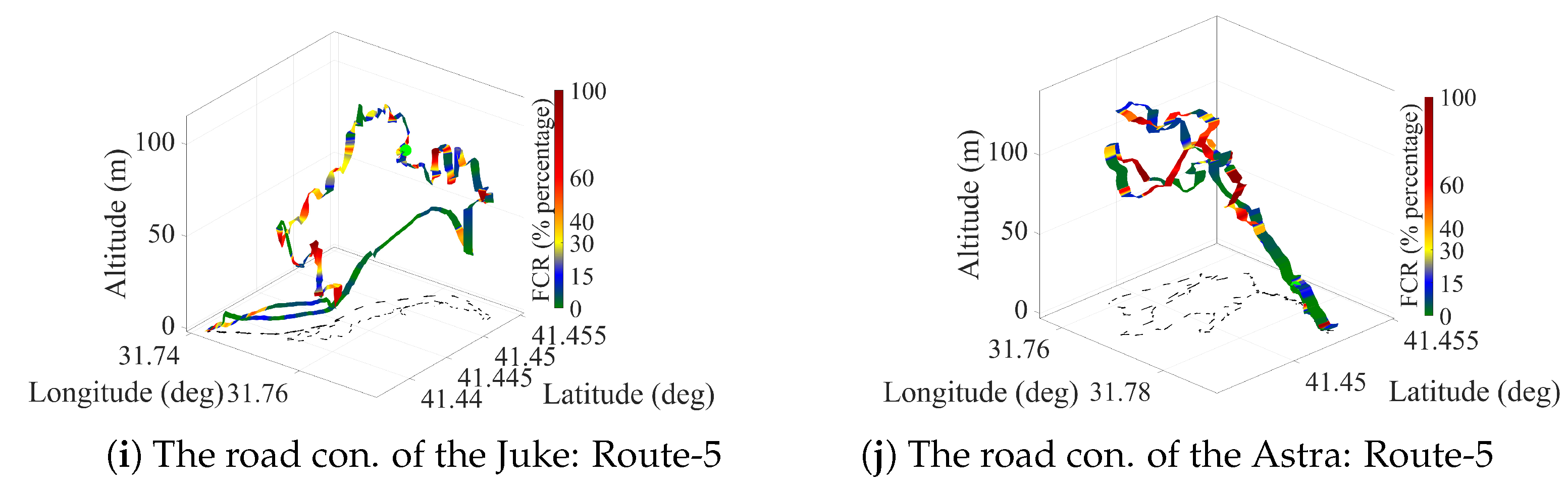


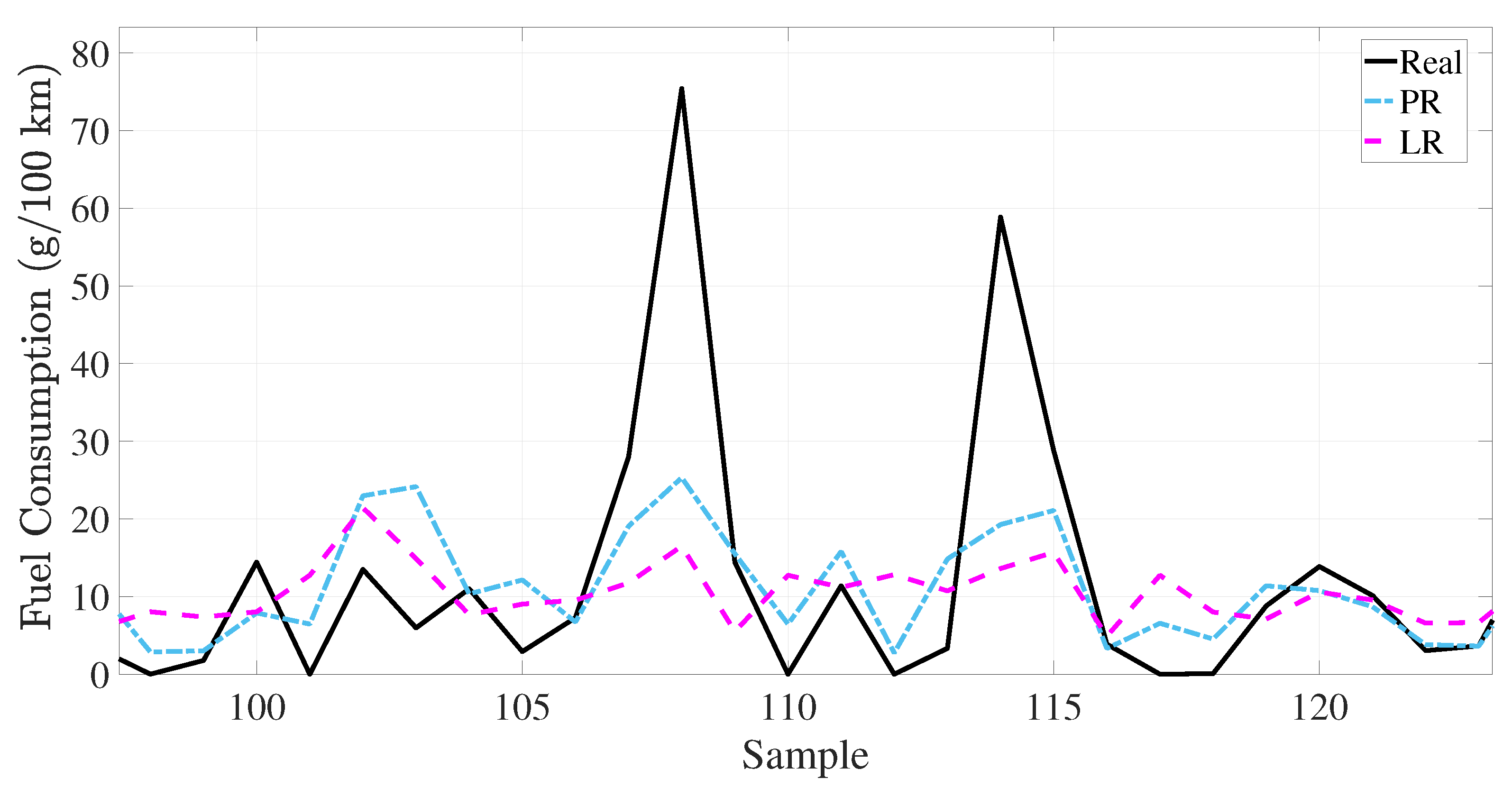

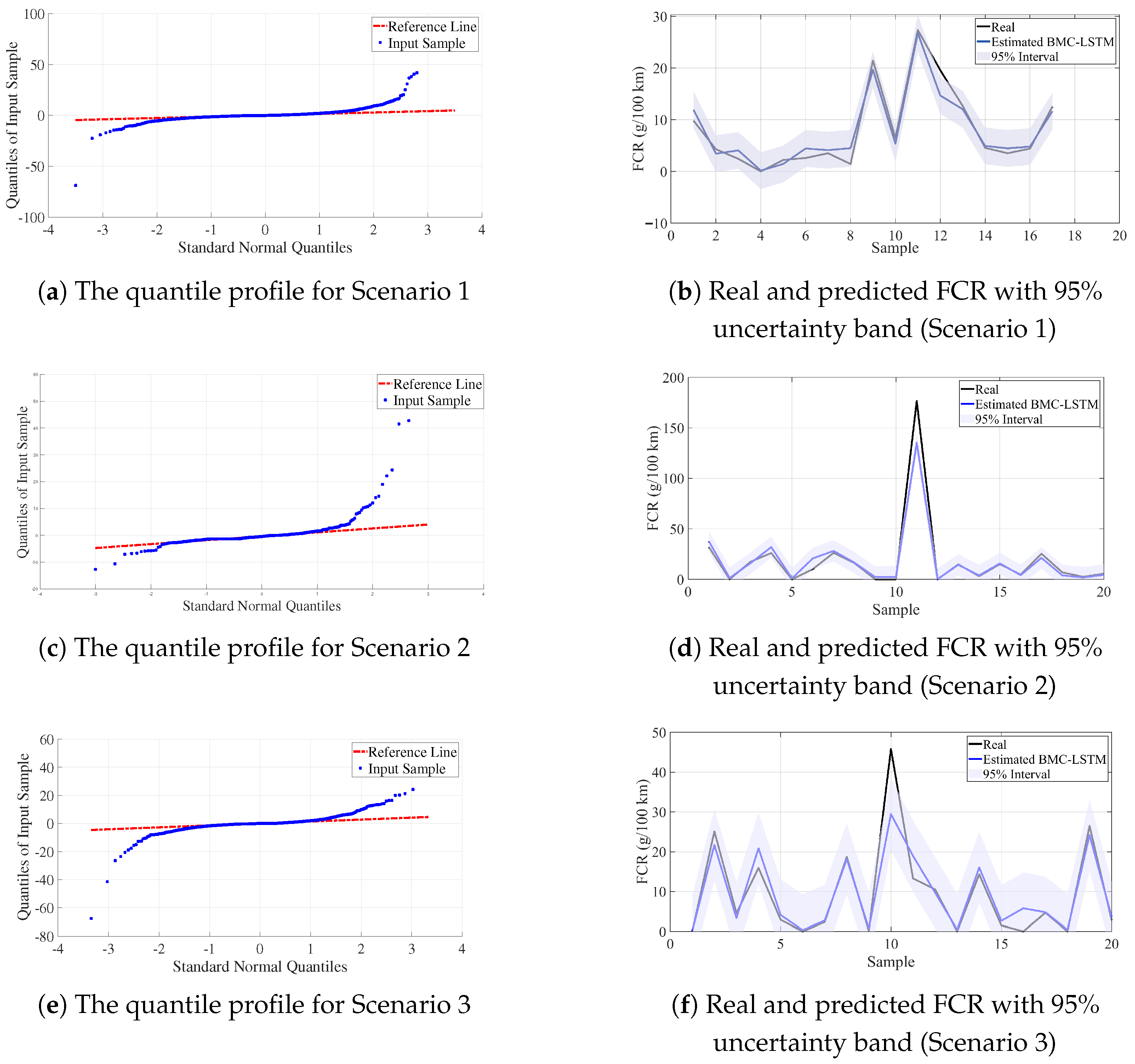
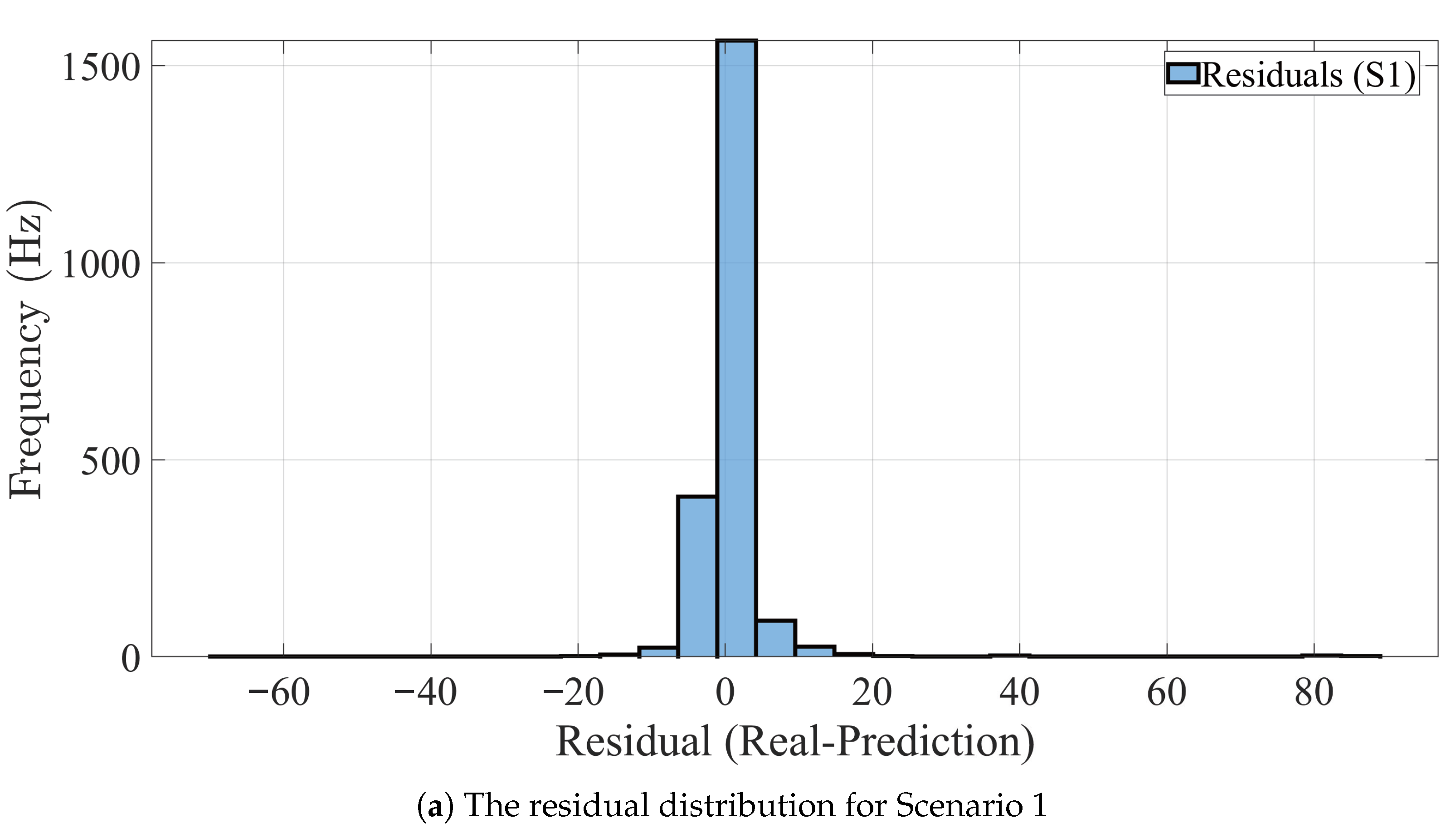
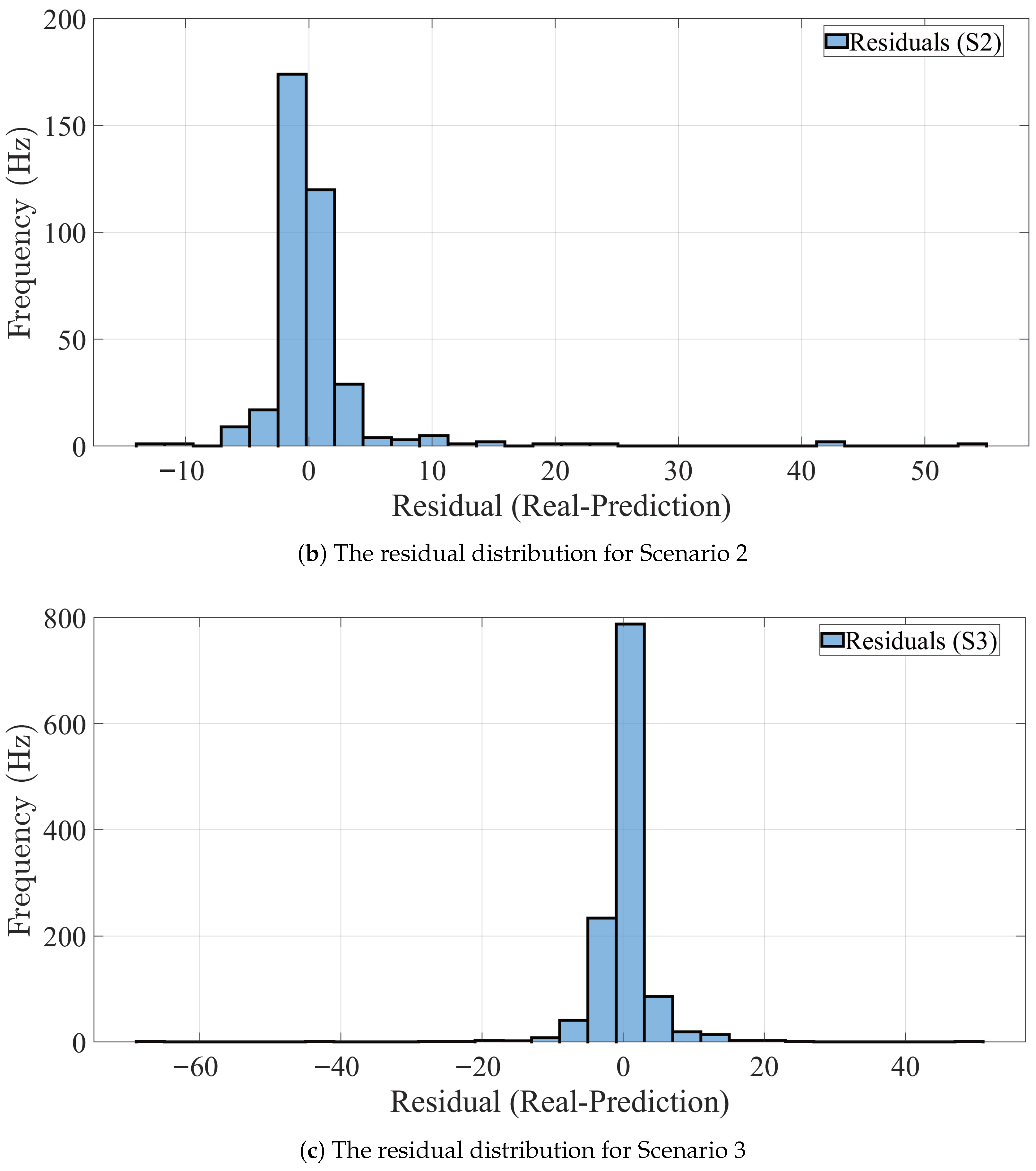
| Drive Name | Samples (N) | Dur. Time (min) | Road Cond. | Role in the S1/S2/S3 |
|---|---|---|---|---|
| Juke/Route-1 | 1160 | 19.3 | Flat | Training/Training/Test |
| Juke/Route-2 | 1051 | 17.52 | Extra Urban | Training/Training/Test |
| Juke/Route-3 | 1018 | 16.97 | Semi-flat | Training/Training/Test |
| Juke/Route-4 | 1395 | 23.25 | Flat | Test/Training/Test |
| Juke/Route-5 | 1202 | 20 | Urban | Test/Training/Test |
| Astra/Route-1 | 714 | 11.9 | Flat | Training/Test/Training |
| Astra/Route-2 | 1335 | 22.25 | Semi-Flat | Training/Test/Training |
| Astra/Route-3 | 861 | 14.35 | Urban | Training/Test/Training |
| Astra/Route-4 | 776 | 12.93 | Urban | Test/Test/Training |
| Astra/Route-5 | 1209 | 20.15 | Extra Urban | Test/Test/Training |
| Model | Hidden Layers (First and Second) | Layers | Dropout | Learning Rate | Epochs | Batch Size |
|---|---|---|---|---|---|---|
| BiLSTM | 128–128 | 4 | 0 | 0.001 | 60 | 16 |
| LSTM | 128–128 | 4 | 0 | 0.001 | 60 | 16 |
| BMC-LSTM | [64–180], [64–180] | 4 | [0.1–0.5] | [0.0001–0.01] | 60 | 16 |
| Scenario Number | Model | RMSE | MSE | MAE | |
|---|---|---|---|---|---|
| 1 | BiLSTM | 5.76 | 33.15 | 2.92 | 0.85 |
| 2-Layer LSTM | 9.42 | 88.75 | 4.94 | 0.60 | |
| PR | 13.77 | 189.71 | 7.34 | 0.15 | |
| LR | 14.52 | 210.75 | 8.13 | 0.06 | |
| XGBoost | 9.57 | 91.62 | 4.82 | 0.58 | |
| SVR | 11.05 | 122.08 | 5.91 | 0.44 | |
| BMC-LSTM | 5.54 | 30.66 | 2.04 | 0.86 | |
| 2 | BiLSTM | 8.12 | 65.95 | 3.65 | 0.79 |
| 2-Layer LSTM | 5.75 | 33.11 | 2.37 | 0.90 | |
| PR | 12.67 | 160.49 | 5.91 | 0.09 | |
| LR | 12.85 | 165.15 | 7.37 | 0.06 | |
| XGBoost | 13.48 | 181.62 | 5.89 | 0.45 | |
| SVR | 14.07 | 198.09 | 6.61 | 0.40 | |
| BMC-LSTM | 5.40 | 29.14 | 2.23 | 0.91 | |
| 3 | BiLSTM | 5.70 | 32.46 | 2.69 | 0.91 |
| 2-Layer LSTM | 4.97 | 24.74 | 2.55 | 0.92 | |
| PR | 14.01 | 196.37 | 7.68 | 0.22 | |
| LR | 15.60 | 243.30 | 9.11 | 0.03 | |
| XGBoost | 11.61 | 134.79 | 5.17 | 0.65 | |
| SVR | 13.55 | 183.55 | 6.46 | 0.52 | |
| BMC-LSTM | 4.57 | 20.89 | 2.14 | 0.95 |
| Metric | Scenario 1 | Scenario 2 | Scenario 3 |
|---|---|---|---|
| PICP | 94.12% | 96.51% | 95.86% |
| NLL | 1.9855 | 3.1049 | 2.9385 |
| OOD | 5.88% | 2.96% | 3.89% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Keskin, R.; Belge, E.; Kutoglu, S.H. Optimizing Fuel Consumption Prediction Model Without an On-Board Diagnostic System in Deep Learning Frameworks. Sensors 2025, 25, 7031. https://doi.org/10.3390/s25227031
Keskin R, Belge E, Kutoglu SH. Optimizing Fuel Consumption Prediction Model Without an On-Board Diagnostic System in Deep Learning Frameworks. Sensors. 2025; 25(22):7031. https://doi.org/10.3390/s25227031
Chicago/Turabian StyleKeskin, Rıdvan, Egemen Belge, and Senol Hakan Kutoglu. 2025. "Optimizing Fuel Consumption Prediction Model Without an On-Board Diagnostic System in Deep Learning Frameworks" Sensors 25, no. 22: 7031. https://doi.org/10.3390/s25227031
APA StyleKeskin, R., Belge, E., & Kutoglu, S. H. (2025). Optimizing Fuel Consumption Prediction Model Without an On-Board Diagnostic System in Deep Learning Frameworks. Sensors, 25(22), 7031. https://doi.org/10.3390/s25227031







