Urea Detection in Phosphate Buffer and Artificial Urine: A Simplified Kinetic Model of a pH-Sensitive EISCAP Urea Biosensor
Abstract
1. Introduction
2. Materials and Methods
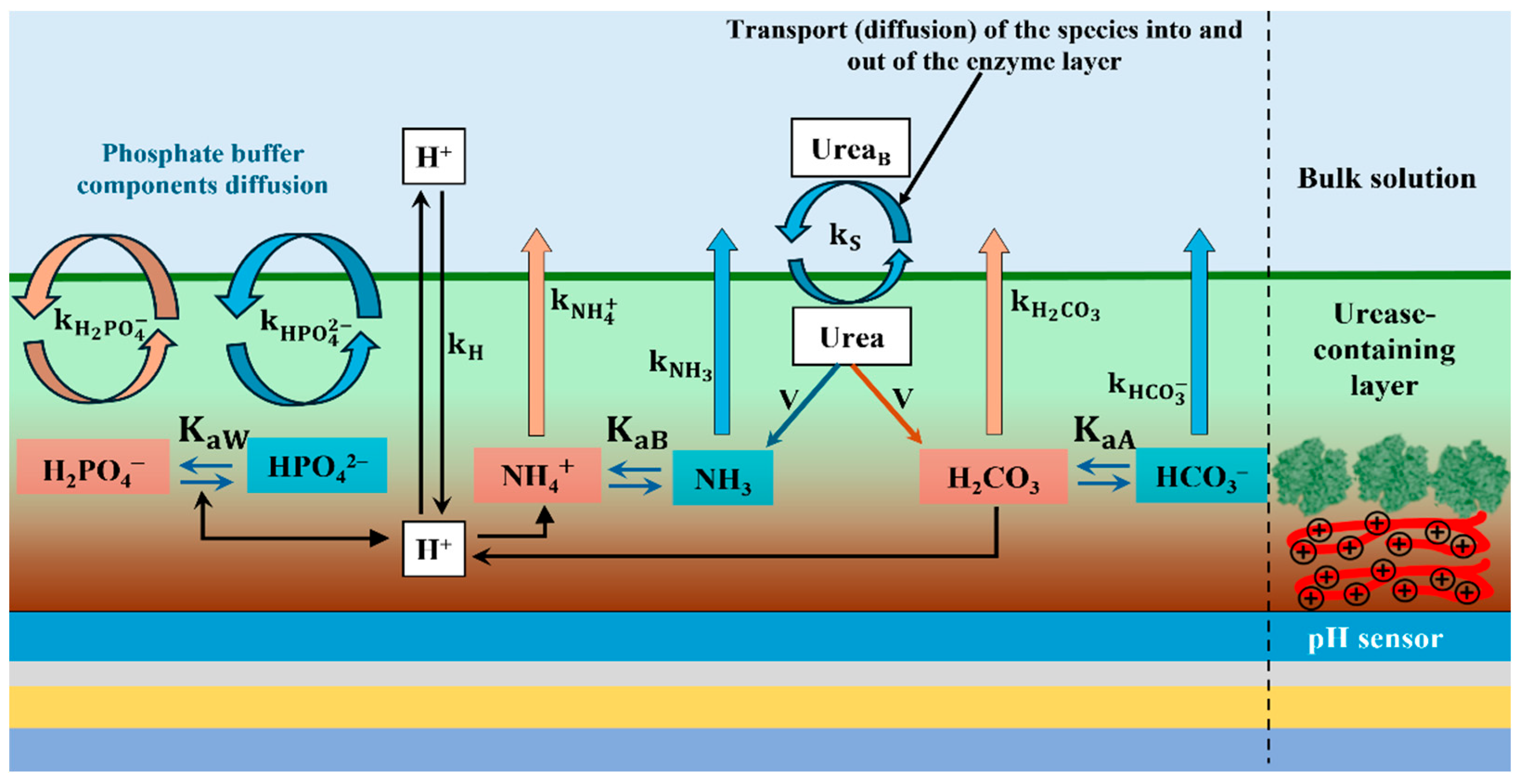
2.1. Diffusion-Kinetic Model Theory
- The geometry of the sensing layer does not have to be defined in kinetic model.
- Enzymatic reaction takes place by Michaelis–Menten kinetics, reaction occurs under steady-state conditions (i.e., ), and concentrations are constant.
- Dissociation constants are the same in both layers.
- All species, except the enzyme, diffuse bidirectionally through the enzyme layer, with transport rate constants being the same in both directions, independent of protonation (i.e., , etc.) and equal to each other (i.e., ) and that makes normalized constants .
2.2. Fitting and Minimization
3. Results and Discussion
3.1. Validation of Our Approach Against Glab et al.’s [24] Results
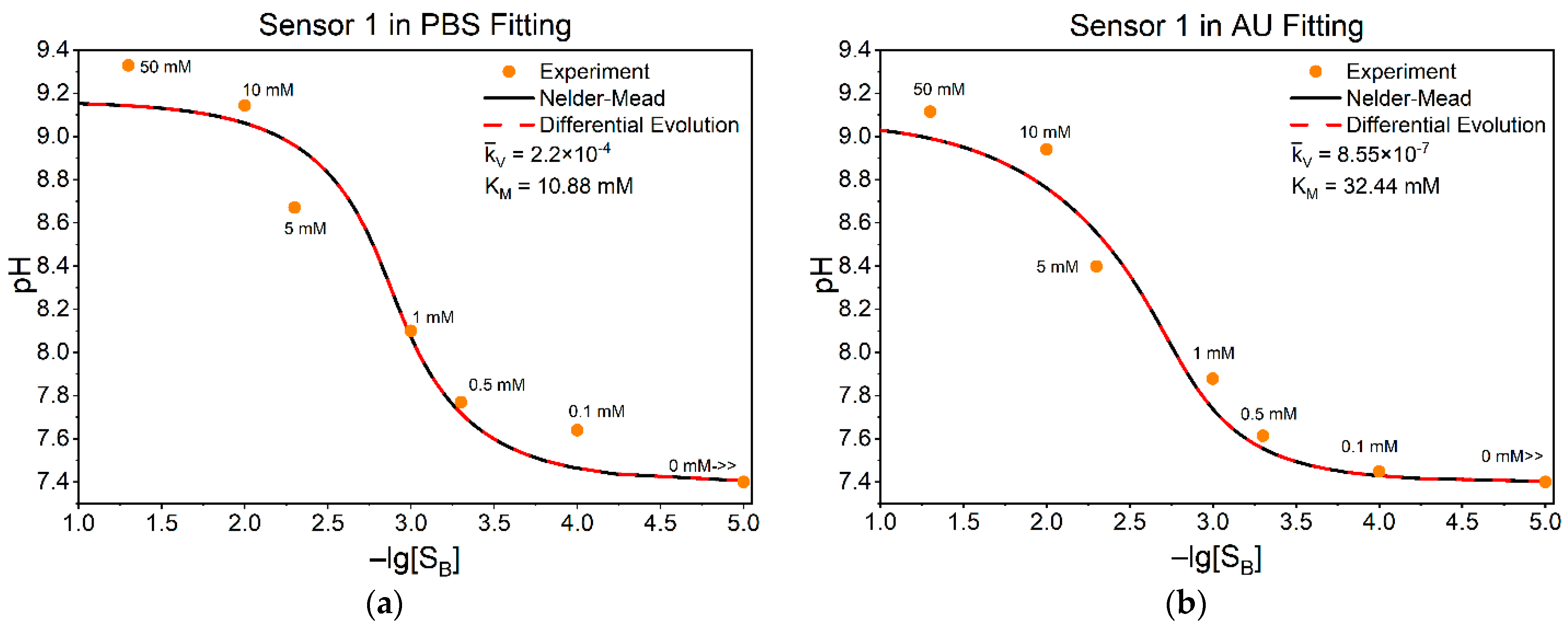
3.2. Experimental Verification
3.3. Fitting Model to Our Experimental Data
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| EISCAP | Electrolyte–insulator–semiconductor capacitor |
| PAH | Polyallylamine hydrochloride |
| KM | Michaelis–Menten constant (mm) |
| Normalized maximum reaction rate | |
| PBS | Phosphate-buffered saline |
| AU | Artificial urine |
| H(H+) | Hydrogen ion |
| V | Reaction rate |
| Vmax | Maximum reaction rate constant |
| [X] | Concentration of substance X |
| S | Substrate(urea) concentration |
| A | Product A (carbonic acid) |
| HA | Deprotonated product A (bicarbonate) |
| B | Product B (ammonia) |
| HB | Protonated product B (ammonium ion) |
| Z | Non–protolytic product |
| nX | Stoichiometric coefficient of X |
| W | Dihydrogen of PBS |
| HW | Monohydrogen of PBS |
| KaX | Dissociation constant of X |
| kX | Transport rate constant of X |
| Normalized transport rate constant of X | |
| Buffer concentration | |
| Ha | Normalized hydrogen ion concentration |
| NM | Nelder–Mead minimization method |
| DE | differential evolution minimization method |
| SA | simulated annealing minimization method |
| NIP | Nonlinear interior point minimization method |
| RS | Random search minimization method |
| CONCAP | Constant-capacitance measurement technique |
| χ2 | Chi-square error |
| D | Diffusion constant of substrate |
| l | Length of enzyme layer |
| t | Thickness of enzyme layer |
| Subscripts | |
| B | In bulk solution |
| X | Any species mentioned (i.e., S, A, HA, B, etc.) |
| exp | Experimental |
| Superscripts | |
| B | ) |
References
- Poghossian, A.; Schöning, M.J. Recent Progress in Silicon-Based Biologically Sensitive Field-Effect Devices. Curr. Opin. Electrochem. 2021, 29, 100811. [Google Scholar] [CrossRef]
- Koncki, R. Recent Developments in Potentiometric Biosensors for Biomedical Analysis. Anal. Chim. Acta 2007, 599, 7–15. [Google Scholar] [CrossRef]
- Singh, S.; Sharma, M.; Singh, G. Recent Advancements in Urea Biosensors for Biomedical Applications. IET Nanobiotechnol. 2021, 15, 358–379. [Google Scholar] [CrossRef]
- Gounden, V.; Bhatt, H.; Jialal, I. Renal Function Tests; StatPearls Publishing: Treasure Island, FL, USA, 2024. [Google Scholar] [PubMed]
- Pundir, C.S.; Jakhar, S.; Narwal, V. Determination of Urea with Special Emphasis on Biosensors: A Review. Biosens. Bioelectron. 2019, 123, 36–50. [Google Scholar] [CrossRef]
- Dhawan, G.; Sumana, G.; Malhotra, B.D. Recent Developments in Urea Biosensors. Biochem. Eng. J. 2009, 44, 42–52. [Google Scholar] [CrossRef]
- Singh, M.; Verma, N.; Garg, A.K. Urea Biosensors. Sens. Actuators B Chem. 2008, 134, 345–351. [Google Scholar] [CrossRef]
- Chou, J.C.; Wu, C.Y.; Lin, S.H.; Kuo, P.Y.; Lai, C.H.; Nien, Y.H.; Lai, T.Y. The Analysis of the Urea Biosensors Using Different Sensing Matrices via Wireless and Microfluidic Measurement Systems. Sensors 2019, 19, 3004. [Google Scholar] [CrossRef]
- Özbek, O.; Berkel, C.; Isildak, Ö.; Isildak, I. Potentiometric Urea Biosensors. Clin. Chim. Acta 2022, 524, 154–163. [Google Scholar] [CrossRef]
- Lonsdale, R.; Harvey, J.N.; Mulholland, A.J. A Practical Guide to Modelling Enzyme Catalysed Reactions. Chem. Soc. Rev. 2012, 41, 3025–3038. [Google Scholar] [CrossRef]
- Garcia-Viloca, M.; Gao, J.; Karplus, M.; Truhlar, D.G. How Enzymes Work: Analysis by Modern Rate Theory and Computer Simulations. Science 2004, 303, 186–195. [Google Scholar] [CrossRef]
- Saeedfar, K.; Heng, L.Y.; Ling, T.L.; Rezayi, M. Potentiometric Urea Biosensor Based on an Immobilized Fullerene–Urease Bioconjugate. Sensors 2013, 13, 16851–16866. [Google Scholar] [CrossRef]
- Welden, M.; Severins, R.; Poghossian, A.; Wege, C.; Bongaerts, J.; Siegert, P.; Keusgen, M.; Schöning, M.J. Detection of Acetoin and Diacetyl by a Tobacco Mosaic Virus-Assisted Field-Effect Biosensor. Chemosensors 2022, 10, 218. [Google Scholar] [CrossRef]
- Poghossian, A.; Jablonski, M.; Koch, C.; Bronder, T.S.; Rolka, D.; Wege, C.; Schöning, M.J. Field-Effect Biosensor Using Virus Particles as Scaffolds for Enzyme Immobilization. Biosens. Bioelectron. 2018, 110, 168–174. [Google Scholar] [CrossRef]
- Schöning, M.J.; Brinkmann, D.; Rolka, D.; Demuth, C.; Poghossian, A. CIP-Suitable “Non-Glass” pH Sensor Based on a Ta2O5-Gate EIS Structure. Sens. Actuators B Chem. 2005, 111, 423–429. [Google Scholar] [CrossRef]
- Perumal, V.; Hashim, U. Advances in Biosensors: Principle, Architecture, and Applications. J. Appl. Biomed. 2014, 12, 1–15. [Google Scholar] [CrossRef]
- Sarigul, N.; Korkmaz, F.; Kurultak, İ. A New Artificial Urine Protocol to Better Imitate Human Urine. Sci. Rep. 2019, 9, 20159. [Google Scholar] [CrossRef]
- Khan, L.B.; Read, H.M.; Ritchie, S.R.; Proft, T. Artificial Urine for Teaching Urinalysis Concepts and Diagnosis of Urinary Tract Infection in the Medical Microbiology Laboratory. J. Microbiol. Biol. Educ. 2017, 18, 46. [Google Scholar] [CrossRef]
- Hwang, C.; Lee, W.J.; Kim, S.D.; Park, S.; Kim, J.H. Recent Advances in Biosensor Technologies for Point-of-Care Urinalysis. Biosensors 2022, 12, 1020. [Google Scholar] [CrossRef]
- Morais, P.V.; Gomes, V.F.; Silva, A.C.; Dantas, N.O.; Schöning, M.J.; Siqueira, J.R. Nanofilm of ZnO Nanocrystals/Carbon Nanotubes as Biocompatible Layer for Enzymatic Biosensors in Capacitive Field-Effect Devices. J. Mater. Sci. 2017, 52, 12314–12325. [Google Scholar] [CrossRef]
- Rahmanian, R.; Mozaffari, S.A.; Abedi, M. Disposable Urea Biosensor Based on Nanoporous ZnO Film Fabricated from Omissible Polymeric Substrate. Mater. Sci. Eng. C 2015, 57, 387–396. [Google Scholar] [CrossRef]
- Tsokolakyan, A.; Poghosyan, T.; Hayrapetyan, V.A.; Petrosyan, D.; Simonyan, K.; Badasyan, A.; Buniatyan, V.; Karschuck, T.; Welden, M.; Iken, H.; et al. Detection of Urea in Artificial Urine Using Capacitive Field-Effect Biosensors Modified with a Stacked Polyelectrolyte–Enzyme Bilayer. In Proceedings of the 15th International Workshop on Engineering of Functional Interfaces (ENFI), Linz, Austria, 29–30 August 2024; Available online: https://www.jku.at/fileadmin/gruppen/170/Downloads/ENFI_2024_Book_of_Abstracts.pdf (accessed on 29 August 2024).
- Glab, S.; Hulanicki, A. Theoretical Model of the Response of pH Based Enzyme Sensors. Electroanalysis 1991, 3, 361–364. [Google Scholar] [CrossRef]
- Glab, S.; Koncki, R.; Hulanicki, A. Kinetic Model of pH Based Potentiometric Enzymic Sensors. Part 1. Theoretical Considerations. Analyst 1991, 116, 453–458. [Google Scholar] [CrossRef]
- Glab, S.; Koncki, R.; Holona, I. Kinetic Model of pH Based Potentiometric Enzymic Sensors. Part 2. Method of Fitting. Analyst 1992, 117, 1671–1674. [Google Scholar] [CrossRef]
- Glab, S.; Koncki, R.; Hulanicki, A. Kinetic Model of pH Based Potentiometric Enzymic Sensors. Part 3. Experimental Verification. Analyst 1992, 117, 1675–1678. [Google Scholar] [CrossRef]
- Koncki, R.; Kopczewska, E.; Glab, S. Comparison of pH Membrane Enzyme Electrodes for Urea with Covalently Bound Enzyme. Anal. Lett. 1994, 27, 475–486. [Google Scholar] [CrossRef]
- Koncki, R.; Leszczyński, P.; Hulanicki, A.; Gła̧b, S. Urea Sensors Based on Glass pH Electrodes with Physically Immobilized Urease. Anal. Chim. Acta 1992, 257, 67–72. [Google Scholar] [CrossRef]
- Blaedel, W.J.; Kissel, T.R.; Boguslaski, R.C. Kinetic Behavior of Enzymes Immobilized in Artificial Membranes. Anal. Chem. 1972, 44, 2030–2037. [Google Scholar] [CrossRef]
- Hameka, H.F.; Rechnitz, G.A. Steady State Theory of Biocatalytic Membrane Electrodes. Anal. Chem. 1981, 53, 1586–1590. [Google Scholar] [CrossRef]
- Hameka, H.F.; Rechnitz, G.A. Theory of the Biocatalytic Membrane Electrode. J. Phys. Chem. 1983, 87, 1235–1241. [Google Scholar] [CrossRef]
- Brady, J.E.; Carr, P.W. Theoretical Evaluation of the Steady State Response of Potentiometric Enzyme Electrodes. Anal. Chem. 1980, 52, 977–980. [Google Scholar] [CrossRef]
- Morf, W.E.; Lindner, E.; Simon, W. Theoretical Treatment of the Dynamic Response of Ion Selective Membrane Electrodes. Anal. Chem. 1975, 47, 1596–1601. [Google Scholar] [CrossRef]
- Jochum, P.; Kowalski, B.B. A Coupled Two Compartment Model for Immobilized Enzyme Electrodes. Anal. Chim. Acta 1982, 144, 25–38. [Google Scholar] [CrossRef]
- Eddowes, M.J. Response of an Enzyme Modified pH Sensitive Ion Selective Device: Influence of Buffering Capacity of the Analyte Solution. Sens. Actuators B 1985, 7, 97–115. [Google Scholar] [CrossRef]
- Eddowes, M.J.; Pedley, D.G.; Webb, B.C. Response of a Glucose Oxidase Modified Ion Sensitive Field Effect Transistor in Buffered and Unbuffered Solutions. Sens. Actuators 1985, 7, 233–244. [Google Scholar] [CrossRef]
- Varanasi, S.; Stevens, R.L.; Ruckenstein, E. Design of Enzyme pH Electrodes. AIChE J. 1987, 33, 558–572. [Google Scholar] [CrossRef]
- Varanasi, S.; Ogundiran, S.O.; Ruckenstein, E. Design and Performance of Potentiometric Enzyme pH Electrodes. Biosensors 1988, 3, 269–287. [Google Scholar] [CrossRef]
- Caras, S.D.; Janata, J.; Saupe, D.; Schmitt, K. pH Based Enzyme Potentiometric Sensors. Part 1. Theory. Anal. Chem. 1985, 57, 1917–1920. [Google Scholar] [CrossRef] [PubMed]
- Caras, S.D.; Petelenz, D.; Janata, J. pH Based Enzyme Potentiometric Sensors. Part 2. Glucose Sensitive Field Effect Transistor. Anal. Chem. 1985, 57, 1920–1923. [Google Scholar] [CrossRef]
- Caras, S.D.; Janata, J. pH Based Enzyme Potentiometric Sensors. Part 3. Penicillin-sensitive field effect transistor. Anal. Chem. 1985, 57, 1924–1926. [Google Scholar] [CrossRef]
- Moynihan, H.J.; Wang, N.-H.L. Analysis of Urea Hydrolysis by Immobilized Urease in Urea-Sensing Electrodes. Biotechnol. Prog. 1987, 3, 90–100. [Google Scholar] [CrossRef]
- Bell, P.R. Acids and Bases: Their Quantitative Behaviour; Methuen: London, UK, 1969. [Google Scholar]
- Hulanicki, A. Reactions of Acids and Bases in Analytical Chemistry; Ellis Horwood: Chichester, UK, 1989. [Google Scholar]
- Morf, W.E. Theoretical Evaluation of Enzyme Electrodes and Enzyme Reactors. Microchim. Acta 1980, 74, 317–332. [Google Scholar] [CrossRef]
- Weiner, P.H.; Parcher, J.F. Improved urea electrode. Anal. Chem. 1973, 45, 417–422. [Google Scholar] [CrossRef]
- Tranh Minh, C.; Broun, G. Construction and study of electrodes using crosslinked enzymes. Anal. Chem. 1975, 47, 1359–1361. [Google Scholar] [CrossRef]
- Morf, W.E. The Principles of Ion Selective Electrodes and Membrane Transport; Elsevier: New York, NY, USA, 1981. [Google Scholar]
- Cambiaso, A.; Delfino, L.; Grattarola, M.; Verreschi, G.; Ashworth, D.; Maines, A.; Vadgama, P. Modelling and Simulation of a Diffusion Limited Glucose Biosensor. Sens. Actuators B 1996, 33, 203–207. [Google Scholar] [CrossRef]
- Cooney, M.J. Kinetic Measurements for Enzyme Immobilization. In Enzyme Stabilization and Immobilization; Methods in Molecular Biology, Vol. 1504; Humana Press: New York, NY, USA, 2017; Chapter 17; pp. 215–232. [Google Scholar] [CrossRef]
- Johnson, K.A.; Goody, R.S. The Original Michaelis Constant: Translation of the 1913 Michaelis–Menten Paper. Biochemistry 2011, 50, 8264–8269. [Google Scholar] [CrossRef]
- Koncki, R.; Severins, R.; Jablonski, M.; Zaborowski, M.; Głąb, S. Simplex Method for the Computation of Analytical Parameters of Potentiometric Sensors. Anal. Chim. Acta 1993, 273, 477–483. [Google Scholar] [CrossRef]
- Wolfram Research, Inc. Mathematica, Version 13.3; Wolfram Research, Inc.: Champaign, IL, USA, 2023.
- Poghossian, A.; Schöning, M.J. Capacitive field-effect EIS chemical sensors and biosensors: A status report. Sensors 2020, 20, 5639. [Google Scholar] [CrossRef] [PubMed]
- Lue, C.-E.; Yu, T.-C.; Yang, C.-M.; Pijanowska, D.G.; Lai, C.-S. Optimization of urea-EnFET based on Ta2O5 layer with post annealing. Sensors 2011, 11, 4562–4571. [Google Scholar] [CrossRef]
- American Medical Laboratories. Urea, Urine (Random). AML Labs. Available online: https://www.aml.co.il/en/lab_tests/urea-urine-random/ (accessed on 11 October 2025).
- Cesareo, S.D.; Langton, S.R. Kinetic Properties of Helicobacter pylori Urease Compared with Jack Bean Urease. FEMS Microbiol. Lett. 1992, 99, 15–21. [Google Scholar] [CrossRef]
- Sigma-Aldrich. Urease from Canavalia Ensiformis; Product No. U1500; Sigma-Aldrich: St. Louis, MO, USA, 2025; Available online: https://www.sigmaaldrich.com/AM/en/product/sigma/u1500 (accessed on 9 May 2025).
- Brooks, T.; Keevil, C.W. A Simple Artificial Urine for the Growth of Urinary Pathogens. Lett. Appl. Microbiol. 1997, 24, 203–206. [Google Scholar] [CrossRef] [PubMed]
- Chutipongtanate, S.; Thongboonkerd, V. Systematic Comparisons of Artificial Urine Formulas for In Vitro Cellular Study. Anal. Biochem. 2010, 402, 110–112. [Google Scholar] [CrossRef] [PubMed]
- Atkins, P.W. Physical Chemistry, 1st ed.; Oxford University Press: Oxford, UK, 1978; p. 775. [Google Scholar]
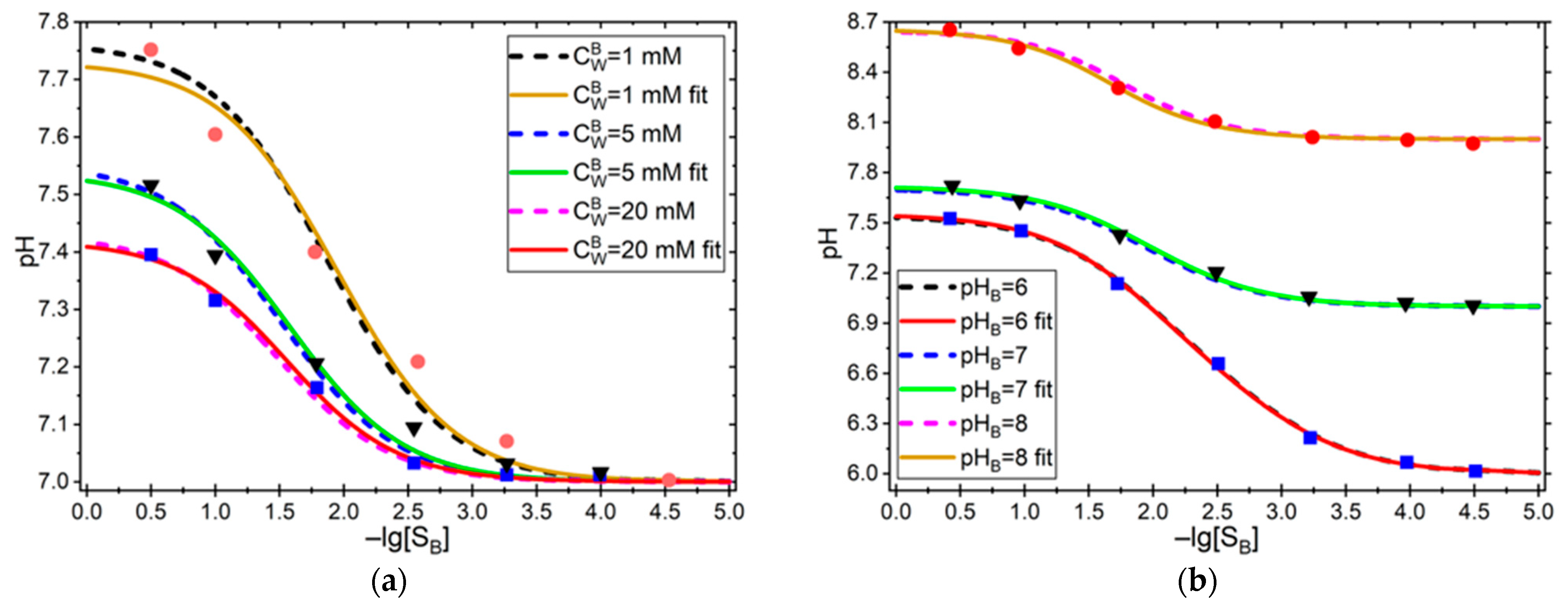


| Constants | Values | Results from Ref. [24] | Our Approach | |||
|---|---|---|---|---|---|---|
| (mM) | (mM) | |||||
| (mM) | 1 | 0.41 | 13.1 | 0.39 | 11.18 | 5.33 |
| 5 | 1.50 | 32.1 | 1.46 | 27.57 | 3.01 | |
| 20 | 4.62 | 33.3 | 4.52 | 28.43 | 0.4 | |
| 6 | 3.05 | 11.2 | 3.08 | 11.51 | 0.21 | |
| 7 | 1.90 | 10.7 | 1.93 | 10 | 2.3 | |
| 8 | 0.86 | 16.5 | 0.87 | 21.11 | 7.1 | |
| Methods | PBS | AU | ||
|---|---|---|---|---|
| , M/L × s | , mM | , M/L × s | , mM | |
| Our method | 0.20 | 10.88 | 7.95 × 10−4 | 32.45 |
| Lineweaver–Burk | 0.20 | 10.88 | 7.95 × 10−4 | 32.45 |
| Eadie–Hofstee | 0.20 | 10.88 | 7.95 × 10−4 | 32.45 |
| Hanes–Woolf | 0.20 | 10.88 | 7.95 × 10−4 | 32.45 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Simonyan, K.; Tsokolakyan, A.; Buniatyan, V.; Badasyan, A.; Yeranosyan, M. Urea Detection in Phosphate Buffer and Artificial Urine: A Simplified Kinetic Model of a pH-Sensitive EISCAP Urea Biosensor. Sensors 2025, 25, 6596. https://doi.org/10.3390/s25216596
Simonyan K, Tsokolakyan A, Buniatyan V, Badasyan A, Yeranosyan M. Urea Detection in Phosphate Buffer and Artificial Urine: A Simplified Kinetic Model of a pH-Sensitive EISCAP Urea Biosensor. Sensors. 2025; 25(21):6596. https://doi.org/10.3390/s25216596
Chicago/Turabian StyleSimonyan, Karen, Astghik Tsokolakyan, Vahe Buniatyan, Artem Badasyan, and Mkrtich Yeranosyan. 2025. "Urea Detection in Phosphate Buffer and Artificial Urine: A Simplified Kinetic Model of a pH-Sensitive EISCAP Urea Biosensor" Sensors 25, no. 21: 6596. https://doi.org/10.3390/s25216596
APA StyleSimonyan, K., Tsokolakyan, A., Buniatyan, V., Badasyan, A., & Yeranosyan, M. (2025). Urea Detection in Phosphate Buffer and Artificial Urine: A Simplified Kinetic Model of a pH-Sensitive EISCAP Urea Biosensor. Sensors, 25(21), 6596. https://doi.org/10.3390/s25216596









