A Proposed System for Temperature Measurement During Tensile Testing
Abstract
1. Introduction
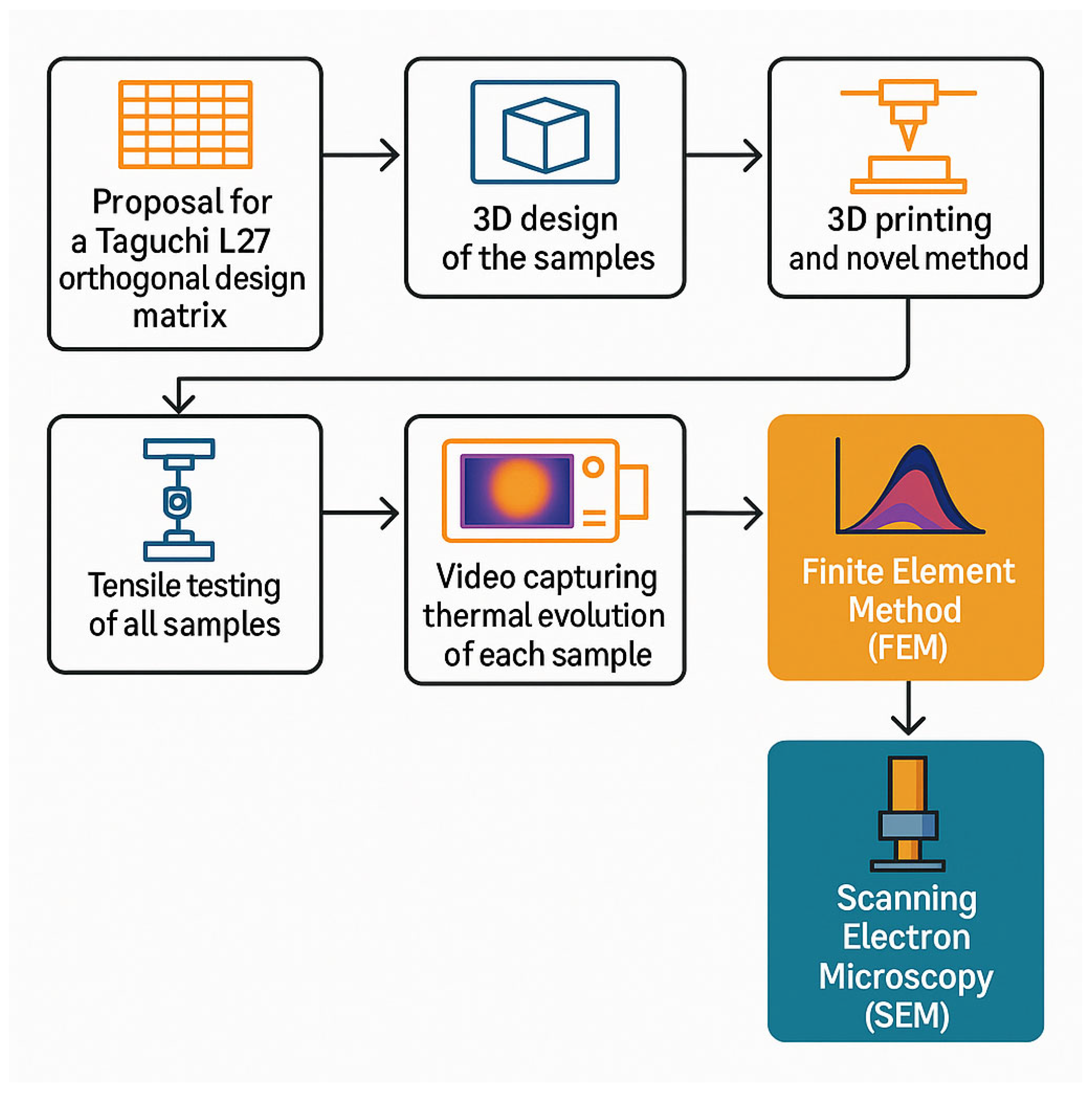
2. Materials and Methods
2.1. Experimental Testing Setup


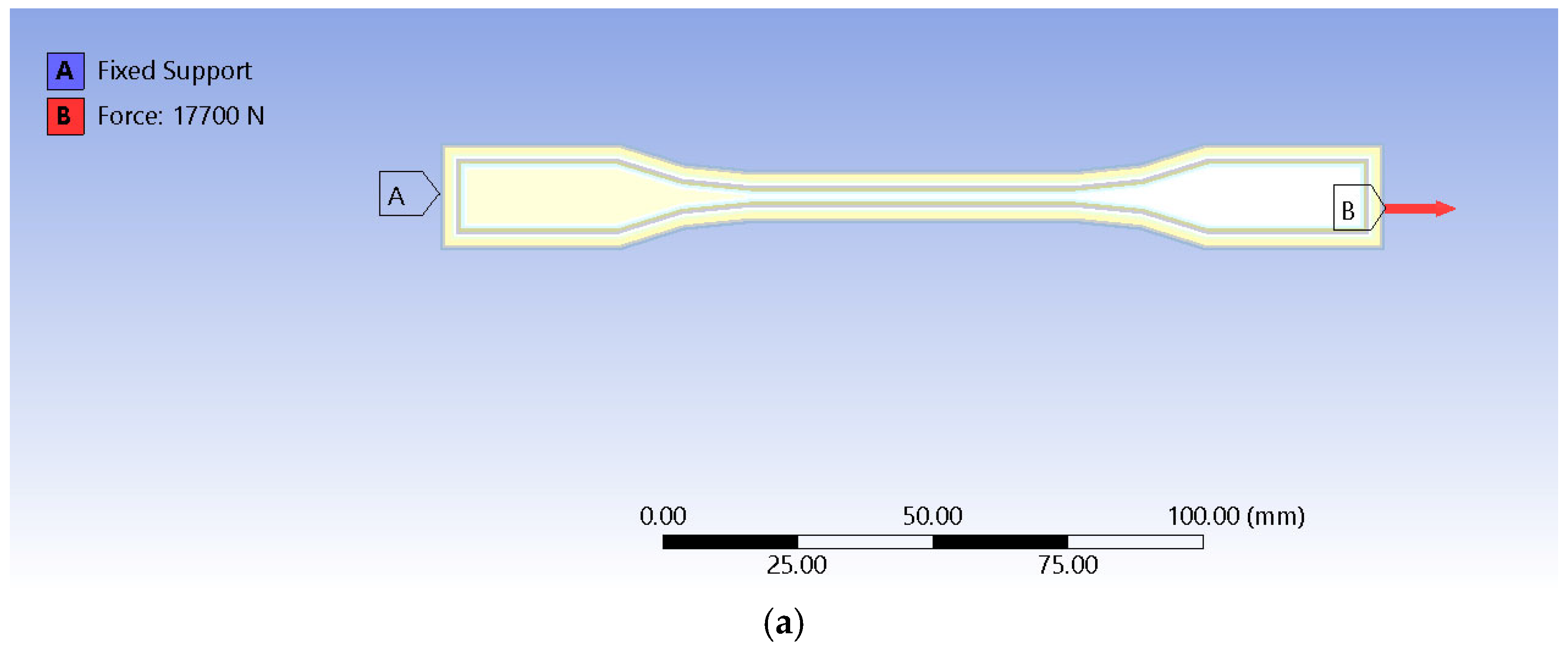
2.2. Setup for Thermal Variation Assessment of the Tensile Test Using Finite Element Method (FEM)



2.3. Setup for Scanning Electron Microscopy (SEM)

3. Results
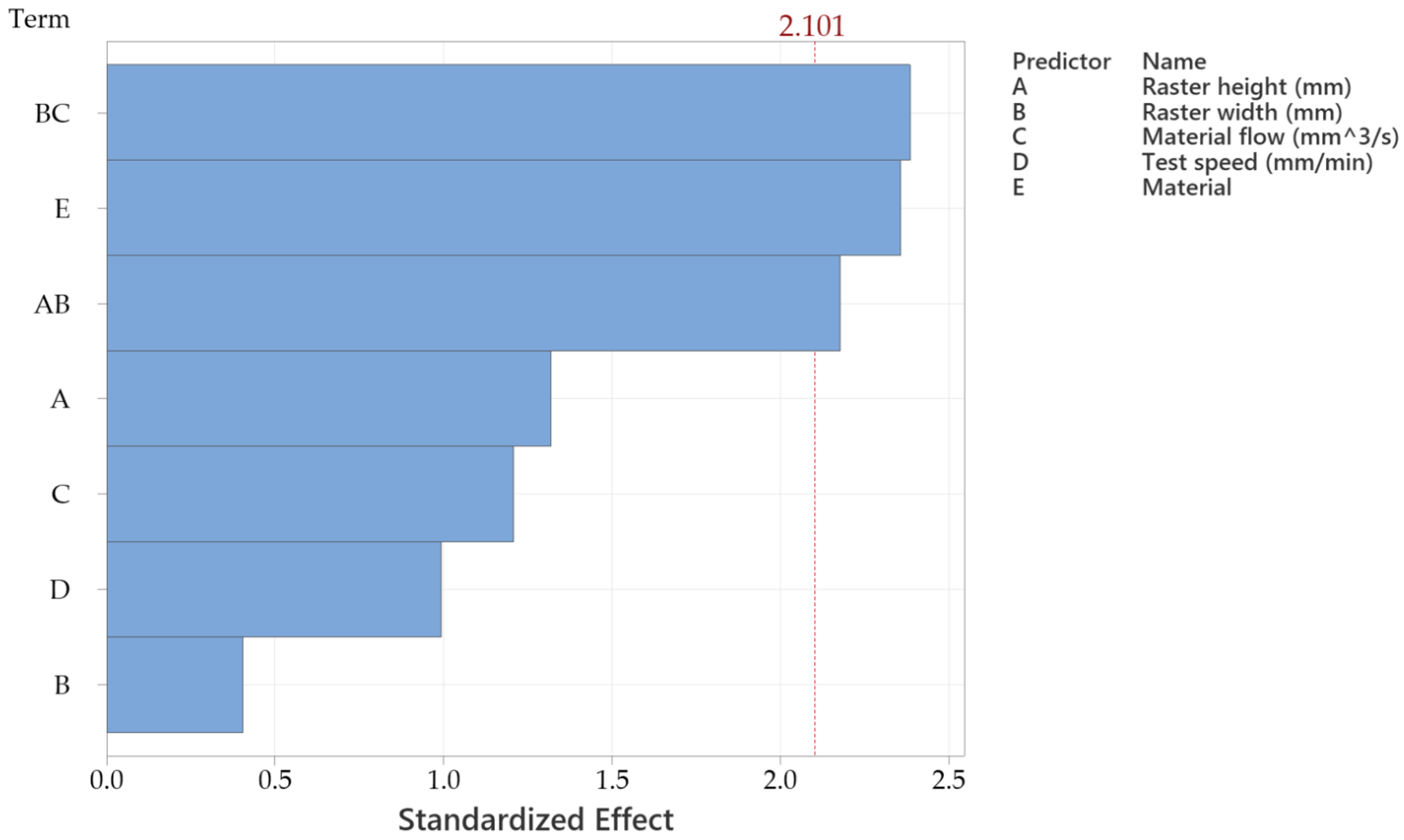
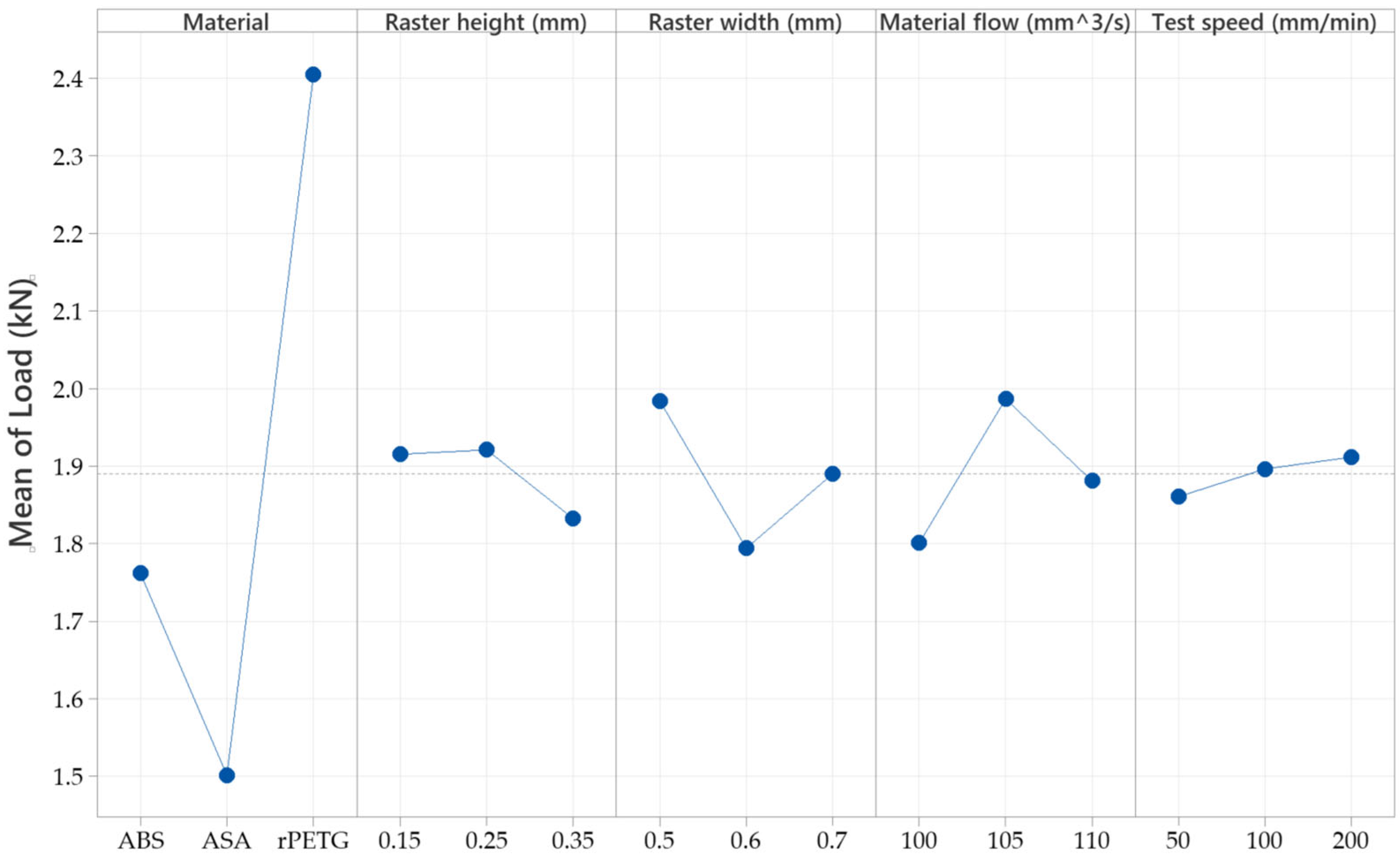
3.1. Statistical Analysis Results

| Source | DF | Seq SS | Contribution | Adj SS | Adj MS | F-Value | p-Value |
|---|---|---|---|---|---|---|---|
| Regression | 7 | 4.24848 | 97.55% | 4.24848 | 0.60693 | 108.19 | 0.000 |
| Raster height (mm) | 1 | 0.03092 | 0.71% | 0.03092 | 0.03092 | 5.51 | 0.030 |
| Raster width (mm) | 1 | 0.03957 | 0.91% | 0.03957 | 0.03957 | 7.05 | 0.016 |
| Material flow (%) | 1 | 0.02880 | 0.66% | 0.02880 | 0.02880 | 5.13 | 0.035 |
| Material | 2 | 3.89919 | 89.53% | 3.75072 | 1.87536 | 334.31 | 0.000 |
| Raster height × Raster width | 1 | 0.12712 | 2.92% | 0.12712 | 0.12712 | 22.66 | 0.000 |
| Raster height × Material flow | 1 | 0.12288 | 2.82% | 0.12288 | 0.12288 | 21.91 | 0.000 |
| Error | 19 | 0.10658 | 2.45% | 0.10658 | 0.00561 | ||
| Lack-of-Fit | 1 | 0.01338 | 0.31% | 0.01338 | 0.01338 | 2.58 | 0.125 |
| Pure Error | 18 | 0.09320 | 2.14% | 0.09320 | 0.00518 | ||
| Total | 26 | 4.35506 | 100.00% |
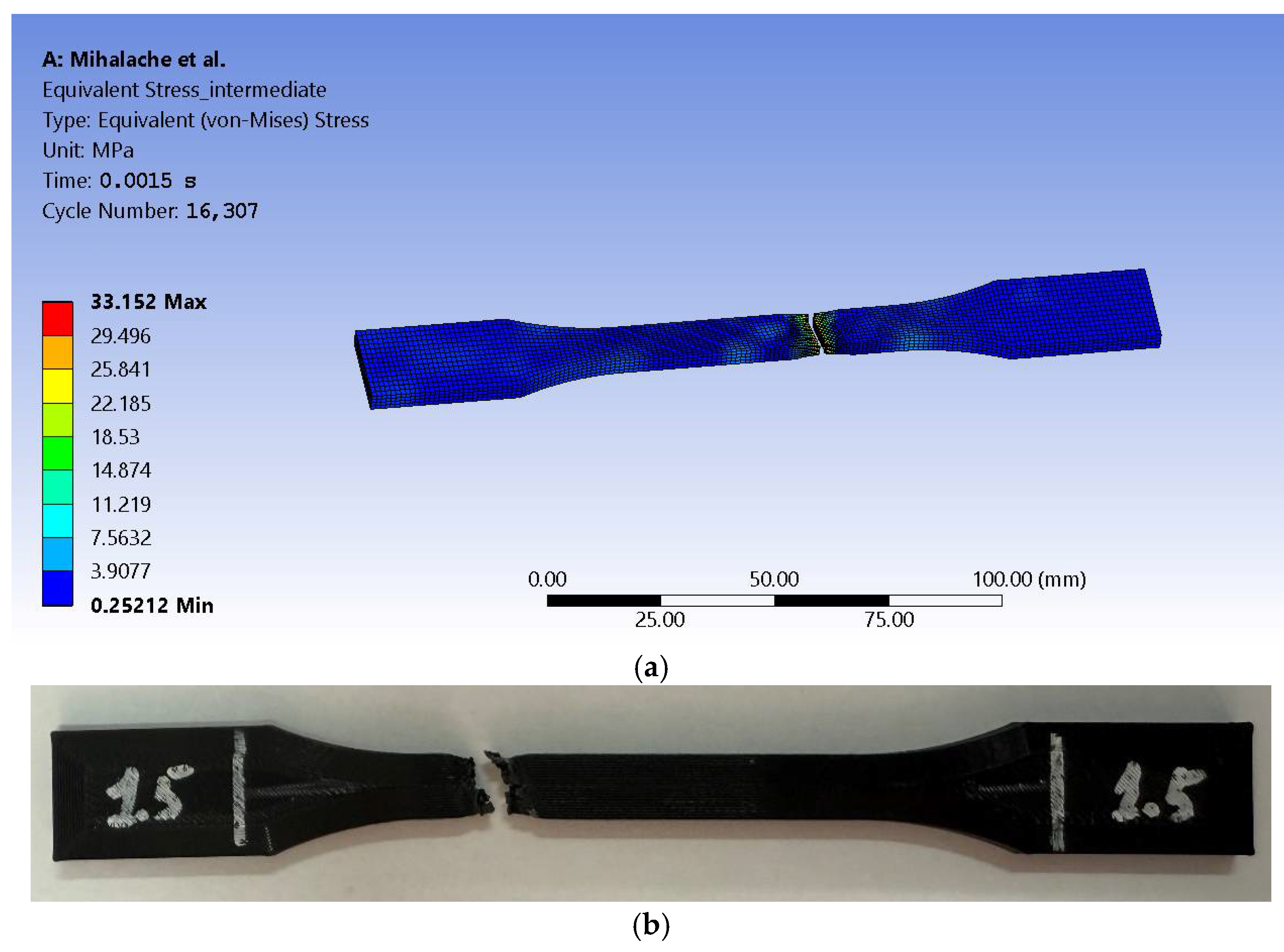
3.2. Finite Element Analysis (FEM) Results

3.3. Scanning Electron Microscopy (SEM) Results
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| ANOVA | analysis of variance |
| DOE | design of experiments |
| FEM | finite element method |
| SEM | scanning electron microscopy |
| DSC | differential scanning calorimetry |
| TGA | thermogravimetric analysis |
| PLA | polylactic acid |
| TPU | thermoplastic polyurethane |
| CF-PLA | carbon fiber-reinforced polylactic acid |
| PMMA | polymethyl methacrylate |
| Tg | glass transition temperature |
| GRA | grey relational analysis |
| TC | thermal conductive |
| TTS | time–temperature superposition |
| UTS | ultimate tensile strength |
| CPPS | cyber–physical production system |
| FEA | finite element analyses |
| FDM | fused deposition modelling |
| ABS | acrylonitrile butadiene styrene |
| ASA | acrylonitrile styrene acrylate |
| rPETG | recycled polyethylene terephthalate glycol-modified |
| PET | polyethylene terephthalate |
References
- Hamidi, M.N.; Abdullah, J.; Mahmud, A.S.; Hassan, M.H.; Zainoddin, A.Y. Influence of thermoplastic polyurethane (TPU) and printing parameters on the thermal and mechanical performance of polylactic acid (PLA)/thermoplastic polyurethane (TPU) polymer. Polym. Test. 2025, 143, 108697. [Google Scholar] [CrossRef]
- Jin, P.; Pan, T.; Li, Y.; Zhong, T.; Jiang, J.; Pu, C.; Ma, C. Performance and thermal properties of 3D printed CF-reinforced PLA monofilaments. Coatings 2024, 14, 1479. [Google Scholar] [CrossRef]
- Švantner, M.; Lang, V.; Skála, J.; Kohlschütter, T.; Šroub, J.; Muzika, L.; Klepáček, J.; Honner, M. Compact thermographic device with built-in active reference element for increased measurement accuracy. Eng. Proc. 2023, 51, 17. [Google Scholar]
- Pei, Y.; Shen, Z.; Zhou, J.; Yang, B. Experimental and theoretical thermal performance analysis of additively manufactured polymer vacuum insulation panels. Appl. Therm. Eng. 2024, 256, 123957. [Google Scholar] [CrossRef]
- Kang, C.; Peng, L.; Li, Y.; Zong, J. Mechanical performance of structural polymethyl methacrylate joints at different temperatures. Polymers 2024, 16, 3243. [Google Scholar] [CrossRef]
- Rezayiye, R.K.; Laurent, K.; Nooralishahi, P.; Ibarra-Castanedo, C.; Maldague, X. Thermal data augmentation approach for the detection of corrosion in pipes using deep learning and finite element modelling. Eng. Proc. 2023, 51, 20. [Google Scholar]
- Kahya, C.; Tunçel, O.; Çavuşoğlu, O.; Tüfekci, K. Thermal annealing optimization for improved mechanical performance of PLA parts produced via 3D printing. Polym. Test. 2025, 144, 108735. [Google Scholar] [CrossRef]
- Fujita, R.; Kudo, N.; Abe, S.; Mohammad Fikry, M.J.; Koyanagi, J.; Ogihara, S.; Nagano, H. Non-destructive fatigue evaluation through thermophysical properties using lock-in thermography. Eng. Proc. 2023, 51, 34. [Google Scholar]
- Demarbaix, A.; Juste, E.; Verlaine, T.; Strazzeri, I.; Quinten, J.; Notebaert, A. Investigating defect detection in advanced ceramic additive manufacturing using active thermography. NDT 2024, 2, 504–518. [Google Scholar] [CrossRef]
- Roudný, P.; Syrový, T. Thermal conductive composites for FDM 3D printing: A review, opportunities and obstacles, future directions. J. Manuf. Process. 2022, 83, 667–677. [Google Scholar] [CrossRef]
- Nguyen, K.Q.; Vuillaume, P.Y.; Hu, L.; Vachon, A.; Diouf-Lewis, A.; Marcoux, P.L.; Robert, M.; Elkoun, S. Effect of in situ thermal treatment on interlayer adhesion of 3D printed polyetherimide (PEI) parts produced by fused deposition modeling (FDM). Mater. Today Commun. 2024, 39, 108588. [Google Scholar] [CrossRef]
- Castillo, M.; Monroy, R.; Ahmad, R. Design of experiments to compare the mechanical properties of polylactic acid using material extrusion three-dimensional-printing thermal parameters based on a cyber–physical production system. Sensors 2023, 23, 9833. [Google Scholar] [CrossRef]
- ISO 527-1:2019; Plastics—Determination of Tensile Properties—Part 1: General Principles. International Organization for Standardization: Geneva, Switzerland, 2019.
- Sajjadi, S.A.; Ghasemi, F.A.; Rajaee, P.; Fasihi, M. Evaluation of fracture properties of 3D printed high impact polystyrene according to essential work of fracture: Effect of raster angle. Addit. Manuf. 2022, 59, 103191. [Google Scholar] [CrossRef]
- Cantrell, J.; Rohde, S.; Damiani, D.; Gurnani, R.; DiSandro, L.; Anton, J.; Young, A.; Jerez, A.; Steinbach, D.; Kroese, K.; et al. Experimental characterization of the mechanical properties of 3D printed ABS and Polycarbonate parts, Chapter 11. In Advancement of Optical Methods in Experimental Mechanics; Springer: Berlin/Heidelberg, Germany, 2016; Volume 3, pp. 89–105. [Google Scholar]
- Wypych, G. Handbook of Polymers, 2nd ed.; ChemTec Publishing: Toronto, ON, Canada, 2016. [Google Scholar]
- NETZSCH Analyzing & Testing. Thermal Characterization of Polymers: Thermoplastics, Thermoplastic Elastomers, Elastomers and Thermosets. 2020. Available online: https://analyzing-testing.netzsch.com (accessed on 17 June 2025).
- Paesano, A. Handbook of Sustainable Polymers for Additive Manufacturing; CRC Press: Boca Raton, FL, USA, 2022. [Google Scholar]
- NETZSCH Group. Thermal Analysis and Rheology in Polymer Additive Manufacturing, 1st ed.; Netzsch Buch: Selb, Germany, 2023. [Google Scholar]
- Mihalache, A.M.; Ermolai, V.; Sover, A.; Nagît, G.; Boca, M.A.; Slatineanu, L.; Hrituc, A.; Dodun, O.; Rîpanu, M.I. Tensile behavior of joints of strip ends made of polymeric materials. Polymers 2022, 14, 4990. [Google Scholar] [CrossRef]
- Galeja, M.; Hejna, A.; Kosmela, P.; Kulawik, A. Static and dynamic mechanical properties of 3D printed ABS as a function of raster angle. Materials 2020, 13, 297. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Ye, H.; Yuan, L.; Luo, C.; Ren, X.; Yu, Q.; Chen, J.; Gao, Q.; Lei, Y.; Cheng, Y.; et al. The effect of weak interface on the fracture behavior of material extrusion 3D-printed polyetherimide. Appl. Mater. Today 2023, 34, 101905. [Google Scholar] [CrossRef]
- Ayatollahia, M.R.; Nabavi-Kivia, A.; Bahramia, B.; Yahyab, M.Y.; Khosravani, M.R. The influence of in-plane raster angle on tensile and fracture strengths of 3D-printed PLA specimens. Eng. Fract. Mech. 2020, 237, 10722. [Google Scholar] [CrossRef]
- Belgen, M.H. Structural stress measurements with an infrared radiometer. ISA Trans. 1967, 6, 49–53. [Google Scholar]
- Wong, A.K.; Sparrow, J.G.; Dunn, S.A. On the revised theory of the thermoelastic effect. J. Phys. Chem. Solids 1988, 49, 395–400. [Google Scholar] [CrossRef]
- Pron, H.; Bissieux, C. 3-D thermal modelling applied to stress-induced anisotropy of thermal conductivity. Int. J. Therm. Sci. 2004, 43, 1161–1169. [Google Scholar] [CrossRef]
- Alarifi, I.M. Mechanical properties and numerical simulation of FDM 3D printed PETG/carbon composite unit structures. J. Mater. Res. Technol. 2023, 23, 656–669. [Google Scholar] [CrossRef]
- Torrado Perez, A.R.; Roberson, D.A.; Wicker, R.B. Fracture surface analysis of 3D-printed tensile specimens of novel ABS-based materials. J. Fail. Anal. Preven. 2014, 14, 343–353. [Google Scholar] [CrossRef]
- Cahyadi, W. Mechanical Properties of 3D Printed Acrylonitrile Styrene Acrylate. Master’s Thesis, South Dakota State University, Brookings, SD, USA, 2019. [Google Scholar]
- Sedlak, J.; Joska, Z.; Jansky, J.; Zouhar, J.; Kolomy, S.; Slany, M.; Svasta, A.; Jirousek, J. Analysis of the mechanical properties of 3D-printed plastic samples subjected to selected degradation effects. Materials 2023, 16, 3268. [Google Scholar] [CrossRef] [PubMed]

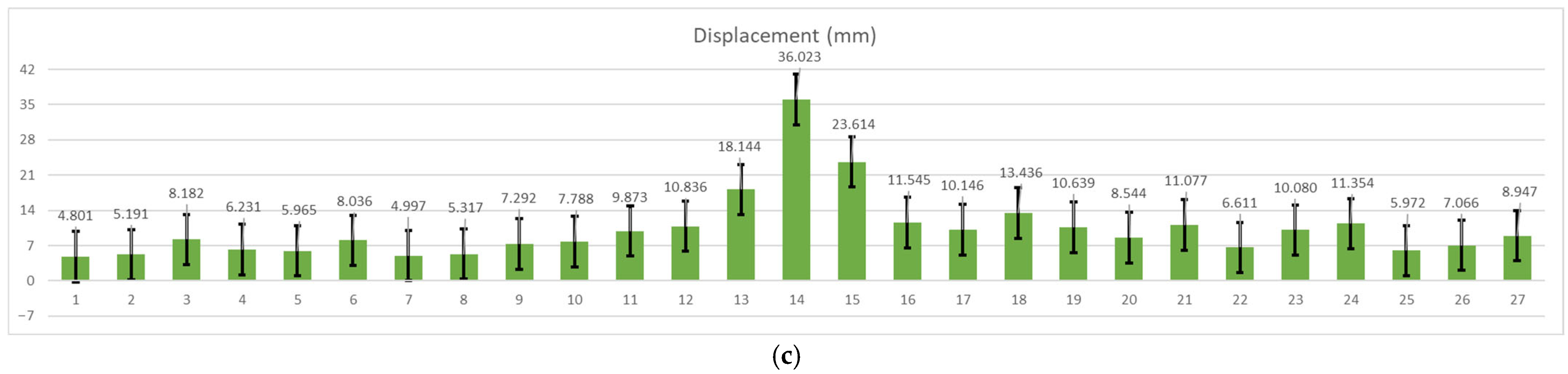



| Run Ord. | Material | Raster Height (mm) | Raster Width (mm) | Material Flow (%) | Test Speed (m/s) (mm/min) | Avg. Fracture Temp. (°C) | Avg. Load (N) | Avg. Displacement (mm) |
|---|---|---|---|---|---|---|---|---|
| 1 | ABS | 0.15 | 0.5 | 100 | 50 | 37.66 | 37.663 | 45.165 |
| 2 | 100 | 50.16 | 50.163 | 60.165 | ||||
| 3 | 200 | 75.16 | 75.163 | 90.165 | ||||
| 4 | 0.25 | 0.6 | 105 | 50 | 38.96 | 38.963 | 46.705 | |
| 5 | 100 | 51.46 | 51.463 | 61.705 | ||||
| 6 | 200 | 76.46 | 76.463 | 91.705 | ||||
| 7 | 0.35 | 0.7 | 110 | 50 | 40.26 | 40.263 | 48.245 | |
| 8 | 100 | 52.76 | 52.763 | 63.245 | ||||
| 9 | 200 | 77.76 | 77.763 | 93.245 | ||||
| 10 | ASA | 0.15 | 0.6 | 110 | 50 | 40.19 | 40.188 | 48.195 |
| 11 | 100 | 52.69 | 52.688 | 63.195 | ||||
| 12 | 200 | 77.69 | 77.688 | 93.195 | ||||
| 13 | 0.25 | 0.7 | 100 | 50 | 37.74 | 37.738 | 45.235 | |
| 14 | 100 | 50.24 | 50.238 | 60.235 | ||||
| 15 | 200 | 75.24 | 75.238 | 90.235 | ||||
| 16 | 0.35 | 0.5 | 105 | 50 | 38.96 | 38.963 | 46.685 | |
| 17 | 100 | 51.46 | 51.463 | 61.685 | ||||
| 18 | 200 | 76.46 | 76.463 | 91.685 | ||||
| 19 | rPETG | 0.15 | 0.7 | 105 | 50 | 38.96 | 38.963 | 46.725 |
| 20 | 100 | 51.46 | 51.463 | 61.725 | ||||
| 21 | 200 | 76.46 | 76.463 | 91.725 | ||||
| 22 | 0.25 | 0.5 | 110 | 50 | 40.19 | 40.188 | 48.175 | |
| 23 | 100 | 52.69 | 52.688 | 63.175 | ||||
| 24 | 200 | 77.69 | 77.688 | 93.175 | ||||
| 25 | 0.35 | 0.6 | 100 | 50 | 37.74 | 37.738 | 45.215 | |
| 26 | 100 | 50.24 | 50.238 | 60.215 | ||||
| 27 | 200 | 75.24 | 75.238 | 90.215 |
| Property | ABS | ASA | rPETG |
|---|---|---|---|
| Cp [J/g∙K] | 1.3–1.6 | 1.4 | 1.0–1.20 |
| k [W/m·K] | 0.128–0.187 | 0.2 | 0.24–0.3 |
| [mm2/s] | 0.11–0.17 | 0.13–0.18 | 0.12–0.18 |
| Source | DF | Seq SS | Contribution | Adj SS | Adj MS | F-Value | p-Value |
|---|---|---|---|---|---|---|---|
| Regression | 8 | 121.530 | 64.50% | 121.530 | 15.1912 | 4.09 | 0.006 |
| Raster height (mm) | 1 | 6.456 | 3.43% | 6.456 | 6.4560 | 1.74 | 0.204 |
| Raster width (mm) | 1 | 0.605 | 0.32% | 0.605 | 0.6050 | 0.16 | 0.691 |
| Material flow (%) | 1 | 5.423 | 2.88% | 5.423 | 5.4230 | 1.46 | 0.243 |
| Test speed (mm/min) | 1 | 3.661 | 1.94% | 3.661 | 3.6610 | 0.99 | 0.334 |
| Material | 2 | 66.641 | 35.37% | 31.860 | 15.9300 | 4.29 | 0.030 |
| Raster height × Raster width | 1 | 17.613 | 9.35% | 17.613 | 17.6131 | 4.74 | 0.043 |
| Raster width × Material flow | 1 | 21.131 | 11.22% | 21.131 | 21.1313 | 5.69 | 0.028 |
| Error | 18 | 66.877 | 35.50% | 66.877 | 3.7154 | ||
| Total | 26 | 188.407 | 100.00% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mihalache, M.A.; Merticaru, V.; Ermolai, V.; Andrusca, L.; Cimpoesu, N.; Negoescu, F. A Proposed System for Temperature Measurement During Tensile Testing. Sensors 2025, 25, 5494. https://doi.org/10.3390/s25175494
Mihalache MA, Merticaru V, Ermolai V, Andrusca L, Cimpoesu N, Negoescu F. A Proposed System for Temperature Measurement During Tensile Testing. Sensors. 2025; 25(17):5494. https://doi.org/10.3390/s25175494
Chicago/Turabian StyleMihalache, Marius Andrei, Vasile Merticaru, Vasile Ermolai, Liviu Andrusca, Nicanor Cimpoesu, and Florin Negoescu. 2025. "A Proposed System for Temperature Measurement During Tensile Testing" Sensors 25, no. 17: 5494. https://doi.org/10.3390/s25175494
APA StyleMihalache, M. A., Merticaru, V., Ermolai, V., Andrusca, L., Cimpoesu, N., & Negoescu, F. (2025). A Proposed System for Temperature Measurement During Tensile Testing. Sensors, 25(17), 5494. https://doi.org/10.3390/s25175494







