Center-of-Gravity-Aware Graph Convolution for Unsafe Behavior Recognition of Construction Workers
Abstract
1. Introduction
- We propose a novel center-of-gravity-aware spatio-temporal graph convolutional network (CoG-STGCN). The model addresses the shortcomings of existing methods by explicitly incorporating CoG dynamics into the graph construction process.
- We conduct a systematic study to identify unsafe behaviors that lead to fall accidents in high-risk areas of construction sites (e.g., floor edges, openings).
- We identify, define, and categorize a set of high-risk unsafe behaviors based on their impact on human balance. This provides a specific basis for risk assessment in such scenarios.
2. Related Works
2.1. Human Pose Estimation Model
2.2. Skeleton-Based Human Action Recognition
3. Methods
3.1. Overall Framework
3.2. YOLOv8-Pose
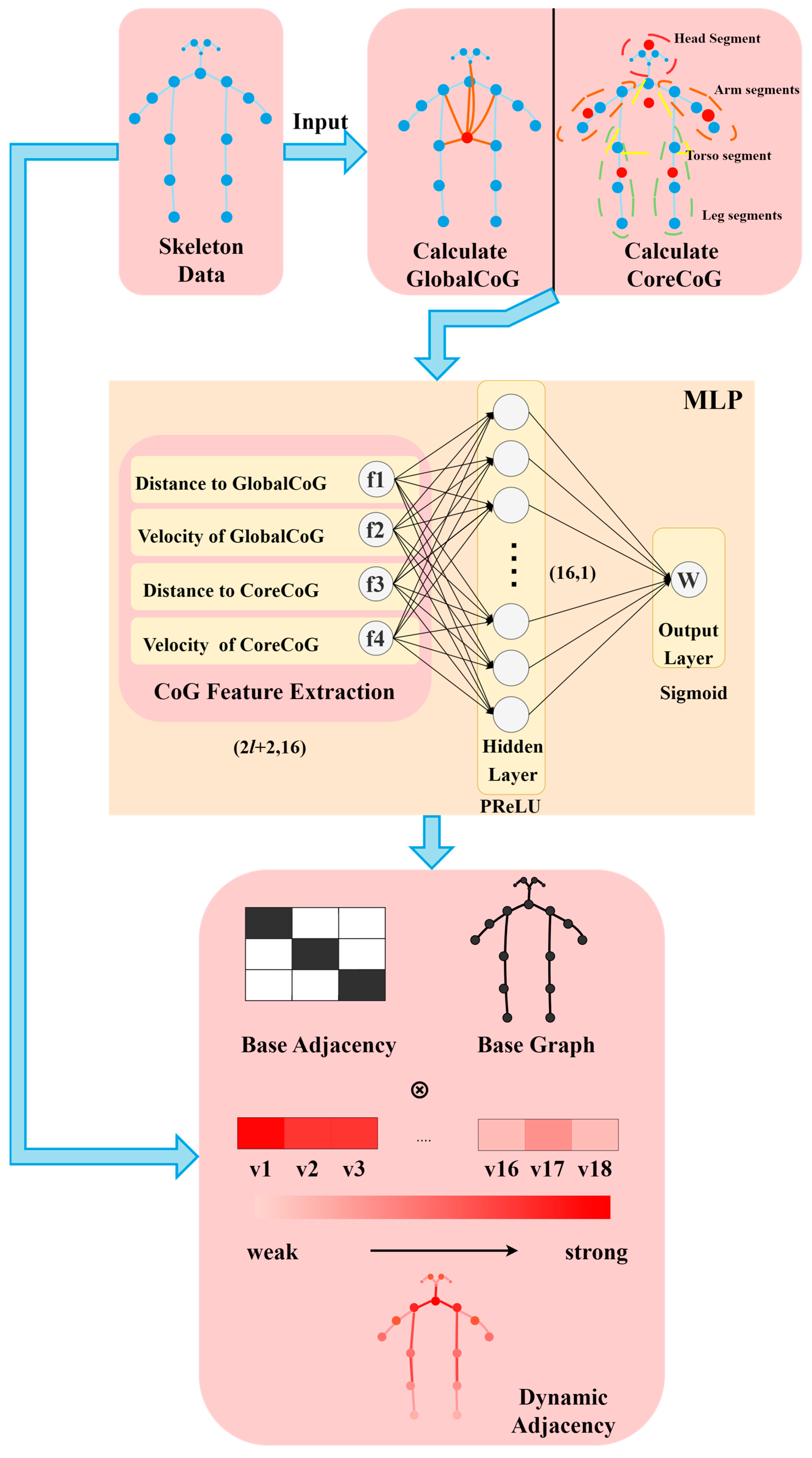
3.3. The Proposed COG-STGCN Model
3.3.1. ST-GCN Model
3.3.2. Center-of-Gravity-Based Improvement to the ST-GCN Model
4. Experiments and Result Analysis
4.1. Data Collection
- Fixed Train-Validation-Test Split: This protocol was used for initial model development and hyperparameter tuning. The 480 video clips were first partitioned into a training set (384 clips, 80%), a validation set (48 clips, 10%), and a test set (48 clips, 10%). Subsequently, data augmentation techniques, including horizontal flipping and random scaling, were applied exclusively to the training set, expanding it from 384 to 1152 samples. This strategy provides a consistent and static test bed for comparing model performance during the development phase.
- Five-Fold Cross-Validation: To obtain a more reliable and generalized assessment of the final model’s performance, we employed a five-fold cross-validation scheme. The entire dataset of 480 clips was randomly partitioned into five equal, non-overlapping folds. In each of the five iterations, four folds (384 clips) were used for training, while the remaining fold (96 clips) served as the validation set. Similar to the fixed split, the training data in each iteration were augmented to 1152 samples. The final performance metrics were then averaged across all five folds. This approach minimizes the potential bias from a single, arbitrary data split.
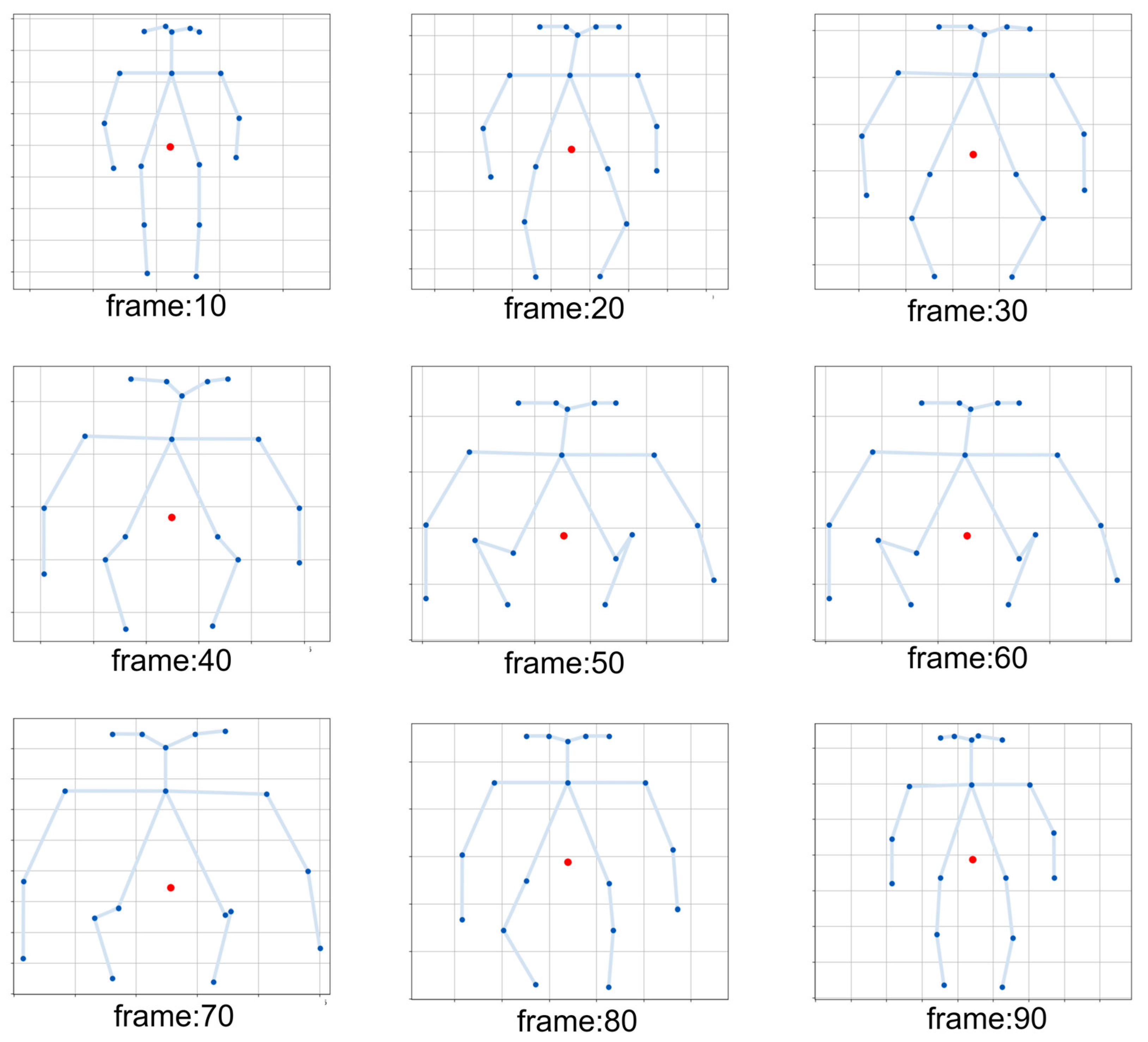
4.2. Validation of CoG Calculation Effectiveness
- Comparison of CoG position with biomechanical reference points in static standardized posture
- 2.
- Stability observation of CoG trajectories in dynamic processes
- 3.
- Positive Impact on Downstream Behavior Recognition Task Performance
4.3. Experimental Setup and Model Training
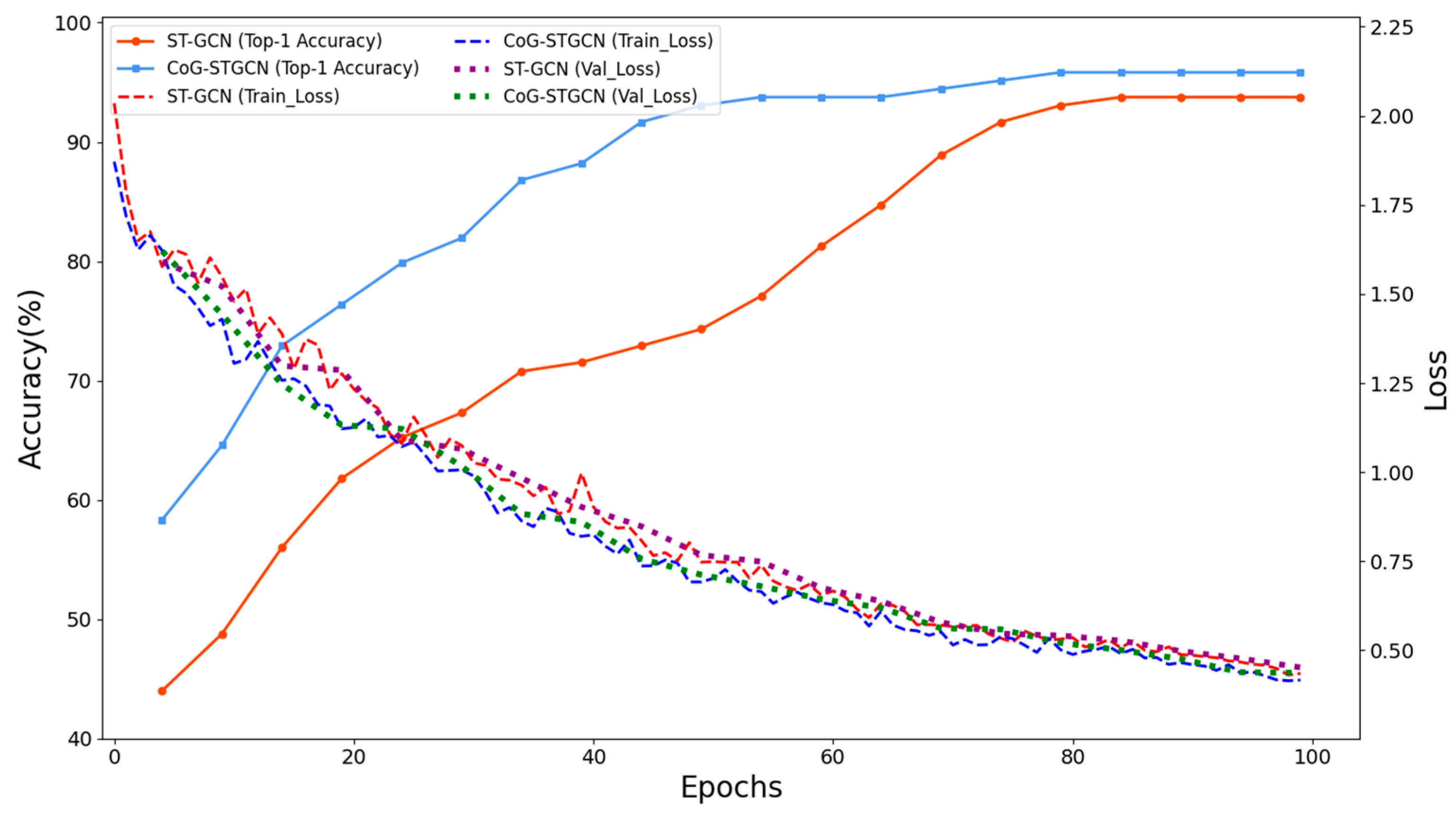
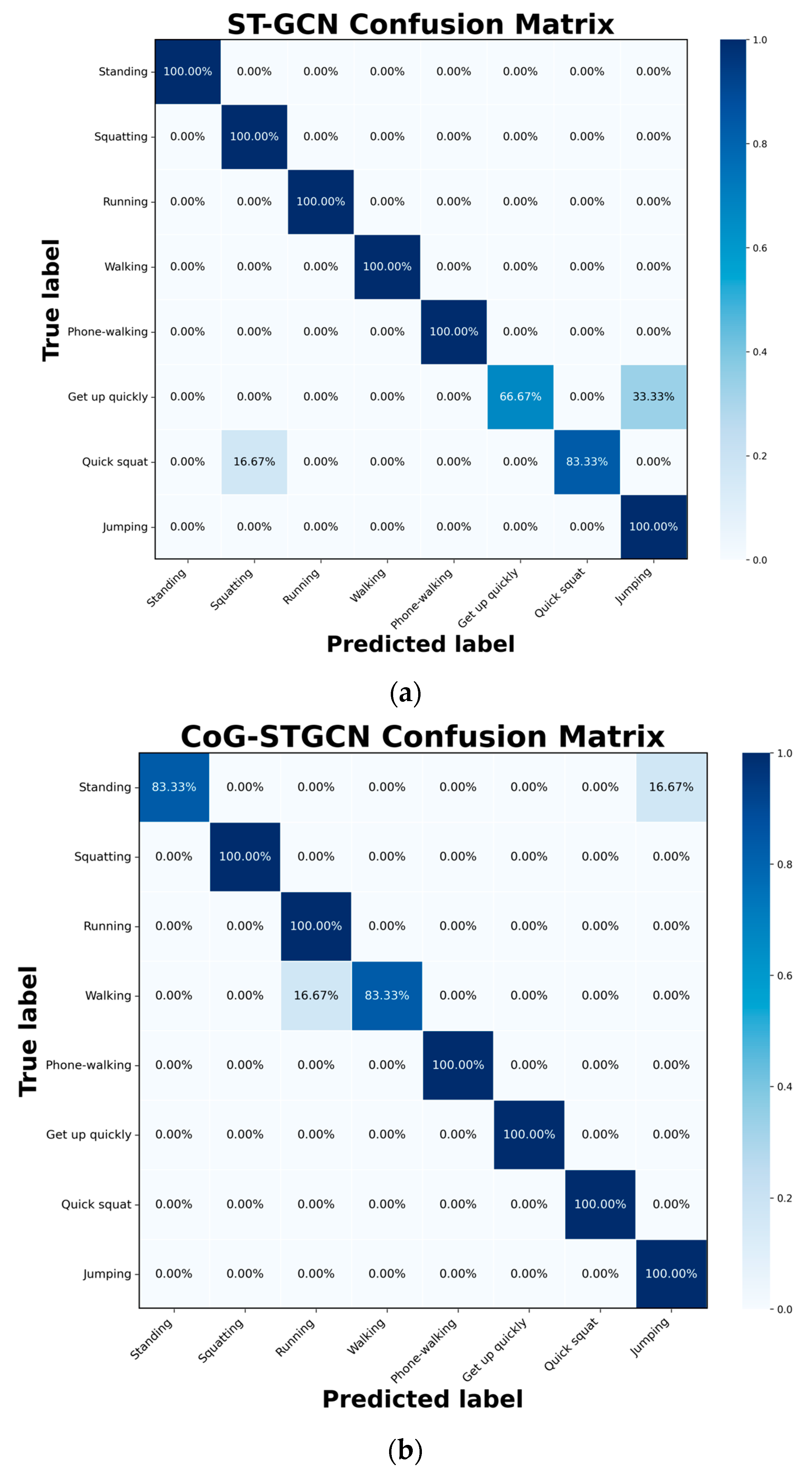
4.4. Experimental Results and Analysis
4.5. Application Demonstration and Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chen, J.; Li, K.; Deng, Z.; Wang, S.; Cheng, X. A Correlation Analysis of Construction Site Fall Accidents Based on Text Mining. Front. Built Environ. 2021, 7, 690071. [Google Scholar] [CrossRef]
- Lim, J.-S.; Song, K.-I.; Lee, H.-L. Real-Time Location Tracking of Multiple Construction Laborers. Sensors 2016, 16, 1869. [Google Scholar] [CrossRef] [PubMed]
- Zhu, Z.; Ren, X.; Chen, Z. Integrated detection and tracking of workforce and equipment from construction jobsite videos. Autom. Constr. 2017, 81, 161–171. [Google Scholar] [CrossRef]
- Shaikh, M.B.; Chai, D. RGB-D Data-Based Action Recognition: A Review. Sensors 2021, 21, 4246. [Google Scholar] [CrossRef] [PubMed]
- Yan, S.; Xiong, Y.; Lin, D. Spatial temporal graph convolutional networks for skeleton-based action recognition. In Proceedings of the AAAI Conference on Artificial Intelligence, New Orleans, LA, USA, 2–7 February 2018. [Google Scholar]
- Li, Z.; Zhang, A.; Han, F.; Zhu, J.; Wang, Y. Worker Abnormal Behavior Recognition Based on Spatio-Temporal Graph Convolution and Attention Model. Electronics 2023, 12, 2915. [Google Scholar] [CrossRef]
- Li, P.; Wu, F.; Xue, S.; Guo, L. Study on the Interaction Behaviors Identification of Construction Workers Based on ST-GCN and YOLO. Sensors 2023, 23, 6318. [Google Scholar] [CrossRef] [PubMed]
- Lee, B.; Hong, S.; Kim, H. Determination of workers’ compliance to safety regulations using a spatio-temporal graph convolution network. Adv. Eng. Inform. 2023, 56, 101942. [Google Scholar] [CrossRef]
- Cao, Z.; Hidalgo, G.; Simon, T.; Wei, S.-E.; Sheikh, Y. OpenPose: Realtime Multi-Person 2D Pose Estimation Using Part Affinity Fields. IEEE Trans. Pattern Anal. Mach. Intell. 2021, 43, 172–186. [Google Scholar] [CrossRef] [PubMed]
- Cheng, B.; Xiao, B.; Wang, J.; Shi, H.; Van Gool, L. HigherHRNet: Scale-Aware Representation Learning for Bottom-Up Human Pose Estimation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 14–19 June 2020; pp. 5385–5394. [Google Scholar]
- Papandreou, G.; Zhu, T.; Chen, L.-C.; Gidaris, S.; Kokkinos, I.; Murphy, K. PersonLab: Person Pose Estimation and Instance Segmentation with a Bottom-Up, Part-Based, Geometric Embedding Model. In Proceedings of the Computer Vision–ECCV 2018, Munich, Germany, 8–14 September 2018; pp. 282–299. [Google Scholar]
- Ren, S.; He, K.; Girshick, R.; Sun, J. Faster R-CNN: Towards Real-Time Object Detection with Region Proposal Networks. arXiv 2015, arXiv:1506.01497. [Google Scholar] [CrossRef] [PubMed]
- Redmon, J.; Divvala, S.; Girshick, R.; Farhadi, A. You Only Look Once: Unified, Real-Time Object Detection. arXiv 2015, arXiv:1506.02640. [Google Scholar]
- Liu, W.; Anguelov, D.; Erhan, D.; Szegedy, C.; Reed, S.; Fu, C.-Y.; Berg, A.C. SSD: Single Shot MultiBox Detector. In Proceedings of the Computer Vision–ECCV 2016, Amsterdam, The Netherlands, 8–16 October 2016; pp. 21–37. [Google Scholar]
- Fang, H.S.; Li, J.; Tang, H.; Xu, C.; Zhu, H.; Xiu, Y.; Lu, C. AlphaPose: Whole-Body Regional Multi-Person Pose Estimation and Tracking in Real-Time. IEEE Trans. Pattern Anal. Mach. Intell. 2023, 45, 7157–7173. [Google Scholar] [CrossRef] [PubMed]
- Sun, K.; Xiao, B.; Liu, D.; Wang, J. Deep High-Resolution Representation Learning for Human Pose Estimation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 5686–5696. [Google Scholar]
- He, K.; Gkioxari, G.; Dollár, P.; Girshick, R. Mask R-CNN. In Proceedings of the 2017 IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 2961–2969. [Google Scholar]
- Maji, D.; Nagori, S.; Mathew, M.; Poddar, D. Yolo-Pose: Enhancing Yolo for Multi Person Pose Estimation Using Object Keypoint Similarity Loss. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 19–24 June 2022; pp. 2637–2646. [Google Scholar]
- Du, Y.; Wang, W.; Wang, L. Hierarchical recurrent neural network for skeleton based action recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 1110–1118. [Google Scholar]
- Du, Y.; Fu, Y.; Wang, L. Skeleton based action recognition with convolutional neural network. In Proceedings of the ACCV 2016 Workshops, Taipei, Taiwan, 20–24 November 2016; pp. 105–119. [Google Scholar]
- Shi, L.; Zhang, Y.; Cheng, J.; Lu, H. Two-Stream Adaptive Graph Convolutional Networks for Skeleton-Based Action Recognition. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 12026–12035. [Google Scholar]
- Liu, Z.; Zhang, H.; Chen, Z.; Wang, Z.; Ouyang, W. Disentangling and Unifying Graph Convolutions for Skeleton-Based Action Recognition. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 143–152. [Google Scholar]
- Chen, Y.; Zhang, Z.; Yuan, C.; Li, B.; Deng, Y.; Hu, W. Channel-Wise Topology Refinement Graph Convolution for Skeleton-Based Action Recognition. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, QC, Canada, 10–17 October 2021; pp. 13359–13368. [Google Scholar]
- Winter, D.A. Biomechanics and Motor Control of Human Movement, 4th ed.; John Wiley & Sons: Hoboken, NJ, USA, 2009; p. 86. [Google Scholar]
- de Leva, P. Adjustments to Zatsiorsky-Seluyanov’s segment inertia parameters. J. Biomech. 1996, 29, 1223–1230. [Google Scholar] [CrossRef] [PubMed]
- Winter, D.A. Human balance and posture control during standing and walking. Gait Posture 1995, 3, 193–214. [Google Scholar] [CrossRef]
- Freeman, R. Neurogenic orthostatic hypotension. N. Engl. J. Med. 2008, 358, 615–624. [Google Scholar] [CrossRef] [PubMed]
- van der Beek, A.J.; van Gaalen, L.C.; Frings-Dresen, M.H. Working postures and activities of lorry drivers: A reliability study of on-site observation and recording on a laptop computer. Appl. Ergon. 1992, 23, 331–336. [Google Scholar] [CrossRef] [PubMed]
- Stavrinos, D.; Byington, K.W.; Schwebel, D.C. Distracted walking: Cell phones increase injury risk for pedestrians. Accid. Anal. Prev. 2011, 43, 150–155. [Google Scholar] [CrossRef] [PubMed]
- Kay, W.; Carreira, J.; Simonyan, K.; Zhang, B.; Hillier, C.; Vijayanarasimhan, S.; Viola, F.; Green, T.; Back, T.; Natsev, P.; et al. The Kinetics Human Action Video Dataset. arXiv 2017, arXiv:1705.06950. [Google Scholar] [CrossRef]


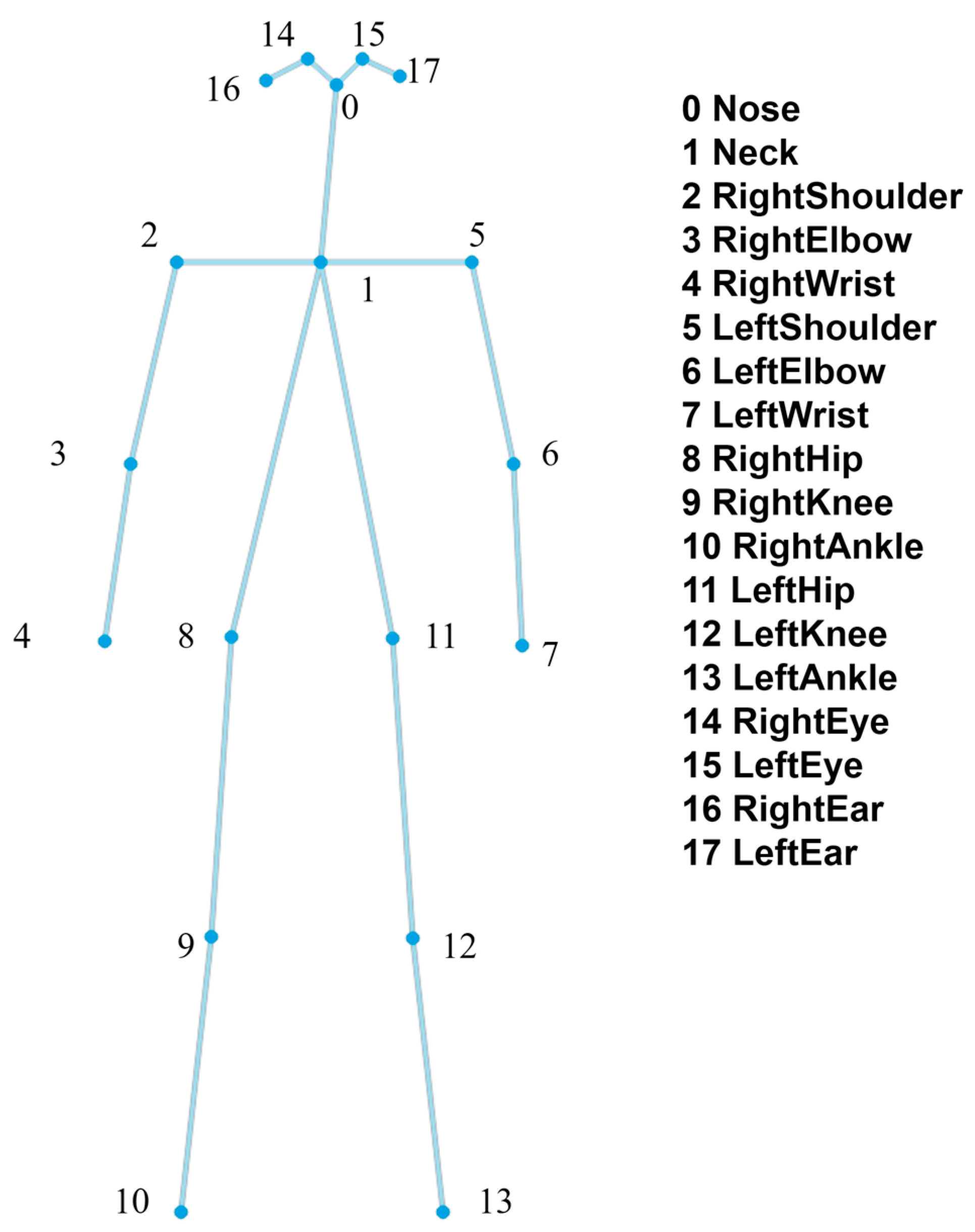






| Model | Input Size (Pixels) | AP (%) | AP@50 (%) | Params (M) | FLOPs (G) |
|---|---|---|---|---|---|
| Bottom-Up | |||||
| OpenPose (VGG19) [9] | - | 61.8 | 84.9 | 49.5 | 221.4 |
| HigherHRNet (HRNet-W32) [10] | 512 × 512 | 67.1 | 86.2 | 28.6 | 47.9 |
| Top-Down | |||||
| AlphaPose (ResNet-50) [15] | 320 × 256 | 73.3 | 89.2 | 28.1 | 26.7 |
| Mask R-CNN (ResNet-50-FPN) [17] | - | 67.0 | 87.3 | 42.3 | 260 |
| One-stage | |||||
| YOLOv8s-pose | 640 × 640 | 59.2 | 85.8 | 11.6 | 30.2 |
| Body Segment | Keypoint Index | Weight |
|---|---|---|
| Head | 0 | 0.08 |
| Trunk | 1, 11, 8 | 0.44 |
| Left Arm | 5 | 0.07 |
| Right Arm | 2 | 0.07 |
| Left Leg | 11 | 0.17 |
| Right Leg | 8 | 0.17 |
| ID | Core Region | Keypoint Index |
|---|---|---|
| l1 | Head | 0, 14, 15, 16, 17 |
| l2 | Trunk | 1, 8, 11 |
| l3 | Left Arm | 5, 6, 7 |
| l4 | Right Arm | 2, 3, 4 |
| l5 | Left Leg | 11, 12, 13 |
| l6 | Right Leg | 8, 9, 10 |
| Category | Action | Description |
|---|---|---|
| Significant CoG Displacement | Running | Large inertia, difficult to stop or turn quickly. |
| Jumping | High impact upon landing, poor stability. | |
| Quick Squat | Rapid CoG drop, prone to dizziness or instability. | |
| Getting up Quickly | Rapid CoG rise, prone to dizziness or instability. | |
| Unstable Posture | Squatting | Legs prone to fatigue, reduced coordination when standing up. |
| Distracted Attention | Phone-walking | Complete disregard for frontal and lateral road conditions. |
| Safe Behaviors | Standing | CoG stable, strong stability. |
| Walking | Small CoG displacement, wide field of view. |
| Methods | Accuracy (Top-1) | Comparison with Baseline |
|---|---|---|
| ST-GCN(Baseline) | 93.75% | - |
| CoG-STGCN (f1 + f2 + f3 + f4) | 95.83% | +2.08% |
| w/o Dist_GlobalCoG (f1) | 95.21% | +1.46% |
| w/o Vel_GlobalCoG (f2) | 93.96% | +0.21% |
| w/o Dist_CoreCoG (f3) | 94.79% | +1.04% |
| w/o Vel_CoreCoG (f4) | 94.17% | +0.42% |
| Model | Metric | Cross Validation | Average ± Std Dev | ||||
|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | |||
| ST-GCN | Accuracy | 0.9270 | 0.9479 | 0.9062 | 0.9375 | 0.9270 | 0.9291 ± 0.0146 |
| Macro-F1 | 0.9283 | 0.9491 | 0.9075 | 0.9384 | 0.9281 | 0.9303 ± 0.0146 | |
| CoG-STGCN | Accuracy | 0.9375 | 0.9583 | 0.9167 | 0.9583 | 0.9375 | 0.9417 ± 0.0169 |
| Macro-F1 | 0.9387 | 0.9594 | 0.9177 | 0.9592 | 0.9384 | 0.9427 ± 0.0169 | |
| Models | Accuracy (Top-1) | Accuracy (Top-5) | Params (M) | FLOPs (G) |
|---|---|---|---|---|
| ST-GCN [5] | 30.7% | 52.8% | 3.10 | 16.30 |
| 2s-AGCN [21] | 36.1% | 58.7% | 6.94 | 37.30 |
| Deep LSTM [5] | 16.4% | 35.3% | - | - |
| MS-G3D [22] | 38.0% | 60.9% | 6.44 | 24.50 |
| CTR-GCN [23] | - | - | 5.84 | 7.88 |
| CoG-STGCN (ours) | 33.1% | 55.7% | 3.16 | 16.95 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jin, P.; Guo, S.; Li, C. Center-of-Gravity-Aware Graph Convolution for Unsafe Behavior Recognition of Construction Workers. Sensors 2025, 25, 5493. https://doi.org/10.3390/s25175493
Jin P, Guo S, Li C. Center-of-Gravity-Aware Graph Convolution for Unsafe Behavior Recognition of Construction Workers. Sensors. 2025; 25(17):5493. https://doi.org/10.3390/s25175493
Chicago/Turabian StyleJin, Peijian, Shihao Guo, and Chaoqun Li. 2025. "Center-of-Gravity-Aware Graph Convolution for Unsafe Behavior Recognition of Construction Workers" Sensors 25, no. 17: 5493. https://doi.org/10.3390/s25175493
APA StyleJin, P., Guo, S., & Li, C. (2025). Center-of-Gravity-Aware Graph Convolution for Unsafe Behavior Recognition of Construction Workers. Sensors, 25(17), 5493. https://doi.org/10.3390/s25175493






