Sub-ppb Methane Detection via EMD–Wavelet Adaptive Thresholding in Wavelength Modulation TDLAS: A Hybrid Denoising Approach for Trace Gas Sensing
Abstract
1. Introduction
2. Principles and Approaches
2.1. Empirical Mode Decomposition (EMD)
2.2. Wavelet Adaptive Thresholding
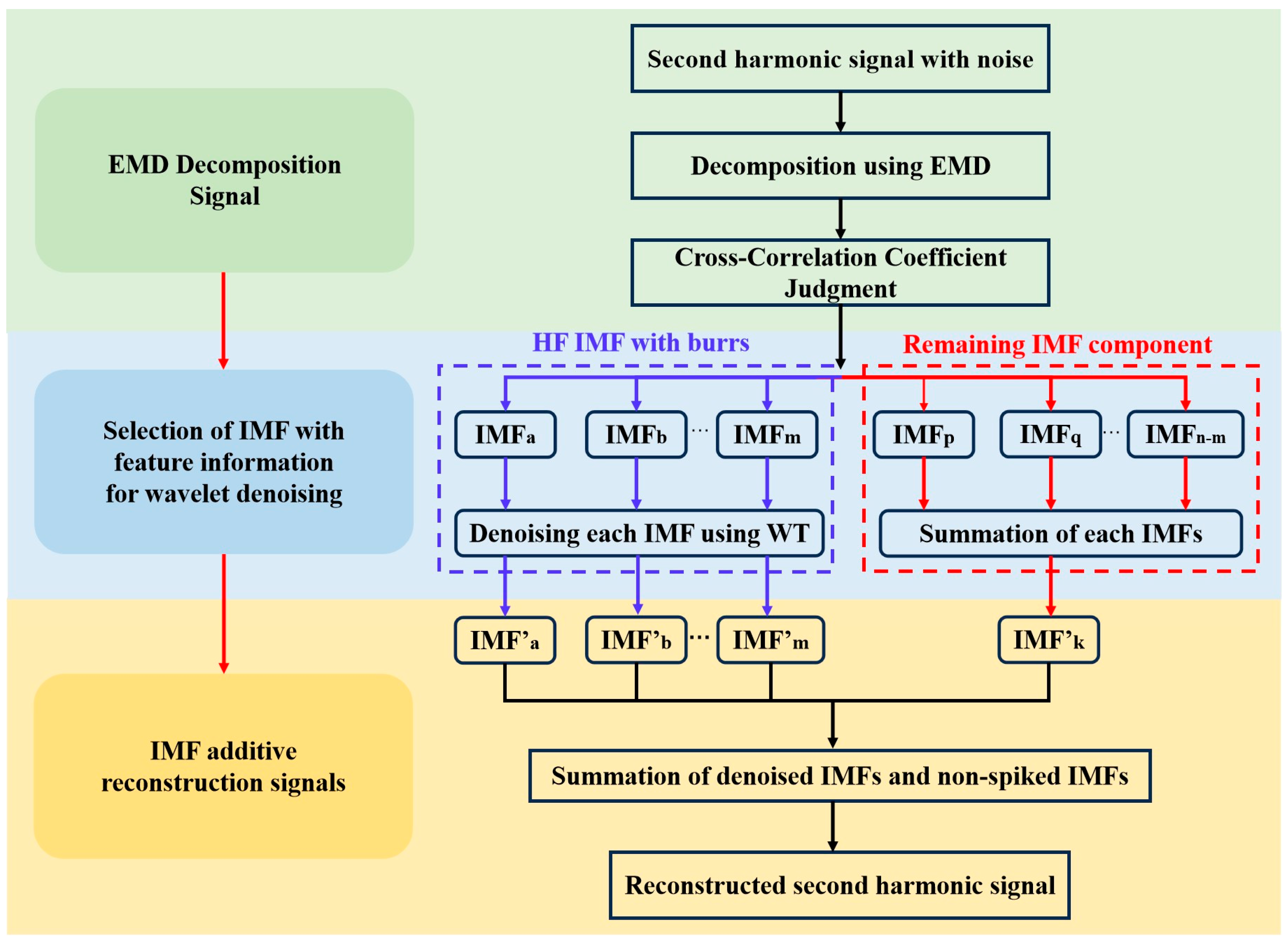
2.3. EMD–Wavelet Adaptive Thresholding Denoising Framework
3. Simulation Analysis
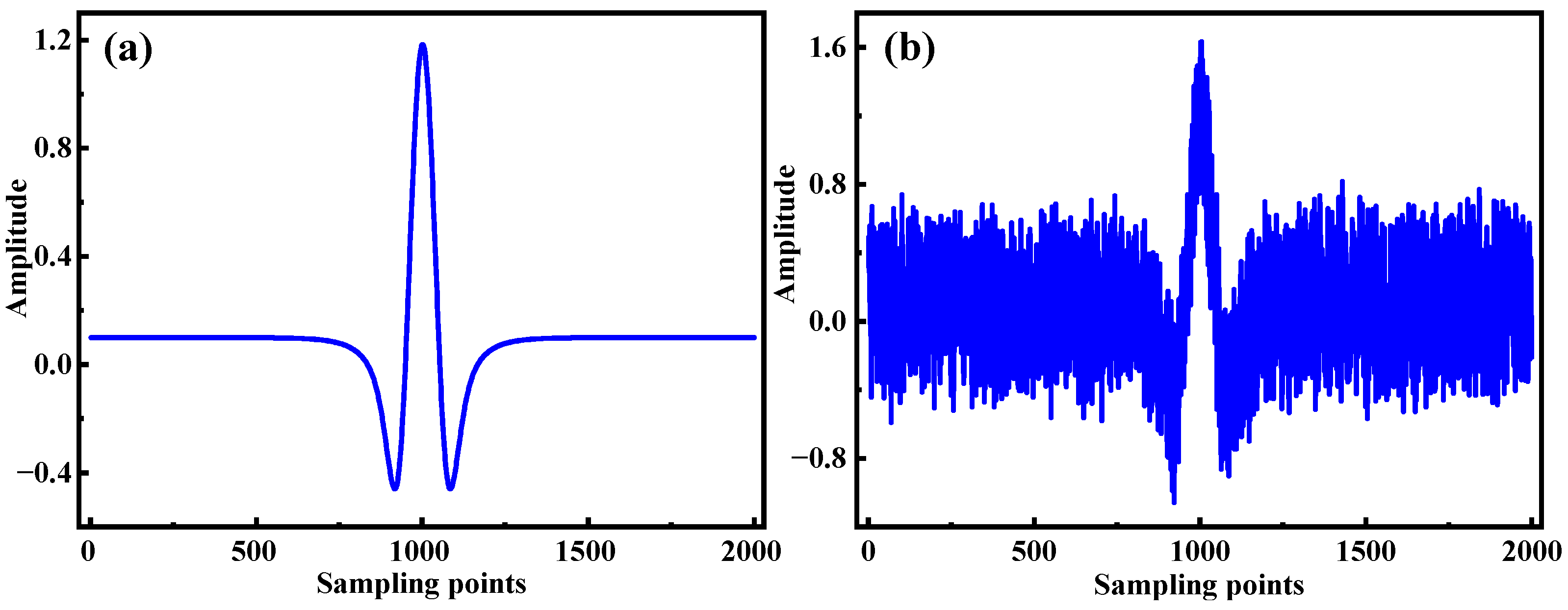
3.1. Simulation Model
3.2. Performance Analysis of EMD–Wavelet Adaptive Thresholding
3.3. Comparison Analysis with Other Methods
4. Experiments
4.1. Experimental System
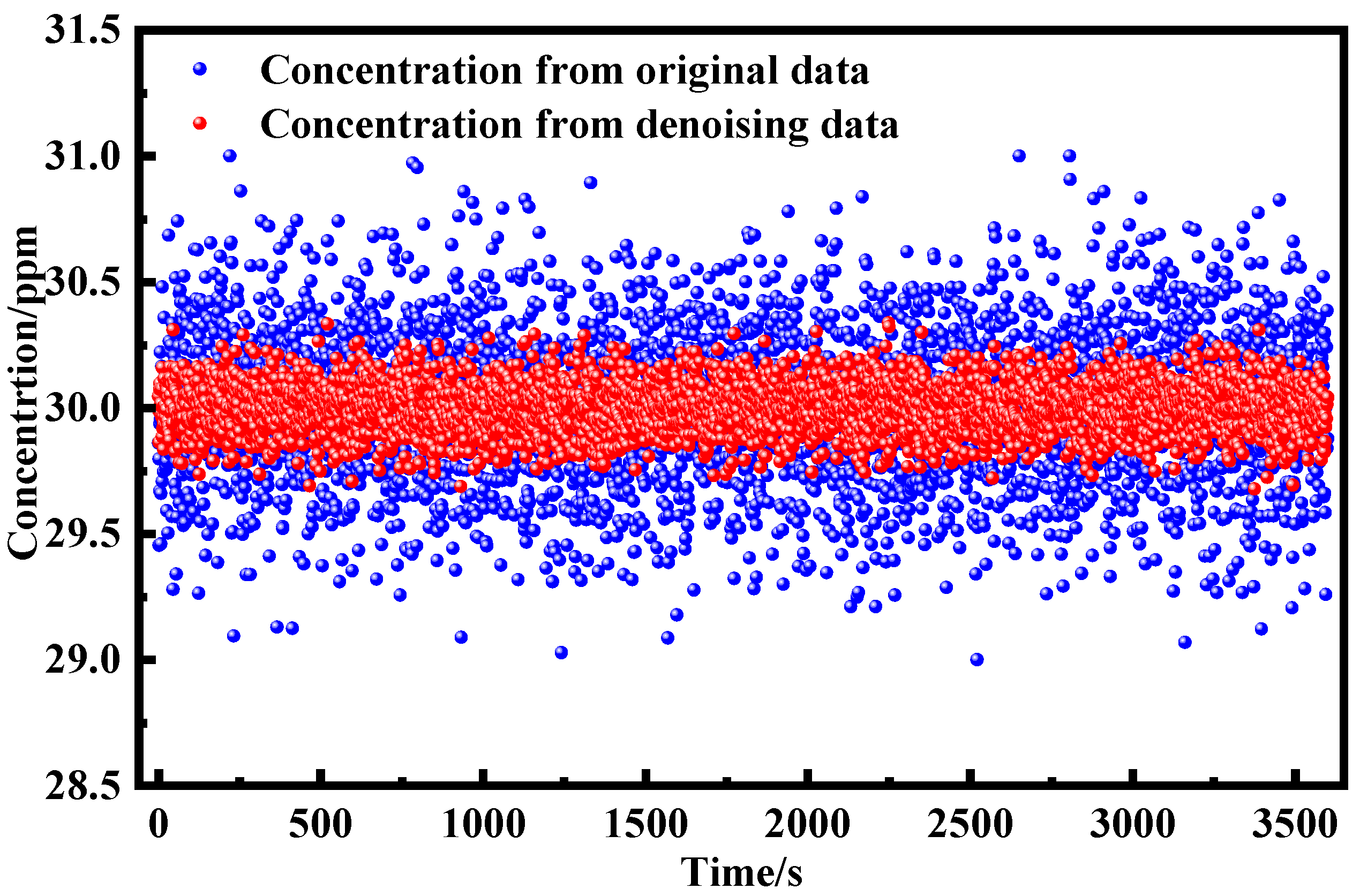
4.2. Experimental Results and Discussion
4.3. Performance Evaluation
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ma, J.; Fan, E.; Liu, H.; Zhang, Y.; Mai, C.; Li, X.; Jin, W.; Guan, B. Microscale Fiber Photoacoustic Spectroscopy for in Situ and Real-Time Trace Gas Sensing. Adv. Photonics 2024, 6, 066008. [Google Scholar] [CrossRef]
- Sun, H.; Qiao, S.; He, Y.; Sun, X.; Ma, Y. Parts-per-Quadrillion Level Gas Molecule Detection: CO-LITES Sensing. Light Sci. Appl. 2025, 14, 180. [Google Scholar] [CrossRef] [PubMed]
- Zhang, S.; Bi, T.; Del’Haye, P. On-the-Fly Precision Spectroscopy with a Dual-Modulated Tunable Diode Laser and Hz-Level Referencing to a Cavity. Adv. Photonics 2024, 6, 046003. [Google Scholar] [CrossRef]
- Shao, M.; Ji, C.; Tan, J.; Du, B.; Zhao, X.; Yu, J.; Man, B.; Xu, K.; Zhang, C.; Li, Z. Ferroelectrically Modulate the Fermi Level of Graphene Oxide to Enhance SERS Response. Opto-Electron. Adv. 2023, 6, 230094. [Google Scholar] [CrossRef]
- You, R.; Kang, H.; Zhang, X.; Zheng, S.; Shao, L.; Han, J.; Feng, G. Cubic Nonlinear Scanning for Improved TDLAS-Based Methane Concentration Detection. Int. J. Hydrogen Energy 2024, 86, 14–23. [Google Scholar] [CrossRef]
- Kong, R.; Huang, J.; Liu, P.; Zhou, X. Real-Time Breath Gas Analysis of Methane Using a Multipass Cell-Based near-Infrared Gas Sensor. Biomed. Opt. Express 2024, 15, 4207–4219. [Google Scholar] [CrossRef]
- Wu, X.; Li, Q.; Chen, J.; Chen, Q.; Yu, M. Estimation of Staphylococcus Total Viable Count in Different Contamination States of Central Venous Catheters in Hemodialysis Centers Based on Tunable Diode Laser Wavelength-Modulation Spectroscopy. Microw. Opt. Technol. Lett. 2024, 66, e34329. [Google Scholar] [CrossRef]
- Wang, Q.; Sun, P.; Zhang, Z.; Cai, Y.; Huang, W.; Pang, T.; Wu, B.; Xia, H.; Guo, Q. Method of Adaptive Wide Dynamic Range Gas Concentration Detection Based on Optimized Direct Absorption Spectroscopy. Opt. Express 2023, 31, 16770–16780. [Google Scholar] [CrossRef]
- Lan, L.; Zhang, C.; Wang, Y.; Xie, Y.; Wang, L.; Yang, C. Long-Tune Natural Logarithmic Wavelength Modulation Spectroscopy for Gas Sensing. Sensors 2024, 24, 7365. [Google Scholar] [CrossRef]
- Liang, W.; Yao, M. Suppression of Interference Fringes in Wavelength Modulation Spectroscopy Based on Convolutional Neural Networks. Opt. Commun. 2025, 574, 131201. [Google Scholar] [CrossRef]
- Zhou, Y.; Ren, Y.; Gao, F.; Liu, Z.; Hu, D. Refrigeration Experiments of Gas Wave Rotor Based on Calibration-Free WMS-TDLAS Method. Exp. Therm. Fluid Sci. 2024, 155, 111206. [Google Scholar] [CrossRef]
- Shi, Y.; Hu, Z.; Niu, M.; Li, T.; Li, H.; Liu, H.; Li, X. High-Sensitive Double Incidence Multi-Pass Cell for Trace Gas Detection Based on TDLAS. Sens. Actuators B-Chem. 2024, 412, 135829. [Google Scholar] [CrossRef]
- Liang, W. Interference Fringes Suppression for Wavelength Modulation Spectroscopy Based on Maximal Overlap Discrete Wavelet Transformation. Measurement 2025, 253, 117471. [Google Scholar] [CrossRef]
- Xie, Y.; Xiong, H.; Feng, S.; Pan, N.; Li, C.; Liu, Y.; Zhang, Y.; Shao, L.; Lu, G.; Liu, K.; et al. Sensitivity improvement of quartz-enhanced photoacoustic spectroscopy using the stochastic resonance method. Photoacoustics 2025, 43, 100707. [Google Scholar] [CrossRef] [PubMed]
- Liang, L.; Liu, Z. Fringe Pattern Preprocessing via Adaptive Multidirectional Empirical Mode Decomposition. Opt. Express 2024, 32, 43512–43533. [Google Scholar] [CrossRef]
- Guo, C.; Wang, Q. Laser Self-Mixing Interference Displacement Signal Filtering Method Based on Empirical Mode Decomposition and Wavelet Threshold. Meas. Sci. Technol. 2024, 35, 045201. [Google Scholar] [CrossRef]
- Wang, S.; Yan, M.; Jiang, J.; Li, Z.; Chen, A.; Tan, K.; Liu, T. Improved Spectral Demodulation Algorithm with EEMDAD for Sapphire Fiber Fabry-Perot High-Temperature Sensing. Appl. Opt. 2022, 61, 8405–8413. [Google Scholar] [CrossRef]
- Esmaili, P.; Martiri, L.; Esmaili, P.; Cristaldi, L. Cycle-Informed Triaxial Sensor for Smart and Sustainable Manufacturing. Sensors 2025, 25, 4431. [Google Scholar] [CrossRef]
- Zhou, H.; Xie, C.; Hu, Y.; Shen, F.; Xing, K.; Wang, B.; Wang, Y. Lidar Signal Processing Method for Atmospheric Coherence Length Measurement Based on the WD-ADMF. Appl. Opt. 2024, 63, 3343–3348. [Google Scholar] [CrossRef]
- Cheikh, F.; Benhassine, N.E.; Sbaa, S. Fetal Phonocardiogram Signals Denoising Using Improved Complete Ensemble (EMD) with Adaptive Noise and Optimal Thresholding of Wavelet Coefficients. Biomed. Eng.-Biomed. Tech. 2022, 67, 237–247. [Google Scholar] [CrossRef]
- Jenkal, W.; Latif, R.; Laaboubi, M. ECG Signal Denoising Using an Improved Hybrid DWT-ADTF Approach. Cardiovasc. Eng. Technol. 2024, 15, 77–94. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Y.; Chang, S.; Zhang, Y.; Xia, H. Application of the Hilbert-Huang Transform to Evaluate Signals in Chromatic Confocal Spectral Interferometry. Appl. Opt. 2024, 63, 9088–9096. [Google Scholar] [CrossRef]
- Chang, X.; Shen, C.; Liu, S.; Zheng, D.; Wang, S.; Yang, C.; Huang, N.E.; Bian, L. Robust Kramers-Kronig Holographic Imaging with Hilbert-Huang Transform. Opt. Lett. 2023, 48, 4161–4164. [Google Scholar] [CrossRef] [PubMed]
- Li, M.; Chen, J.; Chen, M. Spectroscopic Interferometer: Larger Measurement Range Using Wavelet Threshold Denoising and Adaptive Peak Extraction. Opt. Commun. 2024, 557, 130344. [Google Scholar] [CrossRef]
- Liu, R.L.; Zhang, D.; Yao, J.; Zhang, M. Processing of Laser Doppler Velocity Signal Based on Wavelet Threshold De-Noising. Laser Optoelectron. Prog. 2017, 54, 120701. [Google Scholar] [CrossRef]
- Qiu, H.; Lan, J.; Hu, Q.; Zhang, H.; Xu, Y.; Hao, X.; Li, Z. An Enhancement Filtering Method Based on CEEMDAN-EP-WTD for TDLAS Gas Sensing. Infrared Phys. Technol. 2024, 141, 105466. [Google Scholar] [CrossRef]
- Lin, L.; Wang, S.; Wang, K.; Zhao, Z.; Li, G. A Multi-Band Spectral Data Fusion Method for Improving the Accuracy of Quantitative Spectral Analysis. J. Pharm. Biomed. Anal. 2025, 254, 116585. [Google Scholar] [CrossRef]
- Li, S.; Zhao, Q.; Liu, J.; Zhang, X.; Hou, J. Noise Reduction of Steam Trap Based on SSA-VMD Improved Wavelet Threshold Function. Sensors 2025, 25, 1573. [Google Scholar] [CrossRef]
- Cheng, L.; Zhang, S.; Qi, Z.; Wang, X.; Chen, Y.; Feng, P. Research on eLoran Weak Signal Extraction Based on Wavelet Hard Thresholding Processing. Remote Sens. 2024, 16, 3012. [Google Scholar] [CrossRef]
- Wang, Z.-Y.; Xiang, Z.-R.; Zhi, J.-Y.; Ding, T.-C.; Zou, R. A Novel Physiological Signal Denoising Method Coupled with Multispectral Adaptive Wavelet Denoising (MAWD) and Unsupervised Source Counting Algorithm (USCA). J. Eng. Res. 2024, 12, 175–189. [Google Scholar] [CrossRef]
- Subhedar, J.; Urooj, S.; Mahajan, A. Retinal Optical Coherence Tomography Image Denoising Using Modified Soft Thresholding Wavelet Transform. Trait. Signal 2023, 40, 1179–1185. [Google Scholar] [CrossRef]
- Li, S.; Zhu, X.; Zhou, D. Power Quality Disturbance Signal Denoising and Detection Based on Improved DBO-VMD Combined with Wavelet Thresholding. Electr. Power Syst. Res. 2025, 238, 111193. [Google Scholar] [CrossRef]
- Liu, K.; Wang, L.; Tan, T.; Wang, G.; Zhang, W.; Chen, W.; Gao, X. Highly Sensitive Detection of Methane by Near-Infrared Laser Absorption Spectroscopy Using a Compact Dense-Pattern Multipass Cell. Sens. Actuators B-Chem. 2015, 220, 1000–1005. [Google Scholar] [CrossRef]
- Tian, X.; Cheng, G.; Chen, J.; Liu, K. Research on the Enhancement of Signal-to-Noise Ratio by Radio Frequency White Noise in Compact Dense-Pattern Multipass Cell for Trace Gas Detection. Microw. Opt. Technol. Lett. 2023, 65, 1108–1112. [Google Scholar] [CrossRef]









| IMFs | Correlation Coefficient | IMFs | Correlation Coefficient |
|---|---|---|---|
| IMF1 | 0.0082 | IMF6 | 0.5755 |
| IMF2 | 0.0042 | IMF7 | 0.1575 |
| IMF3 | 0.0155 | IMF8 | 0.1216 |
| IMF4 | 0.8454 | IMF9 | 0.1491 |
| IMF5 | 0.7925 | Res | 0.000594 |
| Denoising Method | RMSE/% | SNR | CC/% |
|---|---|---|---|
| Noisy signal | 0.7105 | 7.5182 | 56.14 |
| EMD | 0.0241 | 23.4028 | 99.7016 |
| Wavelet hard thresholding | 0.0194 | 26.8846 | 99.8713 |
| Wavelet soft thresholding | 0.0107 | 27.4227 | 99.9037 |
| Wavelet adaptive thresholding | 0.0218 | 24.8721 | 99.7713 |
| EMD–Wavelet Adaptive Thresholding | 0.0067 | 29.7885 | 99.9503 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mu, T.; Tian, X.; Ni, P.; Chen, S.; Cao, Y.; Cheng, G. Sub-ppb Methane Detection via EMD–Wavelet Adaptive Thresholding in Wavelength Modulation TDLAS: A Hybrid Denoising Approach for Trace Gas Sensing. Sensors 2025, 25, 5167. https://doi.org/10.3390/s25165167
Mu T, Tian X, Ni P, Chen S, Cao Y, Cheng G. Sub-ppb Methane Detection via EMD–Wavelet Adaptive Thresholding in Wavelength Modulation TDLAS: A Hybrid Denoising Approach for Trace Gas Sensing. Sensors. 2025; 25(16):5167. https://doi.org/10.3390/s25165167
Chicago/Turabian StyleMu, Tong, Xing Tian, Peiren Ni, Shichao Chen, Yanan Cao, and Gang Cheng. 2025. "Sub-ppb Methane Detection via EMD–Wavelet Adaptive Thresholding in Wavelength Modulation TDLAS: A Hybrid Denoising Approach for Trace Gas Sensing" Sensors 25, no. 16: 5167. https://doi.org/10.3390/s25165167
APA StyleMu, T., Tian, X., Ni, P., Chen, S., Cao, Y., & Cheng, G. (2025). Sub-ppb Methane Detection via EMD–Wavelet Adaptive Thresholding in Wavelength Modulation TDLAS: A Hybrid Denoising Approach for Trace Gas Sensing. Sensors, 25(16), 5167. https://doi.org/10.3390/s25165167





