Research on Miniaturized UHF Sensing Technology for PD Detection in Power Equipment Based on Symmetric Cut Theory
Abstract
1. Introduction
2. Sensor Design Principles
2.1. Planar Monopole Sensor
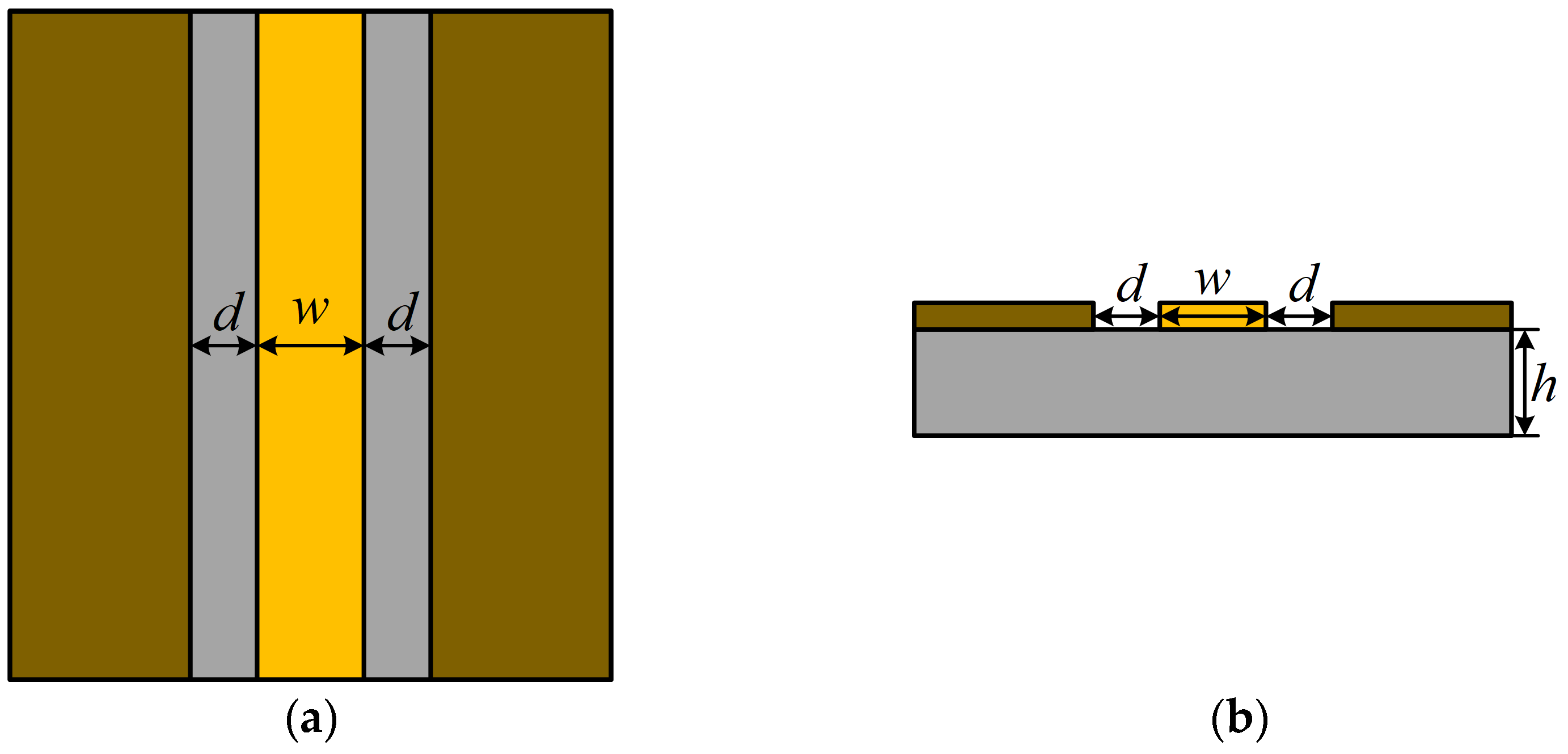
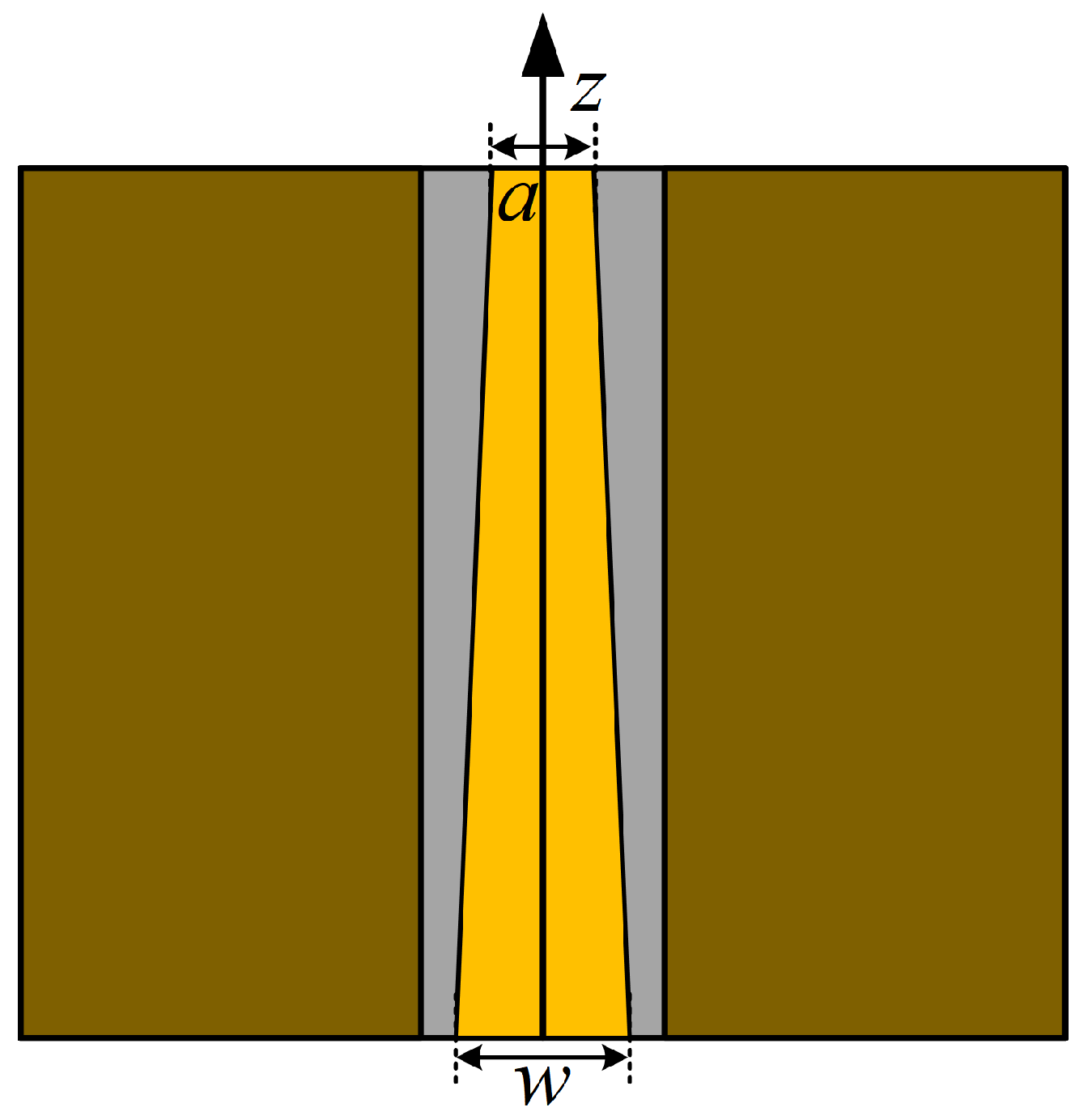
2.2. Theory of Symmetric Cut Miniaturization
2.3. Coplanar Waveguide Feed
3. UHF Sensor Design and Optimization
3.1. Sensor Design
3.1.1. Sensor Body Design
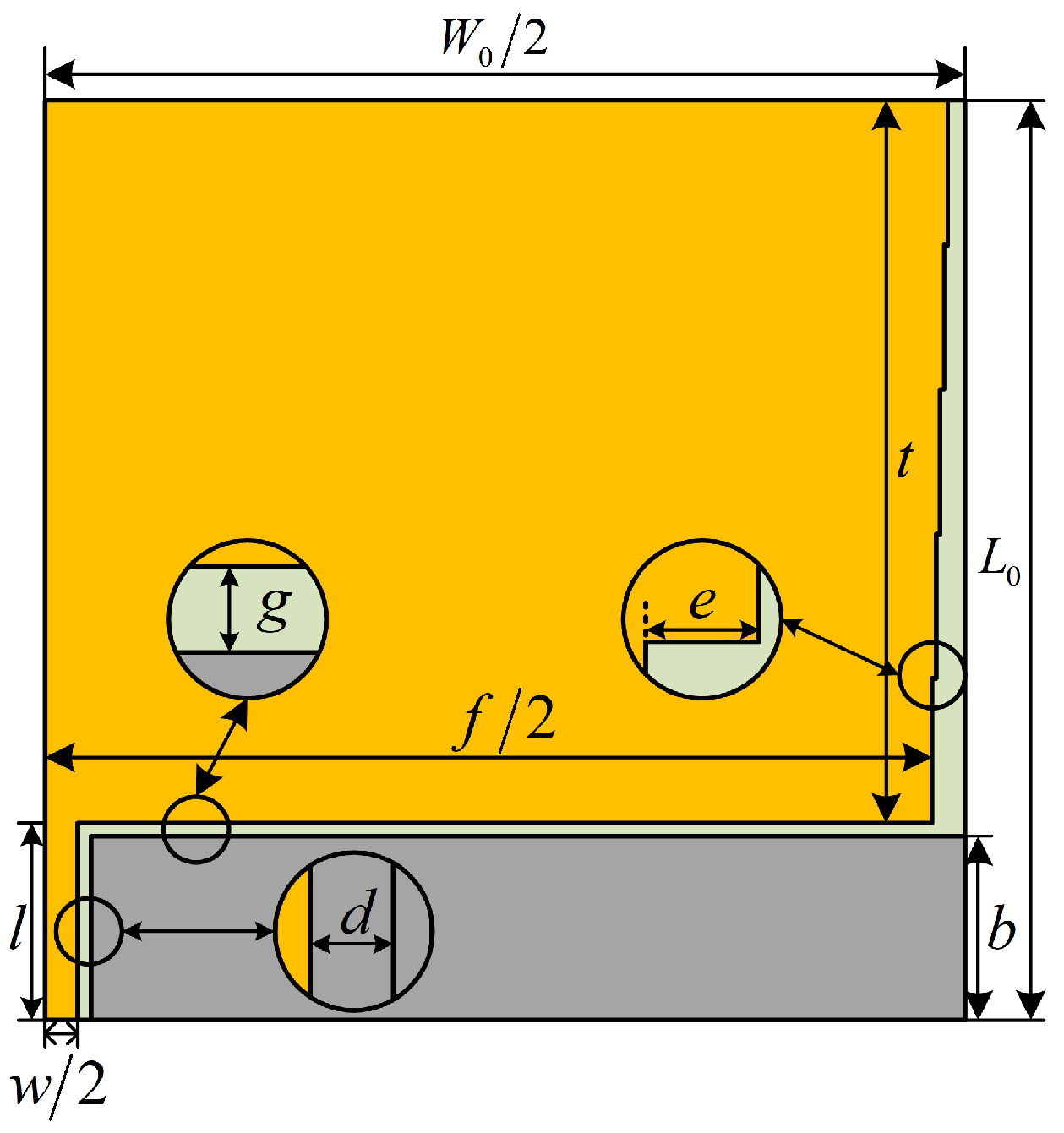
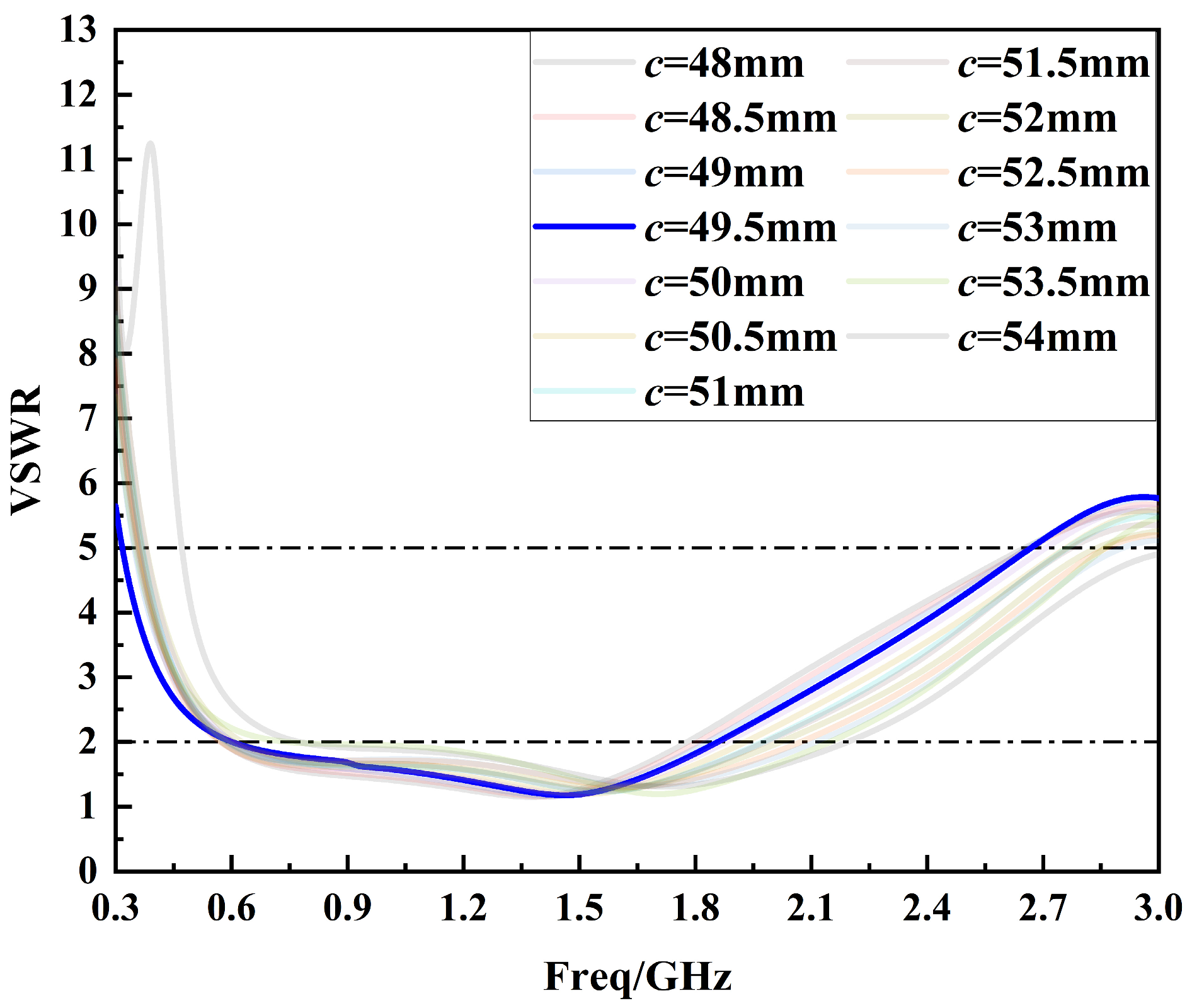
3.1.2. Symmetric Cut Miniaturization Optimization
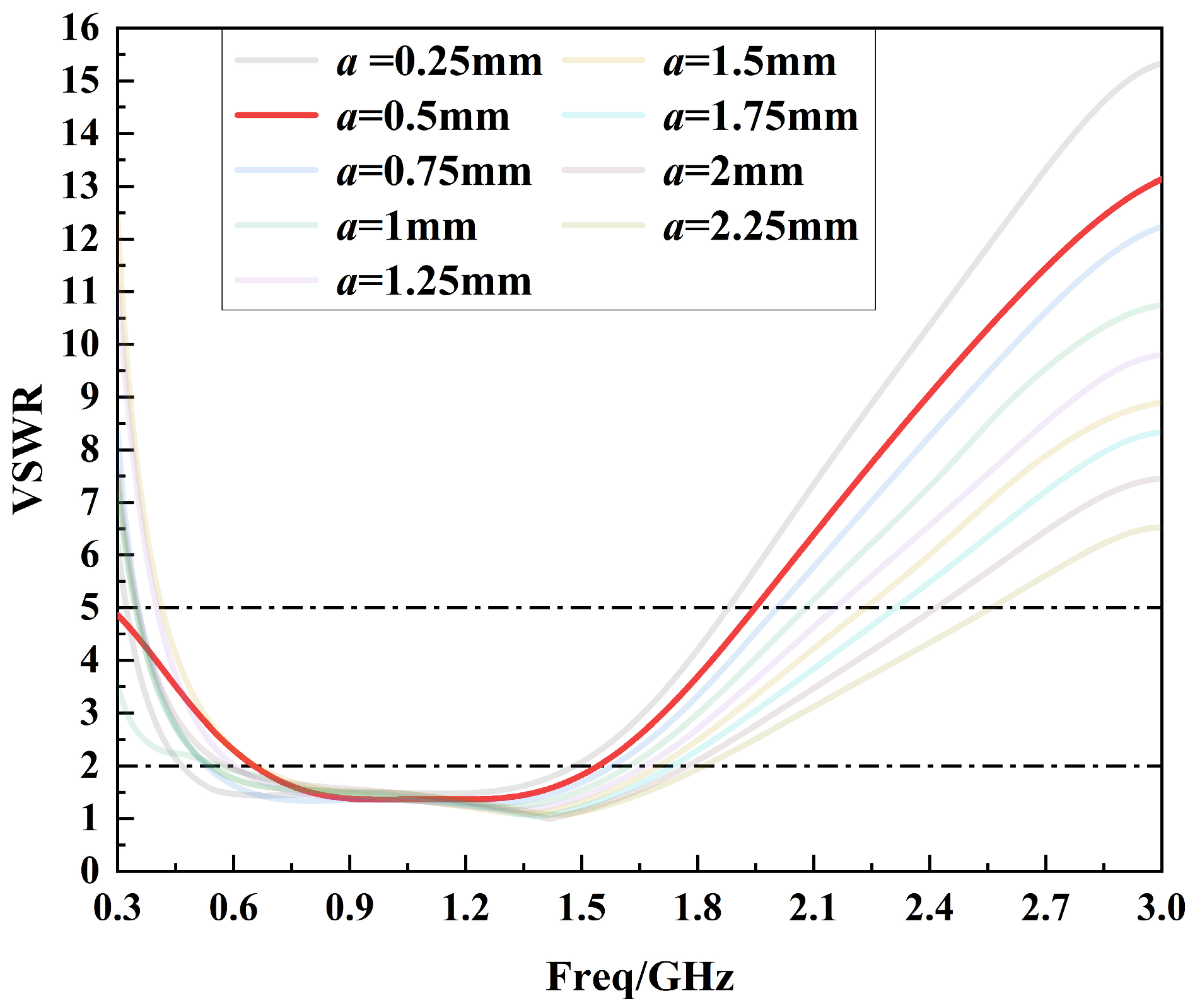
3.1.3. Asymptotic Treatment of CPW Feed Line
3.2. Optimization of Sensor Parameters
4. Sensor Performance Analysis
4.1. Voltage Standing Wave Ratio
4.2. Gain
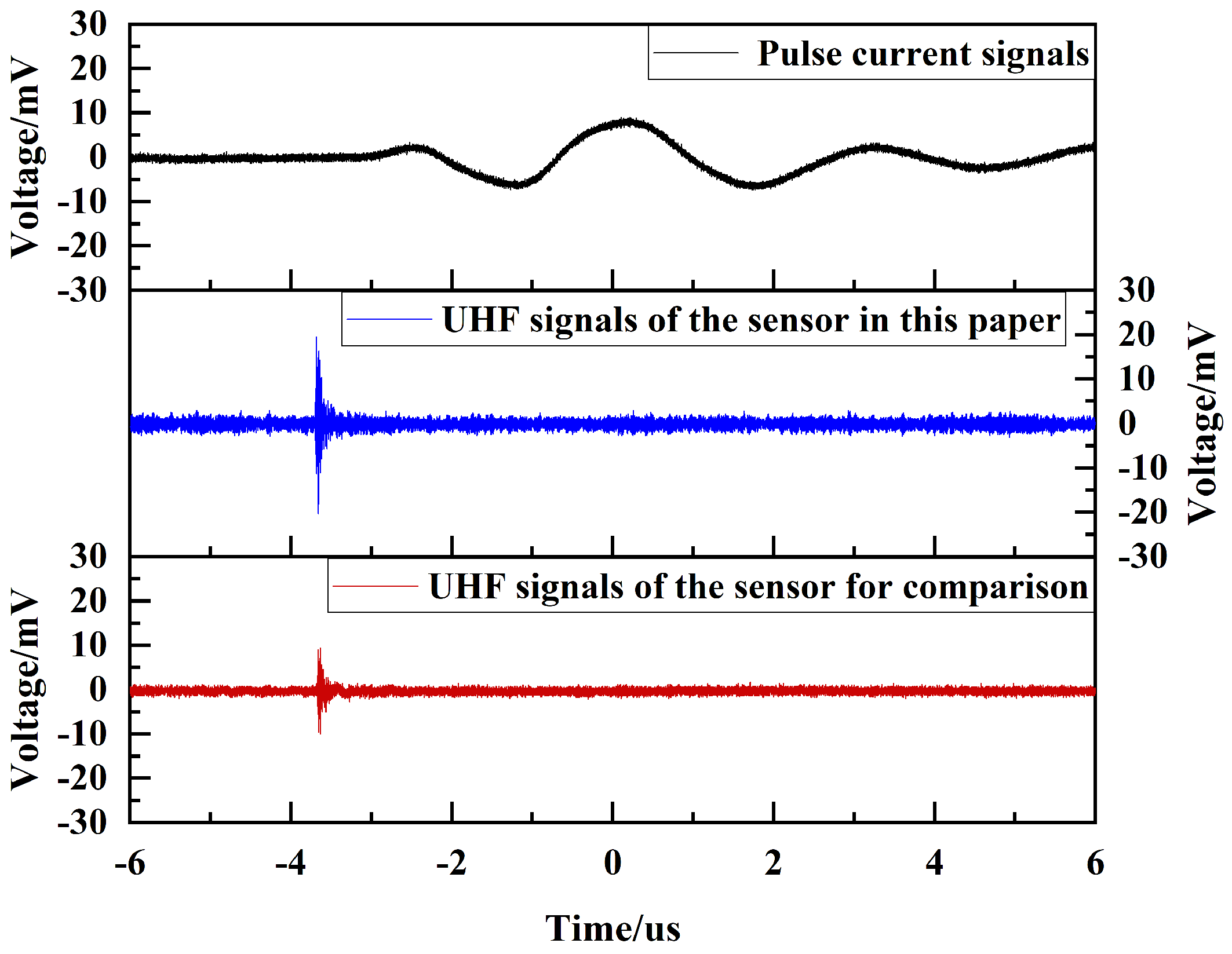
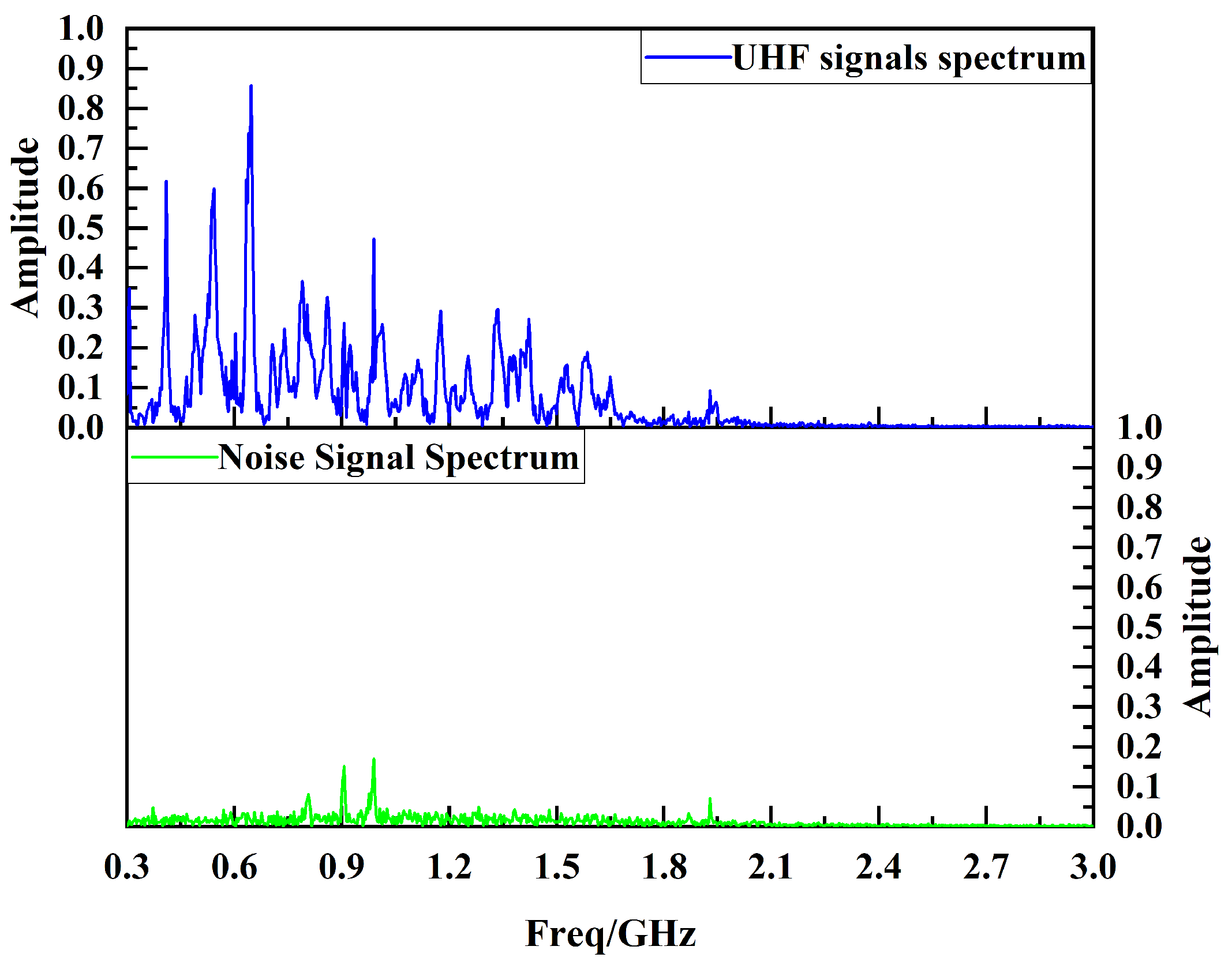
4.3. PD Perception Experimental Test
5. Conclusions
- By miniaturizing the sensor through the symmetric cut miniaturization theory, the size of the sensor is reduced by 50% to only 70 mm × 70 mm with a thickness of 1.6 mm. The sensor has a wide detection band with a VSWR of less than 2 in the 427 MHz~1.54 GHz band and a VSWR of less than 5 in the 300 MHz~1.95 GHz band, which can cover the main frequency band of PD detection; in the 300 MHz~1.5 GHz band, the maximum gain and average gain of the E-plane of the sensor are 4.76 dB and 1.02 dB, respectively, and the performance of the sensor gain is good.
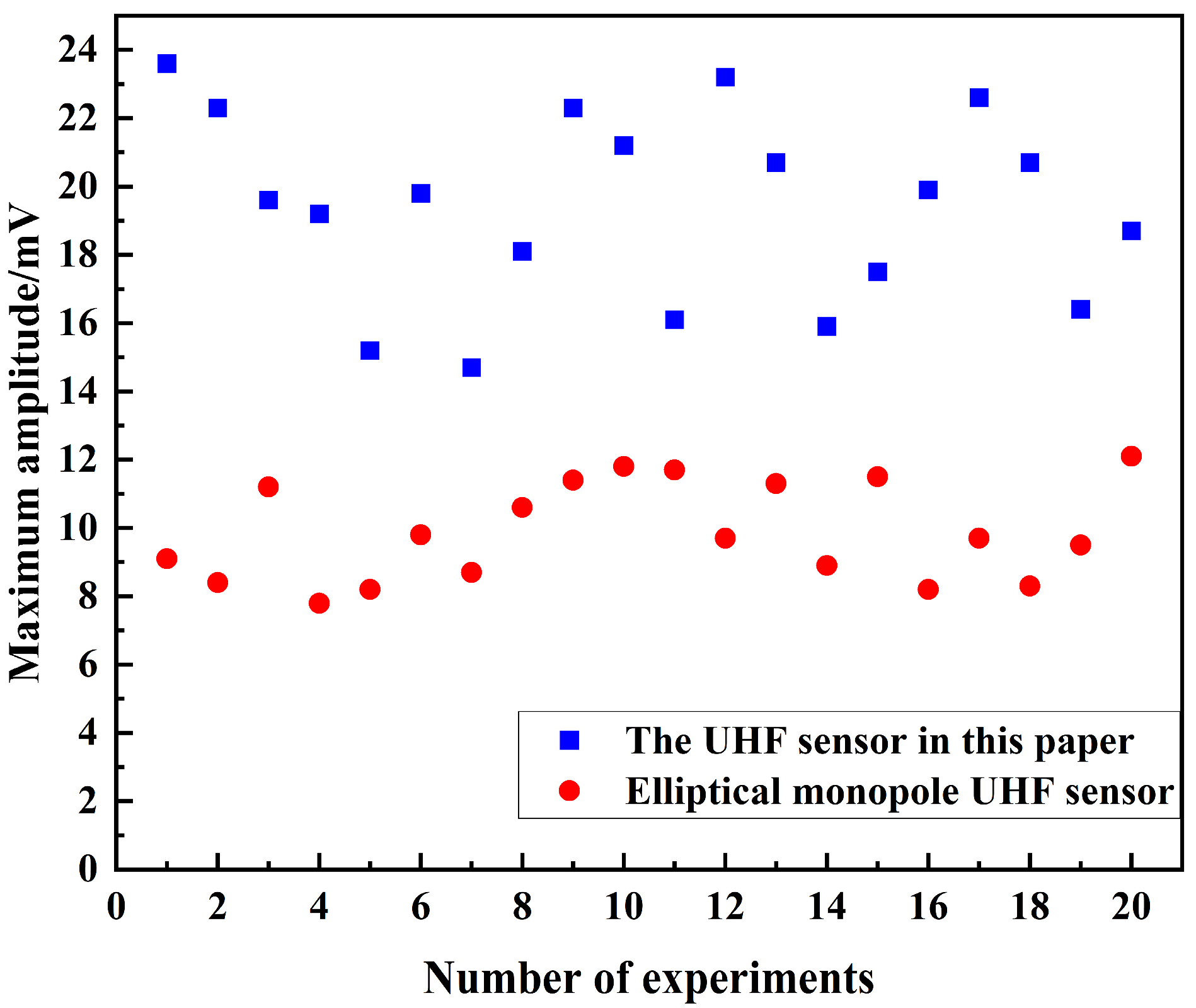
- The experimental results show that the UHF sensor designed by the symmetric cut theory in this paper has excellent PD sensing performance on the basis of a substantial reduction of the sensor structure size; compared to the highly sensitive elliptical monopole UHF sensor, the sensing sensitivity of the UHF sensor designed in this paper is improved by about 95%.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhang, D.Z.; Tong, J.; Xia, B.K. Humidity-sensing properties of chemically reduced graphene oxide/polymer nanocomposite film sensor based on layer-by-layer nano self-assembly. Sens. Actuator B-Chem. 2014, 197, 66–72. [Google Scholar] [CrossRef]
- Zhang, X.X.; Yu, L.; Wu, X.Q.; Hu, W.H. Experimental Sensing and Density Functional Theory Study of H2S and SOF2 Adsorption on Au-Modified Graphene. Adv. Sci. 2015, 2, 10. [Google Scholar] [CrossRef]
- Cui, H.; Zhang, X.X.; Zhang, J.; Zhang, Y. Nanomaterials-based gas sensors of SF6 decomposed species for evaluating the operation status of high-voltage insulation devices. High Volt. 2019, 4, 242–258. [Google Scholar] [CrossRef]
- Liu, Z.H.; Wang, Y.Q.; Chen, X.; Meng, X.K.; Liu, X.L.; Yao, J.Q. An optical fiber sensing method for partial discharge in the HVDC cable system. Int. J. Electr. Power Energy Syst. 2021, 128, 9. [Google Scholar] [CrossRef]
- Zhang, G.; Chen, K.; Tian, H.; Lu, C.; Li, X.; Zhang, X. Ultra-Compact Built-in Flexible Broadband UHF Monopole Antenna Sensing Technology. High Volt. Eng. 2023, 49, 1475–1485. [Google Scholar] [CrossRef]
- Gao, W.S.; Ding, D.W.; Liu, W.D.; Huang, X.H. Investigation of the Evaluation of the PD Severity and Verification of the Sensitivity of Partial-Discharge Detection Using the UHF Method in GIS. IEEE Trans. Power Deliv. 2014, 29, 38–47. [Google Scholar]
- Xavier, G.V.R.; Serres, A.J.R.; da Costa, E.G.; de Oliveira, A.C.; Nobrega, L.; de Souza, V.C. Design and Application of a Metamaterial Superstrate on a Bio-Inspired Antenna for Partial Discharge Detection through Dielectric Windows. Sensors 2019, 19, 4255. [Google Scholar] [CrossRef]
- Wang, P.; Ma, S.J.; Akram, S.; Meng, P.F.; Castellon, J.; Li, Z.Z.; Montanari, G.C. Design of an Effective Antenna for Partial Discharge Detection in Insulation Systems of Inverter-fed Motors. IEEE Trans. Ind. Electron. 2022, 69, 13727–13735. [Google Scholar] [CrossRef]
- Xavier, G.V.R.; da Costa, E.G.; Serres, A.J.R.; Nobrega, L.; Oliveira, A.C.; Sousa, H.F.S. Design and Application of a Circular Printed Monopole Antenna in Partial Discharge Detection. IEEE Sens. J. 2019, 19, 3718–3725. [Google Scholar] [CrossRef]
- Wang, Y.Q.; Wang, Z.; Li, J.F. UHF Moore Fractal Antennas for Online GIS PD Detection. IEEE Antennas Wirel. Propag. Lett. 2017, 16, 852–855. [Google Scholar] [CrossRef]
- Feng, X.; Liu, H.; Zhang, D.; Cui, Y.; Xue, S.; Zhao, Y. A RF Antenna Design Method for Partial Discharge Detection Based on Coplanar Waveguide Feeding. In Proceedings of the 2022 IEEE International Conference on Power Systems and Electrical Technology (PSET), Aalborg, Denmark, 13–15 October 2022. [Google Scholar] [CrossRef]
- Zhang, G.; Chen, K.; Li, X.; Wang, K.; Fang, R.; Liu, J. GIS_PD Detection Flexible Built-in Miniaturized Archimedes Helical Antenna Sensor. High Volt. Eng. 2022, 48, 2244–2254. [Google Scholar] [CrossRef]
- Tian, J.W.; Zhang, G.Z.; Ming, C.; He, L.Y.; Liu, Y.; Liu, J.B.; Zhang, X.X. Design of a Flexible UHF Hilbert Antenna for Partial Discharge Detection in Gas-Insulated Switchgear. IEEE Antennas Wirel. Propag. Lett. 2023, 22, 794–798. [Google Scholar] [CrossRef]
- Yadam, Y.R.; Ramanujam, S.; Arunachalam, K. An Ultrawideband Conical Monopole With Radome for Detection of Partial Discharges. IEEE Sens. J. 2021, 21, 18764–18772. [Google Scholar] [CrossRef]
- Sharma, M.K.; Kumar, M.; Saini, J.P. Design and Analysis of a Compact UWB-MIMO Antenna with Improved Isolation for UWB/WLAN Applications. Wirel. Pers. Commun. 2021, 119, 2913–2928. [Google Scholar] [CrossRef]
- Gao, G.P.; Hu, B.; Zhang, J.S. Design of a Miniaturization Printed Circular-Slot UWB Antenna by the Half-Cutting Method. IEEE Antennas Wirel. Propag. Lett. 2013, 12, 567–570. [Google Scholar] [CrossRef]
- Guo, J.Y.; Feng, W.K.; Friedt, J.M.; Zhao, Q.; Sato, M. A Half-Cut Compact Monopole Antenna for SFCW Radar-Based Concrete Wall Monitoring With a Passive Cooperative Target. IEEE Geosci. Remote Sens. Lett. 2020, 17, 973–977. [Google Scholar] [CrossRef]
- Mondal, K. Half cutting dual-band circularly polarized monopole antenna for wireless communications. AEU-Int. J. Electron. Commun. 2021, 142, 11. [Google Scholar] [CrossRef]
- Sun, M.; Zhang, Y.P.; Lu, Y.L. Miniaturization of Planar Monopole Antenna for Ultrawideband Radios. IEEE Trans. Antennas Propag. 2010, 58, 2420–2425. [Google Scholar] [CrossRef]
- Chair, R.; Mak, C.L.; Kai-Fong, L.; Kwai-Man, L.; Kishk, A.A. Miniature wide-band half U-slot and half E-shaped patch antennas. IEEE Trans. Antennas Propag. 2005, 53, 2645–2652. [Google Scholar] [CrossRef]
- Xue, H.G.; Yang, X.X.; Ma, Z.W. A Novel Microstrip-CPW Fed Planar Slot Antenna with Broadband and Circular Polarization. IEEE Antennas Wirel. Propag. Lett. 2015, 14, 1392–1395. [Google Scholar] [CrossRef]
- Chai, H.; Phung, B.T.; Mitchell, S. Application of UHF Sensors in Power System Equipment for Partial Discharge Detection: A Review. Sensors 2019, 19, 1029. [Google Scholar] [CrossRef] [PubMed]
- Prakoso, T.; Ngah, R.; Rahman, T.A.; Okonkwo, U.A.K.; Ghassemlooy, Z. An evaluation of half-cut technique for microwave-photonic access-point antenna miniaturization. In Proceedings of the 2011 IEEE International RF & Microwave Conference, Seremban, Malaysia, 12–14 December 2011. [Google Scholar] [CrossRef]
- Bai, R. Simulation Study of Low-Profile Unidirectional Radiating Planar Helical Antenna Model. Master’s Thesis, Jilin University, Changchun, China, 2019. [Google Scholar]
- Uwiringiyimana, J.P.; Khayam, U.; Suwarno; Montanari, G.C. Design and Implementation of Ultra-Wide Band Antenna for Partial Discharge Detection in High Voltage Power Equipment. IEEE Access 2022, 10, 10983–10994. [Google Scholar] [CrossRef]
- Satyam; Limbakar, D.; Rauniyar, P.S.; Deepthi, G.; Supriya, J.S.; Madhavi, K.V. Compact UWB Patch Antenna for Partial Discharge detection using Dual Rampart Line Structure, Slots and DGS. In Proceedings of the 8th International Conference on Communication and Electronics Systems (ICCES), Coimbatore, India, 1–3 June 2023. [Google Scholar] [CrossRef]
- Zhang, X.Y.; Duan, W.; Pan, Y.M. High-Gain Filtering Patch Antenna without Extra Circuit. IEEE Trans. Antennas Propag. 2015, 63, 5883–5888. [Google Scholar] [CrossRef]
- Zhang, H.T.; Zhang, G.Z.; Zhang, X.X.; Tian, H.L.; Lu, C.Y.; Liu, J.B.; Zhang, Y. PD Flexible Built-In High-Sensitivity Elliptical Monopole Antenna Sensor. Sensors 2022, 22, 4982. [Google Scholar] [CrossRef] [PubMed]


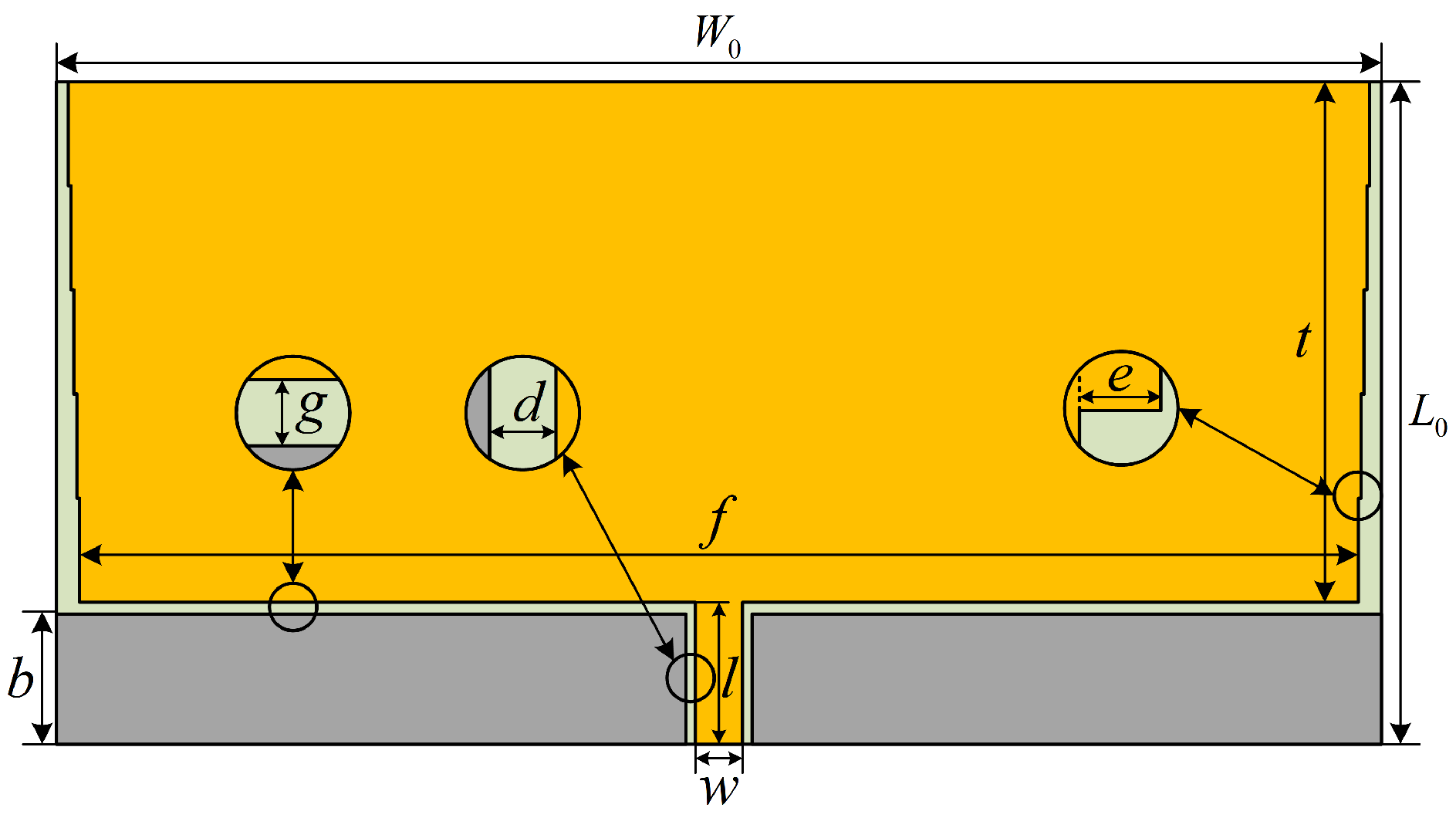


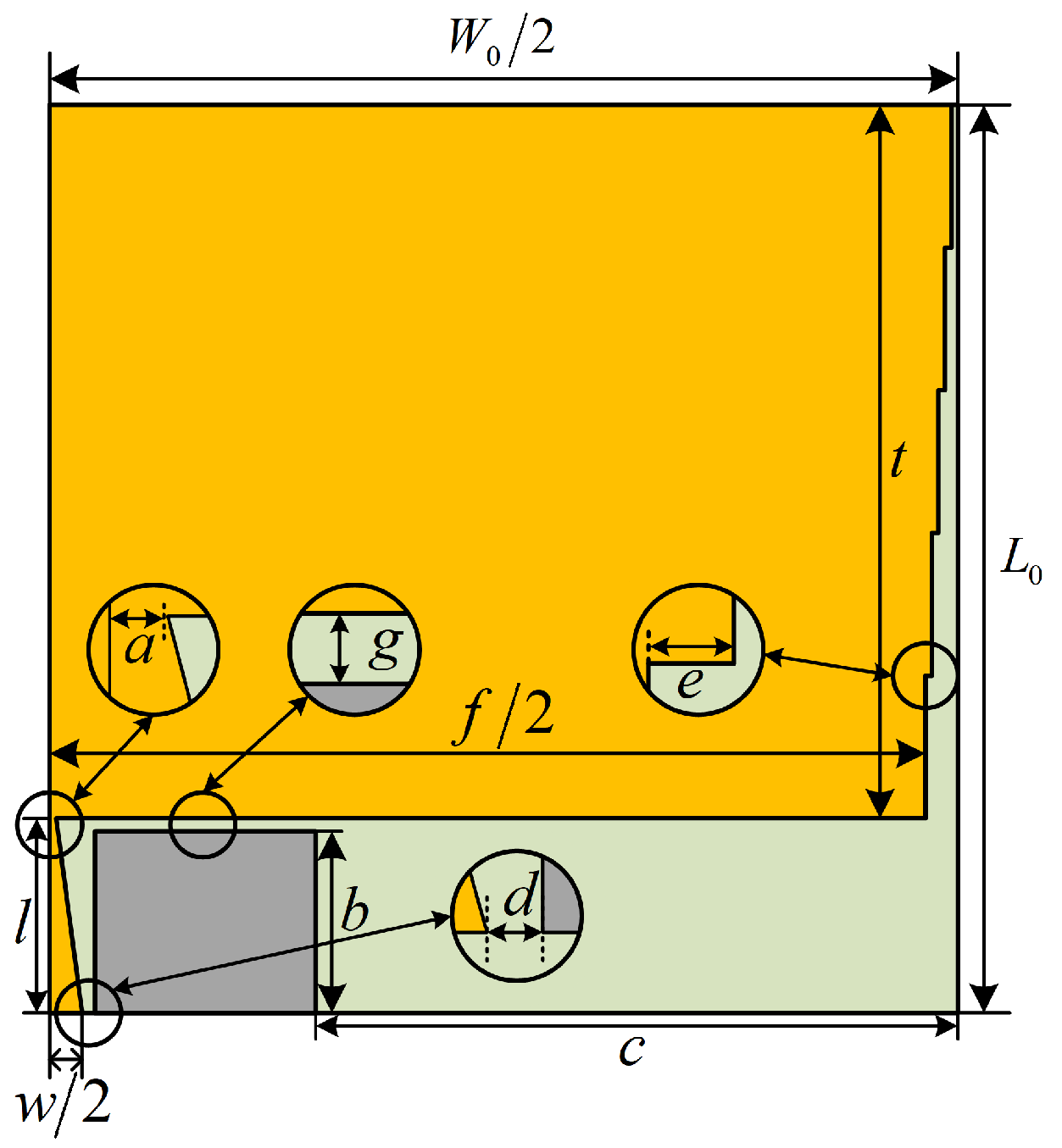






| Parameter Name | Notation | Value (mm) |
|---|---|---|
| Length of patch | t | 55 |
| Width of patch | f | 135 |
| Width of steps | e | 0.3 |
| Height of ground plate | b | 14 |
| Spacing between feed line and ground plate | d | 0.5 |
| Gap between patch and ground plate | g | 1 |
| Length of feed line | l | 15 |
| Width of feed line | w | 5 |
| Parameter Name | Notation | Value (mm) |
|---|---|---|
| Length of patch | t | 55 |
| Width of patch | f/2 | 67.5 |
| Width of steps | e | 0.5 |
| Height of ground plate | b | 14 |
| Spacing between feed line and ground plate | d | 0.5 |
| Gap between patch and ground plate | g | 1 |
| Length of feed line | l | 15 |
| Bottom width of the feed line | w/2 | 2.5 |
| Top width of the feed line | a | 0.5 |
| Distance between ground plate and outer edge of the dielectric substrate | c | 49.5 |
| Number of Experiments | Average Amplitude of the Sensor in This Paper (mV) | Average Amplitude of the Comparison Sensor (mV) | Percentage Improvement |
|---|---|---|---|
| 1~4 | 21.18 | 9.13 | 131.98% |
| 5~8 | 16.95 | 9.33 | 81.67% |
| 9~12 | 20.07 | 11.15 | 80% |
| 13~16 | 18.5 | 9.98 | 85.37% |
| 17~20 | 20.14 | 9.9 | 103.47% |
| 1~20 | 19.385 | 9.895 | 95.91% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, B.; Duan, C.; Wang, J.; Zhang, L.; Zhang, G.; Zhang, G.; Li, G. Research on Miniaturized UHF Sensing Technology for PD Detection in Power Equipment Based on Symmetric Cut Theory. Sensors 2024, 24, 3313. https://doi.org/10.3390/s24113313
Xu B, Duan C, Wang J, Zhang L, Zhang G, Zhang G, Li G. Research on Miniaturized UHF Sensing Technology for PD Detection in Power Equipment Based on Symmetric Cut Theory. Sensors. 2024; 24(11):3313. https://doi.org/10.3390/s24113313
Chicago/Turabian StyleXu, Bowen, Chaoqian Duan, Jiangfan Wang, Lei Zhang, Guozhi Zhang, Guoguang Zhang, and Guangke Li. 2024. "Research on Miniaturized UHF Sensing Technology for PD Detection in Power Equipment Based on Symmetric Cut Theory" Sensors 24, no. 11: 3313. https://doi.org/10.3390/s24113313
APA StyleXu, B., Duan, C., Wang, J., Zhang, L., Zhang, G., Zhang, G., & Li, G. (2024). Research on Miniaturized UHF Sensing Technology for PD Detection in Power Equipment Based on Symmetric Cut Theory. Sensors, 24(11), 3313. https://doi.org/10.3390/s24113313






