A Modeling Method for Thermal Error Prediction of CNC Machine Equipment Based on Sparrow Search Algorithm and Long Short-Term Memory Neural Network
Abstract
1. Introduction
2. Thermal Error Modeling Principle
2.1. Key Temperature-Sensitive Points Screening
- 1.
- Initialize the membership values, .
- 2.
- Calculate the cluster centers by Equation (7).
- 3.
- Update by Equation (5).
- 4.
- Compute the value of the objective function by Equation (8).
- 5.
- If or , then stop; otherwise, return to step 2.
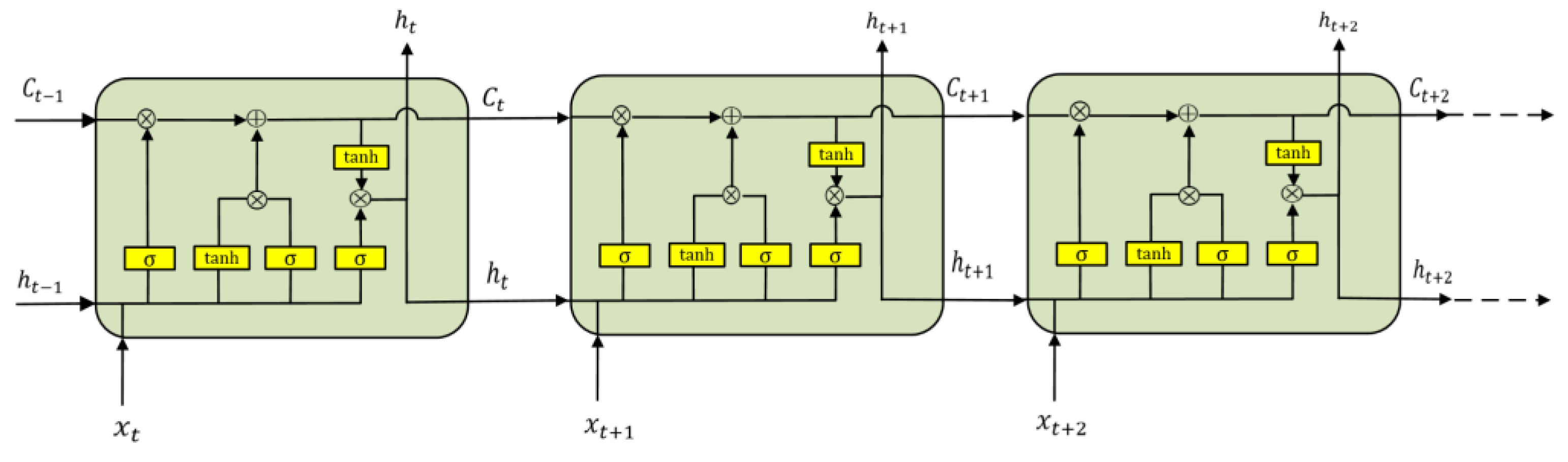
2.2. Long Short-Term Memory Neural Network
2.3. Principle of Sparrow Search Algorithm
- 1.
- Initialize the population.
- 2.
- Determine the fitness function.
- 3.
- Update the location of the discoverer.
- 4.
- Update the location of the joiner.
- 5.
- Update the location of the scout.
2.4. Thermal Error Prediction Model Based on SSA-LSTMNN
- 1.
- Determine the structure of LSTMNN, randomly initialize the parameters and thresholds of the neural network, and prepare the data set, including the training set and test set.
- 2.
- Set the parameters of the SSA, including:
- (1)
- Iteration times of the algorithm. This parameter determines the running time of the program and the stability of the model. Here, the number of iterations is set to 50.
- (2)
- The total number of populations, N, here set to 30.
- (3)
- The percentage of discoverers, here set to 20%.
- (4)
- The scout ratio, here set at 15%.
- (5)
- The safety threshold, here set to 0.8.
- (6)
- The dimensionality of the problem space to be optimized. Here, we wanted to optimize the number of iterations, learning rate, and the number of nodes of hidden layer units of the LSTMNN, so the algorithm dimension is set to 3.
- 3.
- Determine the fitness function. In this paper, the root mean square error (RMSE) between the predicted value of the SSA-LSTMNN model and the actual value is used as the fitness function. Calculate the fitness function value of each sparrow, and sort according to the fitness value to select the current optimal position and the worst position.
- 4.
- Update the positions of all members, including discoverers, joiners, and scouts, according to the Equations (19)–(21).
- 5.
- Obtain the current optimal value and compare it with the previous optimal value. If the current optimal value is better than the previous one, update the global optimal value; otherwise, do not update, and return to the step 4, continuing to iterate until the maximum number of iterations is met.
- 6.
- The optimal solution selected after the termination iteration of the algorithm is used to determine the parameters and thresholds of the LSTMNN for network model training. The SSA-LSTMNN modeling process is shown in Figure 3.
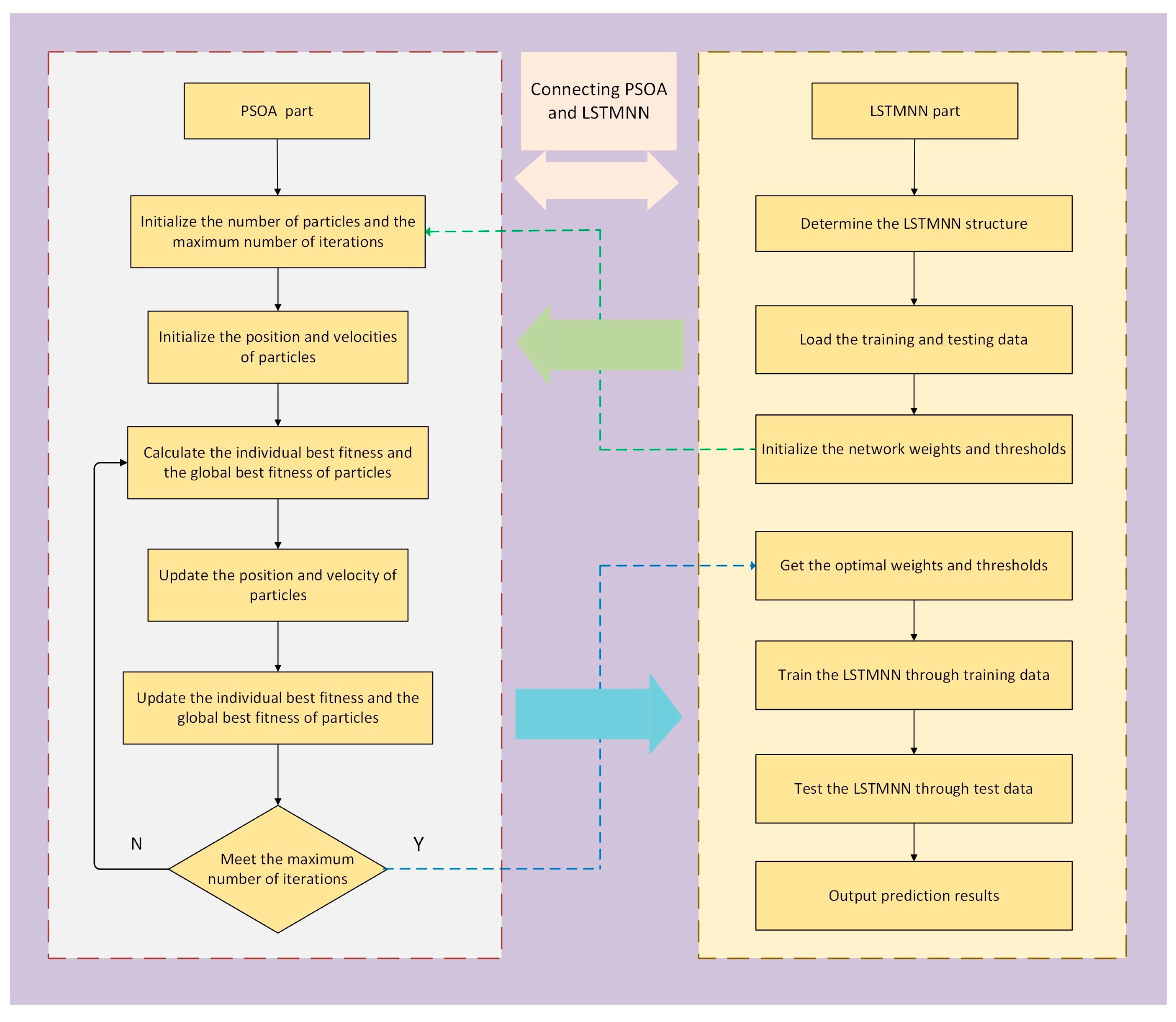
2.5. Thermal Error Prediction Model Based on PSOA-LSTMNN
- 1.
- Determine the structure of the LSTMNN; prepare the data set, including the test and training set; and initialize the thresholds and parameters of the neural network randomly.
- 2.
- Initialize the parameters of the PSOA. Set the total number of particle swarm to 30 and the maximum number of iterations to 50.
- 3.
- Random initialization of the position and velocity vectors of each particle.
- 4.
- Determine the fitness function. The Root Mean Square Error (RMSE) of the predicted and actual values of the PSOA-LSTMNN model is used as the fitness function to calculate the individual best fitness function and the global best fitness function of the particles.
- 5.
- Update the particle’s velocity and position vectors.
- 6.
- Update the individual best-fit function values and global best-fit function values of the particles.
- 7.
- Judge whether the algorithm meets the end condition. If it does not, return to step 5 to continue iteration; if yes, continue to step 8.
- 8.
- Feed the optimal parameters optimized by the PSOA to the LSTMNN for model training. The process of thermal error prediction by the PSOA-LSTMNN model is shown in Figure 4.
3. Experimental Process
4. Establishment of the Thermal Error Prediction Model
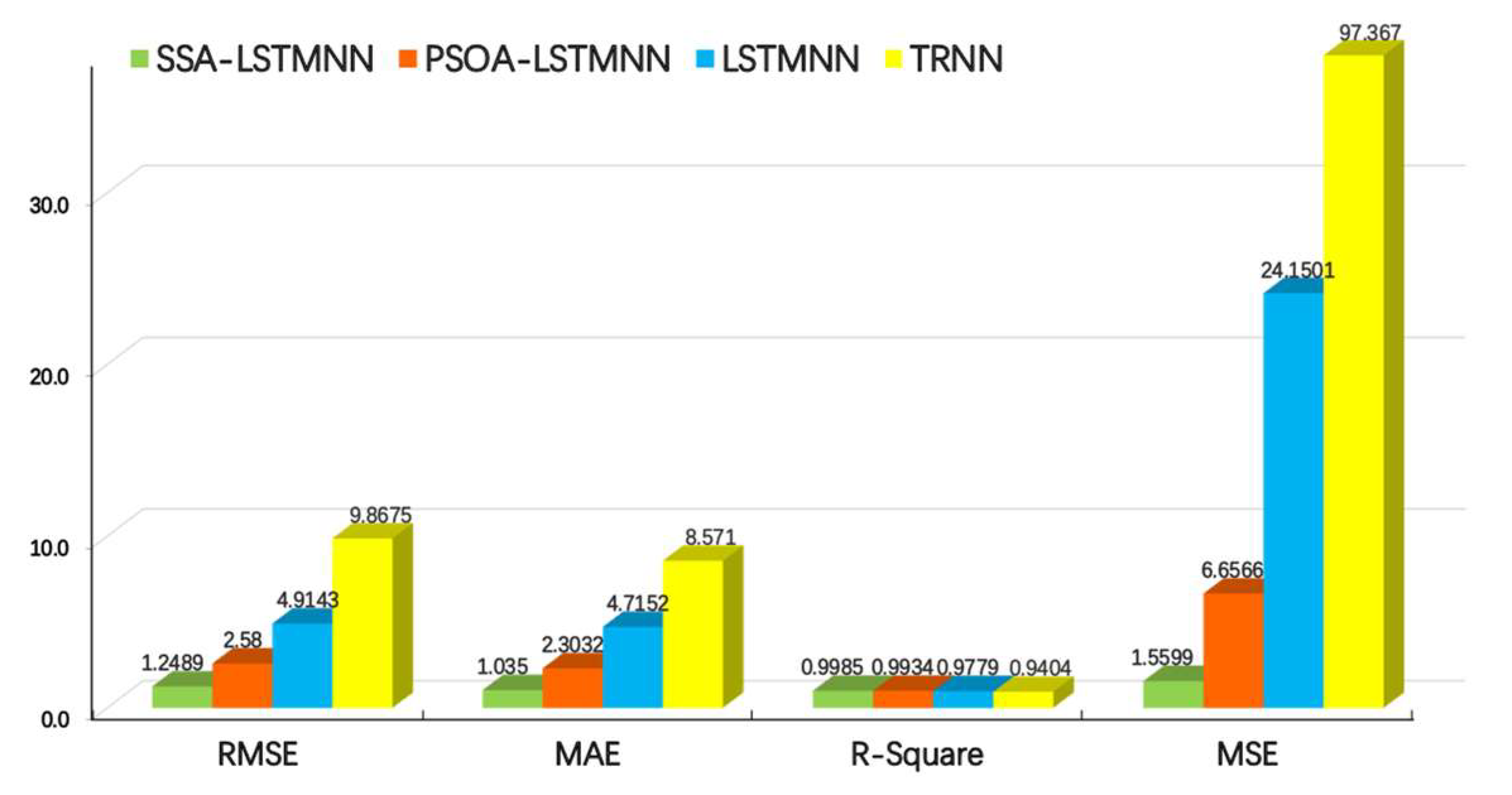
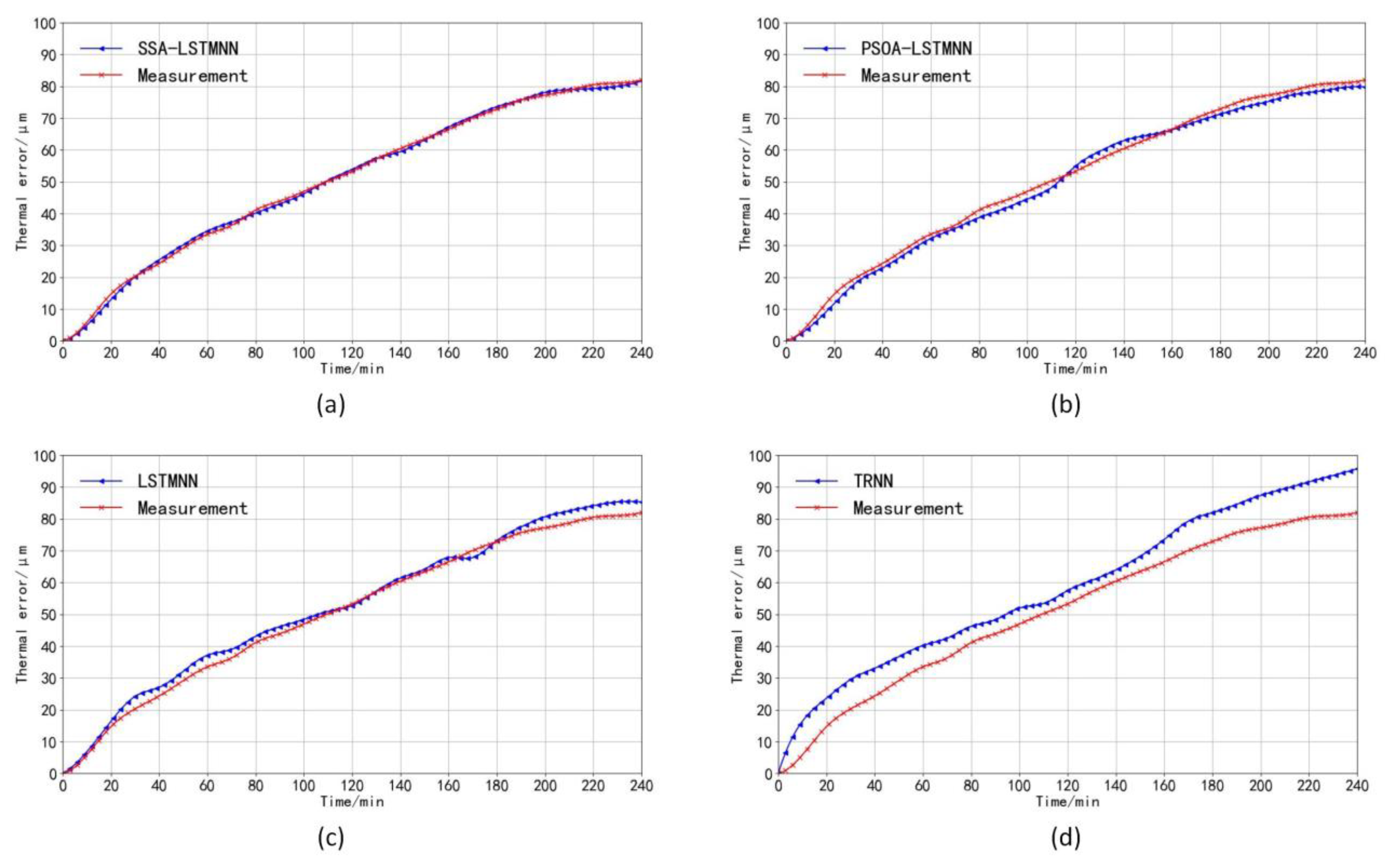
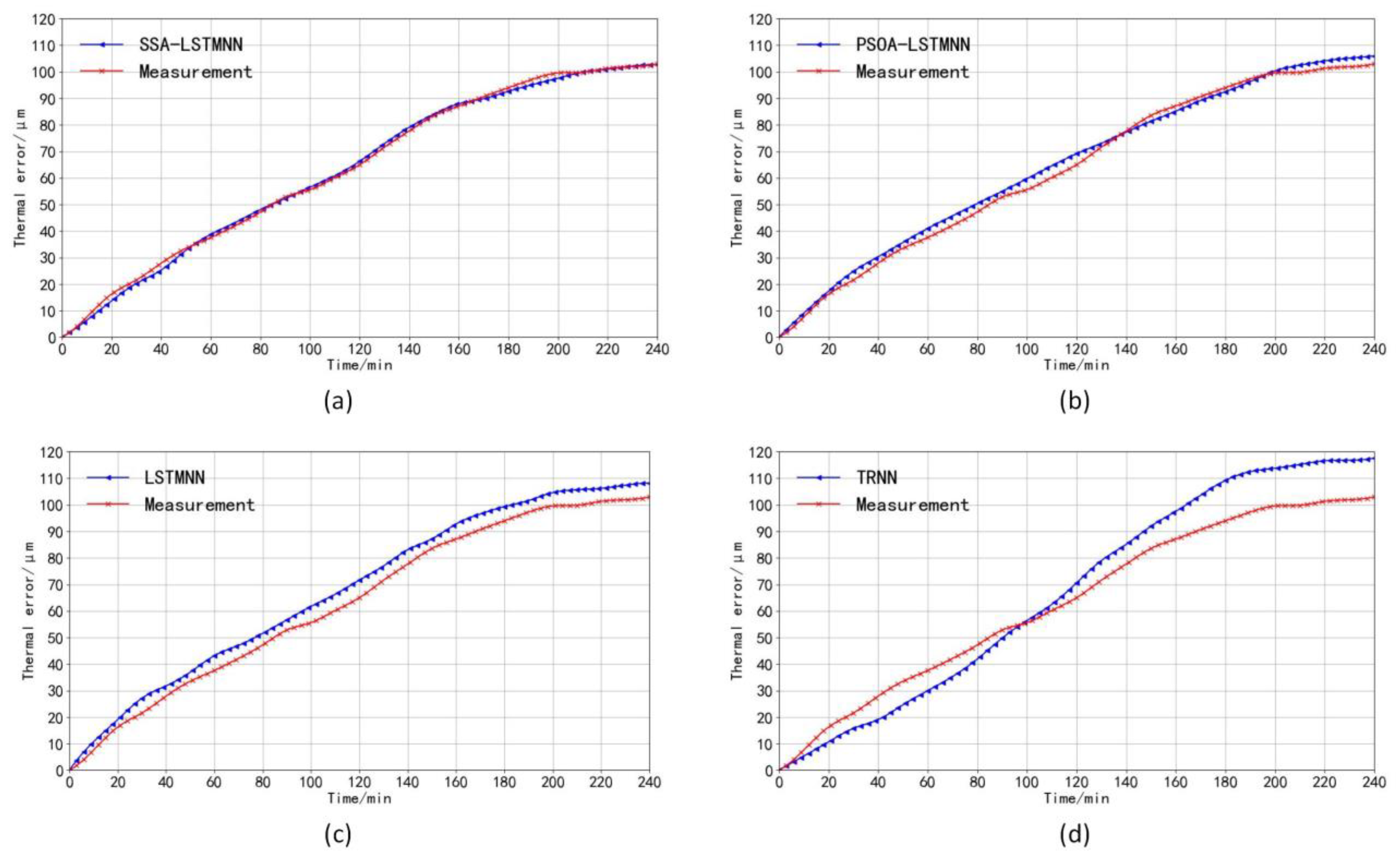
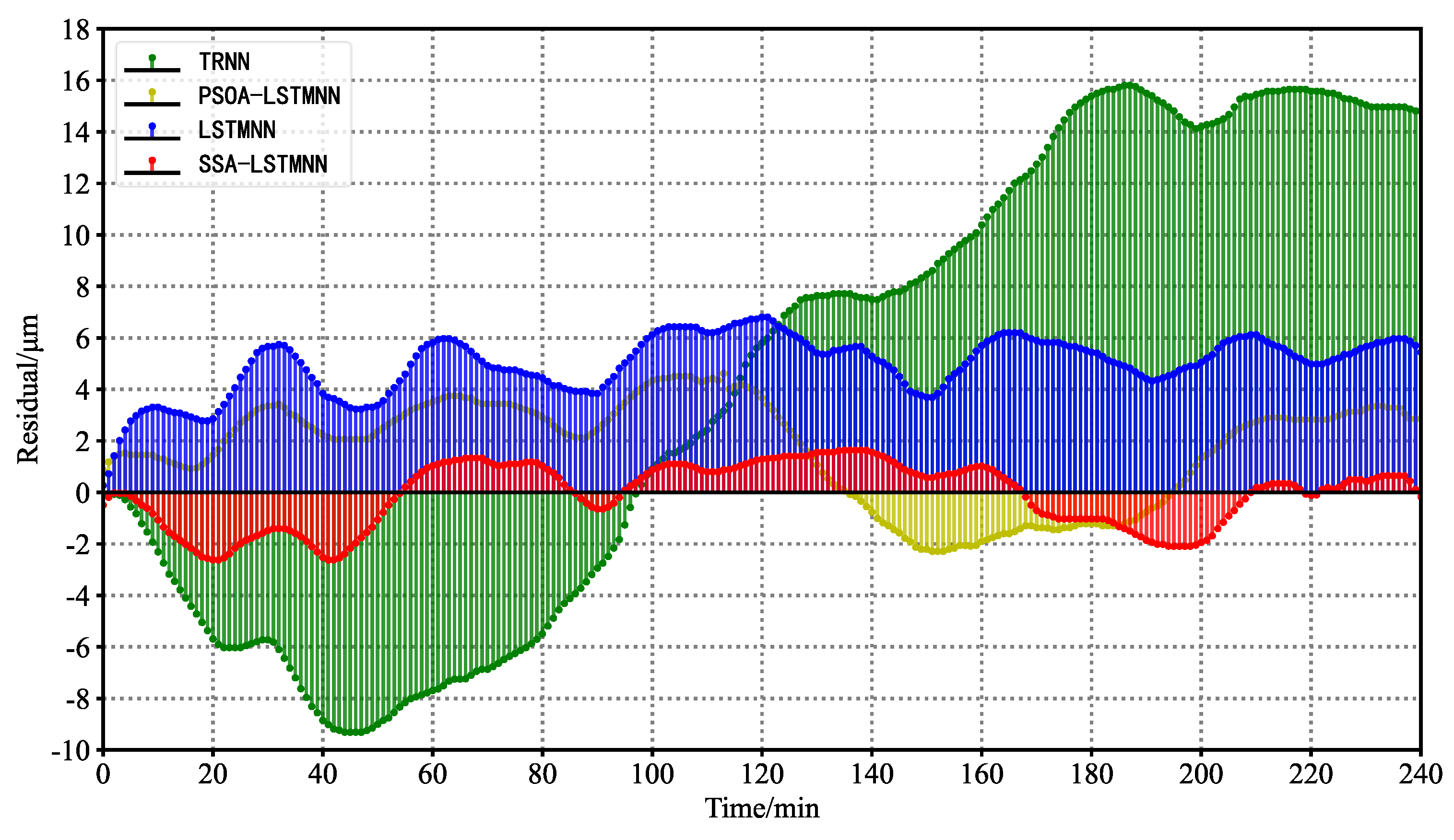
5. Performance Analysis of Thermal Error Prediction Model
6. Conclusions
- 1.
- Firstly, the FCMCA was used to reduce the 13 temperature measuring points of the CNCME to 4, which eliminates the collinearity problem caused by excessive redundant data of the CNCME temperature, reduces the calculation amount of the thermal error prediction modeling process, and improves the model accuracy.
- 2.
- Secondly, the SSA-LSTMNN model was used to train the temperature rise data of key temperature-sensitive points and the thermal error data collected in real-time to build the thermal error prediction model. The long short-term memory recurrent neural network differs from the traditional recurrent neural network in that it takes into account the influence of the temperature rise data of the current moment and the historical moment on the thermal error of the machine tool, which ensures the accuracy of the prediction results. The sparrow search algorithm allows the LSTMNN to be modeled with optimal parameters, optimizing the performance of the LSTMNN and thus enhancing the robustness and strengthening the stability of the model.
- 3.
- Finally, the experimental validation was performed under three different working conditions of the machine tool and compared with the PSOA-LSTMNN, LSTMNN, and TRNN prediction models. The final results show that the SSA-LSTMNN model outperforms the other three models in the evaluation of performance metrics such as RMSE, MAE, R2, and MSE, and the average of the fluctuation range of the residual values of the thermal error prediction results of the SSA-LSTMNN model on two different speed test sets is 44%, 48%, and 82% lower than that of the PSOA-LSTMNN, LSTMNN, and TRNN, respectively. The experimental outcomes demonstrate that the proposed SSA-LSTMNN model in this paper achieves good results; we verified its applicability and its possible generalization, thus showing that the model has a certain industrial application value and is a research prospect in the field of CNCME.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mareš, M.; Horejš, O.; Havlík, L. Thermal error compensation of a 5-axis machine tool using indigenous temperature sensors and CNC integrated Python code validated with a machined test piece. Precis. Eng. 2020, 66, 21–30. [Google Scholar] [CrossRef]
- Li, Y.; Yu, M.; Bai, Y.; Hou, Z.; Wu, W. A review of thermal error modeling methods for machine tools. Appl. Sci. 2021, 11, 5216. [Google Scholar] [CrossRef]
- Wu, C.; Xiang, S.; Xiang, W. Thermal Error Modeling of Rotary Axis Based on Convolutional Neural Network. ASME J. Manuf. Sci. Eng. 2021, 143, 051013. [Google Scholar]
- Katageri, P.; Suresh, B.S.; Pasha Taj, A. An approach to identify and select optimal temperature-sensitive measuring points for thermal error compensation modeling in CNC machines: A case study using cantilever beam. Mater. Today Proc. 2021, 45, 264–269. [Google Scholar] [CrossRef]
- Lei, M.; Yang, J.; Wang, S.; Zhao, L.; Xia, P.; Jiang, G.; Mei, X. Semi-supervised modeling and compensation for the thermal error of precision feed axes. Int. J. Adv. Manuf. Technol. 2019, 104, 4629–4640. [Google Scholar] [CrossRef]
- Liu, K.; Li, T.; Li, T.; Liu, Y.; Wang, Y.; Jia, Z. Thermal behavior analysis of horizontal CNC lathe spindle and compensation for radial thermal drift error. Int. J. Adv. Manuf. Technol. 2018, 95, 1293–1301. [Google Scholar] [CrossRef]
- Huang, Z.; Liu, Y.; Du, L.; Yang, H. Thermal error analysis, modeling and compensation of five-axis machine tools. J. Mech. Sci. Technol. 2020, 34, 4295–4305. [Google Scholar]
- Dai, Y.; Li, Y.; Li, Z.; Wen, W.; Zhan, S. Temperature measurement point optimization and experimental research for Bi-rotary Milling Head of Five-axis CNC Machine Tool. Int. J. Adv. Manuf. Technol. 2022, 121, 309–322. [Google Scholar] [CrossRef]
- Yao, X.; Hu, T.; Yin, G.; Cheng, C. Thermal error modeling and prediction analysis based on OM algorithm for machine tool’s spindle. Int. J. Adv. Manuf. Technol. 2020, 106, 3345–3356. [Google Scholar] [CrossRef]
- Shi, H.; Jiang, C.; Yan, Z.; Tao, T.; Mei, X. Bayesian neural network-based thermal error modeling of feed drive system of CNC machine tool. Int. J. Adv. Manuf. Technol. 2020, 108, 3031–3044. [Google Scholar] [CrossRef]
- Mares, M.; Horejs, O.; Straka, M.; Sveda, J.; Kozlok, T. An update of thermal error compensation model via on-machine measurement. MM Sci. J. 2022, 2022, 6275–6282. [Google Scholar] [CrossRef]
- Li, Z.; Li, G.; Xu, K.; Tang, X.; Dong, X. Temperature-sensitive point selection and thermal error modeling of spindle based on synthetical temperature information. Int. J. Adv. Manuf. Technol. 2021, 113, 1029–1043. [Google Scholar] [CrossRef]
- Xiang, S.; Deng, M.; Li, H.; Du, Z.; Yang, J. Cross-rail deformation modeling, measurement and compensation for a gantry slideway grinding machine considering thermal effects. Meas. Sci. Technol. 2019, 30, 065007. [Google Scholar] [CrossRef]
- Li, Y.; Zhao, J.; Ji, S. Thermal positioning error modeling of machine tools using a bat algorithm-based back-propagation neural network. Int. J. Adv. Manuf. Technol. 2018, 97, 2575–2586. [Google Scholar] [CrossRef]
- Liu, Y.; Miao, E.; Liu, H.; Chen, Y. Robust machine tool thermal error compensation modelling based on temperature-sensitive interval segmentation modelling technology. Int. J. Adv. Manuf. Technol. 2020, 106, 655–669. [Google Scholar] [CrossRef]
- Tan, F.; Yin, G.; Zheng, K.; Wang, X. Thermal error prediction of machine tool spindle using segment fusion LSSVM. Int. J. Adv. Manuf. Technol. 2021, 116, 99–114. [Google Scholar] [CrossRef]
- Hu, J.; Zhou, Z.; Liu, Q.; Lou, P.; Yan, J.; Li, R. Key point selection in large-scale FBG temperature sensors for thermal error modeling of heavy-duty CNC machine tools. Front. Mech. Eng. 2019, 14, 442–451. [Google Scholar] [CrossRef]
- Zhang, T.; Ye, W.; Shan, Y. Application of sliced inverse regression with fuzzy clustering for thermal error modeling of CNC machine tool. Int. J. Adv. Manuf. Technol. 2016, 85, 2761–2771. [Google Scholar] [CrossRef]
- Li, Y.; Zhao, J.; Ji, S.; Liang, F. The selection of temperature-sensitivity points based on K-harmonic means clustering and thermal positioning error modeling of machine tools. Int. J. Adv. Manuf. Technol. 2019, 100, 2333–2348. [Google Scholar] [CrossRef]
- Than, V.-T.; Ngo, T.-T.; Su, D.-Y.; Wang, C.-C. A study on thermal displacement of CNC horizontal lathe based on movable component temperatures. Aust. J. Mech. Eng. 2022, 20, 1–11. [Google Scholar] [CrossRef]
- Krstić, V.; Milčić, D.; Madić, M.; Milčić, M.; Milovančević, M. Prediction of Friction Torque and Temperature on Axial Angular Contact Ball Bearings for Threaded Spindle Using Artificial Neural Network. J. Vib. Eng. Technol. 2022, 10, 1473–1480. [Google Scholar] [CrossRef]
- Abdulshahed, A.M.; Longstaff, A.P.; Fletcher, S. A cuckoo search optimisation-based Grey prediction model for thermal error compensation on CNC machine tools. Grey Syst. Theory Appl. 2017, 7, 146–155. [Google Scholar] [CrossRef]
- Fu, G.; Gong, H.; Gao, H.; Gu, T.; Cao, Z. Integrated thermal error modeling of machine tool spindle using a chicken swarm optimization algorithm-based radial basic function neural network. Int. J. Adv. Manuf. Technol. 2019, 105, 2039–2055. [Google Scholar] [CrossRef]
- Yang, B.; Liu, Z. Thermal error modeling by integrating GWO and ANFIS algorithms for the gear hobbing machine. Int. J. Adv. Manuf. Technol. 2020, 109, 2441–2456. [Google Scholar] [CrossRef]
- Li, B.; Tian, X.; Zhang, M. Thermal error modeling of machine tool spindle based on the improved algorithm optimized BP neural network. Int. J. Adv. Manuf. Technol. 2019, 105, 1497–1505. [Google Scholar] [CrossRef]
- Li, Z.; Zhu, B.; Wang, B.; Wang, Q. Thermal Error Modeling of Electric Spindle Based on Particle Swarm Optimization SVM Neural Network. Int. J. Adv. Manuf. Technol. 2022, 121, 7215–7227. [Google Scholar] [CrossRef]
- Jia, G.; Cao, J.; Zhang, X.; Huang, N. Ambient temperature-induced thermal error modelling for a special CMM at the workshop level based on the integrated temperature regression method. Int. J. Adv. Manuf. Technol. 2022, 121, 5767–5778. [Google Scholar] [CrossRef]
- Cao, W.; Li, H.; Li, Q. A method of thermal error prediction modeling for CNC machine tool spindle system based on linear correlation. Int. J. Adv. Manuf. Technol. 2022, 118, 3079–3090. [Google Scholar] [CrossRef]
- Yue, H.-T.; Guo, C.-G.; Li, Q.; Zhao, L.-J.; Hao, G.-B. Thermal error modeling of CNC milling machining spindle based on an adaptive chaos particle swarm optimization algorithm. J. Braz. Soc. Mech. Sci. Eng. 2020, 42, 427. [Google Scholar] [CrossRef]
- Fan, J.; Wang, P.; Tao, H.; Pan, R. A thermal deformation prediction method for grinding machine’spindle. Int. J. Adv. Manuf. Technol. 2022, 118, 1125–1139. [Google Scholar] [CrossRef]
- Li, Z.L.; Zhu, B.; Dai, Y.; Zhu, W.M.; Wang, Q.H.; Wang, B.D. Thermal error modeling of motorized spindle based on Elman neural network optimized by sparrow search algorithm. Int. J. Adv. Manuf. Technol. 2022, 121, 349–366. [Google Scholar] [CrossRef]
- Gao, X.; Guo, Y.; Hanson, D.A.; Liu, Z.; Zan, T. Thermal Error Prediction of Ball Screws Based on PSO-LSTM. Int. J. Adv. Manuf. Technol. 2021, 116, 1721–1735. [Google Scholar] [CrossRef]
- Yang, H.; Xing, R.; Du, F. Thermal error modelling for a high-precision feed system in varying conditions based on an improved Elman network. Int. J. Adv. Manuf. Technol. 2020, 106, 279–288. [Google Scholar]
- Abdulshahed, A.M.; Longstaff, A.P.; Fletcher, S. The application of ANFIS prediction models for thermal error compensation on CNC machine tools. Appl. Soft Comput. 2015, 27, 158–168. [Google Scholar] [CrossRef]
- Olabode, O.F.; Fletcher, S.; Longstaff, A.P.; Bell, A. Core temperature measurement using ultrasound for high precision manufacturing processes. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2023, 237, 09544054221150662. [Google Scholar] [CrossRef]
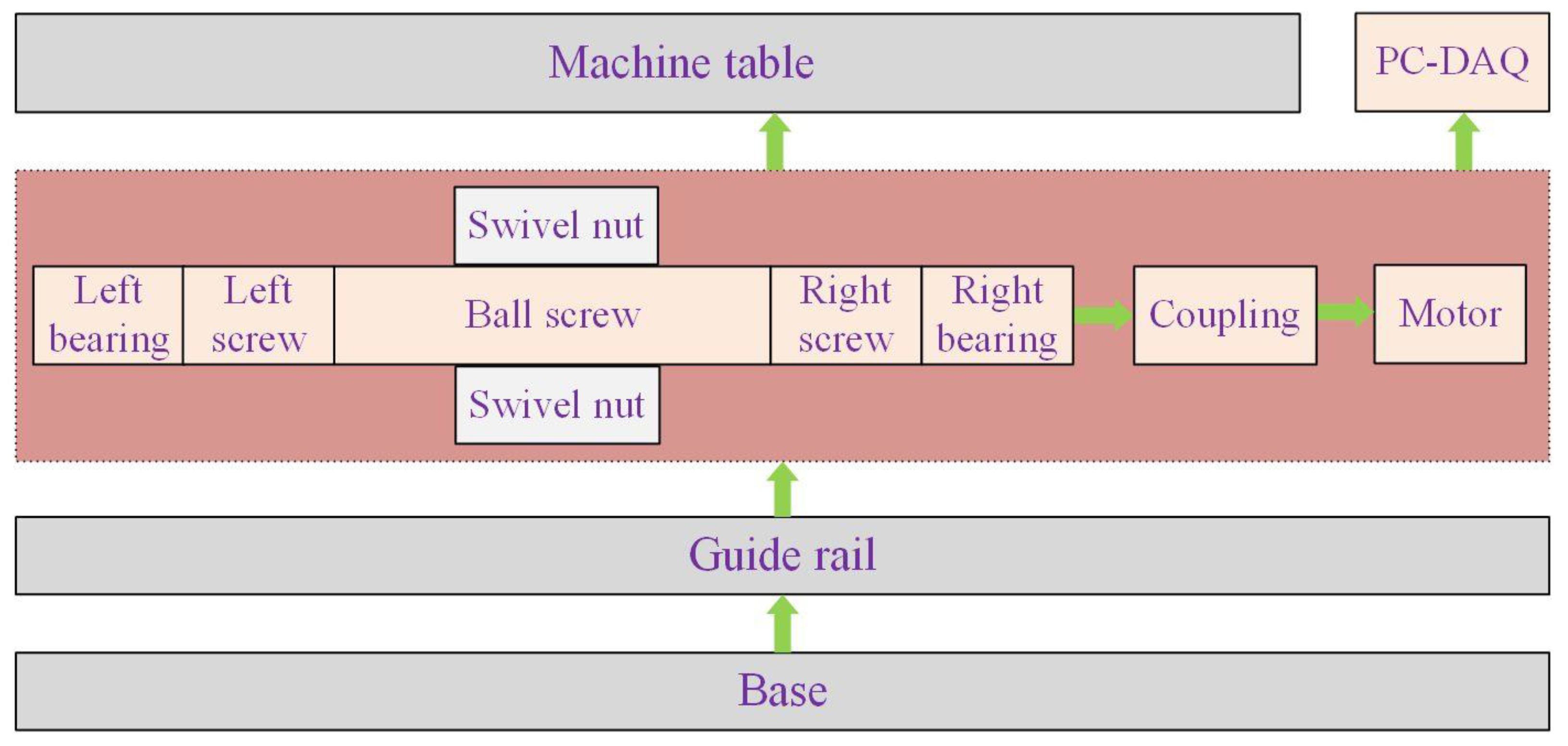






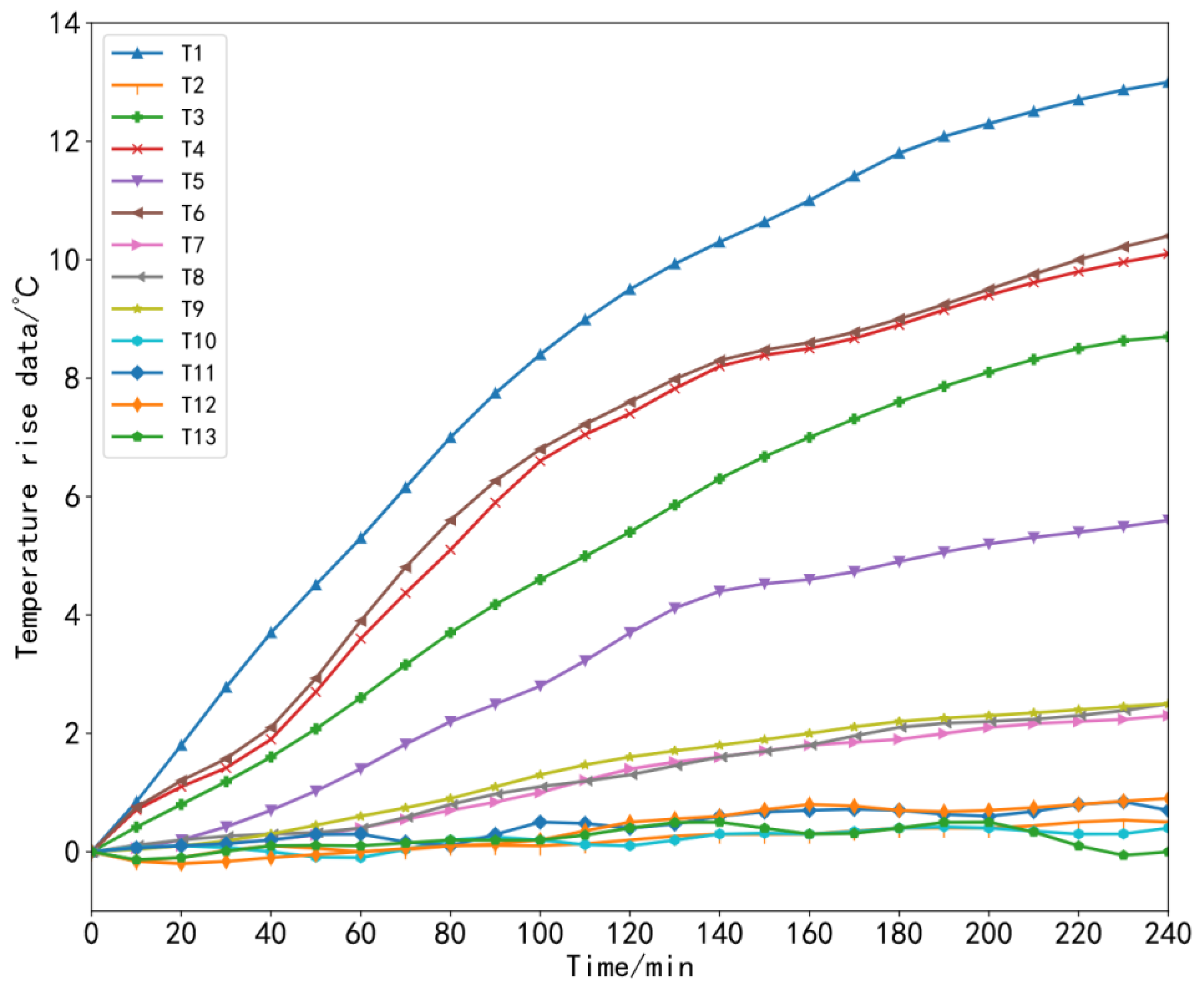
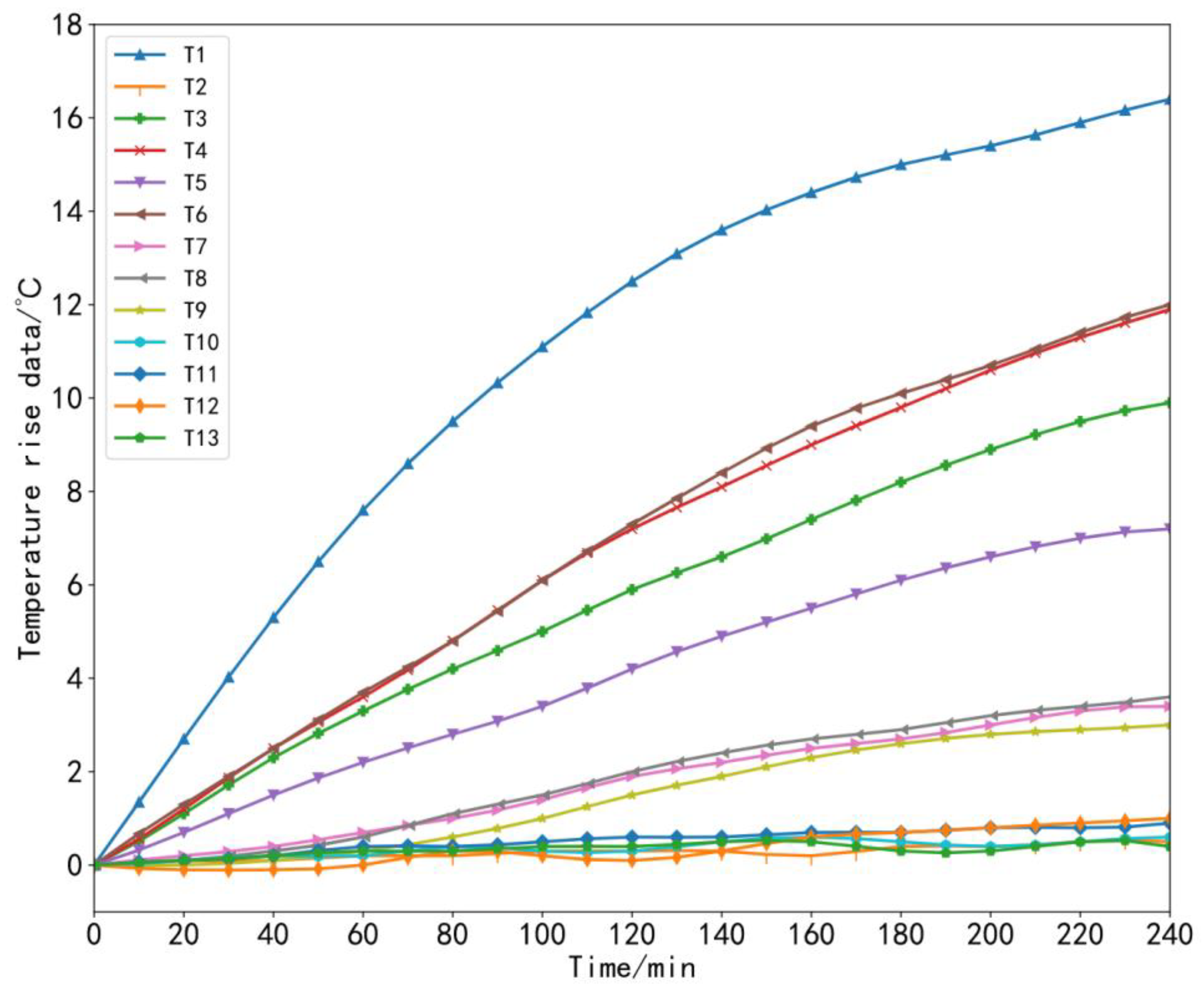
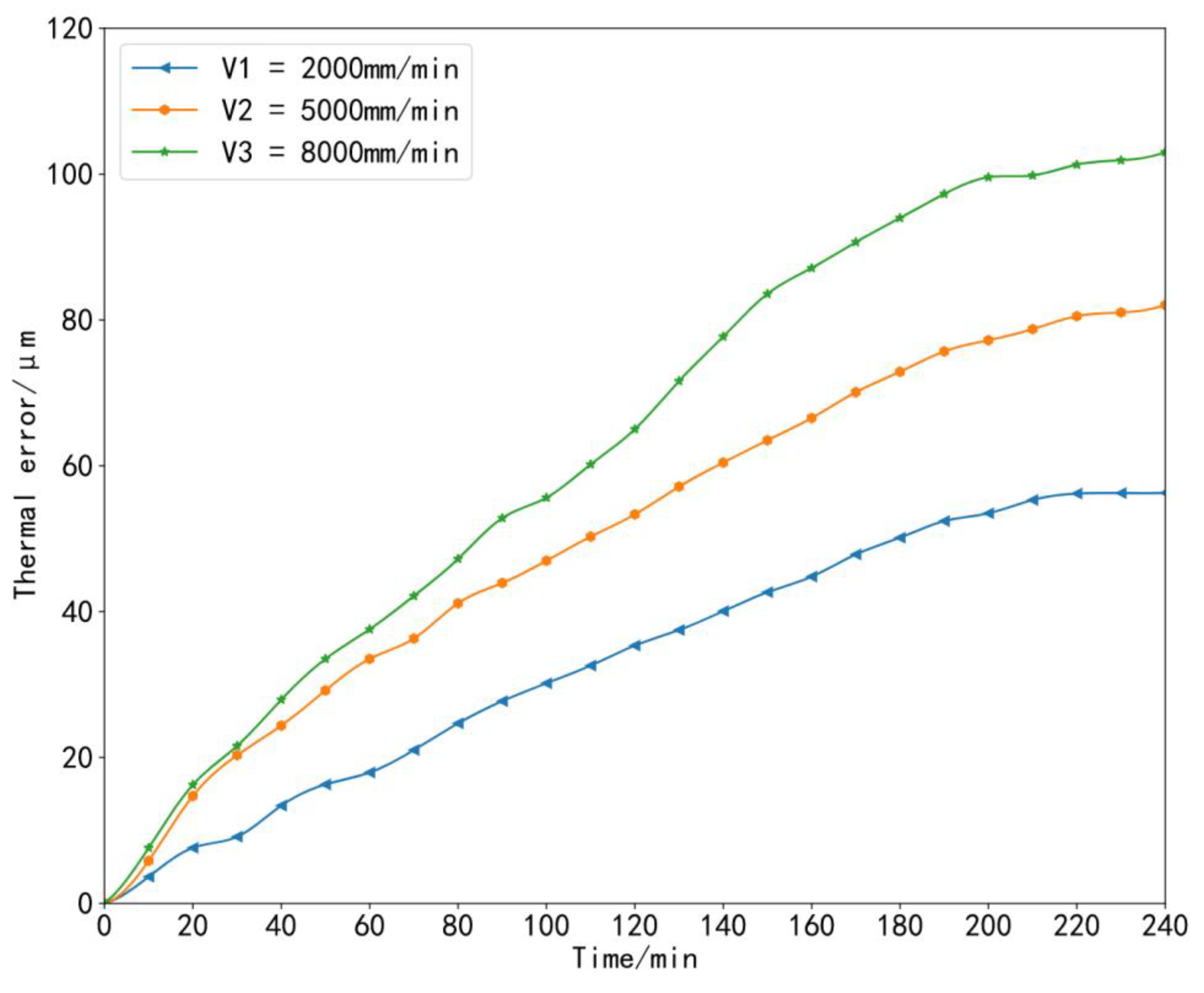
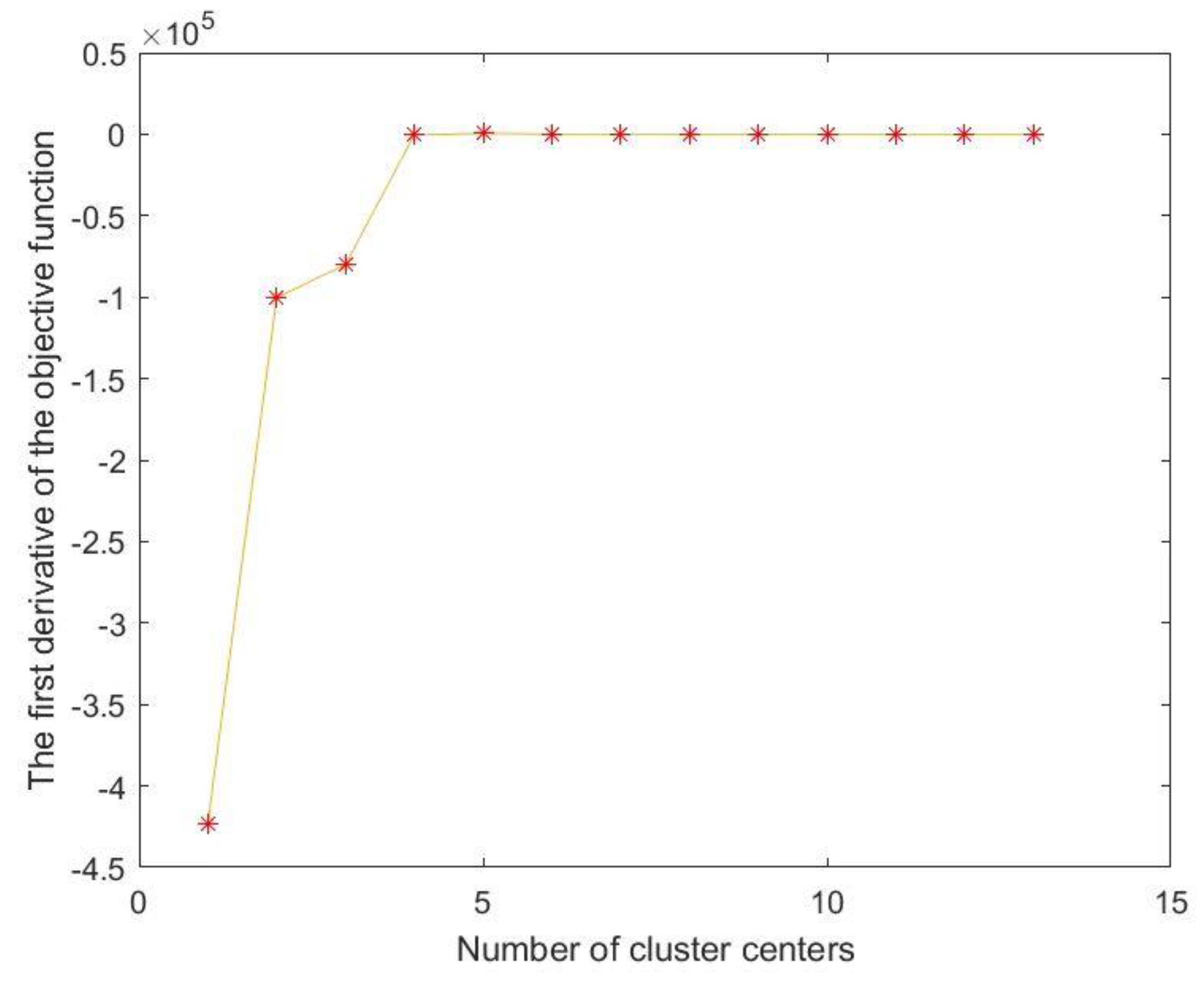

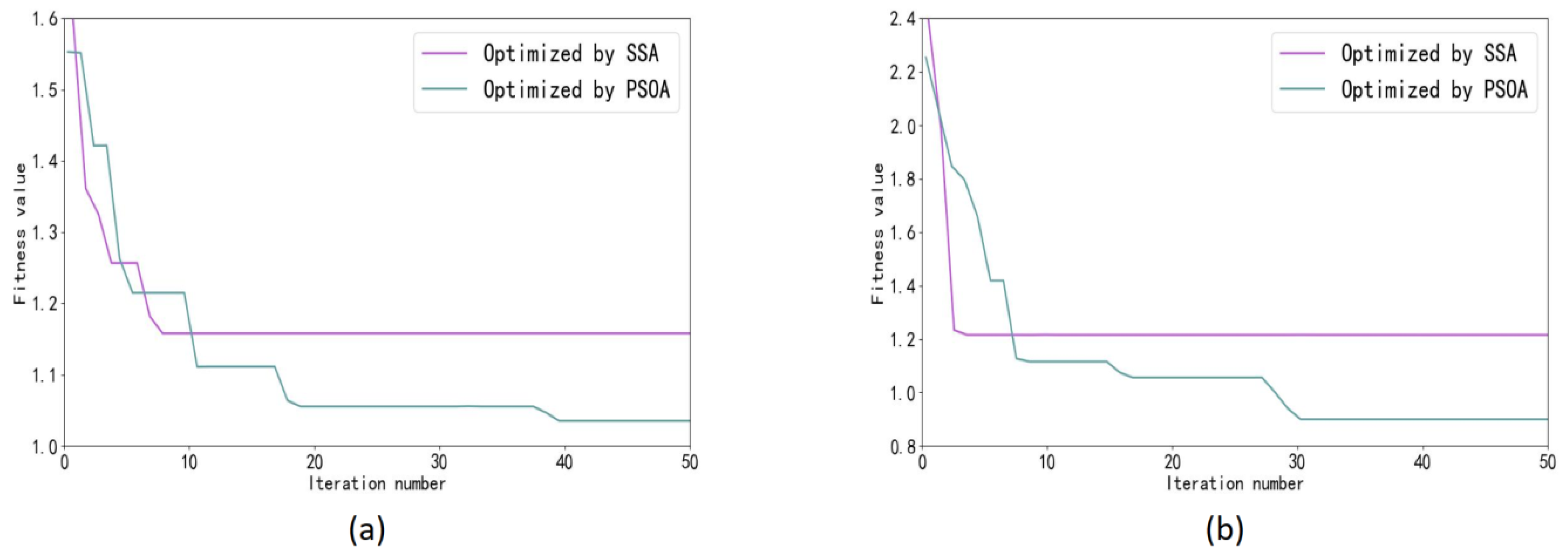




| Serial Number of the Temperature Measuring Point | Location of the Temperature Measuring Point |
|---|---|
| T1 | Motor |
| T2 | Motor coupling |
| T3 | Swivel nut |
| T4, T5, T6 | Left screw seat, ball screw, right screw seat |
| T7, T8, T9 | Left guide rail, guide rail, right guide rail |
| T10 | Workbench |
| T11, T12 | Bed left, bed right |
| T13 | Ambient temperature |
| C(i,j) | T1 | T2 | T3 | T4 | T5 | T6 | T7 | T8 | T9 | T10 | T11 | T12 | T13 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| center 1 | 0.000234 | 0.001224 | 0.335729 | 0.998207 | 0.035849 | 0.982883 | 0.013371 | 0.007053 | 0.011702 | 0.001914 | 0.982883 | 0.000951 | 0.002788 |
| center 2 | 0.998523 | 0.000334 | 0.031218 | 0.000502 | 0.005748 | 0.006271 | 0.003097 | 0.001539 | 0.002659 | 0.000559 | 0.006271 | 0.000274 | 0.000757 |
| center 3 | 0.000518 | 0.981659 | 0.136941 | 0.000429 | 0.075572 | 0.003759 | 0.291295 | 0.087032 | 0.209473 | 0.075572 | 0.978889 | 0.988877 | 0.957454 |
| center 4 | 0.000725 | 0.016783 | 0.496113 | 0.000862 | 0.882832 | 0.007088 | 0.692237 | 0.904376 | 0.776166 | 0.882832 | 0.018639 | 0.009898 | 0.039001 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, Y.; Xia, X.; Guo, Y. A Modeling Method for Thermal Error Prediction of CNC Machine Equipment Based on Sparrow Search Algorithm and Long Short-Term Memory Neural Network. Sensors 2023, 23, 3600. https://doi.org/10.3390/s23073600
Gao Y, Xia X, Guo Y. A Modeling Method for Thermal Error Prediction of CNC Machine Equipment Based on Sparrow Search Algorithm and Long Short-Term Memory Neural Network. Sensors. 2023; 23(7):3600. https://doi.org/10.3390/s23073600
Chicago/Turabian StyleGao, Ying, Xiaojun Xia, and Yinrui Guo. 2023. "A Modeling Method for Thermal Error Prediction of CNC Machine Equipment Based on Sparrow Search Algorithm and Long Short-Term Memory Neural Network" Sensors 23, no. 7: 3600. https://doi.org/10.3390/s23073600
APA StyleGao, Y., Xia, X., & Guo, Y. (2023). A Modeling Method for Thermal Error Prediction of CNC Machine Equipment Based on Sparrow Search Algorithm and Long Short-Term Memory Neural Network. Sensors, 23(7), 3600. https://doi.org/10.3390/s23073600






