DSF Core: Integrated Decision Support for Optimal Scheduling of Lifetime Extension Strategies for Industrial Equipment
Abstract
1. Introduction
- The direct sensorial input needed is the historical and real-time information about analysed stops (failures, strategies), i.e., start-end time, related machine component and reason for each instance. Usually, the aforementioned stop information cannot be recorded directly thanks to sensorial data, may be only manually registered, may have not been performed at all or performed incompletely or inaccurately. In these cases, the stop intervals should be identified based on the behaviour of other sensorial time series (e.g., based on zero or absent values), whereas failure diagnosis algorithms should infer the related component and stop reason, especially in the case of failures accompanied by some anomaly. Failure diagnosis may be performed, e.g., using failure mode and effects analysis [5] or probabilistic graphical models [6] [such as Bayesian methods [7] in general or the time-dependent dynamic Bayesian networks [8]].
- From degradation models, the DSF Core may receive the parameters of the Weibull distributions characterizing the lifetime of machine components with respect to various failure types. In relation to this, it may also receive real-time equivalent age and load information, which assess the respective degradation levels and degradation speeds, in accordance with the generic references [11,12]. There are also references about the reliability of specific common machine components considered in this work, such as bearing [13] and sample-detector [14].
- Thanks to extensive cost information, directly provided as input or computed based on [15] or by the DSF Core itself, the algorithm is able to perform short-term as well as long-term (using Monte Carlo simulation) assessment of the economic KPI, considering costs and profit both during production and during voluntary (strategies) and involuntary stops (failures).
1.1. Related Work on Decision Support and Optimization Plans
1.2. Related Work on Cost Analysis and Cost Modelling Tools
1.3. Related Work on Life Cycle Assessment and Integration with Life Cycle Cost
- Cradle-to-gate: raw material extraction and material production until the exit of the product from the factory;
- Cradle-to-grave: raw material extraction, material production, exit of the final product from the factory, as well as the use, demolition and waste phases;
- Cradle-to-cradle: raw material extraction, material production, exit of the final product from the factory, as well as the phases of use, demolition, waste, recycling and extensive reuse of the waste.
- air (global warming potential, ozone layer depletion potential,…);
- Water (water depletion, eutrophication potential,…);
- Energy (cumulative energy demand, fossil fuel depletion,…);
- Soil (land occupation, acidification potential,…);
- Human (human toxicity potential from chemicals and pollutants released,…);
- Other (minerals depletion, solid waste,…).
1.4. Contributions of This Work beyond the State of the Art
2. Materials and Methods
- During refurbishment of a static component, maintenance of movable components of the same machine is impossible. In this case, the movable components may either be replaced or remain as they are. For some movable components, replacement may be compulsory in this case.
- The reverse is true. During maintenance of a movable component, refurbishment of the same machine is impossible.
- 1
- Pre-optimization for corrective strategies : Assuming initially that a strategy is always applied to a component and only as soon as possible after the component has failed, this phase finds the optimal strategy for each component after its failure. The initial solution considers the lightest compulsory corrective strategy for each failure type. The lightest compulsory corrective strategy to be applied after a failure is defined by the user, as explained later. For every failure type, the possible corrective strategies are the possible preventive ones which are not lighter than the above.
- 2
- Main optimization for decision variables related to:
- Short-interval average modified KPI threshold per component and strategy applicable to it: The strategy is recommended and applied when the average total modified KPI (based on a modification described later) exceeds the threshold. If the threshold is exceeded for multiple strategies for the same component simultaneously, the heaviest one is selected. (If this happens for multiple maintenance alternatives simultaneously, the one defined first by the user is selected.) If strategies and failure fixations may take place only during working hours or the present time is non-working time, the strategy is assigned the status “urgent” and is applied as soon as possible. Otherwise, it is assigned the status “non-urgent” and is also applied as soon as possible, but only during non-working hours in order not to interrupt the production, which would cause indirect economic loss, since fewer parts would be produced due to the additional downtime. Exceptionally, if refurbishment for the static component has been chosen, any proposed strategy for movable components is assigned the same urgency status as refurbishment.
- Failure probability threshold per component and failure type: The lightest strategy applicable to the component is recommended and applied when the probability of any failure in this component exceeds the threshold. If strategies and failure fixations may take place only during working hours or the present time is non-working time, the strategy is considered “urgent”. Otherwise, it is considered “urgent” (instead of “non-urgent”) if and only if the failure probability until the next non-working timestamp is much higher than the failure probability at the next timestamp, also considering the impact of the strategy on the downtime of components and the time distance until the next non-working timestamp, based on the formulaaccording to the following notation:
- –
- : probability for failure of the component in question to happen at the next timestamp, according to the considered (constant) sampling step;
- –
- : probability for failure of the component in question to happen at the next non-working timestamp;
- –
- n: number of time steps until the next non-working timestamp;
- –
- : difference in percentage of non-working machine components if the strategy is applied and not.
For a particular component and failure type combination, due to high time complexity, the relevant computations take place only at the first consecutive working timestamp for which the computation of urgency makes sense. For the other timestamps among the above, the same urgency is defined. In addition, when the status “non-urgent” is assigned to the recommended strategy at the last working timestamp of a working interval, the strategy is recommended with status “urgent” at the next timestamp (i.e., the first of the next non-working interval). This happens even if the respective failure probability threshold with respect to the load during non-working hours at that timestamp is also exceeded.Exceptionally, if refurbishment of the static component has been chosen, any simultaneously proposed strategy for movable components is assigned the same urgency status as refurbishment. - Corrective strategies “actuators” per component and failure type: Binary variables determining if the optimal corrective strategy for the component as found during the pre-optimization phase will indeed be applied as soon as possible (with status “urgent”) after the component fails.
- : instant individual KPI of type k of component c at the i-th timestamp of the simulation interval under corrective strategies and decision variables ;
- : weighting coefficient of respective KPI .
- Number of strategy types;
- *Failure types;
- *Lightest compulsory corrective strategies;
- Objective function g evaluated based on simulation;
- *Stop types corresponding to decision variables to be excluded from the optimization (these are not considered in Algorithm 1);
- Function sorting strategy types based on their effect (for comparisons with the lightest compulsory strategies to determine which strategies are applicable after each failure).
| Algorithm 1 Algorithm for pre-optimization for corrective strategies |
|
- *Strategy types;
- *Failure types;
- *Lightest compulsory corrective strategies;
- Objective function g evaluated based on simulation;
- *Stop types corresponding to decision variables to be excluded from the optimization (these are not considered in Algorithm 2);
- Function finding every time the next for which g is to be evaluated;
| Algorithm 2 Algorithm for main optimization for decision variables |
|
2.1. Input Parameters to the DSF Core Training
- Range: The range is per component and failure type during periods with and without production. The load starts from a random number within the range and evolves according to the maximum absolute first-order difference within 1 day defined below.
- Maximum absolute first-order difference within 1 day: This is a single value divided by the average number of timestamps per day to compute the maximum absolute change between two consecutive timestamps, based on the considered sampling step.
- Multiplier during production due to high failure probability until the next timestamp: This is a per ordered pair of possibly equal failure types, where the first corresponds to the multiplier and the second to the failure probability. The probability is considered as high (resulting in the multiplication of load by the multiplier) when it exceeds the corresponding degradation-based probability of failure until the next timestamp at 90% of the respective METTF (discussed later).
- One-off strategy costs: These costs are defined per machine, component and strategy combination. When multiple strategies start simultaneously to be applied to components of a particular machine, only the maximum one-off strategy cost of the started strategies instead of the sum of all of them is paid and is added to the net costs described later.
- Net costs: The stop-type-dependent costs per component are paid during the stop interval. (The DSF Core assumes that they are paid at the beginning of the interval.) They do not include indirect costs, such as cost due to downtime and long-term economic impact, which are taken into account separately.
2.2. Scenarios of Running a Trained DSF Core Model
- Real-time recommendations scenario: The trained model runs (near-) real-time (automatically, and periodically, based on the sampling step considered for training) for the next timestamp (based on the sampling step). When a strategy is needed, relevant recommendation is shown. This requires the following real-time input:
- –
- Stops (production line failures, strategies);
- –
- Predictions from other DSF algorithms (failure probabilities, degradation levels);
- –
- Process data related to the KPIs (unless already used directly by other DSF algorithms instead).
- Simulation scenario: The trained model runs (manually) for a future time interval, thus simulating (under the trained optimal strategy selection policy and considering the current status of the production line) the following:
- –
- When–what failures will happen;
- –
- When–what strategies will be recommended;
- –
- Future independent KPIs;
- –
- Future production time percentage.
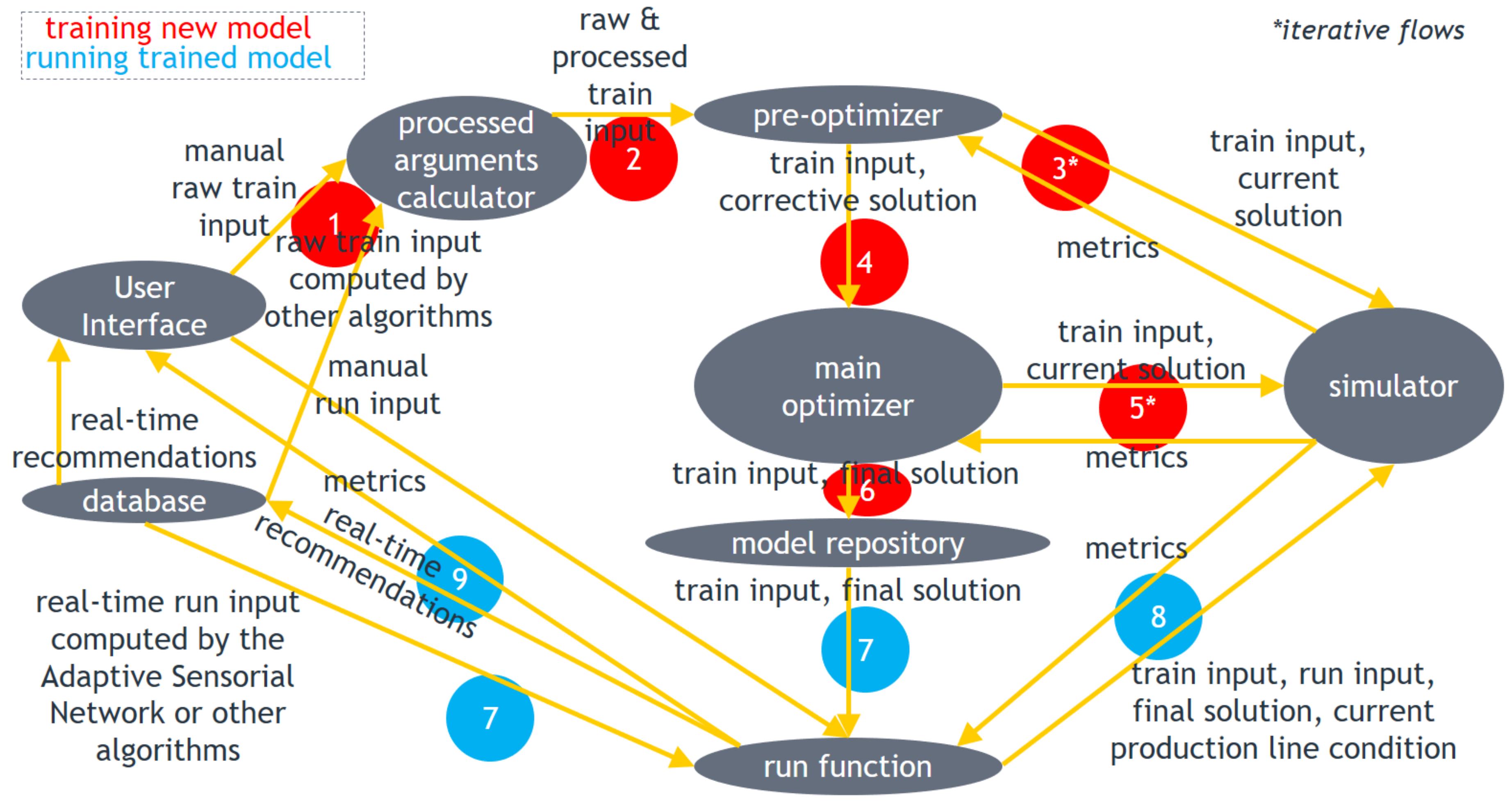
2.3. DSF Core Internal Architecture (Information Flow)
- Database: data repository where sensorial data and outputs of algorithms may be stored for future use by the same or other algorithms within the DSF;
- User Interface: helps the end user interact with the DSF Core by inserting inputs and visualizing outputs;
- Processed arguments calculator: computes additional training input arguments based on those defined by the user or on output of third-party algorithms;
- Pre-optimizer: optimizes the corrective strategies based on Algorithm 1;
- Main optimizer: optimizes the preventive strategy application policy based on Algorithm 2;
- Simulator: simulates the evolution of the production line condition to evaluate the objective function;
- Model repository: working directory where files including the input, processed and trained parameters related to the trained DSF Core models are stored so that the models can run in the future;
- Run function: runs trained DSF Core models based on the aforementioned run scenarios.
3. Results and Discussion
3.1. Application to GORENJE
- 12 power supply units;
- 12 pumps;
- 12 hoses;
- 12 spraying guns.
3.1.1. Training Input for GORENJE
- Power supply unit/pump: maintenance;
- Hose/spraying gun: none.
- Any component—replacement: 0%;
- Pump—maintenance: 10%;
- Spraying gun—maintenance: 5%;
- Power supply unit—maintenance: 20%.
- Range: Load is assumed to equal one during production andzero during intervals without production for any analyzed failure type.
- Maximum absolute first-order difference within 1 day: Load is sectionally constant;
- Multiplier during production due to high failure probability until the next timestamp: One in all cases (no effect assumed);
- Economic: Euros;
- Scrap: discarded parts.
- Economic: one;
- Scrap: 7.5.
- Energy: 0.03 kW·2087 woh/year·0.202 EUR/kWh = 12.65 EUR/year = 0.00606 EUR/woh;
- Gas: 0.6 m/part·793,114 parts/year·1.01 EUR/m = 480,627 EUR/year = 230.280 EUR/woh;
- Material: 2.35 kg/part·793,114 parts/year·1.42 EUR/kg = 2,646,621 EUR/year = 1268.06 EUR/woh
- Labor: (as computed in the “cost input” paragraph below) EUR 258,871/year = 124.03125 EUR/woh.
- Replacement of power supply unit: 1 woh;
- Maintenance of power supply unit: 0.3 woh;
- Replacement of pump: 0.45 woh;
- Other: 0.25 woh.
- Power supply unit: negligible, assumed as 0 (because both fixing the failure and maintenance takes about 20 womin);
- Pump: 0;
- Hose: 15 womin = 0.25 woh (for shortening of the hose);
- Spraying gun: 15 womin = 0.25 woh (for disassembly and cleaning of the gun).
- Replacement of power supply unit: 1.0430377 woh = 0.043459903 woD (woD = working days);
- Maintenance of power supply unit: 0.31291130 woh = 0.013037971 woD;
- Replacement of pump: 0.46936696 woh = 0.019556957 woD;
- Other strategy/hose failure/spraying gun failure: 0.26075942 woh = 0.010864976 woD.
- Replacement of power supply unit: EUR 124.03125;
- Maintenance of power supply unit: EUR 37.209375;
- Replacement of pump: EUR 55.8140625;
- Other: EUR 31.0078125.
3.1.2. Training Results for GORENJE
Optimal Solution
- Preventive replacement is proposed for the hose when its failure probability within the next time step (15 min) exceeds 0.001510.
- Preventive maintenance is proposed for the spraying gun when its failure probability within the next time step (15 min) exceeds 0.001557.
Evaluation Metrics
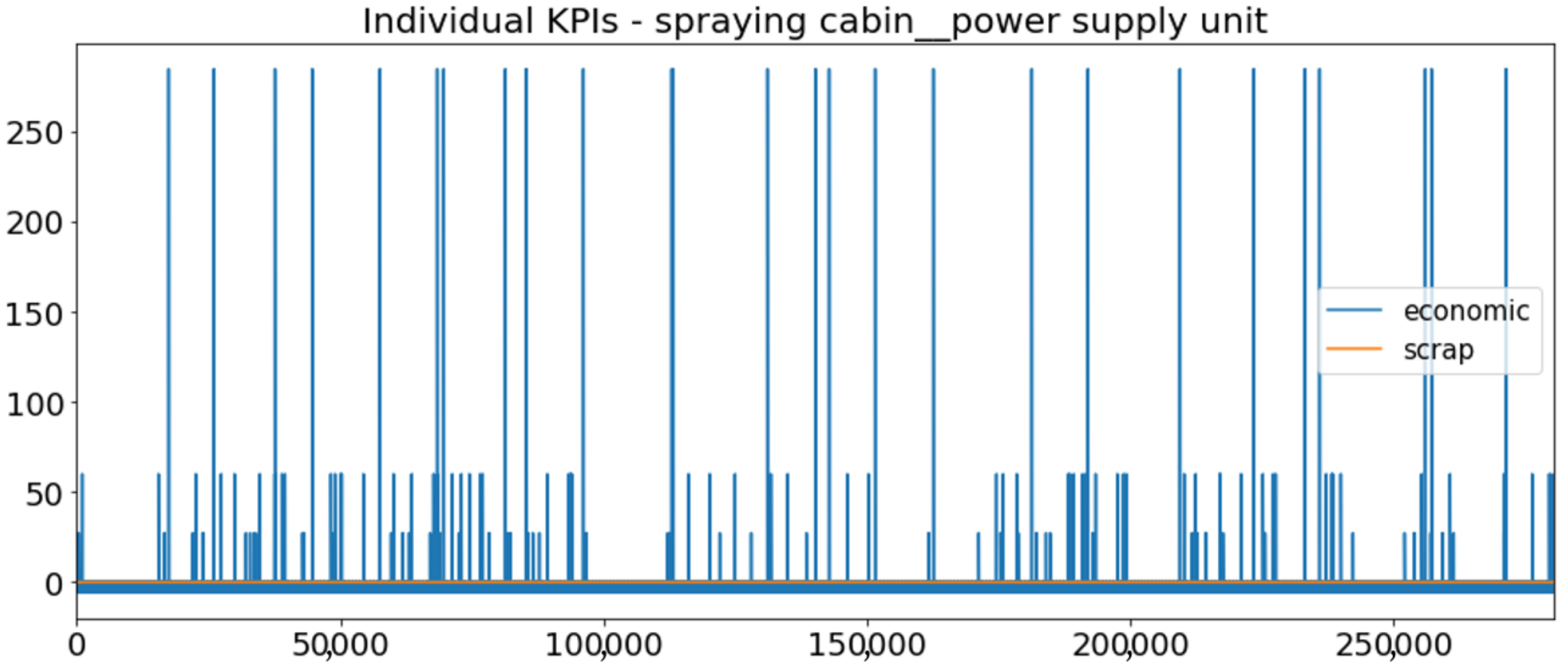
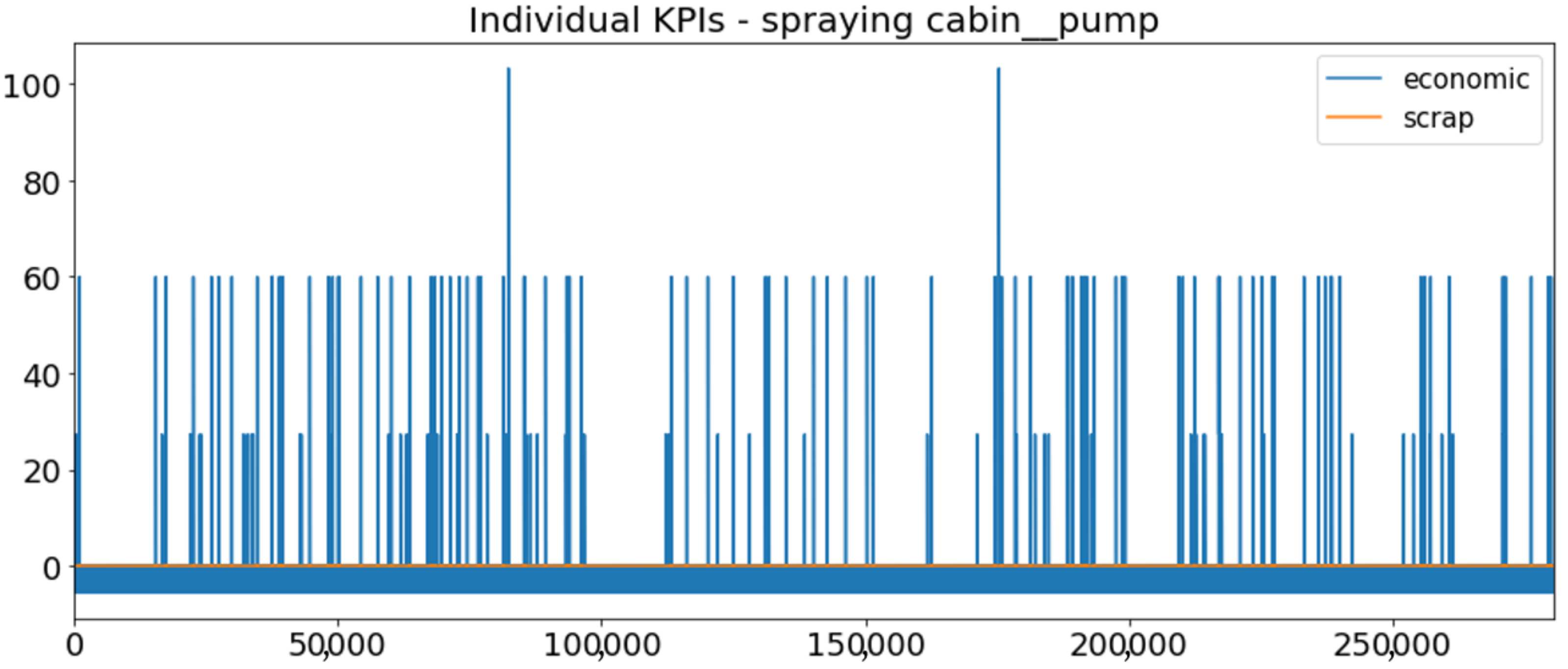
3.1.3. Run Results (Simulation Scenario) for GORENJE
3.1.4. Discussion of the Training Results for GORENJE
3.2. Application to HWH
3.2.1. Training Input for HWH
- Static component—failure: refurbishment;
- Motor/spindle—lubricant: none;
- Any other failure type: replacement.
- Static component—refurbishment—failure: 0%;
- Motor—maintenance:
- –
- Mechanical fatigue: 100%;
- –
- Lubricant: 0%.
- Motor—replacement:
- –
- Mechanical fatigue: 0%;
- –
- Lubricant: 0%.
- Spindle—maintenance:
- –
- Mechanical fatigue: 100%;
- –
- Lubricant: 0%.
- Spindle—replacement:
- –
- Mechanical fatigue: 0%;
- –
- Lubricant: 0%.
- Range: In most cases, it is assumed that normal usage corresponds to average load of 1, ranging from 0.5 to 1.5, as it depends on the way the equipment is used, expressed by potential sensorial data relevant to load calculation throughout working (instead of welding) time. Exceptionally, the load during working time for the static component is assumed by the pilot to range from 0.9 to 1.1. Furthermore, for the sample-detector failure type, load is assumed to exactly equal one during working time (and zero otherwise) only for the purpose of economic penalty evaluation as a function of equivalent age, because the sample-detector failures may be better forecast based on process data anomalies rather than equivalent age. In addition, for the lubricant failure type of the motor and the spindle, load is assumed to exactly equal one during the whole time, including non-working intervals.
- Maximum absolute first-order difference within 1 day: 0.72.
- Multiplier during production due to high failure probability until the next timestamp: one in all cases (no effect assumed).
- Energy: EUR 520/year = 0.33 EUR/woh;
- Gas: 0.025 m/part·50,000 parts/year· EUR 1.6/kg·1.225 kg/m = 2450 EUR/year = 1.565 EUR/woh;
- Labor: 0.05 min/part·50,000 parts/year· EUR 27.4/h = 1141.67 EUR/year = 0.7293 EUR/woh;
- Pressurized air: EUR 220/year = 0.14 EUR/woh;
- Cooling water: EUR 200/year = 0.13 EUR/woh.
- Refurbishment of static component (excluding the compulsory simultaneous replacement of the motor and the spindle): TTRstatic,refurbishment + TTRfwm = 16 woh;
- Replacement of motor: TTRmotor,replacement + TTRfwm = 8 woh;
- Replacement of spindle: TTRmotor,replacement + TTRfwm = 8 woh;
- Replacement of sample-holder: TTRsh,replacement + TTRfwm = 1 woh;
- Replacement of sample-detector: TTRsd,replacement + TTRfwm = 1 woh;
- Refurbishment of static components and replacement of all movable components: TTRstatic,refurbishment + TTRmotor,replacement + TTRspindle,replacement + TTRsh,replacement + TTRsd,replacement + TTRfwm = 20 woh.
- One-off duration: TTRfwm = 7 woh;
- Refurbishment of static component (excluding the compulsory simultaneous replacement of the motor and the spindle): TTRstatic,refurbishment = 9 woh;
- Replacement of any movable component: TTRmotor,replacement = TTRspindle,replacement = TTRsh,replacement = TTRsd,replacement = 1 woh.
3.2.2. Training Results for HWH
Optimal Solution
- Preventive maintenance is proposed for the:
- –
- Motor when:
- *
- The short-interval average modified KPI for the maintenance of this component exceeds ;
- *
- Its lubricant failure probability within the next time step (3 h) exceeds .
- –
- Spindle when the short-interval average modified KPI for the maintenance of this component exceeds .
- Preventive replacement is proposed for the
- –
- Sample-holder when its failure probability within the next time step (3 h) exceeds ;
- –
- Sample-detector when its failure probability within the next time step (3 h) exceeds .
Evaluation Metrics
3.2.3. Run Results (Simulation Scenario) for HWH
3.2.4. Discussion of the Training Results for HWH
3.3. Application to ZORLUTEKS
- 14 roller coatings (one for each of the 16 analysed rollers except the 2 standalone—the other 14 coated rollers are in pairs);
- 16 double bearing-lubricant pairs (one for each roller);
- 10 inverters;
- 11 motors.
3.3.1. Training Input for ZORLUTEKS
- Any component—replacement: 0% for each failure type;
- Roller coating—maintenance: 10%;
- Double bearing-lubricant pair—maintenance:
- –
- Bearing mechanical fatigue: 100%;
- –
- Bearing lubricant: 0%.
- Motor—maintenance (lubrication):
- –
- Complete: 100%;
- –
- Lubricant: 0%.
- Motor—maintenance (winding):
- –
- Complete: 10%;
- –
- Lubricant: 100%.
- Range: Normally, load is assumed to equal one during production and zero during intervals without production for any mechanical fatigue of bearing and complete motor failure. For the other failure types, load is assumed asone all the time. The only exceptions which apply are related to the multipliers discussed below.
- Maximum absolute first-order difference within 1 day: load is sectionally constant.
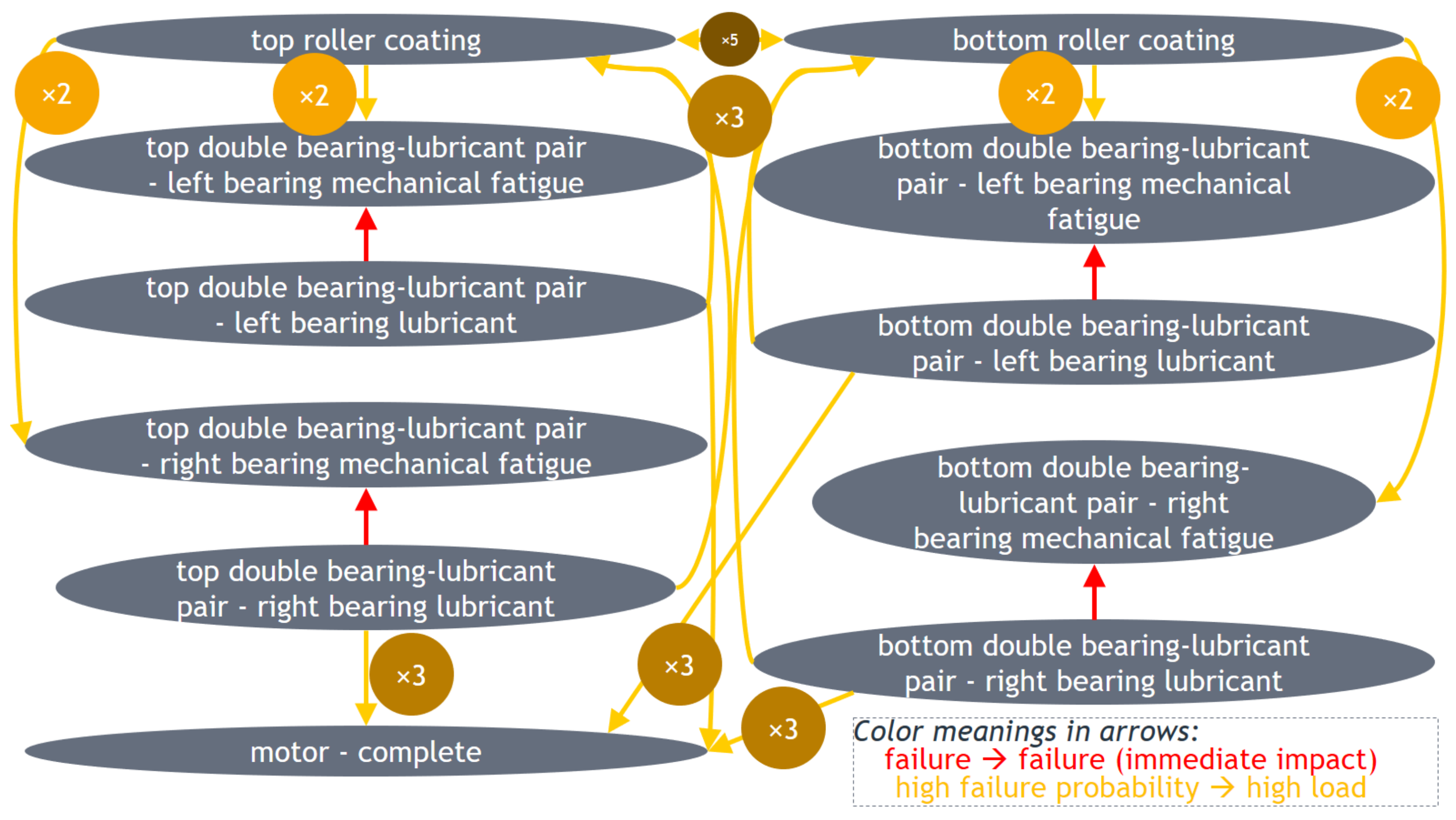
- Multiplier during production due to high failure probability until the next timestamp: According to the orange arrows in Figure 13, load with respect to a particular failure type (arrow end) is assumed to be multiplied by the respective number when the probability of failure of another type (arrow start) within the next elementary time interval (i.e., interval with length equal to the sampling step) is relatively high (i.e., higher than the theoretical degradation-based probability corresponding to 90% of METTF). The red arrows indicate the aforementioned failure correlations.
- economic: EUR.
- energy: kWh.
- other environmental: kg.
- Water: 0.0023 m/(m of fabric) · 33.55 (Mm of fabric)/year · 0.165 EUR/m = 12,732 EUR/year = 1.4525 EUR/h;
- Energy: 0.0051 kWh/(m of fabric) · 33.55 (Mm of fabric)/year · 0.07 EUR/kWh = 11,977 EUR/year = 1.3663 EUR/h;
- Steam: 0.41 kg/(m of fabric) · 33.55 (Mm of fabric)/year · 0.012EUR/kg = 165,066 EUR/year = 18.8303 EUR/h
- Material (fabric): 31.58 (Mm of fabric)/year · 0.48 EUR/(m of fabric) = 15,158,400 EUR/year = 1729 EUR/h;
- Labor: 225 Phs/month·2.3 EUR/Ph = 517.5 EUR/month = 6210 EUR/year = 0.7084189 EUR/h (may be considered as negligible compared to the other production costs—paid also during stops).
- Energy: 0.0051 kWh/(m of fabric) · 33.55 (Mm of fabric)/year = 171,105 kWh/year = 19.5192 kW → 3355 kWh/year = 0.382729 kW = 0.191365 kWh/(30 min) for each of the 51 components;
- Other environmental (total resulting from the following): 14,084.3 t/year = 1606.70 kg/h → 276,163 kg/year = 31.5039 kg/h = 15.7520 kg/(30 min) for each of the 51 components:
- –
- Water: 0.0023 m/(m of fabric) · 33.55 (Mm of fabric)/year = 77,165 m/year = 77,165 kg/year;
- –
- Chemicals: 0.0075 kg/(m of fabric) · 33.55 (Mm of fabric)/year = 251,625 kg/year;
- –
- Steam: 0.41 kg/(m of fabric) · 33.55 (Mm of fabric)/year = 13,755.5 t/year.
- Economic: 1;
- Energy: 0.07;
- Other environmental: (12,732 + 124,741 + 165,066)/(77,165 + 251,625 + 13,755,500) = 0.021481.
- Roller coating: 435 min = 7.25 h;
- Double bearing-lubricant pair: 80 min = 1.33…h (the maintenance is applied in parallel to the production);
- Motor: 210 min = 3.5 h (except for lubrication, for which the duration is 20 min = 0.33…h—the lubrication is applied in parallel to the production).
- Replacement/maintenance of roller coating: 7.5620232 woh = 0.31508430 woD;
- Replacement of double bearing-lubricant pair: 1.3907169 woh = 0.057946538 woD;
- Replacement/maintenance (winding) of motor: 3.6506319 woh = 0.15210967 woD.
- Roller coating: 36 kg;
- Double bearing-lubricant pair: 13 kg;
- Motor: 100 kg (lubricant: 0.1 kg).
3.3.2. Training Results for ZORLUTEKS—Model with Paired Coated Rollers
Optimal Solution
- Coating of the bottom roller when its failure probability within the next time step (30 min) exceeds ;
- Coating of the top roller when its failure probability within the next time step (30 min) exceeds (close to the case of the coating of the bottom roller);
- Double bearing-lubricant pair of any roller when the short-interval average modified KPI for the maintenance of this component exceeds −5.723695048214355;
- Motor (lubrication) when the short-interval average modified KPI for the maintenance (lubrication) of this component exceeds −5.723695048214355.
Evaluation Metrics
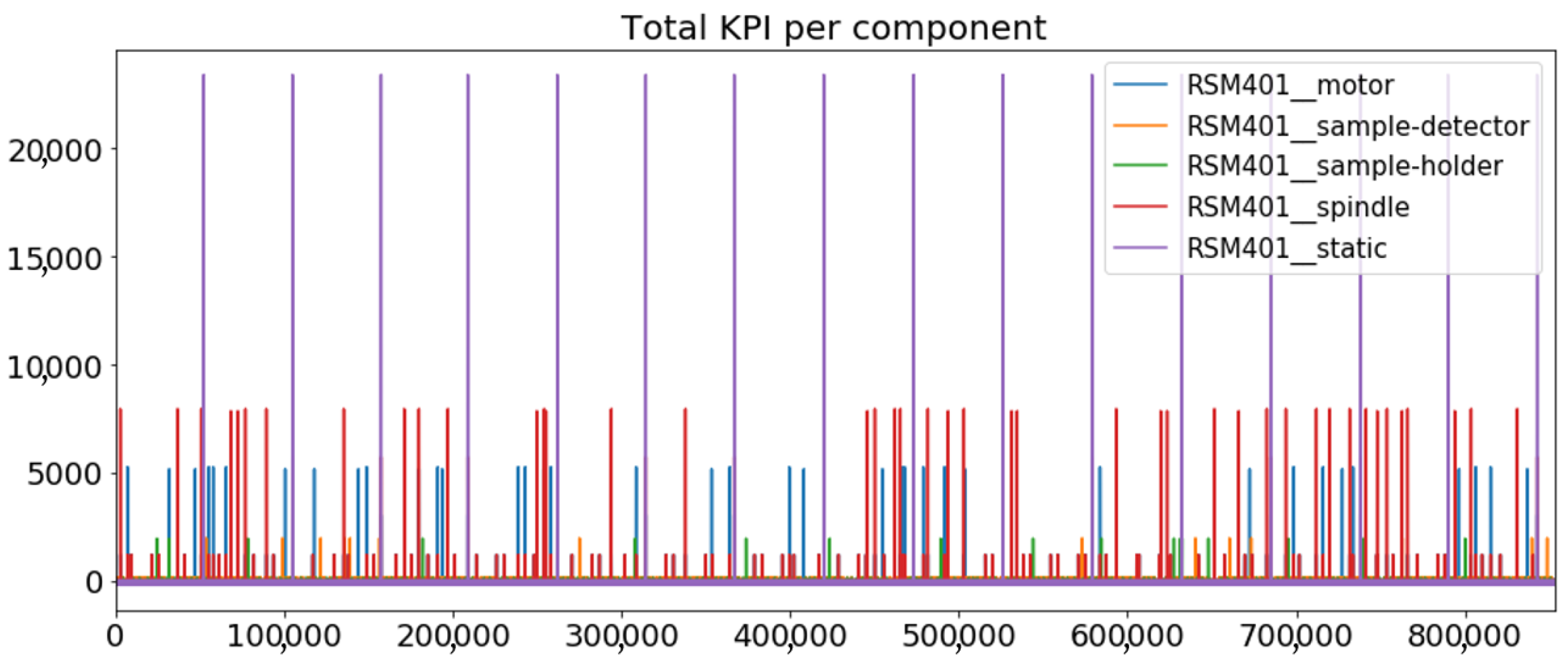
3.3.3. Run Results (Simulation Scenario) for ZORLUTEKS—Model with Paired Coated Rollers
3.3.4. Training Results for ZORLUTEKS—Model with Standalone Uncoated Roller
Optimal Solution
- double bearing-lubricant pair when:
- –
- Its left bearing lubricant failure probability within the next time step (30 min) exceeds ;
- –
- Its right bearing lubricant failure probability within the next time step (30 min) exceeds .
- Motor when its lubricant failure probability within the next time step (30 min) exceeds (in which case the maintenance is lubrication).
Evaluation Metrics
3.3.5. Run Results (Simulation Scenario) for ZORLUTEKS—Model with Standalone Uncoated Roller
3.3.6. Discussion of the Training Results for ZORLUTEKS
4. Conclusions, Limitations and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AHP | analytic hierarchy process |
| CAGR | compound annual growth rate |
| CO2 | carbon dioxide |
| CV | coefficient of variation |
| DSF | Decision Support Framework |
| Easy-LCA | name of software mentioned in [18] |
| EoL | End of Life |
| EOLI | EoL impact |
| ETTF | Equivalent Time To Failure |
| FMOLP | fuzzy multi-objective linear programming model |
| GDL | gas diffusion layer |
| ISO | International Organization for Standardization |
| KPI | Key Performance Indicator |
| LCA | Life Cycle Assessment |
| LCC | Life Cycle Cost |
| LCPlanner | name of software mentioned in [18] |
| MCDA | multi-criteria decision analysis |
| MCDM | multi-criteria decision methodology |
| MEA | membrane electrolyte assembly |
| METTF | Mean ETTF |
| MINLP | mixed integer non-linear programming |
| MRO | Maintenance, Repair and Overhaul |
| MSD | mean stop duration |
| MTTF | Mean Time To Failure |
| NOx | any mono-nitrogen oxide |
| NRV | net recoverable value |
| Ph | person hour |
| PQI | process quality improvement |
| QFD | quality function deployment |
| QFDNavi | name of software mentioned in [18] |
| RUP | remaining usage potential |
| SCR | setup cost reduction |
| SOx | any sulphur oxide |
| weh | welding hours |
| woD | working days |
| woh | working hours |
| womin | working minutes |
References
- Remanufacturing Market Study. Available online: http://www.remanufacturing.eu/assets/pdfs/remanufacturing-market-study.pdf (accessed on 24 November 2022).
- Europe MRO Distribution Market Size, Share & Trends Analysis Report by Distribution Channel (Direct, Indirect), by Maintenance Type, by Sourcing/Service Type, by Product, by Application, and Segment Forecasts, 2022–2030. Available online: https://www.grandviewresearch.com/industry-analysis/europe-maintenance-repair-overhaul-mro-distribution-market (accessed on 24 November 2022).
- Paterson, D.A.; Ijomah, W.L.; Windmill, J.F. End-of-life decision tool with emphasis on remanufacturing. J. Clean. Prod. 2017, 148, 653–664. [Google Scholar] [CrossRef]
- Wang, K.; Tian, J.; Pecht, M.; Xu, A. A Prognostics and Health Management Based Method for Refurbishment Decision Making for Electromechanical Systems. IFAC-PapersOnLine 2015, 48, 454–459. [Google Scholar] [CrossRef]
- Wu, Z.; Liu, W.; Nie, W. Literature review and prospect of the development and application of FMEA in manufacturing industry. Int. J. Adv. Manuf. Technol. 2021, 112, 1409–1436. [Google Scholar] [CrossRef]
- Saada, M.; Meng, Q. An efficient algorithm for anomaly detection in a flight system using dynamic bayesian networks. In Proceedings of the International Conference on Neural Information Processing (ICONIP), Doha, Qatar, 12–15 November 2012; Huang, T., Zeng, Z., Li, C., Leung, C.S., Eds.; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- von der Linden, W.; Dose, V.; von Toussaint, U. Bayesian Probability Theory: Applications in the Physical Sciences; Cambridge University Press: Cambridge, UK, 2014. [Google Scholar]
- Murphy, K.P. Dynamic Bayesian Networks: Representation, Inference and Learning. Ph.D. Dissertation, University of California, Berkeley, CA, USA, 2002. [Google Scholar]
- Rossini, R.; Conzon, D.; Prato, G.; Pastrone, C.; Reis, J.; Gonçalves, G. REPLICA: A Solution for Next Generation IoT and Digital Twin Based Fault Diagnosis and Predictive Maintenance. In Proceedings of the Conference on Security, Artificial Intelligence, and Modeling for the Next Generation Internet of Things (SAM IoT), Online, 17–18 September 2020. [Google Scholar]
- Kolokas, N.; Vafeiadis, T.; Ioannidis, D.; Tzovaras, D. A generic fault prognostics algorithm for manufacturing industries using unsupervised machine learning classifiers. Simul. Modell. Pract. Theory 2020, 103, 102109. [Google Scholar] [CrossRef]
- Soyer, R.; Mazzuchi, T.A.; Singpurwalla, N.D. (Eds.) Mathematical Reliability: An Expository Perspective; Springer Science+Business Media: New York, NY, USA, 2004. [Google Scholar]
- Escobar, L.A.; Meeker, W.Q. A Review of Accelerated Test Models. Stat. Sci. 2006, 21, 552–577. [Google Scholar] [CrossRef]
- Radial Ball Bearings Life and Load Ratings. Available online: https://www.astbearings.com/radial-ball-bearings-life-and-load-ratings.html (accessed on 24 November 2022).
- Reliability and Lifetime of LEDs. Available online: https://www.farnell.com/Reliability-and%20lifetime-of-LEDs.pdf?ICID=I-CT-TECH-RES-CLA-SEP_21-0 (accessed on 24 November 2022).
- Amaitik, N.; Zhang, M.; Wang, Z.; Xu, Y.; Thomson, G.; Xiao, Y.; Kolokas, N.; Maisuradze, A.; Garcia, O.; Peschl, M. Cost Modelling to Support Optimum Selection of Life Extension Strategy for Industrial Equipment in Smart Manufacturing. Circ. Econ. Sust. 2022, 2, 1425–1444. [Google Scholar] [CrossRef]
- Fontana, A.; Barni, A.; Leone, D.; Spirito, M.; Tringale, A.; Ferraris, M.; Reis, J.; Goncalves, G. Circular Economy Strategies for Equipment Lifetime Extension: A Systematic Review. Sustainability 2021, 13, 1117. [Google Scholar] [CrossRef]
- Brundage, M.P.; Bernstein, W.Z.; Hoffenson, S.; Chang, Q.; Nishi, H.; Kliks, T.; Morris, K.C. Analyzing environmental sustainability methods for use earlier in the product life cycle. J. Clean. Prod. 2018, 187, 877–892. [Google Scholar] [CrossRef]
- Kobayashi, H. Strategic evolution of eco-products: A product life cycle planning methodology. Res. Eng. Des. 2005, 16, 1–16. [Google Scholar] [CrossRef]
- Bianchini, A.; Rossi, J.; Pellegrini, M. Overcoming the Main Barriers of Circular Economy Implementation through a New Visualization Tool for Circular Business Models. Sustainability 2019, 11, 6614. [Google Scholar] [CrossRef]
- Reike, D.; Vermeulen, W.J.V.; Witjes, S. The circular economy: New or Refurbished as CE 3.0?—Exploring Controversies in the Conceptualization of the Circular Economy through a Focus on History and Resource Value Retention Options. Resour. Conserv. Recycl. 2018, 135, 246–264. [Google Scholar] [CrossRef]
- Stoycheva, S.; Marchese, D.; Paul, C.; Padoan, S.; Juhmani, A.-s.; Linkov, I. Multi-criteria decision analysis framework for sustainable manufacturing in automotive industry. J. Clean. Prod. 2018, 187, 257–272. [Google Scholar] [CrossRef]
- Ziout, A.; Azab, A.; Atwan, M. A holistic approach for decision on selection of end-of-life products recovery options. J. Clean. Prod. 2014, 65, 497–516. [Google Scholar] [CrossRef]
- Banasik, A.; Bloemhof-Ruwaard, J.M.; Kanellopoulos, A.; Claassen, G.D.H.; van der Vorst, J.G.A.J. Multi-criteria decision making approaches for green supply chains: A review. Flex. Serv. Manuf. J. 2018, 30, 366–396. [Google Scholar] [CrossRef]
- Kamble, S.S.; Gunasekaran, A.; Gawankar, S.A. Sustainable Industry 4.0 framework: A systematic literature review identifying the current trends and future perspectives. Process. Saf. Environ. Prot. 2018, 117, 408–425. [Google Scholar] [CrossRef]
- Ren, S.; Zhang, Y.; Liu, Y.; Sakao, T.; Huisingh, D.; Almeida, C.M.V.B. A comprehensive review of big data analytics throughout product life cycle to support sustainable smart manufacturing: A framework, challenges and future research directions. J. Clean. Prod. 2019, 210, 1343–1365. [Google Scholar] [CrossRef]
- Suzanne, E.; Absi, N.; Borodin, V. Toward circular economy in production planning: Challenges and Opportunities. Eur. J. Oper. Res. 2019, 287, 168–190. [Google Scholar] [CrossRef]
- Kumar, A.; Shankar, R.; Thakur, L.S. A big data driven sustainable manufacturing framework for condition-based maintenance prediction. J. Comput. Sci. 2018, 27, 428–439. [Google Scholar] [CrossRef]
- Omwando, T.A.; Otieno, W.A.; Farahani, S.; Ross, A.D. A Bi-Level fuzzy analytical decision support tool for assessing product remanufacturability. J. Clean. Prod. 2018, 174, 1534–1549. [Google Scholar] [CrossRef]
- Alamerew, Y.A.; Brissaud, D. Circular economy assessment tool for end of life product recovery strategies. J. Remanuf. 2019, 9, 169–185. [Google Scholar] [CrossRef]
- Dehghanbaghi, M.; Hosseininasab, H.; Sadeghieh, A. A hybrid approach to support recovery strategies (a case study). J. Clean. Prod. 2016, 113, 717–729. [Google Scholar] [CrossRef]
- Mangum, D.; Thurston, D.L. Incorporating component reuse, remanufacture, and recycle into product portfolio design. IEEE Trans. Eng. Manag. 2002, 49, 479–490. [Google Scholar] [CrossRef]
- Rahimifard, S.; Coates, G.; Staikos, T.; Edwards, C.; Abu-Bakar, M. Barriers, drivers and challenges for sustainable product recovery and recycling. Int. J. Sustain. Eng. 2009, 2, 80–90. [Google Scholar] [CrossRef]
- Rose, C. Design for Environment: A Method for Formulating End-of-Life Strategies. Ph.D. Dissertation, Stanford University, Stanford, CA, USA, November 2000. [Google Scholar]
- Zwolinski, P.; Ontiveros, M.A.L.; Brissaud, D. Integrated design of remanufacturable products based on product profile. J. Clean. Prod. 2005, 14, 1333–1345. [Google Scholar] [CrossRef]
- Lebreton, B.; Tuma, A. A quantitative approach to assessing the profitability of car and truck tire remanufacturing. Int. J. Prod. Econ. 2006, 104, 639–652. [Google Scholar] [CrossRef]
- Toffel, M.W. Manufacturer strategies for end-of-life product recovery. In Proceedings of the Conference on European Electronics Take-back Legislation: Impacts on Business Strategy and Global Trade, Fontainebleau, France, 17–18 October 2002. [Google Scholar]
- Seitz, M.A.; Wells, B.E. Challenging the implementation of corporate sustainability: The case of automotive engine remanufacturing. Bus. Process Manag. J. 2006, 12, 822–836. [Google Scholar] [CrossRef]
- González, B.; Adenso-Díaz, B. A bill of materials-based approach for end-of-life decision making in design for the environment. Int. J. Prod. Res. 2005, 43, 2071–2099. [Google Scholar] [CrossRef]
- Willems, B.; Dewulf, W.; Duflou, J.R. A method to assess lifetime prolongation capabilities of products. Int. J. Sustain. Manuf. 2008, 1, 122–144. [Google Scholar] [CrossRef]
- Xanthopoulos, A.; Iakovou, E. On the optimal design of the disassembly and recovery process. J. Waste Manag. 2009, 29, 1702–1711. [Google Scholar] [CrossRef] [PubMed]
- Boks, C.; Stevels, A. Ranking ecodesign priorities from quantitative uncertainty assessment for end-of-life scenarios. In Proceedings of the IEEE International Symposium on Electronics and the Environment, Denver, CO, USA, 9 May 2001; pp. 76–81. [Google Scholar]
- Saman, A.; Zhang, G. A multi-objective facility location model for closed-loop supply chain network under uncertain demand and return. Appl. Math. Modell. 2013, 37, 4165–4176. [Google Scholar]
- Krikke, H.R.; Harten, A.V.; Schuur, P.C. On a medium term of product recovery and disposal strategy for durable assembly products. Int. J. Prod. Res. 1998, 36, 111–139. [Google Scholar] [CrossRef]
- Kumar, V.; Shirodkar, P.S.; Camelio, J.A.; Sutherland, J.W. Value flow characterization during product life cycle to assist in recovery decisions. Int. J. Prod. Res. 2007, 45, 4555–4572. [Google Scholar] [CrossRef]
- Zussman, E.; Kriwet, A.; Selieger, G. Disassembly-oriented assessment methodology to support design for recycling. Ann. CIRP 1994, 43, 9–14. [Google Scholar] [CrossRef]
- Hula, A.; Jalili, K.; Hamza, K.; Skerlos, S.J.; Saitou, K. Multi-criteria decision making for optimization of product disassembly under multiple situations. J. Environ. Sci. Technol. 2003, 37, 5303–5313. [Google Scholar] [CrossRef] [PubMed]
- Bakar, M.S.; Rahimifard, S. Computer-aided recycling process planning for end-of-life electrical and electronic equipment. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2007, 221, 1369–1374. [Google Scholar] [CrossRef]
- Iakovou, E.; Moussiopoulos, N.; Xanthopoulos, A.; Achillas, C.; Michailidis, N.; Chatzipanagioti, M.; Koroneos, C.; Bouzakis, K.D.; Kikis, V. A methodological framework for end-of-life management of electronic products. Resour. Conserv. Recycl. 2009, 53, 329–339. [Google Scholar] [CrossRef]
- Caudill, R.J.; Dickinson, D.A. Sustainability and end-of-life product management: A case study of electronics collection scenarios. In Proceedings of the IEEE International Symposium on Electronics and the Environment, Scottsdale, AZ, USA, 10–13 May 2004; pp. 132–137. [Google Scholar]
- Ziout, A.; Azab, A.; Altarazi, S.; ElMaraghy, W.H. Multi-criteria decision support for sustainability assessment of manufacturing system reuse. CIRP J. Manuf. Sci. Technol. 2013, 6, 59–69. [Google Scholar] [CrossRef]
- Wang, X.; Lu, X.; Zhang, S. Study on the waste liquid crystal display treatment: Focus on the resource recovery. J. Hazard. Mater. 2013, 244–245, 342–347. [Google Scholar] [CrossRef] [PubMed]
- Staikos, T.; Rahimifard, S. A decision model for waste management in the footwear industry. Int. J. Prod. Res. 2007, 45, 4403–4422. [Google Scholar] [CrossRef]
- Chan, J.W.K. Product end-of-life options selection: Grey relational analysis approach. Int. J. Prod. Res. 2008, 46, 2889–2912. [Google Scholar] [CrossRef]
- Fernandez, I.; Puente, J.; Garcia, N.; Gomez, A. A decision-making support system on a products recovery management framework. A fuzzy approach. Concurr. Eng. Res. Appl. 2008, 16, 129–138. [Google Scholar] [CrossRef]
- Gehin, A.; Zwoliniski, P.; Brissaud, D. A tool to implement sustainable end-of-life strategies in the product development phase. J. Clean. Prod. 2008, 16, 566–576. [Google Scholar] [CrossRef]
- Giudice, F.; La Rosa, G.; Risitano, A. Product recovery-cycles design. Feature Based Prod.-Life-Cycle Model. 2003, 109, 165–185. [Google Scholar]
- Srinivasan, S.; Khan, S.H. Multi-stage manufacturing/re-manufacturing facility location and allocation model under uncertain demand and return. Int. J. Adv. Manuf. Technol. 2018, 94, 2847–2860. [Google Scholar] [CrossRef]
- Farahani, S.; Otieno, W.; Omwando, T. The optimal disposition policy for remanufacturing systems with variable quality returns. Comput. Ind. Eng. 2020, 140, 106218. [Google Scholar] [CrossRef]
- Farahani, S.; Otieno, W.; Barah, M. Environmentally friendly disposition decisions for end-of-life electrical and electronic products: The case of computer remanufacture. J. Clean. Prod. 2019, 224, 25–39. [Google Scholar] [CrossRef]
- Bentaha, M.-L.; Voisin, A.; Marangé, P. A decision tool for disassembly process planning under end-of-life product quality. Int. J. Prod. Econ. 2020, 219, 386–401. [Google Scholar] [CrossRef]
- Su, T.-S. Optimal lot-sizing decisions with integrated purchasing, manufacturing and assembling for remanufacturing systems. Iran. J. Fuzzy Syst. 2018, 15, 1–26. [Google Scholar]
- Chan, S.L.; Lu, Y.; Wang, Y. Data-driven cost estimation for additive manufacturing in cybermanufacturing. J. Manuf. Syst. 2018, 46, 115–126. [Google Scholar] [CrossRef]
- Yang, Y.; Li, L. Cost modeling and analysis for Mask Image Projection Stereolithography additive manufacturing: Simultaneous production with mixed geometries. Int. J. Prod. Econ. 2018, 206, 146–158. [Google Scholar] [CrossRef]
- Mahadik, A.; Masel, D. Implementation of Additive Manufacturing Cost Estimation Tool (AMCET) Using Break-down Approach. Procedia Manuf. 2018, 17, 70–77. [Google Scholar] [CrossRef]
- Chang, N.L.; Ho-Baillie, A.W.Y.; Vak, D.; Gao, M.; Green, M.A.; Egan, R.J. Manufacturing cost and market potential analysis of demonstrated roll-to-roll perovskite photovoltaic cell processes. Sol. Energy Mater. Sol. Cells 2018, 174, 314–324. [Google Scholar] [CrossRef]
- Khorasani, M.; Ghasemi, A.H.; Rolfe, B.; Gibson, I. Additive manufacturing a powerful tool for the aerospace industry. Rapid Prototyp. J. 2021, 28, 87–100. [Google Scholar] [CrossRef]
- Dey, B.K.; Bhuniya, S.; Sarkar, B. Involvement of controllable lead time and variable demand for a smart manufacturing system under a supply chain management. Expert Syst. Appl. 2021, 184, 115464. [Google Scholar] [CrossRef]
- França, W.T.; Barros, M.V.; Salvador, R.; de Francisco, A.C.; Moreira, M.T.; Piekarski, C.M. Integrating life cycle assessment and life cycle cost: A review of environmental-economic studies. Int J Life Cycle Assess 2021, 26, 244–274. [Google Scholar] [CrossRef]
- Vieira, D.R.; Calmon, J.L.; Coelho, F.Z. Life cycle assessment (LCA) applied to the manufacturing of common and ecological concrete: A review. Constr. Build. Mater. 2016, 124, 656–666. [Google Scholar] [CrossRef]
- Amicarelli, V.; Bux, C.; Spinelli, M.P.; Lagioia, G. Life cycle assessment to tackle the take-make-waste paradigm in the textiles production. Waste Manag. 2022, 151, 10–27. [Google Scholar] [CrossRef]
- Ferrari, A.M.; Volpi, L.; Settembre-Blundo, D.; García-Muiña, F.E. Dynamic life cycle assessment (LCA) integrating life cycle inventory (LCI) and Enterprise resource planning (ERP) in an industry 4.0 environment. J. Clean. Prod. 2021, 286, 125314. [Google Scholar] [CrossRef]
- Reisinger, J.; Kugler, S.; Kovacic, I.; Knoll, M. Parametric Optimization and Decision Support Model Framework for Life Cycle Cost Analysis and Life Cycle Assessment of Flexible Industrial Building Structures Integrating Production Planning. Buildings 2022, 12, 162. [Google Scholar] [CrossRef]
- Selicati, V.; Cardinale, N.; Dassisti, M. Cycle Thinking in assessing manufacturing sustainability: A review of hybrid approaches. J. Clean. Prod. 2021, 286, 124932. [Google Scholar] [CrossRef]
- Chang, Y.-J.; Sproesser, G.; Neugebauer, S.; Wolf, K.; Scheumann, R.; Pittner, A.; Rethmeier, M.; Finkbeiner, M. Environmental and Social Life Cycle Assessment of Welding Technologies. Procedia CIRP 2015, 26, 293–298. [Google Scholar] [CrossRef]
- Duan, Z.; Huang, Q.; Zhang, Q. Life cycle assessment of mass timber construction: A review. Build. Environ. 2022, 221, 109320. [Google Scholar] [CrossRef]
- Müller, A.; Friedrich, L.; Reichel, C.; Herceg, S.; Mittag, M.; Neuhaus, D.H. A comparative life cycle assessment of silicon PV modules: Impact of module design, manufacturing location and inventory. Sol. Energy Mater. Sol. Cells 2021, 230, 111277. [Google Scholar] [CrossRef]
- Kolokas, N.; Ioannidis, D.; Tzovaras, D. Multi-Step Energy Demand and Generation Forecasting with Confidence Used for Specification-Free Aggregate Demand Optimization. Energies 2021, 14, 3162. [Google Scholar] [CrossRef]
- Galbraith, C.S. Quantifying the association between discrete event time series with applications to digital forensics. J. R. Stat. Soc. A 2020, 183, 1005–1027. [Google Scholar] [CrossRef]











| Input Data | Optimization Criteria | Decisions | Methods | Reference(s) |
|---|---|---|---|---|
| - | economic (costs, profit, net present value…), environmental (greenhouse gas, energy, life-cycle-assessment-based, water, waste,…), other (service level, social) | decisions for green supply chains about production–distribution planning, inventory management | multi-criteria decision methodology (MCDM) [analytic hierarchy process (AHP), analytic network process, decision-making trial and evaluation laboratory, elimination and choice expressing reality, preference ranking organization method for enrichment of evaluations, technique for order of preference by similarity to ideal solution, utility additive, -constraint, goal programming, weighting method] (+interpretive structural modelling) | [23,24] |
| product performance, historical product design, customer demands, assembly requirements, environment impacts,… | - | intelligent product and service design | data mining, artificial intelligence, big data analysis (deep learning on diverse input) | [25] |
| {historical faults, product quality} → {failure forecasting, products lifetime} | - | intelligent production (predictive maintenance planning,…) | ||
| material delivery, energy (maybe predicted by process variables) | energy efficiency (of shop-floor material handling) | intelligent production (material route),… | ||
| product operation status → equipment performance, product quality monitoring, historical faults, customer evaluation | - | intelligent maintenance and service (customer service, product support, maintenance) | ||
| product life cycle history ({product design index, maintenance history, operation status,…} → {remaining lifetime, degradation status}, environmental factors,…) | environmental | intelligent recovery (reuse, remanufacturing, repair, recycling, disposal,…) | ||
| linking equipment and process data to inspection and metrology data | product quality and yield | - | ||
| logistics data | shop-floor logistics (productivity, delivery time) | - | ||
| - | environmental,… | design |
| [17] |
| costs (setup, penalty, overload, lost sales, inventory holding) | disassembly lot-sizing (scheduling)
| various | [26] |
| production, setup, holding costs associated to (re)manufacturing | from product to raw material recycling
| ||
| setup, production, inventory costs | by-products vs. co-products
| ||
| costs | greenhouse gas emissions and energy consumption
| ||
| failure probability threshold (determining replacement decision) | replacement/ maintenance cost | replacement | gas turbine measurements → failure probability (supervised classification with fuzzy unordered rule induction algorithm) | [27] |
| - | environmental, economic, social | material alternatives in manufacturing | multi-criteria decision analysis (MCDA) | [21] |
| data from a local control drive remanufacturing company | technological, economic, resource utilization, environmental metrics | - (only a continuous remanufacturability score is the output) | fuzzy inference system | [28] |
| environmental (EOLI, CO2-SO2 emissions, energy), economic [NRV, logistic–disassembly cost, product cost (incineration, recycling, landfill)], societal (number of employees and their exposure to hazardous materials) | remanufacturing, reconditioning, refurbishment, cannibalization, repair, recycling | mathematical optimization, MCDM (selected in the respective paper), empirical methods | [29] |
| - | working status, quality, disassemblability, cleanability, repair–replacement ability, spare parts availability, market for recovered 2nd-hand products, green design and hazardous waste | reuse/resell, product upgrade (repair, remanufacturing, refurbishment), materials recovery (cannibalization, recycling), disposal | fuzzy logic | [30] |
| item useful life time [31,32], technology/design cycle [33,34,35], wear-out life [33,35], standard or interchangeable item [36,37], number of components [33], product architecture and level of integration [33,34], disassembly effort [38,39,40], materials separability [34], investment costs [41,42], recovery process cost [43], new item value [34,44], used item value [34], lost sale in primary market [34,45], EoL product location [46], collection cost [34,41,42], demand volume [41], cost of legal compliance [47], regulations on recycled quota [48], energy yield [49], material yield [50], liquid and solid waste impact [50], air emissions [49,50], hazardous material contents [51], reason for discard, purpose of ownership, consumer opinion toward used product [43], damages/benefit to human health [52,53], society involvement in recovery programs [54], green party pressure [55], fuel cell cost data [for end and bipolar plates, membrane electrolyte assembly (MEA) [gas diffusion layer (GDL), anode and cathode catalyst, membrane], gaskets, current collectors, electrical jumpers, bolts], disassembly time (to unplug electrical jumpers, unscrew end plate bolts, and remove end and bipolar plates, current collector, gasket, MEA assembly, GDLs, cathode and anode catalysts and membrane) | engineering (product, process), business (market, supply–demand, legal-political), environmental (resources, pollution), societal (targeted segment, overall society) |
| exhaustive enumeration, mathematical optimization, multi-criteria (selected with AHP in the respective paper), clustering, empirical | [22] |
| cost, environmental, quality | upgrade/maintenance, product/component reuse, material recycling, disposal | quality function deployment (QFD) (transforms qualitative user demands into quantitative parameters,…) | [18] |
| environmental effectiveness of recovery cycles (intensity of resource use in terms of extension of the product’s useful life) | design alternative |
| [56] |
| total supply chain cost | quantities shipped among supplier, processing/assembling/ reprocessing/sorting and dismantling/disposal units, distribution hubs, retailers, customers | mixed integer linear programming (selected in respective paper), fuzzy logic, branch and bound, spanning tree and prufer number, stochastic programming, goal programming | [57] |
| expected (based on Markov chain) frequency of accepting products for remanufacturing/rejecting disposed products/disposing products due to storage capacity limits/customer order completion delays/storing recoverable products/discarding products during remanufacturing, expected revenue from remanufacturing a returned product [quality follows normal, exponential or beta (in respective paper) distribution], salvage cost, cost of recoverable products inventory establishment, cost of customer order completion delay, holding cost of returned products, cost of discarding recoverable product during remanufacturing (fixed unit costs) | profit | optimal minimum quality to accept into remanufacturing facility and quantity of parts to purchase from external suppliers, recoverable products inventory capacity | mixed integer non-linear programming (MINLP), queueing model, continuous time Markov chain, quasi-birth–death process, matrix-geometric method | [58] |
| total profit of facility | optimal minimum quality to remanufacture, sales, quantity of purchased/disassembled/ remanufactured/refurbished/ disposed products/parts, inventory levels, binary variables for setup of remanufacturing/disassembly/ refurbishing | MINLP → quadratic mixed integer programming | [59] |
quality of product (or subassembly, or component) → revenue (health state of product, its parts and sub-parts considered as random variables)
| disassembly profit (revenue by recovered parts – disassembly costs) | disassembly alternatives (level) in remanufacturing | quality modeled using RUP [considered as normal distribution truncated in [0,1]] | [60] |
| costs, CO2 emissions, lead time | lot size (units) per component purchased/released per manufacturing/assembling machine | fuzzy multi-objective linear programming model (FMOLP) | [61] |
| Input Data | Cost Types | Methods | Reference(s) |
|---|---|---|---|
| manufacturing | predictive analytics modelling, least absolute shrinkage and selection operator and elastic net modelling 1, process-oriented feature extraction | [62] |
| raw material price, initial investment | labor, part material, energy, support material, overheads | fixed values of parameters | [63] |
| few primary user parameters, optional secondary user parameters to increase estimation accuracy | machine, material, labor, post-processing | break-down (build time estimated by considering activities undergone by machine for preparation of a layer and multiplying it by total number of layers) | [64] |
| module dimensions and format, factory assumptions and cost inputs, production equipment assumptions, materials | manufacturing (sum of tool and facility, spare parts, footprint, electricity, material cost-usage) | Monte Carlo analysis to estimate cost distribution | [65] |
| product type, design method, machining condition parameters (tool diameter/tip, cutting/free movement feed rate, cut depth, step over) | machining, printing (process), material, labor, post-processing | calculating parameters affecting air manifold production price (cost types) (machining simulations performed with “Power mill 2018 software”) | [66] |
| vendor’s/buyer’s holding cost, cost of replacing imperfect goods, cumulative distribution function, mean/variance of lead time, buyer’s ordering cost, backorder cost, coefficient of variance per time period, batch size, initial probability of shifting out-of-control from in-control state, vendor’s initial setup cost, demand scaling parameter, scaling/shape parameters related to advertising demand function, annual fractional cost of capital investment, variation constant of product tool/die cost, machine running cost, scaling parameters related to PQI/SCR, reorder point for buyer, expected backorder quantity/on-hand inventory, mean lead time demand | vendor [holding, setup, variable production, defective, process quality improvement (PQI), setup cost reduction (SCR), advertisement] | exact computations also considering assumptions based on bibliography | [67] |
| Component | Scale () | Shape () | METTF |
|---|---|---|---|
| Power supply unit | 144 D = 34.3 woD | 2 | 128 D = 30.4 woD |
| Pump | 4.8 years = 1.1 working years = 417 woD | 2 | 4.3 years = 370 woD |
| Other | 33 D = 7.9 woD | 2 | 29 D = 7.0 woD |
| Component | Strategy | Gross | Net |
|---|---|---|---|
| Power supply unit | Maintenance | 257.209375 | 220 |
| Replacement | 3334.03125 | 3210 | |
| Pump | Maintenance | 76.0078125 | 45 |
| Replacement | 840.8140625 | 785 | |
| Hose | Replacement | 146.0078125 | 115 |
| Spraying gun | Maintenance | 181.0078125 | 150 |
| Replacement | 3686.0078125 | 3655 |
| Economic (EUR/Year) | Scrap (Discarded Parts/Year) | Total | |||||
|---|---|---|---|---|---|---|---|
| Ideal | Per Component | −45,542 | 62.167 | −45,076 | |||
| Total | −182,168 | 248.667 | −180,303 | ||||
| Component | Actual | Extra | Actual | Extra | Actual | Extra | |
| Initial = corrective solution | Hose | −39,639 | 5903 | 57.086 | −5.081 | −39,211 | 5865 |
| Power supply unit | −40,965 | 4577 | 57.086 | −5.081 | −40,537 | 4539 | |
| Pump | −41,799 | 3743 | 57.086 | −5.081 | −41,371 | 3705 | |
| Spraying gun | −39,080 | 6462 | 57.086 | −5.081 | −38,652 | 6424 | |
| Total | −161,482 | 20,686 | 228.343 | −20.323 | −159,770 | 20,533 | |
| Final solution | Hose | −41,412 | 4130 | 60.474 | −1.692 | −40,958 | 4118 |
| Power supply unit | −43,446 | 2096 | 60.474 | −1.692 | −42,992 | 2084 | |
| Pump | −44,281 | 1261 | 60.474 | −1.692 | −43,827 | 1248 | |
| Spraying gun | −40,735 | 4807 | 60.474 | −1.692 | −40,281 | 4795 | |
| Total | −169,873 | 12,295 | 241.897 | −6.770 | −168,059 | 12,244 | |
| Component | Stop Type | Initial = Corrective Solution | Final Solution |
|---|---|---|---|
| Hose | Failure | 2464 | 1275 |
| Replacement | 2464 | 3726 | |
| Power supply unit | Failure | 665 | 666 |
| Maintenance | 665 | 666 | |
| Replacement | 0 | 0 | |
| Pump | Failure | 56 | 56 |
| Maintenance | 56 | 56 | |
| Replacement | 0 | 0 | |
| Spraying gun | Failure | 2585 | 1436 |
| Maintenance | 2585 | 3726 | |
| Replacement | 0 | 0 |
| Ideal | Initial = Corrective Solution | Final Solution |
|---|---|---|
| 23.8095% | 23.6471% | 23.7553% |
| Economic (EUR/Year) | Scrap (Discarded Parts/Year) | Total (Yearly) | |||||
|---|---|---|---|---|---|---|---|
| Model | Actual | Extra | Actual | Extra | Actual | Extra | |
| Initial = corrective solution | Quartet () | −161,482 | 20,686 | 228.343 | −20.323 | −159,770 | 20,533 |
| Total | −1938 K | 248,229 | 2740.12 | −243.88 | −1917 K | 246,400 | |
| Final solution | Quartet () | −169,873 | 12,295 | 241.897 | −6.770 | -168,059 | 12,244 |
| Total | −2038 K | 147,542 | 2902.76 | −81.24 | −2017 K | 146,933 | |
| Component | Failures | Strategies |
|---|---|---|
| Static | single failure type | refurbishment |
| Motor | mechanical fatigue 1, lubricant | maintenance 2, replacement |
| Spindle | mechanical fatigue, lubricant | maintenance, replacement |
| Sample-holder | single failure type | replacement |
| Sample-detector | single failure type | replacement |
| Component | Failure Type | Scale () | Shape () | METTF |
|---|---|---|---|---|
| Static | Failure | 1179.02 woD | 127.53015316411776 (so that CV = 0.01) 1 | 18 years 2 = 1173.75 woD |
| Motor/Spindle | Mechanical fatigue | 24.9 years = 4.45 working years = 1625.36 woD | 1.5 | 22.50 years = 1467.29 woD |
| Lubricant | 5 years = 1826.25 D | 2 | 4.43 years = 1618.47 D | |
| Sample-holder | Failure | 150,000 parts = 3 years = 195.63 woD | 3 | 2.68 years = 174.69 woD |
| Component | Strategy | Duration-Dependent (Gross) | Duration-Independent | Total (Gross) | Total (Net) |
|---|---|---|---|---|---|
| Static | Refurbishment | not studied | not studied | 21,730 | 21,534.7 |
| Motor | Maintenance | 223.2 | 1070 | 1293.2 | 1097.9 |
| Replacement | 223.2 | 3120 | 3343.2 | 3147.9 | |
| Spindle | Maintenance | 223.2 | 1060 | 1283.2 | 1087.9 |
| Replacement | 223.2 | 5810 | 6033.2 | 5837.9 | |
| Sample-holder | Replacement | 27.9 | 101 | 128.9 | 128.9 |
| Sample-detector | Replacement | 27.9 | 121 | 148.9 | 148.9 |
| Component | Ideal | Initial = Corrective Solution | Final Solution | ||
|---|---|---|---|---|---|
| Actual | Extra | Actual | Extra | ||
| Motor | −99,094 | −97,301 | 1793 | −97,695 | 1398 |
| Sample-detector | −99,094 | −97,931 | 1162 | −98,166 | 927 |
| Sample-holder | −99,094 | −98,336 | 758 | −98,870 | 223 |
| Spindle | −99,094 | −96,314 | 2780 | −97,317 | 1776 |
| Static | −99,094 | −97,801 | 1293 | −97,801 | 1293 |
| Total | −495,468 | −487,682 | 7786 | −489,850 | 5618 |
| Component | Stop Type | Initial = Corrective Solution | Final Solution |
|---|---|---|---|
| Motor | Lubricant | 46 | 29 |
| Mechanical fatigue | 60 | 38 | |
| Maintenance | 46 | 82 | |
| Replacement | 76 | 54 | |
| Sample-detector | Failure | 158 | 14 |
| Replacement | 158 | 1631 | |
| Sample-holder | Failure | 104 | 16 |
| Replacement | 104 | 258 | |
| Spindle | Lubricant | 57 | 28 |
| Mechanical fatigue | 66 | 34 | |
| Maintenance | 57 | 82 | |
| Replacement | 82 | 50 | |
| Static | Failure | 16 | 16 |
| Refurbishment | 16 | 16 |
| Component | Failures | Strategies |
|---|---|---|
| Roller coating | single failure type | maintenance (=grinding), replacement |
| Double bearing-lubricant pair | left bearing mechanical fatigue, right bearing mechanical fatigue, left bearing lubricant, right bearing lubricant | maintenance (=lubricant replacement for both bearings), replacement |
| Motor | complete, lubricant | maintenance (lubrication and winding alternatives), replacement |
| Operation | Mean Output Fabric Area (Mm/Year) | Time Percentage (%) | ||||
|---|---|---|---|---|---|---|
| Bleaching | Washing | Total | Bleaching | Washing | Total | |
| Route | 27.72 | 0.34 | 28.06 | 54.28 | 0.72 | 55.00 |
| Repair | 3.33 | 1.63 | 4.96 | 7.55 | 4.25 | 11.80 |
| Sample | 0.00 | 0.00 | 0.00 | 0.01 | 0.00 | 0.01 |
| Total | 31.05 | 1.97 | 33.02 | 61.84 | 4.97 | 66.81 |
| Component | Mean (min) | CV | Weibull Scale (min) | Weibull Shape |
|---|---|---|---|---|
| Roller coating | 65.031579 | 1.8217826 | 41.612199 | 0.5832355 |
| Double bearing-lubricant pair | 53.293333 | 2.9996844 | 17.292100 | 0.4113669 |
| Motor | 31.915254 | 0.4667525 | 36.030221 | 2.2688522 |
| Component | Failure Type | Scale () | Shape () | METTF |
|---|---|---|---|---|
| Roller coating | Failure | 2 years = 730.5 D | 3 | 1.785959 years = 652.3215 D |
| Double bearing-lubricant pair | Mechanical fatigue of particular bearing (model with paired coated rollers) | 7 years = 2556.75 D | 1.5 | 6.319217 years = 2308.094 D |
| Mechanical fatigue of particular bearing (model with standalone uncoated roller) | 4.5 years = 1643.625 D | 1.5 | 4.062354 years = 1483.775 D | |
| Lubricant for particular bearing | 3 years = 1095.75 D | 1 15 | 2.896992 years = 1058.126 D | |
| Motor | Complete (model with paired coated rollers) | 3 years = 1095.75 D | 1.5 | 2.708236 years = 989.1832 D |
| Complete (model with standalone uncoated roller) | 2 years = 730.5 D | 1.5 | 1.805491 years = 659.4554 D | |
| Lubricant | 4 years = 1461 D | 3 | 3.571918 years = 1304.643 D |
| Component | Strategy | Gross | Net |
|---|---|---|---|
| Roller coating | Maintenance | 1307 | 175 |
| Replacement | 1582 | 450 | |
| Double bearing-lubricant pair | Maintenance | 6 | 6 |
| Replacement | 1458 | 326 | |
| Motor | Maintenance (lubrication) | 21 | 21 |
| Maintenance (winding) | 1282 | 150 | |
| Replacement | 4132 | 3000 |
| Component | Bad Whiteness Probability | Expected Waiting Time Due to Bad Whiteness | Expected Gross Profit Loss Due to Bad Whiteness |
|---|---|---|---|
| Roller coating | 41% | 9.4 min | EUR 464 |
| Double bearing-lubricant pair | 43% | 9.9 min | EUR 487 |
| Motor | 14% | 3.2 min | EUR 159 |
| Component | Failure Type | Corrective Strategy |
|---|---|---|
| Coating of any roller | Failure | replacement |
| Double bearing-lubricant pair of any roller | Left bearing lubricant | maintenance |
| Left bearing mechanical fatigue | replacement | |
| Right bearing lubricant | maintenance | |
| Right bearing mechanical fatigue | maintenance | |
| Motor | Complete | maintenance (winding) |
| Lubricant | maintenance (lubrication) |
| Economic (EUR/Year) | Energy (kWh/Year) | Other Environmental (kg/Year) | Total (Yearly) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Ideal | Per Component | −206,863 | 3355 | 276,163 | −200,696 | ||||
| Total | −103,4314 | 16,775 | 1,380,814 | −1,003,478 | |||||
| Component | Actual | Extra | Actual | Extra | Actual | Extra | Actual | Extra | |
| Initial solution | Coating of bottom roller | −199,778 | 7084 | 3269 | −86 | 269,093 | −7070 | −193,769 | 6927 |
| Coating of top roller | −199,761 | 7102 | 3269 | −86 | 269,093 | −7070 | −193,751 | 6944 | |
| Double bearing-lubricant pair of bottom roller | −200,623 | 6240 | 3269 | −86 | 269,093 | −7070 | −194,614 | 6082 | |
| Double bearing-lubricant pair of top roller | −200,628 | 6235 | 3269 | −86 | 269,093 | −7070 | −194,619 | 6077 | |
| Motor | −200,889 | 5974 | 3269 | −86 | 269,093 | −7070 | −194,880 | 5816 | |
| Total | −1.002 M | 32,635 | 16,346 | −429 | 1.345 M | −35,349 | −971,632 | 31,846 | |
| Corrective solution | Coating of bottom roller | −200,199 | 6664 | 3278 | −77 | 269,854 | −6309 | −194,173 | 6523 |
| Coating of top roller | −200,148 | 6715 | 3278 | −77 | 269,855 | −6308 | −194,122 | 6574 | |
| Double bearing-lubricant pair of bottom roller | −201,406 | 5457 | 3278 | −77 | 269,824 | −6339 | −195,381 | 5315 | |
| Double bearing-lubricant pair of top roller | −201,387 | 5476 | 3278 | −77 | 269,824 | −6339 | −195,361 | 5335 | |
| Motor | −201,415 | 5448 | 3278 | −77 | 269,820 | −6342 | −195,389 | 5306 | |
| Total | −1.005 M | 29,759 | 16,390 | −385 | 1.349 M | −31,637 | −974,425 | 29,053 | |
| Final solution | Coating of bottom roller | −202,717 | 4145 | 3297 | −58 | 271,432 | −4731 | −196,656 | 4040 |
| Coating of top roller | −202,686 | 4177 | 3297 | −58 | 271,434 | −4729 | −196,621 | 4075 | |
| Double bearing-lubricant pair of bottom roller | −202,391 | 4472 | 3297 | −58 | 271,426 | −4737 | −196,326 | 4370 | |
| Double bearing-lubricant pair of top roller | −202,351 | 4512 | 3297 | −58 | 271,426 | −4737 | −196,286 | 4410 | |
| Motor | −202,084 | 4779 | 3297 | −58 | 271,425 | −4738 | −196,019 | 4677 | |
| Total | −1.012 M | 22,084 | 16,487 | −288 | 1.357 M | −23,672 | −981,922 | 21,556 | |
| Component | Stop Type | Initial Solution | Corrective Solution | Final Solution |
|---|---|---|---|---|
| Coating of bottom roller | Failure | 202 | 187 | 47 |
| Maintenance | 202 | 0 | 113 | |
| Replacement | 0 | 187 | 47 | |
| Coating of top roller | Failure | 204 | 192 | 57 |
| Maintenance | 204 | 0 | 104 | |
| Replacement | 0 | 192 | 57 | |
| Double bearing-lubricant pair of bottom roller | Left bearing lubricant | 5 | 20 | 0 |
| Left bearing mechanical fatigue | 204 | 50 | 33 | |
| Right bearing lubricant | 1 | 23 | 0 | |
| Right bearing mechanical fatigue | 173 | 46 | 28 | |
| Maintenance | 383 | 89 | 3291 | |
| Replacement | 0 | 50 | 33 | |
| Double bearing-lubricant pair of top roller | Left bearing lubricant | 2 | 21 | 0 |
| Left bearing mechanical fatigue | 184 | 51 | 33 | |
| Right bearing lubricant | 4 | 17 | 0 | |
| Right bearing mechanical fatigue | 191 | 55 | 34 | |
| Maintenance | 381 | 93 | 3259 | |
| Replacement | 0 | 51 | 33 | |
| Motor | Complete | 87 | 90 | 75 |
| Lubricant | 57 | 54 | 6 | |
| Maintenance (lubrication) | 57 | 54 | 3025 | |
| Maintenance (winding) | 87 | 90 | 75 | |
| Replacement | 0 | 0 | 0 |
| Ideal | Initial Solution | Corrective Solution | Final Solution |
|---|---|---|---|
| 100.0000% | 99.7490% | 99.7748% | 99.8318% |
| Component | Failure Type | Corrective Strategy |
|---|---|---|
| Double bearing-lubricant pair | Left bearing lubricant | replacement |
| Left bearing mechanical fatigue | replacement | |
| Right bearing lubricant | replacement | |
| Right bearing mechanical fatigue | maintenance | |
| Motor | Complete | maintenance (winding) |
| Lubricant | maintenance (lubrication) |
| Economic (EUR/Year) | Energy (kWh/Year) | Other Environmental (kg/Year) | Total (Yearly) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Ideal | Per Component | −206,863 | 3355 | 276,163 | −200,696 | ||||
| Total | −413,725 | 6710 | 552,325 | −401,391 | |||||
| Component | Actual | Extra | Actual | Extra | Actual | Extra | Actual | Extra | |
| Initial solution | Double bearing-lubricant pair | −202,088 | 4774 | 3301 | −54 | 271,717 | −4446 | −196,020 | 4675 |
| Motor | −202,611 | 4251 | 3301 | −54 | 271,717 | −4446 | −196,544 | 4152 | |
| Total | −404,700 | 9026 | 6602 | −108 | 543,434 | −8891 | −392,564 | 8827 | |
| Corrective solution | Double bearing-lubricant pair | −203,472 | 3390 | 3318 | −37 | 273,083 | −3080 | −197,374 | 3322 |
| Motor | −203,643 | 3220 | 3318 | −37 | 273,077 | −3086 | −197,544 | 3151 | |
| Total | −407,115 | 6611 | 6635 | −75 | 546,160 | −6165 | −394,918 | 6473 | |
| Final solution | Double bearing-lubricant pair | −204,185 | 2678 | 3323 | −32 | 273,512 | −2650 | −198,077 | 2619 |
| Motor | −204,001 | 2862 | 3323 | −32 | 273,509 | −2654 | −197,893 | 2803 | |
| Total | −408,186 | 5540 | 6646 | −64 | 547,021 | −5304 | −395,970 | 5421 | |
| Component | Stop Type | Initial Solution | Corrective Solution | Final Solution |
|---|---|---|---|---|
| Double bearing-lubricant pair | Left bearing lubricant | 2 | 23 | 1 |
| Left bearing mechanical fatigue | 298 | 64 | 55 | |
| Right bearing lubricant | 0 | 10 | 0 | |
| Right bearing mechanical fatigue | 286 | 55 | 45 | |
| Maintenance | 586 | 55 | 1184 | |
| Replacement | 0 | 97 | 56 | |
| Motor | Complete | 121 | 119 | 117 |
| Lubricant | 55 | 57 | 31 | |
| Maintenance (lubrication) | 55 | 57 | 61 | |
| Maintenance (winding) | 121 | 119 | 117 | |
| Replacement | 0 | 0 | 0 |
| Ideal | Initial Solution | Corrective Solution | Final Solution |
|---|---|---|---|
| 100.0000% | 99.9369% | 99.9562% | 99.9623% |
| Economic (EUR/Year) | Energy (kWh/year) | Other Environmental (kg/Year) | Total (Yearly) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Model | Actual | Extra | Actual | Extra | Actual | Extra | Actual | Extra | |
| Initial solution | Motor of type 2_2 () | −1.000 M | 34236 | 16323 | −452 | 1.344 M | −37,219 | −970,074 | 33,404 |
| Motor of type 2_3_7 | −1.002 M | 32,635 | 16,346 | −429 | 1.345 M | −35,349 | −971,632 | 31,846 | |
| Motor of type 2_3_4.5 | −994,133 | 40,180 | 16,251 | −524 | 1.338 M | −43,150 | −964,261 | 39,217 | |
| Motor of type 1 () | −404,700 | 9026 | 6602 | −108 | 543,434 | −8891 | −392,564 | 8827 | |
| Motor of type 0 () | −202,585 | 4277 | 3302 | −53 | 271,766 | −4396 | −196,516 | 4179 | |
| Inverter of type 9 () | −206,686 | 177 | 3352 | −2.6 | 275,947 | −216 | −200,524 | 172 | |
| Inverter of type 10 () | −206,742 | 121 | 3353 | −1.8 | 276,017 | −145 | −200,578 | 118 | |
| Total | −10.28 M | 272 K | 167.5 K | −3558 | 13.79 M | −293 K | −9.97 M | 266 K | |
| Corrective solution | Motor of type 2_2 () | −1.002 M | 31,900 | 16,363 | −412 | 1.347 M | −33,862 | −972,335 | 31,143 |
| Motor of type 2_3_7 | −1.005 M | 29,759 | 16,390 | −385 | 1.349 M | −31,637 | −974,425 | 29,053 | |
| Motor of type 2_3_4.5 | −1.004 M | 30,275 | 16,383 | −392 | 1.349 M | −32,196 | −973,923 | 29,556 | |
| Motor of type 1 () | −407,115 | 6611 | 6635 | −75 | 546,160 | −6165 | −394,918 | 6473 | |
| Motor of type 0 () | −202,585 | 4277 | 3302 | −53 | 271,766 | −4396 | −196,516 | 4179 | |
| Inverter of type 9 () | −206,686 | 177 | 3352 | −2.6 | 275,947 | −216 | −200,524 | 172 | |
| Inverter of type 10 () | −206,742 | 121 | 3353 | −1.8 | 276,017 | −145 | −200,578 | 118 | |
| Total | -10.31 M | 243 K | 168.0 K | −3116 | 13.83 M | −256 K | −10.0 M | 237 K | |
| Final solution | Motor of type 2_2 () | −1.011 M | 23,197 | 16,473 | −302 | 1.356 M | −24,840 | −980,836 | 22,642 |
| Motor of type 2_3_7 | −1.012 M | 22,084 | 16,487 | −288 | 1.357 M | −23,672 | −981,922 | 21,556 | |
| Motor of type 2_3_4.5 | −1.010 M | 23,864 | 16,467 | −308 | 1.355 M | −25,341 | −980,180 | 23,298 | |
| Motor of type 1 () | −408,186 | 5540 | 6646 | −64 | 547,021 | −5304 | −395,970 | 5421 | |
| Motor of type 0 () | −202,790 | 4073 | 3304 | −51 | 271,967 | −4195 | −196,717 | 3979 | |
| Inverter of type 9 () | −206,723 | 139 | 3353 | −2.1 | 275,993 | −169 | −200,560 | 136 | |
| Inverter of type 10 () | −206,742 | 121 | 3353 | −1.8 | 276,017 | −145 | −200,578 | 118 | |
| Total | −10.37 M | 182 K | 168.7 K | −2356 | 13.89 M | −194 K | −10.1 M | 178 K | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kolokas, N.; Ioannidis, D.; Tzovaras, D. DSF Core: Integrated Decision Support for Optimal Scheduling of Lifetime Extension Strategies for Industrial Equipment. Sensors 2023, 23, 1332. https://doi.org/10.3390/s23031332
Kolokas N, Ioannidis D, Tzovaras D. DSF Core: Integrated Decision Support for Optimal Scheduling of Lifetime Extension Strategies for Industrial Equipment. Sensors. 2023; 23(3):1332. https://doi.org/10.3390/s23031332
Chicago/Turabian StyleKolokas, Nikolaos, Dimosthenis Ioannidis, and Dimitrios Tzovaras. 2023. "DSF Core: Integrated Decision Support for Optimal Scheduling of Lifetime Extension Strategies for Industrial Equipment" Sensors 23, no. 3: 1332. https://doi.org/10.3390/s23031332
APA StyleKolokas, N., Ioannidis, D., & Tzovaras, D. (2023). DSF Core: Integrated Decision Support for Optimal Scheduling of Lifetime Extension Strategies for Industrial Equipment. Sensors, 23(3), 1332. https://doi.org/10.3390/s23031332






