A Novel Simulated Annealing-Based Hyper-Heuristic Algorithm for Stochastic Parallel Disassembly Line Balancing in Smart Remanufacturing
Abstract
1. Introduction
2. Literature Review
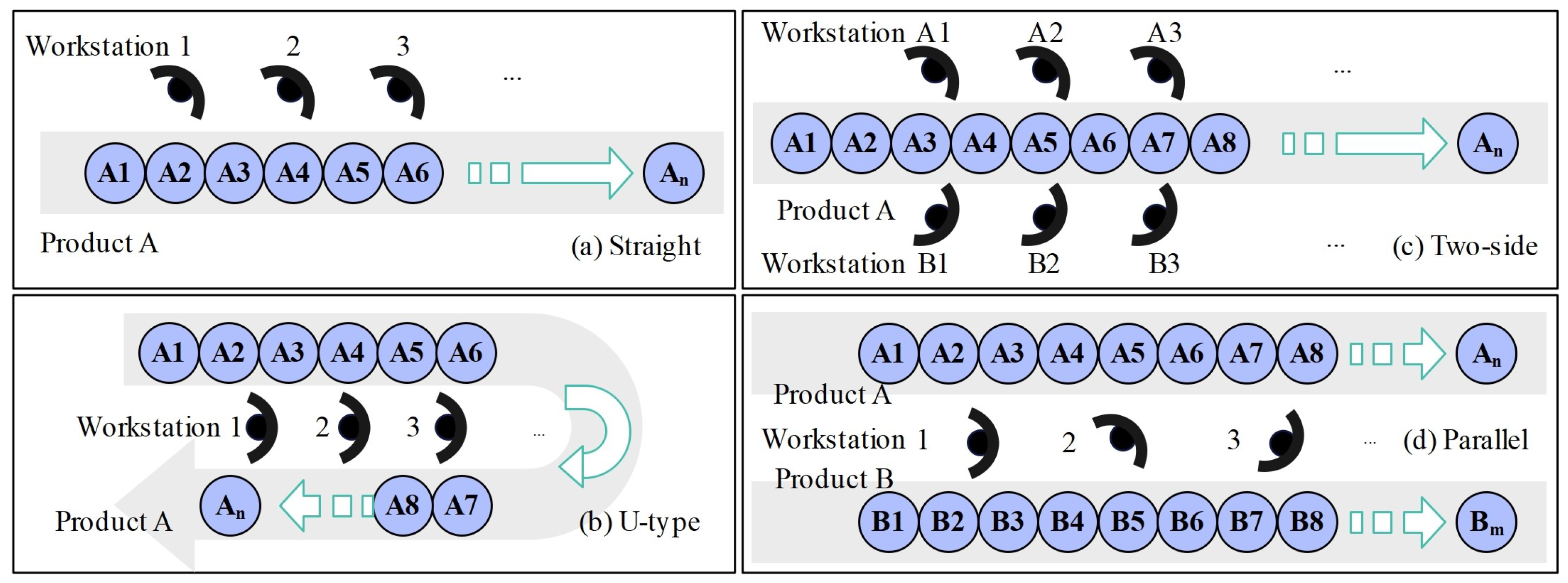
2.1. Layout Type of Disassembly Line
2.2. Optimization Algorithms for DLBP
2.3. The Categories of EoL Product in DLBP
2.4. Research Gaps and Challenges
- The majority of disassembly line layout types are straight with a determined environment [41], which cannot fully model the actual disassembly scenario. Straight disassembly lines are incapable of disassembling multi-type EoL products simultaneously [42]. The mathematical model of the predetermined scenario cannot reflect the actual characteristics of both disassembly lines and EoL products.
- The increasing complexity of the mathematical model and the uncertain conditions of DLBP limit the performance of existing optimisation algorithms. The single-objective optimisation of DLBP is linear. However, the multi-objective optimisation of DLBP-SP becomes a nonlinear and NP problem with higher computational complexity than DLBP. With the development of artificial intelligence methods, novel optimisation algorithms need to be proposed to deal with multi-objective optimization with uncertain conditions and obtain better optimisation performance.
- The condition of EoL products is uncertain, and the disassembly sequence is also divergent. These uncertain characteristics of EoL products will lead to uncertain disassembly process sequence and time of EoL products. Most EoL products in DLBP are based on benchmark test datasets or WEEE equipment. The number of disassembly tasks of these EoL products is relatively small. The precedence constraints are relatively simple as well. Industrial equipment is another category that has great potential value for remanufacturing [37].
3. Stochastic Parallel Disassembly Line Balancing Problem
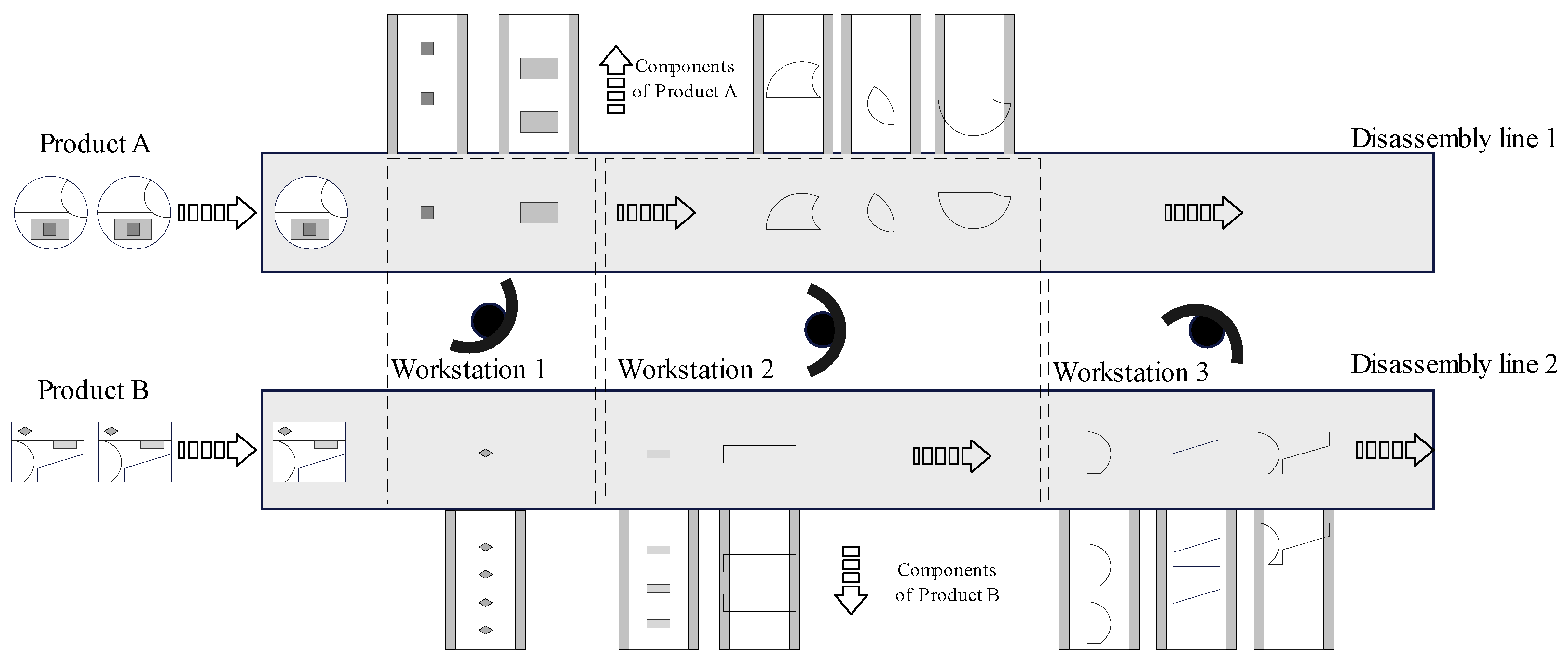
3.1. Problem Description
3.2. Notations and Assumptions of DLBP-SP
- Two disassembly lines are designed to be adjacent and parallel, and the workstations are located sequentially between them.
- The cycle time of each disassembly line is pre-defined and can be different.
- Workstations are operated by skilled workers who can work on single or both parallel disassembly lines and spend no travel time.
- The workstations can only be allocated and process a single disassembly task at a time.
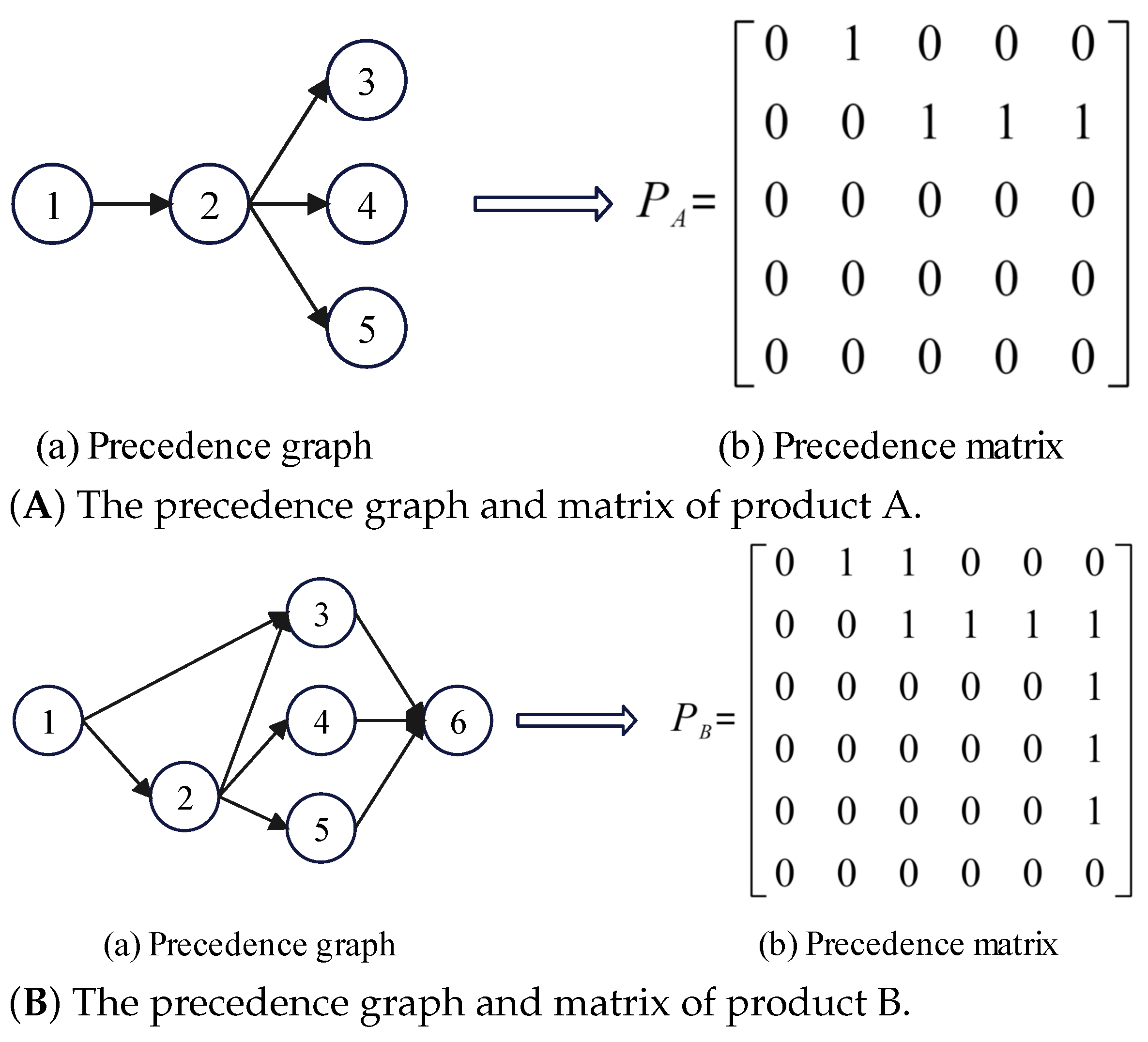
- The precedence constraints and mean disassembly time of each disassembly task are known. Moreover, the precedence constraints of disassembly tasks should be satisfied during the disassembly process.
- The EoL products are completely disassembled into their simplest single components. The revenue from each disassembled component is known.
- Each disassembly task’s actual process time is stochastic, following the standard normal distribution.
- The sum of the actual process time of assigned disassembly tasks to a workstation should not exceed the cycle time. If exceeded, the number of workstations should be added for taking the remaining disassembly tasks into new cycle time.
- Materials and instruments are sufficient and infinite.
3.3. Mathematical Model of DLBP-SP
3.3.1. Cycle Time of Parallel Disassembly Lines
3.3.2. Multi-Objective Optimisation of DLBP-SP
3.3.3. The Lower Bound
3.4. The Explanatory Example
4. The Proposed Hyper-Heuristic Algorithm for DLBP-SP
4.1. Encoding Strategy
4.2. Procedures of the Proposed Hyper-Heuristic Algorithm
4.2.1. Low-Level Heuristic Algorithms
- NSGA2 [51]: adopts fast sorting and elite strategy for improving the convergence and accuracy of the algorithm and proposes the congestion degree for ensuring the variety and distribution of solutions. NSGA2 has good convergence for solving multi-objective optimisation problems. However, the distribution of the optimal solutions from NSGA2 is not uniform.
- SPEA2 [52]: adopts the fine-grained fitness assignment strategy and density information that is suitable for solving multi-objective optimisation problems. SPEA2 has faster convergence and low computational complexity compared to the other two algorithms.
- MOEAD [53]: transforms the multi-objective optimisation problem into multiple sub-scalar problems. Each sub-scalar problem is composed of the uniformly distributed weight vector and optimises each sub-scalar problem through an aggregation function to solve the multi-objective problems. However, the computational complexity of MOEAD is the highest among LLHs.
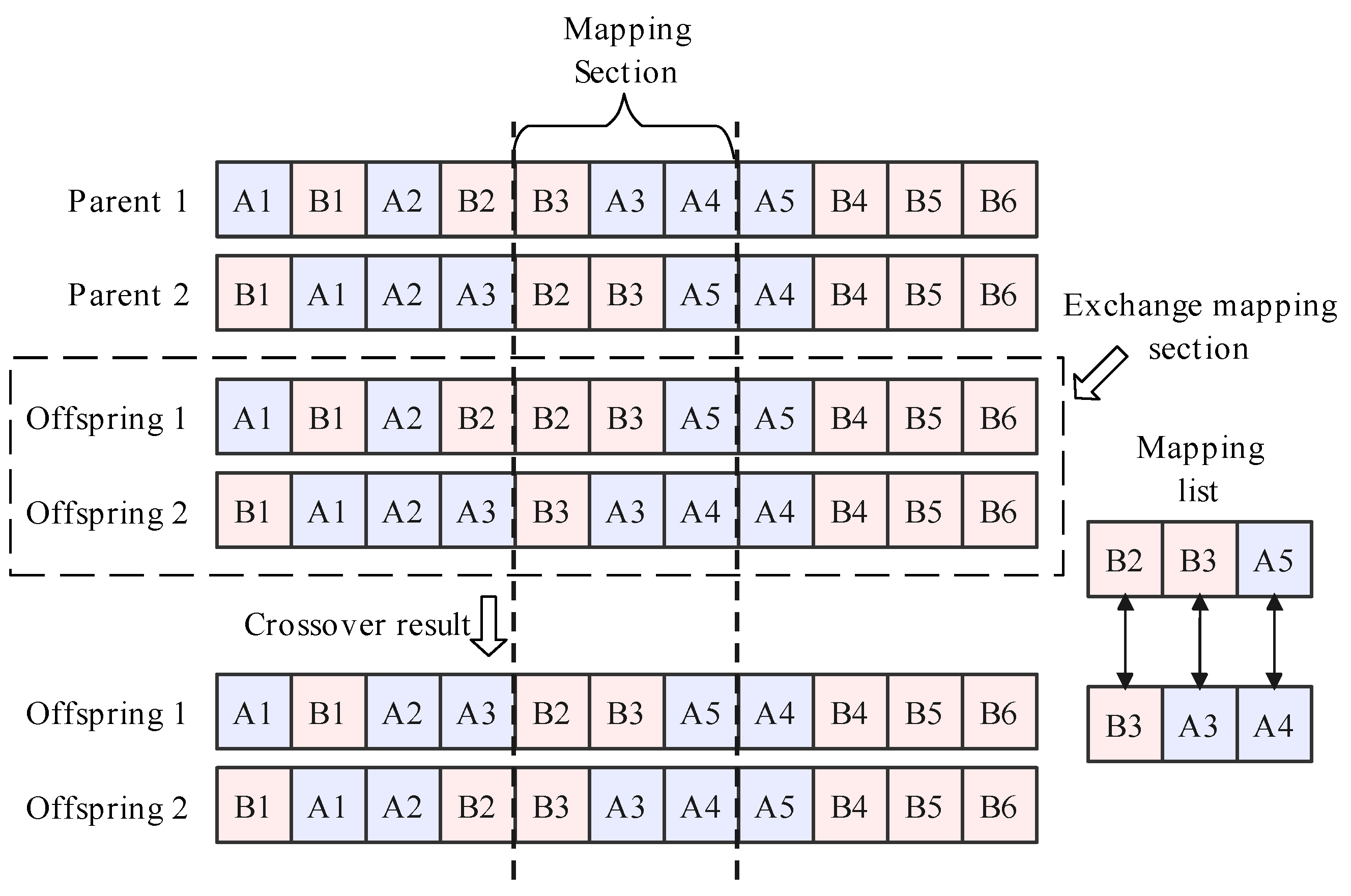
4.2.2. Partially Mapped Crossover
4.2.3. Single-Point Insertion Mutation
4.3. Simulated Annealing Based High-Level Heuristic Algorithm
| Algorithm 1Proposed SA based HH. |
|
4.4. Decoding Process
5. Computational Experiments
5.1. Comparison Experiment
5.1.1. Description of the Collected Dataset
5.1.2. Results and Analysis
5.2. Case Study
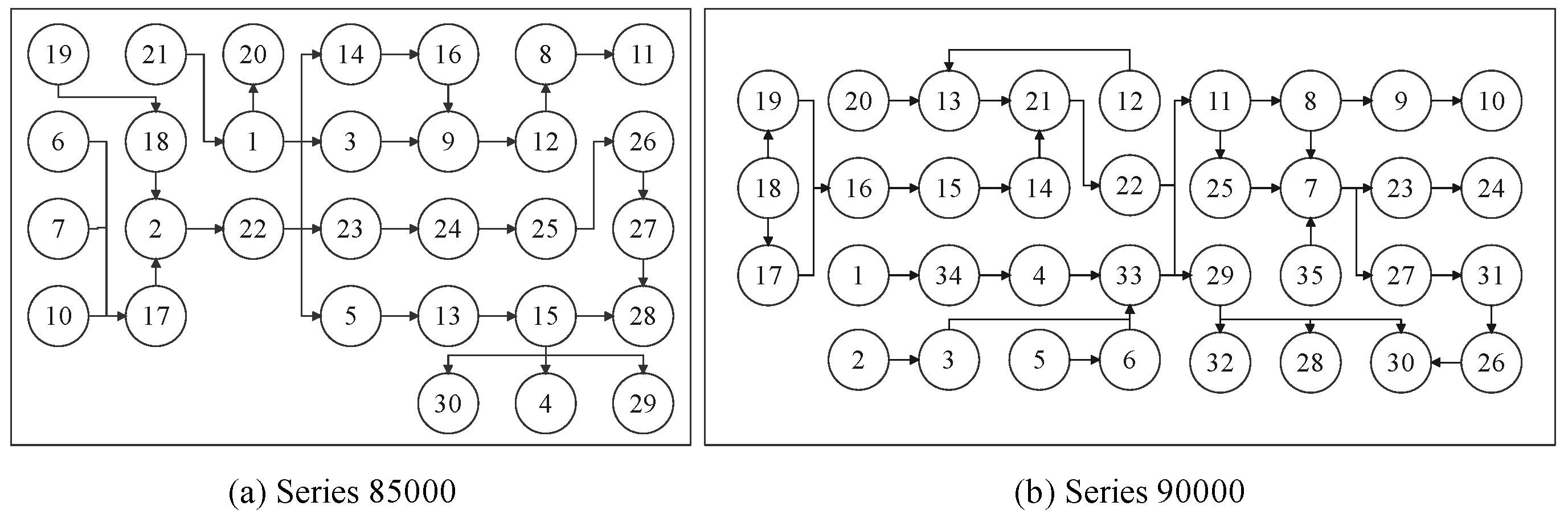
5.2.1. Descriptions of the Gearboxes
5.2.2. Experiments and Analysis
5.2.3. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Bill of Materials of Splitter Gearboxes
| No. | Description (Parts) | Quality (Q) | Mean Process Time (t) | Deviation (D) | Revenue (r) |
|---|---|---|---|---|---|
| 1 | Housing | 1 | 8.2 | 2.1 | 25.3 |
| 2 | Cover | 1 | 10.4 | 3.5 | 43.5 |
| 3 | Bearing 6010 | 1 | 5.6 | 1.2 | 12.6 |
| 4 | Pinion gear | 2 | 3.4 | 1.4 | 6.6 |
| 5 | Sealing ring 45 × 65 × 8 | 2 | 7.6 | 2.2 | 4.8 |
| 6 | Oil plug 3/8 | 2 | 4.8 | 2.0 | 2.2 |
| 7 | Oil drain plug 3/8 | 1 | 5.2 | 1.6 | 1.4 |
| 8 | Key 12*25 | 1 | 2.6 | 0.8 | 0.7 |
| 9 | Snap ring UNI 7435-50 | 2 | 6.4 | 4.2 | 4.7 |
| 10 | Oil dipstick with vent | 1 | 7.3 | 1.4 | 2.6 |
| 11 | Male P.T.O. shaft 13/8 Z6 | 1 | 8.4 | 3.4 | 23.4 |
| 12 | Ring gear | 1 | 18.7 | 5.2 | 4.3 |
| 13 | Bearing 6009 | 4 | 5.4 | 1.3 | 11.2 |
| 14 | Sealing ring 50*65*8 | 1 | 4.7 | 1.4 | 2.5 |
| 15 | Cap DIN 470 D.38 | 5 | 10.5 | 4.5 | 1.5 |
| 16 | Bearing 6210 | 1 | 10.2 | 3.5 | 15.6 |
| 17 | Gasket | 4 | 4.8 | 1.6 | 60.4 |
| 18 | Washer Grower d.8 | 12 | 15.6 | 1.2 | 67.9 |
| 19 | Nut M8 | 12 | 25.2 | 2.4 | 7.2 |
| 20 | Peg UNI 8751 6*24 | 8 | 10.4 | 1.6 | 0.8 |
| 21 | Socket cap screw M8*45 | 12 | 27.6 | 3.6 | 42.2 |
| 22 | Gasket | 1 | 8.5 | 1.4 | 14.3 |
| 23 | Snap ring UNI 7435-48 | 1 | 3.4 | 1.2 | 2.3 |
| 24 | Ring | 1 | 4.7 | 2.1 | 3.7 |
| 25 | Spring | 1 | 2.6 | 1.4 | 2.3 |
| 26 | Spring ring | 1 | 8.6 | 2.4 | 4.2 |
| 27 | Ball | 3 | 4.2 | 0.9 | 12.7 |
| 28 | Female P.T.O. shaft—13/8 Z6 | 1 | 4.6 | 1.6 | 16.6 |
| 29 | Female P.T.O. shaft short 13/8 | 1 | 5.2 | 1.4 | 20.7 |
| 30 | Female P.T.O. shaft long 13/8 | 1 | 3.4 | 0.8 | 23.4 |
| No. | Description (Parts) | Quality (Q) | Mean Process Time (t) | Deviation (D) | Revenue (r) |
|---|---|---|---|---|---|
| 1 | Socket cap screw M6×20 | 4 | 9.2 | 1.2 | 14.2 |
| 2 | Oil level plug | 1 | 2.4 | 1.1 | 1.4 |
| 3 | Gasket | 1 | 1.2 | 0.4 | 0.6 |
| 4 | Gasket | 1 | 6.5 | 2.4 | 1.4 |
| 5 | Socket cap screw | 10 | 23.1 | 6.4 | 31.2 |
| 6 | Peg ø 6 | 2 | 2.6 | 0.6 | 0.2 |
| 7 | Snap ring ø 58 | 3 | 9.6 | 3.2 | 5.4 |
| 8 | Bearing type 6010 | 5 | 28 | 6 | 63 |
| 9 | Cap DIN 470 | 2 | 4.2 | 1.8 | 0.6 |
| 10 | Pinion Gear | 2 | 3.4 | 1.4 | 6.6 |
| 11 | Sealing ring ø | 3 | 11.4 | 2.1 | 7.2 |
| 12 | Oil dipstick with vent | 1 | 7.3 | 1.4 | 2.6 |
| 13 | Gasket | 3 | 3.6 | 1.2 | 45.3 |
| 14 | O-Ring | 2 | 8.2 | 2.2 | 0.6 |
| 15 | Corteco Ring | 2 | 10.4 | 3.8 | 6.4 |
| 16 | Gasket | 2 | 16.4 | 6.4 | 23.6 |
| 17 | Flange SAE B | 1 | 12.7 | 4.2 | 16.6 |
| 18 | Socket cap screw | 6 | 13.8 | 1.8 | 21.1 |
| 19 | Flange SAE A | 1 | 14.2 | 4.1 | 23.5 |
| 20 | Oil drain plug 3/8 | 1 | 5.2 | 1.6 | 1.4 |
| 21 | Housing | 1 | 8.4 | 2.2 | 25.4 |
| 22 | Gasket | 1 | 8.5 | 1.4 | 14.3 |
| 23 | Ring gear | 1 | 18.7 | 5.2 | 4.3 |
| 24 | Male P.T.O. shaft 13/8 | 1 | 4.6 | 1.6 | 16.4 |
| 25 | Bearing type 6210 | 1 | 10.2 | 3.5 | 15.6 |
| 26 | Ball | 3 | 4.2 | 0.9 | 12.7 |
| 27 | Spring | 1 | 2.6 | 1.4 | 2.3 |
| 28 | Female P.T.O. shaft 13/8 long | 1 | 3.4 | 0.8 | 23.4 |
| 29 | Cap DIN 470 | 3 | 6.3 | 2.7 | 0.9 |
| 30 | Female P.T.O. shaft 1-3/8 | 1 | 7.3 | 2.4 | 18.4 |
| 31 | Spring ring | 1 | 8.6 | 2.4 | 4.1 |
| 32 | Female P.T.O. shaft 13/8 short | 1 | 5.2 | 1.4 | 20.7 |
| 33 | Cover | 1 | 10.8 | 2.4 | 24.8 |
| 34 | Cap | 1 | 8.6 | 2.2 | 8.2 |
| 35 | Ring | 1 | 4.8 | 1.8 | 3.8 |
References
- Zhang, X.G.; Zhang, M.Y.; Zhang, H.; Jiang, Z.G.; Liu, C.H.; Cai, W. A review on energy, environment and economic assessment in remanufacturing based on life cycle assessment method. J. Clean. Prod. 2020, 255, 120160. [Google Scholar] [CrossRef]
- Middendorf, P.; Blümel, R.; Hinz, L.; Raatz, A.; Kästner, M.; Reithmeier, E. Pose Estimation and Damage Characterization of Turbine Blades during Inspection Cycles and Component-Protective Disassembly Processes. Sensors 2022, 22, 5191. [Google Scholar] [CrossRef] [PubMed]
- Mete, S.; Çil, Z.A.; Özceylan, E.; Ağpak, K. Resource constrained disassembly line balancing problem. IFAC-PapersOnLine 2016, 49, 921–925. [Google Scholar] [CrossRef]
- Rizova, M.I.; Wong, T.C.; Ijomah, W. A systematic review of decision-making in remanufacturing. Comput. Ind. Eng. 2020, 147, 106681. [Google Scholar] [CrossRef]
- Priyono, A.; Ijomah, W.; Bititci, U.S. Disassembly for remanufacturing: A systematic literature review, new model development and future research needs. J. Ind. Eng. Manag. (JIEM) 2016, 9, 899–932. [Google Scholar] [CrossRef]
- Gungor, A.; Gupta, S.M. A solution approach to the disassembly line balancing problem in the presence of task failures. Int. J. Prod. Res. 2001, 39, 1427–1467. [Google Scholar] [CrossRef]
- Wang, K.; Li, X.; Gao, L. Modeling and optimization of multi-objective partial disassembly line balancing problem considering hazard and profit. J. Clean. Prod. 2019, 211, 115–133. [Google Scholar] [CrossRef]
- Çil, Z.A.; Mete, S.; Serin, F. Robotic Disassembly Line Balancing Problem: A Mathematical Model and Ant Colony Optimization Approach. Appl. Math. Model. 2020, 86, 335–348. [Google Scholar] [CrossRef]
- Agrawal, S.; Tiwari, M. A collaborative ant colony algorithm to stochastic mixed-model U-shaped disassembly line balancing and sequencing problem. Int. J. Prod. Res. 2008, 46, 1405–1429. [Google Scholar] [CrossRef]
- Wang, K.; Gao, L.; Li, X. A multi-objective algorithm for U-shaped disassembly line balancing with partial destructive mode. Neural Comput. Appl. 2020, 32, 12715–12736. [Google Scholar] [CrossRef]
- Wang, K.; Li, X.; Gao, L. A multi-objective discrete flower pollination algorithm for stochastic two-sided partial disassembly line balancing problem. Comput. Ind. Eng. 2019, 130, 634–649. [Google Scholar] [CrossRef]
- Kucukkoc, I. Balancing of two-sided disassembly lines: Problem definition, MILP model and genetic algorithm approach. Comput. Oper. Res. 2020, 124, 105064. [Google Scholar] [CrossRef]
- Roshani, A.; Fattahi, P.; Roshani, A.; Salehi, M.; Roshani, A. Cost-oriented two-sided assembly line balancing problem: A simulated annealing approach. Int. J. Comput. Integr. Manuf. 2012, 25, 689–715. [Google Scholar] [CrossRef]
- Aydemir-Karadag, A.; Turkbey, O. Multi-objective optimization of stochastic disassembly line balancing with station paralleling. Comput. Ind. Eng. 2013, 65, 413–425. [Google Scholar] [CrossRef]
- Wang, K.; Li, X.; Gao, L.; Li, P.; Gupta, S.M. A genetic simulated annealing algorithm for parallel partial disassembly line balancing problem. Appl. Soft Comput. 2021, 107, 107404. [Google Scholar] [CrossRef]
- McGovern, S.M.; Gupta, S.M. Ant colony optimization for disassembly sequencing with multiple objectives. Int. J. Adv. Manuf. Technol. 2006, 30, 481–496. [Google Scholar] [CrossRef]
- Altekin, F.T.; Kandiller, L.; Ozdemirel, N.E. Disassembly line balancing with limited supply and subassembly availability. In Proceedings of the Environmentally Conscious Manufacturing III International Society for Optics and Photonics, Providence, RI, USA, 29–30 October 2003; Volume 5262, pp. 59–70. [Google Scholar]
- Altekin, F.T.; Kandiller, L.; Ozdemirel, N.E. Profit-oriented disassembly-line balancing. Int. J. Prod. Res. 2008, 46, 2675–2693. [Google Scholar] [CrossRef]
- Igarashi, K.; Yamada, T.; Gupta, S.M.; Inoue, M.; Itsubo, N. Disassembly system modeling and design with parts selection for cost, recycling and CO2 saving rates using multi criteria optimization. J. Manuf. Syst. 2016, 38, 151–164. [Google Scholar] [CrossRef]
- Özceylan, E.; Paksoy, T. Interactive fuzzy programming approaches to the strategic and tactical planning of a closed-loop supply chain under uncertainty. Int. J. Prod. Res. 2014, 52, 2363–2387. [Google Scholar] [CrossRef]
- McGovern, S.M.; Gupta, S.M. Greedy algorithm for disassembly line scheduling. In Proceedings of the SMC’03 Conference Proceedings: 2003 IEEE International Conference on Systems, Man and Cybernetics. Conference Theme-System Security and Assurance (Cat. No. 03CH37483), Washington, DC, USA, 5–8 October 2003; Volume 2, pp. 1737–1744. [Google Scholar]
- McGovern, S.M.; Gupta, S.M. Combinatorial optimization methods for disassembly line balancing. In Proceedings of the Environmentally Conscious Manufacturing IV International Society for Optics and Photonics, Philadelphia, PA, USA, 25–28 October 2004; Volume 5583, pp. 53–66. [Google Scholar]
- Kalayci, C.B.; Gupta, S.M. Simulated annealing algorithm for solving sequence-dependent disassembly line balancing problem. IFAC Proc. Vol. 2013, 46, 93–98. [Google Scholar] [CrossRef]
- Kalayci, C.B.; Gupta, S.M. Ant colony optimization for sequence-dependent disassembly line balancing problem. J. Manuf. Technol. Manag. 2013, 24, 413–427. [Google Scholar] [CrossRef]
- Kalayci, C.B.; Polat, O.; Gupta, S.M. A hybrid genetic algorithm for sequence-dependent disassembly line balancing problem. Ann. Oper. Res. 2016, 242, 321–354. [Google Scholar] [CrossRef]
- Saif, U.; Guan, Z.; Zhang, L.; Mirza, J.; Lei, Y. Hybrid Pareto artificial bee colony algorithm for assembly line balancing with task time variations. Int. J. Comput. Integr. Manuf. 2017, 30, 255–270. [Google Scholar] [CrossRef]
- Kalayci, C.B.; Gupta, S.M. Artificial bee colony algorithm for solving sequence-dependent disassembly line balancing problem. Expert Syst. Appl. 2013, 40, 7231–7241. [Google Scholar] [CrossRef]
- Kalayci, C.B.; Gupta, S.M. A tabu search algorithm for balancing a sequence-dependent disassembly line. Prod. Plan. Control 2014, 25, 149–160. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, K.; Zhu, L.; Wang, Y. A Pareto improved artificial fish swarm algorithm for solving a multi-objective fuzzy disassembly line balancing problem. Expert Syst. Appl. 2017, 86, 165–176. [Google Scholar] [CrossRef]
- Zhu, L.; Zhang, Z.; Wang, Y. A Pareto firefly algorithm for multi-objective disassembly line balancing problems with hazard evaluation. Int. J. Prod. Res. 2018, 56, 7354–7374. [Google Scholar] [CrossRef]
- Paprocka, I.; Skołud, B. A Predictive Approach for Disassembly Line Balancing Problems. Sensors 2022, 22, 3920. [Google Scholar] [CrossRef]
- Mcgovern, S.M.; Gupta, S.M. Combinatorial optimization analysis of the unary NP-complete disassembly line balancing problem. Int. J. Prod. Res. 2007, 45, 4485–4511. [Google Scholar] [CrossRef]
- Özceylan, E.; Kalayci, C.B.; Güngör, A.; Gupta, S.M. Disassembly line balancing problem: A review of the state of the art and future directions. Int. J. Prod. Res. 2019, 57, 4805–4827. [Google Scholar] [CrossRef]
- Avikal, S.; Jain, R.; Yadav, H.; Mishra, P. A New Heuristic for Disassembly Line Balancing Problems with AND/OR Precedence Relations. In Proceedings of the Second International Conference on Soft Computing for Problem Solving (SocProS 2012), 28–30 December 2012; Springer: New Delhi, India, 2014; pp. 519–525. [Google Scholar]
- Xiao, S.; Wang, Y.; Yu, H.; Nie, S. An entropy-based adaptive hybrid particle swarm optimization for disassembly line balancing problems. Entropy 2017, 19, 596. [Google Scholar] [CrossRef]
- Kalayci, C.B.; Hancilar, A.; Gungor, A.; Gupta, S.M. Multi-objective fuzzy disassembly line balancing using a hybrid discrete artificial bee colony algorithm. J. Manuf. Syst. 2015, 37, 672–682. [Google Scholar] [CrossRef]
- Ngu, H.J.; Lee, M.D.; Bin Osman, M.S. Review on current challenges and future opportunities in Malaysia sustainable manufacturing: Remanufacturing industries. J. Clean. Prod. 2020, 273, 123071. [Google Scholar] [CrossRef]
- Pistolesi, F.; Lazzerini, B.; Dalle Mura, M.; Dini, G. EMOGA: A hybrid genetic algorithm with extremal optimization core for multiobjective disassembly line balancing. IEEE Trans. Ind. Inform. 2017, 14, 1089–1098. [Google Scholar] [CrossRef]
- Yang, Y.; Yuan, G.; Zhuang, Q.; Tian, G. Multi-objective low-carbon disassembly line balancing for agricultural machinery using MDFOA and fuzzy AHP. J. Clean. Prod. 2019, 233, 1465–1474. [Google Scholar] [CrossRef]
- Cao, J.; Xia, X.; Wang, L.; Zhang, Z.; Liu, X. A Novel Multi-Efficiency Optimization Method for Disassembly Line Balancing Problem. Sustainability 2019, 11, 6969. [Google Scholar] [CrossRef]
- Laili, Y.; Li, Y.; Fang, Y.; Pham, D.T.; Zhang, L. Model review and algorithm comparison on multi-objective disassembly line balancing. J. Manuf. Syst. 2020, 56, 484–500. [Google Scholar] [CrossRef]
- Sitcharangsie, S.; Ijomah, W.; Wong, T.C. Decision makings in key remanufacturing activities to optimise remanufacturing outcomes: A review. J. Clean. Prod. 2019, 232, 1465–1481. [Google Scholar] [CrossRef]
- Vanegas Pena, P.; Peeters, J.; Cattrysse, D.; Duflou, J.; Tecchio, P.; Mathieux, F.; Ardente, F. Study for a Method to Assess the Ease of Disassembly of Electrical and Electronic Equipment. Method Development and Application to a Flat Panel Display Case Study; European Union: Brussels, Belgium, 2016. [Google Scholar]
- Nadarajah, S.; Kotz, S. The cycle time distribution. Int. J. Prod. Res. 2008, 46, 3133–3141. [Google Scholar] [CrossRef]
- Özcan, U. Balancing stochastic parallel assembly lines. Comput. Oper. Res. 2018, 99, 109–122. [Google Scholar] [CrossRef]
- Benitez-Hidalgo, A.; Nebro, A.J.; Garcia-Nieto, J.; Oregi, I.; Del Ser, J. jMetalPy: A Python framework for multi-objective optimization with metaheuristics. Swarm Evol. Comput. 2019, 51, 100598. [Google Scholar] [CrossRef]
- Gökçen, H.; Ağpak, K.; Benzer, R. Balancing of parallel assembly lines. Int. J. Prod. Econ. 2006, 103, 600–609. [Google Scholar] [CrossRef]
- Bentaha, M.L.; Battaïa, O.; Dolgui, A. Disassembly line balancing problem with fixed number of workstations under uncertainty. IFAC Proc. Vol. 2014, 47, 3522–3526. [Google Scholar] [CrossRef]
- Burke, E.K.; Gendreau, M.; Hyde, M.; Kendall, G.; Ochoa, G.; Özcan, E.; Qu, R. Hyper-heuristics: A survey of the state of the art. J. Oper. Res. Soc. 2013, 64, 1695–1724. [Google Scholar] [CrossRef]
- Burke, E.K.; Hyde, M.R.; Kendall, G.; Ochoa, G.; Özcan, E.; Woodward, J.R. A classification of hyper-heuristic approaches: Revisited. In Handbook of Metaheuristics; Springer: Berlin/Heidelberg, Germany, 2019; pp. 453–477. [Google Scholar]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Zitzler, E.; Laumanns, M.; Thiele, L. SPEA2: Improving the strength Pareto evolutionary algorithm. TIK-Report 2001, 103. [Google Scholar] [CrossRef]
- Zhang, Q.; Li, H. MOEA/D: A multiobjective evolutionary algorithm based on decomposition. IEEE Trans. Evol. Comput. 2007, 11, 712–731. [Google Scholar] [CrossRef]
- Drake, J.H.; Kheiri, A.; Özcan, E.; Burke, E.K. Recent advances in selection hyper-heuristics. Eur. J. Oper. Res. 2020, 285, 405–428. [Google Scholar] [CrossRef]
- Wang, L.; Guo, Y.Y.; Zhang, Z.L.; Xia, X.H.; Cao, J.H. Generalized growth decision based on cascaded failure information: Maximizing the value of retired mechanical products. J. Clean. Prod. 2020, 269, 122176. [Google Scholar] [CrossRef]
- Zitzler, E.; Thiele, L.; Laumanns, M.; Fonseca, C.M.; Da Fonseca, V.G. Performance assessment of multiobjective optimizers: An analysis and review. IEEE Trans. Evol. Comput. 2003, 7, 117–132. [Google Scholar] [CrossRef]
- Mincă, E.; Filipescu, A.; Cernega, D.; Șolea, R.; Filipescu, A.; Ionescu, D.; Simion, G. Digital Twin for a Multifunctional Technology of Flexible Assembly on a Mechatronics Line with Integrated Robotic Systems and Mobile Visual Sensor—Challenges towards Industry 5.0. Sensors 2022, 22, 8153. [Google Scholar] [CrossRef] [PubMed]
- Indri, M.; Lachello, L.; Lazzero, I.; Sibona, F.; Trapani, S. Smart sensors applications for a new paradigm of a production line. Sensors 2019, 19, 650. [Google Scholar] [CrossRef] [PubMed]
- Garcia, P.P.; Santos, T.G.; Machado, M.A.; Mendes, N. Deep Learning Framework for Controlling Work Sequence in Collaborative Human—Robot Assembly Processes. Sensors 2023, 23, 553. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Wu, F.; Lyu, C.; Li, S.; Ye, J.; Qu, X. Deep dispatching: A deep reinforcement learning approach for vehicle dispatching on online ride-hailing platform. Transp. Res. Part E Logist. Transp. Rev. 2022, 161, 102694. [Google Scholar] [CrossRef]




| Notations | Definition and Description |
|---|---|
| m | Number of disassembly line, m = 1, 2 |
| Number of disassembly tasks on disassembly line , where I is the number of components of EoL product | |
| K | Number of workstations, , where K is the maximum number of workstations |
| j | The position of the disassembly process, , where J is the maximum number . |
| Revenue from disassembly task i | |
| Fix operation cost per unit time for workstations | |
| Operating cost of workstations for parallel disassembly lines | |
| Operating cost of workstations for single disassembly line | |
| Cycle time of disassembly line m | |
| Cycle time of parallel disassembly lines | |
| Operation time of workstation k | |
| Coefficient value of and | |
| Stochastic disassembly time of task i on disassembly line m | |
| Average disassembly time of task i on disassembly line m | |
| Variance of task i on disassembly line m | |
| Confidence level | |
| Standard normal distribution function | |
| Theoretical minimum number of workstations | |
| I | Workload smoothness index |
| P | Overall profit from complete disassembly process |
| The set of predecessors of task i on disassembly line m | |
| The set of predecessors of task i on disassembly line m | |
| = | |
| = | |
| = | |
| = | |
| = |
| Cycle Time of Disassembly Line 1 () | 15 | ||||
|---|---|---|---|---|---|
| Task ID () | 1 | 2 | 3 | 4 | 5 |
| Average disassembly time () | 4 | 6 | 3 | 4 | 2 |
| Variance () | 0.50 | 1.20 | 0.70 | 0.60 | 0.20 |
| Precedence constraints | - | 1 | 1, 2 | 1, 2 | 1, 2 |
| Cycle Time of Disassembly Line 2 () | 20 | |||||
|---|---|---|---|---|---|---|
| Task ID () | 1 | 2 | 3 | 4 | 5 | 6 |
| Average disassembly time () | 3 | 4 | 2 | 6 | 7 | 4 |
| Variance () | 0.40 | 0.30 | 0.10 | 1.20 | 1.50 | 0.30 |
| Precedence constraints | - | 1 | 1, 2 | 1, 2, 3 | 1, 2 | 1, 2, 3, 4 |
| = 60 | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| = 4, = 3 | |||||||||||
| TaskID | A1 | A2 | A3 | A4 | A5 | B1 | B2 | B3 | B4 | B5 | B6 |
| 16 | 24 | 12 | 16 | 8 | 9 | 12 | 6 | 18 | 21 | 12 | |
| 8.00 | 19.20 | 11.20 | 9.60 | 3.20 | 3.60 | 2.70 | 0.90 | 10.80 | 13.50 | 2.70 | |
| Number of Workstation | 1 | 2 | 3 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Sequential task ID | A1 | B1 | A2 | B2 | B3 | A3 | A4 | A5 | B4 | B5 | B6 |
| 16 | 9 | 24 | 12 | 6 | 12 | 16 | 8 | 18 | 21 | 12 | |
| i | 8.00 | 3.60 | 19.20 | 2.70 | 0.90 | 11.2 | 9.60 | 3.20 | 10.80 | 13.50 | 2.70 |
| Sum of | 49 | 54 | 51 | ||||||||
| Operating rate (%) | 76.67 | 90.00 | 85.00 | ||||||||
| Problem | Low Task Variances | High Task Variance | ||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| LB | TS | GSA | HH | LB | TS | GSA | HH | LB | TS | GSA | HH | LB | TS | GSA | HH | |||||
| Jaeschke–Jaeschke | 9 | 9 | 10 | 14 | 7 | 8 | 8 | 8 | 8 | 10 | 9 | 9 | 7 | 11 | 10 | 8 | 8 | 13 | 13 | 10 |
| 10 | 10 | 8 | 10 | 10 | 10 | 9 | 12 | 12 | 12 | 8 | 14 | 14 | 10 | 10 | 15 | 15 | 12 | |||
| 18 | 10 | 7 | 7 | 7 | 7 | 7 | 8 | 8 | 8 | 7 | 9 | 9 | 8 | 8 | 11 | 11 | 9 | |||
| Jackson–Jaeschke | 11 | 9 | 10 | 14 | 8 | 9 | 9 | 9 | 8 | 11 | 10 | 10 | 8 | 11 | 11 | 10 | 8 | 13 | 13 | 11 |
| 10 | 10 | 9 | 12 | 12 | 12 | 9 | 14 | 14 | 14 | 9 | 14 | 14 | 12 | 10 | 15 | 15 | 14 | |||
| 21 | 18 | 5 | 5 | 5 | 5 | 5 | 6 | 6 | 6 | 6 | 6 | 6 | 6 | 6 | 7 | 7 | 6 | |||
| Jackson–Jackson | 11 | 11 | 10 | 13 | 9 | 11 | 11 | 11 | 9 | 12 | 12 | 12 | 9 | 11 | 11 | 11 | 9 | 14 | 13 | 12 |
| 14 | 14 | 8 | 9 | 9 | 8 | 8 | 9 | 9 | 8 | 8 | 9 | 9 | 8 | 8 | 10 | 10 | 9 | |||
| 21 | 14 | 7 | 7 | 7 | 7 | 7 | 7 | 7 | 7 | 7 | 7 | 7 | 7 | 7 | 8 | 8 | 7 | |||
| Roszieg–Jackson | 25 | 11 | 18 | 21 | 11 | 11 | 11 | 11 | 11 | 12 | 12 | 12 | 11 | 13 | 12 | 11 | 11 | 14 | 13 | 12 |
| 21 | 21 | 10 | 10 | 10 | 10 | 10 | 11 | 10 | 10 | 10 | 11 | 10 | 10 | 10 | 12 | 12 | 11 | |||
| 25 | 14 | 10 | 10 | 10 | 10 | 10 | 11 | 11 | 11 | 11 | 11 | 11 | 11 | 10 | 12 | 12 | 11 | |||
| Roszieg–Roszieg | 25 | 25 | 18 | 25 | 14 | 14 | 14 | 15 | 14 | 15 | 15 | 15 | 14 | 16 | 16 | 15 | 14 | 17 | 17 | 16 |
| 21 | 21 | 13 | 15 | 14 | 15 | 14 | 16 | 15 | 15 | 14 | 16 | 16 | 15 | 14 | 18 | 17 | 16 | |||
| 32 | 25 | 11 | 11 | 11 | 11 | 11 | 11 | 11 | 11 | 11 | 11 | 11 | 11 | 11 | 13 | 12 | 11 | |||
| Sawyer–Roszieg | 30 | 25 | 41 | 32 | 13 | 15 | 14 | 14 | 13 | 15 | 15 | 15 | 14 | 16 | 15 | 15 | 14 | 17 | 17 | 15 |
| 47 | 25 | 14 | 14 | 14 | 14 | 14 | 15 | 15 | 15 | 14 | 16 | 15 | 14 | 14 | 18 | 17 | 15 | |||
| 54 | 21 | 13 | 14 | 14 | 14 | 14 | 15 | 15 | 15 | 14 | 16 | 15 | 14 | 14 | 18 | 17 | 15 | |||
| Sawyer–Sawyer | 30 | 30 | 36 | 41 | 18 | 21 | 20 | 21 | 18 | 22 | 22 | 22 | 19 | 24 | 22 | 21 | 19 | 27 | 26 | 23 |
| 36 | 36 | 19 | 22 | 22 | 23 | 19 | 24 | 24 | 25 | 20 | 25 | 24 | 23 | 20 | 28 | 28 | 25 | |||
| 75 | 54 | 11 | 12 | 12 | 12 | 11 | 13 | 13 | 13 | 12 | 13 | 13 | 12 | 12 | 14 | 14 | 13 | |||
| Gunther–Sawyer | 35 | 30 | 61 | 75 | 14 | 15 | 15 | 15 | 14 | 16 | 16 | 16 | 14 | 17 | 16 | 15 | 14 | 19 | 18 | 16 |
| 69 | 54 | 14 | 16 | 15 | 16 | 14 | 17 | 17 | 17 | 15 | 18 | 17 | 16 | 15 | 20 | 19 | 17 | |||
| 81 | 36 | 16 | 19 | 18 | 19 | 16 | 20 | 19 | 20 | 17 | 21 | 20 | 19 | 17 | 24 | 23 | 20 | |||
| Gunther–Gunther | 35 | 35 | 61 | 69 | 17 | 19 | 19 | 19 | 17 | 20 | 20 | 20 | 17 | 22 | 21 | 19 | 17 | 25 | 24 | 21 |
| 69 | 69 | 16 | 18 | 17 | 18 | 16 | 19 | 19 | 19 | 16 | 20 | 20 | 18 | 16 | 24 | 22 | 19 | |||
| 81 | 61 | 15 | 17 | 17 | 17 | 16 | 18 | 18 | 18 | 16 | 20 | 19 | 18 | 16 | 23 | 22 | 19 | |||
| Kilbridge–Gunther | 45 | 35 | 79 | 81 | 14 | 15 | 15 | 15 | 15 | 16 | 16 | 16 | 15 | 17 | 17 | 15 | 15 | 19 | 19 | 16 |
| 69 | 69 | 17 | 18 | 18 | 18 | 17 | 19 | 19 | 19 | 17 | 20 | 19 | 18 | 17 | 22 | 22 | 20 | |||
| 184 | 61 | 12 | 13 | 13 | 13 | 12 | 14 | 14 | 14 | 13 | 15 | 15 | 13 | 13 | 17 | 16 | 14 | |||
| Kilbridge–Kilbridge | 45 | 45 | 79 | 184 | 11 | 12 | 12 | 12 | 12 | 12 | 12 | 12 | 12 | 12 | 12 | 12 | 12 | 13 | 13 | 12 |
| 92 | 92 | 13 | 14 | 14 | 14 | 14 | 15 | 15 | 15 | 14 | 15 | 15 | 14 | 14 | 16 | 16 | 15 | |||
| 138 | 110 | 10 | 10 | 10 | 10 | 11 | 11 | 11 | 11 | 11 | 11 | 11 | 11 | 11 | 12 | 12 | 11 | |||
| Hahn-Kilbridge | 53 | 45 | 2338 | 92 | 13 | 14 | 14 | 14 | 14 | 15 | 15 | 15 | 14 | 15 | 15 | 14 | 14 | 16 | 16 | 15 |
| 2004 | 69 | 16 | 18 | 18 | 18 | 17 | 19 | 19 | 19 | 17 | 19 | 19 | 18 | 17 | 21 | 21 | 19 | |||
| 2338 | 184 | 10 | 10 | 10 | 11 | 11 | 11 | 11 | 11 | 11 | 11 | 11 | 11 | 11 | 12 | 12 | 11 | |||
| Hahn-Hahn | 53 | 53 | 2004 | 4676 | 11 | 12 | 12 | 12 | 11 | 13 | 13 | 13 | 12 | 13 | 13 | 12 | 12 | 14 | 14 | 13 |
| 2806 | 2806 | 11 | 12 | 12 | 12 | 11 | 13 | 12 | 12 | 12 | 13 | 12 | 12 | 12 | 14 | 15 | 13 | |||
| 4676 | 3507 | 8 | 8 | 8 | 8 | 8 | 9 | 8 | 8 | 9 | 9 | 9 | 9 | 9 | 9 | 9 | 9 | |||
| Tonge-Hahn | 70 | 53 | 293 | 2004 | 20 | 22 | 22 | 23 | 16 | 24 | 24 | 24 | 21 | 25 | 25 | 23 | 21 | 28 | 27 | 24 |
| 410 | 2806 | 14 | 13 | 13 | 16 | 14 | 14 | 14 | 17 | 15 | 14 | 14 | 16 | 15 | 16 | 16 | 17 | |||
| 468 | 3507 | 12 | 13 | 13 | 13 | 12 | 14 | 14 | 14 | 13 | 14 | 14 | 13 | 13 | 16 | 16 | 14 | |||
| Tonge-Tonge | 70 | 70 | 364 | 410 | 19 | 21 | 21 | 21 | 19 | 22 | 22 | 22 | 19 | 23 | 23 | 21 | 19 | 26 | 26 | 22 |
| 468 | 468 | 16 | 17 | 17 | 17 | 16 | 18 | 18 | 18 | 16 | 19 | 19 | 17 | 16 | 21 | 21 | 18 | |||
| 527 | 293 | 19 | 22 | 22 | 22 | 19 | 23 | 23 | 23 | 20 | 24 | 24 | 22 | 20 | 27 | 27 | 23 | |||
| Wee-Mag-Tonge | 75 | 70 | 50 | 320 | 42 | 55 | 50 | 55 | 42 | 63 | 62 | 64 | 43 | 63 | 62 | 56 | 43 | 71 | 67 | 65 |
| 52 | 364 | 40 | 48 | 45 | 48 | 40 | 57 | 55 | 57 | 40 | 60 | 56 | 54 | 40 | 66 | 62 | 61 | |||
| 54 | 527 | 35 | 42 | 40 | 41 | 36 | 49 | 44 | 48 | 35 | 54 | 48 | 41 | 36 | 58 | 56 | 53 | |||
| Wee-Mag-Wee-Mag | 75 | 75 | 50 | 56 | 57 | 77 | 67 | 77 | 57 | 95 | 90 | 95 | 58 | 103 | 98 | 79 | 59 | 113 | 109 | 98 |
| 52 | 52 | 58 | 82 | 74 | 81 | 58 | 104 | 103 | 105 | 60 | 107 | 104 | 82 | 60 | 113 | 112 | 107 | |||
| 56 | 54 | 54 | 67 | 65 | 67 | 55 | 83 | 76 | 82 | 55 | 97 | 91 | 69 | 57 | 108 | 106 | 85 | |||
| Arcus83-Wee-Mag | 83 | 75 | 5048 | 50 | 45 | 59 | 54 | 58 | 46 | 67 | 63 | 65 | 47 | 70 | 63 | 60 | 47 | 74 | 72 | 68 |
| 5408 | 54 | 42 | 50 | 49 | 50 | 42 | 56 | 55 | 56 | 43 | 62 | 60 | 51 | 44 | 70 | 69 | 58 | |||
| 5853 | 56 | 39 | 47 | 46 | 47 | 39 | 51 | 49 | 51 | 40 | 58 | 54 | 48 | 41 | 66 | 61 | 51 | |||
| Arcus83-Arcus83 | 83 | 83 | 5048 | 5408 | 29 | 34 | 34 | 34 | 29 | 36 | 35 | 36 | 31 | 38 | 37 | 34 | 31 | 43 | 42 | 36 |
| 6883 | 6883 | 22 | 25 | 25 | 25 | 22 | 26 | 26 | 26 | 24 | 28 | 28 | 25 | 24 | 31 | 31 | 27 | |||
| 8898 | 6309 | 20 | 23 | 23 | 23 | 20 | 24 | 24 | 24 | 22 | 26 | 26 | 24 | 22 | 29 | 29 | 25 | |||
| Lutz3-Arcus83 | 89 | 83 | 110 | 6309 | 29 | 31 | 31 | 31 | 29 | 33 | 33 | 33 | 29 | 35 | 35 | 31 | 29 | 39 | 38 | 33 |
| 127 | 7571 | 25 | 27 | 26 | 27 | 25 | 28 | 28 | 28 | 25 | 29 | 29 | 27 | 25 | 32 | 32 | 28 | |||
| 150 | 8898 | 21 | 22 | 22 | 22 | 21 | 23 | 23 | 23 | 21 | 24 | 24 | 22 | 21 | 27 | 27 | 23 | |||
| Lutz3-Lutz3 | 89 | 89 | 110 | 150 | 28 | 30 | 30 | 30 | 28 | 32 | 32 | 32 | 28 | 33 | 33 | 31 | 28 | 37 | 37 | 32 |
| 118 | 118 | 30 | 33 | 33 | 33 | 30 | 35 | 34 | 35 | 30 | 37 | 36 | 33 | 30 | 41 | 40 | 35 | |||
| 137 | 127 | 27 | 29 | 29 | 29 | 27 | 31 | 31 | 31 | 27 | 32 | 32 | 29 | 27 | 36 | 36 | 31 | |||
| Mukherje-Lutz3 | 94 | 89 | 301 | 137 | 28 | 30 | 30 | 30 | 28 | 32 | 32 | 32 | 28 | 33 | 33 | 31 | 28 | 37 | 37 | 32 |
| 324 | 118 | 29 | 31 | 31 | 31 | 29 | 33 | 33 | 33 | 29 | 35 | 35 | 32 | 29 | 39 | 38 | 34 | |||
| 351 | 150 | 25 | 26 | 27 | 26 | 25 | 28 | 28 | 28 | 25 | 29 | 29 | 27 | 25 | 32 | 32 | 28 | |||
| Mukherje-Mukherje | 94 | 94 | 301 | 301 | 29 | 33 | 33 | 33 | 29 | 35 | 35 | 35 | 30 | 36 | 36 | 33 | 30 | 40 | 40 | 35 |
| 301 | 351 | 27 | 30 | 30 | 30 | 27 | 32 | 32 | 32 | 28 | 33 | 33 | 30 | 28 | 37 | 37 | 32 | |||
| 351 | 324 | 26 | 29 | 29 | 29 | 26 | 31 | 31 | 31 | 27 | 32 | 32 | 29 | 27 | 36 | 35 | 31 | |||
| Arcus111-Mukherje | 111 | 94 | 8847 | 301 | 32 | 36 | 36 | 36 | 32 | 39 | 38 | 39 | 33 | 40 | 40 | 37 | 33 | 45 | 45 | 39 |
| 9400 | 324 | 30 | 34 | 34 | 34 | 30 | 36 | 36 | 36 | 31 | 38 | 37 | 34 | 31 | 42 | 42 | 36 | |||
| 10,027 | 351 | 28 | 31 | 31 | 31 | 28 | 33 | 33 | 33 | 29 | 35 | 34 | 32 | 29 | 39 | 38 | 33 | |||
| Arcus111-Arcus111 | 111 | 111 | 8847 | 9400 | 34 | 39 | 39 | 39 | 34 | 42 | 41 | 42 | 35 | 44 | 43 | 40 | 35 | 49 | 48 | 42 |
| 11,378 | 11,378 | 28 | 31 | 31 | 31 | 28 | 33 | 32 | 33 | 28 | 33 | 33 | 31 | 28 | 37 | 37 | 33 | |||
| 17,067 | 10,743 | 23 | 26 | 26 | 26 | 23 | 28 | 28 | 28 | 24 | 29 | 29 | 26 | 24 | 32 | 32 | 28 | |||
| Bartholdi-Arcus111 | 148 | 111 | 564 | 11,378 | 25 | 26 | 26 | 26 | 25 | 28 | 28 | 28 | 25 | 29 | 29 | 26 | 25 | 31 | 31 | 28 |
| 705 | 11,570 | 22 | 24 | 24 | 24 | 22 | 25 | 25 | 25 | 23 | 26 | 26 | 24 | 23 | 28 | 28 | 25 | |||
| 805 | 7571 | 28 | 31 | 31 | 31 | 28 | 33 | 33 | 33 | 28 | 35 | 34 | 31 | 28 | 37 | 38 | 33 | |||
| Bartholdi-Bartholdi | 148 | 148 | 513 | 564 | 22 | 23 | 24 | 23 | 22 | 24 | 25 | 24 | 23 | 25 | 25 | 23 | 23 | 27 | 28 | 24 |
| 626 | 626 | 19 | 20 | 20 | 20 | 19 | 21 | 21 | 21 | 20 | 21 | 22 | 20 | 20 | 23 | 23 | 21 | |||
| 805 | 705 | 16 | 17 | 17 | 17 | 16 | 17 | 17 | 17 | 17 | 18 | 18 | 17 | 17 | 19 | 19 | 18 | |||
| Lee-Bartholdi | 205 | 148 | 1510 | 564 | 26 | 28 | 29 | 28 | 26 | 30 | 30 | 30 | 27 | 31 | 31 | 28 | 27 | 34 | 34 | 30 |
| 2077 | 626 | 21 | 22 | 23 | 22 | 21 | 23 | 23 | 23 | 22 | 24 | 24 | 22 | 22 | 26 | 26 | 23 | |||
| 2832 | 705 | 17 | 18 | 18 | 18 | 17 | 19 | 19 | 19 | 18 | 19 | 19 | 18 | 18 | 20 | 21 | 19 | |||
| Lee-Lee | 205 | 205 | 1699 | 2643 | 23 | 25 | 25 | 25 | 23 | 26 | 26 | 26 | 23 | 27 | 27 | 25 | 23 | 29 | 29 | 26 |
| 2266 | 2266 | 22 | 23 | 23 | 23 | 22 | 23 | 24 | 24 | 22 | 24 | 24 | 23 | 22 | 26 | 26 | 24 | |||
| 2832 | 2454 | 19 | 19 | 20 | 20 | 19 | 20 | 20 | 20 | 19 | 21 | 21 | 20 | 19 | 22 | 22 | 21 | |||
| Scholl-Lee | 297 | 205 | 1935 | 2831 | 46 | 50 | 50 | 50 | 46 | 52 | 52 | 52 | 46 | 54 | 54 | 50 | 46 | 60 | 60 | 52 |
| 2247 | 1699 | 46 | 50 | 50 | 50 | 46 | 53 | 53 | 53 | 46 | 54 | 54 | 50 | 46 | 60 | 60 | 52 | |||
| 2787 | 1510 | 42 | 45 | 45 | 45 | 42 | 47 | 47 | 47 | 42 | 49 | 49 | 45 | 42 | 53 | 53 | 47 | |||
| Scholl-Scholl | 297 | 297 | 2049 | 2680 | 62 | 68 | 67 | 67 | 67 | 71 | 71 | 71 | 62 | 73 | 73 | 68 | 62 | 81 | 81 | 71 |
| 2111 | 2111 | 68 | 75 | 75 | 75 | 68 | 78 | 78 | 78 | 68 | 82 | 81 | 75 | 68 | 90 | 90 | 79 | |||
| 2787 | 2247 | 58 | 63 | 63 | 63 | 58 | 66 | 66 | 66 | 58 | 68 | 68 | 63 | 58 | 75 | 74 | 66 | |||
| Computational Results Analysis | VS TS | VS GAS | ||||||
|---|---|---|---|---|---|---|---|---|
| Low Task Variance | High Task Variance | Low Task Variance | High Task Variance | |||||
| Number of better solutions | 6 | 9 | 83 | 91 | 5 | 1 | 80 | 91 |
| Number of identical solutions | 81 | 79 | 9 | 1 | 68 | 75 | 12 | 1 |
| Number of worse solutions | 6 | 5 | 1 | 1 | 20 | 17 | 1 | 1 |
| Rate of better solutions (%) | 6.45% | 9.68% | 89.24% | 97.84% | 5.38% | 1.08% | 86.02% | 97.84% |
| Rate of identical solutions (%) | 87.10% | 84.94% | 9.68% | 1.08% | 73.12% | 80.64% | 12.90% | 1.08% |
| Rate of worse solutions (%) | 6.45% | 5.38% | 1.08% | 1.08% | 21.50% | 18.28% | 1.08% | 1.08% |
| %Gap of TS and GAS | 9.67 | 14.37 | 16.83 | 22.03 | 9.51 | 16.98 | 18.51 | 31.01 |
| %Gap | 9.37 | 14.29 | 7.63 | 13.17 | - | |||
| No. | No. | No. | No. | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 8 | 11 | 8 | 27 | 65 | 15 | 39 | 89 | 22 | 84 | 24 |
| 2 | 8 | 24 | 9 | 27 | 72 | 16 | 67 | 11 | 23 | 84 | 65 |
| 3 | 8 | 65 | 10 | 27 | 89 | 17 | 67 | 24 | 24 | 84 | 72 |
| 4 | 8 | 72 | 11 | 39 | 11 | 18 | 67 | 65 | 25 | 84 | 89 |
| 5 | 8 | 89 | 12 | 39 | 24 | 19 | 67 | 72 | |||
| 6 | 27 | 11 | 13 | 39 | 65 | 20 | 67 | 89 | |||
| 7 | 27 | 24 | 14 | 39 | 72 | 21 | 84 | 11 |
| No. | K | I | P | MOEAD | SPEA2 | NSGAII | SA | HH | ||
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 8 | 10 | 51 | 781.8 | 359.8 | 6 | 6 | 7 | 6 | 7 |
| 2 | 8 | 24 | 39 | 421.3 | 495.8 | 5 | 5 | 6 | 5 | 6 |
| 3 | 8 | 60 | 31 | 1866.6 | 479.8 | 6 | 6 | 7 | 7 | 7 |
| 4 | 8 | 65 | 31 | 8127.6 | 79.8 | 6 | 6 | 7 | 7 | 7 |
| 5 | 8 | 108 | 29 | 3259.8 | 403.8 | 7 | 7 | 8 | 7 | 7 |
| 6 | 27 | 10 | 38 | 3991.9 | 259.8 | 8 | 8 | 8 | 8 | 8 |
| 7 | 27 | 24 | 25 | 620.2 | 443.8 | 5 | 5 | 5 | 5 | 5 |
| 8 | 27 | 60 | 16 | 619.8 | 209.8 | 9 | 9 | 9 | 9 | 10 |
| 9 | 27 | 65 | 15 | 1767.9 | −995.2 | 10 | 10 | 11 | 11 | 11 |
| 10 | 27 | 108 | 13 | 102.9 | 671.8 | 6 | 6 | 7 | 6 | 7 |
| 11 | 50 | 10 | 33 | 681.2 | 529.8 | 6 | 6 | 6 | 6 | 6 |
| 12 | 50 | 24 | 20 | 1505.8 | 109.8 | 5 | 5 | 5 | 5 | 5 |
| 13 | 50 | 60 | 11 | 124.1 | 499.8 | 7 | 7 | 8 | 7 | 8 |
| 14 | 50 | 65 | 10 | 127.9 | 159.8 | 6 | 6 | 8 | 7 | 8 |
| 15 | 50 | 108 | 8 | 486.8 | −1870.2 | 9 | 9 | 10 | 10 | 10 |
| 16 | 60 | 10 | 32 | 803.4 | 529.8 | 6 | 6 | 6 | 6 | 6 |
| 17 | 60 | 24 | 19 | 290.9 | 599.8 | 3 | 3 | 3 | 3 | 3 |
| 18 | 60 | 60 | 10 | 19.9 | 749.8 | 11 | 10 | 10 | 11 | 11 |
| 19 | 60 | 65 | 9 | 142.6 | 39.8 | 6 | 6 | 7 | 6 | 7 |
| 20 | 60 | 108 | 7 | 46.6 | 299.8 | 3 | 3 | 3 | 3 | 3 |
| 21 | 90 | 10 | 30 | 1154.6 | 519.8 | 6 | 6 | 7 | 6 | 7 |
| 22 | 90 | 24 | 17 | 797.4 | 379.8 | 6 | 6 | 6 | 6 | 6 |
| 23 | 90 | 60 | 8 | 25.3 | 649.8 | 6 | 6 | 7 | 6 | 7 |
| 24 | 90 | 65 | 8 | 256.3 | −340.2 | 6 | 6 | 7 | 6 | 7 |
| 25 | 90 | 108 | 6 | 116.0 | 309.8 | 10 | 10 | 10 | 10 | 10 |
| Best number in 25 times | 8 | 7 | 22 | 12 | 24 | |||||
| Rate (%) | 32 | 28 | 88 | 48 | 96 | |||||
| Workstation No. | Working Load Balance | Profit | Time | (%) | Task Sequence on Each Workstation |
|---|---|---|---|---|---|
| 1 | 124.12 | 499.8 | 184.2 | 61.4% | ‘A6’→‘B5’→‘B35’→‘B2’→‘B20’ |
| 2 | 239.0 | 79.7% | ‘A21’→‘B6’→‘A10’ | ||
| 3 | 287.5 | 95.8% | ‘B18’→‘B1’→‘B3’→‘B34’→‘B19’→‘B12’→‘B4’ | ||
| 4 | 281.0 | 93.7% | ‘A1’→‘B13’→‘A19’→‘B33’→‘A7’ | ||
| 5 | 265.5 | 88.5% | ‘B17’→‘A20’→‘A18’→‘A17’ | ||
| 6 | 260.0 | 86.7% | ‘B16’→‘B15’→‘B14’→‘B21’→‘B22’→‘B29’ | ||
| 7 | 288.8 | 96.3% | ‘A2’→‘A22’→‘A23’→‘B32’→‘A3’→‘B11’→‘B28’ | ||
| 8 | 271.5 | 90.5% | ‘A24’→‘A14’→‘A5’→‘B8’ | ||
| 9 | 279.8 | 93.2% | ‘B25’→‘A25’→‘A16’→‘B7’→‘B23’→‘B9’ | ||
| 10 | 279.2 | 93.0% | ‘A26’→‘A27’→‘A9’→‘B24’→‘A13’→‘B27’→‘A15’→‘B31’→‘A4’→‘B26’→‘A29’ | ||
| 11 | 289.0 | 96.3% | ‘A30’→‘B30’→‘A28’→‘A12’→‘B10’→‘A8’→‘A11’ |
| Workstation No. | Working Load Balance | Profit | Time | (%) | Task Sequence on Each Workstation |
|---|---|---|---|---|---|
| 1 | 19.87 | 749.8 | 53.0 | 88.3% | ‘A19’→‘B35’→‘B2’→‘A6’→‘A18’→‘B1’ |
| 2 | 56.6 | 94.3% | ‘B5’→‘A21’ | ||
| 3 | 44.6 | 89.2% | ‘A1’→‘B20’→‘A20’→‘A7’→‘A10’→‘B18’ | ||
| 4 | 57.8 | 96.3% | ‘B17’→‘B19’→‘B16’→‘B3’→‘B6’→‘B34’ | ||
| 5 | 57.6 | 96.0% | ‘A17’→‘A2’→‘B4’→‘B12’→‘B15’→‘A22’→‘A14’→‘B13’ | ||
| 6 | 51.0 | 85.0% | ‘A23’→‘B3’→‘B14’→‘B21’→‘A5’→‘A24’→‘A13’→‘A3’→‘A15’ | ||
| 7 | 55.4 | 92.3% | ‘A16’→‘A4’→‘A9’→‘A25’→‘A29’→‘A30’→‘A12’→‘A8’ | ||
| 8 | 58.4 | 97.3% | ‘B22’→‘B11’→‘B29’→‘A26’→‘B28’→‘A27’→‘B25’ | ||
| 9 | 49.2 | 82.0% | ‘A28’→‘B32’→‘B8’→‘B9’→‘A11’ | ||
| 10 | 53.8 | 89.7% | ‘B7’→‘B27’→‘B31’→‘B10’→‘B23’→‘B24’→‘B26’→‘B30’ |
| Workstation No. | Working Load Balance | Profit | Time | (%) | Task Sequence on Each Workstation |
|---|---|---|---|---|---|
| 1 | 115.97 | 309.8 | 490.9 | 90.9% | ‘B5’→‘A19’→‘B12’→‘B6’→‘B1’→‘A7’→‘A10’→‘B18’ |
| 2 | 508.1 | 94.1% | ‘B17’→‘A21’→‘A18’→‘A1’→‘B34’→‘B20’→‘B2’→‘B13’→‘B35’ | ||
| 3 | 512.2 | 94.9% | ‘B4’→‘B19’→‘B16’→‘B3’→‘A6’→‘A20’→‘A17’→‘B15’→‘B14’→‘B33’→‘A2’→‘B21’ | ||
| 4 | 519.1 | 96.1% | ‘B22’→‘B29’→‘B11’→‘B28’→‘B25’→‘A22’→‘B8’→‘A14’→‘B9’→‘B32’ | ||
| 5 | 481.4 | 89.1% | ‘A16’→‘B10’→‘A3’→‘B7’→‘B23’→‘A9’→‘B24’→‘A23’→‘B27’→‘A24’→‘A25→‘A26→‘A5’ | ||
| 6 | 413.8 | 76.6% | ‘A12’→‘A13’→‘B31’→‘A15’→‘B26’→‘B30’→‘A30’→‘A8’→‘A11’→‘A29’→‘A27’→‘A4’→‘A28’ |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, Y.; Liu, C.; Zhang, M.; Jia, Y.; Xu, Y. A Novel Simulated Annealing-Based Hyper-Heuristic Algorithm for Stochastic Parallel Disassembly Line Balancing in Smart Remanufacturing. Sensors 2023, 23, 1652. https://doi.org/10.3390/s23031652
Hu Y, Liu C, Zhang M, Jia Y, Xu Y. A Novel Simulated Annealing-Based Hyper-Heuristic Algorithm for Stochastic Parallel Disassembly Line Balancing in Smart Remanufacturing. Sensors. 2023; 23(3):1652. https://doi.org/10.3390/s23031652
Chicago/Turabian StyleHu, Youxi, Chao Liu, Ming Zhang, Yu Jia, and Yuchun Xu. 2023. "A Novel Simulated Annealing-Based Hyper-Heuristic Algorithm for Stochastic Parallel Disassembly Line Balancing in Smart Remanufacturing" Sensors 23, no. 3: 1652. https://doi.org/10.3390/s23031652
APA StyleHu, Y., Liu, C., Zhang, M., Jia, Y., & Xu, Y. (2023). A Novel Simulated Annealing-Based Hyper-Heuristic Algorithm for Stochastic Parallel Disassembly Line Balancing in Smart Remanufacturing. Sensors, 23(3), 1652. https://doi.org/10.3390/s23031652









