Flood Detection in Steel Tubes Using Guided Wave Energy Leakage
Abstract
1. Introduction
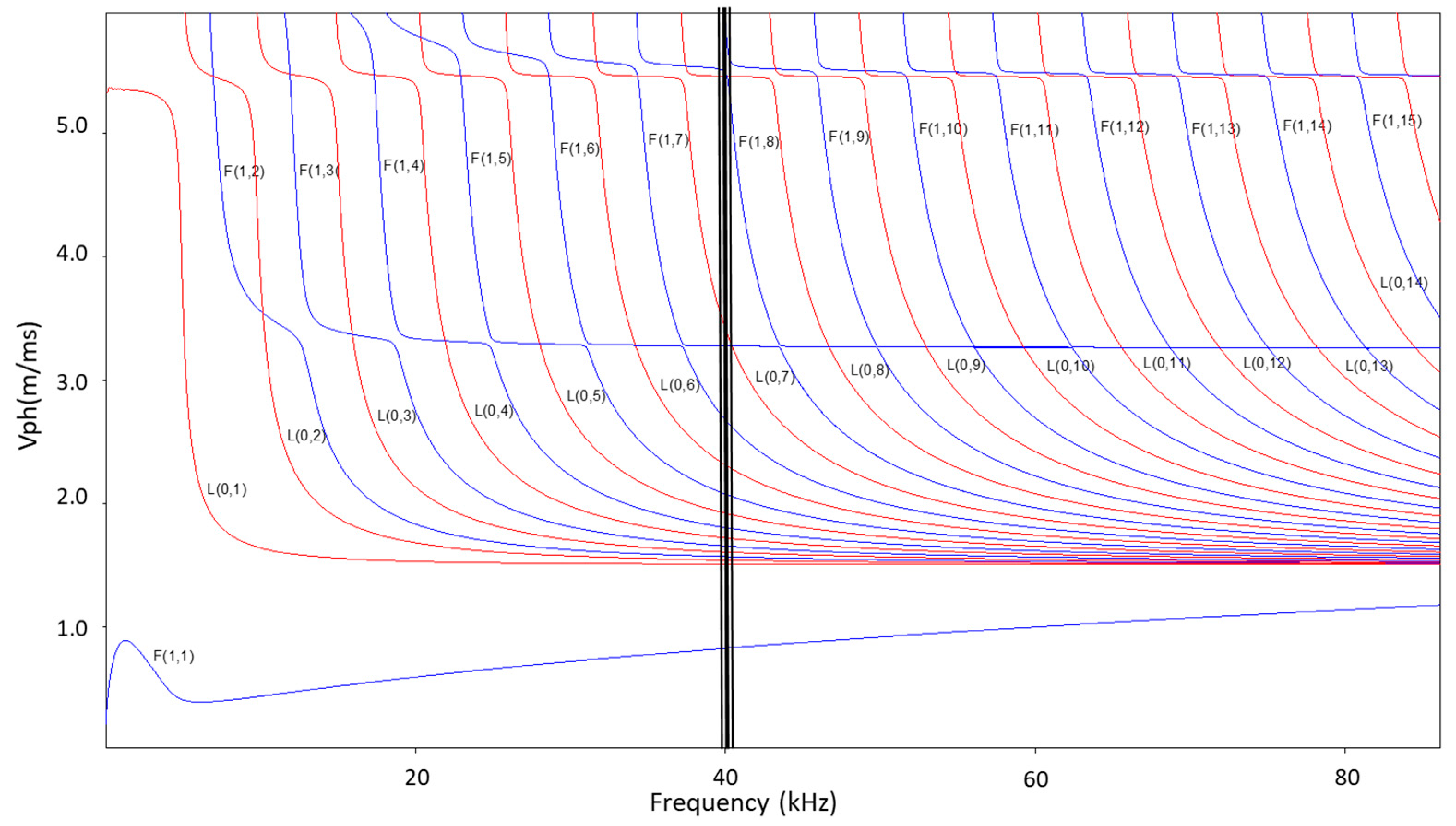
2. Leaky Guided Waves
Dispersion Curves and Mode Shapes
3. Wavelet Energy Entropy Signal Processing
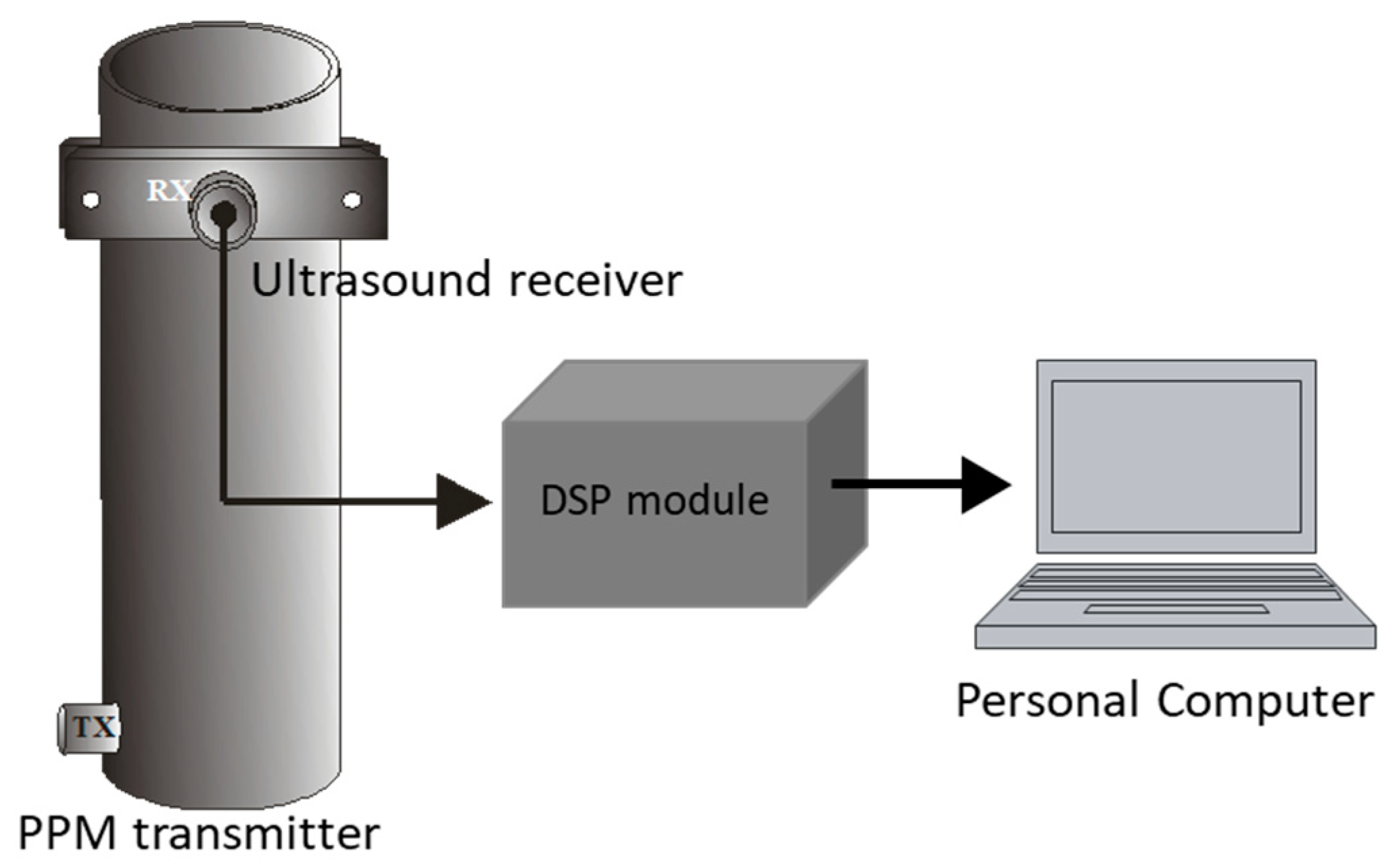
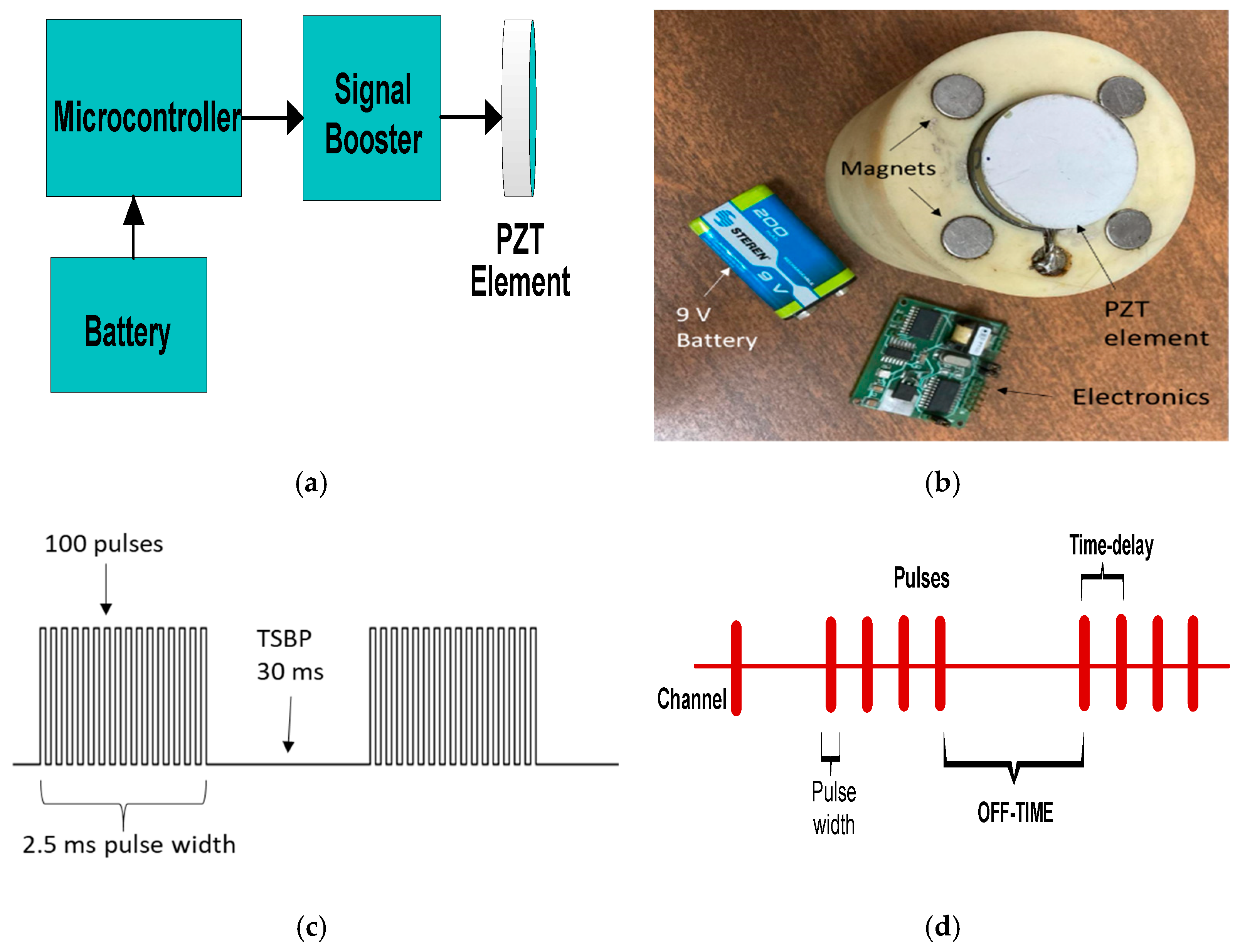
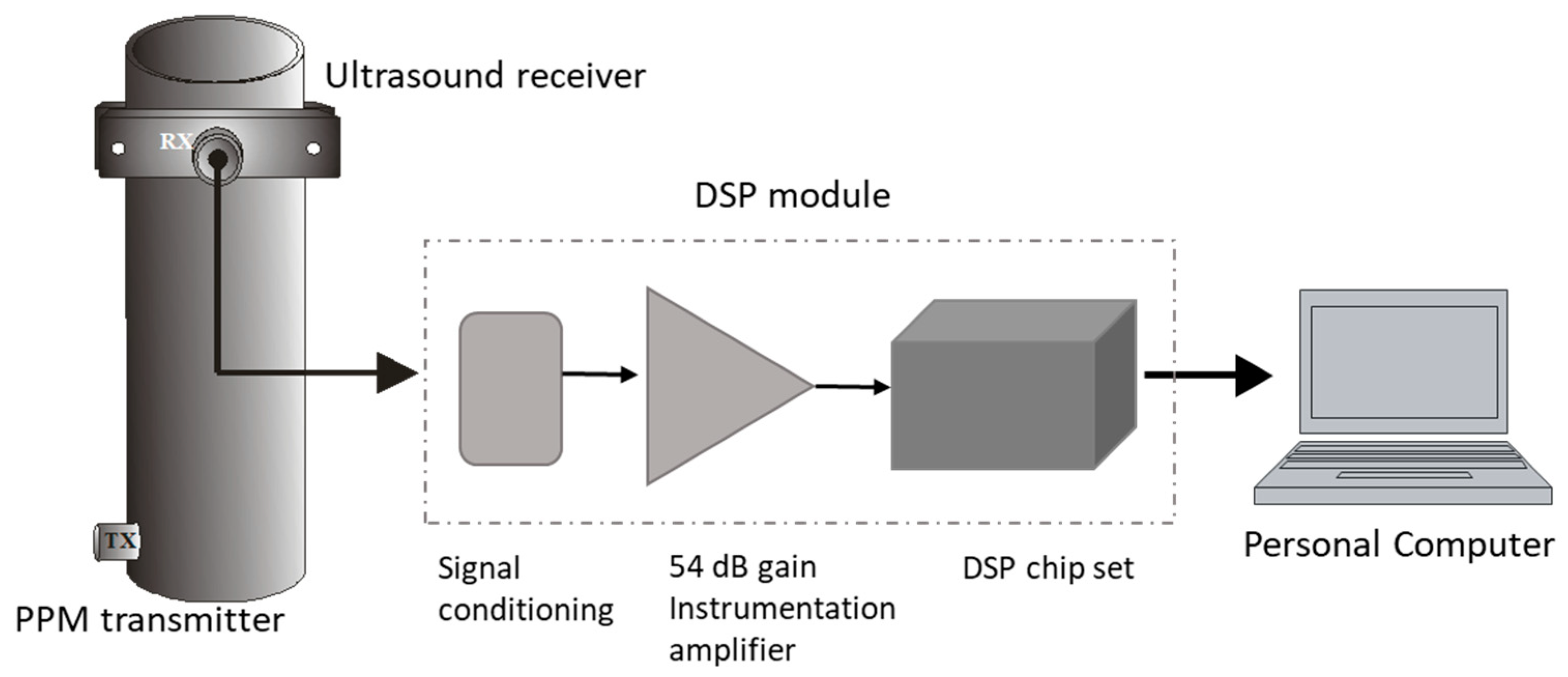
4. FMD-Guided Wave System
5. Experiment Setup
6. Results
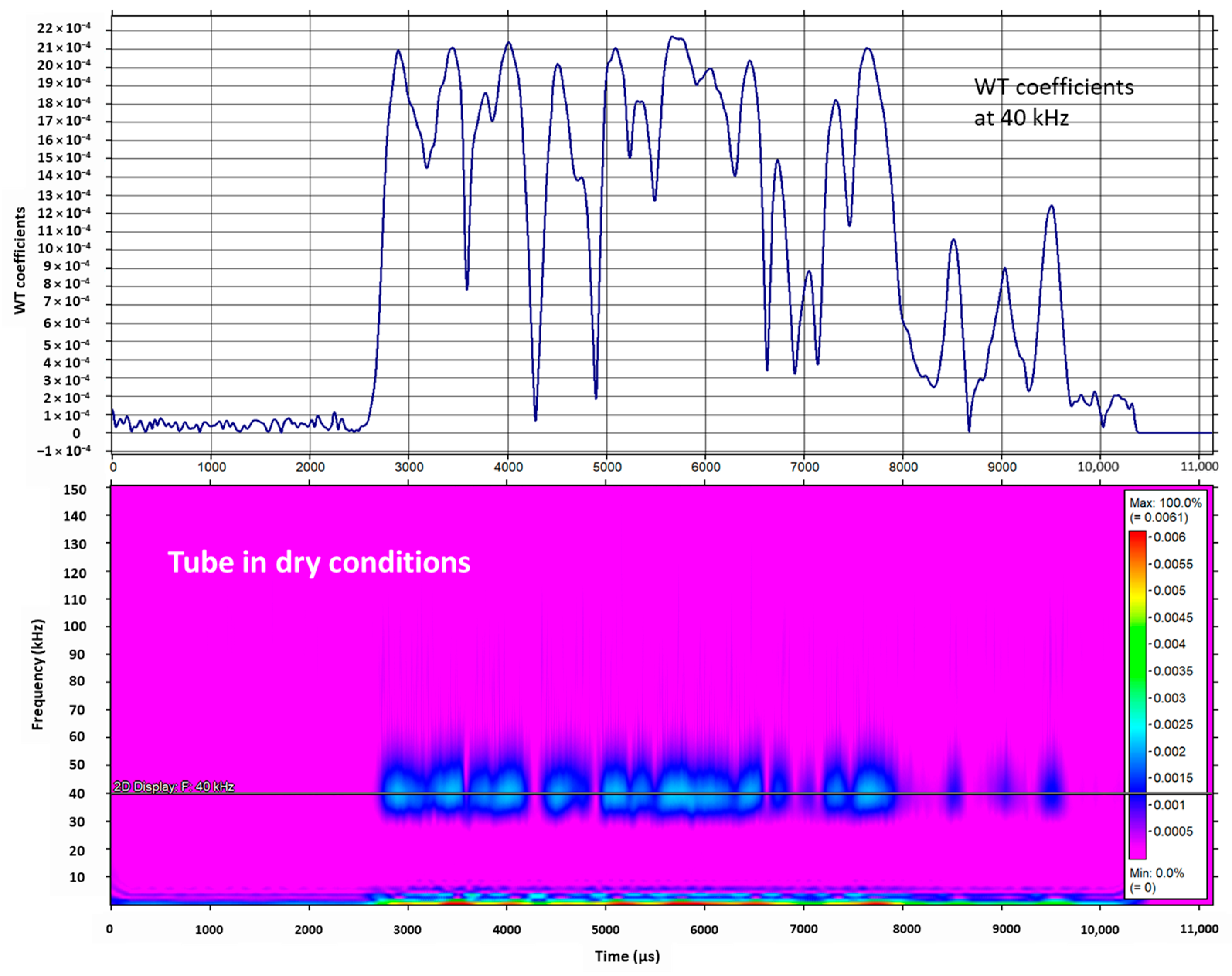
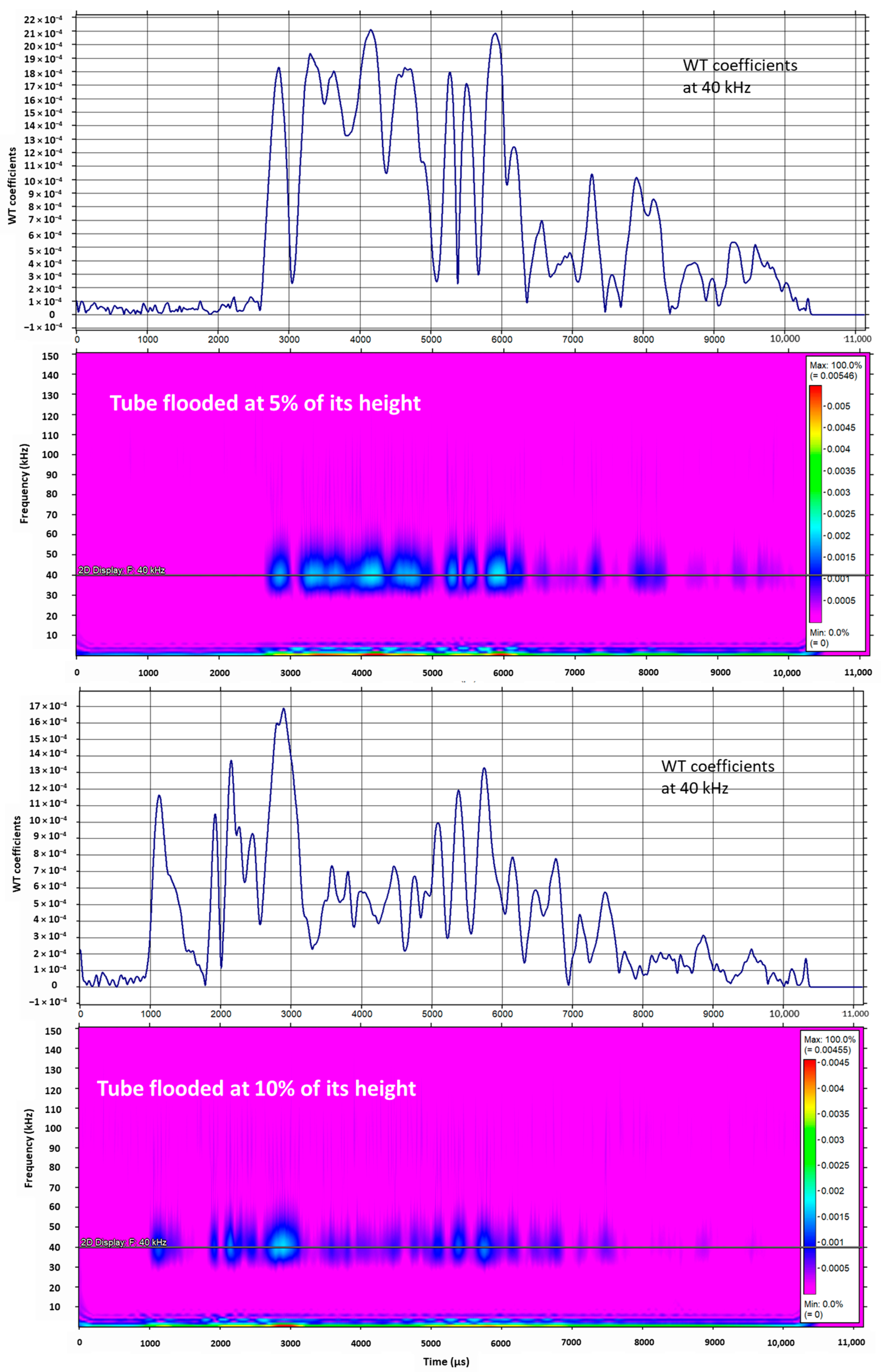
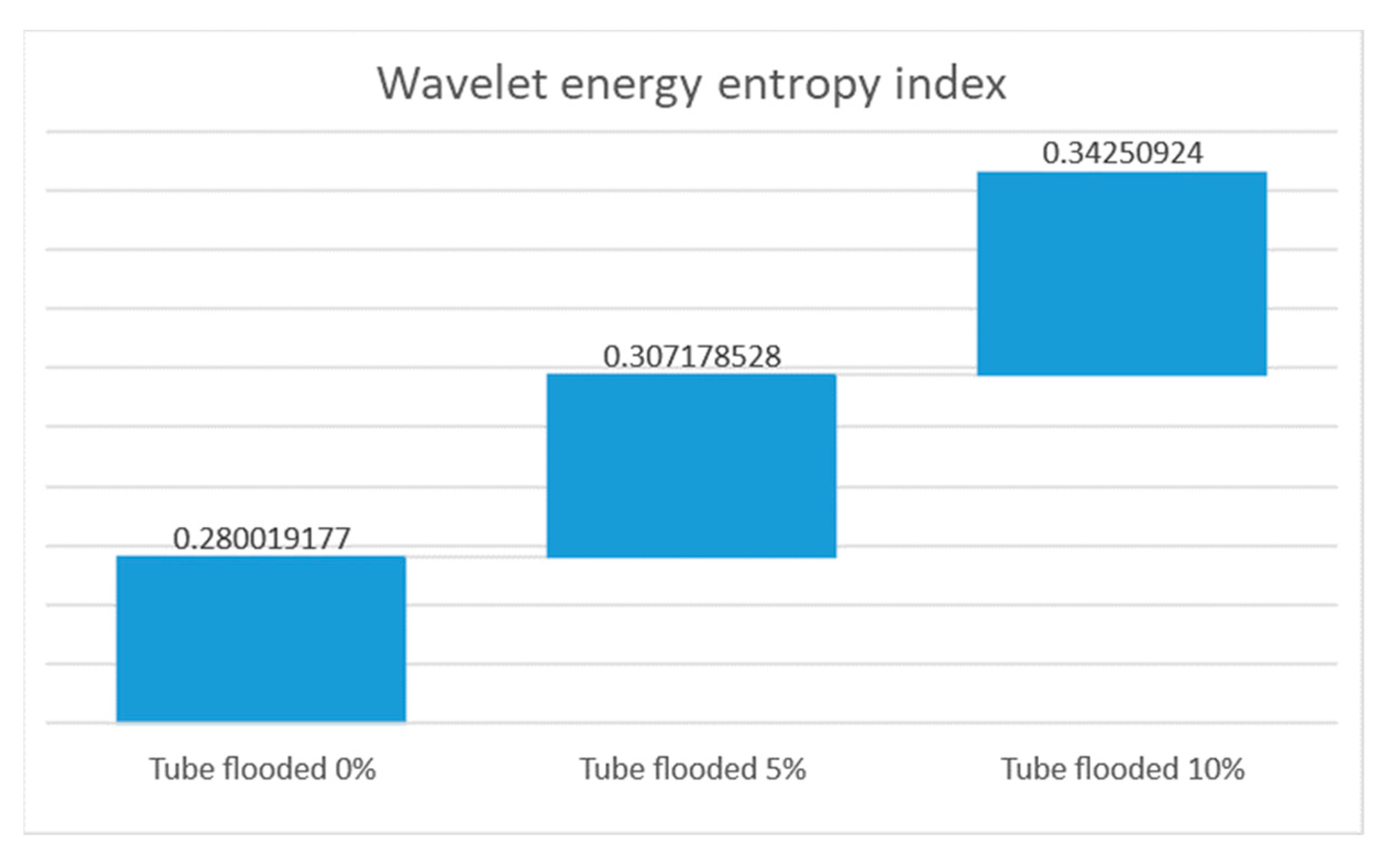
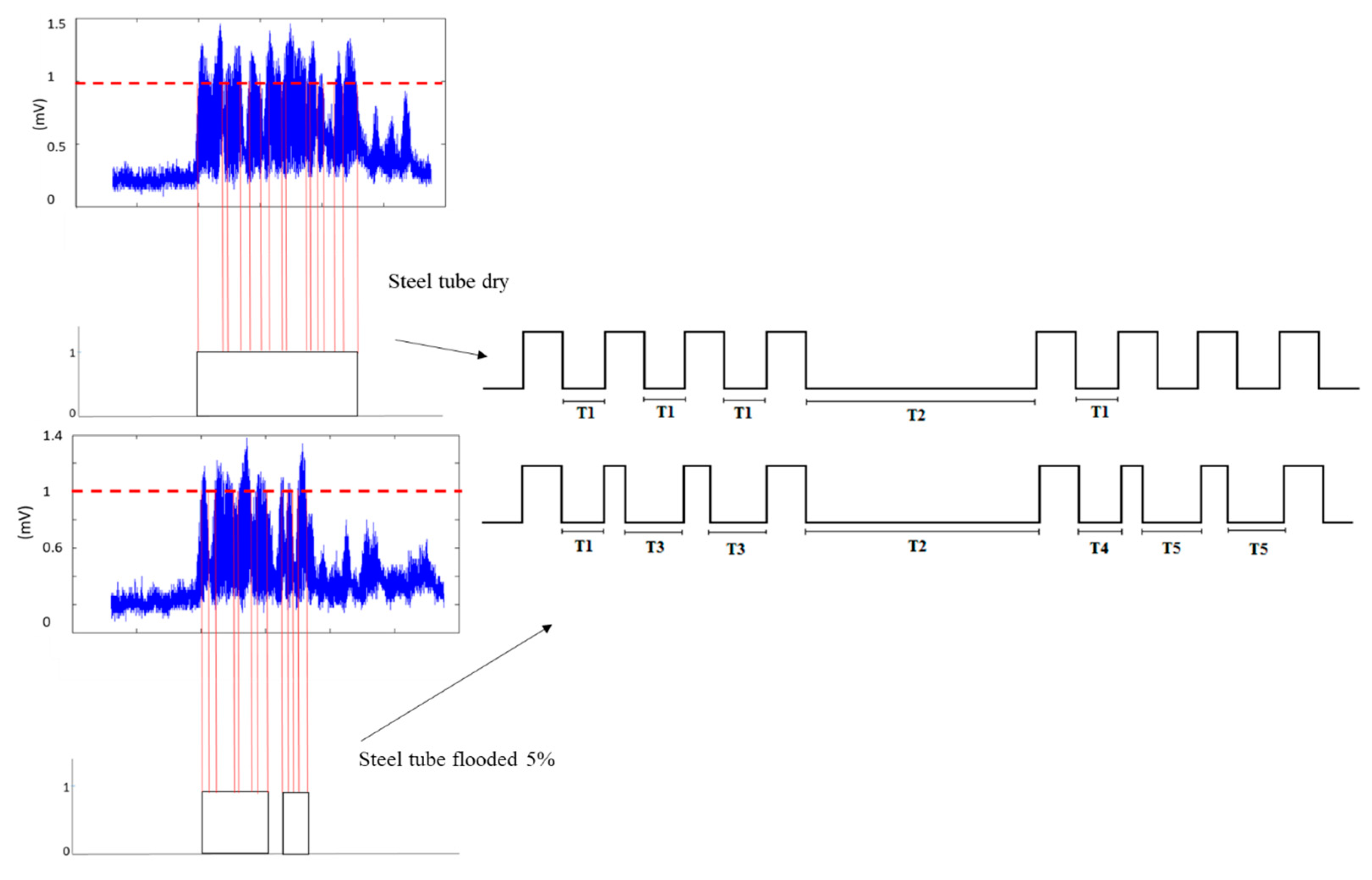
6.1. Off-Line FMD via Wavelet Energy Entropy
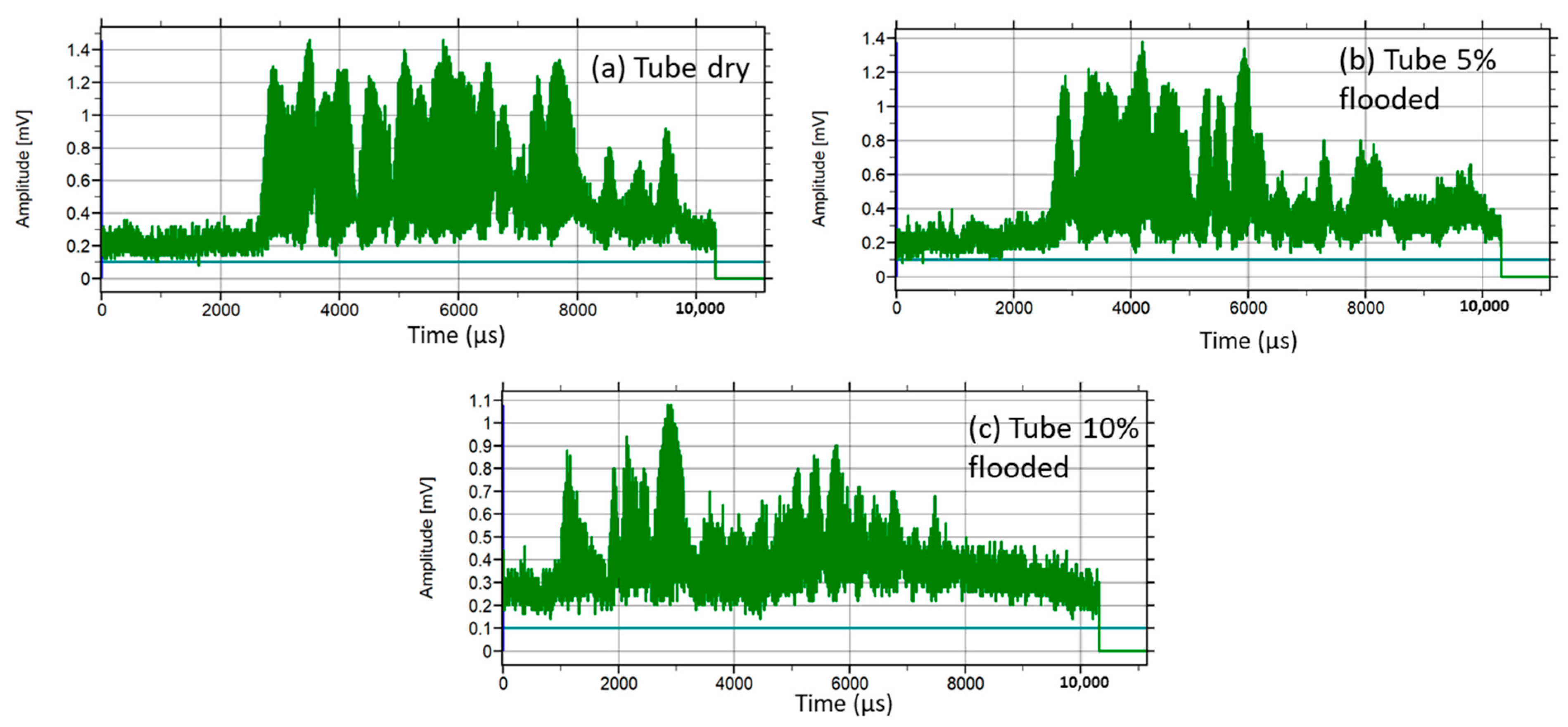
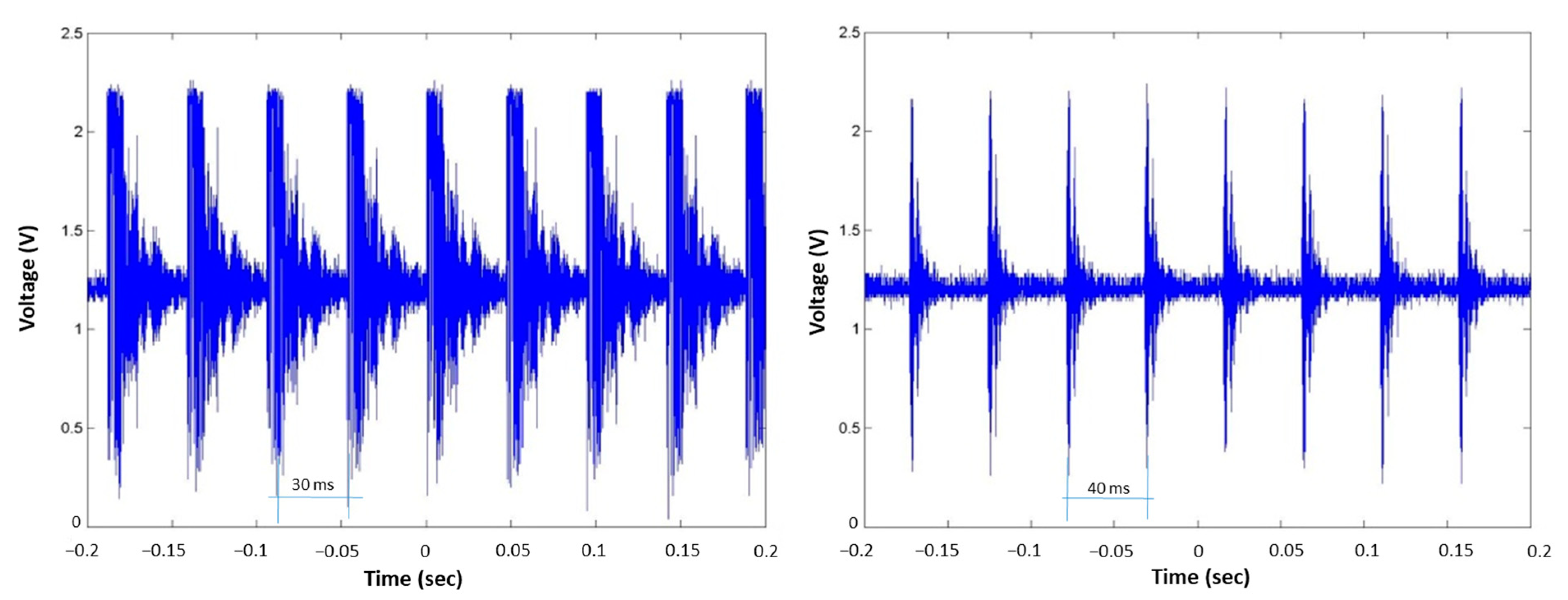
6.2. Real-Time FMD via Time–Space between Pulses
7. Conclusions and Further Work
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- ISO19902; Petroleum and Natural Gas Industries—Fixed Steel Offshore Structures. International Organization for Standardization (ISO): Geneva, Switzerland, 2007.
- Nelson, A.; Sanderson, D.J.; Thurlbeck, S.D. Stress Redistribution in Platform Substructures due to Primary Member Damage and Its Effect on Structural Reliability; HSE Books: London, UK, 2004. [Google Scholar]
- Burdekin, F.M.; Talai-faz, B.; Brennan, F.P.; Dover, W. Experimental Validation 450 of the Ultimate Strength of Brace Members with Circumferential Cracks; HSE Books: London, UK, 2002. [Google Scholar]
- Abdallah El-Reedy, M. Assessment of existing structures and repairs. In Offshore Structures, 2nd ed.; Gulf Professional Publishing: Kidlington, UK, 2020; pp. 419–542. ISBN 9780128161913. [Google Scholar]
- Christ, R.D.; Wernli Sr, R.L. Chapter 18—Ancillary Sensors. In The ROV Manual, 2nd ed.; Butterworth-Heinemann: Oxford, UK, 2013; pp. 477–500. ISBN 9780080982885. [Google Scholar]
- Sevan’kaev, A.V.; Lloyd, D.C.; Edwards, A.A.; Moquet, J.E.; Nugis, V.Y.; Mikhailova, G.M.; Potetnya, O.I.; Khvostunov, I.K.; Guskova, A.K.; Baranov, A.E.; et al. Cytogenic Investigations of Serious Overexposures to an Industrial Gamma Radiography Source. Radiat. Prot. Dosim. 2002, 102, 201–206. [Google Scholar] [CrossRef] [PubMed]
- Gnanasekaran, T.S. Cytogenetic biological dosimetry assays: Recent developments and updates. Radiat. Oncol. J. 2021, 39, 159–166. [Google Scholar] [CrossRef] [PubMed]
- Hayward, G.; Pearson, J.; Stirling, G. An intelligent ultrasonic inspection system for flooded member detection in offshore structures. IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 1993, 40, 512–521. [Google Scholar] [CrossRef]
- Hartmann, M.; Kaajakari, V. Ultrasonic Nanostructured Thin Film Transducers for Flooded Member Detection. In Proceedings of the 2008 17th Biennial University/Government/Industry Micro/Nano Symposium, Louisville, KY, USA, 13–16 July 2008; pp. 212–214. [Google Scholar] [CrossRef]
- Mijarez, R.; Gaydecki, P.; Burdekin, M. Continuous monitoring guided wave encoded sensor for oil rig flooded member detection. Insight Non-Destruct. Test. Cond. Monit 2005, 47, 748–751. [Google Scholar]
- Mijarez, R.; Gaydecki, P.; Burdekin, M. Flood member detection for real-time structural health monitoring of sub-sea structures of offshore steel oilrigs Smart Mater. Struct 2007, 16, 1857–1869. [Google Scholar]
- Mijarez, R. and Gaydecki, P. Automatic guided wave PPM communication system for potential SHM of flooding members in sub-sea oil rigs. Smart Mater. Struct 2013, 22, 055031. [Google Scholar]
- Rizzo, P. 11—Sensing solutions for assessing and monitoring underwater systems. In Sensor Technologies for Civil Infrastructures, Woodhead Publishing Series in Civil and Structural Engineering, 2nd ed.; Lynch, J.P., Sohn, H., Wang, M.L., Eds.; Woodhead Publishing: Cambridge, MA, USA, 2022; pp. 355–376. ISBN 9780081027066. [Google Scholar]
- Bingham, J.; Hinders, M.; Friedman, A. Lamb wave detection of limpet mines on ship hulls. Ultrasonics 2009, 49, 706–722. [Google Scholar] [CrossRef]
- Na, W.B.; Kundu, T. Underwater pipeline inspection using guided waves. J. Press Vessel. Technol. 2002, 124, 196–200. [Google Scholar] [CrossRef]
- Koduru, J.P.; Rose, J.L. Mode controlled guided wave tomography using annular array transducers for SHM of water loaded plate like structures. Smart Mater. Struct. 2013, 22, 125021. [Google Scholar]
- Chen, J.; Su, Z.; Cheng, L. Identification of corrosion damage in submerged structures using fundamental anti-symmetric lamb waves. Smart Mater. Struct. Jan. 2010, 19, 015004. [Google Scholar] [CrossRef]
- Rizzo, P.; Han, J.G.; Ni, X.L. Structural health monitoring of immersed structures by means of guided ultrasonic waves. J. Intell Mater. Syst. Struct. Sep. 2010, 21, 1397–1407. [Google Scholar] [CrossRef]
- Pavlakovic, B.N. Leaky Guided Ultrasonic Waves in NDT. Ph.D. Thesis, Imperial College, London, UK, October 1998. [Google Scholar]
- Aristégui, C.; Lowe, M.; Cawley, P. Guided waves in fluid-filled pipes surrounded by different fluids. Ultrasonics 2001, 39, 367–375. [Google Scholar] [CrossRef]
- Long, R.; Lowe, M.; Cawley, P. Attenuation characteristics of the fundamental modes that propagate in buried iron water pipes. Ultrasonics 2003, 41, 509–519. [Google Scholar] [CrossRef] [PubMed]
- Fan, Z.; Lowe, M.J.S.; Castaings, M.; Bacon, C. Torsional waves propagation along a waveguide of arbitrary cross section immersed in a perfect fluid. J. Acoust. Soc. Am. 2008, 124, 2002–2010. [Google Scholar] [CrossRef]
- Rose, J.L. Ultrasonic Waves in Solid Media; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar]
- Chimenti, D.E.; Nayfeh, A.H. Leaky lamb waves in fibrous composite laminates. J. Appl. Phys. 1985, 58, 4531–4538. [Google Scholar] [CrossRef]
- Shuvalov, A.L.; Poncelet, O.; Deschamps, M. Analysis of the dispersion spectrum of fluid-loaded anisotropic plates: Leaky-wave branches. J. Sound Vib. 2006, 296, 494–517. [Google Scholar] [CrossRef]
- Wu, J.R.; Zhu, Z.M. The propagation of lamb waves in a plate bordered with layers of a liquid. J. Acoust. Soc. Am. 1992, 91, 861–867. [Google Scholar] [CrossRef]
- Yu, L.; Tian, Z. Case study of guided wave propagation in a one-side water-immersed steel plate. Case Stud. Nondestruct. Test. Eval. 2015, 3, 1–8, ISSN 2214-6571. [Google Scholar] [CrossRef]
- Nayfeh, A.H.; Chimenti, D.E. Propagation of guided waves in fluid-coupled plates of fiber-reinforced composite. J. Acoust. Soc. Am. 1988, 83, 1736–1743. [Google Scholar] [CrossRef]
- Ahmad, F.; Kiyani, N.; Yousaf, F.; Shams, M. Guided waves in a fluid-loaded transversely isotropic plate. Math. Probl. Eng. 2002, 8, 151–159. [Google Scholar] [CrossRef]
- Belloncle, G.; Luppé, F.; Franklin, H.; Conoir, J.M. Influence of the slow wave on the relation between the angular resonances and the leaky guided modes properties for a poroelastic plate embedded in water. Ultrasonics 2004, 42, 511–514. [Google Scholar] [CrossRef] [PubMed]
- Dayal, V. Longitudinal waves in homogeneous anisotropic cylindrical bars immersed in fluid. J. Acoust. Soc. Am. 1993, 93, 1249–1255. [Google Scholar] [CrossRef]
- Nagy, P.B. Longitudinal guided wave propagation in a transversely isotropic rod immersed in fluid. J. Acoust. Soc. Am. 1995, 98, 454–457. [Google Scholar] [CrossRef]
- Berliner, M.J.; Solecki, R. Wave propagation in fluid-loaded, transversely isotropic cylinders. Part I. Analytical formulation. J. Acoust. Soc. Am. 1996, 99, 1841–1847. [Google Scholar] [CrossRef]
- Ahmad, F. Guided waves in a transversely isotropic cylinder immersed in a fluid. J. Acoust. Soc. Am. 2001, 109, 886–890. [Google Scholar] [CrossRef]
- Thomson, W.T. Transmission of elastic waves through a stratified solid medium. J. Appl. Phys. 1950, 21, 89–93. [Google Scholar] [CrossRef]
- Haskell, N.A. The dispersion of surface waves on multilayered media. Bull. Seismol. Soc. Am. 1953, 43, 17–34. [Google Scholar] [CrossRef]
- Knopoff, L. A matrix method for elastic wave problems. Bull. Seismol. Soc. Am. 1964, 54, 431–438. [Google Scholar] [CrossRef]
- Randall, M.J. Fast programs for layered half-space problems. Bull. Seismol. Soc. Am. 1967, 57, 1299–1315. [Google Scholar] [CrossRef]
- Lowe, M. Matrix techniques for modeling ultrasonic waves in multilayered media, IEEE Transactions on Ultrasonics. Ferroelectr. Freq. Control. 1995, 42, 525–542. [Google Scholar] [CrossRef]
- Maess, M.; Wagner, N.; Gaul, L. Dispersion curves of fluid filled elastic pipes by standard FE models and eigenpath analysis. J. Sound Vib. 2006, 296, 264–276. [Google Scholar] [CrossRef]
- Sorohan, S.; Constantin, N.; Gavan, M.; Anghel, V. Extraction of dispersion curves for waves propagating in free complex waveguides by standard finite element codes. Ultrasonics 2011, 51, 503–515. [Google Scholar] [CrossRef] [PubMed]
- Hayashi, T.; Song, W.J.; Rose, J.L. Guided wave dispersion curves for a bar with an arbitrary cross-section, a rod and rail example. Ultrasonics 2003, 41, 175–183. [Google Scholar] [CrossRef]
- Bartoli, I.; Marzani, A.; Lanza di Scalea, F.; Viola, E. Modeling wave propagation in damped waveguides of arbitrary cross-section. J. Sound Vib. 2006, 295, 685–707. [Google Scholar] [CrossRef]
- Nilsson, C.M.; Finnveden, S. Waves in thin-walled fluid-filled ducts with arbitrary cross-sections. J. Sound Vib. 2008, 310, 58–76. [Google Scholar] [CrossRef]
- Mazzotti, M.; Marzani, A.; Bartoli, I.; Viola, E. Guided waves dispersion analysis for prestressed viscoelastic waveguides by means of the SAFE method. Int. J. Solids Struct. 2012, 49, 2359–2372. [Google Scholar] [CrossRef]
- Gunawan, A.; Hirose, S. Boundary element analysis of guided waves in a bar with an arbitrary cross-section. Eng. Anal. Bound. Elem. 2005, 29, 913–924. [Google Scholar] [CrossRef]
- Mazzotti, M.; Bartoli, I.; Marzani, A.; Viola, E. A 2.5 D boundary element formulation for modeling damped waves in arbitrary cross-section waveguides, cavities. J. Comput. Phys. 2013, 248, 363–382. [Google Scholar] [CrossRef]
- Mazzotti, M.; Marzani, A.; Bartoli, I. Dispersion analysis of leaky guided waves in fluid-loaded waveguides of generic shape. Ultrasonics 2014, 54, 408–418, 0041-624X. [Google Scholar] [CrossRef]
- Pavlakovic, B.; Lowe, M. Disperse User Manual: A System for Generating Dispersion Curves; Imperial College: London, UK, 2003. [Google Scholar]
- Rose, J.L.; Ditri, J.J.; Pilarski, A.; Rajana, K.; Carr, F. A guided wave inspection technique for nuclear steam generator tubing. NDTE Int. 1994, 27, 6. [Google Scholar] [CrossRef]
- Hong, J.C.; Kim, Y.Y. The optimal selection of mother wavelet shape for the best time-frequency localization of the continuous wavelet transform. Smart Structures and Materials 2003. In Modeling, Signal Processing, and Control; SPIE: San Diego, CA, USA, 2003. [Google Scholar]
- Mijarez, R.; Baltazar, A.; Rodríguez, J.; Ramírez-Niño, J. Damage detection in ACSR cables based on ultrasonic guided waves. Dyna 2014, 81, 226–233. [Google Scholar] [CrossRef]
- Torrence, C.; Compo, G. A practical guide to wavelet analysis. Bull. Am. Meteorol. Soc. 1998, 79, 61–78. [Google Scholar] [CrossRef]
- Daubechies, I. Ten lectures on wavelets. In CBMS-NSF Conference on Wavelets and Applications; SIAM: Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 1992; pp. 1–337. [Google Scholar]
- Addison, P.S. The Illustrated Wavelet Transform Handbook: Introductory Theory and Applications in Science, Engineering, Medicine and Finance; CRC Press: Boca Raton, FL, USA, 2002. [Google Scholar]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Gaydecki, P. Foundations of Digital Signal Processing: Theory, Algorithms and Hardware Design; The Institute of Electrical Engineers: London, UK, 2004. [Google Scholar]
- AGU-Vallen Wavelet, Vallen Systeme GmbH© 2023–2005. Available online: https://www.vallen.de/knowledgebase/agu-vallen-wavelet (accessed on 18 November 2022).
- Mijarez, R.; Solis, L.; Martinez, F. A continuous health monitoring guided wave FMD system for retrofit to existing offshore oilrigs. AIP Conf. Proc. 2010, 1211, 1697–1704. [Google Scholar]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mijarez, R. Flood Detection in Steel Tubes Using Guided Wave Energy Leakage. Sensors 2023, 23, 1334. https://doi.org/10.3390/s23031334
Mijarez R. Flood Detection in Steel Tubes Using Guided Wave Energy Leakage. Sensors. 2023; 23(3):1334. https://doi.org/10.3390/s23031334
Chicago/Turabian StyleMijarez, Rito. 2023. "Flood Detection in Steel Tubes Using Guided Wave Energy Leakage" Sensors 23, no. 3: 1334. https://doi.org/10.3390/s23031334
APA StyleMijarez, R. (2023). Flood Detection in Steel Tubes Using Guided Wave Energy Leakage. Sensors, 23(3), 1334. https://doi.org/10.3390/s23031334





