Design and Analysis of an Extended Simply Supported Beam Piezoelectric Energy Harvester
Abstract
1. Introduction
2. Design and Modeling
3. Experiment
4. Results
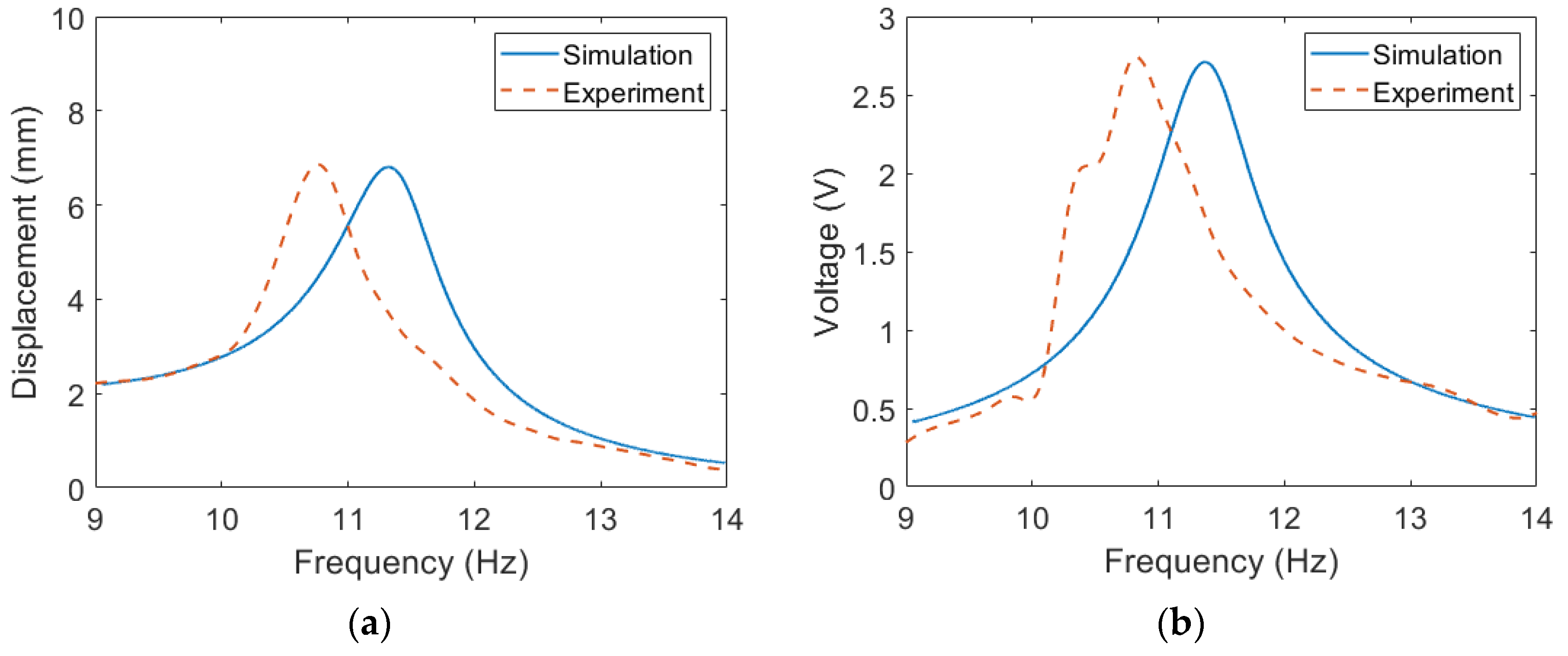
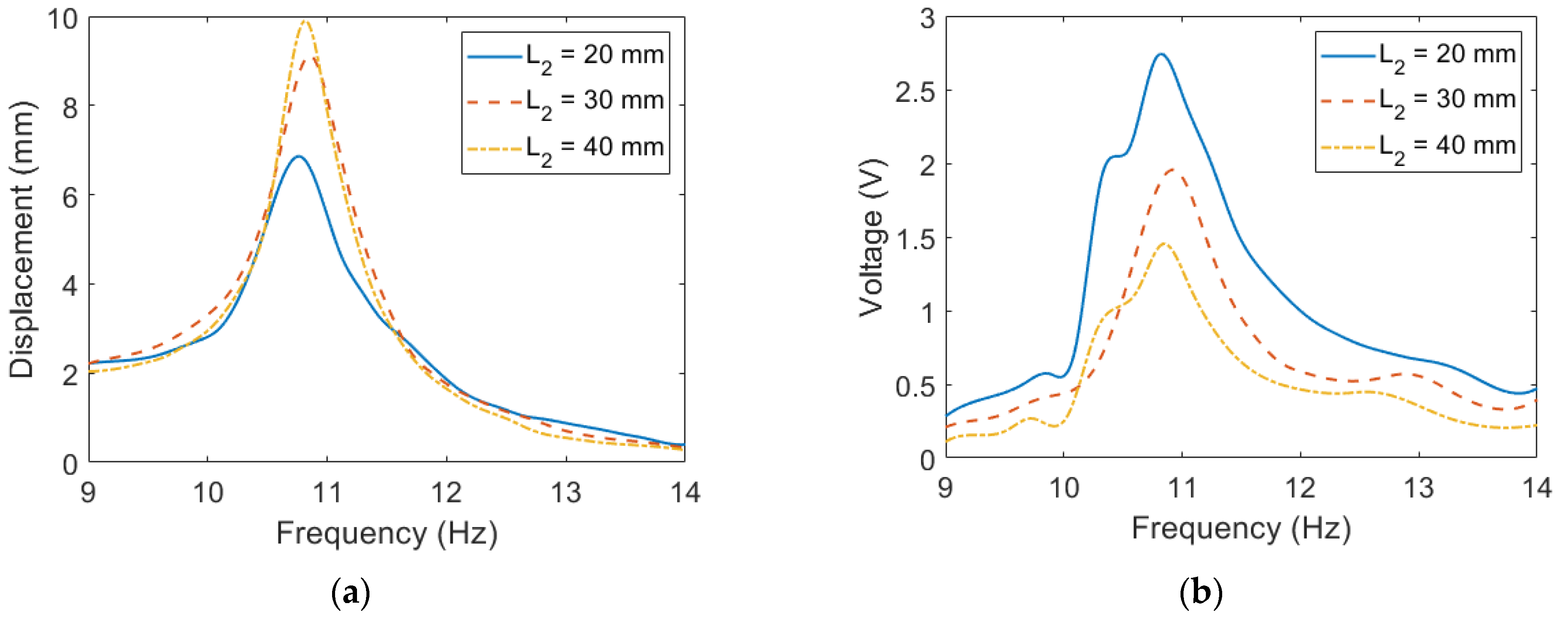
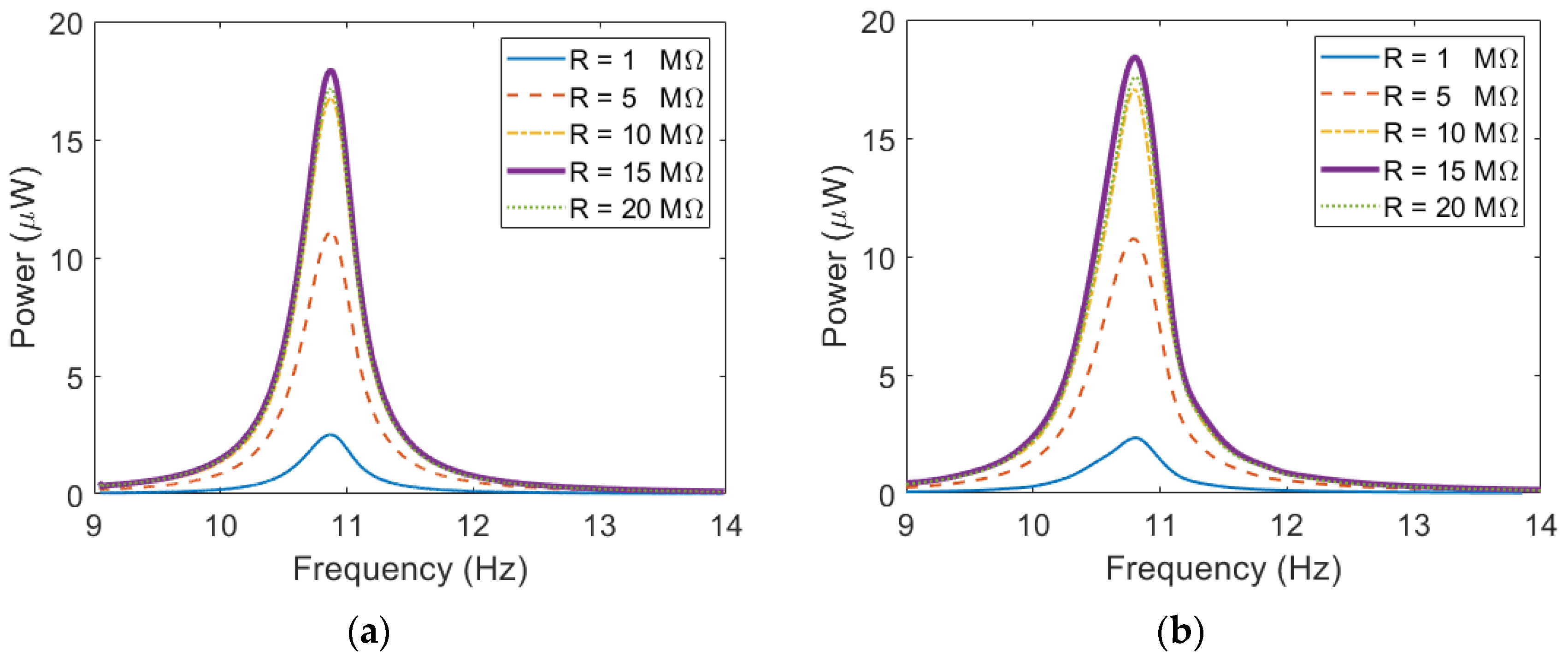
4.1. ESSB PEH under Base Excitations
4.2. ESSB PEH with Torsional Springs under Base Excitations
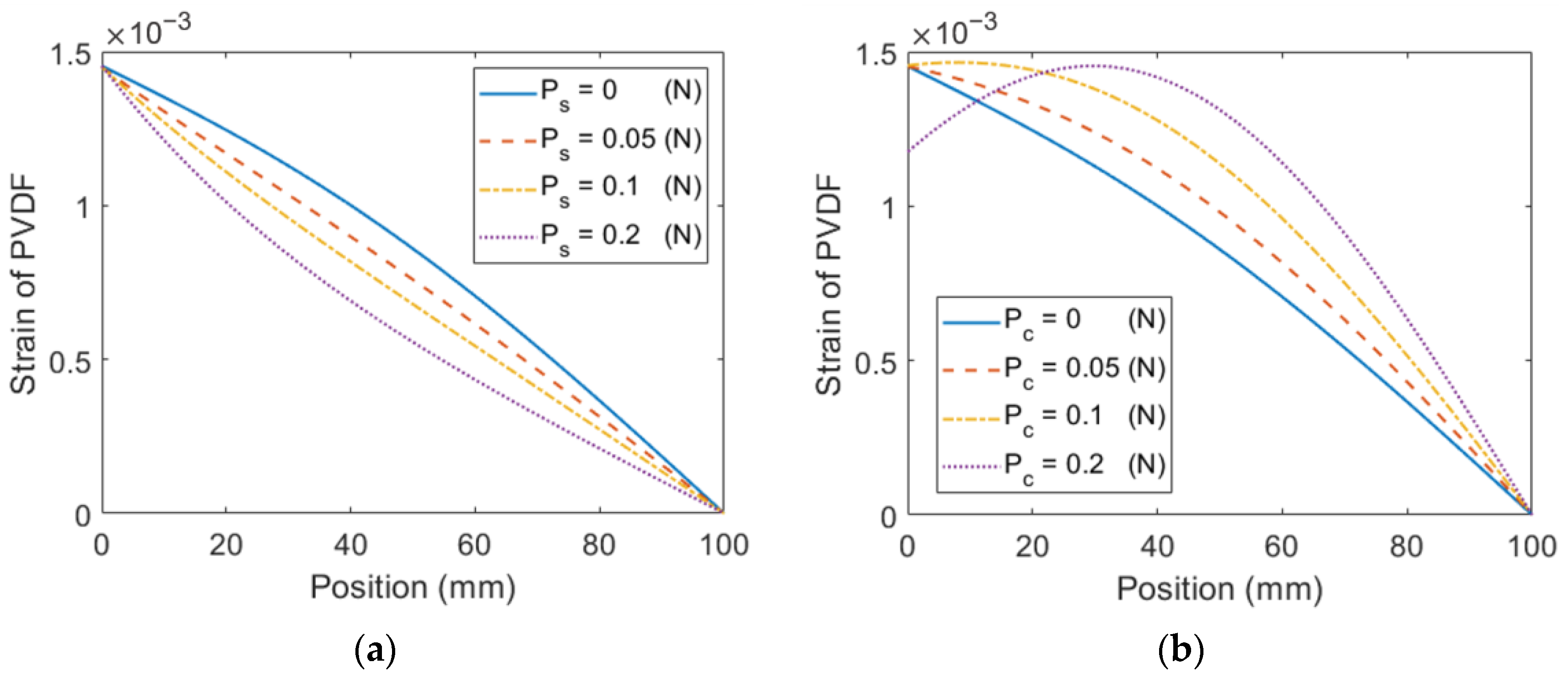
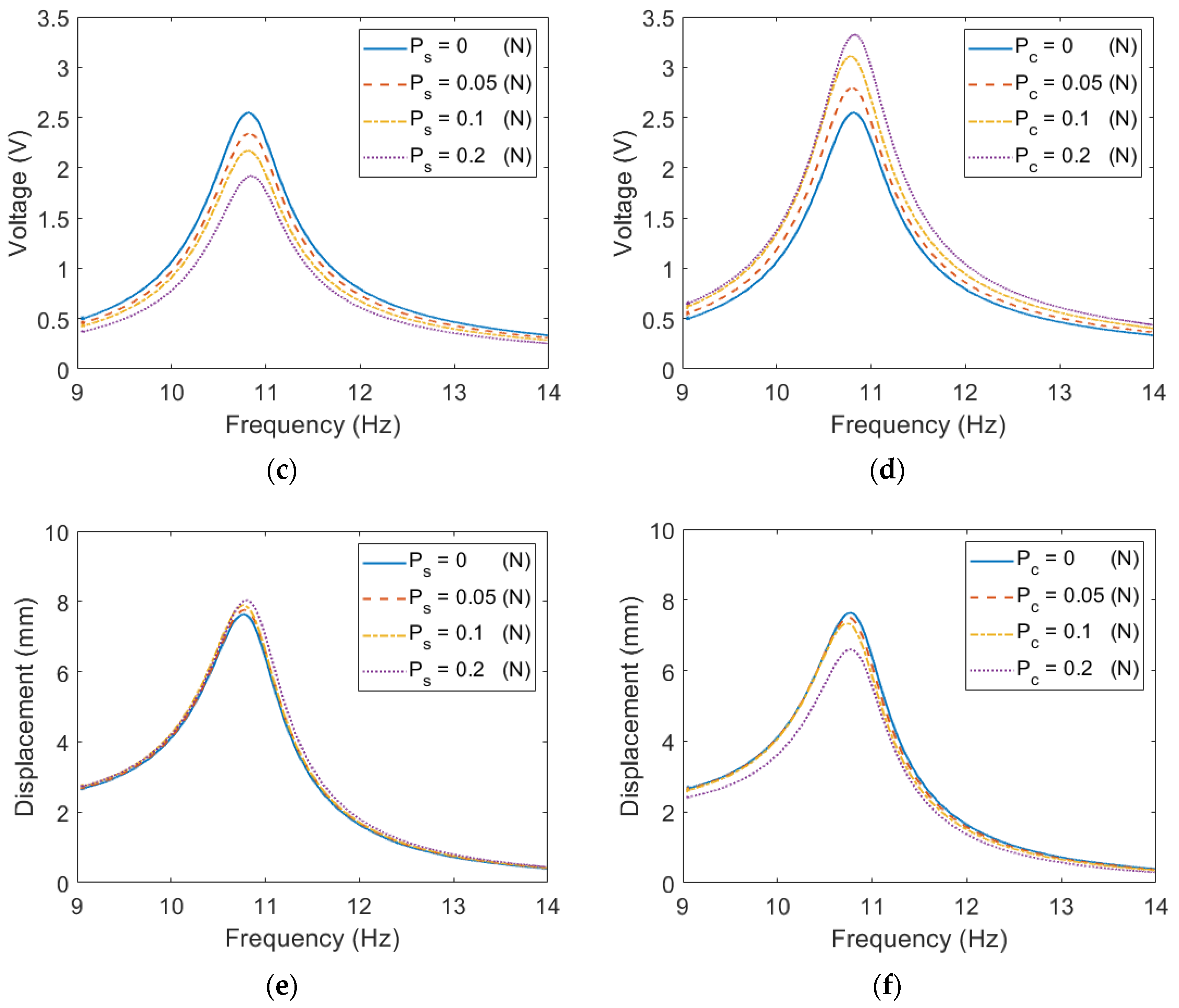
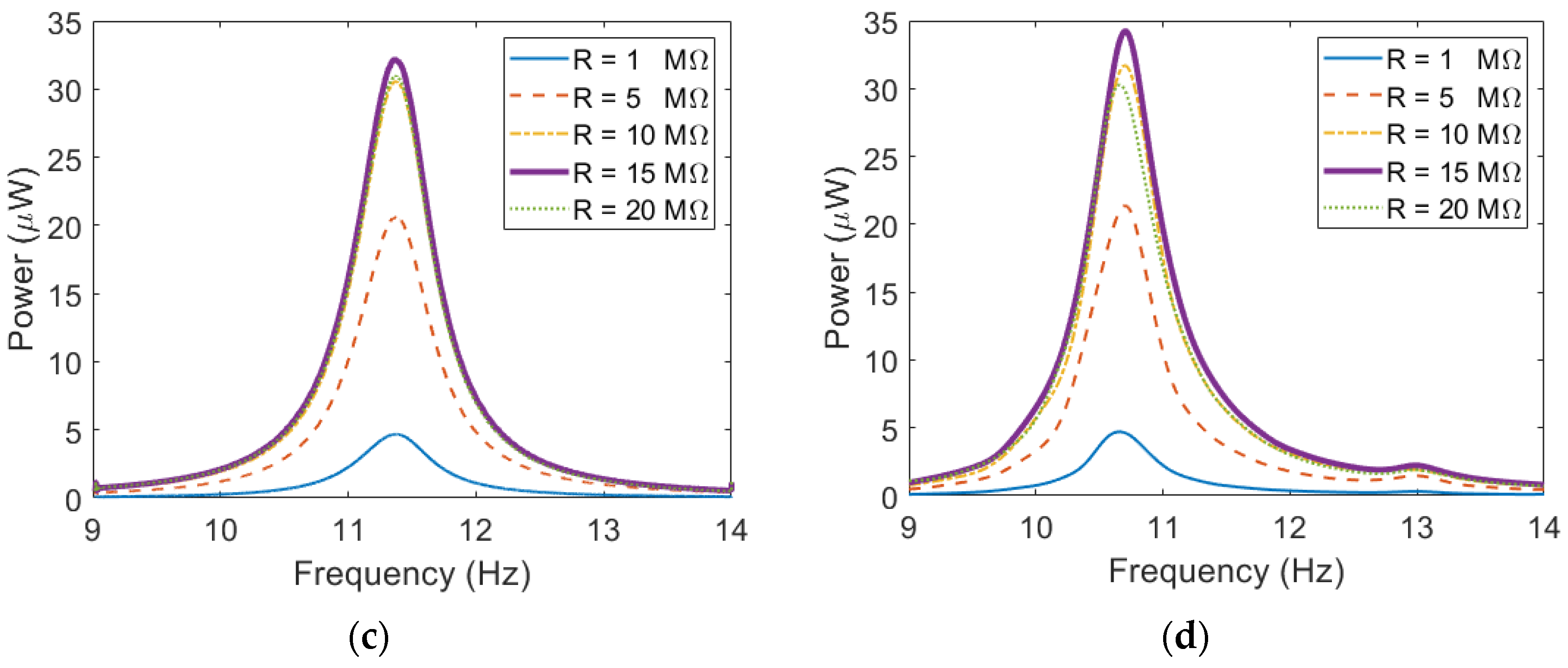
4.3. ESSB PEH with Axial Preload under Base Excitations
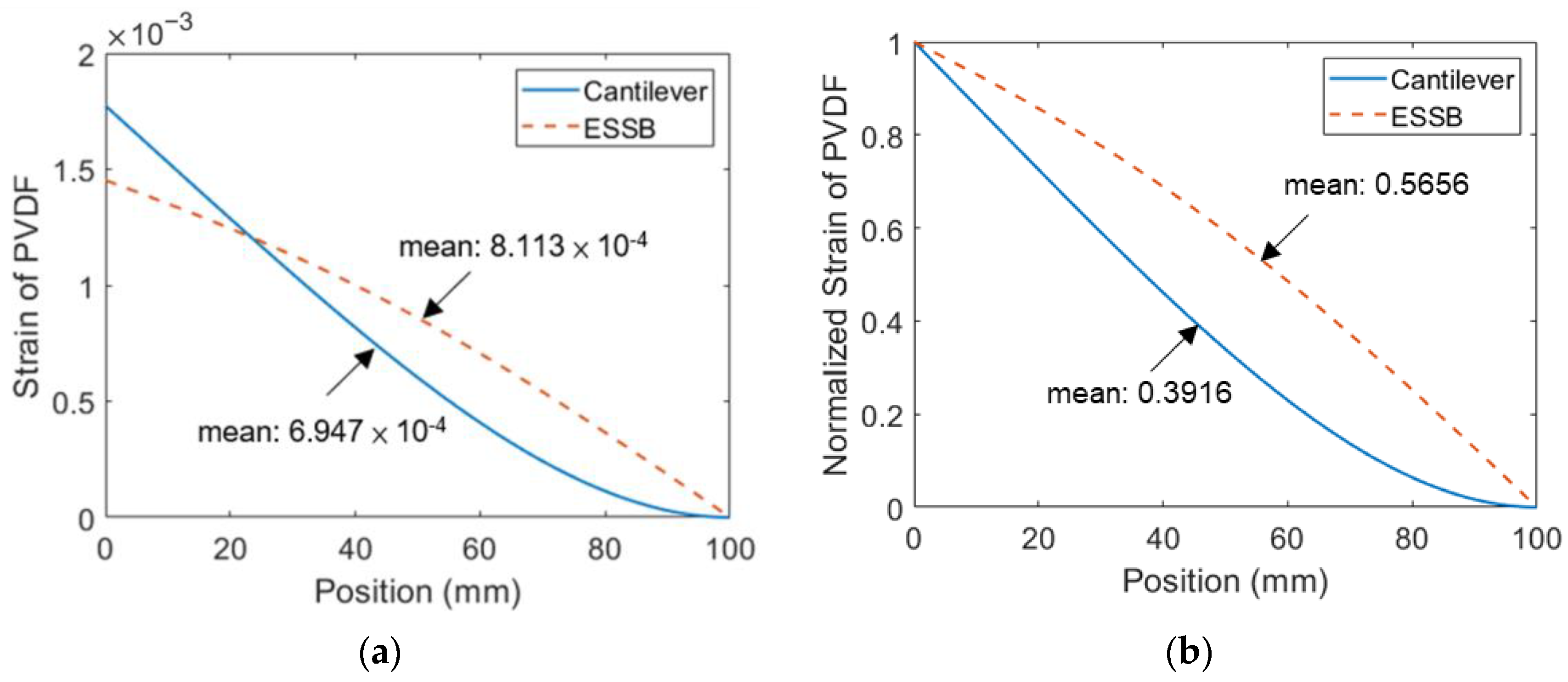
4.4. Comparison between the ESSB PEH and the Cantilevered PEH
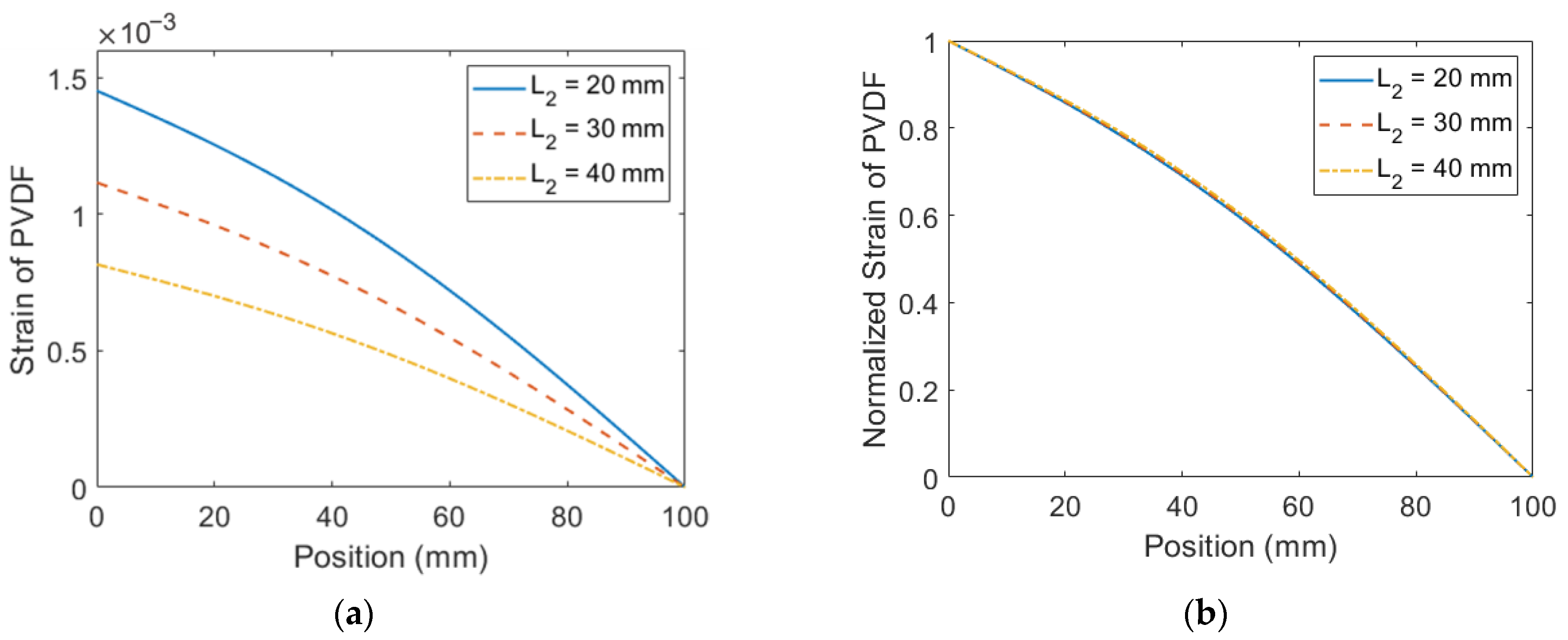
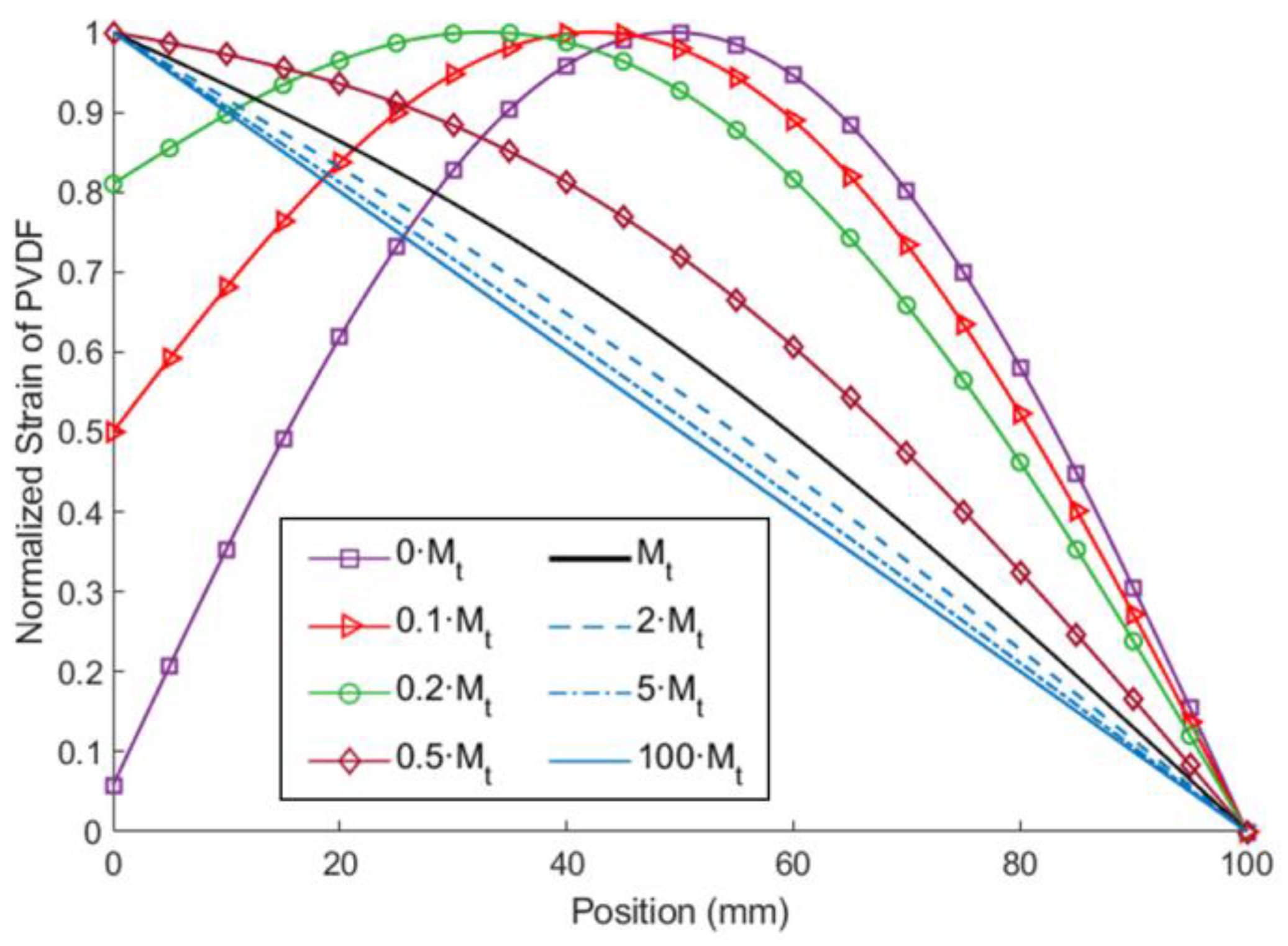
4.5. Influence of Tip Mass on Strain Distribution of the ESSB PEH
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Qi, S.; Shuttleworth, R.; Olutunde Oyadiji, S.; Wright, J. Design of a multiresonant beam for broadband piezoelectric energy harvesting. Smart Mater. Struct. 2010, 19, 094009. [Google Scholar] [CrossRef]
- Wu, H.; Tang, L.; Yang, Y.; Soh, C.K. A novel two-degrees-of-freedom piezoelectric energy harvester. J. Intell. Mater. Syst. Struct. 2012, 24, 357–368. [Google Scholar] [CrossRef]
- Erturk, A.; Renno, J.M.; Inman, D.J. Modeling of Piezoelectric Energy Harvesting from an L-shaped Beam-mass Structure with an Application to UAVs. J. Intell. Mater. Syst. Struct. 2009, 20, 529–544. [Google Scholar] [CrossRef]
- Li, X.; Upadrashta, D.; Yu, K.; Yang, Y. Analytical modeling and validation of multi-mode piezoelectric energy harvester. Mech. Syst. Signal Process. 2019, 124, 613–631. [Google Scholar] [CrossRef]
- Su, W.-J.; Shih, H.-A. A U-shaped multi-modal bi-directional piezoelectric energy harvester. Appl. Phys. Lett. 2018, 113, 071905. [Google Scholar] [CrossRef]
- Cao, Y.; Cao, D.; He, G.; Ge, X.; Hao, Y. Vibration analysis and distributed piezoelectric energy harvester design for the L-shaped beam. Eur. J. Mech. A/Solids 2021, 87, 104214. [Google Scholar] [CrossRef]
- Ferrari, M.; Ferrari, V.; Guizzetti, M.; Marioli, D.; Taroni, A. Piezoelectric multifrequency energy converter for power harvesting in autonomous microsystems. Sens. Actuators A Phys. 2008, 142, 329–335. [Google Scholar] [CrossRef]
- Liu, J.Q.; Fang, H.-B.; Xu, Z.-Y.; Mao, X.-H.; Shen, X.-C.; Chen, D.; Liao, H.; Cai, B.-C. A MEMS-based piezoelectric power generator array for vibration energy harvesting. Microelectron. J. 2008, 39, 802–806. [Google Scholar] [CrossRef]
- Xue, H.; Hu, Y.; Wang, Q.M. Broadband piezoelectric energy harvesting devices using multiple bimorphs with different operating frequencies. IEEE Trans Ultrason. Ferroelectr. Freq. Control 2008, 55, 2104–2108. [Google Scholar] [CrossRef]
- Sebald, G.; Kuwano, H.; Guyomar, D.; Ducharne, B. Experimental Duffing oscillator for broadband piezoelectric energy harvesting. Smart Mater. Struct. 2011, 20, 102001. [Google Scholar] [CrossRef]
- Yan, Z.; Sun, W.; Hajj, M.R.; Zhang, W.; Tan, T. Ultra-broadband piezoelectric energy harvesting via bistable multi-hardening and multi-softening. Nonlinear Dyn. 2020, 100, 1057–1077. [Google Scholar] [CrossRef]
- Zhao, D.; Wang, X.; Cheng, Y.; Liu, S.; Wu, Y.; Chai, L.; Liu, Y.; Cheng, Q. Analysis of single-degree-of-freedom piezoelectric energy harvester with stopper by incremental harmonic balance method. Mater. Res. Express 2018, 5, 055502. [Google Scholar] [CrossRef]
- Yang, Z.; Zu, J. Toward Harvesting Vibration Energy from Multiple Directions by a Nonlinear Compressive-Mode Piezoelectric Transducer. IEEE/ASME Trans. Mechatron. 2016, 21, 1787–1791. [Google Scholar] [CrossRef]
- Abdelkefi, A.; Barsallo, N. Comparative modeling of low-frequency piezomagnetoelastic energy harvesters. J. Intell. Mater. Syst. Struct. 2014, 25, 1771–1785. [Google Scholar] [CrossRef]
- Stanton, S.C.; McGehee, C.C.; Mann, B.P. Nonlinear dynamics for broadband energy harvesting: Investigation of a bistable piezoelectric inertial generator. Phys. D Nonlinear Phenom. 2010, 239, 640–653. [Google Scholar] [CrossRef]
- Zou, H.-X.; Zhang, W.-M.; Li, W.-B.; Hu, K.-M.; Wei, K.-X.; Peng, Z.-K.; Meng, G. A broadband compressive-mode vibration energy harvester enhanced by magnetic force intervention approach. Appl. Phys. Lett. 2017, 110, 163904. [Google Scholar] [CrossRef]
- Roundy, S.; Leland, E.S.; Baker, J.; Carleton, E.; Reilly, E.; Lai, E.; Otis, B.; Rabaey, J.M.; Sundararajan, V.; Wright, P.K. Improving Power Output for Vibration-Based Energy Scavengers. IEEE Pervasive Comput. 2005, 4, 28–36. [Google Scholar] [CrossRef]
- Goldschmidtboeing, F.; Woias, P. Characterization of different beam shapes for piezoelectric energy harvesting. J. Micromech. Microeng. 2008, 18, 104013. [Google Scholar] [CrossRef]
- Benasciutti, D.; Moro, L.; Zelenika, S.; Brusa, E. Vibration energy scavenging via piezoelectric bimorphs of optimized shapes. Microsyst. Technol. 2009, 16, 657–668. [Google Scholar] [CrossRef]
- Dietl, J.M.; Garcia, E. Beam Shape Optimization for Power Harvesting. J. Intell. Mater. Syst. Struct. 2010, 21, 633–646. [Google Scholar] [CrossRef]
- Reilly, E.K.; Burghardt, F.; Fain, R.; Wright, P. Powering a wireless sensor node with a vibration-driven piezoelectric energy harvester. Smart Mater. Struct. 2011, 20, 125006. [Google Scholar] [CrossRef]
- Paquin, S.; St-Amant, Y. Improving the performance of a piezoelectric energy harvester using a variable thickness beam. Smart Mater. Struct. 2010, 19, 105020. [Google Scholar] [CrossRef]
- Čeponis, A.; Mažeika, D.; Bakanauskas, V. Trapezoidal Cantilevers with Irregular Cross-Sections for Energy Harvesting Systems. Appl. Sci. 2017, 7, 134. [Google Scholar] [CrossRef]
- Emad, A.; Mahmoud, M.A.E.; Ghoneima, M.; Dessouky, M. Testing and evaluation of stretching strain in clamped–clamped beams for energy harvesting. Smart Mater. Struct. 2016, 25, 115006. [Google Scholar] [CrossRef]
- Hajati, A.; Kim, S.-G. Ultra-wide bandwidth piezoelectric energy harvesting. Appl. Phys. Lett. 2011, 99, 083105. [Google Scholar] [CrossRef]
- Liu, W.; Yuan, Z.; Zhang, S.; Zhu, Q. Enhanced broadband generator of dual buckled beams with simultaneous translational and torsional coupling. Appl. Energy 2019, 251, 113412. [Google Scholar] [CrossRef]
- Li, Z.; Naguib, H.E. Effect of revolute joint mechanism on the performance of cantilever piezoelectric energy harvester. Smart Mater. Struct. 2019, 28, 085043. [Google Scholar] [CrossRef]
- Li, Z.; Yang, Z.; Naguib, H.E. Introducing revolute joints into piezoelectric energy harvesters. Energy 2020, 192, 116604. [Google Scholar] [CrossRef]
- Yang, Z.; Wang, Y.Q.; Zuo, L.; Zu, J. Introducing arc-shaped piezoelectric elements into energy harvesters. Energy Convers. Manag. 2017, 148, 260–266. [Google Scholar] [CrossRef]
- Lu, Z.-Q.; Chen, J.; Ding, H.; Chen, L.-Q. Two-span piezoelectric beam energy harvesting. Int. J. Mech. Sci. 2020, 175, 105532. [Google Scholar] [CrossRef]
- Patel, R.; Tanaka, Y.; McWilliam, S.; Mutsuda, H.; Popov, A.A. Simply-supported multi-layered beams for energy harvesting. J. Intell. Mater. Syst. Struct. 2017, 28, 740–759. [Google Scholar] [CrossRef]
- Rajora, A.; Dwivedi, A.; Vyas, A.; Gupta, S.; Tyagi, A. Energy Harvesting Estimation from the Vibration of a Simply Supported Beam. Int. J. Acoust. Vib. 2017, 22, 186–193. [Google Scholar] [CrossRef]
- Dehghan Hamani, I.; Tikani, R.; Assadi, H.; Ziaei-Rad, S. Energy harvesting from moving harmonic and moving continuous mass traversing on a simply supported beam. Measurement 2020, 150, 107080. [Google Scholar] [CrossRef]
- Chen, Y.; Yan, Z. Nonlinear analysis of axially loaded piezoelectric energy harvesters with flexoelectricity. Int. J. Mech. Sci. 2020, 173, 105473. [Google Scholar] [CrossRef]
- Assadi, H.; Dehghan Hamani, I.; Tikani, R.; Ziaei-Rad, S. An experimental and analytical piezoelectric energy harvesting from a simply supported beam with moving mass. J. Intell. Mater. Syst. Struct. 2016, 27, 2408–2415. [Google Scholar] [CrossRef]
- Xu, C.; Liang, Z.; Ren, B.; Di, W.; Luo, H.; Wang, D.; Wang, K.; Chen, Z. Bi-stable energy harvesting based on a simply supported piezoelectric buckled beam. J. Appl. Phys. 2013, 114, 114507. [Google Scholar] [CrossRef]
- Zhu, Y.; Zu, J.; Su, W. Broadband energy harvesting through a piezoelectric beam subjected to dynamic compressive loading. Smart Mater. Struct. 2013, 22, 045007. [Google Scholar] [CrossRef]
- Xu, C.; Ren, B.; Di, W.; Liang, Z.; Jiao, J.; Li, L.; Li, L.; Zhao, X.; Luo, H.; Wang, D. Cantilever driving low frequency piezoelectric energy harvester using single crystal material 0.71Pb(Mg1/3Nb2/3)O3-0.29PbTiO3. Appl. Phys. Lett. 2012, 101, 033502. [Google Scholar] [CrossRef]
- Liu, W.Q.; Badel, A.; Formosa, F.; Wu, Y.P.; Agbossou, A. Wideband energy harvesting using a combination of an optimized synchronous electric charge extraction circuit and a bistable harvester. Smart Mater. Struct. 2013, 22, 125038. [Google Scholar] [CrossRef]
- Liu, W.; Formosa, F.; Badel, A.; Wu, Y.; Agbossou, A. Self-powered nonlinear harvesting circuit with a mechanical switch structure for a bistable generator with stoppers. Sens. Actuators A Phys. 2014, 216, 106–115. [Google Scholar] [CrossRef]
- Liu, W.; Formosa, F.; Badel, A. Optimization study of a piezoelectric bistable generator with doubled voltage frequency using harmonic balance method. J. Intell. Mater. Syst. Struct. 2016, 28, 671–686. [Google Scholar] [CrossRef]
- Li, Z.; Saadatnia, Z.; Yang, Z.; Naguib, H. A hybrid piezoelectric-triboelectric generator for low-frequency and broad-bandwidth energy harvesting. Energy Convers. Manag. 2018, 174, 188–197. [Google Scholar] [CrossRef]
- Yang, Z.; Zu, J. High-efficiency compressive-mode energy harvester enhanced by a multi-stage force amplification mechanism. Energy Convers. Manag. 2014, 88, 829–833. [Google Scholar] [CrossRef]
- Yang, Z.; Zu, J.; Luo, J.; Peng, Y. Modeling and parametric study of a force-amplified compressive-mode piezoelectric energy harvester. J. Intell. Mater. Syst. Struct. 2016, 28, 357–366. [Google Scholar] [CrossRef]
- Chang, H.-L.; Su, W.-J. Design and development of a high-performance tensile-mode piezoelectric energy harvester based on a three-hinged force-amplification mechanism. Smart Mater. Struct. 2022, 31, 075018. [Google Scholar] [CrossRef]
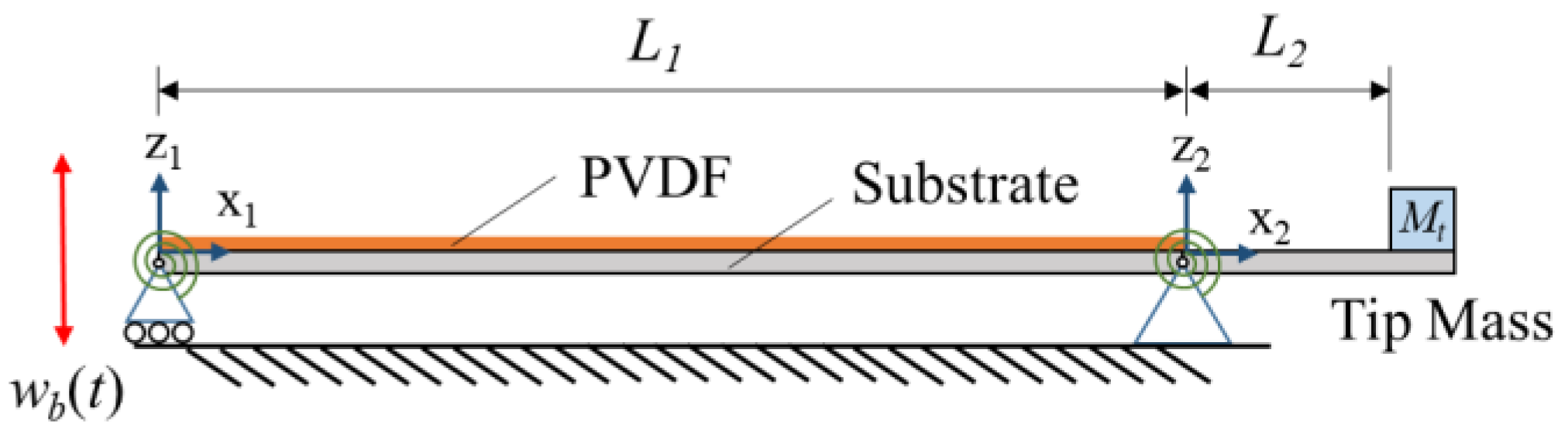
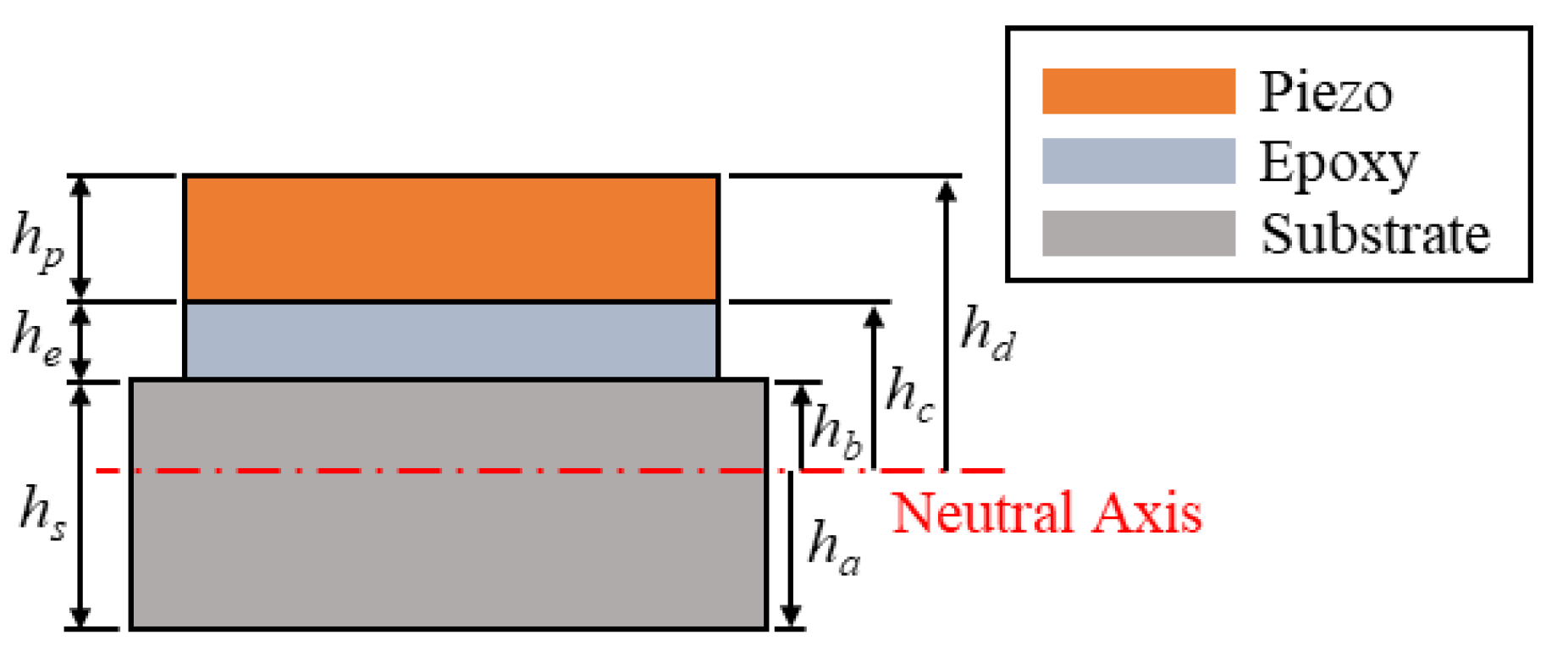

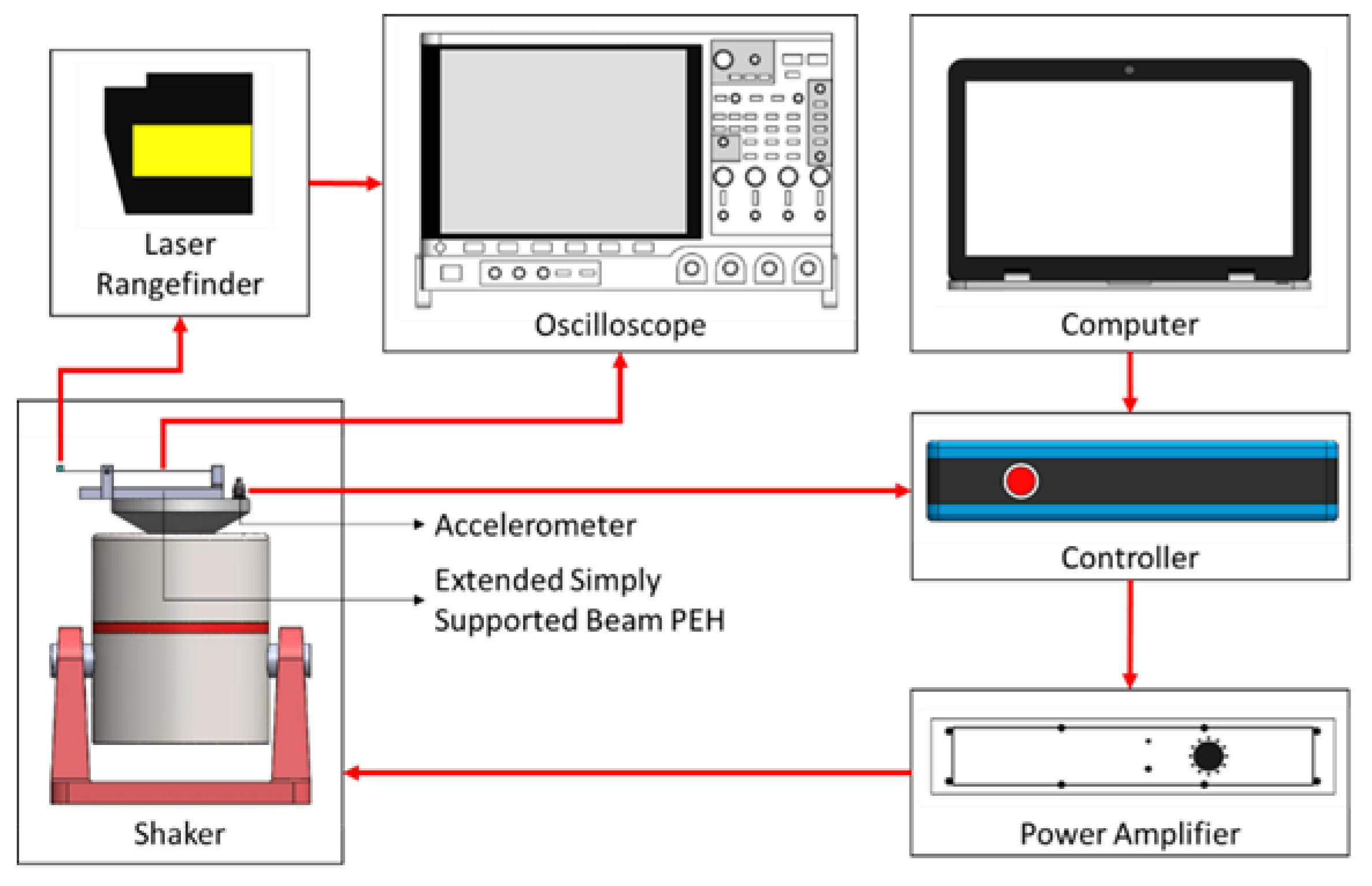
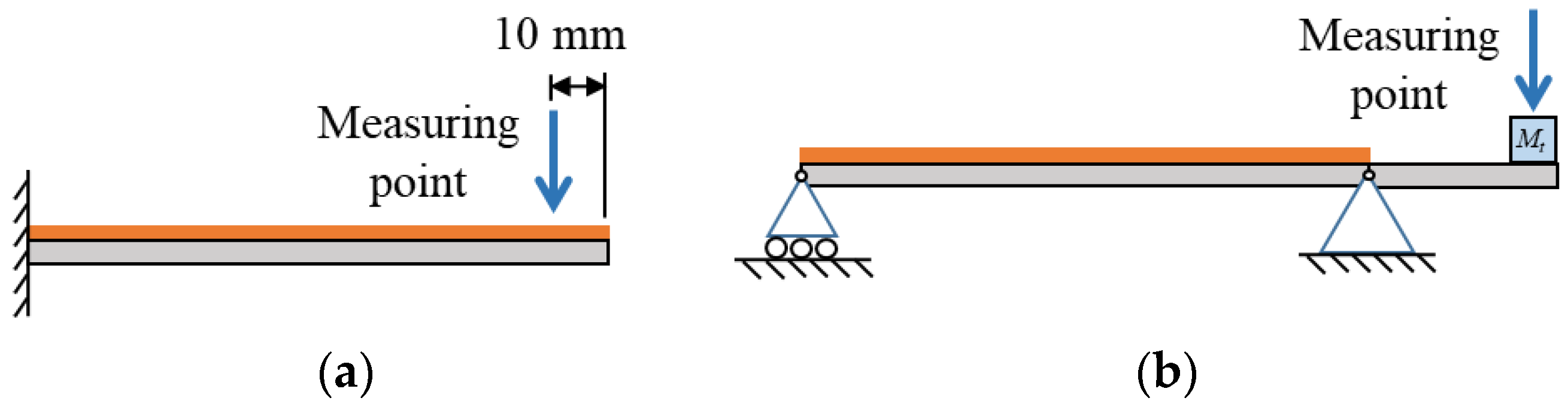



| Symbol | Description | Value | ||
|---|---|---|---|---|
| Config. 1 | Config. 2 | Config. 3 | ||
| L2 | Length of the extended beam | 20 mm | 30 mm | 40 mm |
| Mt | Tip mass | 4.9 g | 1.9 g | 0.9 g |
| ζ | damping ratio | 0.035 | 0.0265 | 0.0245 |
| bx | Width of the extended beam | 12.7 mm | ||
| hx | Thickness of the extended beam | 0.1 mm | ||
| ρx | Density of the extended beam | 7930 kg/m3 | ||
| Yx | Young’s modulus of the extended beam | 193 GPa | ||
| L1 | Length of the main beam | 100 mm | ||
| bs | Width of the substrate | 12.7 mm | ||
| hs | Thickness of the substrate | 0.1 mm | ||
| ρs | Density of the substrate | 7930 kg/m3 | ||
| Ys | Young’s modulus of the substrate | 193 Gpa | ||
| be | Width of the epoxy | 10 mm | ||
| he | Thickness of the epoxy | 0.09 mm | ||
| ρe | Density of the epoxy | 1200 kg/m3 | ||
| Ye | Young’s modulus of the epoxy | 27 Mpa | ||
| bp | Width of the PVDF | 10 mm | ||
| hp | Thickness of the PVDF | 0.2 mm | ||
| ρp | Density of the PVDF | 1780 kg/m3 | ||
| Yp | Young’s modulus of the PVDF | 2.9 Gpa | ||
| Cp | Capacitance of the PVDF | 1 nF | ||
| d31 | Piezoelectric constant of the PVDF | 16 pm/V | ||
| Symbol | Description | Value | |||
|---|---|---|---|---|---|
| Config. A | Config. B | Config. C | Config. D | ||
| k1 | Stiffness | 0 N/rad | 10−3 N/rad | 10−2 N/rad | 10−1 N/rad |
| Le | Length of the extended beam | 21.9 mm | 22.1 mm | 23.9 mm | 26.2 mm |
| Mt | Tip mass | 4.4 g | 4.33 g | 3.83 g | 3.33 g |
| Symbol | Description | Value | |||
|---|---|---|---|---|---|
| Config. A | Config. B | Config. C | Config. D | ||
| k1 | Stiffness | 0 N/rad | 10−3 N/rad | 10−2 N/rad | 10−1 N/rad |
| Le | Length of the extended beam | 21.9 mm | 21.8 mm | 20 mm | 12.2 mm |
| Mt | Tip mass | 4.4 g | 4.64 g | 7.4 g | 50.6 g |
| Symbol | Description | Value | |||
|---|---|---|---|---|---|
| Config. A | Config. B | Config. C | Config. D | ||
| Ps | Pre-stretching load | 0 N | 0.05 N | 0.1 N | 0.2 N |
| Le | Length of the extended beam | 21.9 mm | 22.9 mm | 23.8 mm | 25.1 mm |
| Mt | Tip mass | 4.4 g | 4.12 g | 3.9 g | 3.61 g |
| Symbol | Description | Value | |||
|---|---|---|---|---|---|
| Config. A | Config. B | Config. C | Config. D | ||
| k1 | Pre-compressing load | 0 N | 0.05 N | 0.1 N | 0.2 N |
| Le | Length of the extended beam | 21.9 mm | 20.8 mm | 19.5 mm | 18.5 mm |
| Mt | Tip mass | 4.4 g | 4.74 g | 5.2 g | 4.9 g |
| Tip Mass | Mean of Normalized Strain |
|---|---|
| 0·Mt | 0.6465 |
| 0.1·Mt | 0.7146 |
| 0.2·Mt | 0.7379 |
| 0.5·Mt | 0.6405 |
| Mt | 0.5656 |
| 2·Mt | 0.5316 |
| 5·Mt | 0.5124 |
| 100·Mt | 0.5006 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Su, W.-J.; Tseng, C.-H. Design and Analysis of an Extended Simply Supported Beam Piezoelectric Energy Harvester. Sensors 2023, 23, 5895. https://doi.org/10.3390/s23135895
Su W-J, Tseng C-H. Design and Analysis of an Extended Simply Supported Beam Piezoelectric Energy Harvester. Sensors. 2023; 23(13):5895. https://doi.org/10.3390/s23135895
Chicago/Turabian StyleSu, Wei-Jiun, and Chu-Hsiang Tseng. 2023. "Design and Analysis of an Extended Simply Supported Beam Piezoelectric Energy Harvester" Sensors 23, no. 13: 5895. https://doi.org/10.3390/s23135895
APA StyleSu, W.-J., & Tseng, C.-H. (2023). Design and Analysis of an Extended Simply Supported Beam Piezoelectric Energy Harvester. Sensors, 23(13), 5895. https://doi.org/10.3390/s23135895







