On the Problem of Double-Filtering in PPP-RTK
Abstract
1. Introduction
2. Optimal Provider-Filter vs. Misspecified User-Filter
2.1. Non-Random Corrections as a Basic Principle
2.2. Optimal Provider-Filter
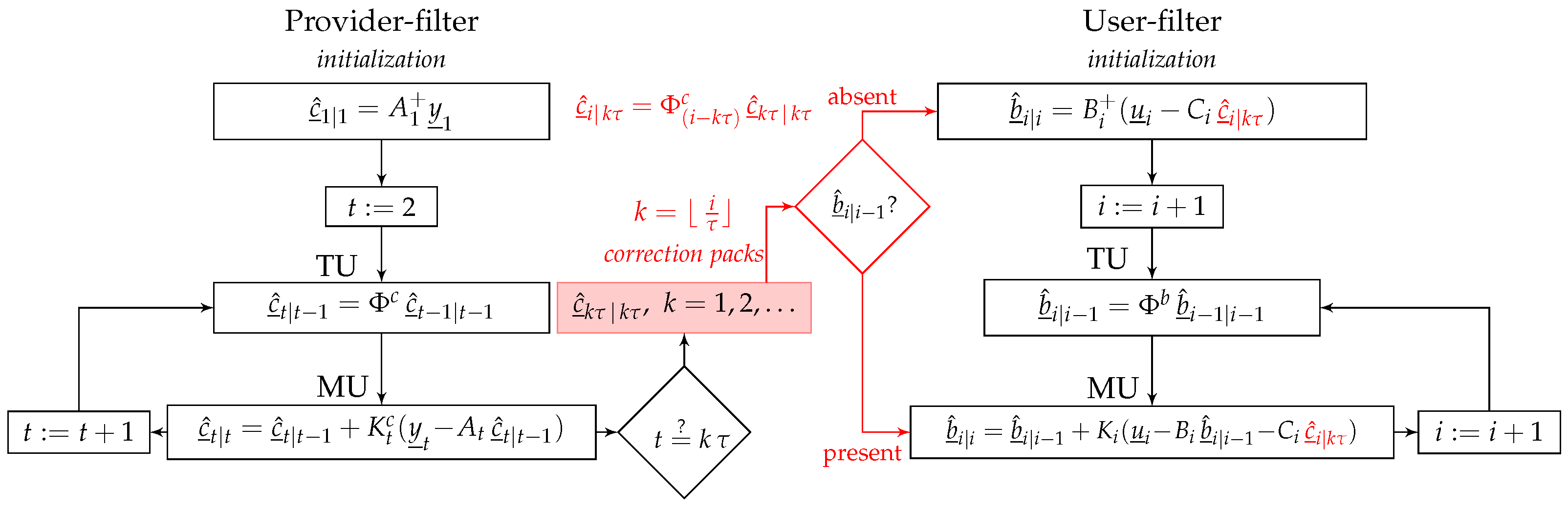
2.3. Misspecified User-Filter
3. On the Choice of the Inverse-Weight Matrix
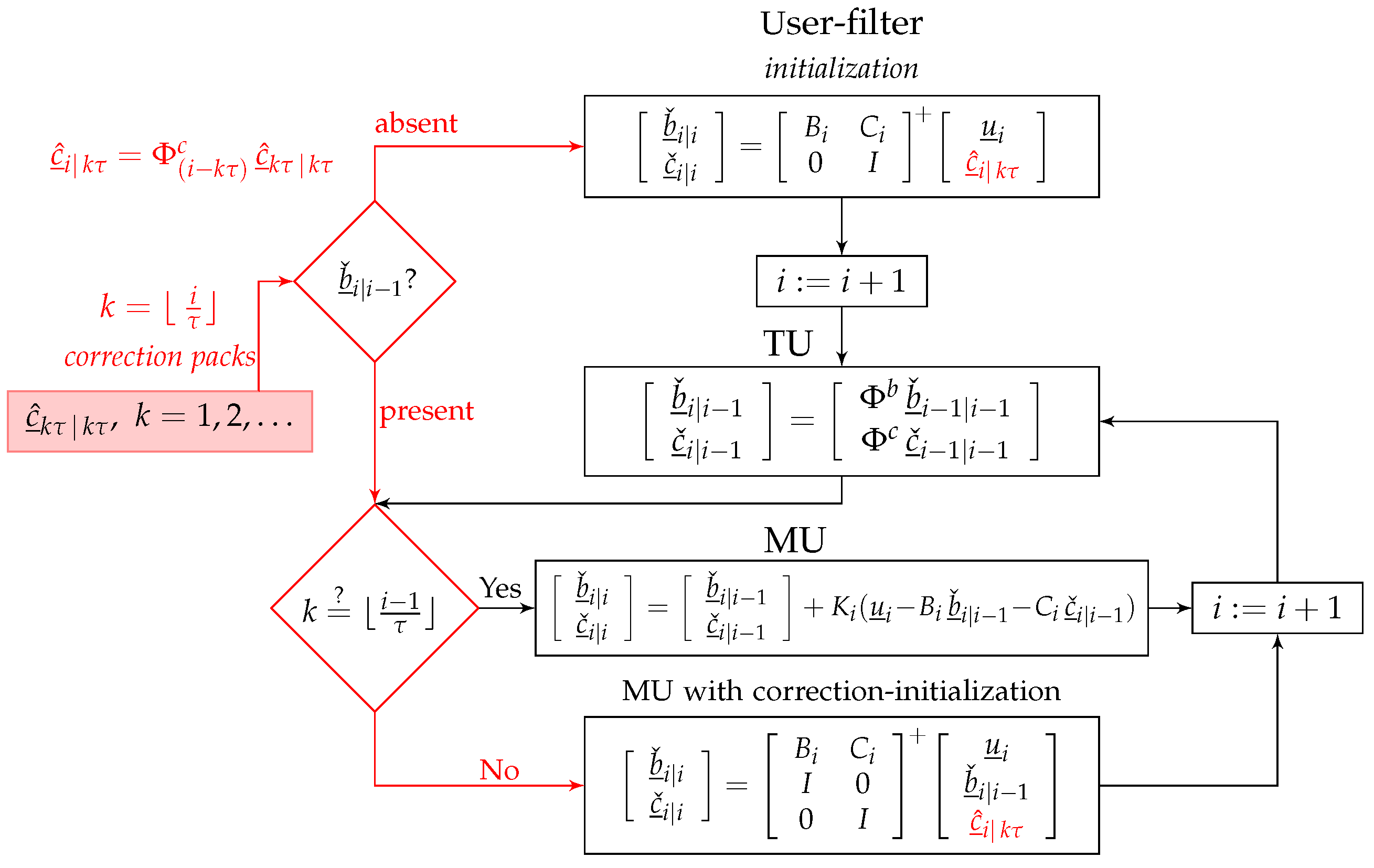
4. User-Filter with Correctional Update
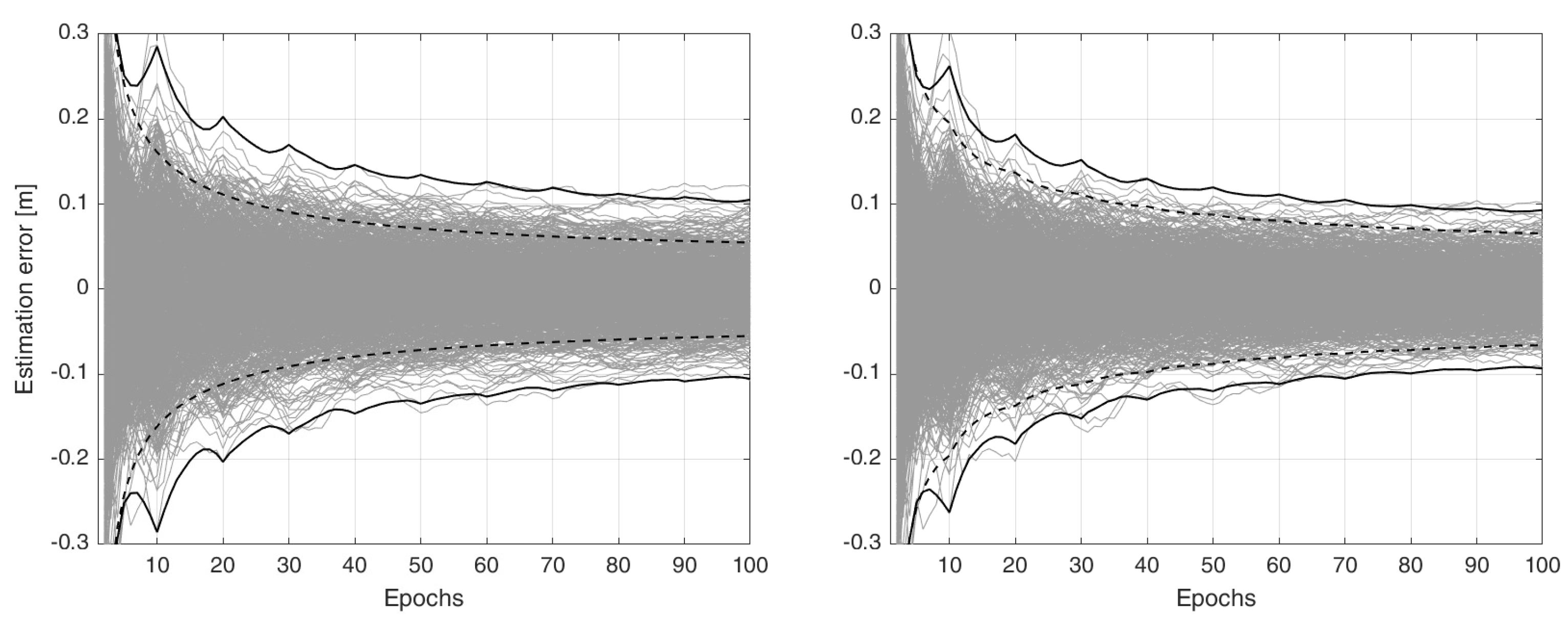
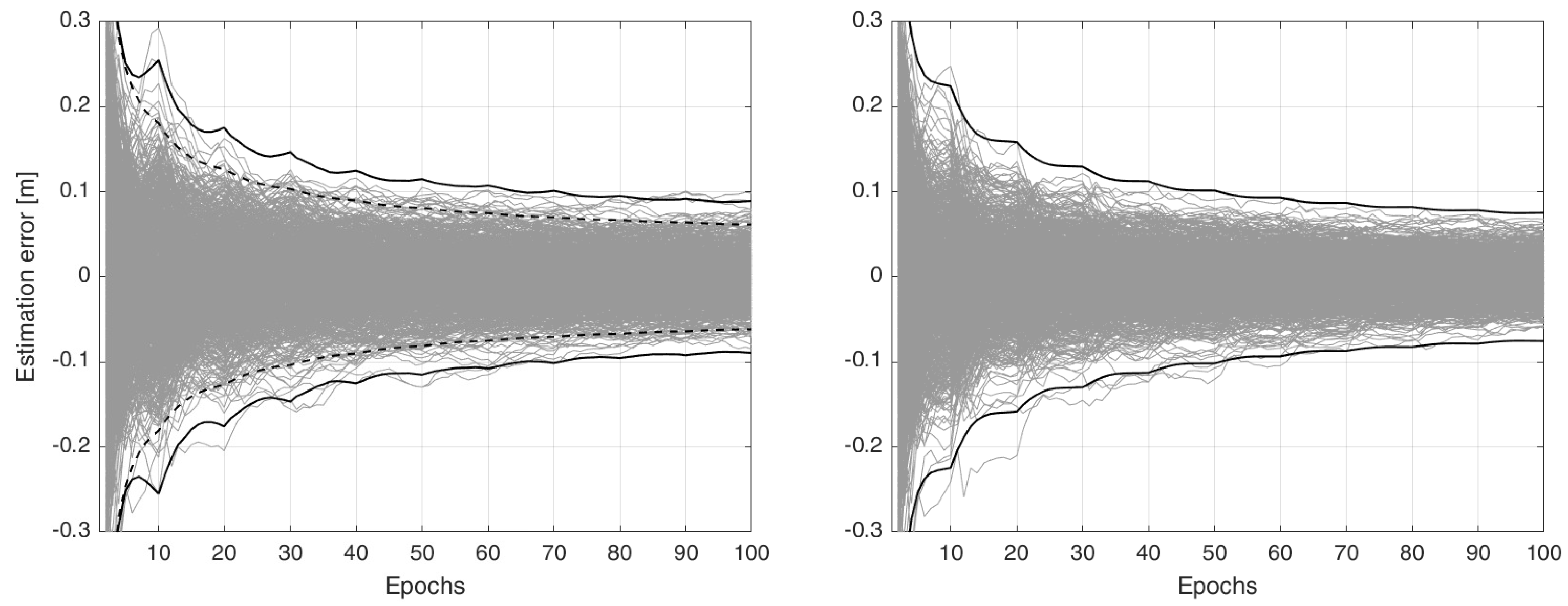
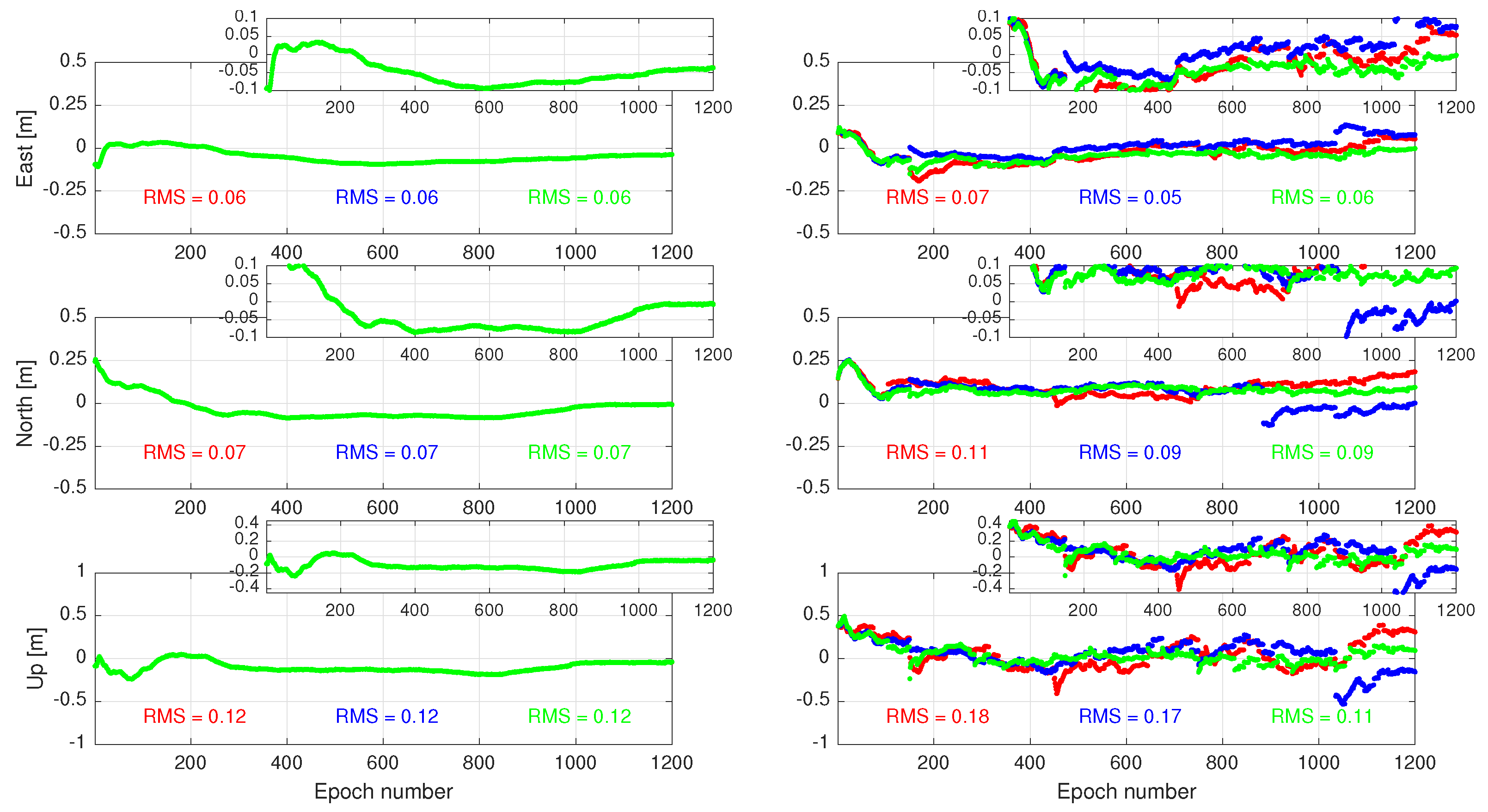
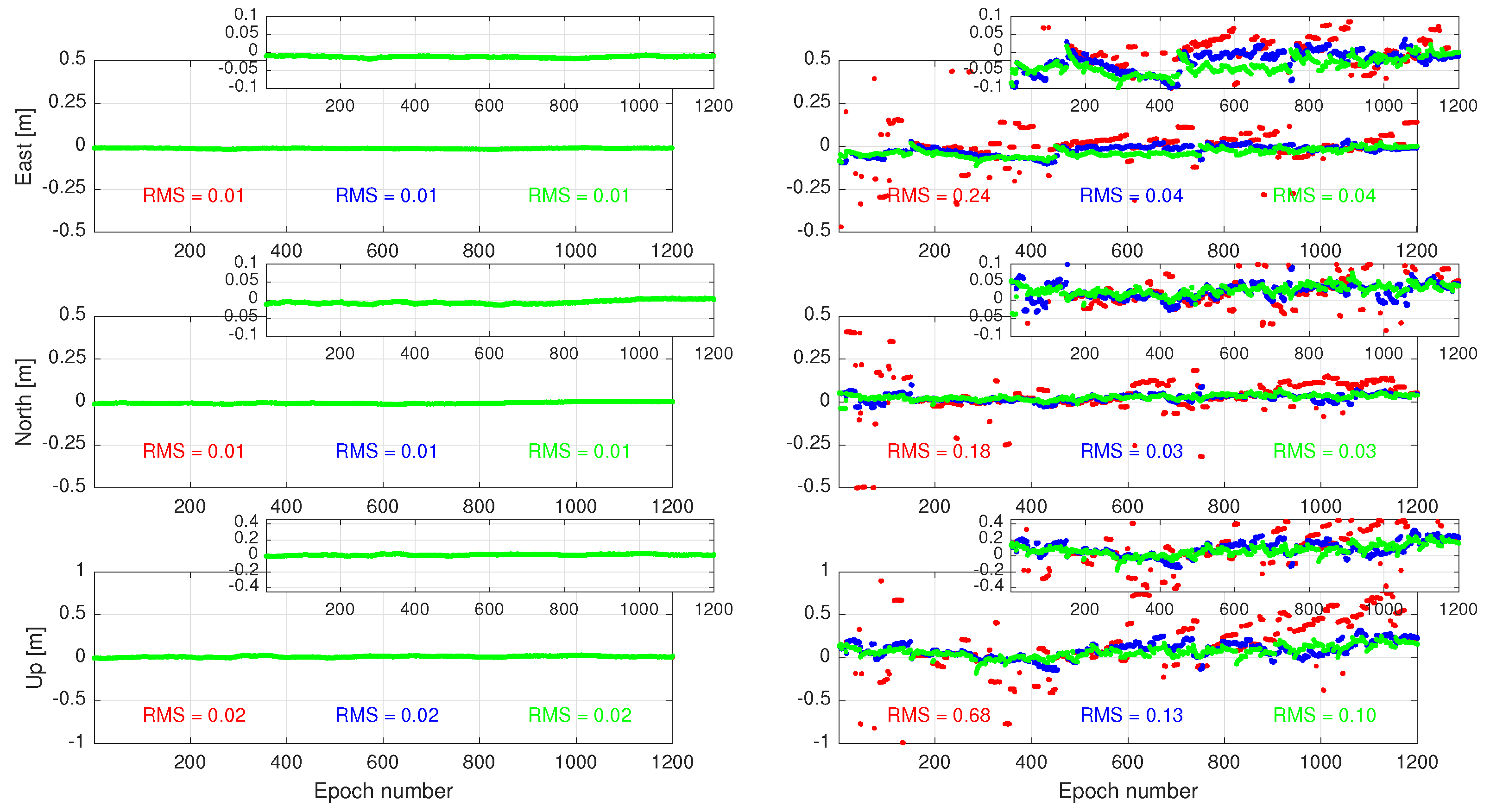
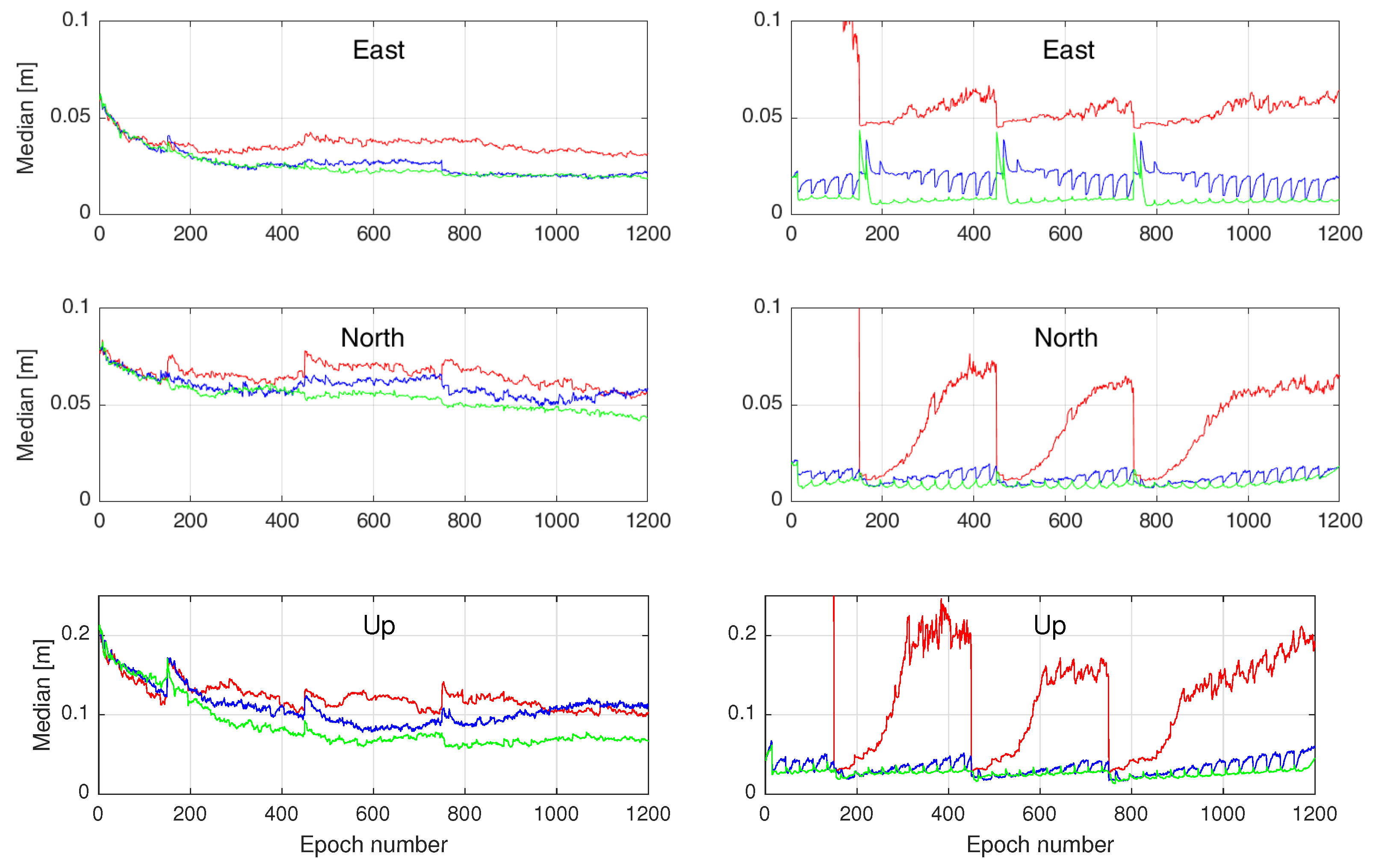
5. A Single-Station PPP-RTK Example
6. Conclusions and Outlook
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Supplementary Proofs
References
- Wubbena, G.; Schmitz, M.; Bagg, A. PPP-RTK: Precise Point Positioning using state-space representation in RTK networks. In Proceedings of the ION GNSS, Long Beach, CA, USA, 13–16 September 2005; pp. 13–16. [Google Scholar]
- Laurichesse, D.; Mercier, F. Integer ambiguity resolution on undifferenced GPS phase measurements and its application to PPP. In Proceedings of the 20th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS 2007), Fort Worth, TX, USA, 25–28 September 2007; pp. 839–848. [Google Scholar]
- Collins, P.; Bisnath, S.; Lahaye, F.; Heroux, P. Undifferenced GPS ambiguity resolution using the decoupled clock model and ambiguity datum fixing. Navigation 2010, 57, 123–135. [Google Scholar] [CrossRef]
- Teunissen, P.J.G.; Odijk, D.; Zhang, B. PPP-RTK: Results of CORS Network-Based PPP with Integer Ambiguity Resolution. J. Aeronaut. Astronaut. Aviat. 2010, 42, 223–229. [Google Scholar]
- Geng, J.; Bock, Y. Triple-frequency GPS precise point positioning with rapid ambiguity resolution. J. Geod. 2013, 87, 449–460. [Google Scholar] [CrossRef]
- Wang, K.; Khodabandeh, A.; Teunissen, P.J.G. A study on predicting network corrections in PPP-RTK processing. Adv. Space Res. 2017, 60, 1463–1477. [Google Scholar] [CrossRef]
- Khodabandeh, A. Single-station PPP-RTK: Correction latency and ambiguity resolution performance. J. Geod. 2021, 95, 1–24. [Google Scholar] [CrossRef]
- Odijk, D.; Teunissen, P.J.G.; Khodabandeh, A. Single-Frequency PPP-RTK: Theory and Experimental Results. IAG Symp. 2014, 139, 167–173. [Google Scholar]
- Psychas, D.; Khodabandeh, A.; Teunissen, P.J.G. Impact and mitigation of neglecting PPP-RTK correctional uncertainty. GPS Solut. 2022, 26, 33. [Google Scholar] [CrossRef]
- Teunissen, P.J.G.; Khodabandeh, A.; Psychas, D. A generalized Kalman filter with its precision in recursive form when the stochastic model is misspecified. J. Geod. 2021, 95, 108. [Google Scholar] [CrossRef]
- Kalman, R.E. A new approach to linear filtering and prediction problems. J. Basic Eng. 1960, 82, 35–45. [Google Scholar] [CrossRef]
- Simon, D. Optimal State Estimation: Kalman, H [Infinity] and Nonlinear Approaches; John Wiley and Sons: Hoboken, NJ, USA, 2006. [Google Scholar]
- Khodabandeh, A.; Teunissen, P.J.G. An analytical study of PPP-RTK corrections: Precision, correlation and user-impact. J. Geod. 2015, 89, 1109–1132. [Google Scholar] [CrossRef]
- Leick, A.; Rapoport, L.; Tatarnikov, D. GPS Satellite Surveying, 4th ed.; John Wiley and Sons: Hoboken, NJ, USA, 2015. [Google Scholar]
- Odijk, D.; Zhang, B.; Khodabandeh, A.; Odolinski, R.; Teunissen, P.J.G. On the estimability of parameters in undifferenced, uncombined GNSS network and PPP-RTK user models by means of S-system theory. J. Geod. 2015, 90, 15–44. [Google Scholar] [CrossRef]
- Teunissen, P.J.G.; Montenbruck, O. (Eds.) Springer Handbook of Global Navigation Satellite Systems; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Zhang, B.; Liu, T.; Yuan, Y. GPS receiver phase biases estimable in PPP-RTK networks: Dynamic characterization and impact analysis. J. Geod. 2018, 92, 659–674. [Google Scholar] [CrossRef]
- Teunissen, P.J.G. Dynamic Data Processing; Series on Mathematical Geodesy and Positioning; Delft University Press: Delft, The Netherlands, 2001. [Google Scholar]
- Teunissen, P.J.G. Adjustment Theory: An Introduction; Series on Mathematical Geodesy and Positioning; Delft University Press: Delft, The Netherlands, 2000. [Google Scholar]
- Vollath, U.; Talbot, N.C.; Glocker, M.; Chen, X.; Leandro, R. GNSS Signal Processing with Delta Phase. WO2012151006 A1, 8 November 2012. [Google Scholar]
- Laurichesse, D. The CNES Real-time PPP with undifferenced integer ambiguity resolution demonstrator. In Proceedings of the 24th International Technical Meeting of The Satellite Division of the Institute of Navigation (ION GNSS 2011), Portland, OR, USA, 20–23 September 2011; pp. 654–662. [Google Scholar]
- Leandro, R.F.; Santos, M.C.; Langley, R.B. Analyzing GNSS data in precise point positioning software. GPS Solut. 2011, 15, 1–13. [Google Scholar] [CrossRef]
- Maybeck, P. Stochastic Models, Estimation, and Control; Academic Press: Cambridge, MA, USA, 1979; Volume 1, Republished in 1994. [Google Scholar]
- Petovello, M.G.; O’Keefe, K.; Lachapelle, G.; Cannon, M.E. Consideration of time-correlated errors in a Kalman filter applicable to GNSS. J. Geod. 2009, 83, 51–56. [Google Scholar] [CrossRef]
- Verhagen, S.; Teunissen, P.J.G. The ratio test for future GNSS ambiguity resolution. GPS Solut. 2013, 17, 535–548. [Google Scholar] [CrossRef]
- Teunissen, P.J.G.; Khodabandeh, A. BLUE, BLUP and the Kalman filter: Some new results. J. Geod. 2013, 87, 461–473. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khodabandeh, A.; Teunissen, P.J.G.; Psychas, D. On the Problem of Double-Filtering in PPP-RTK. Sensors 2023, 23, 229. https://doi.org/10.3390/s23010229
Khodabandeh A, Teunissen PJG, Psychas D. On the Problem of Double-Filtering in PPP-RTK. Sensors. 2023; 23(1):229. https://doi.org/10.3390/s23010229
Chicago/Turabian StyleKhodabandeh, A., P. J. G. Teunissen, and D. Psychas. 2023. "On the Problem of Double-Filtering in PPP-RTK" Sensors 23, no. 1: 229. https://doi.org/10.3390/s23010229
APA StyleKhodabandeh, A., Teunissen, P. J. G., & Psychas, D. (2023). On the Problem of Double-Filtering in PPP-RTK. Sensors, 23(1), 229. https://doi.org/10.3390/s23010229







