Two Models for Time-Domain Simulation of Hybrid Magnetic Bearing’s Characteristics
Abstract
:1. Introduction
- -
- the rotor of the bearing can rotate at very high speeds. The maximum rotational speed is limited by the critical speed of the rotor and stable rotation of the rotor achieved by the control system,
- -
- magnetic bearings generate low losses, caused mainly due to eddy currents and hysteresis in the magnetic material of the stator and rotor. Additionally, at very high speeds, the losses are also caused by friction between the rotor surface and the air. The losses in magnetic bearings are 5 to 20 times lower than in conventional bearings at high speed [4], which significantly reduces operating costs,
- -
- magnetic bearings are lubricant-free; therefore, they do not require sealings, nor a lubrication system, which reduces their maintenance costs,
- -
- magnetic bearings are free of contamination wear, which makes them ideal for use in clean and sterile environments,
- -
- the load of the bearing is limited mainly by the size of the bearing. However, the bearing load also depends on the type of the magnetic material, as well as on the stator construction,
- -
- vibrations of the rotor are isolated from the machine body. Additionally, vibrations of the rotor can be actively suppressed by the control system by adjusting the stiffness and dumping factor of the bearing,
- -
- the control system of the magnetic bearing allows for the easy implementation of the online diagnostics for the electric machine because it can access the position of the rotor and control currents. These signals can be used to determine the operating conditions and performance of the rotating machine,
- -
- magnetic bearings can compensate unbalanced forces of the rotor by the control system,
- -
- the lifetime of the magnetic bearings is almost unlimited because it operates contactless.
2. Description of the Hybrid Magnetic Bearing
3. Dynamic Simulation Model
3.1. Implementation of the Flux-Circuit Directly Coupled Magnetic Equivalent Circuit
3.2. Implementation of the Field-Circuit Indirectly Coupled Finite Element Model
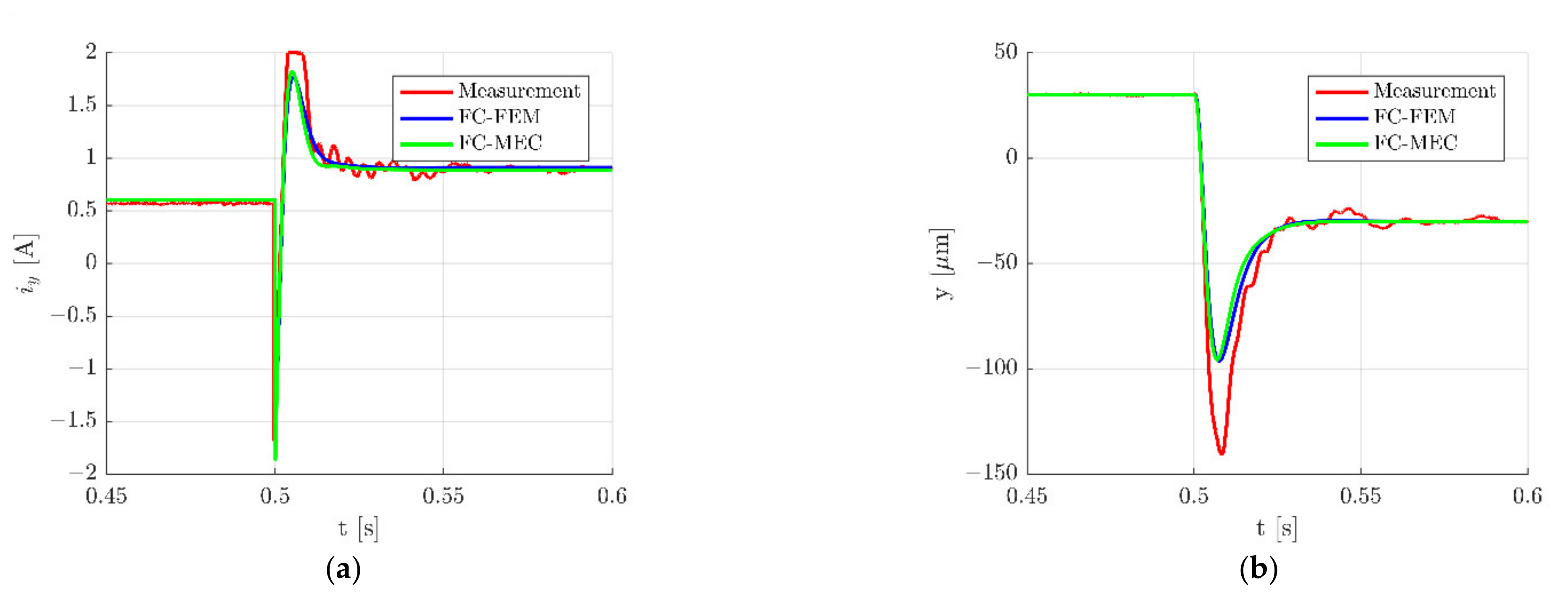
4. Simulation Results
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Sikora, B.M.; Piłat, A.K. Analytical modeling and experimental validation of the six pole axial active magnetic bearing. Appl. Math. Model. 2022, 104, 50–66. [Google Scholar] [CrossRef]
- Nielsen, K.K.; Bahl, C.R.H.; Dagnaes, N.A.; Santos, I.F.; Bjørk, R. A passive permanent magnetic bearing with increased axial lift relative to radial stiffness. IEEE Trans. Magn. 2021, 57, 8300108. [Google Scholar] [CrossRef]
- Liu, G.; Zhu, H.; Wu, M.; Zhang, W. Principle and performance analysis for heteropolar permanent magnet biased radial hybrid magnetic bearing. IEEE Trans. Appl. Supercond. 2020, 30, 3602704. [Google Scholar] [CrossRef]
- Schweitzer, G.; Maslen, H. Magnetic Bearings, Theory, Design, and Application to Rotating Machinery; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Mystkowski, A.; Pawluszewicz, E.; Dragašiusb, E. Robust nonlinear position-flux zero-bias control for uncertain AMB system. Int. J. Control 2015, 88, 1619–1629. [Google Scholar] [CrossRef]
- Gosiewski, Z.; Mystkowski, A. Robust control of active magnetic suspension: Analytical and experimental results. Mech. Syst. Signal Process. 2008, 22, 1297–1303. [Google Scholar] [CrossRef]
- Zhang, D.; Liu, T.; He, C.; Wu, T. A new 2-D multi-slice time-stepping finite element method and its application in analyzing the transient characteristics of induction motors under symmetrical sag conditions. Access IEEE 2018, 6, 47036–47046. [Google Scholar] [CrossRef]
- Ho, S.L.; Niu, S.; Fu, W.N. Transient analysis of a magnetic gear integrated brushless permanent magnet machine using circuit-field-motion coupled time-stepping finite element method. IEEE Trans. Magn. 2010, 46, 2074–2077. [Google Scholar] [CrossRef]
- Barański, M. Field-circuit analysis of lspms motor supplied with distorted voltage. Electr. Eng. 2017, 91, 287–297. [Google Scholar] [CrossRef]
- Nowak, L.; Mikołajewicz, J. Field-circuit model of the dynamics of electromechanical device supplied by electronic power converters. Compel 2004, 23, 977–985. [Google Scholar] [CrossRef]
- Piłat, A. Modelling, investigation, simulation, and PID current control of active magnetic levitation FEM model. In Proceedings of the 18th International Conference on Methods & Models in Automation & Robotics (MMAR 2013), Międzyzdroje, Poland, 26–29 August 2013; pp. 299–304. [Google Scholar]
- Pietrowski, W. 3D analysis of influence of stator winding asymmetry on axial flux. Compel 2013, 32, 1278–1286. [Google Scholar] [CrossRef]
- Tomczuk, B.; Wajnert, D. Field—circuit model of the radial active magnetic bearing system. Electr. Eng. 2018, 100, 2319–2328. [Google Scholar] [CrossRef] [Green Version]
- Waindok, A.; Piekielny, P. Analysis of an iron-core and ironless railguns powered sequentially. Compel 2018, 37, 1707–1721. [Google Scholar] [CrossRef]
- Mohammed, O.A.; Liu, Z.; Liu, S.; Abed, N.Y. Finite-element-based nonlinear physical model of iron-core transformers for dynamic simulations. IEEE Trans. Magn. 2006, 42, 1027–1030. [Google Scholar] [CrossRef]
- Wajnert, D.; Sykulski, J.K.; Tomczuk, B. An enhanced dynamic simulation model of a hybrid magnetic bearing taking account of the sensor noise. Sensors 2020, 20, 1116. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Qian, J.; Chen, X.; Chen, H.; Zeng, L.; Li, X. Magnetic field analysis of lorentz motors using a novel segmented magnetic equivalent circuit method. Sensors 2013, 13, 1664–1678. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wajnert, D.; Tomczuk, B. Nonlinear magnetic equivalent circuit of the hybrid magnetic bearing. Compel 2019, 38, 1190–1203. [Google Scholar] [CrossRef]
- Wajnert, D. Comparison of two constructions of hybrid magnetic bearings. Prz. Elektrotechniczn 2019, 95, 53–58. [Google Scholar] [CrossRef]
- Franklin, G.F.; Powell, J.D.; Emami-Naeini, A. Feedback Control of Dynamic Systems; Pearson: Upper Saddle River, NJ, USA, 2002. [Google Scholar]
- Burden, R.; Faires, J.D. Numerical Analysis; Brooks/Cole: Boston, MA, USA, 2011. [Google Scholar]
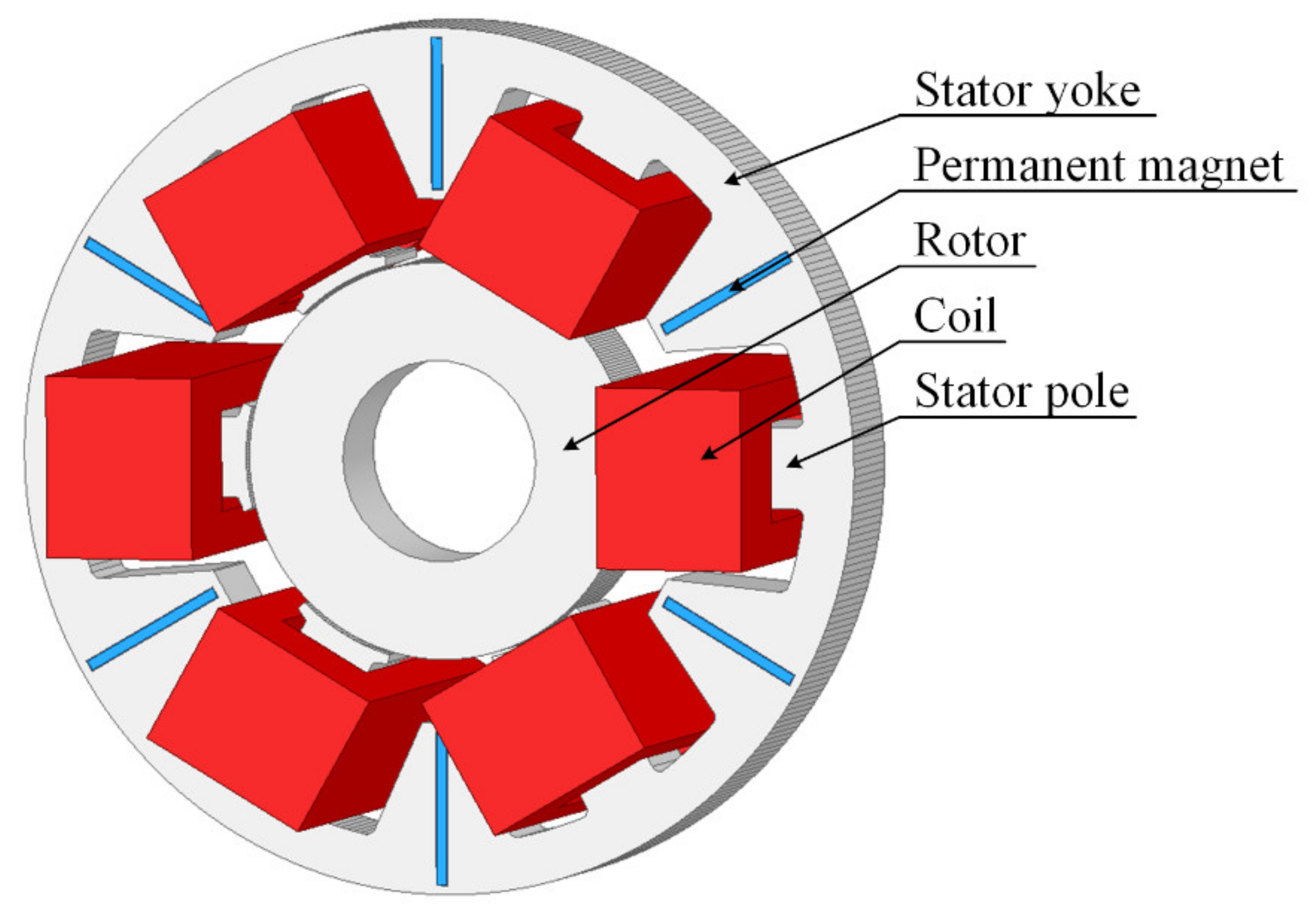
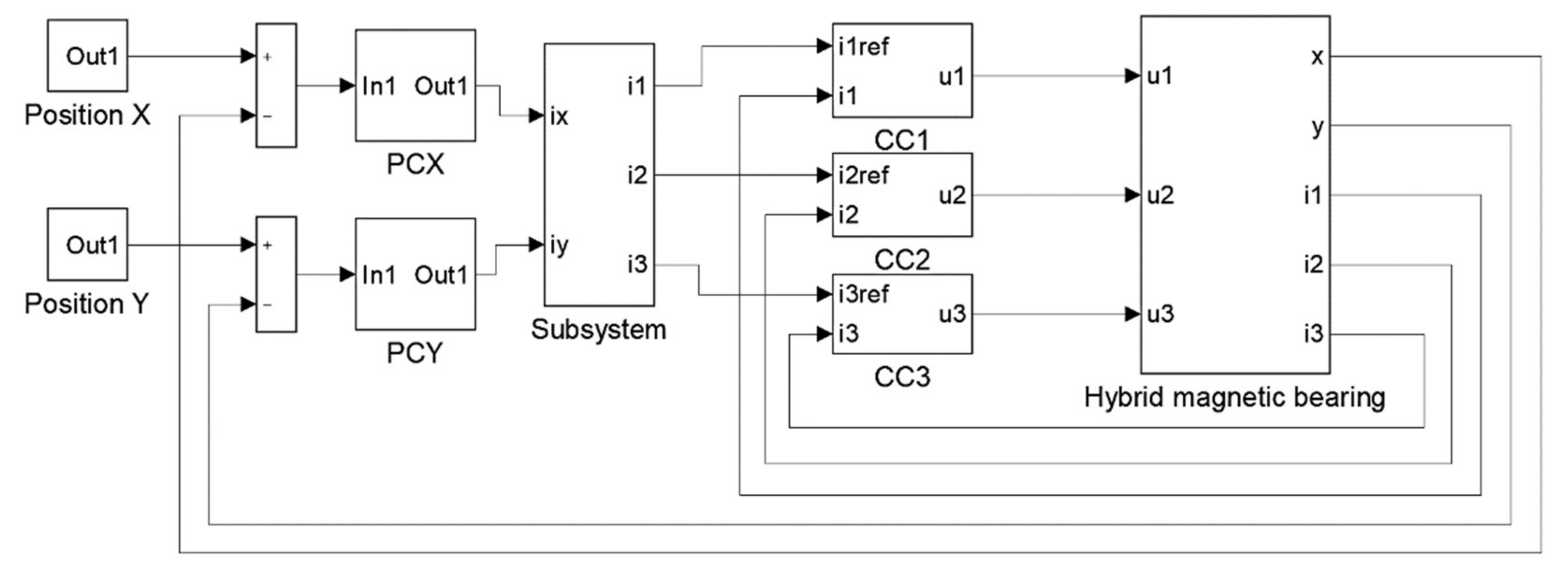

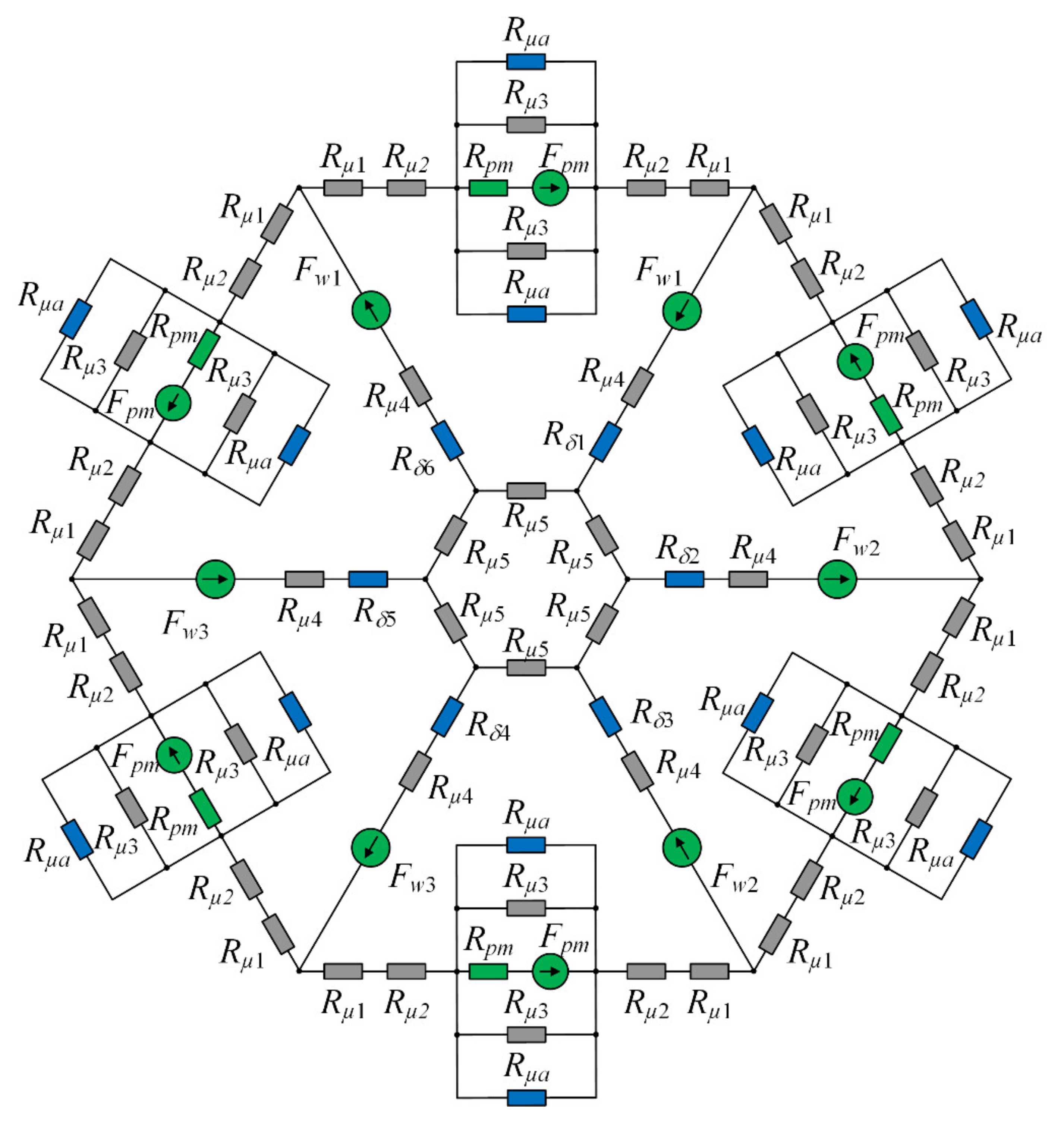
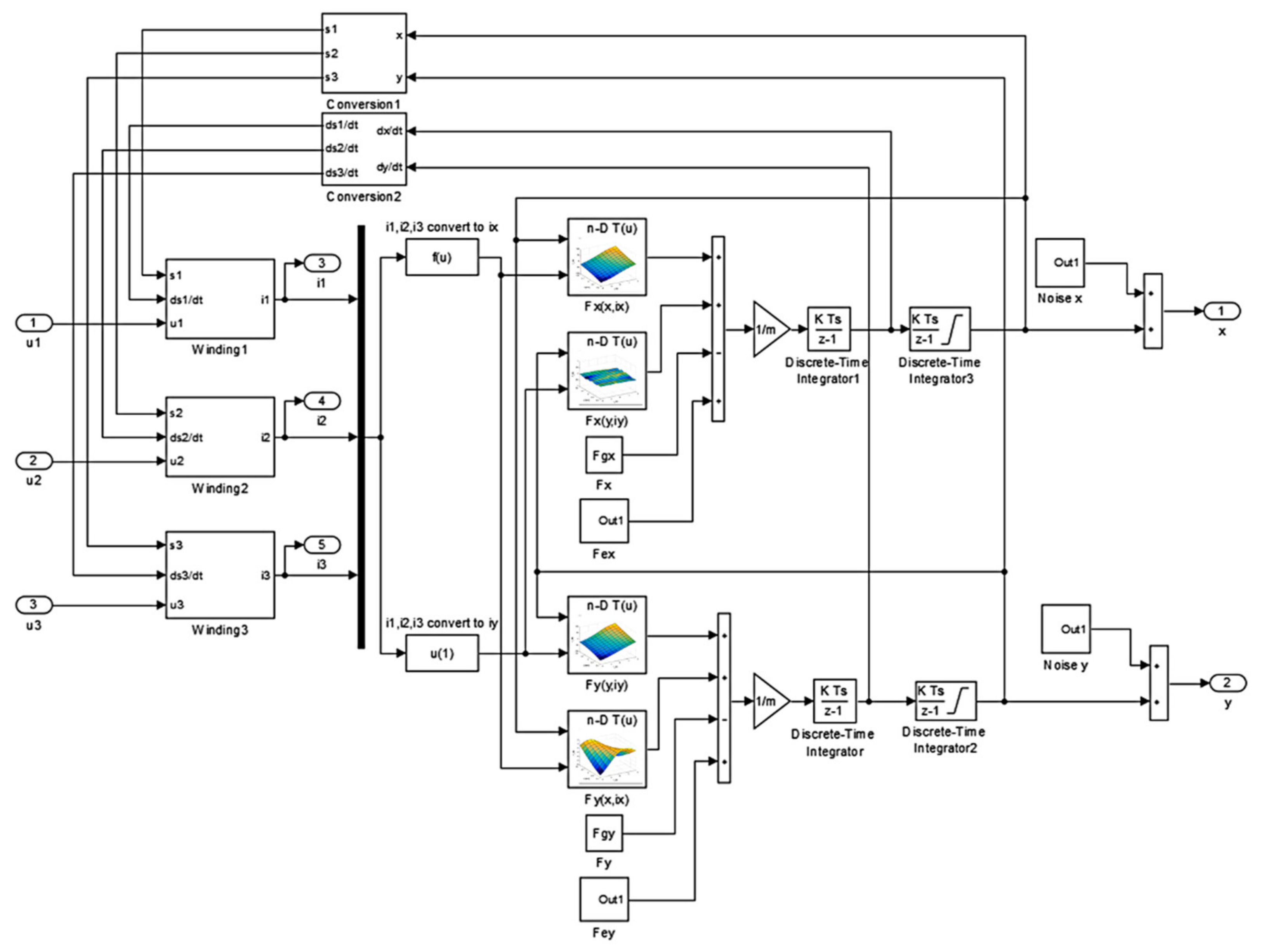

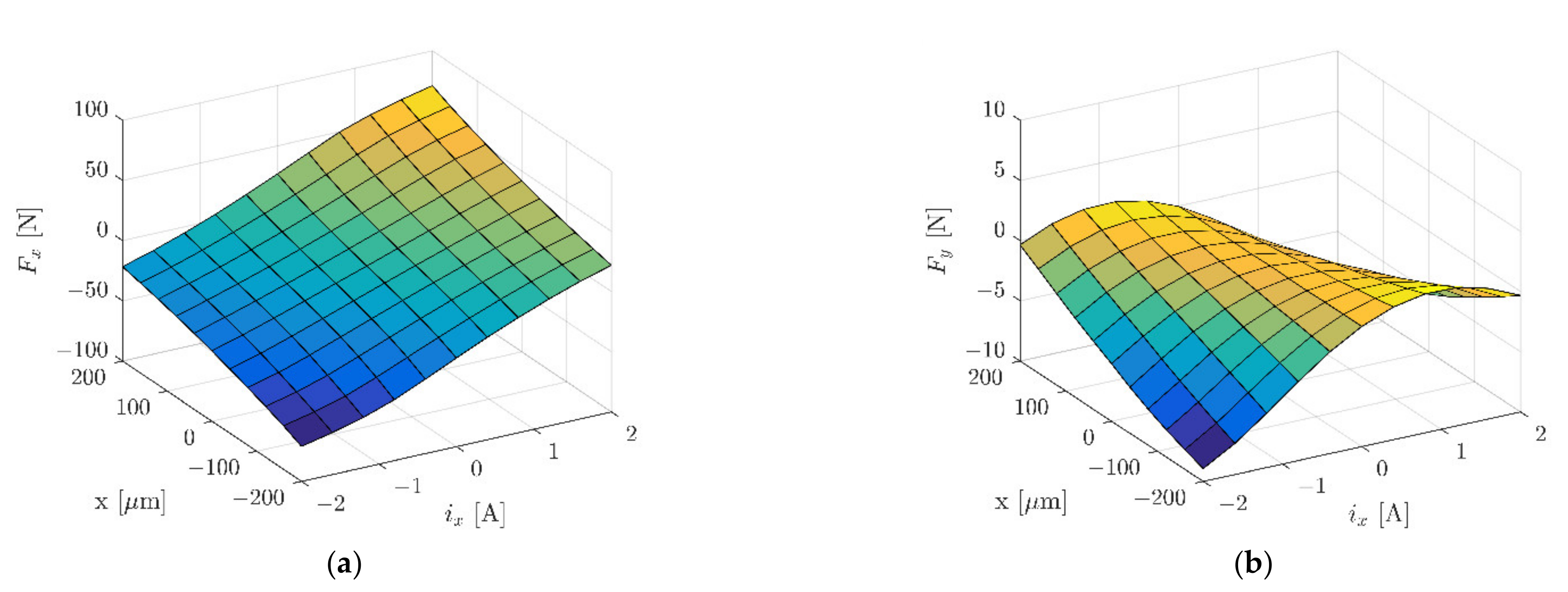

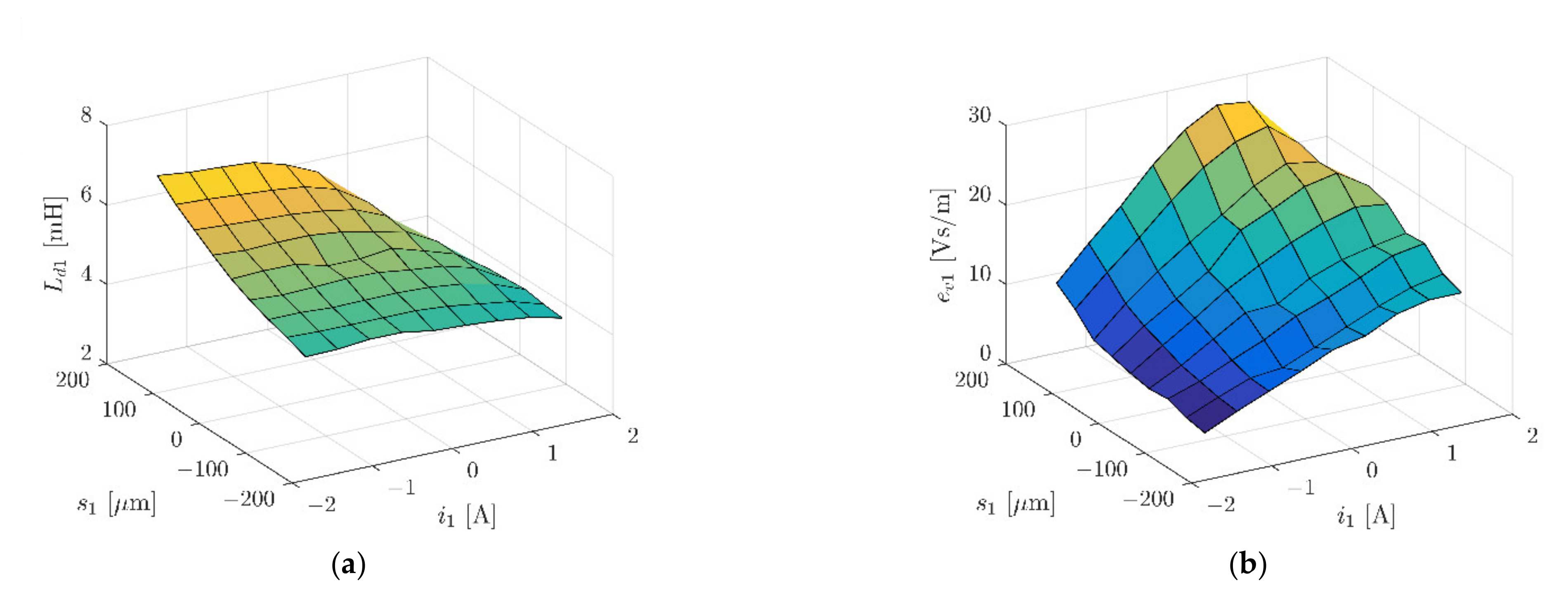

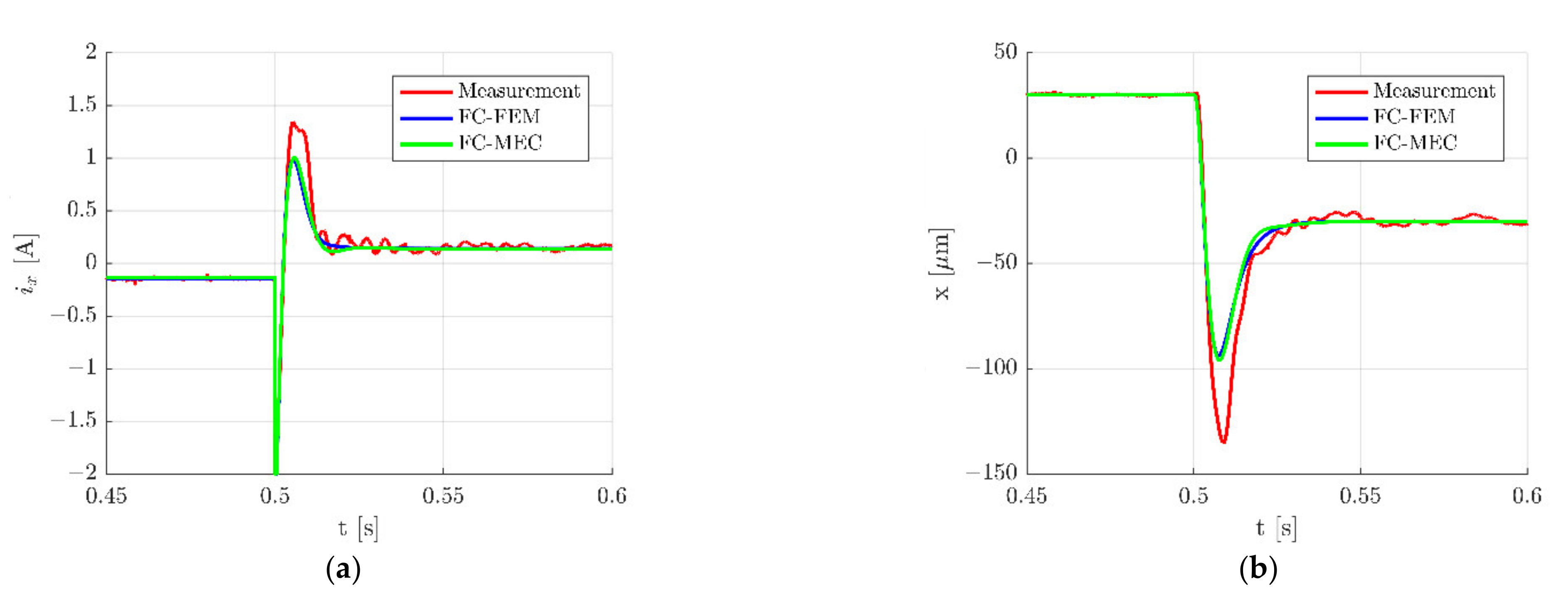
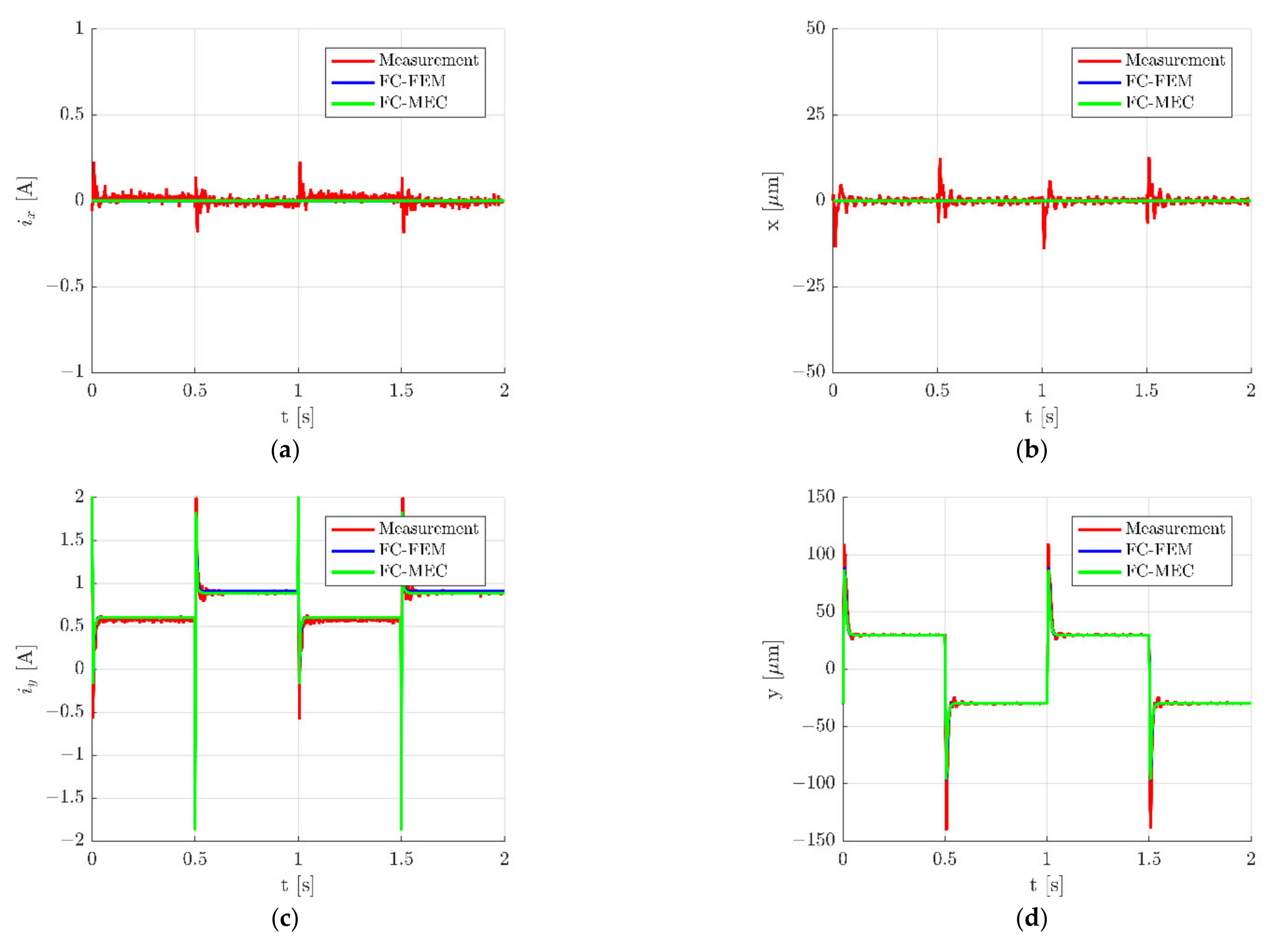

| Abbreviation | Full Form |
|---|---|
| CC | Current controller |
| FC-FEM | Field-circuit indirectly coupled finite element model |
| FC-MEC | Flux-circuit directly coupled magnetic equivalent circuit |
| FEA | Finite element analysis |
| FEM | Finite element method |
| HMB | Hybrid magnetic bearing |
| MEC | Magnetic equivalent circuit |
| ODE | Ordinary differential equation |
| PCX | Position controller for the x-axis |
| PCY | Position controller for the y-axis |
| PM | Permanent magnet |
| RSME | Root square mean error |
| A | Cross-section area of the magnetic path |
| Velocity-induced voltage | |
| Eccentricity | |
| Magnetic force for the x- and y-axis | |
| Maximal force for the x- and y-axis | |
| Magnetomotive force of the permanent magnet | |
| Magnetomotive forces of windings | |
| Initial force for the x- and y-axis | |
| g | Gravitational acceleration |
| Coercive force of the permanent magnet | |
| Currents of the windings | |
| Carter’s factor | |
| Position stiffness | |
| Current stiffness | |
| l | Length of the magnetic path |
| Dynamic inductance | |
| m | Mass of the rotor |
| N | Winding number of turns |
| Reluctance of the permanent magnet | |
| Reluctances of air-gaps | |
| Reluctances of stator and rotor paths | |
| x, y | Position of the rotor along the x- and y-axis |
| λ | Leakage factor of the windings |
| µ | Magnetic permeability |
| ν(B) | Magnetic reluctivity |
| Ψ | Linkage flux |
| ω | Rotational speed of the rotor |
| Parameter | Value |
|---|---|
| Position stiffness in the x-axis, ksx | 105.93 N/mm |
| Position stiffness in the y-axis, ksy | 106.03 N/mm |
| Current stiffness in the x-axis, kix | 21.97 N/A |
| Current stiffness in the y-axis, kiy | 22.00 N/A |
| Initial force in the x-axis, F0x | 21.84 N |
| Initial force in the y-axis, F0y | 22.53 N |
| Maximal force in the x-axis, Fmaxx | 41.84 N |
| Maximal force in the y-axis, Fmaxy | 46.09 N |
| Dynamic inductance, Ld | 5.27 mH |
| Velocity-induced voltage, ev | 15.56 Vs/m |
| RMSEx | RMSEix | RMSEy | RMSEiy | |
|---|---|---|---|---|
| FC-FEM | 15.48 μm | 215.8 mA | 2.764 μm | 48.85 mA |
| FC-MEC | 15.79 μm | 221.2 mA | 2.723 μm | 39.96 mA |
| RMSEx | RMSEix | RMSEy | RMSEiy | |
|---|---|---|---|---|
| FC-FEM | 1.620 μm | 25.66 mA | 15.09 μm | 205.6 mA |
| FC-MEC | 1.631 μm | 25.76 mA | 15.34 μm | 207.1 mA |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wajnert, D.; Tomczuk, B. Two Models for Time-Domain Simulation of Hybrid Magnetic Bearing’s Characteristics. Sensors 2022, 22, 1567. https://doi.org/10.3390/s22041567
Wajnert D, Tomczuk B. Two Models for Time-Domain Simulation of Hybrid Magnetic Bearing’s Characteristics. Sensors. 2022; 22(4):1567. https://doi.org/10.3390/s22041567
Chicago/Turabian StyleWajnert, Dawid, and Bronisław Tomczuk. 2022. "Two Models for Time-Domain Simulation of Hybrid Magnetic Bearing’s Characteristics" Sensors 22, no. 4: 1567. https://doi.org/10.3390/s22041567
APA StyleWajnert, D., & Tomczuk, B. (2022). Two Models for Time-Domain Simulation of Hybrid Magnetic Bearing’s Characteristics. Sensors, 22(4), 1567. https://doi.org/10.3390/s22041567






