Diversion Detection in Small-Diameter HDPE Pipes Using Guided Waves and Deep Learning
Abstract
1. Introduction
- To propose, design, and test piezoelectric transducer arrays, electronic circuits, signal designing and processing, and DNN models required to develop a DNN-based UGW detection scheme.
- To implement and evaluate a DNN-based UGW detection scheme, for detecting diversions in HDPE pipes.
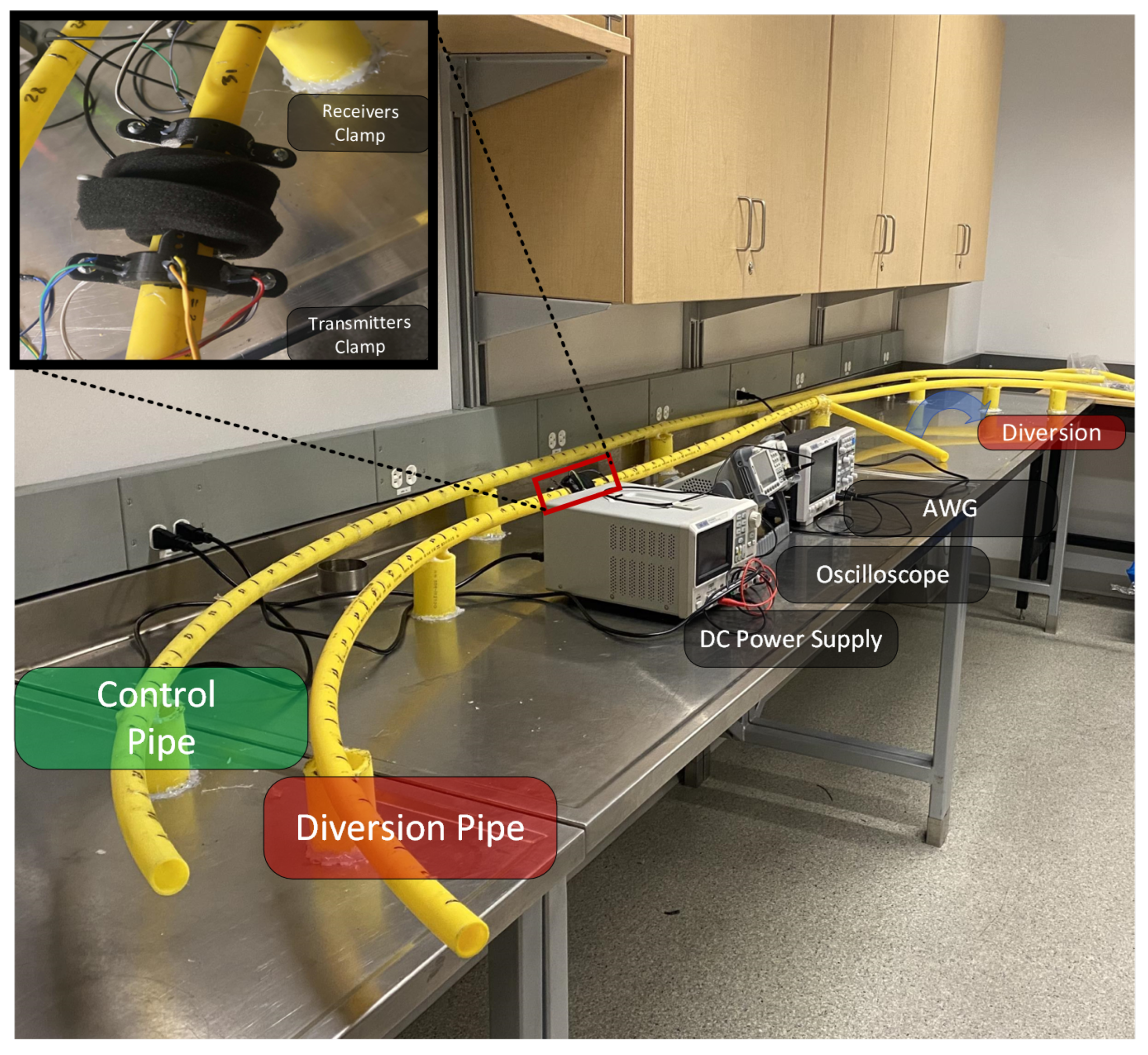
2. System Specifications
3. Signal Design and Processing
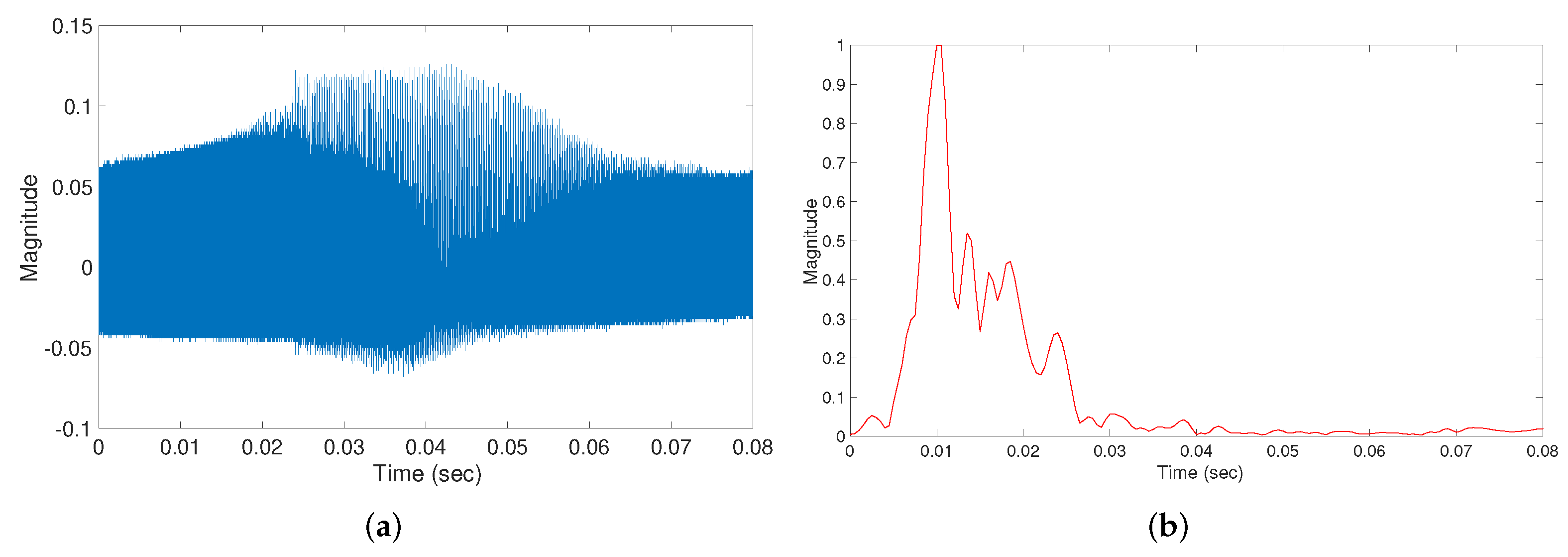
3.1. Transmitted Signal Design
3.2. Received Signal Processing
4. Data Collection
5. DNN Architectures
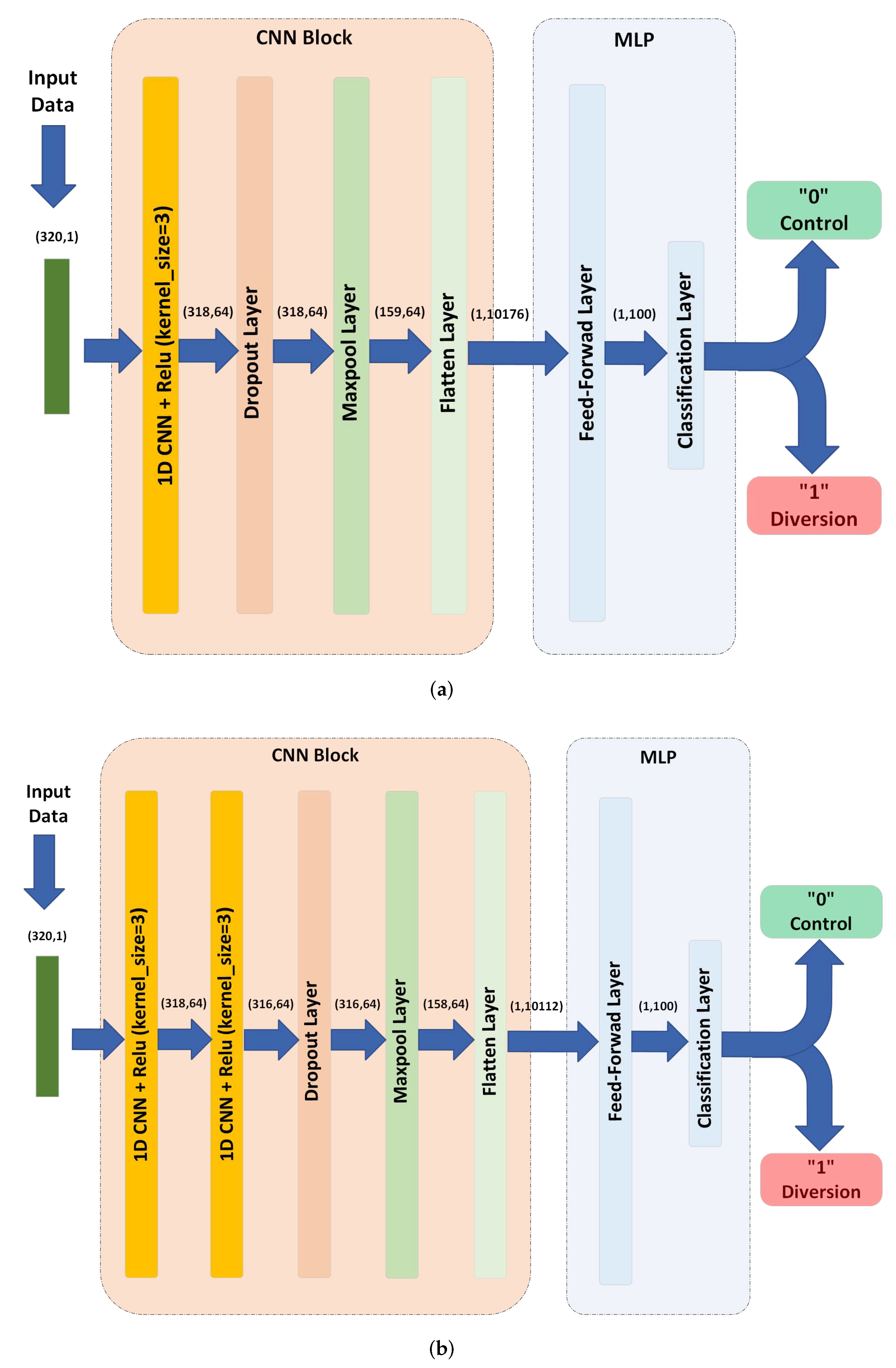
5.1. CNN Based Model
5.2. LSTM Based Models
5.3. CNN-LSTM Based Models
5.4. Multilayer Perceptron
6. Experimental Protocol and Results Discussion
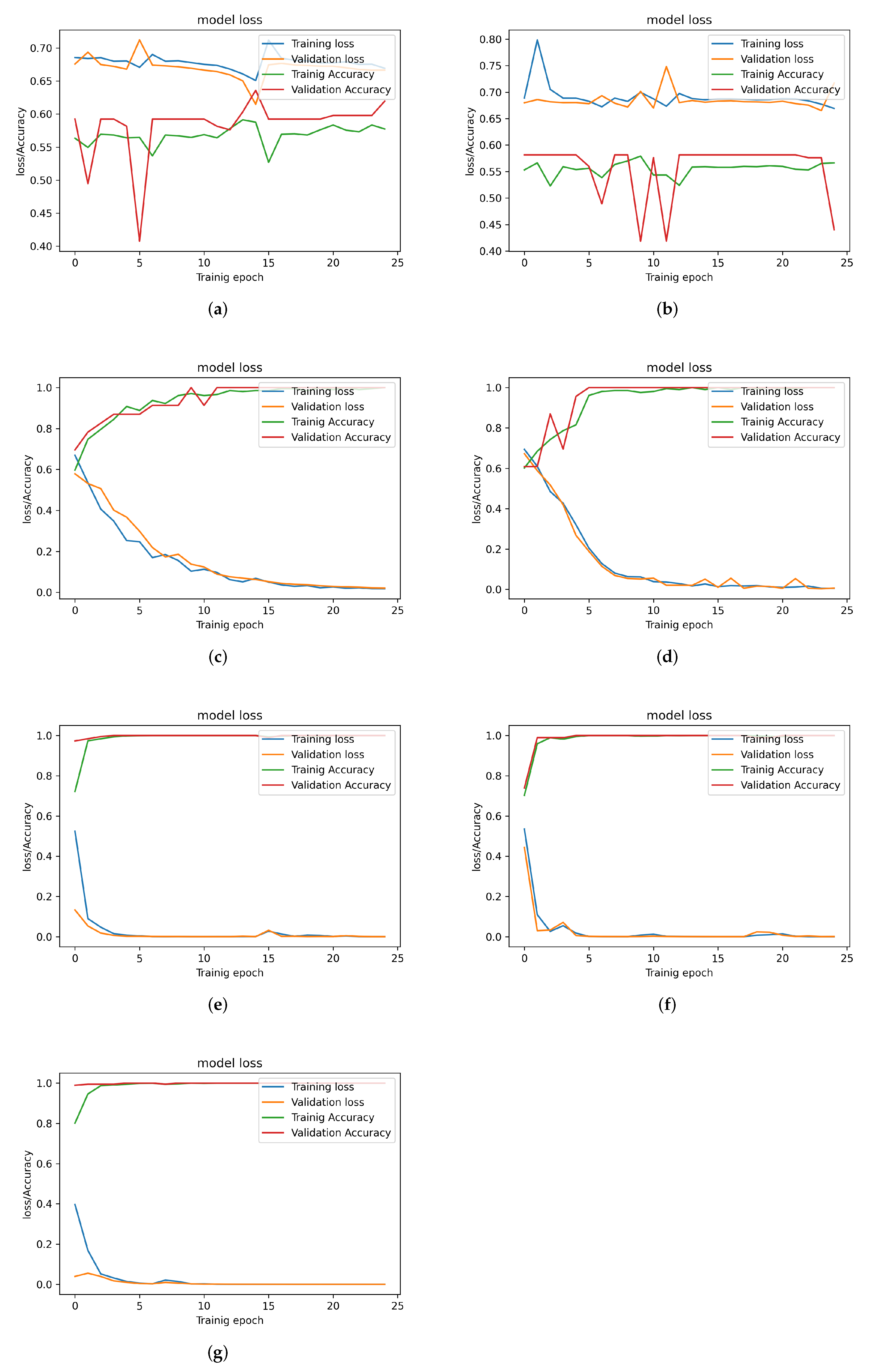
6.1. Experimental Protocols
- Accuracy: The accuracy is the percentage of data points that are classified correctly by the algorithm over the total number of data points. Mathematically, the accuracy can be expressed aswhere is the number of the correctly classified positive points (diversions), is the number of misclassified negative points (control), is the number of correctly classified positive points, and is the number of misclassified negative points.
- AUC: The area under the receiver operating characteristic (ROC) curve (AUC) is a metric that measures the ability of a classifier to distinguish between classes across all possible classification thresholds. Therefore, it measures the performance of a model irrespective of the classification threshold.
- Precision: If it is required to evaluate a model only on classifying the positive samples, precision is used. Precision is the ratio of positive samples classified correctly to total positive samples, which can be expressed as
- Recall: The recall describes the ratio of correctly classified positive samples over the total number of the positive samples, which is given by
- F1-score: F1-score is the harmonic mean of the precision and the recall values, which can be expressed as
6.2. Discussion of the Results
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Baroudi, U.; Al-Roubaiey, A.A.; Devendiran, A. Pipeline Leak Detection Systems and Data Fusion: A Survey. IEEE Access 2019, 7, 97426–97439. [Google Scholar] [CrossRef]
- Ho, M.; El-Borgi, S.; Patil, D.; Song, G. Inspection and monitoring systems subsea pipelines: A review paper. Struct. Health Monit. 2020, 19, 606–645. [Google Scholar] [CrossRef]
- Liu, Z.; Kleiner, Y. State of the art review of inspection technologies for condition assessment of water pipes. Measurement 2013, 46, 1–15. [Google Scholar] [CrossRef]
- International Atomic Energy Agency. Ageing Management for Nuclear Power Plants; Number NS-G-2.12 in Specific Safety Guides; International Atomic Energy Agency: Vienna, Austria, 2009. [Google Scholar]
- Lowe, S.; Sanderson, R.; Boulgouris, N.; Haig, A.; Balachandran, W. Inspection of Cylindrical Structures Using the First Longitudinal Guided Wave Mode in Isolation for Higher Flaw Sensitivity. IEEE Sensors J. 2015, 16, 706–714. [Google Scholar] [CrossRef]
- Chen, H.P.; Niu, X.; Marques, H. Transducer Array Optimisation for Guided Wave Testing of Pipes Using Finite Element Numerical Simulations and Experimental Studies. In Proceedings of the 8th International Conference on Structural Health Monitoring of Intelligent Infrastructure (SHMII-8), Brisbane, Australia, 5–8 December 2017. [Google Scholar]
- Abbas, M.; Shafiee, M. Structural Health Monitoring (SHM) and Determination of Surface Defects in Large Metallic Structures using Ultrasonic Guided Waves. Sensors 2018, 18, 3958. [Google Scholar] [CrossRef] [PubMed]
- Moradi, S. Defect Detection and Classification in Sewer Pipeline Inspection Videos Using Deep Neural Networks. Ph.D. Dissertation, Concordia University, Montreal, QC, Canada, 2020. [Google Scholar]
- Surrey Now Leader. Surrey a Leader in Natural Gas Theft. 2014. Available online: https://www.surreynowleader.com/news/surrey-a-leader-in-natural-gas-theft/ (accessed on 12 October 2022).
- CBC News. Fake Farm Concealed Underground Grow-Op in Langley, B.C. 2013. Available online: https://www.cbc.ca/news/canada/british-columbia/fake-farm-concealed-underground-grow-op-in-langley-b-c-1.1388770/ (accessed on 12 October 2022).
- McNeney, K.; (FortisBC, Victoria, BC, Canada); Leyland, M.; (FortisBC, Victoria, BC, Canada). Personal communication, 2020.
- Reuters. Mexico Fuel Pipeline Blast Kills 73, Witnesses Describe Horror. 2019. Available online: https://www.reuters.com/article/us-mexico-fuel-theft-blast-idUSKCN1PD033/ (accessed on 14 October 2022).
- Bloomberg. A Gas Heist Gone Wrong, an Explosion, and 137 Deaths in Mexico. 2019. Available online: https://www.bloomberg.com/news/features/2019-06-26/a-gas-heist-gone-wrong-an-explosion-and-137-deaths-in-mexico/ (accessed on 14 October 2012).
- Usamentiaga, R.; Venegas, P.; Guerediaga, J.; Vega, L.; Molleda, J.; Bulnes, F.G. Infrared Thermography for Temperature Measurement and Non-Destructive Testing. Sensors 2014, 14, 12305–12348. [Google Scholar] [CrossRef] [PubMed]
- Adedeji, K.B.; Hamam, Y.; Abe, B.T.; Abu-Mahfouz, A.M. Towards Achieving a Reliable Leakage Detection and Localization Algorithm for Application in Water Piping Networks: An Overview. IEEE Access 2017, 5, 20272–20285. [Google Scholar] [CrossRef]
- Serey, V.; Micheau, P.; Rénier, M.; Castaings, M.; Masson, P.; Quaegebeur, N. Selective generation of ultrasonic guided waves in a bi-dimensional waveguide. Struct. Health Monit. 2019, 18, 1324–1336. [Google Scholar] [CrossRef]
- Olisa, S.C.; Khan, M.A.; Starr, A. Review of Current Guided Wave Ultrasonic Testing (GWUT) Limitations and Future Directions. Sensors 2021, 21, 811. [Google Scholar] [CrossRef] [PubMed]
- Lowe, P.S.; Lais, H.; Paruchuri, V.; Gan, T.H. Application of Ultrasonic Guided Waves for Inspection of High Density Polyethylene Pipe Systems. Sensors 2020, 20, 3184. [Google Scholar] [CrossRef]
- Yan, S.; Li, Y.; Zhang, S.; Song, G.; Zhao, P. Pipeline Damage Detection Using Piezoceramic Transducers: Numerical Analyses with Experimental Validation. Sensors 2018, 18, 2106. [Google Scholar] [CrossRef]
- Ghavamian, A.; Mustapha, F.; Baharudin, B.H.T.; Yidris, N. Detection, Localisation and Assessment of Defects in Pipes Using Guided Wave Techniques: A Review. Sensors 2018, 18, 4470. [Google Scholar] [CrossRef]
- Yang, D.; Cui, Y.; Yu, Z.; Yuan, H. Deep Learning Based Steel Pipe Weld Defect Detection. Appl. Artif. Intell. 2021, 35, 1237–1249. [Google Scholar] [CrossRef]
- Ouadah, A. Pipeline Defects Risk Assessment Using Machine Learning and Analytical Hierarchy Process. In Proceedings of the 2018 International Conference on Applied Smart Systems (ICASS), Médéa, Algeria, 24–25 November 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Dib, G.; Karpenko, O.; Koricho, E.; Khomenko, A.; Haq, M.; Udpa, L. Ensembles of Novelty Detection Classifiers for Structural Health Monitoring using Guided Waves. Smart Mater. Struct. 2017, 27, 015003. [Google Scholar] [CrossRef]
- Yaacoubi, S.; El Mountassir, M.; Ferrari, M.; Dahmene, F. Measurement investigations in tubular structures health monitoring via ultrasonic guided waves: A case of study. Measurement 2019, 147, 106800. [Google Scholar] [CrossRef]
- García-Gómez, J.; Gil-Pita, R.; Rosa-Zurera, M.; Romero, A.; Jimenez Garrido, J.; García, V. Smart Sound Processing for Defect Sizing in Pipelines Using EMAT Actuator Based Multi-Frequency Lamb Waves. Sensors 2018, 18, 802. [Google Scholar] [CrossRef]
- Azuara, G.; Ruiz, M.; Barrera, E. Damage Localization in Composite Plates Using Wavelet Transform and 2-D Convolutional Neural Networks. Sensors 2021, 21, 5825. [Google Scholar] [CrossRef]
- Melville, J.; Supreet, A.K.; Deemer, C.; Harley, J. Structural Damage Detection Using Deep Learning of Ultrasonic Guided Waves. In AIP Conference Proceedings; AIP Publishing LLC: Melville, NY, USA, 2017; Volume 1949. [Google Scholar] [CrossRef]
- Hesser, D.; Kocur, G.; Markert, B. Active source localization in wave guides based on machine learning. Ultrasonics 2020, 106, 106144. [Google Scholar] [CrossRef]
- Sun, H.; Peng, L.; Wang, S.; Huang, S.; Qu, K. Development of Frequency-Mixed Point-Focusing Shear Horizontal Guided-Wave EMAT for Defect Inspection Using Deep Neural Network. IEEE Trans. Instrum. Meas. 2021, 70, 1–14. [Google Scholar] [CrossRef]
- Popovic, B. Generalized chirp-like polyphase sequences with optimum correlation properties. IEEE Trans. Inf. Theory 1992, 38, 1406–1409. [Google Scholar] [CrossRef]
- Niu, X.; Chen, H.P.; Marques, H. Optimising circumferential piezoelectric transducer arrays of pipelines through linear superposition analysis. In Proceedings of the The sixth International symposium on Life-Cycle Civil Engineering (IALCCE 2018), Ghent, Belgium, 28–31 October 2018. [Google Scholar]
- Yan, S.; Zhang, B.; Song, G.; Lin, J. PZT-Based Ultrasonic Guided Wave Frequency Dispersion Characteristics of Tubular Structures for Different Interfacial Boundaries. Sensors 2018, 18, 4111. [Google Scholar] [CrossRef]
- Barry, R.; Cheema, B.; Dhillon, G.; Krabben, M.; Lowe, J. Detection and Localization of Gas Diversions in Below-Grade Polyethylene Pipes; Capstone Report; University of British Columbia: Vancouver, BC, Canada, 2019. [Google Scholar]
- Diogo, A.R.; Moreira, B.; Gouveia, C.A.J.; Tavares, J.M.R.S. A Review of Signal Processing Techniques for Ultrasonic Guided Wave Testing. Metals 2022, 12, 936. [Google Scholar] [CrossRef]
- Cruz, F.; Simas Filho, E.; Albuquerque, M.; Silva, I.; Farias, C.; Gouvêa, L. Efficient Feature Selection for Neural Network Based Detection of Flaws in Steel Welded Joints Using Ultrasound Testing. Ultrasonics 2016, 73, 1–8. [Google Scholar] [CrossRef]
- Lin, J.C. Channel Estimation Assisted by Postfixed Pseudo-Noise Sequences Padded with Null Samples for Mobile OFDM Communications. In Proceedings of the 2008 IEEE Wireless Communications and Networking Conference, Las Vegas, NV, USA, 31 March 2008–3 April 2008; pp. 846–851. [Google Scholar] [CrossRef]
- Alsharif, M.; Saad, M.; Siala, M.; Ballal, T.; Boujemaa, H.; Al-Naffouri, T. Zadoff-Chu coded ultrasonic signal for accurate range estimation. In Proceedings of the 2017 25th European Signal Processing Conference (EUSIPCO), Kos, Greece, 28 August–2 September 2017; pp. 1250–1254. [Google Scholar] [CrossRef]
- Venkitaraman, A.; Chatterjee, S.; Händel, P. Hilbert Transform, Analytic Signal, and Modulation Analysis for Graph Signal Processing. arXiv 2016, arXiv:1611.05269. [Google Scholar]
- Bertovic, M. Human Factors in Non-Destructive Testing (NDT): Risks and Challenges of Mechanised NDT. Ph.D. Thesis, Technische Universitaet Berlin, Berlin, Germany, 2015. [Google Scholar] [CrossRef]
- Ewald, V.; Groves, R.; Benedictus, R. DeepSHM: A Deep Learning Approach for Structural Health Monitoring Based on Guided Lamb Wave Techniques. Sensors Smart Struct. Technol. Civil Mech. Aerosp. Syst. 2019, 10970, 84–99. [Google Scholar] [CrossRef]
- Ordóñez, F.J.; Roggen, D. Deep Convolutional and LSTM Recurrent Neural Networks for Multimodal Wearable Activity 552 Recognition. Sensors 2016, 16, 115. [Google Scholar] [CrossRef]








| Dataset | Control | Diversion | Total |
|---|---|---|---|
| Training | 718 | 886 | 1604 |
| Validation | 104 | 125 | 229 |
| Testing | 184 | 275 | 459 |
| Model | Performance Metrics | ||||
|---|---|---|---|---|---|
| Accuracy | Recall | Precision | F1-Score | AUC | |
| LSTM | 0.655 (±0.021) | 0.845 (±0.036) | 0.708 (±0.017) | 0.767 (±0.004) | 0.637 (±0.001) |
| 2-LSTM | 0.638 (±0.0242) | 0.909 (±0.04) | 0.627 (±0.025) | 0.74 (±0.003) | 0.627 (±0.048) |
| CNN | 0.821 (±0.04) | 0.921 (±0.04) | 0.79 (±0.064) | 0.85 (±0.026) | 0.915 (±0.02) |
| 2-CNN | 0.837 (±0.0167) | 0.89 (±0.036) | 0.83 (±0.038) | 0.85 (±0.01) | 0.92 (±0.009) |
| CNN-LSTM | 0.801 (±0.03) | 0.822 (±0.13) | 0.82 (±0.061) | 0.81 (±0.05) | 0.890 (±0.01) |
| CNN-(2-LSTM) | 0.822 (±0.04) | 0.77 (±0.12) | 0.91 (±0.05) | 0.82 (±0.06) | 0.920 (±0.006) |
| (2-CNN)-LSTM | 0.903 (±0.02) | 0.9014 (±0.06) | 0.905 (±0.04) | 0.921 (±0.025) | 0.926 (±0.006) |
| Model | Performance Metrics | ||||
|---|---|---|---|---|---|
| Accuracy | Recall | Precision | F1-Score | AUC | |
| LSTM | 0.544 (±0.037) | 0.817 (±0.291) | 0.58 (±0.150) | 0.61 (±0.104) | 0.562 (±0.067) |
| 2-LSTM | 0.58 (±0.0182) | 0.891 (±0.197) | 0.64 (±0.121) | 0.71 (±0.064) | 0.6185 (±0.118) |
| CNN | 0.991 (±0.007) | 0.9991 (±0.002) | 0.995 (±0.004) | 0.999 (±0.0002) | 0.995 (±0.004) |
| 2-CNN | 0.997 (±0.003) | 0.997 (±0.003) | 0.998 (±0.003) | 0.998 (±0.002) | 0.997 (±0.0094) |
| CNN-LSTM | 0.996 (±0.00065) | 0.992 (±0.007) | 0.998 (±0.001) | 0.999 (±0.0004) | 0.998 (±0.0045) |
| CNN-(2-LSTM) | 0.993 (±0.00130) | 0.994 (±0.008) | 0.993 (±0.002) | 0.992 (±0.00098) | 0.994 (±0.0031) |
| (2-CNN)-LSTM | 0.996 (±0.001) | 0.998 (±0.006) | 0.998 (±0.0023) | 0.999 (±0.00003) | 0.999 (±0.0023) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zayat, A.; Obeed, M.; Chaaban, A. Diversion Detection in Small-Diameter HDPE Pipes Using Guided Waves and Deep Learning. Sensors 2022, 22, 9586. https://doi.org/10.3390/s22249586
Zayat A, Obeed M, Chaaban A. Diversion Detection in Small-Diameter HDPE Pipes Using Guided Waves and Deep Learning. Sensors. 2022; 22(24):9586. https://doi.org/10.3390/s22249586
Chicago/Turabian StyleZayat, Abdullah, Mohanad Obeed, and Anas Chaaban. 2022. "Diversion Detection in Small-Diameter HDPE Pipes Using Guided Waves and Deep Learning" Sensors 22, no. 24: 9586. https://doi.org/10.3390/s22249586
APA StyleZayat, A., Obeed, M., & Chaaban, A. (2022). Diversion Detection in Small-Diameter HDPE Pipes Using Guided Waves and Deep Learning. Sensors, 22(24), 9586. https://doi.org/10.3390/s22249586






