Machine Learning Models for Slope Stability Classification of Circular Mode Failure: An Updated Database and Automated Machine Learning (AutoML) Approach

Abstract

Slope failures lead to large casualties and catastrophic societal and economic consequences, thus potentially threatening access to sustainable development. Slope stability assessment, offering potential long-term benefits for sustainable development, remains a challenge for the practitioner and researcher. In this study, for the first time, an automated machine learning (AutoML) approach was proposed for model development and slope stability assessments of circular mode failure. An updated database with 627 cases consisting of the unit weight, cohesion, and friction angle of the slope materials; slope angle and height; pore pressure ratio; and corresponding stability status has been established. The stacked ensemble of the best 1000 models was automatically selected as the top model from 8208 trained models using the H2O-AutoML platform, which requires little expert knowledge or manual tuning. The top-performing model outperformed the traditional manually tuned and metaheuristic-optimized models, with an area under the receiver operating characteristic curve (AUC) of 0.970 and accuracy (ACC) of 0.904 based on the testing dataset and achieving a maximum lift of 2.1. The results clearly indicate that AutoML can provide an effective automated solution for machine learning (ML) model development and slope stability classification of circular mode failure based on extensive combinations of algorithm selection and hyperparameter tuning (CASHs), thereby reducing human efforts in model development. The proposed AutoML approach has the potential for short-term severity mitigation of geohazard and achieving long-term sustainable development goals.

1. Introduction

Natural hazards like landslide and subsidence have been acknowledged as a major factor disturbing sustainable development in developing countries [1,2,3,4]. For example, a catastrophic landfill slope failure occurred on 20 December 2015, in Guangming, Shenzhen, China, took the lives of 69 people [5]. The risk assessment and management of natural hazard will have a short-term benefit for severity mitigation and a long-term benefit for achieving sustainable development goals [1].

The evaluation of slope stability is of primary importance for natural hazard risk assessment and management in mountain areas. Numerous efforts have been made for slope stability assessment [6,7,8,9]. However, slope stability assessment for circular mode failure, a typical problem, still remains a challenge for the practitioner and researcher due to inherent complexity and uncertainty [10]. An extensive body of literature exists regarding slope stability assessments of circular failure, and significant progress has been achieved. Three main categories of assessment approaches have emerged: analytical approaches, numerical approaches, and machine learning (ML)-based approaches [11,12,13]. Limited equilibrium methods, such as the simplified Bishop, Spencer, and Morgenstern-Price methods, are commonly used analytical approaches and have been routinely used in practice. Generally, geometrical data, physical and shear strength parameters (unit weight, cohesion, and friction angle), and the pore pressure ratio are required in limited equilibrium methods [14,15]. However, the results vary across different methods due to different assumptions [9]. Numerical approaches (e.g., finite element methods) have been widely adopted for slope stability assessment. However, due to the requirement of numerous expensive input parameters, these models can be applied only in limited cases [16]. Recently, ML-based approaches have led to giant strides in slope stability assessment. A summary of the slope stability assessments of circular failure using ML approaches is given in Table 1. Among the various ML approaches used, artificial neural networks (ANNs) are widely utilized for slope stability assessment due to their simple structure and acceptable accuracy [11,17,18]. Recently, sophisticated ML algorithms, including but not limited to support vector machine (SVM), decision tree (DT), extreme learning machine (ELM), random forest (RF), and gradient boosting machine (GBM) algorithms, have been utilized for slope stability assessment. Hyperparameter tuning is a fundamental step required for accurate ML modeling [19,20]. As listed in Table 1, grid search (GS) and metaheuristic methods, such as the artificial bee colony (ABC) algorithm, genetic algorithm (GA), and particle swarm optimization (PSO), have been utilized for hyperparameter tuning in ML-based slope stability assessment. For example, Qi and Tang [16] simultaneously trained six firefly algorithm (FA)-optimized ML models, including multilayer perceptron neural network, logistic regression (LR), DT, RF, SVM, and GBM models, based on 148 cases of circular mode failure. The FA-optimized SVM was selected as the final model, with an area under the receiver operating characteristic curve (AUC) of 0.967 for the testing dataset. The performance of eight ensemble learning approaches was compared by [12] based on a dataset with 444 cases of circular mode failure. A stacked model was selected as the final model, with an AUC of 0.9452 for the testing dataset.

Table 1. Summary of the slope stability assessment of circular mode failure using MLs.

Reference	Data Size (Stable/Failure)	Input Features	Data Preprocessing	ML Algorithm Selection	Hyperparameter Tuning	Final Model and Performance
[21]	82 (38/44)	$\gamma$, $c$, $\phi$, $\beta$, $H$, $r_u$	/	BP	Trial and error GA	GA-optimized BP was selected as the final model, with an AUC of 0.455 for the testing dataset.
[22]	32 (14/18)	$\gamma$, $c$, $\phi$, $\beta$, $H$, $r_u$	/	ANN	Trial and error	The ANN achieved an ACC of 1.00 for the testing dataset in two cases.
[23]	46 (17/29)	$\gamma$, $c$, $\phi$, $\beta$, $H$, $r_u$	Data normalization	SVM	PSO	PSO-SVM achieved an ACC of 0.8125 for the testing dataset.
[24]	168 (84/84)	$\gamma$, $c$, $\phi$, $\beta$, $H$, $r_u$	Data normalization	LSSVM	FA	The FA-optimized LSSVM achieved an AUC of 0.86 for the testing dataset.
[25]	168 (84/84)	$\gamma$, $c$, $\phi$, $\beta$, $H$, $r_u$	Data normalization	RBF LSSVM ELM	Orthogonal least squares GA Trial and error	The GA-ELM was selected as the final model, with an AUC of 0.8706 for the testing dataset.
[26]	82 (49/33)	$\gamma$, $c$, $\phi$, $\beta$, $H$, $r_u$	/	NB	/	NB achieved an ACC of 0.846 for the testing dataset.
[27]	107 (48/59)	$\gamma$, $c$, $\phi$, $\beta$, $H$, $r_u$	/	RF SVM Bayes GSA	Ten-fold CV	The GSA was selected as the final model, with an AUC of 0.889 for the testing dataset.
[17]	168 (84/84)	$\gamma$, $c$, $\phi$, $\beta$, $H$, $r_u$	Data normalization	GP QDA SVM ADB-DT ANN KNN Classifier ensemble	GA	The optimum ensemble classifier was selected as the final model, with an AUC of 0.943 for the testing dataset.
[16]	148 (78/70)	$\gamma$, $c$, $\phi$, $\beta$, $H$, $r_u$	Data normalization	LR DT RF GBM SVM BP	FA GS	The FA-optimized SVM was selected as the final model, with an AUC of 0.967 for the testing dataset.
[18]	221 (115/106)	$\gamma$, $c$, $\phi$, $\beta$, $H$, $r_u$	Data normalization	ANN SVM RF GBM	Five-fold CV	The GBM-based model was selected as the final model, with an AUC of 0.900 for the testing dataset.
[28]	87 (42/45)	$\gamma$, $c$, $\phi$, $\beta$, $H$, $r_u$	/	J48	Trial and error	J48 achieved an ACC of 0.9231 for the testing dataset.
[13]	257 (123/134)	$\gamma$, $c$, $\phi$, $\beta$, $H$, $r_u$	/	XGB RF LR SVM BC LDA KNN DT MLP GNB XRT Stacked ensemble	ABC PSO	The stacked ensemble was selected as the final model, with an AUC of 0.904 for the testing dataset.
[11]	153 (83/70)	$\gamma$, $c$, $\phi$, $\beta$, $H$, $r_u$	Data normalization and outlier removing	KNN SVM SGD GP QDA GNB DT ANN Bagging ensemble Heterogeneous ensemble	GS	An ensemble classifier based on extreme gradient boosting was selected as the final model, with an AUC of 0.914 for the testing dataset.
[29]	19 (13/6)	$\gamma$, $c$, $\phi$, $\beta$, $H$, $r_u$	Data normalization	K-means cluster	HS	K-means clustering optimized by HS achieved an ACC of 0.89 for all datasets.
[12]	444 (224/220)	$\gamma$, $c$, $\phi$, $\beta$, $H$, $r_u$	Data normalization	AdaBoost GBM Bagging XRT RF HGB Voting Stacked	GS	A stacked model was selected as the final model, with an AUC of 0.9452 for the testing dataset.
[30]	422 (226/196)	$\gamma$, $c$, $\phi$, $\beta$, $H$, $r_u$	Data normalization	MDMSE	GS	The MDMSE model achieved an AUC of 0.8810 for the testing dataset.

Note: Abbreviations in this table are explained in Abbreviations.

Although ML-based models have been widely applied, some studies have been based on a small number of samples, which may affect the generalization ability of the classifier. Moreover, most ML models have been manually developed by researchers with expert knowledge in a trial-and-error approach. In fact, exhaustive steps, including data preprocessing [31], feature engineering [32], ML algorithm selection [33], and hyperparameter tuning, are involved in practical applications of ML. Among them, model selection and hyperparameter tuning remain challenges for successful ML-based modeling [34]. Based on the no-free-lunch theorem [35], there is no algorithm that outperforms all others in all problems. Therefore, at present, according to prior experience, candidate off-the-shelf models are trained with a training dataset and validated by researchers. The ML model that provides the best performance is considered the final model and tested with an out-of-box testing dataset. This traditional workflow makes the model development process knowledge-based and time-consuming [36], and might yield unsatisfactory results [37]. However, most practitioners and researchers lack the knowledge and expertise required to build satisfactory ML models. Hence, an objective workflow with less human effort is needed, providing a basis for the concept of automated ML (AutoML) [38].

From the perspective of automation, AutoML is a systematic framework that automates algorithm selection and hyperparameter tuning and explores different combinations of factors with minimal human intervention [34,39,40,41]. AutoML has been successfully applied for ML modeling in a variety of fields, including tunnel displacement prediction [36], tunnel boring machine performance prediction [34], and earthquake casualty and economic loss prediction [42]. Thus, the generalization ability of this approach has been confirmed.

In the present study, an updated database with 627 cases consisting of the unit weight, cohesion, and friction angle of the slope materials: slope angle and height, pore pressure ratio, and corresponding stability status of circular mode failure, has been collected. For the first time, an AutoML approach was proposed for slope stability classification. The top model was selected from 8208 trained ML models by exploring numerous combinations of algorithm selection and hyperparameter tuning (CASHs) with minimal human intervention.

The major contribution of this paper is highlighted as follows:

(a)

A large database consisting of 627 cases has been collected for slope stability classification.

(b)

Based on the updated dataset, an AutoML approach was proposed for slope stability classification without the need for manual trial and error. The proposed AutoML approach outperformed the existing ML models by achieving superior performance.

The rest of this paper is organized as follows: the updated database and methodology are presented in Section 2 and Section 3, respectively. Section 4 presents and discusses experimental results. Finally, the conclusions and further work are presented in Section 5.

2. Database

As listed in Table 1, the input features relevant to the slope stability assessment of the circular failure model (schematic illustrated in inset of Figure 1) mainly include the unit weight, cohesion, and friction angle of the slope materials, the slope angle and height, and the pore pressure ratio. Moreover, these features are fundamental input parameters for limit equilibrium methods, such as the simplified Bishop method [15,43]. Based on the previous research listed in Table 1, an updated database consisting of 627 cases was obtained from previous studies [11,12,16,24,30,44] and is listed in Appendix A. The database consists of the unit weight, cohesion, and friction angle of the slope materials, the slope angle and height, the pore pressure ratio, and the corresponding stability status. The numbers of positive (stable) and negative (failure) samples are 311 and 316, respectively. The statistics of the input features are summarized in Table 2. To better visualize the collected dataset, ridgeline plots showing the density distributions of the input features based on kernel density estimation [3] are presented in Figure 1. As shown, the collected dataset was distributed in a wide range of regions, and the distribution was not symmetric.

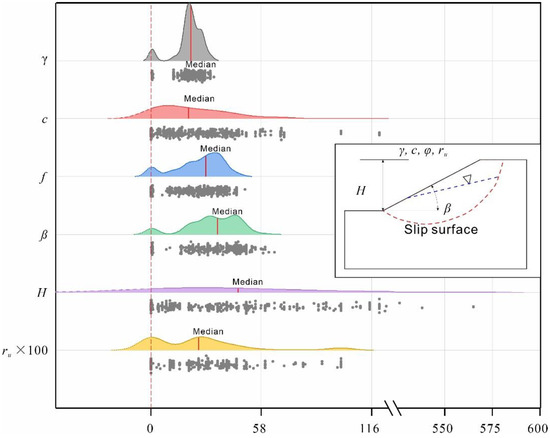
Figure 1. Ridgeline plots showing the density distributions of the input features. The inset shows a schematic diagram of the circular failure model.

Table 2. Summary of the input feature statistics.

Input Feature	Notation	Range	Median	Mean	Std.
Unit weight (kN/m3)	$\gamma$	0.492–33.160	20.959	20.185	7.044
Cohesion (kPa)	$c$	0–300.00	19.690	25.600	31.036
Friction angle (°)	$\phi$	0–49.500	28.800	25.308	12.331
Slope angle (°)	$\beta$	0.302–65.000	34.980	32.605	13.711
Slope height (m)	$H$	0.018–565.000	45.800	90.289	120.140
Pore pressure ratio	$r_u$	0–1.000	0.250	0.254	0.260

The Pearson correlation coefficient (R) was adopted to further reveal the linear correlations between input features and the slope stability status and is shown in the lower left half of the panels in Figure 2. As shown, relatively poor linear correlations with correlation coefficients lower than 0.5 were observed between the input features and the slope stability status. Significant linear correlations (R = 0.71, 0.71, and 0.68) were noted for the unit weight, friction angle, and slope angle. Additionally, a moderate correlation (R = 0.51) was found between the unit weight and slope height.

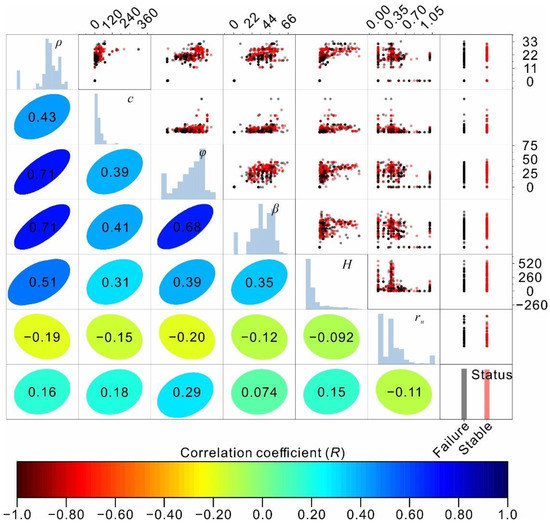
Figure 2. Scatter matrix showing the collected dataset. The panels in the upper right show the data points, and the lower left half of the figure shows the correlation coefficients between the features and the slope stability status.

Furthermore, the multivariate principal component analysis (PCA) technique [45] was applied to enhance the visualization of the statistical relationships among features. The PCA results shown in Figure 3 demonstrate that the first three principal components (PC1-PC3) account for 79.09% of the entire multivariate variance in space. PC1 is mainly associated with the unit weight, friction angle, and slope angle. PC2 corresponds to the pore pressure ratio. Moreover, overlapping among failure and stability classes can be clearly observed. In other words, the decision boundary for separating slope failure and stability is highly nonlinear and complex.

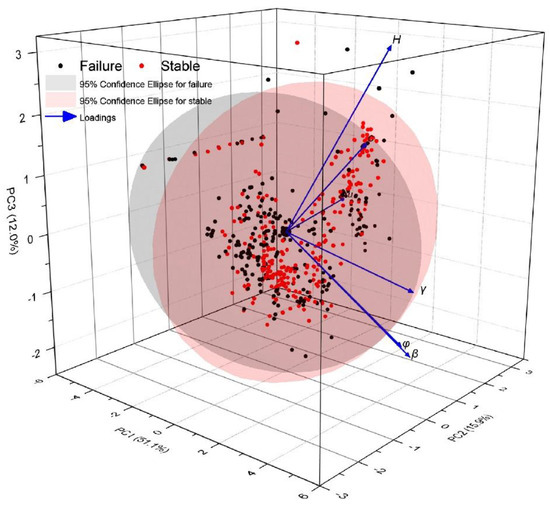
Figure 3. 3D PCA score plot of the input features.

3. Methodology

3.1. AutoML

From the perspective of automation, AutoML is a systematic model that automates the algorithm selection and hyperparameter tuning processes and explores different CASHs with minimal human intervention [34,39,40]. More formally, the CASH problem can be stated as follows. Let $A=\{A^1,A^2,\cdots ,A^R\}$ be a set of ML algorithms, $\mathrm{\Lambda }=\{{\mathrm{\Lambda }}^1,{\mathrm{\Lambda }}^2,\cdots ,{\mathrm{\Lambda }}^R\}$ be the corresponding hyperparameters, and $L$ be the loss function. When adopting k-fold cross validation (CV), the training dataset $D_{training}$ is divided into subsets $\{D_{training}^{(1)},D_{training}^{(2)},\cdots ,D_{training}^{(k)}\}$ and $\{D_{validation}^{(1)},D_{validation}^{(2)},\cdots ,D_{validation}^{(k)}\}$. The CASH problem is defined as

$$A^{*}{}_{{\lambda }^{*}}\in \underset{A^{(j)}\in A,{\lambda }^{(j)}\in \mathrm{\Lambda }}{\arg \min }\frac{1}{k}{\displaystyle \sum _{i=1}^{k}L(A_{\lambda }^{(j)},D_{training}^{(i)},D_{validation}^{(i)})}$$

(1)

Generally, AutoML consists of the following three key components: a search space, a search strategy, and a performance evaluation strategy [40] (schematically illustrated in Figure 4). The search space refers to a set of hyperparameters and the range of each hyperparameter. The search strategy refers to the strategy of selecting the optimal hyperparameters from the search space. Grid search and Bayesian optimization are commonly used search strategies. The performance evaluation strategy refers to the method used to evaluate the performance of the trained models.

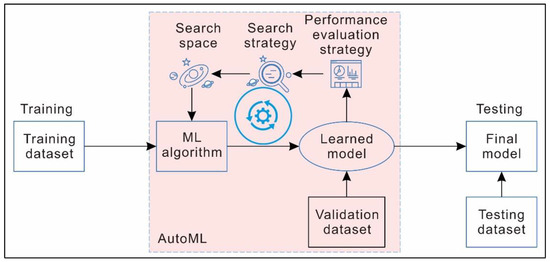
Figure 4. Schematic diagram showing the workflow of AutoML.

Various open-source platforms, such as AutoKeras, AutoPyTorch, AutoSklearn, AutoGluon, and H2O AutoML, have been developed to facilitate the adoption of AutoML [46]. Previous studies [47,48] have demonstrated the strong feature of H2O AutoML for processing large and complicated datasets by quickly searching the optimal model without the need for manual trial and error. Moreover, H2O AutoML provides a user interface for non-experts to import and split datasets, identify the response column, and automatically train and tune models. Therefore, in the present study, the H2O AutoML platform was adopted for the automated assessment of slope.

The H2O AutoML platform includes the following commonly used ML algorithms: generalized linear model (GLM), distributed random forest (DRF), extremely randomized tree (XRT), deep neural network (DNN), and GBM algorithms [49]. The abovementioned ML algorithms in the H2O AutoML platform are briefly described as follows.

GLM is an extended form of a linear model. Given the input variable x, the conditional probability of the output class falling within the class c of observations is defined as follows:

$${\widehat{y}}_c=Pr(y=c|x)=\frac{e{x}^T{\beta }_c+{\beta }_{c0}}{{\displaystyle \sum _{k=1}^K(e{x}^T{\beta }_k+{\beta }_{k0})}}$$

(2)

where ${\beta }_c$ is the vector of coefficients for class c.

The DRF is an ensemble learning approach based on decision trees. In the DRF training process, multiple decision trees are built. To reduce the variance, the final prediction was obtained by aggregating the outputs from all decision trees.

Similar to the DRF, XRT is based on multiple decision trees, but randomization is strongly emphasized to reduce the variance with little influence on the bias. The following main innovations are involved in the XRT process: random division of split nodes using cut points and full adoption of the entire training dataset instead of a bootstrap sample for the growth of trees.

The DNN in H2O AutoML is based on a multilayer feedforward artificial neural network with multiple hidden layers. There are a large number of hyperparameters involved in DNN training, which makes it notoriously difficult to manually tune. Cartesian and random grid searches are available in H2O AutoML for DNN hyperparameter optimization.

GBM is an ensemble learning method. The basic idea of GBM is to combine weak base learners (usually decision trees) for the generation of strong learners. The objective is to minimize the error in the objective function through an iterative process using gradient descent.

In addition, stacked ensembles can be built using either the best-performing models or all the trained models.

3.2. Search Space and Search Strategy

In the present study, a random grid search was adopted for hyperparameter tuning in the search space. When adopting k-fold CV, the hyperparameter tuning process can be described as follows (schematically illustrated in Figure 5). First, possible combinations of the tuned parameters are generated. Then, CV is performed using a possible parameter combination. The training dataset is divided into k equal-sized subsets. A single subset is treated as the validation subset, while the remaining subsets are adopted for classification training. The average accuracy from k validation sets is computed and adopted as the performance measure of the k-CV classifier model. The above process is repeated for all possible parameter combinations. A ranking of all trained classifiers by model performance is obtained. The classifier that yields the highest accuracy is selected.

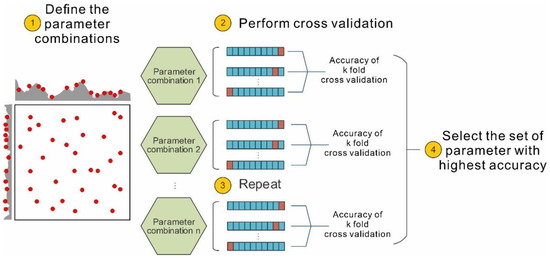
Figure 5. Schematic diagram showing hyperparameter tuning based on the k-fold CV and random grid search methods.

3.3. Performance Evaluation Measures

In the present study, widely applied criteria, including the accuracy (ACC), AUC, sensitivity (SEN), specificity (SPE), positive predictive value (PPV), negative predictive value (NPV), and Matthews correlation coefficient (MCC), were adopted for performance evaluation (Table 3). The AUC can be interpreted as follows: an AUC equal to 1.0 indicates perfect discriminative ability, an AUC value from 0.9 to 1.0 indicates highly accurate discriminative ability, an AUC value from 0.7 to 0.9 indicates moderately accurate discriminative ability, an AUC value from 0.5 to 0.7 demonstrates inaccurate discriminative ability, and an AUC less than 0.5 indicates no discriminative ability.

Table 3. Confusion matrix and performance measures for slope stability assessment.

	Predicted	Stable	Failure
Actual
Stable		True positive (TP)	False negative (FN)	Sensitivity: $SEN=\frac{TP}{TP+FN}$ (The ideal value is 1, whereas the worst is zero.)
Failure		False positive (FP)	True negative (TN)	Specificity $SPE=\frac{TN}{FP+TN}$ (The ideal value is 1, whereas the worst is zero.)
		Positive predictive value (PPV) $PPV=\frac{TP}{TP+FP}$ (The ideal value is 1, whereas the worst is zero.)	Negative predictive value (NPV) $NPV=\frac{TN}{FN+TN}$ (The ideal value is 1, whereas the worst is zero.)	Accuracy $ACC=\frac{TP+TN}{TP+FN+FP+TN}$ (The ideal value is 1, whereas the worst is zero.) Matthews correlation coefficient $MCC=\frac{TP\cdot TN-FP\cdot FN}{\sqrt{(TP+FP)\cdot (TP+FN)\cdot (TN+FP)\cdot (TN+FN)}}$ (The ideal value is 1.)

3.4. Slope Stability Assessment through AutoML

In the present study, the H2O AutoML approach was adopted for ML model development for slope stability classification (schematic illustrated in Figure 6). First, the database listed in Appendix A was randomly divided into training and testing datasets at a ratio of 80% to 20%, respectively. ML models, including GLM, DRF, XRT, DNN, and GBM were automated and developed (schematic illustrated in Figure 6). To enhance the reliability and performance, the common 10-fold CV was performed. A full list of tuned hyperparameters and the corresponding searchable values are given in Table 4. Stacked ensembles were developed based on the best-performing models and all the tuned models. A leaderboard ranking the mode performance accuracy was achieved. The leader models were saved and evaluated on the testing dataset.

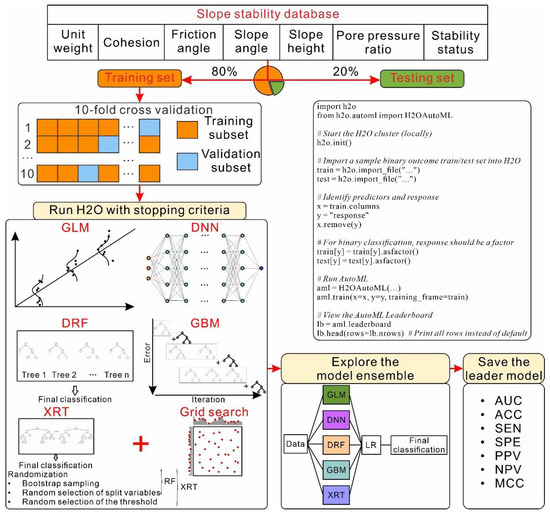
Figure 6. Flowchart of the AutoML-based slope stability classification.

Table 4. The hyperparameter search space for GS optimization for AutoML-based slope stability classification.

Algorithm	Parameter	Searchable values
DNN	Adaptive learning rate time smoothing factor (epsilon)	$\{{10}^{-6},{10}^{-7},{10}^{-8},{10}^{-9}\}$
	Hidden layer size (hidden)	Grid search 1: {20}, {50}, {100}
		Grid search 2: {20, 20}, {50, 50}, {100, 100}
		Grid search 3: {20, 20, 20}, {50, 50, 50}, {100, 100, 100}
	Hidden_dropout_ratio	Grid search 1: {0.1}, {0.2}, {0.3}, {0.4}, {0.5}
		Grid search 2: {0.1, 0.1}, {0.2, 0.2}, {0.3, 0.3}, {0.4, 0.4}, {0.5, 0.5}
		Grid search 3: {0.1, 0.1, 0.1}, {0.2, 0.2, 0.2} {0.3, 0.3, 0.3}, {0.4, 0.4, 0.4}, {0.5, 0.5, 0.5}
	Input_dropout_ratio	{0.0, 0.05, 0.1, 0.15, 0.2}
	Adaptive learning rate time decay factor (rho)	{0.9, 0.95, 0.99}
GLM	Regularization distribution between L1 and L2 (alpha)	{0.0, 0.2, 0.4, 0.6, 0.8, 1.0}
GBM	Column sampling rate (col_sample_rate)	{0.4, 0.7, 1.0}
	Column sample rate per tree (col_sample_rate_per_tree)	{0.4, 0.7, 1.0}
	Maximum tree depth (max_depth)	{3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17}
	Minimum number of observations for a leaf (min_rows)	{1, 5, 10, 15, 30, 100}
	Minimum relative improvement in squared error reduction (min_split_improvement)	$\{{10}^{-4},{10}^{-5}\}$
	Row sampling rate (sample_rate)	{0.50, 0.60, 0.70, 0.80, 0.90, 1.00}

The AutoML process was implemented using H2O AutoML (3.36.1.2) with an Intel(R) Xeon(R) E-2176M @ 2.70 GHz CPU with 64 GB RAM. The maximum time allotted to run generation classifiers, except for the stacked ensembles, was set to 3600 s.

4. Results and Discussions

4.1. Performance Analysis

A total of 8208 ML models, including bypass CV models, were trained with the H2O AutoML platform and saved. The top five models from the leaderboard were selected and listed in Table 4 for testing. The performance evaluation metrics for the top five models on the testing dataset are listed in Table 5.

Table 5. Comparison of the performance of the selected top-five models from AutoML in slope stability assessments of circular mode failure based on the selected test data.

Model ID	Model Type	Hyperparameters	AUC	Confusion Matrix				Performance Measures
H2O1	Stacked ensemble	The base models are the top-1000 trained models, and the metalearner is a GLM. A logit transformation is used for the predicted probabilities.	0.970		Predicted	Stable	Failure	SEN = 0.968 SPE = 0.841 PPV = 0.857 NPV = 0.964 ACC = 0.904 MCC = 0.815
				Actual
				Stable		60	2
				Failure		10	53
H2O2	GBM	score_tree_interval = 5; ntrees = 105; max_depth = 7; stopping_metric = logloss; stopping_tolerance = 0.045; learn_rate = 0.1; learn_rate_annealing = 1; sample_rate = 1; col_sample_rate = 0.4; col_sample_rate_change_per_level = 1; col_sample_rate_per_tree = 0.7	0.968		Predicted	Stable	Failure	SEN = 0.903 SPE = 0.937 PPV = 0.933 NPV = 0.908 ACC = 0.920 MCC = 0.840
				Actual
				Stable		56	6
				Failure		4	59
H2O3	DRF	Ntrees = 50; max_depth = 20	0.963		Predicted	Stable	Failure	SEN = 0.839 SPE = 0.968 PPV = 0.963 NPV = 0.859 ACC = 0.904 MCC = 0.815
				Actual
				Stable		52	10
				Failure		2	61
H2O4	XR	score_tree_interval = 5; max_after_balance_size = 5; max_confusion_matrix_size = 20; ntrees = 50; max_depth = 20; stopping_metric = logloss; stopping_tolerance = 0.045; sample_rate = 0.632	0.963		Predicted	Stable	Failure	SEN = 0.871 SPE = 0.937 PPV = 0.931 NPV = 0.881 ACC = 0.904 MCC = 0.810
				Actual
				Stable		54	8
				Failure		4	59
H2O5	GBM	score_tree_interval = 5; ntrees = 97; max_depth = 7; stopping_metric = logloss; stopping_tolerance = 0.045; learn_rate = 0.1; learn_rate_annealing = 1; sample_rate = 0.8; col_sample_rate = 0.8; col_sample_rate_change_per_level = 1; col_sample_rate_per_tree = 0.8	0.960		Predicted	Stable	Failure	SEN = 0.968 SPE = 0.810 PPV = 0.833 NPV = 0.962 ACC = 0.888 MCC = 0.786
				Actual
				Stable		60	2
				Failure		12	51

As listed in Table 5, the stacked ensemble of the best 1000 models (H2O₁) ranked as the top-performing model. The corresponding ROC curves are shown in Figure 7, which clearly indicates that the top-performing model is capable of providing highly accurate discriminative ability, with AUC of 0.999 and 0.970 for the training and testing dataset, respectively. The model performance was further evaluated using gain and lift charts (Figure 8). A gain chart measures the effectiveness of a classifier based on the percentage of correct classifications obtained with the model versus the percentage of correct classifications obtained by chance (i.e., the baseline). As shown, for the top model, only 30% of the population is required to achieve an accuracy of 60%, compared to 30% for the random model. The top classifier is capable of achieving a maximum lift of 2.1. In other words, when only 10% of the sample was selected, the average accuracy of the top model was approximately two times higher than that of the random model.

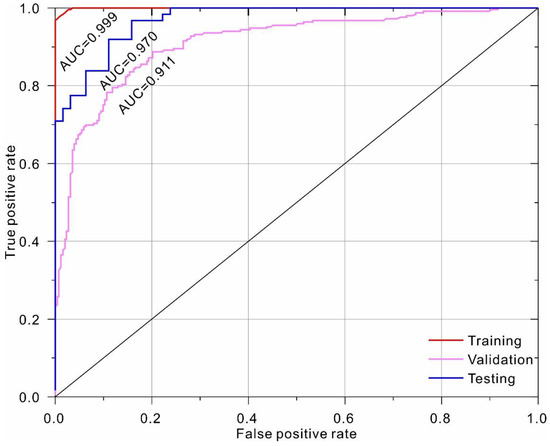
Figure 7. ROC curve of the top-performing model (H2O₁) from AutoML.

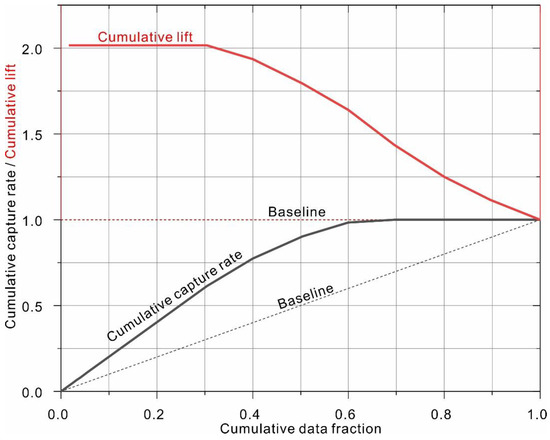
Figure 8. Cumulative gain and lift charts for the top-performing model (H2O₁) based on testing data.

Figure 9 demonstrates the correlation between NPV and PPV for the obtained top-five classification models based on the testing dataset. As shown, the top-performing model (H2O₁) falls within zone 2, in which the obtained NPV is greater than the PPV. This result indicates that the top-performing model (H2O₁) tends to classify slope status as a failure (negative status) more often than stable (positive status). In other words, the top-performing model (H2O₁) may overestimate stability.

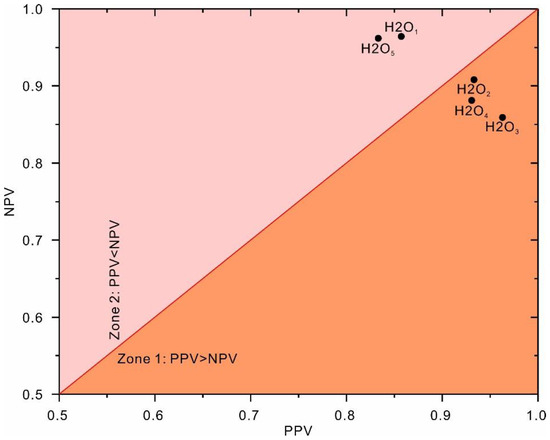
Figure 9. Correlation between the NPV and PPV values of the classification models based on the testing dataset.

4.2. Model Interpretation

In the present study, the partial dependence plot graphically revealing the input–output relationship was adopted for model interpretation. The partial dependence plot has been considered as one of the most popular model agnostic tools due to the advantages of simple definition and easy implementation. The partial dependence relations of the input features in the top-performing model (H2O₁) are shown in Figure 10. In partial dependence plots, features with greater variability have more significant effects on the model [18,50]. As shown, the top-performing model (H2O₁) is highly influenced by the slope height and friction angle.

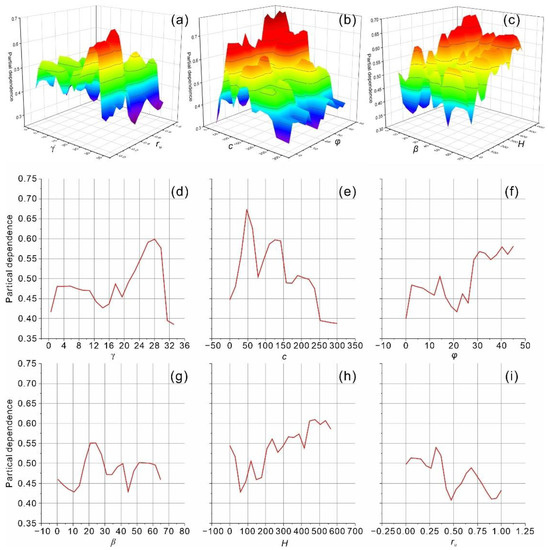
Figure 10. Partial dependence plots of the input features in the top-performing model (H2O₁) for the classification of slope stability. (a) Unit weight and pore pressure ratio, (b) cohesion and friction angle, (c) slope angle and slope height, (d) unit weight, (e) cohesion, (f) friction angle, (g) slope angle, (h) slope height, and (i) pore pressure ratio.

4.3. Validation of the AutoML Model in ACADS Example

Furthermore, the predictive capacity of the top-performing model (H2O₁) was validated on the Australian Association for Computer-Aided Design (ACADS) referenced slope example EX1, which is a simple homogeneous slope. The slope is 20 m long and 10 m high. The geometry and material properties are shown in Figure 11. With the parameters listed in Figure 11, the example slope was estimated to fail [43]. The top-performing model (H2O₁) successfully classified the slope example as a failure case.

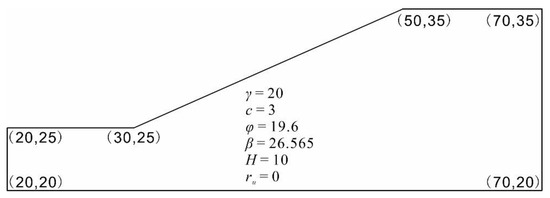
Figure 11. ACADS reference slope example EX1 (Unit: m).

4.4. Comparison with Exiting Models

To further assess performance, the top-performing model (H2O₁) from the AutoML approach was further compared with a manually derived ML model for slope stability assessment (Table 6). As shown in Table 6, in the previous studies, the firefly algorithm optimized SVM (FA-SVM) provides the best performance with an AUC of 0.967 [16], followed by ensemble classifiers on the extreme gradient boosting (XGB-CM) [11]. Obviously, the top-performing model (H2O₁) is of better generalization ability than the existing models shown in Table 6 with the largest AUC and ACC values. These comparative results clearly indicate that the top-performing model (H2O₁) from AutoML approach is capable of providing better generalization performance than the manually derived ML and metaheuristics-optimized model.

Table 6. Comparison of different ML models for slope stability assessments of circular mode failure.

Reference	Model	AUC	ACC	Reference	Model	AUC	ACC
[24]	BDA LM-ANN SCG-ANN RMV SVM RBP-ANN MO-LSSVM	0.75 0.79 0.81 0.83 0.83 0.84 0.86	/	[25]	RBF LSSVM ELM	/	0.81 0.8706 0.8400
[17]	GA-GP GA-QDA GA-SVM GA-ANN GA-ADB-DT GA-KNN GA-OEC	0.893 0.798 0.908 0.877 0.936 0.908 0.943	/	[27]	RF SVM NB GSA	0.833 0.556 0.667 0.886	/
[16]	FA-LR FA-DT FA-MLP FA-RF FA-GBM FA-SVM	0.822 0.854 0.864 0.957 0.962 0.967	/	[18]	ANN SVM RF GBM	0.888 0.889 0.897 0.900	/
[13]	XGB RF LR SVM BC LDA KNN DT MLP GNB XRT Stacked ensemble	0.77 0.79 0.83 081 0.71 0.80 0.78 0.72 0.83 0.7. 0.74 0.90	/	[11]	KNN SVM SGD GP QDA GNB DT ANN B-KNN B-SVM B-ANN RF AB GBM XGB Heterogeneous ensemble	0.931 0.796 0.688 0.933 0.817 0.775 0.829 0.817 0.938 0.892 0.933 0.904 0.910 0.929 0.950 0.950	0.839 0.806 0.710 0.839 0.774 0.806 0.774 0.806 0.871 0.871 0.839 0.806 0.839 0.774 0.903 0.806
[12]	GBM Bagging Adaboost XRT RF HGB Voting Stacked	0.9199 0.9291 0.9199 0.9519 0.9268 0.8970 0.9588 0.9382	/	[30]	SVM DT LR NB Boosting MDMSE	/	0.8452 0.8333 <0.75 <0.75 0.8214 0.8810
Current study	H2O1 (Stacked Ensemble_Best1000)	0.970	0.904

Note: The best results are shown in bold italics. The results for relatively small sample sets (less than 100) are not presented or compared.

4.5. Advantages and Limitations of the Proposed Approach

Generally, the traditional ML models require workflows which encompass data preprocessing, feature engineering, ML algorithm selection, and hyperparameter tuning to be constructed, and are often developed based on prior experience. Due to varying levels of knowledge, the traditional ML model may not fully exploit the power of ML, resulting in less optimal results than those obtained with other models. Therefore, it is not objective to claim that one algorithm outperforms another without adjusting the hyperparameters. In contrast, AutoML is capable of automatically implementing the above processes and extensively exploring different workflows with minimal human intervention, resulting in a better model. In fact, previous studies [51,52] have reported that AutoML outperformed traditional ML models that were manually developed by data scientists. Moreover, it takes less computational time to train AutoML, with hundreds of optional pipelines, than it does to train a manually derived ML model, often requiring days to tune. In fact, based on the collected dataset, the computational time of AutoML with 8408 pipelines is one hour. Moreover, various commercial and open-source AutoML platforms have been developed, and many successful implementations have been reported. For example, an AutoML vision model was implemented for production recommendation using Google Cloud AutoML without hiring ML engineers [40]. These results may suggest that AutoML is preferred in some cases. However, due to the complex and involved process required to build an AutoML system from scratch, AutoML is still in an early stage of development. At present, AutoML is not fully automated [37,40]. For example, human efforts are still needed for data collection and data cleaning. For now, clear objectives based on high-quality data must be defined for AutoML. Nevertheless, the AutoML approach holds limitations such as black box, and is computationally expensive for large-scale datasets due to extensive searching of different pipelines.

5. Conclusions

In the present study, an updated database consisting of 627 cases was collected for slope stability classification of circular failure model. For the first time, an AutoML approach was proposed for ML model development. Instead of manually building a pipeline for ML algorithm selection and hyperparameter tuning, AutoML is capable of automatically implementing model development and performing extensive searches of different pipelines with minimal human intervention. The stacked ensemble of the best 1000 models was selected as the top model from 8208 ML trained models. The top-performing model provided highly accurate discriminative ability, with an AUC of 0.970 and an ACC of 0.904 for the testing dataset, achieving a maximum lift of 2.1. The trained AutoML model outperformed traditional manually tuned and metaheuristic-optimized models. AutoML was verified as an effective tool for automated ML model development and slope stability assessments of circular failure.

Given the successful use of AutoML for classification of slope stability for circular mode failure, it seems that such a methodology could be useful for short-term severity mitigation of geohazard and achieving long-term sustainable development goals.

Although the proposed AutoML approach shows promising results, it still has some limitations. Beyond the black box nature, among the major shortcomings of AutoML, a solution is their computational complexity. Future works should focus on developing explainable and interpretable ML models by coupling data-driven models with physical models.