Analysis of the Accuracy of Ten Algorithms for Orientation Estimation Using Inertial and Magnetic Sensing under Optimal Conditions: One Size Does Not Fit All
Abstract
1. Introduction
2. Materials and Methods
2.1. Optimal Working Conditions
2.2. Selected Algorithms
2.3. Experimental Setup
2.4. Experimental Protocol
2.5. Data Processing
2.5.1. SP Data Pre-Processing and Synchronization with MIMUs Signals
2.5.2. Orientation Estimation and Error Computation under Optimal Conditions
| Algorithm 1. Pseudocode to detail the orientation estimation process for each SFA. |
| for each pair of MIMUs (Xsens, APDM, and Shimmer) for each angular rate condition (slow, medium, fast) remove the static bias for each gyroscope compute the starting orientation for each MIMU initialize the matrix (#rows = length(), #columns = length()) for each value belonging to between [, ] for each value belonging to between [, ] compute the absolute orientation of each MIMU separately with the SFA under analysis to obtain and refer and to the starting orientation to obtain and , as done in (1) compute the absolute orientation error of and separately using the gold standard to obtain and , as done in (2) convert and into angular rotation errors to obtain and compute the average value between the two absolute errors to obtain compute the RMS of considering only the dynamic parts of the recording to obtain add to the matrix end end find the optimal region of which correspond to the range of which includes its minimum () + 0.5 deg to obtain and find the value of which correspond to the default parameter values to obtain end end |
2.6. Data Analysis
- SFA analytical formulation
- rotation rate magnitude
- different commercial products.
2.6.1. Identification of the Optimal Regions and the Corresponding Errors
- Minimum absolute orientation error which corresponds to the selection of the optimal parameter values: , where is the matrix of the average errors between the two MIMUs of dimensions equal to [length(), length()].
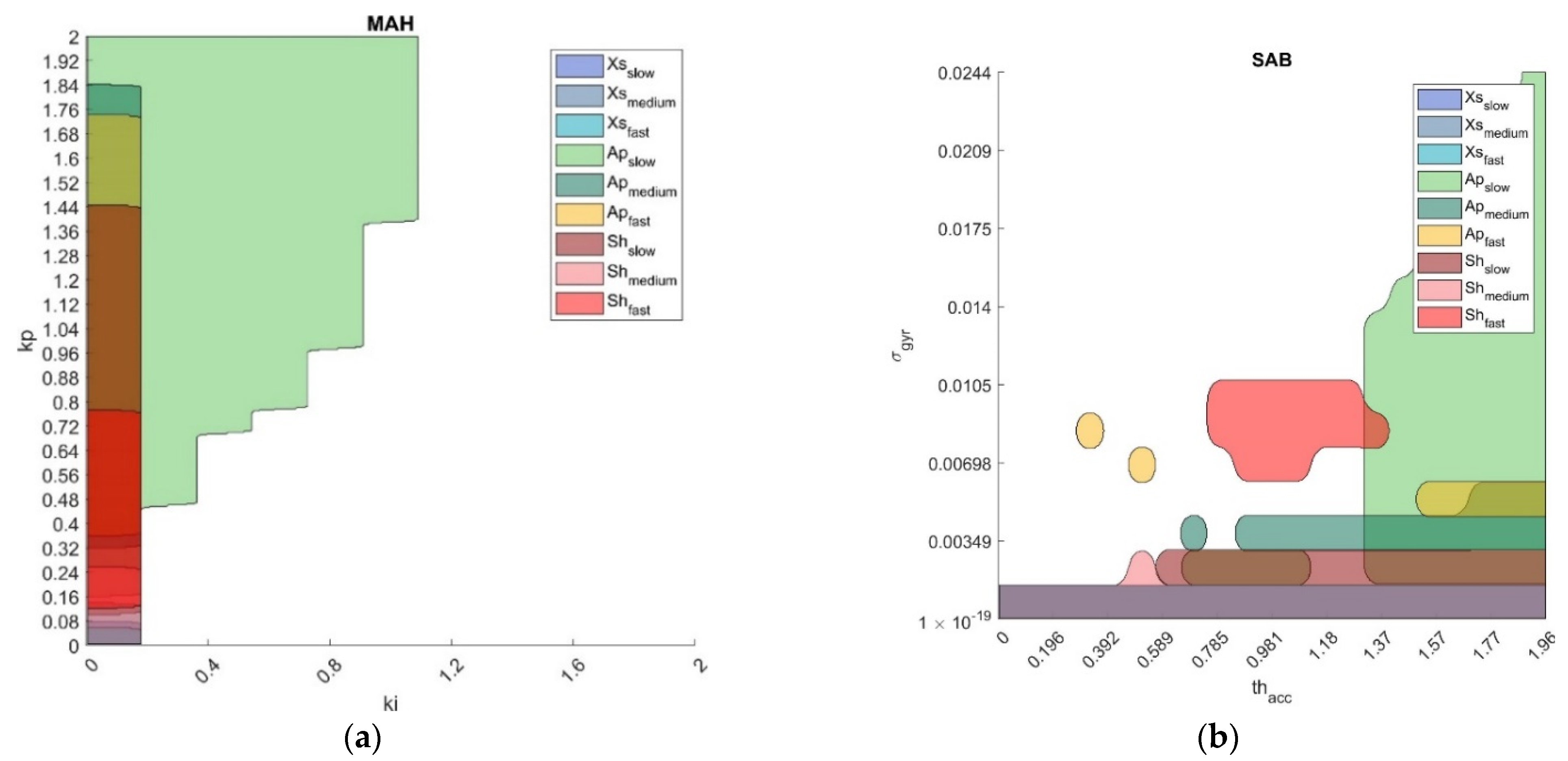
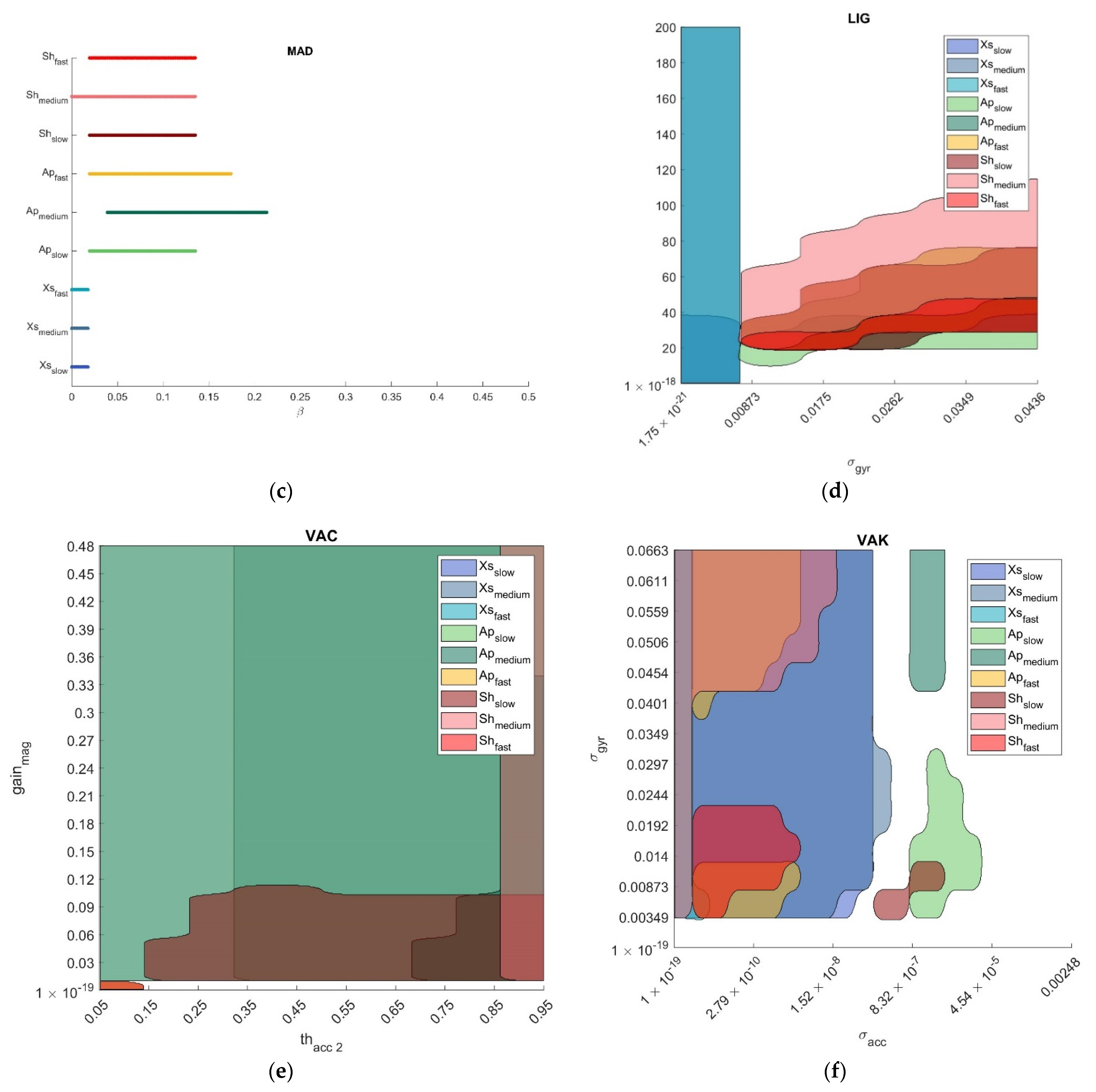
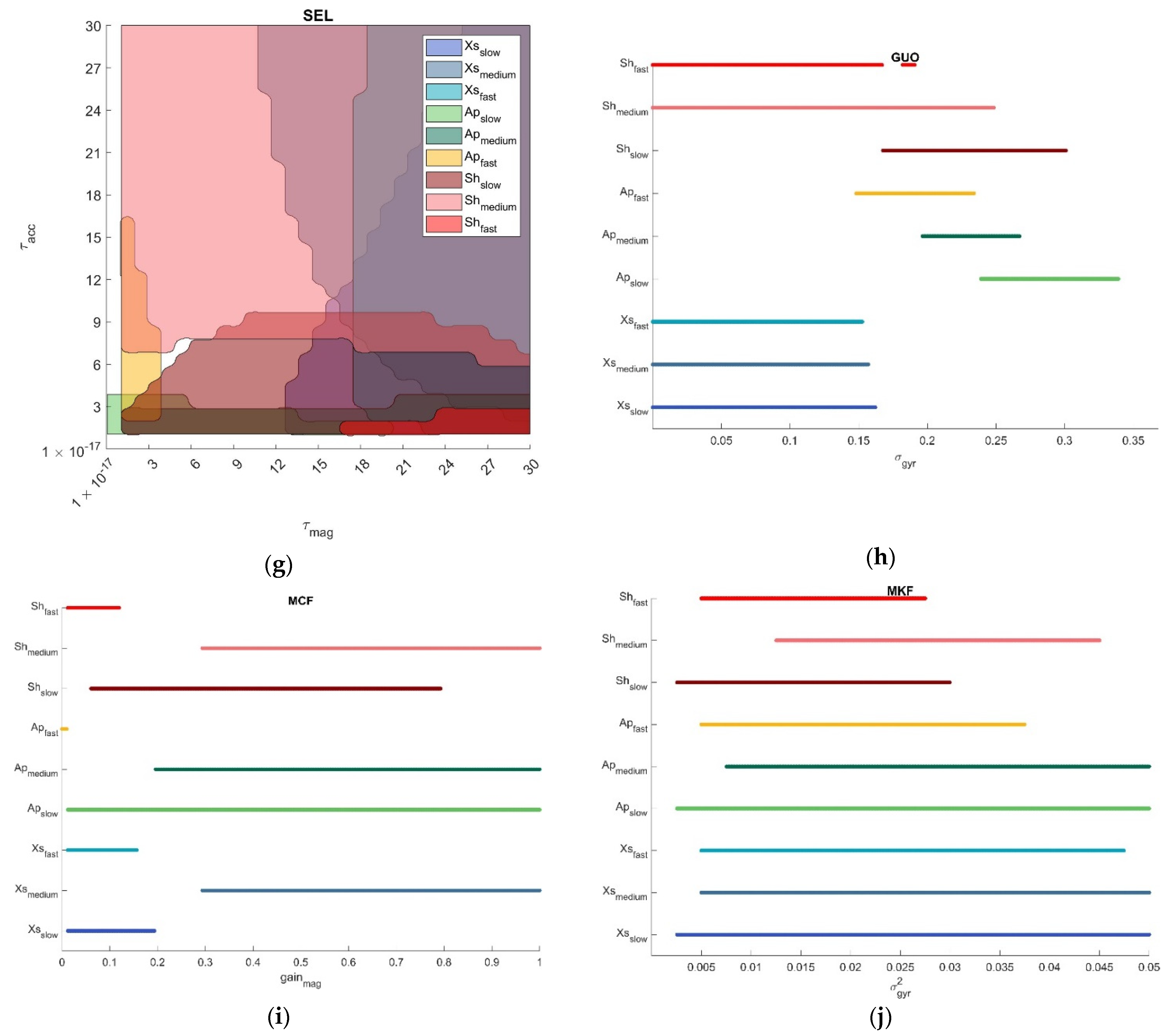
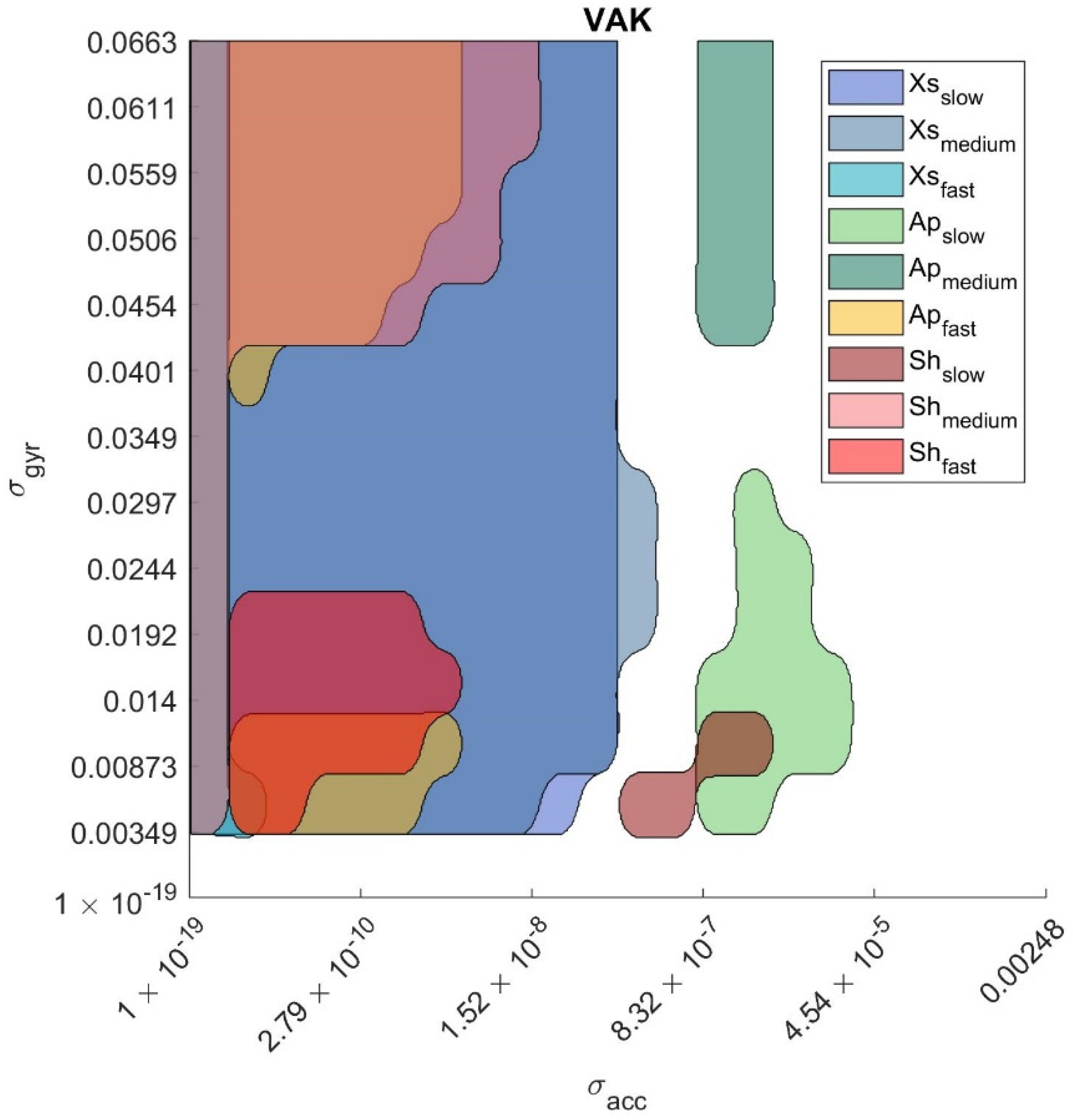
- Optimal parameter region is defined as the range of parameter values for which the relevant orientation errors are equal to the minimum error plus 0.5 deg (i.e., the SP uncertainty band, as stated in Section 2.5.1). These regions are defined as: . An example of optimal region is illustrated in Figure 2 for the VAK filter. When only one parameter was tuned (MAD, VAC, GUO, MKF) was a vector and the optimal region degenerated into a 1D interval.
2.6.2. Identification of the Default Errors
2.6.3. Statistical Analysis to Evaluate the Influence of the SFAs and of the Experimental Factors
2.6.4. Computation Time of the Different SFAs
3. Results
3.1. Optimal and Default Errors
3.2. Optimal Regions
3.3. Influence of the Experimental Factors on the Absolute Accuracy
3.3.1. Influence of the Specific SFA (3 Rotation Rates × 3 Commercial Products)
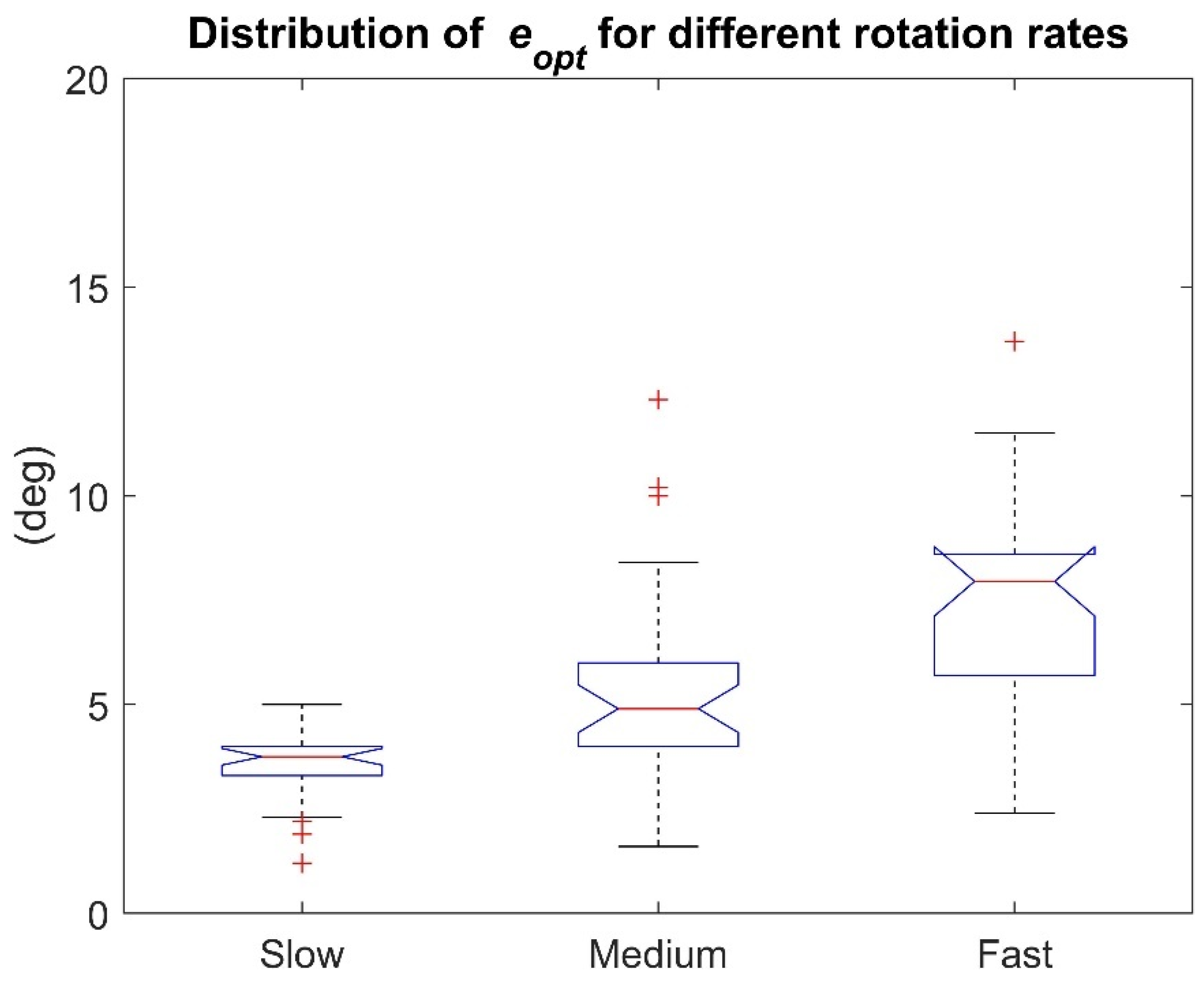
3.3.2. Influence of the Rotation Rate (10 SFA × 3 Commercial Products)
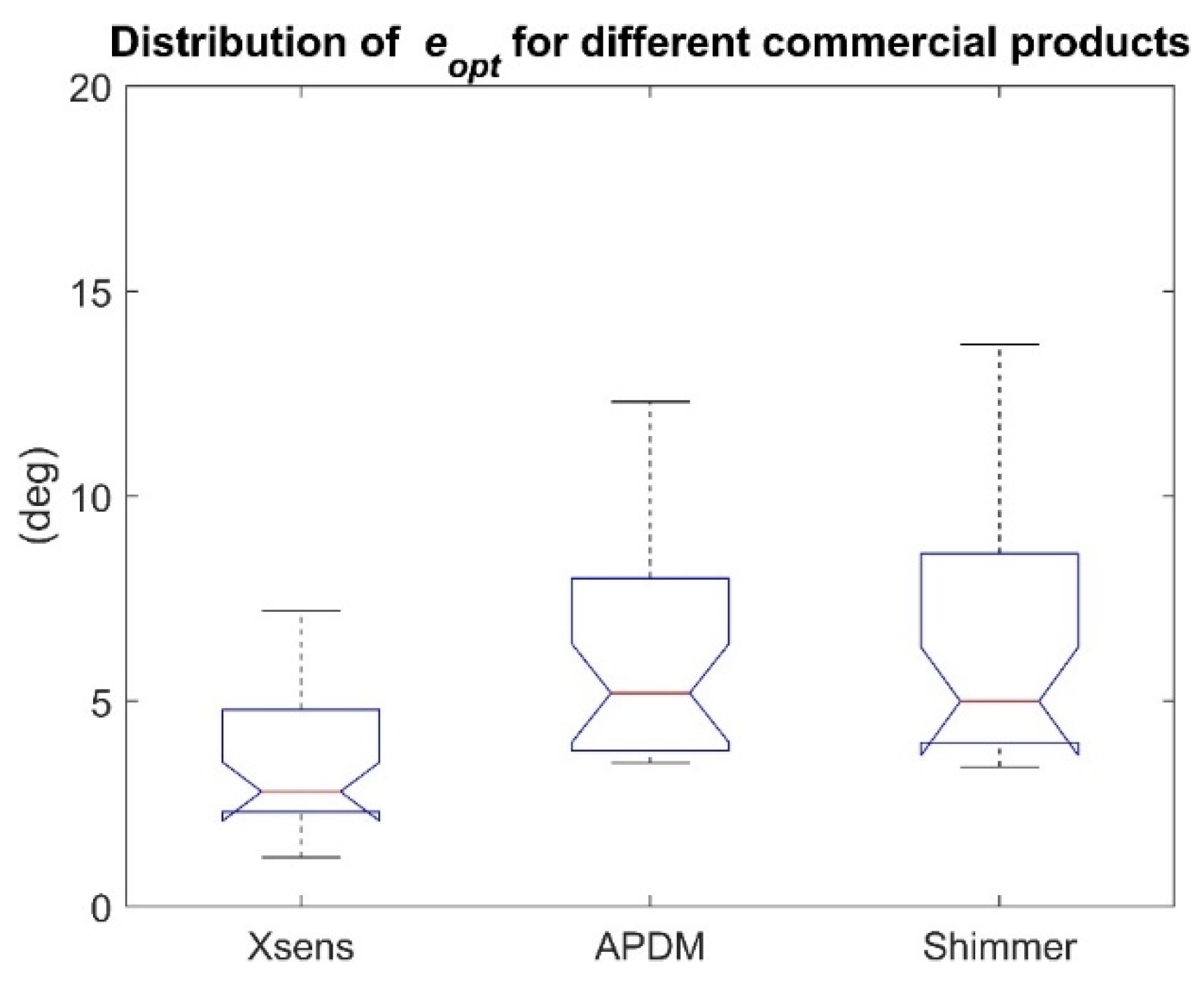
3.3.3. Influence of the Commercial Product (10 SFA × 3 Rotation Rates)
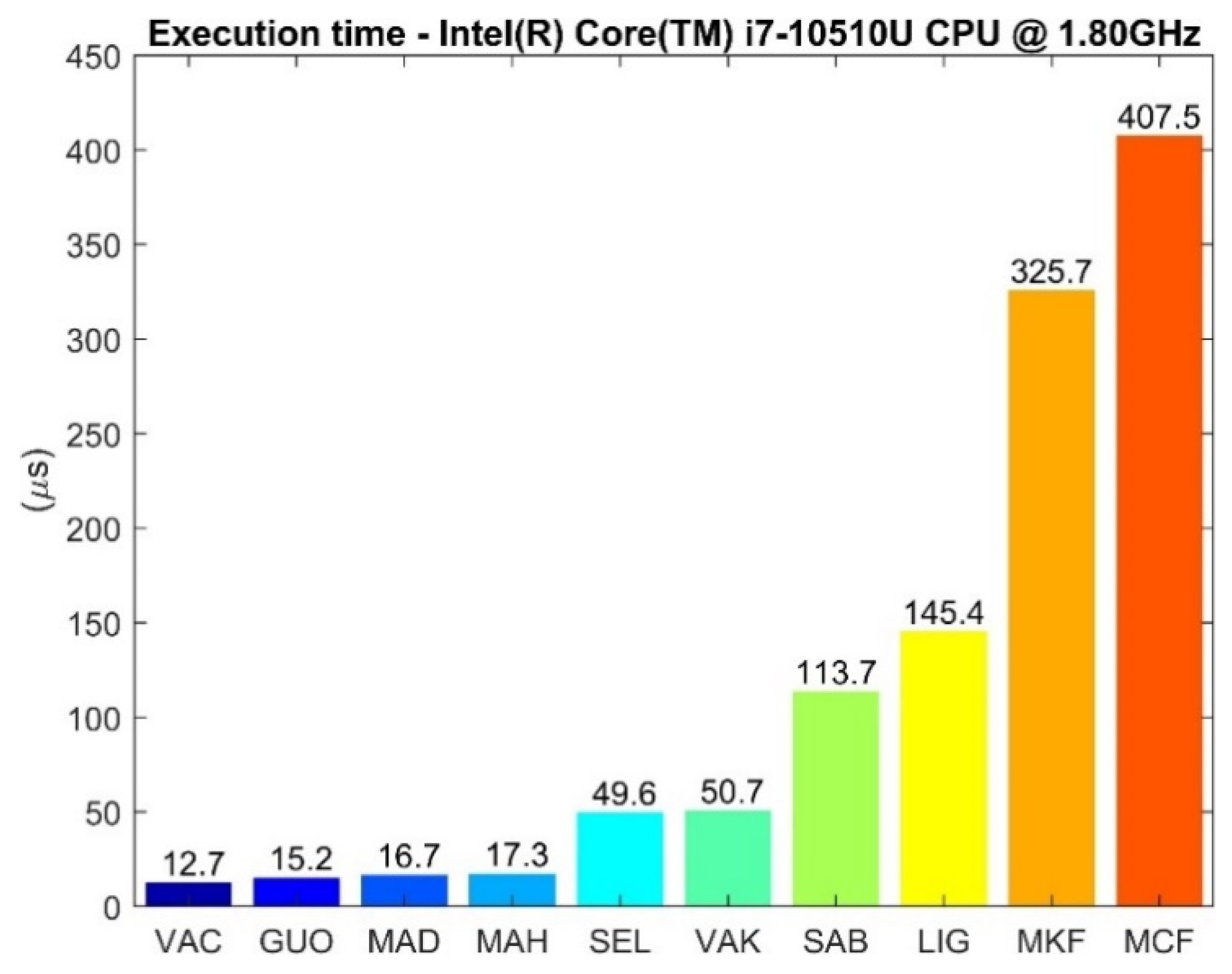
3.4. Computation Time of the Different SFAs
4. Discussion
4.1. The Importance of Properly Tuning Each SFA
4.2. Influence of the SFA and of the Experimental Factors on the Absolute Accuracy
4.3. Computation Time of the SFAs
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Glossary
| CF | complementary filter |
| GCS | global coordinate system |
| KF | Kalman filter |
| LCS | local coordinate system |
| MIMU | magneto-inertial measurement unit |
| RMS | root mean square |
| SFA | sensor fusion algorithm |
| SP | stereo-photogrammetric system |
| STD | standard deviation |
| Absolute orientation | the orientation of the local coordinate system (LCS) of a system with respect to its GCS |
| Absolute orientation error | the difference between the orientation of the LCS of a magneto-inertial measurement unit (MIMU) computed by a sensor fusion algorithm (SFA) and its actual orientation computed by the optical reference (SP) and expressed by the angle given by the axis-angle convention |
| absolute orientation error corresponding to the selection of the default parameter values | |
| minimum absolute orientation error which corresponds to the selection of the optimal parameter values | |
| Optimal parameter region | the range of parameter values for which the orientation errors are equal to plus 0.5 deg |
Appendix A
| First Author | SFA(s) Employed | MIMU(s) Employed | Experimental Protocol | Standard | Declared Errors |
|---|---|---|---|---|---|
| Picerno 2011 [30] | Xsens filter (KF) | 9 Xsens MTw | MIMUs were aligned on a rigid body which was oriented in 12 different poses. Only the static orientation was considered. | none | Differences were up to 11.4 for yaw angle (in an ideal case they should be null). |
| Bergamini 2014 [25] | Madgwick [9] (CF) Sabatini [34] (KF) | 1 APDM-Opal | Manual tasks (slow velocities, short time, and small capture volume). Locomotion task (larger capture volume, three minutes, no static phases). | SP | RMS errors were similar for CF and KF: from 5.5 (manual) to 21 (locomotion) tasks. |
| Lebel 2015 [26] | Xsens filter (KF) APDM filter (KF) Inertial Labs filter (CF) | 4 Xsens-MTx 4 APDM-Opal 4 Inertial Labs-Osv3 | MIMUs attached to a gimbal. Rotation of the gimbal axes to obtain both planar (2D) and 3D motions at quasi-constant low and high rotation rates (90 dps and 180 dps) for 120 s. | SP | Mean errors increased up to 7 when the rotation rate increased, although this was less evident for Xsens filter. |
| Ricci 2016 [27] | APDM filter (KF) Tian [46] (CF) | 6 APDM-Opal | MIMUs attached to a robot arm Static (different orientations) Dynamic (sinusoidal rotations around MIMU axis, the RMS of the angular velocity ranged from 2.1 dps to 150 dps). | Robot angles | In static the maximum errors amounted to 1 for CF and 1.6 for KF. In the dynamic trials, the KF exhibited the best performance. Errors increased when the velocity increased. |
| Ludwig 2018 [28] | Madgwick [9] (CF) Mahony [6] (CF) Marins [47] (KF) | 1 embedded on a quadcopter | The quadrotor flew to perform both loop and random sequences within the volume capture (1m × 1m × 1m). | SP | RMS errors amounted to 11, 13, and 13.3 for Mahony, Madgwick and Marius, respectively. |
| First Author | SFA(s) Employed | MIMU(s) Employed | Experimental Protocol | Standard | Declared Errors |
|---|---|---|---|---|---|
| Young 2009 [7] | Proposed CF Yun [48] (KF) | 1 Orient | Gently movements by hand (20 s). Walking with MIMU on the lower leg (five trials, 30 s each). | SP | RMS inclination (and yaw) errors. Gently movements: 3.2 (9.6) for CF and 5.4 deg (10.1) for KF. Walking: 4 deg (10.9) for CF and 11.9 (31.8) for KF. |
| Fourati 2014 [8] | Proposed CF Xsens filter (KF) | 1 Xsens-Mti 1 Xsens-MTi-G | Manual (3 straight translations along each MIMU axis and a free 3 D motion). | none | Average inclination (and yaw) difference between the estimates of the CF and KF ranged between [1,2,3] ([2,3,4,5]). |
| Madgwick [9] | Proposed CF Xsens filter (KF) | 1 Xsens-MTx | Static. Dynamic (manual motions). | SP | RMS errors in dynamic amounted to 1.1 for the proposed and 1.3 for KF. |
| Valenti 2015 [2] | Proposed CF Sabatini [34] (KF) Madgwick [9] (CF) | PhidgetSpatial 3/3/3 embedded in a quadrotor | The vehicle flew in a volume of 10 m × 10 m × 10 m to perform loop trajectories. | SP | RMS inclination (and yaw) errors amounted to 1.7 (16.6), 2.5 (20.3), and 3 (76.2) for the proposed CF, the KF, and the CF by Madgwick. |
| Marantos 2016 [14] | Proposed CF St iNEMO filter (KF) Mahony [6] (CF) | Designed | MIMU mounted on a gimbal which was subjected to a combined motion in all axes including strong acceleration and ferromagnetic disturbances. | Gimbal encoders | Mean inclination (and yaw) errors amounted to 1.0 (2.5), 5.5 (10.5), and 4.9 (11.5) for the proposed CF, the CF from Mahony and KF. |
| Olivares 2016 [15] | Two proposed KFs (optimal approach vs. algebraic solution) | 1 Wagyromag (designed) | MIMU mounted on a device moved at 3 speeds including high accelerations and magnetic disturbances. | Potentiometer—mounted on the hinge. | Mean RMS errors: 1.5 for KF with optimal approach and 2.1 for KF with algebraic solution. |
| Seel 2017 [16] | Proposed CF Madgwick [9] (CF) | none | Simulated magnetic field environment. | Synthetic ground-truth. | Inclination errors for Madgwick CF were higher than 4. |
| Guo 2017 [17] | Proposed KF Fourati 2014 [8] (CF) Marantos 2016 [14] (CF) Valenti 2016 [2] (KF) | 1 MicroStrain 3DM- GX3-25 | Random movements carried out by hand. | Provided by the proprietary algorithm (not properly a gold standard). | Mean inclination (and yaw) errors amounted to 0.1 (0.1), 0.2 (0.7), 1.3 (0.6), and 2.2 (3.7) for the proposed KF, the CF by Fourati, the CF by Marantos, and the KF by Valenti. |
| Fan 2018 [18] | Basic proposed CF Finite-state proposed CF | 1 Xsens-MTw | Fast MIMU movement up and down (range of 60 cm) close to a big ferromagnetic box. | SP | RMS inclination (and yaw) errors 6 (7) and 1 (1) for basic CF and finite-state CF during large acceleration. RMS Yaw errors 7 and 1 for basic CF and finite-state CF during magnetic disturbances. |
| Weber 2020 [22] | Proposed neural-network See1 2017 [16] (CF) | 1 Myon AG-aktos-t | Roto-translation movements at different speeds including pauses. | SP | RMS errors equal to 1.4 for the neural network and to 2.8 for the CF. |
Appendix B
| STD | Accelerometer (mg) | Gyroscope (deg/s) | Magnetometer (µT) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| x | y | z | x | y | z | x | y | z | |
| Xsens-MTx #1 | 0.86 | 0.80 | 0.85 | 0.38 | 0.39 | 0.37 | 0.06 | 0.04 | 0.04 |
| Xsens-MTX #2 | 0.82 | 0.86 | 0.80 | 0.44 | 0.40 | 0.40 | 0.05 | 0.06 | 0.06 |
| APDM-OPAL #1 | 0.38 | 0.33 | 0.38 | 0.16 | 0.23 | 0.11 | 0.26 | 0.23 | 0.20 |
| APDM-OPAL #2 | 0.34 | 0.32 | 0.35 | 0.16 | 0.27 | 0.19 | 0.26 | 0.25 | 0.20 |
| Shimmer-Shimmer 3 #1 | 1.06 | 0.97 | 1.26 | 0.09 | 0.08 | 0.09 | 0.84 | 0.84 | 0.69 |
| Shimmer-Shimmer 3 #2 | 1.12 | 1.09 | 1.29 | 0.06 | 0.06 | 0.06 | 0.97 | 0.97 | 0.58 |
| Gyroscope Bias (deg/s) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Slow | Medium | Fast | ||||||||
| x | y | z | x | y | z | x | y | z | ||
| Xsens-MTx #1 | before | −0.24 | −1.70 | −0.32 | −0.26 | −1.70 | −0.33 | −0.25 | −1.69 | −0.33 |
| diff | 0.00 | −0.05 | 0.00 | −0.01 | 0.00 | −0.02 | −0.01 | −0.01 | −0.02 | |
| Xsens-MTX #2 | before | −0.26 | 0.76 | 0.42 | −0.26 | 0.76 | 0.43 | −0.28 | 0.74 | 0.41 |
| diff | 0.01 | 0.01 | 0.02 | 0.03 | 0.00 | 0.03 | −0.01 | −0.02 | −0.02 | |
| APDM-OPAL #1 | before | 0.78 | −0.57 | 0.34 | 0.59 | −0.80 | 0.36 | 0.74 | −0.78 | 0.37 |
| diff | 0.08 | 0.04 | −0.02 | −0.12 | −0.02 | 0.00 | −0.02 | 0.12 | −0.01 | |
| APDM-OPAL #2 | before | −1.10 | −0.06 | −0.71 | −1.20 | −0.05 | −0.48 | −1.11 | 0.17 | −0.48 |
| diff | 0.07 | 0.01 | −0.03 | −0.17 | −0.17 | −0.05 | −0.09 | −0.03 | −0.10 | |
| Shimmer-Shimmer 3 #1 | before | −0.03 | −0.06 | −0.01 | −0.02 | −0.05 | 0.01 | −0.03 | −0.07 | 0.02 |
| diff | −0.01 | −0.03 | 0.00 | −0.01 | 0.00 | 0.00 | 0.00 | −0.01 | 0.00 | |
| Shimmer-Shimmer 3 #2 | before | −0.06 | −0.03 | 0.09 | −0.06 | −0.03 | 0.08 | −0.06 | −0.05 | 0.10 |
| diff | −0.01 | −0.03 | 0.01 | −0.01 | −0.03 | 0.01 | −0.01 | −0.03 | 0.03 | |
| Range | A/D Resolution | Alignment Error | |
|---|---|---|---|
| Xsens-MTx | |||
| Accelerometer | ±50 m/s2 | 16 bits | 0.1 deg |
| Gyroscope | ±1200 deg/s | 16 bits | 0.1 deg |
| Magnetometer | ±75 µT | 16 bits | 0.1 deg |
| APDM-OPAL | |||
| Accelerometer | ±16 m/s2 | 14 bits | |
| Gyroscope | ±2000 deg/s | 16 bits | |
| Magnetometer | ±800 µT | 12 bits | |
| Shimmer-Shimmer3 | |||
| Accelerometer | ±16 m/s2 | 16 bits | |
| Gyroscope | ±2000 deg/s | 16 bits | |
| Magnetometer | ±400 µT | 16 bits | |
Appendix C
References
- Cereatti, A.; Trojaniello, D.; Della Croce, U. Accurately measuring human movement using magneto-inertial sensors: Techniques and challenges. In Proceedings of the 2015 IEEE International Symposium on Inertial Sensors and Systems (ISISS) Proceedings, Hapuna Beach, HI, USA, 23–26 March 2015; pp. 1–4. [Google Scholar] [CrossRef]
- Valenti, R.G.; Dryanovski, I.; Xiao, J. Keeping a good attitude: A quaternion-based orientation filter for IMUs and MARGs. Sensors 2015, 15, 19302–19330. [Google Scholar] [CrossRef]
- Sabatini, A.M. Quaternion-Based extended Kalman filter for determining orientation by inertial and magnetic sensing. IEEE Trans. Biomed. Eng. 2006, 53, 1346–1356. [Google Scholar] [CrossRef]
- Luinge, H.J.; Veltink, P.H. Inclination measurement of human movement using a 3-D accelerometer with autocalibration. IEEE Trans. Neural Syst. Rehabil. Eng. 2004, 12, 112–121. [Google Scholar] [CrossRef]
- Roetenberg, D.; Baten, C.T.M.; Veltink, P.H. Estimating body segment orientation by applying inertial and magnetic sensing near ferromagnetic materials. IEEE Trans. Neural Syst. Rehabil. Eng. 2007, 15, 469–471. [Google Scholar] [CrossRef] [PubMed]
- Mahony, R.; Hamel, T.; Pflimlin, J.M. Nonlinear complementary filters on the special orthogonal group. IEEE Trans. Autom. Control 2008, 53, 1203–1218. [Google Scholar] [CrossRef]
- Young, A.D. Comparison of orientation filter algorithms for realtime wireless inertial posture tracking. In Proceedings of the 2009 Sixth International Workshop on Wearable and Implantable Body Sensor Networks, Berkeley, CA, USA, 3–5 June 2009; pp. 59–64. [Google Scholar] [CrossRef]
- Fourati, H.; Manamanni, N.; Afilal, L.; Handrich, Y. Complementary observer for body segments motion capturing by inertial and magnetic sensors. IEEE ASME Trans. Mechatron. 2014, 19, 149–157. [Google Scholar] [CrossRef]
- Madgwick, S.O.H.; Harrison, A.J.L.; Vaidyanathan, R. Estimation of IMU and MARG orientation using a gradient descent algorithm. In Proceedings of the 2011 IEEE International Conference on Rehabilitation Robotics, Zurich, Switzerland, 29 June–1 July 2011; pp. 1–7. [Google Scholar] [CrossRef]
- Calusdian, J.; Yun, X.; Bachmann, E. Adaptive-Gain complementary filter of inertial and magnetic data for orientation estimation. In Proceedings of the IEEE International Conference on Robotics and Automation, Shanghai, China, 9–13 May 2011; pp. 1916–1922. [Google Scholar] [CrossRef]
- Mazzà, C.; Donati, M.; McCamley, J.; Picerno, P.; Cappozzo, A. An optimized Kalman filter for the estimate of trunk orientation from inertial sensors data during treadmill walking. Gait Posture 2012, 35, 138–142. [Google Scholar] [CrossRef] [PubMed]
- Ligorio, G.; Sabatini, A.M. A novel Kalman filter for human motion tracking with an inertial-based dynamic inclinometer. IEEE Trans. Biomed. Eng. 2015, 62, 2033–2043. [Google Scholar] [CrossRef]
- Valenti, R.G.; Dryanovski, I.; Xiao, J. A linear Kalman filter for MARG orientation estimation using the algebraic quaternion algorithm. IEEE Trans. Instrum. Meas. 2016, 65, 467–481. [Google Scholar] [CrossRef]
- Marantos, P.; Koveos, Y.; Kyriakopoulos, K.J. UAV State Estimation Using Adaptive Complementary Filters. IEEE Trans. Control Syst. Technol. 2016, 24, 1214–1226. [Google Scholar] [CrossRef]
- Olivares, A.; Górriz, J.M.; Ramírez, J.; Olivares, G. Using frequency analysis to improve the precision of human body posture algorithms based on Kalman filters. Comput. Biol. Med. 2016, 72, 229–238. [Google Scholar] [CrossRef]
- Seel, T.; Ruppin, S. Eliminating the effect of magnetic disturbances on the inclination estimates of inertial sensors. IFAC PapersOnLine 2017, 50, 8798–8803. [Google Scholar] [CrossRef]
- Guo, S.; Wu, J.; Wang, Z.; Qian, J. Novel MARG-sensor orientation estimation algorithm using fast Kalman filter. J. Sens. 2017, 2017, 8542153. [Google Scholar] [CrossRef]
- Fan, B.; Li, Q.; Liu, T. Improving the accuracy of wearable sensor orientation using a two-step complementary filter with state machine-based adaptive strategy. Meas. Sci. Technol. 2018, 29, 115104. [Google Scholar] [CrossRef]
- Del Rosario, M.B.; Khamis, H.; Ngo, P.; Lovell, N.H.; Redmond, S.J. Computationally efficient adaptive error-state Kalman filter for attitude estimation. IEEE Sens. J. 2018, 18, 9332–9342. [Google Scholar] [CrossRef]
- Majumder, S.; Deen, M.J. A robust orientation filter for wearable sensing applications. IEEE Sens. J. 2020, 20, 14228–14236. [Google Scholar] [CrossRef]
- Esfahani, M.A.; Wang, H.; Wu, K.; Yuan, S. OriNet: Robust 3-D orientation estimation with a single particular IMU. IEEE Robot. Autom. Lett. 2020, 5, 399–406. [Google Scholar] [CrossRef]
- Weber, D.; Gühmann, C.; Seel, T. Neural networks versus conventional filters for inertial-sensor-based attitude estimation. arXiv 2020, arXiv:2005.06897. [Google Scholar]
- Deibe, Á.; Augusto, J.; Nacimiento, A.; Peña, F.L. A Kalman Filter for nonlinear attitude estimation using time variable matrices and quaternions. Sensors 2020, 20, 6731. [Google Scholar] [CrossRef]
- Kalman, R.E. A new approach to linear filtering and prediction problems. J. Fluids Eng. Trans. ASME 1960, 82, 35–45. [Google Scholar] [CrossRef]
- Bergamini, E.; Ligorio, G.; Summa, A.; Vannozzi, G.; Cappozzo, A.; Sabatini, A.M. Estimating orientation using magnetic and inertial sensors and different sensor fusion approaches: Accuracy assessment in manual and locomotion tasks. Sensors 2014, 14, 18625–18649. [Google Scholar] [CrossRef] [PubMed]
- Lebel, K.; Boissy, P.; Hamel, M.; Duval, C. Inertial measures of motion for clinical biomechanics: Comparative assessment of accuracy under controlled conditions—Changes in accuracy over time. PLoS ONE 2015, 10, e79945. [Google Scholar] [CrossRef]
- Ricci, L.; Taffoni, F.; Formica, D. On the orientation error of IMU: Investigating static and dynamic accuracy targeting human motion. PLoS ONE 2016, 11, e0161940. [Google Scholar] [CrossRef]
- Ludwig, S.A.; Burnham, K.D. Comparison of Euler Estimate using extended Kalman filter, Madgwick and Mahony on quadcopter flight data. In Proceedings of the 2018 International Conference on Unmanned Aircraft Systems, Dallas, TX, USA, 12–15 June 2018; pp. 1236–1241. [Google Scholar] [CrossRef]
- Nazarahari, M.; Rouhani, H. 40 Years of sensor fusion for orientation tracking via magnetic and inertial measurement units: Methods, lessons learned, and future challenges. Inf. Fusion 2020, 68, 67–84. [Google Scholar] [CrossRef]
- Picerno, P.; Cereatti, A.; Cappozzo, A. A spot check for assessing static orientation consistency of inertial and magnetic sensing units. Gait Posture 2011, 33, 373–378. [Google Scholar] [CrossRef]
- Caruso, M.; Sabatini, A.M.; Knaflitz, M.; Gazzoni, M.; Della Croce, U.; Cereatti, A. Orientation estimation through magneto-inertial sensor fusion: A Heuristic approach for suboptimal parameters tuning. IEEE Sens. J. 2020, 21, 3408–3419. [Google Scholar] [CrossRef]
- Cavallo, A.; Cirillo, A.; Cirillo, P.; De Maria, G.; Falco, P.; Natale, C.; Pirozzi, S. Experimental comparison of sensor fusion algorithms for attitude estimation. IFAC Proc. Vol. 2014, 47, 7585–7591. [Google Scholar] [CrossRef]
- Caruso, M.; Sabatini, A.M.; Knaflitz, M.; Gazzoni, M.; Della Croce, U.; Cereatti, A. Accuracy of the orientation estimate obtained using four sensor fusion filters applied to recordings of magneto-inertial sensors moving at three rotation rates. In Proceedings of the Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Berlin, Germany, 23–27 July 2019; pp. 2053–2058. [Google Scholar] [CrossRef]
- Sabatini, A.M. Estimating three-dimensional orientation of human body parts by inertial/magnetic sensing. Sensors 2011, 11, 1489–1525. [Google Scholar] [CrossRef]
- Roetenberg, D.; Luinge, H.J.; Baten, C.T.M.; Veltink, P.H. Compensation of magnetic disturbances improves inertial and magnetic sensing of human body segment orientation. IEEE Trans. Neural Syst. Rehabil. Eng. 2005, 13, 395–405. [Google Scholar] [CrossRef]
- Cappozzo, A.; Cappello, A.; Della Croce, U.; Pensalfini, F. Surface-Marker cluster design criteria for 3-D bone movement reconstruction. IEEE Trans. Biomed. Eng. 1997, 44, 1165–1174. [Google Scholar] [CrossRef]
- Caruso, M.; Cereatti, A.; Della Croce, U. MIMU_OPTICAL_SASSARI_DATASET. Available online: https://ieee-dataport.org/documents/mimuopticalsassaridataset (accessed on 29 March 2021). [CrossRef]
- Chardonnens, J.; Favre, J.; Aminian, K. An effortless procedure to align the local frame of an inertial measurement unit to the local frame of another motion capture system. J. Biomech. 2012, 45, 2297–2300. [Google Scholar] [CrossRef]
- Chiari, L.; Della Croce, U.; Leardini, A.; Cappozzo, A. Human movement analysis using stereophotogrammetry. Part 2: Instrumental errors. Gait Posture 2005, 21, 197–211. [Google Scholar] [CrossRef]
- Lee, S.; Lee, D.K. What is the proper way to apply the multiple comparison test? Korean J. Anesthesiol. 2018, 71, 353–360. [Google Scholar] [CrossRef]
- IEEE Electron Devices Society; Microelectromechanical Systems Standards Development Committee; Institute of Electrical and Electronics Engineers; IEEE-SA Standards Board. IEEE Standard for Sensor Performance Parameter Definitions; IEEE: New York, NY, USA, 2014. [Google Scholar]
- Lebel, K.; Boissy, P.; Hamel, M.; Duval, C. Inertial measures of motion for clinical biomechanics: Comparative assessment of accuracy under controlled conditions—Effect of velocity. PLoS ONE 2013, e79945. [Google Scholar] [CrossRef] [PubMed]
- Zedda, A.; Gusai, E.; Caruso, M.; Bertuletti, S.; Baldazzi, G.; Spanu, S.; Riboni, D.; Pibiri, A.; Monticone, M.; Cereatti, A.; et al. DoMoMEA: A Home-Based telerehabilitation system for stroke patients. In Proceedings of the 2020 42nd Annual International Conference of the IEEE Engineering in Medicine & Biology Society (EMBC), Montreal, QC, Canada, 20–24 July 2020; pp. 5773–5776. [Google Scholar] [CrossRef]
- Ludwig, S.A.; Jiménez, A.R. Optimization of gyroscope and accelerometer/magnetometer portion of basic attitude and heading reference system. In Proceedings of the 2018 IEEE International Symposium on Inertial Sensors and Systems (INERTIAL), Lake Como, Italy, 26–29 March 2018; pp. 1–4. [Google Scholar] [CrossRef]
- Cardarelli, S.; Verdini, F.; Mengarelli, A.; Strazza, A.; Di Nardo, F.; Burattini, L.; Fiorettiet, S. Position Estimation of an IMU Placed on Pelvis Through Meta-heuristically Optimised WFLC. In Proceedings of the World Congress on Medical Physics and Biomedical Engineering 2018, Prague, Czech Republic, 3–8 June 2018; pp. 659–664. [Google Scholar]
- Tian, Y.; Wei, H.; Tan, J. An Adaptive-Gain complementary filter for real-time human motion tracking with MARG sensors in free-living environments. IEEE Trans. Neural Syst. Rehabil. Eng. 2013, 21, 254–264. [Google Scholar] [CrossRef] [PubMed]
- Marins, J.L.; Yun, X.; Bachmann, E.R.; McGhee, R.B.; Zyda, M.J. An extended Kalman filter for quaternion-based orientation estimation using MARG sensors. In Proceedings of the Proceedings 2001 IEEE/RSJ International Conference on Intelligent Robots and Systems. Expanding the Societal Role of Robotics in the the Next Millennium (Cat. No.01CH37180), Maui, HI, USA, 29 October–3 November 2001; pp. 2003–2011. [Google Scholar] [CrossRef]
- Yun, X.; Bachmann, E.R. Design, implementation, and experimental results of a quaternion-based Kalman filter for human body motion tracking. IEEE Trans. Robot. 2006, 22, 1216–1227. [Google Scholar] [CrossRef]
- Sabatini, A.M. Awavelet-Based bootstrap method applied to inertial sensor stochastic error modelling using the allan variance. Meas. Sci. Technol. 2006, 17, 2980–2988. [Google Scholar] [CrossRef]
- El-Sheimy, N.; Hou, H.; Niu, X. Analysis and modeling of inertial sensors using allan variance. IEEE Trans. Instrum. Meas. 2008, 57, 140–149. [Google Scholar] [CrossRef]
- Hussen, A.A.; Jleta, I.N. Low-Cost inertial sensors modeling using allan variance. Int. Sch. Sci. Res. Innov. 2015, 9, 1069–1074. [Google Scholar]

| CF | # Params | Default | Default | ||||
| MAH | 2 | kp—inverse gyroscope weight | 1 | rad/s | ki—weight for online bias estimation | 0.3 | rad/s |
| MAD | 1 | β—inverse gyroscope weight | 0.1 | rad/s | / | / | |
| VAC | 9 | gmag—magnetometer weight | 0.01 | a.u. | ath2—threshold for accelerometer vector selection | 0.2 | a.u. |
| SEL | 4 | τacc—accelerometer time constant | 1 | s | τmag—magnetometer time constant | 3 | s |
| MCF | 2 | gmag—magnetometer weight | 0.01 | a.u. | / | / | |
| KF | # Params | Default | Default | ||||
| SAB | 6 | σgyr—inverse gyroscope weight | 0.007 | rad/s | ath—threshold for accelerometer vector selection | 40 | mg |
| LIG | 6 | σgyr—inverse gyroscope weight | 1 | rad/s | cb—Gauss-Markov parameter of the prediction model to set the variance of external acceleration and ferromagnetic disturbances | 1 | a.u. |
| VAK | 3 | σgyr—inverse gyroscope weight | 0.004 | rad/s | σacc—inverse accelerometer weight | 0.014 | m/s2 |
| GUO | 3 | σgyr—inverse gyroscope weight | 0.001 | rad/s | / | / | |
| MKF | 8 | σ2gyr—inverse gyroscope weight | 9.14 × 10−5 | (rad/s)2 | / | / | |
| Influencing Factor | Number of Distributions | Number of Values for Each Distribution |
|---|---|---|
| SFA | 10 (one for each SFA) | 9 (=3 rotation rates × 3 commercial products) |
| Rotation rate | 3 (one for each rotation rate) | 30 (=10 SFAs × 3 commercial products) |
| Commercial product | 3 (one for each commercial product) | 30 (=10 SFAs × 3 rotation rates) |
| CF | KF | ||||||
|---|---|---|---|---|---|---|---|
| Xsens | Slow | MAH | 2.5 | 4.2 | SAB | 2.2 | 67.9 |
| Medium | 2.4 | 11.9 | 2.1 | 96.6 | |||
| Fast | 4.0 | 13.0 | 2.4 | 53.9 | |||
| APDM | Slow | 3.8 | 3.9 | 5.0 | 77.5 | ||
| Medium | 4.8 | 17.7 | 5.7 | 62.6 | |||
| Fast | 8.2 | 12.3 | 8.3 | 9.9 | |||
| Shimmer | Slow | 3.4 | 5.9 | 4.5 | 71.1 | ||
| Medium | 4.6 | 38.2 | 4.9 | 14.5 | |||
| Fast | 7.6 | 17.0 | 8.5 | 30.0 | |||
| Xsens | Slow | MAD | 2.7 | 4.7 | LIG | 1.9 | 3.7 |
| Medium | 2.5 | 5.2 | 2.0 | 3.9 | |||
| Fast | 4.0 | 6.8 | 2.9 | 4.8 | |||
| APDM | Slow | 3.8 | 4.1 | 3.6 | 3.6 | ||
| Medium | 4.6 | 4.6 | 4.9 | 5.0 | |||
| Fast | 8.1 | 8.2 | 4.6 | 4.6 | |||
| Shimmer | Slow | 3.9 | 4.3 | 4.4 | 4.4 | ||
| Medium | 4.9 | 5.2 | 4.0 | 4.2 | |||
| Fast | 8.8 | 8.9 | 6.3 | 6.5 | |||
| Xsens | Slow | VAC | 4.0 | 4.1 | VAK | 1.2 | 22.3 |
| Medium | 5.0 | 5.9 | 1.6 | 21.4 | |||
| Fast | 7.2 | 10.0 | 2.5 | 72.8 | |||
| APDM | Slow | 3.5 | 3.6 | 3.6 | 29.6 | ||
| Medium | 6.1 | 11.8 | 6.0 | 30.4 | |||
| Fast | 8.3 | 15.1 | 9.2 | 81.9 | |||
| Shimmer | Slow | 3.8 | 3.8 | 4.0 | 32.6 | ||
| Medium | 10.2 | 19.2 | 4.4 | 48.8 | |||
| Fast | 11.5 | 23.6 | 8.2 | 100.1 | |||
| Xsens | Slow | SEL | 3.1 | 4.0 | GUO | 2.3 | 3.7 |
| Medium | 2.5 | 4.6 | 2.3 | 4.9 | |||
| Fast | 5.1 | 6.7 | 5.7 | 10.6 | |||
| APDM | Slow | 3.7 | 3.8 | 4.2 | 4.5 | ||
| Medium | 7.1 | 7.3 | 5.1 | 5.3 | |||
| Fast | 8.0 | 8.8 | 9.4 | 12.0 | |||
| Shimmer | Slow | 3.4 | 3.5 | 4.0 | 4.0 | ||
| Medium | 5.0 | 8.4 | 5.1 | 5.7 | |||
| Fast | 9.4 | 11.8 | 13.7 | 16.7 | |||
| Xsens | Slow | MCF | 3.3 | 4.5 | MKF | 4.2 | 4.9 |
| Medium | 6.1 | 6.2 | 4.8 | 8.7 | |||
| Fast | 6.6 | 7.8 | 6.7 | 10.9 | |||
| APDM | Slow | 3.8 | 4.2 | 3.6 | 4.8 | ||
| Medium | 12.3 | 12.3 | 5.3 | 14.3 | |||
| Fast | 7.9 | 9.3 | 7.2 | 10.7 | |||
| Shimmer | Slow | 5.0 | 5.2 | 3.9 | 5.8 | ||
| Medium | 10.0 | 10.1 | 8.4 | 45.2 | |||
| Fast | 8.6 | 12.0 | 9.9 | 19.0 |
| LIG | VAK | MAH | MAD | SAB | SEL | GUO | MKF | VAC | MCF | |
|---|---|---|---|---|---|---|---|---|---|---|
| 3.8 ± 1.4 | 4.5 ± 2.8 | 4.6 ± 2.1 | 4.8 ± 2.2 | 4.8 ± 2.4 | 5.3 ± 2.4 | 5.8 ± 3.7 | 6.0 ± 2.2 | 6.6 ± 2.9 | 7.1 ± 2.9 |
| (deg) | Slow | Medium | Fast |
|---|---|---|---|
| 3.5 ± 0.9 | 5.2 ± 2.5 | 7.3 ± 2.6 |
| Scenario | Optimal Conditions |
|---|---|
| Slow vs. fast | Significantly different (p < 1× 10−4) |
| Slow vs. medium | Significantly different (p < 1× 10−3) |
| Fast vs. medium | Significantly different (p = 0.013) |
| (deg) | Xsens-MTx | APDM-Opal | Shimmer-Shimmer 3 |
|---|---|---|---|
| 3.5 ± 1.7 | 6.0 ± 2.3 | 6.5 ± 2.8 |
| Scenario | Optimal Conditions |
|---|---|
| Xsens vs. APDM | Significantly different (p < 1× 10−5) |
| Xsens vs. Shimmer | Significantly different (p < 1× 10−6) |
| APDM vs. Shimmer | Not significantly different (p = 1) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Caruso, M.; Sabatini, A.M.; Laidig, D.; Seel, T.; Knaflitz, M.; Della Croce, U.; Cereatti, A. Analysis of the Accuracy of Ten Algorithms for Orientation Estimation Using Inertial and Magnetic Sensing under Optimal Conditions: One Size Does Not Fit All. Sensors 2021, 21, 2543. https://doi.org/10.3390/s21072543
Caruso M, Sabatini AM, Laidig D, Seel T, Knaflitz M, Della Croce U, Cereatti A. Analysis of the Accuracy of Ten Algorithms for Orientation Estimation Using Inertial and Magnetic Sensing under Optimal Conditions: One Size Does Not Fit All. Sensors. 2021; 21(7):2543. https://doi.org/10.3390/s21072543
Chicago/Turabian StyleCaruso, Marco, Angelo Maria Sabatini, Daniel Laidig, Thomas Seel, Marco Knaflitz, Ugo Della Croce, and Andrea Cereatti. 2021. "Analysis of the Accuracy of Ten Algorithms for Orientation Estimation Using Inertial and Magnetic Sensing under Optimal Conditions: One Size Does Not Fit All" Sensors 21, no. 7: 2543. https://doi.org/10.3390/s21072543
APA StyleCaruso, M., Sabatini, A. M., Laidig, D., Seel, T., Knaflitz, M., Della Croce, U., & Cereatti, A. (2021). Analysis of the Accuracy of Ten Algorithms for Orientation Estimation Using Inertial and Magnetic Sensing under Optimal Conditions: One Size Does Not Fit All. Sensors, 21(7), 2543. https://doi.org/10.3390/s21072543









