On Systematic Design of Fractional-Order Element Series
Abstract
1. Introduction
2. Theory on Fractional-Order Elements
3. General Immittance Converter in FOEs’ Series Design
3.1. General Immittance Converter Behavior Definition
- Frequency dependent negative resistor - type I (FDNR-I), ,
- Fractional FDNR-I, ,
- Capacitor C, ,
- Capacitive FOE, ,
- Resistor R, ,
- Inductive FOE, ,
- Inductor L,
- Fractional frequency dependent negative resistor-type II (FDNR-II), ,
- FDNR-II, .
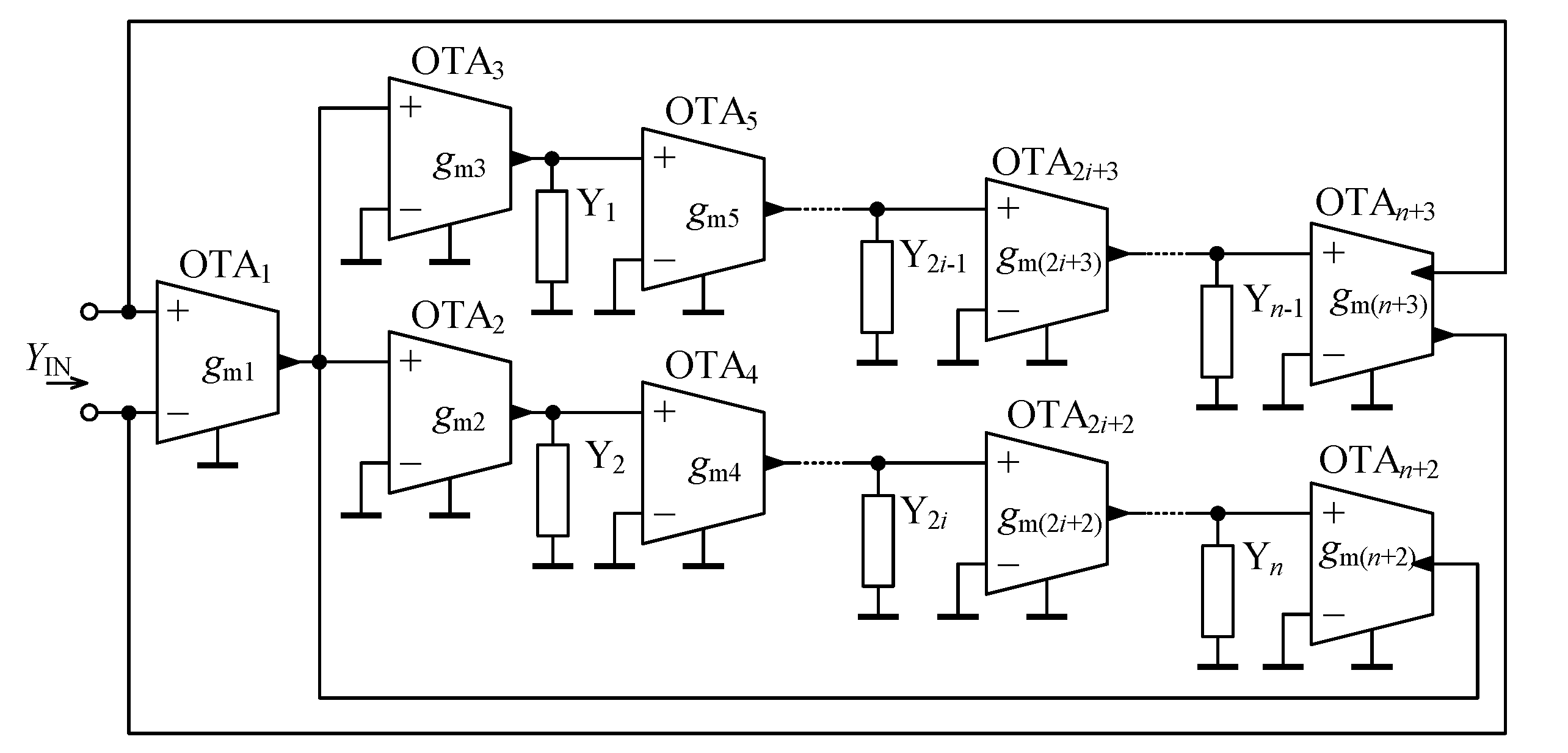
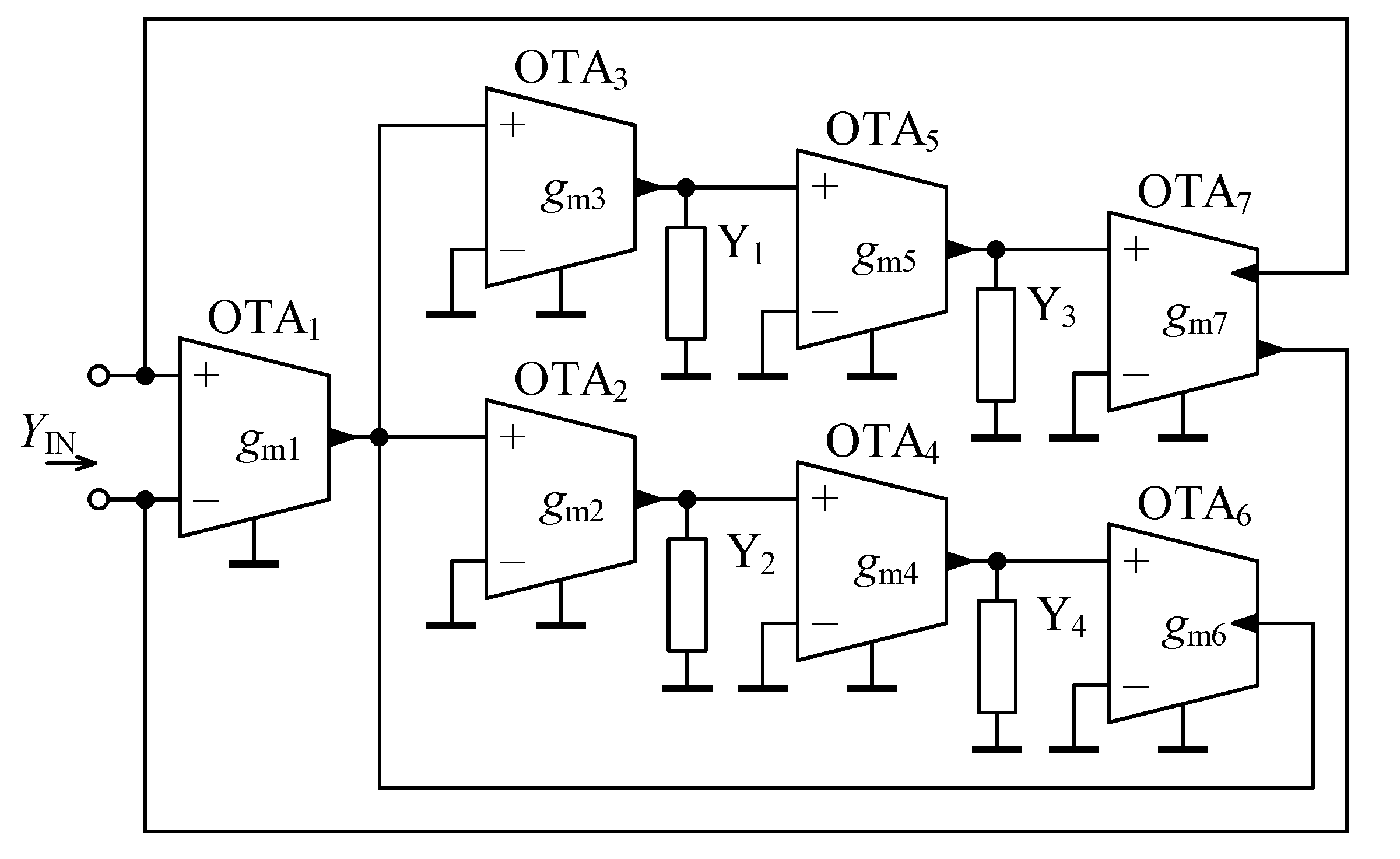
3.2. Proposed Implementation of General Immittance Converter
- Floating fractional-order elements are designed,
- Only grounded external admittances are employed,
- Electronic tunability of is possible by proper adjustment of the transcondutances of the active elements,
- There is no restriction concerning matching between passive (external) or active elements.
4. Performance Analysis of the Proposed Immittance Converter
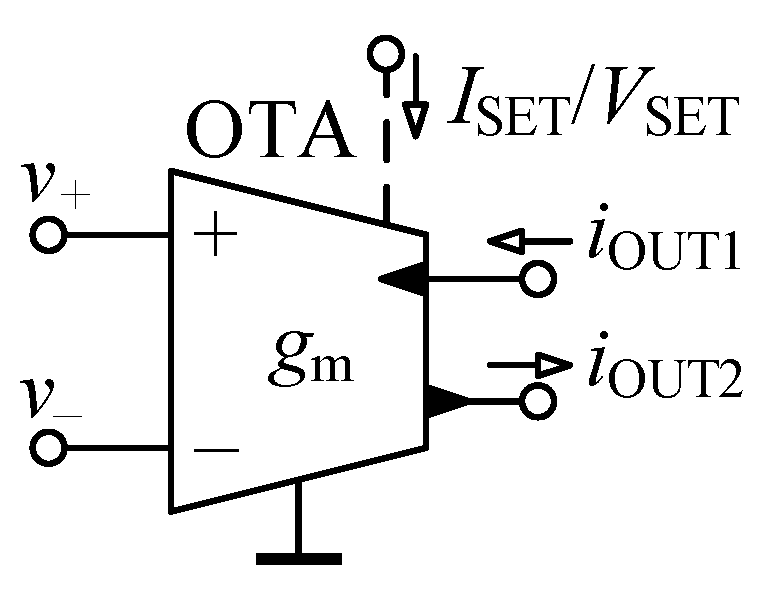
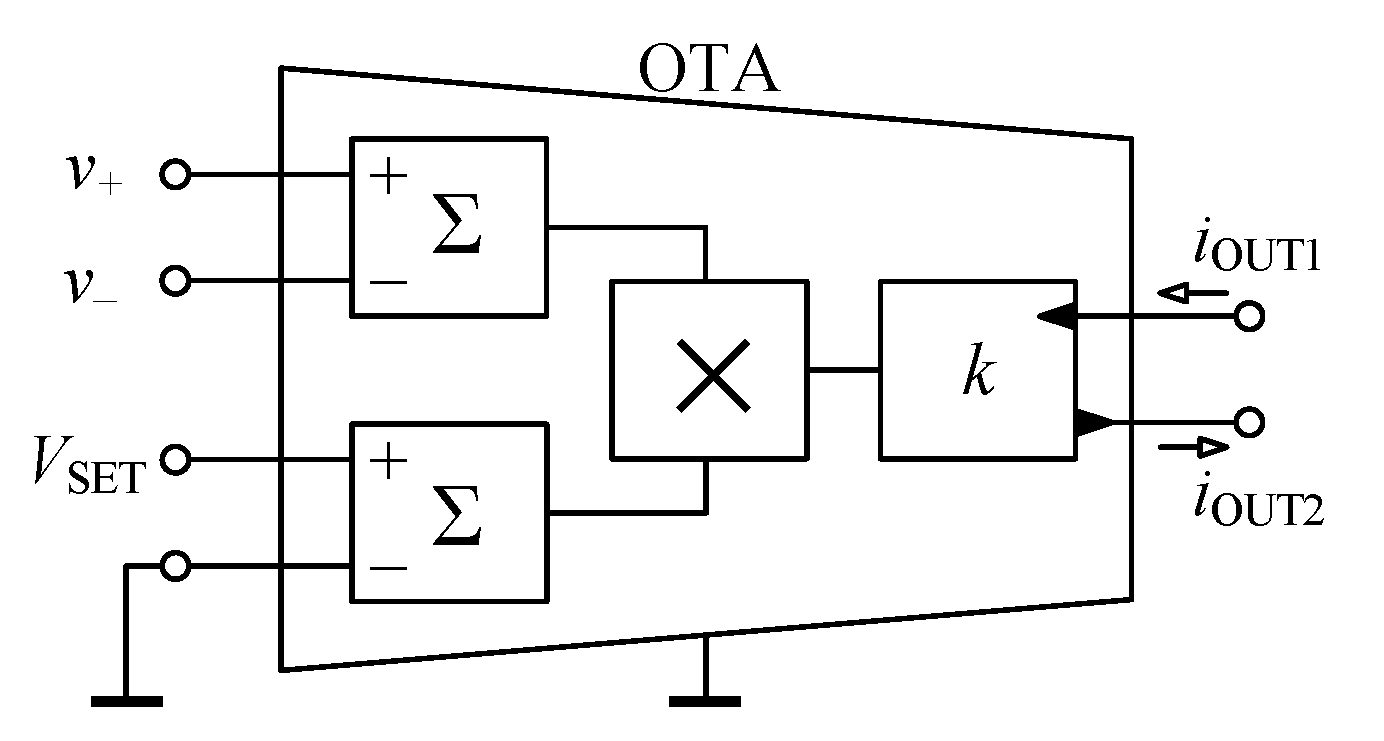
4.1. Properties of Used OTA
4.2. Influence of OTA Parasitics and Optimization of GIC Performance
4.2.1. Nodes A, B, C, D
4.2.2. Node E
4.2.3. Port F
4.3. OTA-Based Circuit with Negative Conductance
5. Simulation Results
5.1. Design of “Seed” FOEs
5.2. Simulation of the GIC
5.3. Optimization of GIC Performance
5.3.1. Optimization Example for
5.3.2. Optimization Example for
5.4. Fractional Band-Pass Filter Design
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CMOS | Complementary metal-oxide semiconductor |
| CPE | Constant-phase element |
| EFI | Elements with fractional impedance |
| FDNR | Frequency dependent negative resistor |
| FOE | Fractional-order element |
| FOFDNR | Fractional order frequency dependent negative resistor |
| GIC | General immittance converter |
| OTA | Operational transconductance amplifier |
| RC | resistor-capacitor |
| TSMC | Taiwan semiconductor manufacturing company |
Appendix A. Variant Combinations of Admittances Y and Their () vs. Final Fractional Order of Z
| 0 | 1 | 0 | 1 | 2.0 |
| 0.2 | 1 | 0 | 1 | 1.8 |
| 0.2 | 1 | 0.2 | 1 | 1.6 |
| 0 | 1 | 0 | 0.2 | 1.2 |
| 0 | 1 | 0 | 0 | 1.0 |
| 0.2 | 1 | 0 | 0 | 0.8 |
| 0.2 | 1 | 0.2 | 0 | 0.6 |
| 0 | 0.2 | 0 | 0.2 | 0.4 |
| 0 | 0.2 | 0 | 0 | 0.2 |
| 0 | 0 | 0 | 0 | 0.0 |
| 0.2 | 0 | 0 | 0 | |
| 0.2 | 0 | 0.2 | 0 | |
| 1 | 0.2 | 0 | 0.2 | |
| 1 | 0.2 | 0 | 0 | |
| 1 | 0 | 0 | 0 | |
| 1 | 0 | 0.2 | 0 | |
| 1 | 0.2 | 1 | 0.2 | |
| 1 | 0.2 | 1 | 0 | |
| 1 | 0 | 1 | 0 |
| 0 | 1 | 0 | 1 | 2.00 | 0.0625 | 0 | 0 | 0 | |
| 0 | 1 | 0.0625 | 1 | 1.9375 | 0.0625 | 0 | 0.0625 | 0 | |
| 0.0625 | 1 | 0.0625 | 1 | 1.875 | 0.25 | 0 | 0 | 0.0625 | |
| 0 | 1 | 0.25 | 1 | 1.75 | 0.25 | 0 | 0 | 0 | |
| 0.0625 | 1 | 0.25 | 1 | 1.6875 | 0.25 | 0 | 0.0625 | 0 | |
| 0.25 | 1 | 0.25 | 1 | 1.50 | 0.25 | 0.0625 | 0.25 | 0.0625 | |
| 0 | 1 | 0 | 0.25 | 1.25 | 0.25 | 0 | 0.25 | 0.0625 | |
| 0 | 1 | 0.0625 | 0.25 | 1.1875 | 0.25 | 0 | 0.25 | 0 | |
| 0.0625 | 1 | 0.0625 | 0.25 | 1.125 | 1 | 0.25 | 0.0625 | 0.25 | |
| 0 | 1 | 0 | 0.0625 | 1.0625 | 1 | 0.0625 | 0 | 0.25 | |
| 0 | 1 | 0 | 0 | 1.00 | 1 | 0 | 0 | 0.25 | |
| 0 | 1 | 0.0625 | 0 | 0.9375 | 1 | 0 | 0.0625 | 0.25 | |
| 0.0625 | 1 | 0.0625 | 0 | 0.875 | 1 | 0.0625 | 0 | 0.0625 | |
| 0 | 1 | 0.25 | 0.0625 | 0.8125 | 1 | 0 | 0 | 0.0625 | |
| 0 | 1 | 0.25 | 0 | 0.75 | 1 | 0 | 0 | 0 | |
| 0.0625 | 1 | 0.25 | 0 | 0.6875 | 1 | 0 | 0.0625 | 0 | |
| 0.25 | 1 | 0.25 | 0.0625 | 0.5625 | 1 | 0.0625 | 0.25 | 0.0625 | |
| 0 | 0.25 | 0 | 0.25 | 0.50 | 1 | 0 | 0.25 | 0.0625 | |
| 0 | 0.25 | 0.0625 | 0.25 | 0.4375 | 1 | 0 | 0.25 | 0 | |
| 0.0625 | 0.25 | 0.0625 | 0.25 | 0.375 | 1 | 0.25 | 1 | 0.25 | |
| 0 | 0.25 | 0 | 0.0625 | 0.3125 | 1 | 0.0625 | 1 | 0.25 | |
| 0 | 0.25 | 0 | 0 | 0.25 | 1 | 0 | 1 | 0.25 | |
| 0 | 0.25 | 0.0625 | 0 | 0.1875 | 1 | 0.0625 | 1 | 0.0625 | |
| 0 | 0.0625 | 0 | 0.0625 | 0.125 | 1 | 0 | 1 | 0.0625 | |
| 0 | 0.0625 | 0 | 0 | 0.0625 | 1 | 0 | 1 | 0 | |
| 0 | 0 | 0 | 0 | 0.00 |
References
- Oldham, K.B.; Spanier, J. The Fractional Calculus: Theory and Applications of Differentiation and Integration to Arbitrary Order; Academic Pr.: Cambridge, MA, USA, 1984. [Google Scholar]
- Podlubny, I. Fractional Differential Equations; Academic Press: San Diego, CA, USA, 1999. [Google Scholar]
- Uchaikin, V.V. Fractional Derivatives for Physicists and Engineers Volume I Background and Theory Volume II Applications; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Povstenko, Y. Linear Fractional Diffusion-Wave Equation for Scientists and Engineers; Springer International Publishing: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- West, B.J. Fractional Calculus View of Complexity: Tomorrows Science; CRC Press/Taylor & Francis Group: Boca Raton, FL, USA, 2016. [Google Scholar]
- Magin, R.L. Fractional Calculus in Bioengineering; Begell House Publishers: Danbury, CT, USA, 2006. [Google Scholar]
- Freeborn, T.J. A Survey of Fractional-Order Circuit Models for Biology and Biomedicine. IEEE J. Emerg. Sel. Top. Circuits Syst. 2013, 3, 416–424. [Google Scholar] [CrossRef]
- Lazović, G.; Vosika, Z.; Lazarević, M.; Simic-Krstić, J.; Koruga, D. Modeling of bioimpedance for human skin based on fractional distributed-order modified Cole model. FME Trans. 2014, 42, 74–81. [Google Scholar] [CrossRef]
- Ionescu, C.; Lopes, A.; Copot, D.; Machado, J.A.T.; Bates, J.H.T. The role of fractional calculus in modeling biological phenomena: A review. Commun. Nonlinear Sci. Numer. Simul. 2017, 51, 141–159. [Google Scholar] [CrossRef]
- Xu, Z.; Chen, W. A fractional-order model on new experiments of linear viscoelastic creep of Hami Melon. Comput. Math. Appl. 2013, 66, 677–681. [Google Scholar] [CrossRef]
- Lopes, A.M.; Machado, J.A.T.; Ramalho, E. On the fractional-order modeling of wine. Eur. Food Res. Technol. 2017, 243, 921–929. [Google Scholar] [CrossRef]
- Machado, J.A.T.; Lopes, A.M. On Fractional-Order Characteristics of Vegetable Tissues and Edible Drinks. In Springer Proceedings in Mathematics & Statistics Fractional Calculus; Springer: Singapore, 2019; pp. 19–35. [Google Scholar] [CrossRef]
- Zhao, J.; Wang, S.; Chang, Y.; Li, X. A novel image encryption scheme based on an improper fractional-order chaotic system. Nonlinear Dyn. 2015, 80, 1721–1729. [Google Scholar] [CrossRef]
- Li, T.; Yang, M.; Wu, J.; Jing, X. A Novel Image Encryption Algorithm Based on a Fractional-Order Hyperchaotic System and DNA Computing. Complexity 2017, 2017, 9010251. [Google Scholar] [CrossRef]
- Petráš, I. Fractional Order Nonlinear Systems Modeling, Analysis and Simulation; Higher Education Press: Beijing, China, 2011. [Google Scholar]
- Petráš, I. Tuning and implementation methods for fractional-order controllers. Fract. Calc. Appl. Anal. 2012, 15, 282–303. [Google Scholar] [CrossRef]
- Monje, C.A.; Chen, Y.; Vinagre, B.M.; Xue, D.; Feliu-Batlle, V. Fractional-Order Systems and Controls Fundamentals and Applications; Springer: London, UK, 2010. [Google Scholar]
- Tepljakov, A. Fractional-Order Modeling and Control of Dynamic Systems; Springer: Berlin, Germany, 2017. [Google Scholar] [CrossRef]
- Maxim, A.; Copot, D.; Copot, C.; Ionescu, C.M. The 5W’s for Control as Part of Industry 4.0: Why, What, Where, Who, and When-A PID and MPC Control Perspective. Inventions 2019, 4, 10. [Google Scholar] [CrossRef]
- Petráš, I. (Ed.) Handbook of Fractional Calculus with Applications: Applications in Control; De Gruyter: Berlin, Germany, 2019; Volume 6. [Google Scholar]
- Bingi, K.; Ibrahim, R.; Karsiti, M.N.; Hassan, S.M.; Harindran, V.R. Fractional-Order Systems and PID Controllers: Using Scilab and Curve Fitting Based Approximation Techniques; Springer: Cham, Switzerland, 2020. [Google Scholar]
- Magin, R.; Ortigueira, M.D.; Podlubny, I.; Trujillo, J. On the fractional signals and systems. Signal Process. 2011, 91, 350–371. [Google Scholar] [CrossRef]
- Mucha, J.; Faundez-Zanuy, M.; Mekyska, J.; Zvoncak, V.; Galáž, Z.; Kiska, T.; Smekal, Z.; Brabenec, L.; Rektorova, I.; Lopez-De-Ipiña, K. Analysis of Parkinson’s Disease Dysgraphia Based on Optimized Fractional Order Derivative Features. In Proceedings of the 2019 27th European Signal Processing Conference (EUSIPCO), A Coruna, Spain, 2–6 September 2019. [Google Scholar] [CrossRef]
- Galaz, Z.; Mucha, J.; Zvoncak, V.; Mekyska, J.; Smekal, Z.; Safarova, K.; Ondrackova, A.; Urbanek, T.; Havigerova, J.M.; Bednarova, J.; et al. Advanced Parametrization of Graphomotor Difficulties in School-Aged Children. IEEE Access 2020, 8, 112883–112897. [Google Scholar] [CrossRef]
- Radwan, A.G.; Elwakil, A.S.; Soliman, A.M. Fractional-order sinusoidal oscillators: Design procedure and practical examples. IEEE Trans. Circuits Syst. I Regul. Pap. 2008, 55, 2051–2063. [Google Scholar] [CrossRef]
- Al-Rabtah, A.; Ertürk, V.S.; Momani, S. Solutions of a fractional oscillator by using differential transform method. Comput. Math. Appl. 2010, 59, 1356–1362. [Google Scholar] [CrossRef]
- Tripathy, M.C.; Mondal, D.; Biswas, K.; Sen, S. Design and performance study of phase-locked loop using fractional-order loop filter. Int. J. Circuit Theory Appl. 2015, 43, 776–792. [Google Scholar] [CrossRef]
- Li, M. Three Classes of Fractional Oscillators. Symmetry 2018, 10, 40. [Google Scholar] [CrossRef]
- Adhikary, A.; Sen, S.; Biswas, K. Practical Realization of Tunable Fractional Order Parallel Resonator and Fractional Order Filters. IEEE Trans. Circuits Syst. I Regul. Pap. 2016, 63, 1142–1151. [Google Scholar] [CrossRef]
- Tsirimokou, G.; Psychalinos, C.; Elwakil, A. Design of CMOS Analog Integrated Fractional-Order Circuits Applications in Medicine and Biology; Springer International Publishing: Cham, Switzerland, 2017. [Google Scholar]
- Shah, Z.M.; Kathjoo, M.Y.; Khanday, F.A.; Biswas, K.; Psychalinos, C. A survey of single and multi-component Fractional-Order Elements (FOEs) and their applications. Microelectron. J. 2019, 84, 9–25. [Google Scholar] [CrossRef]
- Kartci, A.; Herencsar, N.; Machado, J.T.; Brancik, L. History and Progress of Fractional-Order Element Passive Emulators: A Review. Radioengineering 2020, 29, 296–304. [Google Scholar] [CrossRef]
- Tsirimokou, G. A systematic procedure for deriving RC networks of fractional-order elements emulators using MATLAB. AEU Int. J. Electron. Commun. 2017, 78, 7–14. [Google Scholar] [CrossRef]
- Kartci, A.; Agambayev, A.; Farhat, M.; Herencsar, N.; Brancik, L.; Bagci, H.; Salama, K.N. Synthesis and Optimization of Fractional-Order Elements Using a Genetic Algorithm. IEEE Access 2019, 7, 80233–80246. [Google Scholar] [CrossRef]
- He, Q.Y.; Pu, Y.F.; Yu, B.; Yuan, X. Arbitrary-order fractance approximation circuits with high order-stability characteristic and wider approximation frequency bandwidth. IEEE/CAA J. Autom. Sin. 2020, 7, 1425–1436. [Google Scholar] [CrossRef]
- Antoniou, A. Bandpass transformation and realization using frequency-dependent negative-resistance elements. IEEE Trans. Circuit Theory 1971, 18, 297–299. [Google Scholar] [CrossRef]
- Abaci, A.; Yuce, E. Modified DVCC based quadrature oscillator and lossless grounded inductor simulator using grounded capacitor(s). AEU Int. J. Electron. Commun. 2017, 76, 86–96. [Google Scholar] [CrossRef]
- Alpaslan, H.; Yuce, E. Inverting CFOA Based Lossless and Lossy Grounded Inductor Simulators. Circuits Syst. Signal Process. 2015, 34, 3081–3100. [Google Scholar] [CrossRef]
- Adhikary, A.; Sen, P.; Sen, S.; Biswas, K. Design and Performance Study of Dynamic Fractors in Any of the Four Quadrants. Circuits Syst. Signal Process. 2015, 35, 1909–1932. [Google Scholar] [CrossRef]
- Adhikary, A.; Choudhary, S.; Sen, S. Optimal Design for Realizing a Grounded Fractional Order Inductor Using GIC. IEEE Trans. Circuits Syst. I Regul. Pap. 2018, 65, 2411–2421. [Google Scholar] [CrossRef]
- Tripathy, M.C.; Mondal, D.; Biswas, K.; Sen, S. Experimental studies on realization of fractional inductors and fractional-order bandpass filters. Int. J. Circuit Theory Appl. 2015, 43, 1183–1196. [Google Scholar] [CrossRef]
- Freeborn, T.J.; Maundy, B.; Elwakil, A. Fractional Resonance-Based RLβCα Filters. Math. Probl. Eng. 2013, 2013, 726721. [Google Scholar] [CrossRef]
- Jakubowska, A.; Walczak, J. Electronic realizations of fractional-order elements: I. Synthesis of the arbitrary order elements. Poznan Univ. Technol. Acad. J. 2016, 85, 137–148. [Google Scholar]
- Koton, J.; Dvorak, J.; Kubanek, D.; Herencsar, N. Design of Fractional Order Elements’ Series. In Proceedings of the 2019 11th International Conference on Electrical and Electronics Engineering (ELECO), Bursa, Turkey, 28–30 November 2019. [Google Scholar] [CrossRef]
- Kakaei, M.N.; Neshati, J.; Rezaierod, A.R. On the Extraction of the Effective Capacitance from Constant Phase Element Parameters. Prot. Met. Phys. Chem. Surf. 2018, 54, 548–556. [Google Scholar] [CrossRef]
- Koton, J.; Kubanek, D.; Ushakov, P.A.; Maksimov, K. Synthesis of fractional-order elements using the RC-EDP approach. In Proceedings of the 2017 European Conference on Circuit Theory and Design (ECCTD), Catania, Italy, 4–6 September 2017. [Google Scholar] [CrossRef]
- Tsirimokou, G.; Kartci, A.; Koton, J.; Herencsar, N.; Psychalinos, C. Comparative Study of Discrete Component Realizations of Fractional-Order Capacitor and Inductor Active Emulators. J. Circuits Syst. Comput. 2018, 27, 1850170. [Google Scholar] [CrossRef]
- Fakhfakh, M.; Tlelo-Cuautle, E.; Castro-López, R. (Eds.) Analog-RF and Mixed-Signal Circuit Systematic Design; Springer: Berlin, Germany, 2013. [Google Scholar]
- Sánchez-Gaspariano, L.A.; Muñiz Montero, C.; Muñoz Pacheco, J.M.; Sánchez-López, C.; Gómez-Pavón, L.D.C.; Luis-Ramos, A.; Bautista-Castillo, A.I. CMOS Analog Filter Design for Very High Frequency Applications. Electronics 2020, 9, 362. [Google Scholar] [CrossRef]
- Geiger, R.L.; Sánchez-Sinencio, E. Active filter design using operational transconductance amplifiers: A tutorial. IEEE Circuits Devices Mag. 1985, 1, 20–32. [Google Scholar] [CrossRef]
- Sotner, R.; Jerabek, J.; Kartci, A.; Domansky, O.; Herencsar, N.; Kledrowetz, V.; Alagoz, B.B.; Yeroglu, C. Electronically reconfigurable two-path fractional-order PI/D controller employing constant phase blocks based on bilinear segments using CMOS modified current differencing unit. Microelectron. J. 2019, 86, 114–129. [Google Scholar] [CrossRef]
- Razavi, B. Design of Analog CMOS Integrated Circuits; McGraw-Hill: Boston, MA, USA, 2000. [Google Scholar]
- Maloberti, F. Analog Design for CMOS VLSI Systems; Springer: New York, NY, USA, 2001. [Google Scholar]
- Baker, R.J. CMOS Circuit Design, Layout, and Simulation; Wiley-IEEE Press: Hoboken, NJ, USA, 2019. [Google Scholar]
- Kubanek, D.; Freeborn, T.J.; Koton, J.; Dvorak, J. Transfer Functions of Fractional-Order Band-Pass Filter with Arbitrary Magnitude Slope in Stopband. In Proceedings of the 2019 42nd International Conference on Telecommunications and Signal Processing (TSP), Budapest, Hungary, 1–3 July 2019. [Google Scholar] [CrossRef]


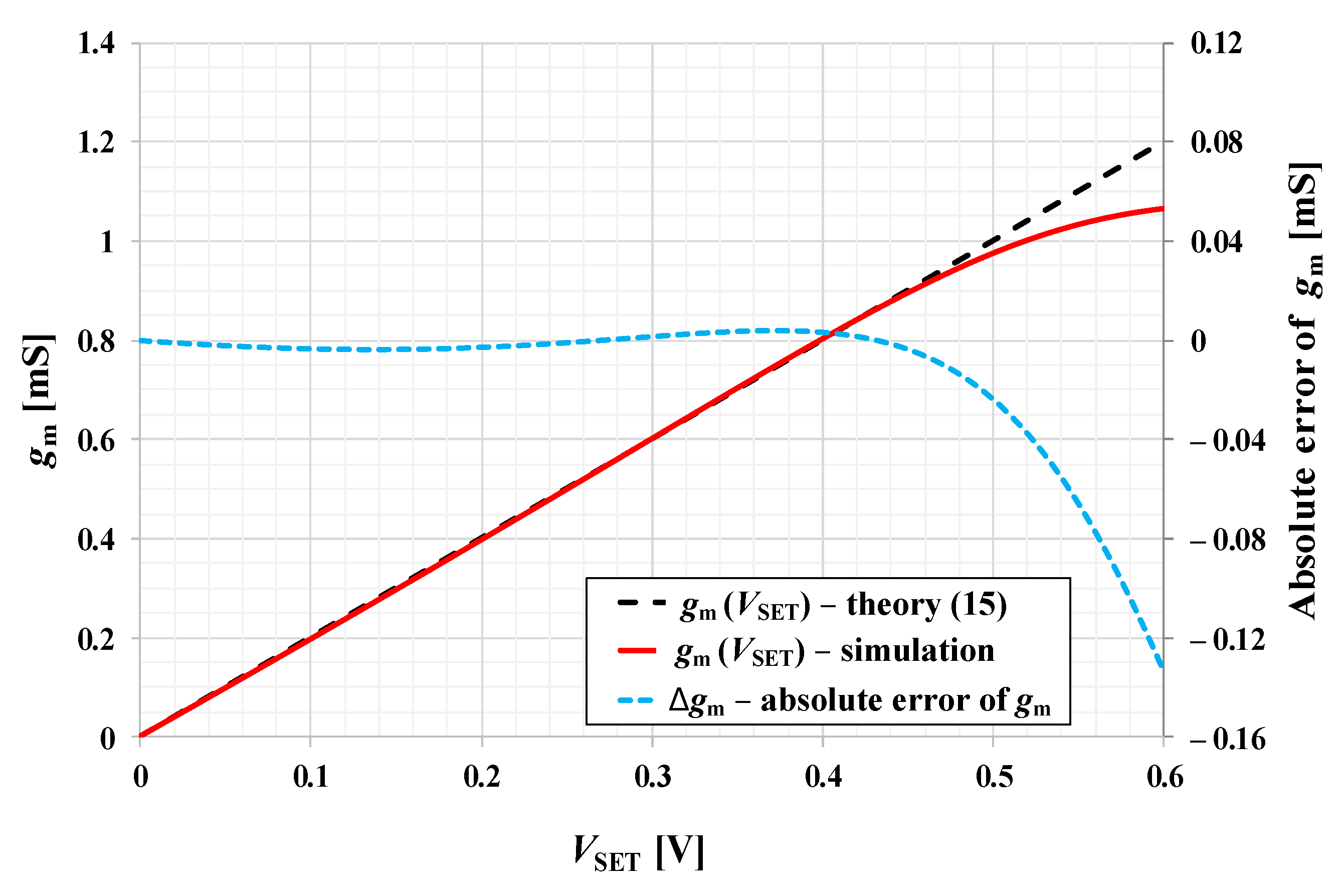

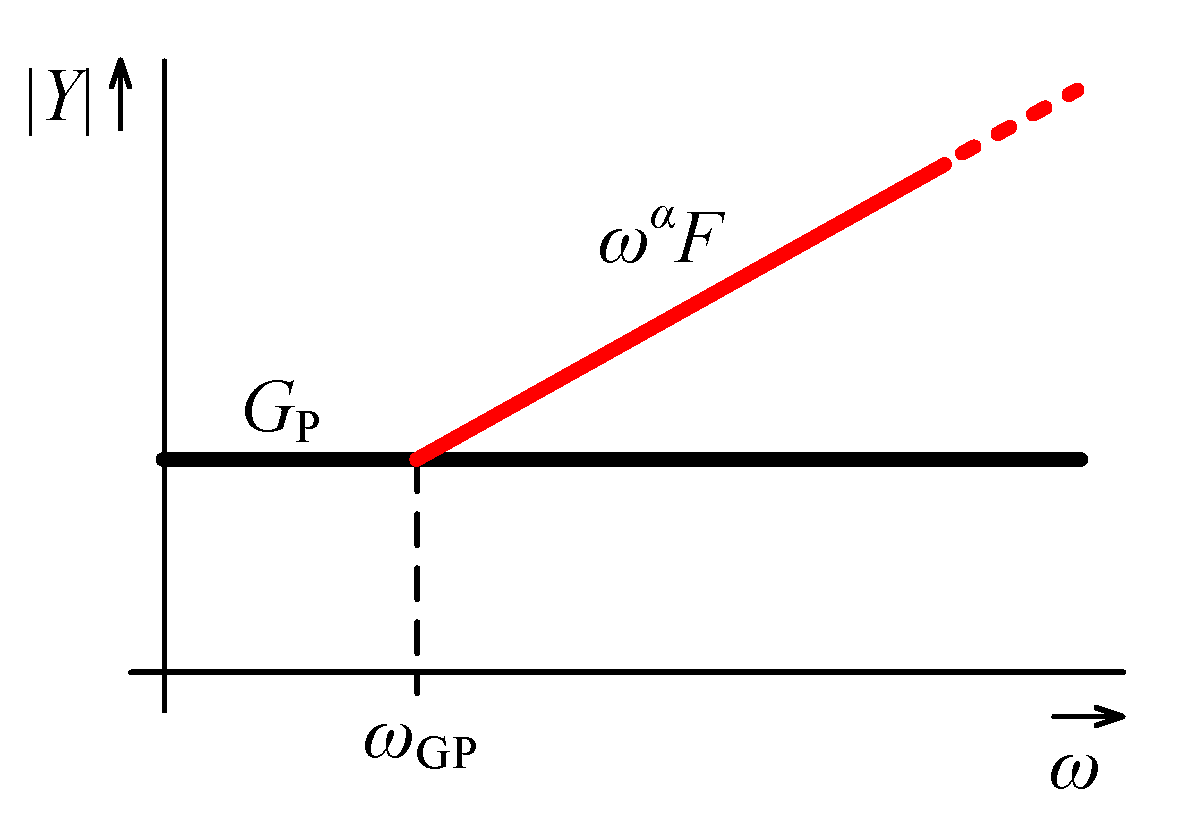



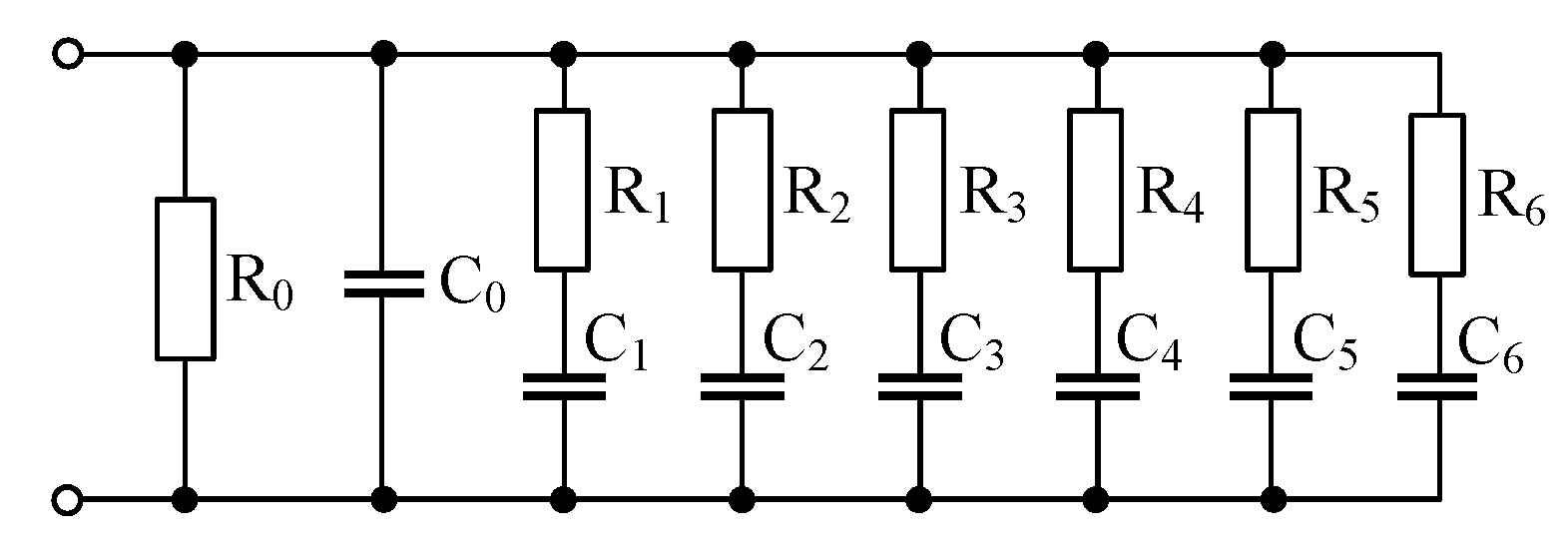
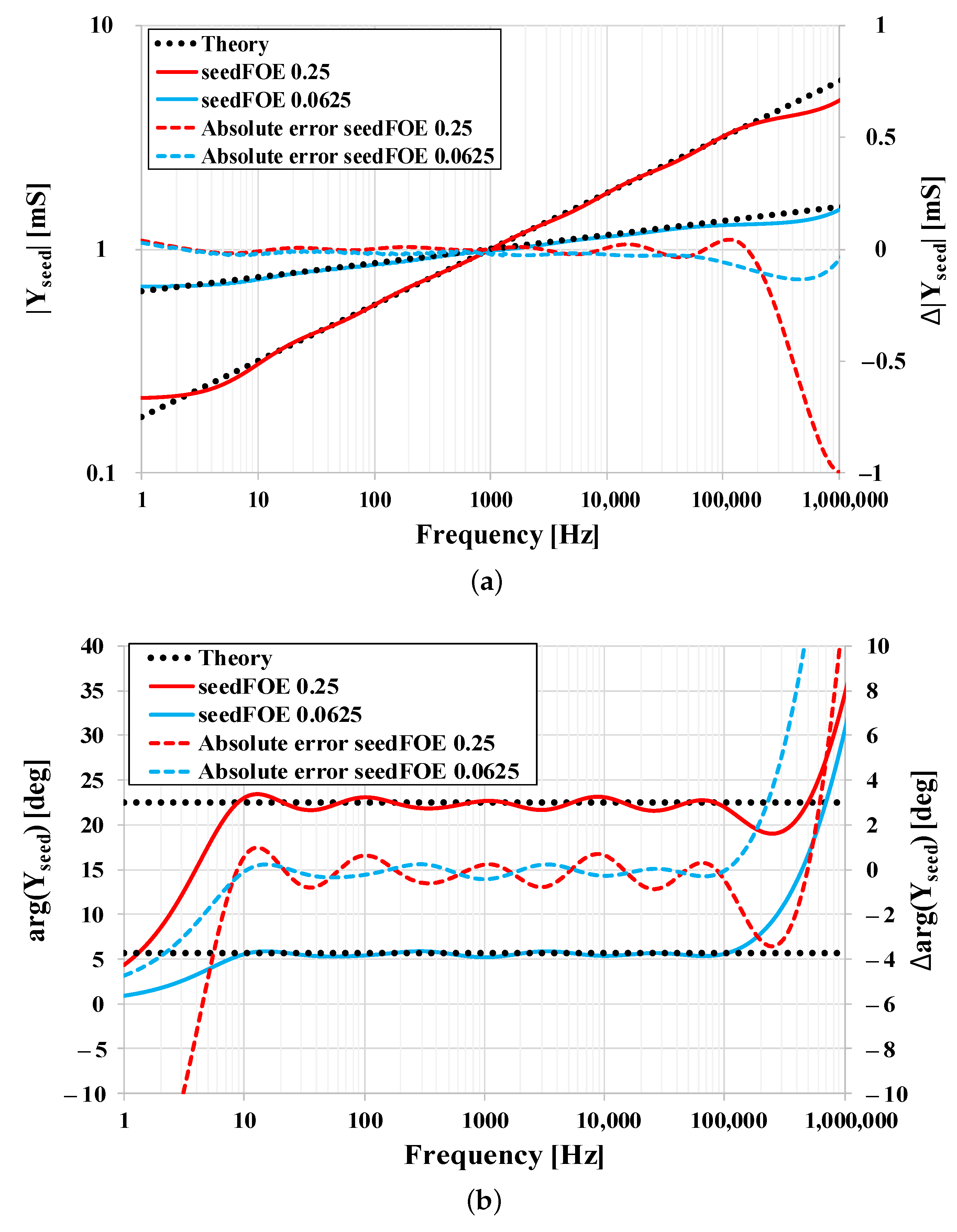


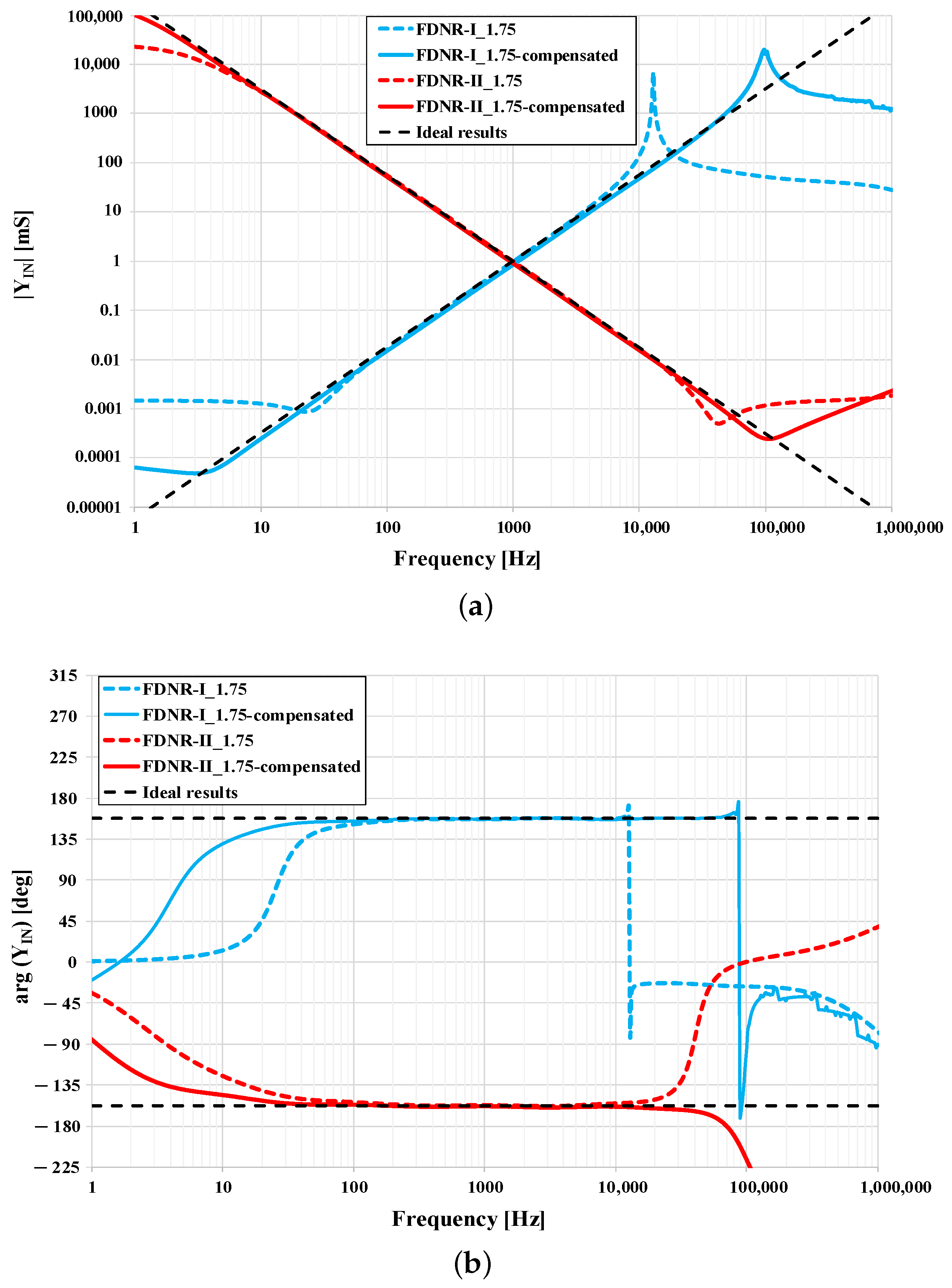
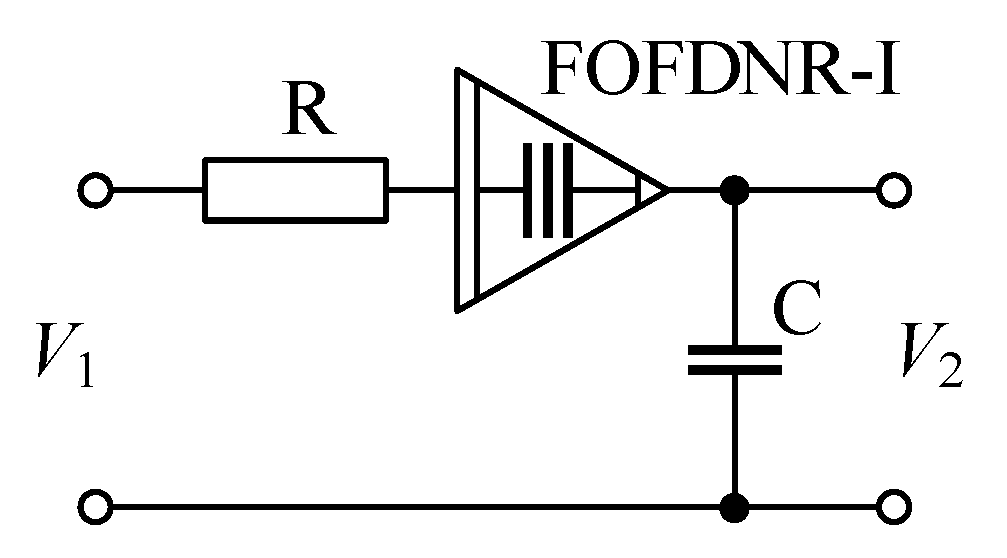

| (k) | 4.64 | 1.47 |
| (k) | 5.11 | 17.8 |
| (k) | 4.02 | 13.3 |
| (k) | 6.81 | 12.0 |
| (k) | 1.15 | 8.20 |
| (k) | 2.20 | 8.20 |
| (k) | 0.59 | 6.81 |
| (nF) | 0.39 | 0.12 |
| (nF) | 2200 | 120 |
| (nF) | 330 | 0.47 |
| (nF) | 56 | 0.39 |
| (nF) | 12 | 1500 |
| (nF) | 47 | 56 |
| (nF) | 2.7 | 6.8 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Koton, J.; Kubanek, D.; Dvorak, J.; Herencsar, N. On Systematic Design of Fractional-Order Element Series. Sensors 2021, 21, 1203. https://doi.org/10.3390/s21041203
Koton J, Kubanek D, Dvorak J, Herencsar N. On Systematic Design of Fractional-Order Element Series. Sensors. 2021; 21(4):1203. https://doi.org/10.3390/s21041203
Chicago/Turabian StyleKoton, Jaroslav, David Kubanek, Jan Dvorak, and Norbert Herencsar. 2021. "On Systematic Design of Fractional-Order Element Series" Sensors 21, no. 4: 1203. https://doi.org/10.3390/s21041203
APA StyleKoton, J., Kubanek, D., Dvorak, J., & Herencsar, N. (2021). On Systematic Design of Fractional-Order Element Series. Sensors, 21(4), 1203. https://doi.org/10.3390/s21041203








