Using Different Combinations of Body-Mounted IMU Sensors to Estimate Speed of Horses—A Machine Learning Approach
Abstract
1. Introduction
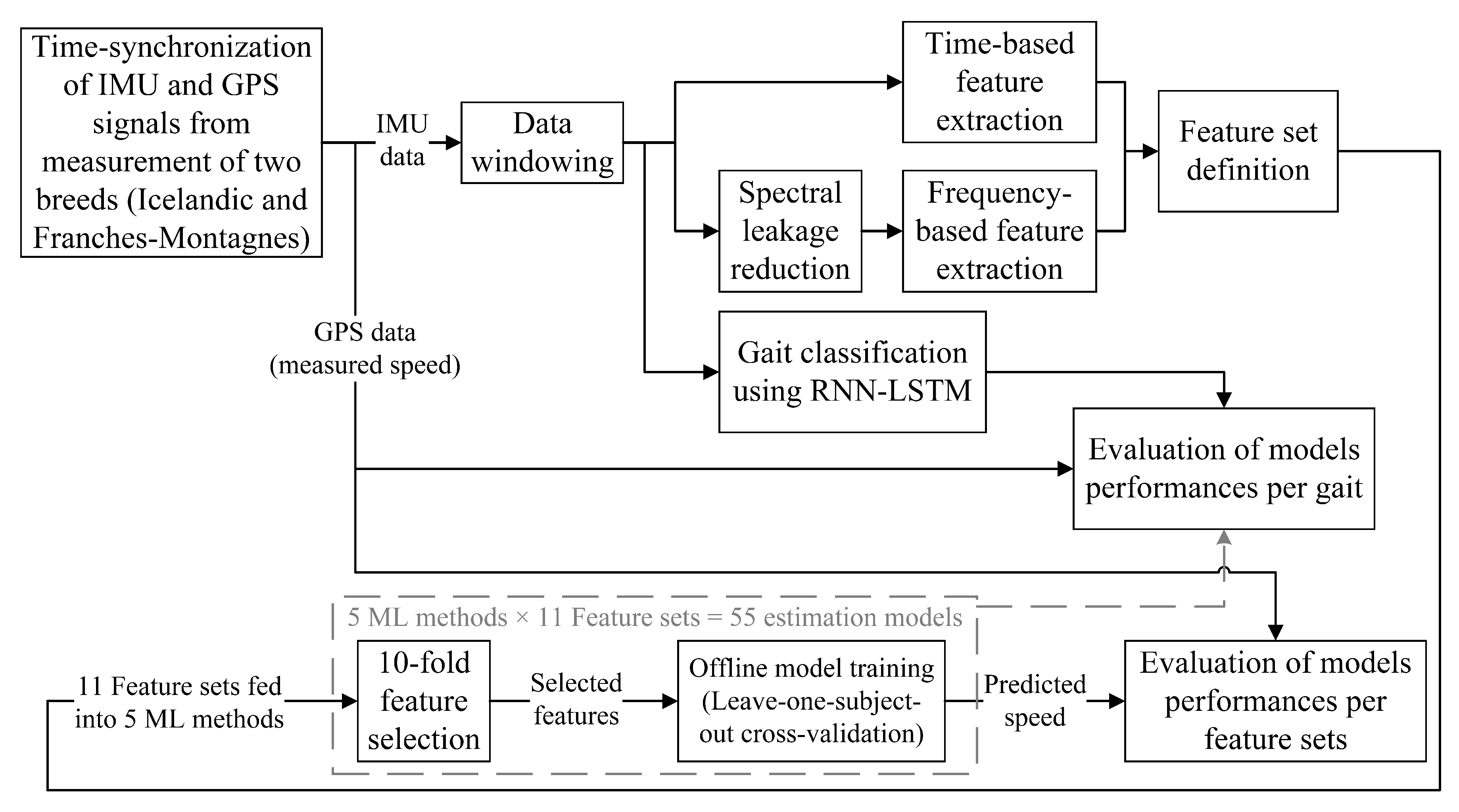
2. Methods
2.1. Data
2.2. Features and Feature Sets
2.3. Feature Selection
2.4. Model Training and Performance Evaluation
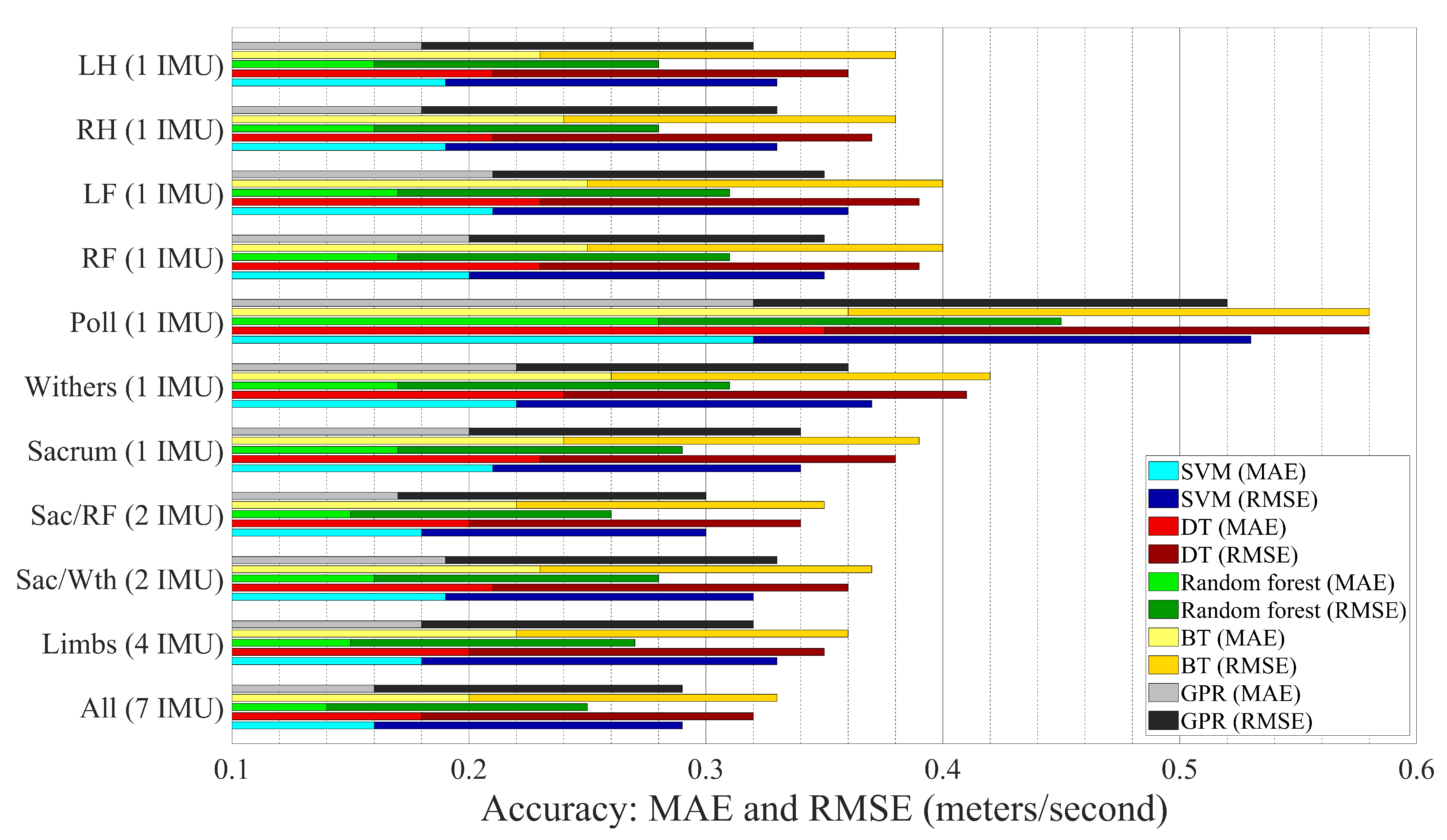
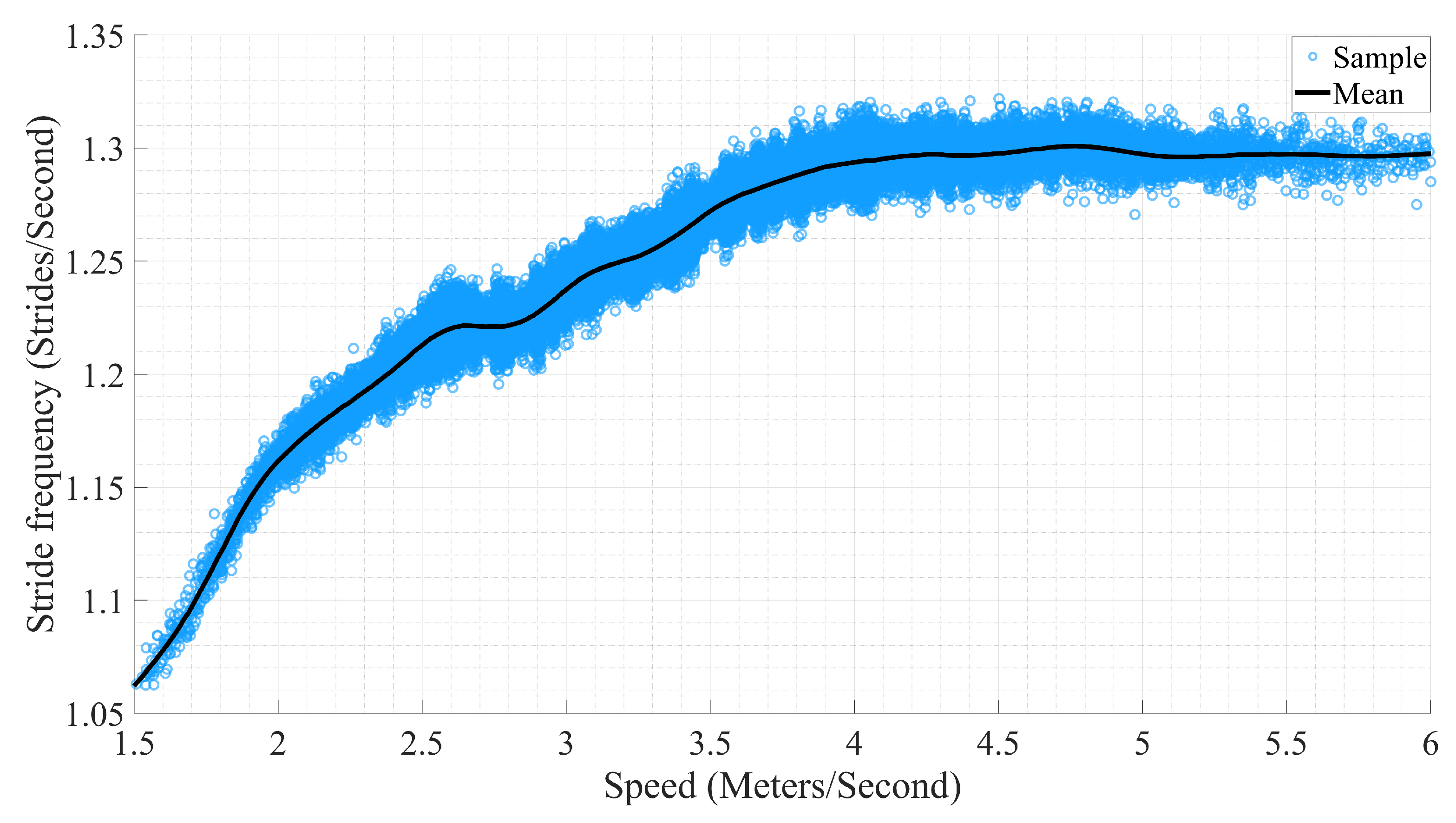
3. Results
3.1. Selected Features
3.2. Feature Set
3.3. Machine Learning Technique
3.4. Gait
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Meira, C.T.; Fortes, M.R.; Farah, M.M.; Porto-Neto, L.R.; Kelly, M.; Moore, S.S.; Pereira, G.L.; Chardulo, L.A.L.; Curi, R.A. Speed Index in the Racing Quarter Horse: A Genome-wide Association Study. J. Equine Vet. Sci. 2014, 34, 1263–1268. [Google Scholar] [CrossRef]
- Witte, T.; Wilson, A. Accuracy of non-differential GPS for the determination of speed over ground. J. Biomech. 2004, 37, 1891–1898. [Google Scholar] [CrossRef] [PubMed]
- Robert, C.; Valette, J.P.; Pourcelot, P.; Audigie, F.; Denoix, J.M. Effects of trotting speed on muscle activity and kinematics in saddlehorses. Equine Vet. J. 2002, 34, 295–301. [Google Scholar] [CrossRef] [PubMed]
- Weishaupt, M.A.; Hogg, H.P.; Auer, J.A.; Wiestner, T. Velocity-dependent changes of time, force and spatial parameters in Warmblood horses walking and trotting on a treadmill. Equine Vet. J. 2010, 42, 530–537. [Google Scholar] [CrossRef] [PubMed]
- Allen, K.J.; Young, L.E.; Franklin, S.H. Evaluation of heart rate and rhythm during exercise. Equine Vet. Educ. 2015, 28, 99–112. [Google Scholar] [CrossRef]
- Williams, J.; Kenworth, K.; Jones, T. The role of heart rate monitoring to assess workload during maintenance interval training in national hunt racehorses. J. Vet. Behav. 2019, 29, 150. [Google Scholar] [CrossRef]
- Moorman, V.J.; Frisbie, D.D.; Kawcak, C.E.; McIlwraith, C.W. The Effect of Horse Velocity on the Output of an Inertial Sensor System. J. Equine Vet. Sci. 2017, 58, 34–39. [Google Scholar] [CrossRef]
- Yigit, T.; Han, F.; Rankins, E.; Yi, J.; McKeever, K.; Malinowski, K. Wearable IMU-based Early Limb Lameness Detection for Horses using Multi-Layer Classifiers. In Proceedings of the 2020 IEEE 16th International Conference on Automation Science and Engineering (CASE), Hong Kong, China, 20–21 August 2020; pp. 955–960. [Google Scholar] [CrossRef]
- Witte, T.H.; Hirst, C.V.; Wilson, A.M. Effect of speed on stride parameters in racehorses at gallop in field conditions. J. Exp. Biol. 2006, 209, 4389–4397. [Google Scholar] [CrossRef]
- Munsters, C.C.; van Iwaarden, A.; van Weeren, R.; Sloet van Oldruitenborg-Oosterbaan, M.M. Exercise testing in Warmblood sport horses under field conditions. Vet. J. 2014, 202, 11–19. [Google Scholar] [CrossRef]
- Farries, G.; Gough, K.F.; Parnell, A.C.; McGivney, B.A.; McGivney, C.L.; McGettigan, P.A.; MacHugh, D.E.; Katz, L.M.; Hill, E.W. Analysis of genetic variation contributing to measured speed in Thoroughbreds identifies genomic regions involved in the transcriptional response to exercise. Anim. Genet. 2019, 50, 670–685. [Google Scholar] [CrossRef]
- Enschede, I.B. KWPN Lineair Scoring. Available online: https://www.kwpn.org/events/empty/studbook-inspections/lineair-scoring (accessed on 20 April 2020).
- König von Borstel, U.; Pasing, S.; Gauly, M. Towards a more objective assessment of equine personality using behavioural and physiological observations from performance test training. Appl. Anim. Behav. Sci. 2011, 135, 277–285. [Google Scholar] [CrossRef]
- Starke, S.; Oosterlinck, M. Reliability of equine visual lameness classification as a function of expertise, lameness severity and rater confidence. Vet. Rec. 2018, 184. [Google Scholar] [CrossRef] [PubMed]
- Gmel, A.I.; Gmel, G.; von Niederhäusern, R.; Weishaupt, M.A.; Neuditschko, M. Should We Agree to Disagree? An Evaluation of the Inter-Rater Reliability of Gait Quality Traits in Franches-Montagnes Stallions. J. Equine Vet. Sci. 2020, 88, 102932. [Google Scholar] [CrossRef] [PubMed]
- Fredricson, I.; Drevemo, S.; Dalin, G.; Hjerten, G.; Björne, K. The application of high-speed cinematography for the quantitative analysis of equine locomotion. Equine Vet. J. 1980, 12, 54–59. [Google Scholar] [CrossRef] [PubMed]
- Ratzlaff, M.H.; Shindell, R.M.; White, K.K. The interrelationships of stride lengths and stride times to velocities of galloping horses. J. Equine Vet. Sci. 1985, 5, 279–283. [Google Scholar] [CrossRef]
- Ericson, C.; Stenfeldt, P.; Hardeman, A.; Jacobson, I. The Effect of Kinesiotape on Flexion-Extension of the Thoracolumbar Back in Horses at Trot. Animals 2020, 10, 301. [Google Scholar] [CrossRef]
- Pfau, T. A method for deriving displacement data during cyclical movement using an inertial sensor. J. Exp. Biol. 2005, 208, 2503–2514. [Google Scholar] [CrossRef]
- Nguyen, K.D.; Chen, I.; Luo, Z.; Yeo, S.H.; Duh, H.B. A Wearable Sensing System for Tracking and Monitoring of Functional Arm Movement. IEEE/ASME Trans. Mechatron. 2011, 16, 213–220. [Google Scholar] [CrossRef]
- Fasel, B.; Duc, C.; Dadashi, F.; Bardyn, F.; Savary, M.; Farine, P.A.; Aminian, K. A wrist sensor and algorithm to determine instantaneous walking cadence and speed in daily life walking. Med. Biol. Eng. Comput. 2017, 55, 1773–1785. [Google Scholar] [CrossRef]
- Feigl, T.; Kram, S.; Woller, P.; Siddiqui, R.H.; Philippsen, M.; Mutschler, C. RNN-aided human velocity estimation from a single IMU. Sensors 2020, 20, 3656. [Google Scholar] [CrossRef]
- Brzostowski, K. Novel approach to human walking speed enhancement based on drift estimation. Biomed. Signal Process. Control. 2018, 42, 18–29. [Google Scholar] [CrossRef]
- Díez, L.E.; Bahillo, A.; Otegui, J.; Otim, T. Step Length Estimation Methods Basedon Inertial Sensors: A Review. IEEE Sens. J. 2018, 18, 6908–6926. [Google Scholar] [CrossRef]
- Varley, M.C.; Fairweather, I.H.; Aughey, R.J. Validity and reliability of GPS for measuring instantaneous velocity during acceleration, deceleration, and constant motion. J. Sports Sci. 2012, 30, 121–127. [Google Scholar] [CrossRef] [PubMed]
- Borresen, J.; Ian Lambert, M. The Quantification of Training Load, the Training Response and the Effect on Performance. Sports Med. 2009, 39, 779–795. [Google Scholar] [CrossRef]
- Roe, G.; Darrall-Jones, J.; Black, C.; Shaw, W.; Till, K.; Jones, B. Validity of 10-HZ GPS and Timing Gates for Assessing Maximum Velocity in Professional Rugby Union Players. Int. J. sports Physiol. Perform. 2017, 12, 836–839. [Google Scholar] [CrossRef]
- Beato, M.; Devereux, G.; Stiff, A. Validity and Reliability of Global Positioning System Units (STATSports Viper) for Measuring Distance and Peak Speed in Sports. J. Strength Cond. Res. 2018, 32, 2831–2837. [Google Scholar] [CrossRef]
- Scott, M.T.; Scott, T.J.; Kelly, V.G. The Validity and Reliability of Global Positioning Systems in Team Sport. J. Strength Cond. Res. 2016, 30, 1470–1490. [Google Scholar] [CrossRef]
- Kingston, J.K.; Soppet, G.M.; Rogers, C.W.; firth, E.C. Use of a global positioning and heart rate monitoring system to assess training load in a group of Thoroughbred racehorses. Equine Vet. J. 2006, 38, 106–109. [Google Scholar] [CrossRef]
- Bazzano, M.; Giudice, E.; Rizzo, M.; Congiu, F.; Zumbo, A.; Arfuso, F.; Di Pietro, S.; Bruschetta, D.; Piccione, G. Application of a combined global positioning and heart rate monitoring system in jumper horses during an official competition—A preliminary study. Acta Vet. Hung. 2016, 64, 189–200. [Google Scholar] [CrossRef]
- Fonseca, R.G.; Kenny, D.A.; Hill, E.W.; Katz, L.M. The association of various speed indices to training responses in Thoroughbred flat racehorses measured with a global positioning and heart rate monitoring system. Equine Vet. J. 2010, 42, 51–57. [Google Scholar] [CrossRef]
- Parkes, R.S.V.; Weller, R.; Pfau, T.; Witte, T.H. The Effect of Training on Stride Duration in a Cohort of Two-Year-Old and Three-Year-Old Thoroughbred Racehorses. Animals 2019, 9, 466. [Google Scholar] [CrossRef] [PubMed]
- Vermeulen, A.D.; Evans, D.L. Measurements of fitness in Thoroughbred racehorses using field studies of heart rate and velocity with a global positioning system. Equine Vet. J. 2006, 38, 113–117. [Google Scholar] [CrossRef] [PubMed]
- Han, H.; McGivney, B.A.; Farries, G.; Katz, L.M.; MacHugh, D.E.; Randhawa, I.A.S.; Hill, E.W. Selection in Australian Thoroughbred horses acts on a locus associated with early two-year old speed. PLoS ONE 2020, 15, e0227212. [Google Scholar] [CrossRef] [PubMed]
- Best, R.; Standing, R. The Spatiotemporal Characteristics of 0–24-Goal Polo. Animals 2019, 9, 446. [Google Scholar] [CrossRef]
- Phinyomark, A.; Petri, G.; Ibáñez-Marcelo, E.; Osis, S.T.; Ferber, R. Analysis of big data in gait biomechanics: Current trends and future directions. J. Med. Biol. Eng. 2018, 38, 244–260. [Google Scholar] [CrossRef]
- Bouwman, A.; Savchuk, A.; Abbaspourghomi, A.; Visser, B. Automated Step Detection in Inertial Measurement Unit Data From Turkeys. Front. Genet. 2020, 11, 207 . [Google Scholar] [CrossRef]
- Zhou, Y.; Romijnders, R.; Hansen, C.; Campen, J.; Maetzler, W.; Hortobágyi, T.; Lamoth, C. The detection of age groups by dynamic gait outcomes using machine learning approaches. Sci. Rep. 2020, 10, 4426. [Google Scholar] [CrossRef]
- Cortes, C.; Vapnik, V. Support-vector networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Rasmussen, C.E.; Williams, C.K.I. Gaussian Processes for Machine Learning; MIT Press: Cambridge, MA, USA, 2008. [Google Scholar]
- Quinlan, J.R. Induction of decision trees. Mach. Learn. 1986, 1, 81–106. [Google Scholar] [CrossRef]
- Friedman, J.H. Stochastic gradient boosting. Comput. Stat. Data Anal. 2002, 38, 367–378. [Google Scholar] [CrossRef]
- Sut, N.; Simsek, O. Comparison of regression tree data mining methods for prediction of mortality in head injury. Expert Syst. Appl. 2011, 38, 15534–15539. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Faber, M.; Johnston, C.; van Weeren, P.R.; Barneveld, A. Repeatability of back kinematics in horses during treadmill locomotion. Equine Vet. J. 2002, 34, 235–241. [Google Scholar] [CrossRef] [PubMed]
- Cano, M.; Vivo, J.; MirÓ, F.; Morales, J.; Galisteo, A. Kinematic characteristics of Andalusian, Arabian and Anglo-Arabian horses: A comparative study. Res. Vet. Sci. 2001, 71, 147–153. [Google Scholar] [CrossRef]
- Robilliard, J.J.; Pfau, T.; Wilson, A.M. Gait characterisation and classification in horses. J. Exp. Biol. 2007, 210, 187–197. [Google Scholar] [CrossRef]
- Gunnarsson, V.; Tijssen, M.; Bjornsdottir, S.; Voskamp, J.; Van Weeren, P.; Back, W.; Rhodin, M.; Persson-Sjodin, E.; Serra Braganca, F. Objective evaluation of stride parameters in the five-gaited Icelandic horse. Comp. Exerc. Physiol. 2018, 14, S52. [Google Scholar] [CrossRef]
- Bosch, S.; Braganca, F.; Marin-Perianu, M.; Marin-Perianu, R.; van der Zwaag, B.J.; Voskamp, J.; Back, W.; van Weeren, P.; Havinga, P. EquiMoves: A Wireless Networked Inertial Measurement System for Objective Examination of Horse Gait. Sensors 2018, 18, 850. [Google Scholar] [CrossRef]
- Glowinski, S.; Łosiński, K.; Kowianski, P.; Waśkow, M.; Bryndal, A.; Grochulska, A. Inertial Sensors as a Tool for Diagnosing Discopathy Lumbosacral Pathologic Gait: A Preliminary Research. Diagnostics 2020, 10, 342. [Google Scholar] [CrossRef]
- OriginGPS-Hornet. Available online: https://origingps.com/product-category/hornet/ (accessed on 25 September 2020).
- Ahmed, N.; Rafiq, J.I.; Islam, M.R. Enhanced Human Activity Recognition Based on Smartphone Sensor Data Using Hybrid Feature Selection Model. Sensors 2020, 20, 317. [Google Scholar] [CrossRef]
- Barwick, J.; Lamb, D.; Dobos, R.; Schneider, D.; Welch, M.; Trotter, M. Predicting Lameness in Sheep Activity Using Tri-Axial Acceleration Signals. Animals 2018, 8, 12. [Google Scholar] [CrossRef]
- Rehman, R.Z.U.; Del Din, S.; Guan, Y.; Yarnall, A.J.; Shi, J.Q.; Rochester, L. Selecting Clinically Relevant Gait Characteristics for Classification of Early Parkinson’s Disease: A Comprehensive Machine Learning Approach. Sci. Rep. 2019, 9, 17269. [Google Scholar] [CrossRef] [PubMed]
- Kamminga, J.W.; Le, D.V.; Meijers, J.P.; Bisby, H.; Meratnia, N.; Havinga, P.J. Robust Sensor-Orientation-Independent Feature Selection for Animal Activity Recognition on Collar Tags. Proc. Acm Interact. Mob. Wearable Ubiquitous Technol. 2018, 2, 1–27. [Google Scholar] [CrossRef]
- Smith, S.W. The Scientist and Engineer’s Guide to Digital Signal Processing; Technical Publishing: San Francisco, CA, USA, 1997. [Google Scholar]
- Peng, J.; Ferguson, S.; Rafferty, K.; Kelly, P. An efficient feature selection method for mobile devices with application to activity recognition. Neurocomputing 2011, 74, 3543–3552. [Google Scholar] [CrossRef]
- Pudil, P.; Novovičová, J.; Kittler, J. Floating search methods in feature selection. Pattern Recognit. Lett. 1994, 15, 1119–1125. [Google Scholar] [CrossRef]
- Mannini, A.; Sabatini, A.M. Walking speed estimation using foot-mounted inertial sensors: Comparing machine learning and strap-down integration methods. Med. Eng. Phys. 2014, 36, 1312–1321. [Google Scholar] [CrossRef]
- Braganca, F.; Broomé, S.; Rhodin, M.; Bjornsdottir, S.; Gunnarsson, V.; Voskamp, J.; Persson-Sjodin, E.; Back, W.; Lindgren, G.; Novoa-Bravo, M.; et al. Improving gait classification in horses by using inertial measurement unit (IMU) generated data and machine learning. Sci. Rep. 2020, 10, 17785. [Google Scholar] [CrossRef]
- Pfau, T.; Boultbee, H.; Davis, H.; Walker, A.; Rhodin, M. Agreement between two inertial sensor gait analysis systems for lameness examinations in horses. Equine Vet. Educ. 2016, 28, 203–208. [Google Scholar] [CrossRef]
- Thompson, R.; Kyriazakis, I.; Holden, A.; Olivier, P.; Ploetz, T. Dancing with Horses: Automated Quality Feedback for Dressage Riders. In Proceedings of the 2015 ACM International Joint Conference on Pervasive and Ubiquitous Computing, Umeda, Osaka, Japan, 9–11 September 2015; pp. 325–336. [Google Scholar] [CrossRef]
- Keegan, K.G.; Kramer, J.; Yonezawa, Y.; Maki, H.; Pai, P.F.; Dent, E.V.; Kellerman, T.E.; Wilson, D.A.; Reed, S.K. Assessment of repeatability of a wireless, inertial sensor-based lameness evaluation system for horses. Am. J. Vet. Res. 2011, 72, 1156–1163. [Google Scholar] [CrossRef]
- Bragança, F.M.; Bosch, S.; Voskamp, J.P.; Marin-Perianu, M.; Van der Zwaag, B.J.; Vernooij, J.C.M.; van Weeren, P.R.; Back, W. Validation of distal limb mounted inertial measurement unit sensors for stride detection in Warmblood horses at walk and trot. Equine Vet. J. 2017, 49, 545–551. [Google Scholar] [CrossRef]
- Clayton, H. Comparison of the stride kinematics of the collected, medium, and extended walks in horses. Am. J. Vet. Res. 1995, 56, 849–852. [Google Scholar]
- Clayton, H.M. Comparison of the stride kinematics of the collected, working, medium and extended trot in horses. Equine Vet. J. 1994, 26, 230–234. [Google Scholar] [CrossRef] [PubMed]
- Schmutz, A.; Chèze, L.; Jacques, J.; Martin, P. A method to estimate horse speed per stride from one IMU with a machine learning method. Sensors 2020, 20, 518. [Google Scholar] [CrossRef] [PubMed]
- Byun, S.; Lee, H.J.; Han, J.W.; Kim, J.S.; Choi, E.; Kim, K.W. Walking-speed estimation using a single inertial measurement unit for the older adults. PLoS ONE 2019, 14, e0227075. [Google Scholar] [CrossRef] [PubMed]
- Zihajehzadeh, S.; Park, E.J. Regression model-based walking speed estimation using wrist-worn inertial sensor. PLoS ONE 2016, 11, e0165211. [Google Scholar] [CrossRef] [PubMed]

| Time-Domain Feature | Equation |
|---|---|
| Maximum | max = Maximum value of the window |
| Minimum | min = Minimum value of the window |
| Mean () | |
| Median | mdn = Median value of the window |
| Standard deviation () | |
| First quartile | p25 = 25th percentile of the window |
| Third quartile | p75 = 75th percentile of the window |
| Kurtosis | |
| Skewness | |
| Frequency-domain Feature | |
| Spectral entropy | |
| Spectral energy | |
| Magnitude of Fourier transform 1st six coefficients | |
| Phase angle of Fourier transform 1st six coefficients |
| Feature Set | IMU Positions | ||||||
|---|---|---|---|---|---|---|---|
| Sacrum | Withers | Poll | RF | LF | RH | LH | |
| All | × | × | × | × | × | × | × |
| Limbs | × | × | × | × | |||
| Sac/Wth | × | × | |||||
| Sac/RF | × | × | |||||
| Sacrum | × | ||||||
| Withers | × | ||||||
| Poll | × | ||||||
| RF | × | ||||||
| LF | × | ||||||
| RH | × | ||||||
| LH | × | ||||||
| Feature Set | SVM | DT | Random Forest | BT | GPR | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| MAE | RMSE | MAE | RMSE | MAE | RMSE | MAE | RMSE | MAE | RMSE | |
| All | 0.16 | 0.29 | 0.18 | 0.32 | 0.14 | 0.25 | 0.20 | 0.33 | 0.16 | 0.29 |
| Limbs | 0.18 | 0.33 | 0.20 | 0.35 | 0.15 | 0.27 | 0.22 | 0.36 | 0.18 | 0.32 |
| Sac/Wth | 0.19 | 0.32 | 0.21 | 0.36 | 0.16 | 0.28 | 0.23 | 0.37 | 0.19 | 0.33 |
| Sac/RF | 0.18 | 0.30 | 0.20 | 0.34 | 0.15 | 0.26 | 0.22 | 0.35 | 0.17 | 0.30 |
| Sacrum | 0.21 | 0.34 | 0.23 | 0.38 | 0.17 | 0.29 | 0.24 | 0.39 | 0.20 | 0.34 |
| Withers | 0.22 | 0.37 | 0.24 | 0.41 | 0.17 | 0.31 | 0.26 | 0.42 | 0.22 | 0.36 |
| Poll | 0.32 | 0.53 | 0.35 | 0.58 | 0.28 | 0.45 | 0.36 | 0.58 | 0.32 | 0.52 |
| RF | 0.20 | 0.35 | 0.23 | 0.39 | 0.17 | 0.31 | 0.25 | 0.40 | 0.20 | 0.35 |
| LF | 0.21 | 0.36 | 0.23 | 0.39 | 0.17 | 0.31 | 0.25 | 0.40 | 0.21 | 0.35 |
| RH | 0.19 | 0.33 | 0.21 | 0.37 | 0.16 | 0.28 | 0.24 | 0.38 | 0.18 | 0.33 |
| LH | 0.19 | 0.33 | 0.21 | 0.36 | 0.16 | 0.28 | 0.23 | 0.38 | 0.18 | 0.32 |
| Feature Set | #1 | #2 | #3 | #4 | #5 | #6 |
|---|---|---|---|---|---|---|
| All | max_gyr | sd_acc | mean_gyro | p75_gyr | fft_acc | max_acc |
| (LH) | (sacrum) | (sacrum) | (LF) | (withers) | (sacrum) | |
| Limbs | max_gyr | p75_gyr | p25_gyr | min_gyr | p75_gyr | p25_gyr |
| (LH) | (LF) | (LH) | (RH) | (RH) | (RF) | |
| Sac/Wth | sd_acc | sd_acc | ent_gyr | p75_acc | ent_acc | skw_acc |
| (withers) | (sacrum) | (sacrum) | (withers) | (sacrum) | (sacrum) | |
| Sac/RF | p25_gyr | sd_acc | max_acc | mean_acc | sd_gyr | sd_gyr |
| (RF) | (sacrum) | (RF) | (sacrum) | (sacrum) | (RF) | |
| Sacrum | min_acc | sd_acc | ent_gyr | sd_gyr | sd_gyr | ent_acc |
| Withers | sd_acc | p75_acc | sd_acc | mean_gyr | ent_acc | sd_gyr |
| Poll | fft_acc | sd_acc | sd_gyr | ent_acc | krt_acc | ent_acc |
| RF | p25_gyr | max_acc | sd_gyr | mdn_gyr | sd_gyr | sd_gyr |
| LF | p75_gyr | max_acc | sd_gyr | sd_acc | sd_gyr | mdn_gyr |
| RH | min_gyr | p75_gyr | mdn_acc | min_acc | mean_gyr | p75_acc |
| LH | max_gyr | p25_gyr | p75_acc | mean_gyr | min_acc | p75_acc |
| Gait | Measured- | Predicted Speed Error | |
|---|---|---|---|
| Speed () () | RMSE () | nRMSE | |
| All | 3.25 () | 0.25 | 7.69% |
| Walk | 1.70 () | 0.20 | 11.76% |
| Trot | 3.30 () | 0.31 | 10.03% |
| Tölt | 3.90 () | 0.28 | 7.18% |
| Canter | 4.95 () | 0.34 | 6.87% |
| Pace | 7.52 () | 0.31 | 4.12% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Darbandi, H.; Serra Bragança, F.; van der Zwaag, B.J.; Voskamp, J.; Gmel, A.I.; Haraldsdóttir, E.H.; Havinga, P. Using Different Combinations of Body-Mounted IMU Sensors to Estimate Speed of Horses—A Machine Learning Approach. Sensors 2021, 21, 798. https://doi.org/10.3390/s21030798
Darbandi H, Serra Bragança F, van der Zwaag BJ, Voskamp J, Gmel AI, Haraldsdóttir EH, Havinga P. Using Different Combinations of Body-Mounted IMU Sensors to Estimate Speed of Horses—A Machine Learning Approach. Sensors. 2021; 21(3):798. https://doi.org/10.3390/s21030798
Chicago/Turabian StyleDarbandi, Hamed, Filipe Serra Bragança, Berend Jan van der Zwaag, John Voskamp, Annik Imogen Gmel, Eyrún Halla Haraldsdóttir, and Paul Havinga. 2021. "Using Different Combinations of Body-Mounted IMU Sensors to Estimate Speed of Horses—A Machine Learning Approach" Sensors 21, no. 3: 798. https://doi.org/10.3390/s21030798
APA StyleDarbandi, H., Serra Bragança, F., van der Zwaag, B. J., Voskamp, J., Gmel, A. I., Haraldsdóttir, E. H., & Havinga, P. (2021). Using Different Combinations of Body-Mounted IMU Sensors to Estimate Speed of Horses—A Machine Learning Approach. Sensors, 21(3), 798. https://doi.org/10.3390/s21030798







