Semi-Automatic Spectral Image Stitching for a Compact Hybrid Linescan Hyperspectral Camera towards Near Field Remote Monitoring of Potato Crop Leaves
Abstract
:1. Introduction
1.1. Context
1.2. Related Works
1.3. Our Contribution and Paper Organization
2. Projective Warps
2.1. Inlier Set of Matching Pairs
2.2. Global Homography Warping (GHW)
2.3. Improved Warping Methods
3. Methodology
3.1. Spatio-Spectral Scanning
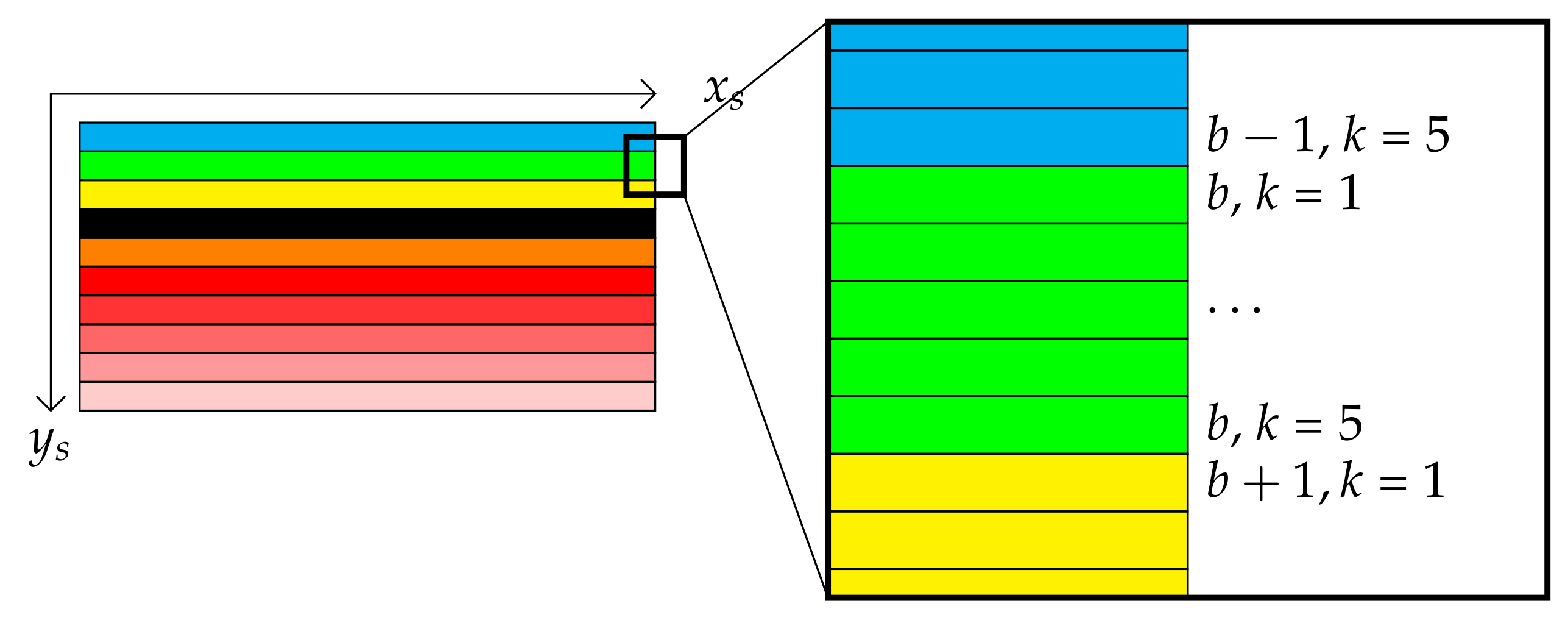
3.2. Sensor Structure
- The 4 first rows are not used.
- 64 spectral stripes (also called bandlets) of 5 by 2048 pixels each enable to inspect the visible wavelength range, represented in the top part of Figure 3.
- A 120 by 2048 pixels rectangle (corresponding to 24 stripes) accounts for a blind area. This area corresponds to a white rectangle in the middle of Figure 3.
- 128 spectral stripes of 5 by 2048 pixels each explore the near infrared domain (NIR).
- The 4 last rows are not used either.
3.3. 3-Axis Representation
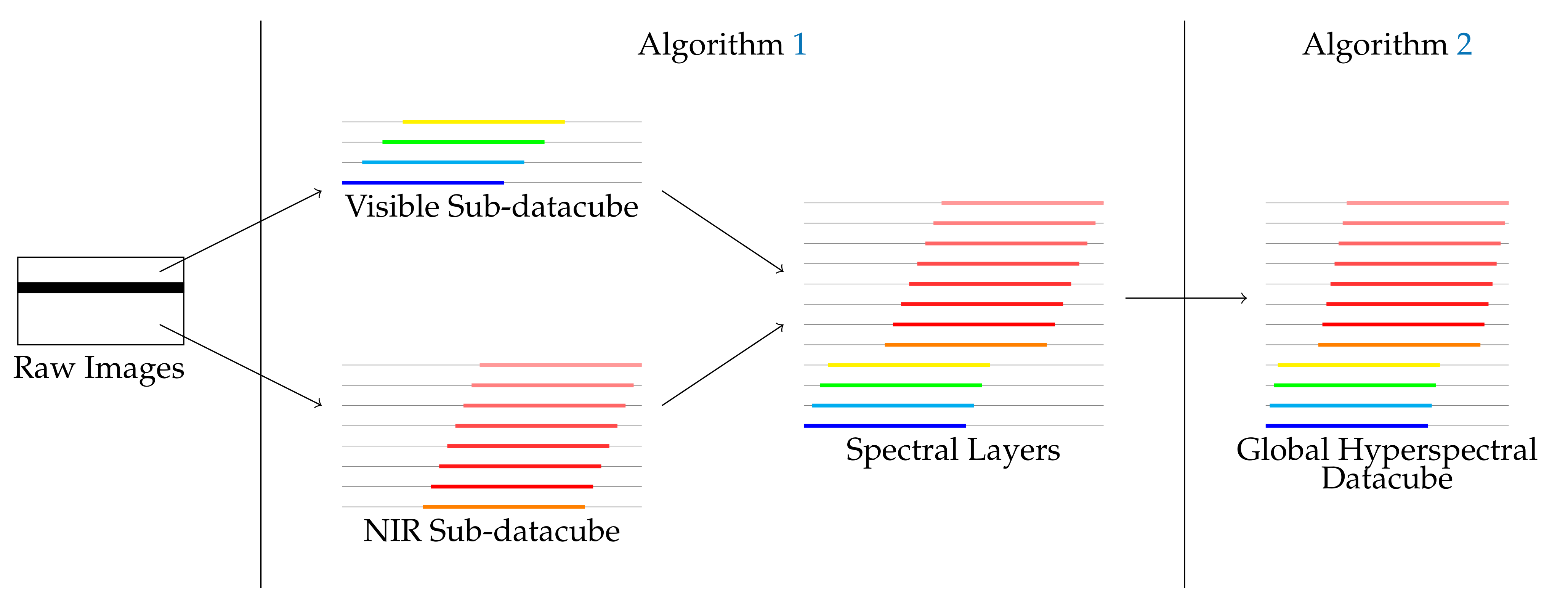
4. Two Proposed Spectral Stitching Methods
4.1. Heuristic Based Spectral Reconstruction (HSR)
- A sub-datacube reconstruction for hyperspectral image reconstruction and extraction of hyperspectral bands;
- A fusion of sub-datacubes based on matching procedures.
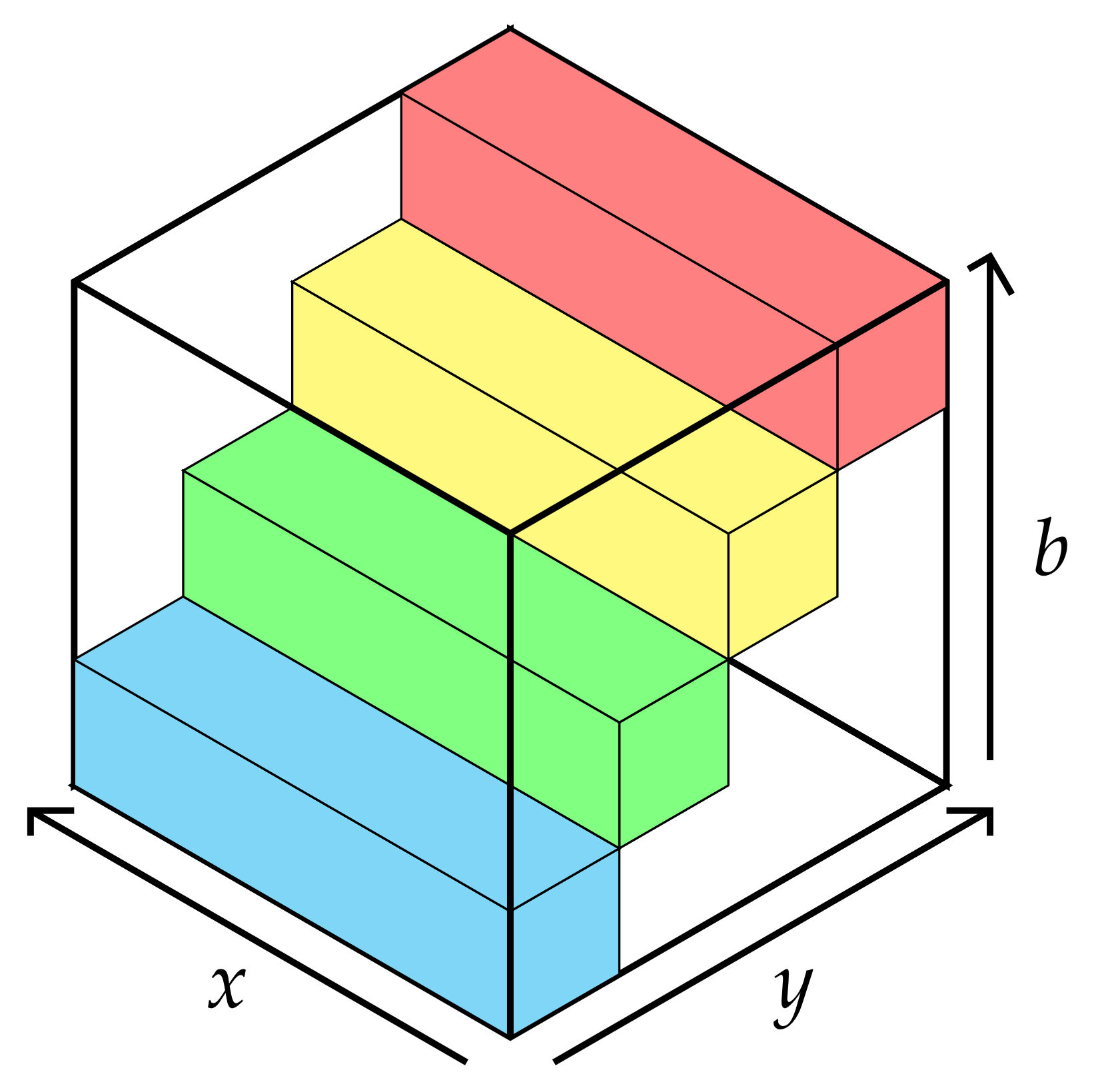
4.1.1. Sub-Datacube Reconstruction
| Algorithm 1 Sub-datacube Reconstruction |
|
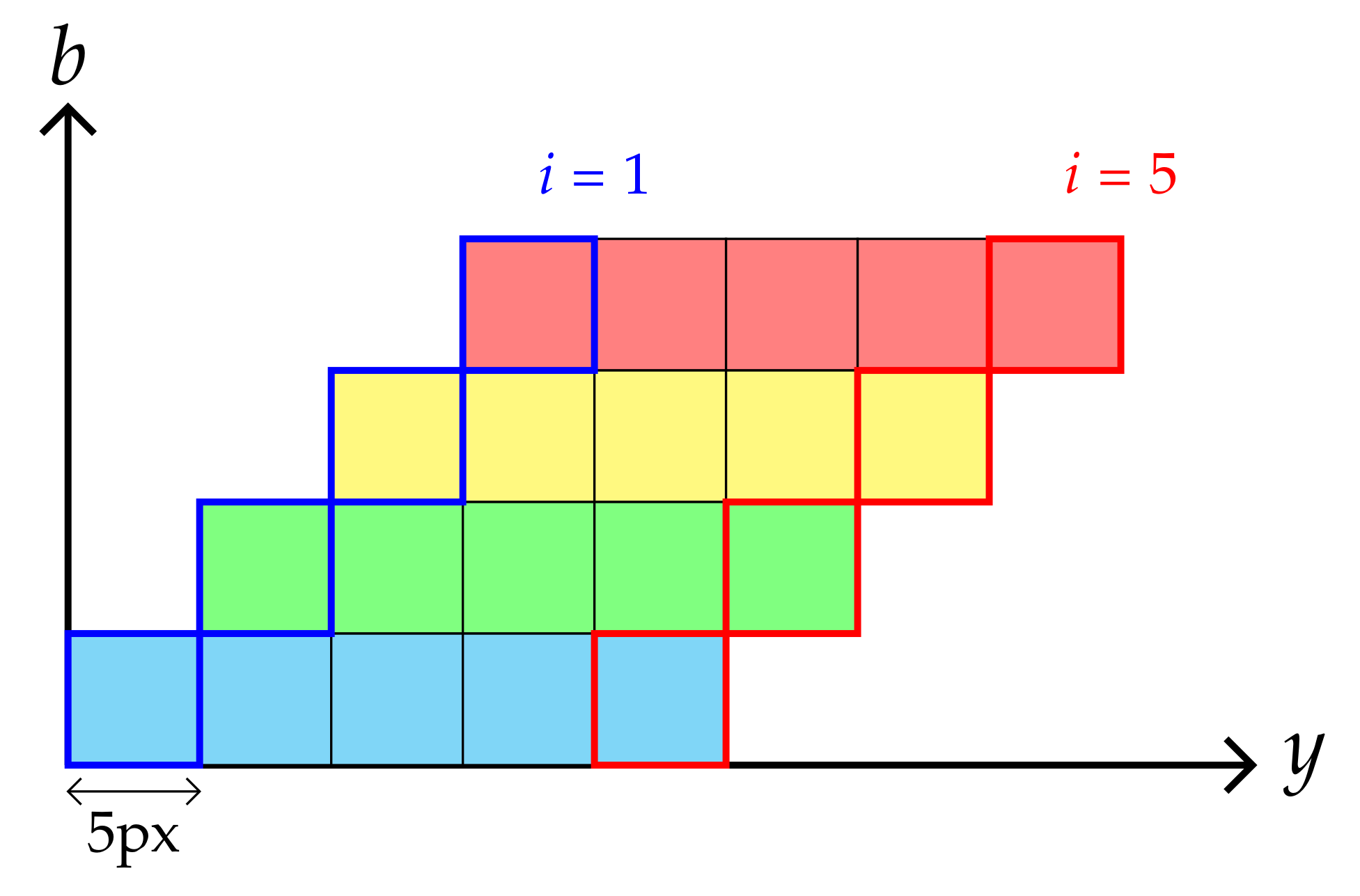
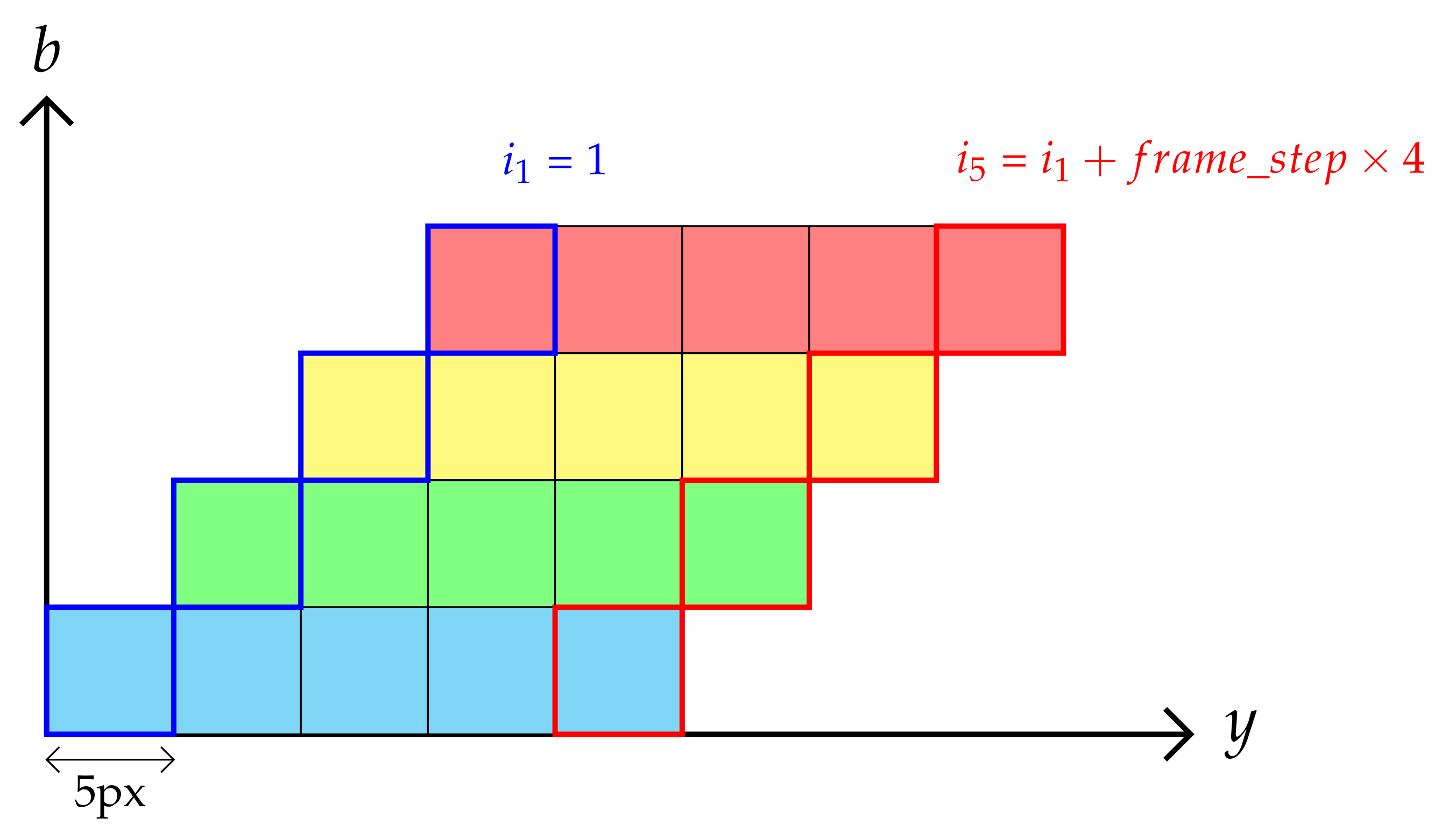
4.1.2. Estimating the Frame Step Parameter
4.1.3. Matching and Fusion of Sub-Datacube
| Algorithm 2 Matching and fusion of sub-datacube. |
|
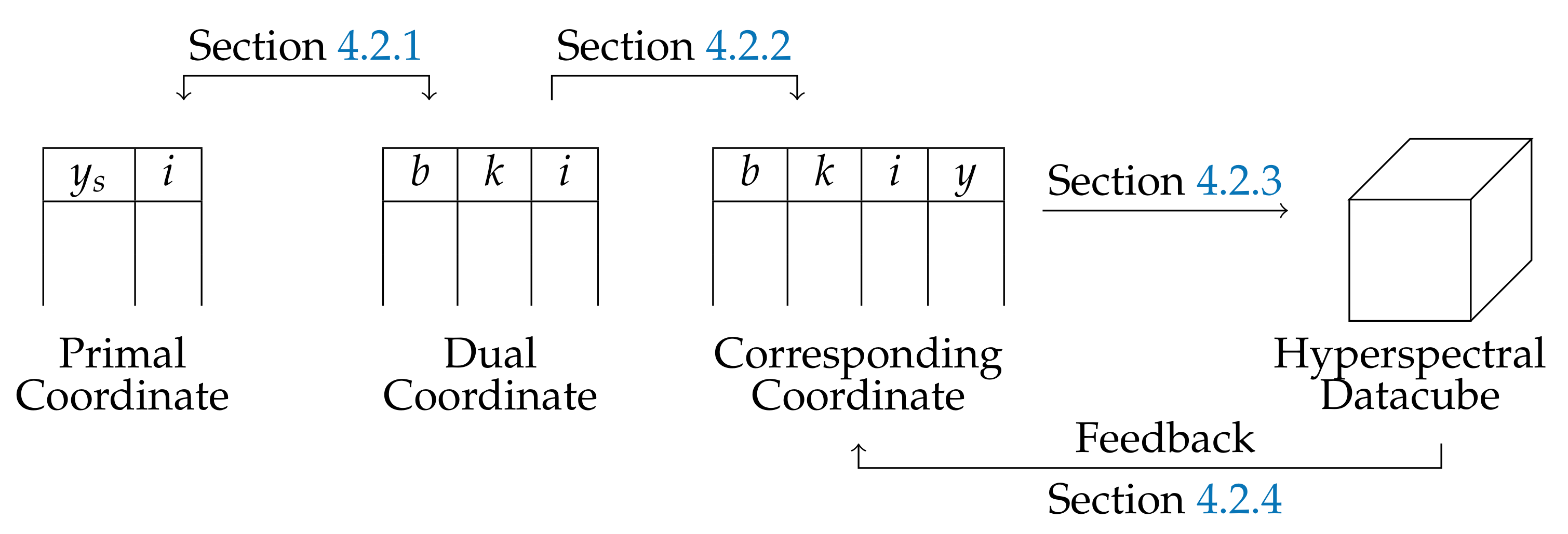
4.2. Physical-Based Spectral Reconstruction (PSR)
4.2.1. First Basis Change
4.2.2. Second Basis Change
4.2.3. Interpolation of the Radiance
| Algorithm 3 Physical-based spectral reconstruction (PSR). |
|
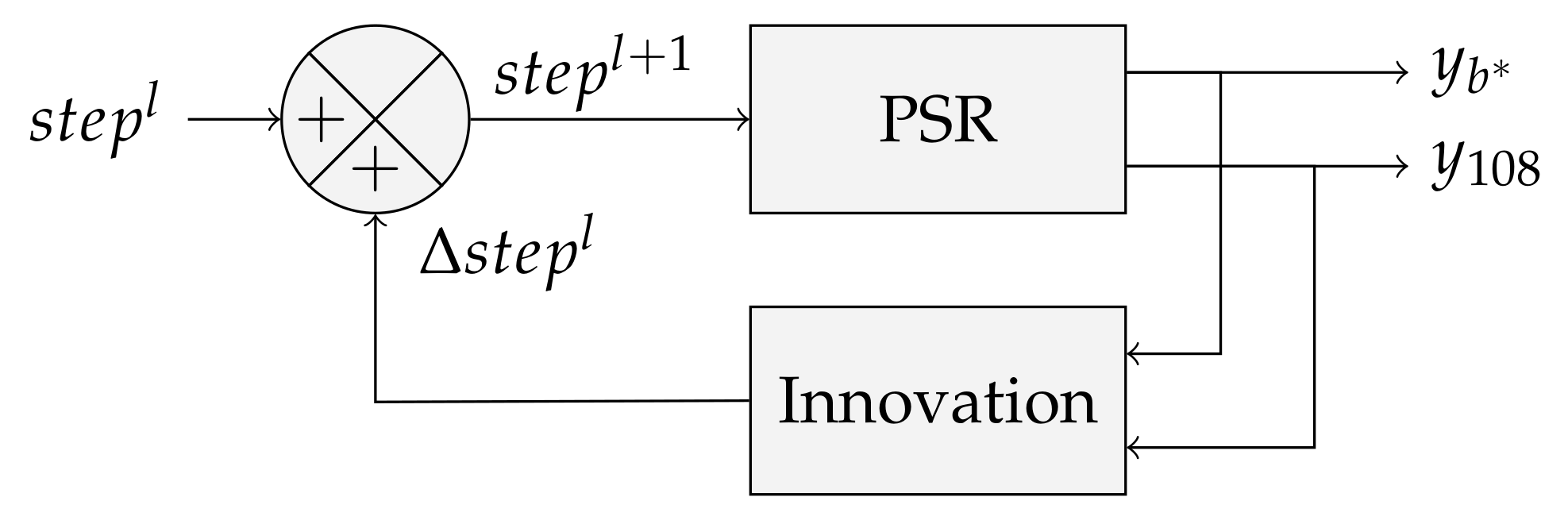
4.2.4. Estimating the Step Parameter
- Initialization.The knowledge of the sensor speed enables to propose an approximate value, expressed in pixels per frame, i.e.,where [mm/s] accounts for the sensor speed and [mm/px] stands for the ground instantaneous field of view derived from the global ground field of view [26]. Since all the parameters are known, it is easy to propose an approximate step parameter as an initial value.
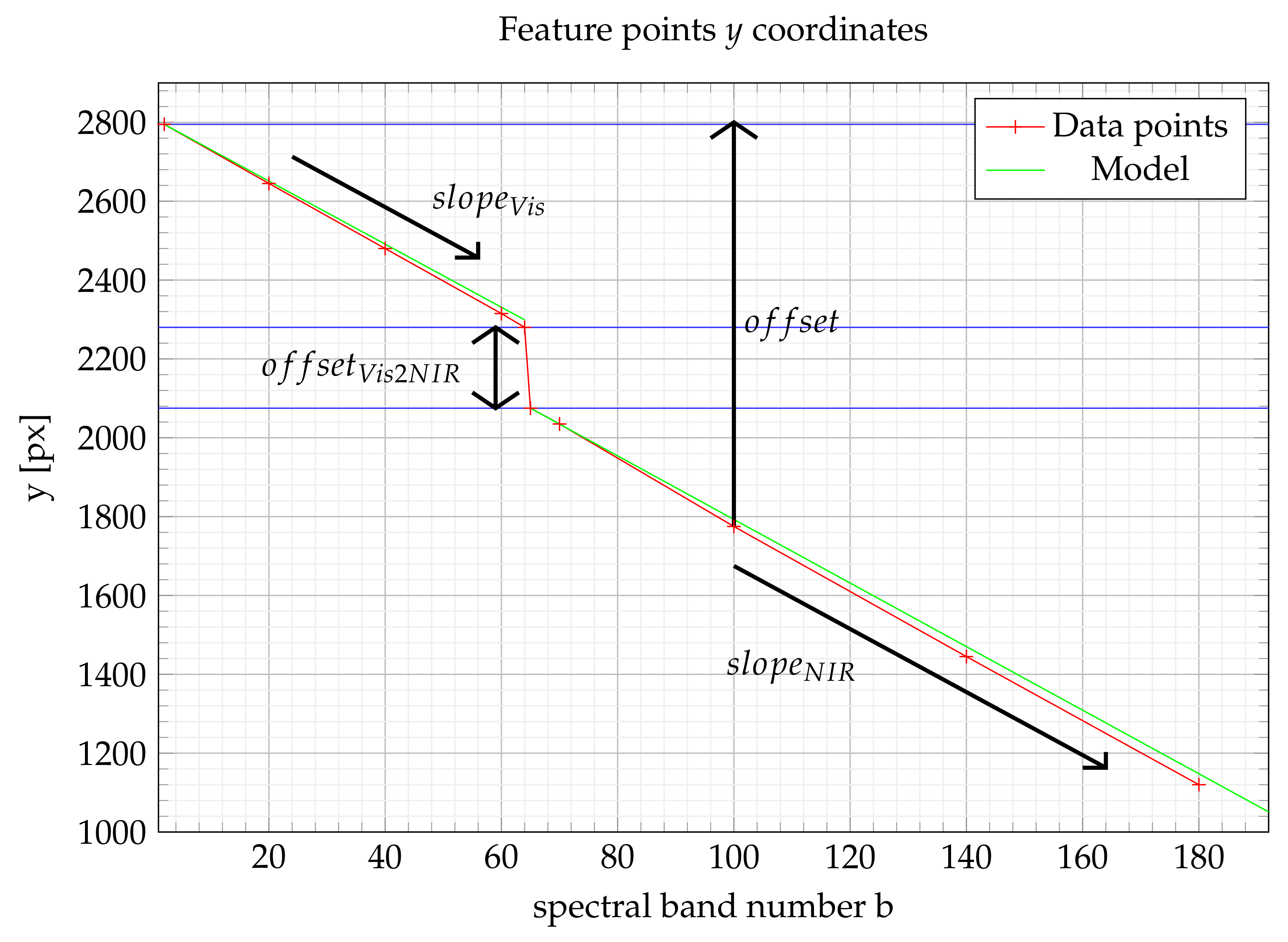
- Update rule.The first run with an estimated speed parameter denoted as leads to a first spectral reconstruction. Tracking a reference point in different bands enables inspecting a potential drift. Let (This band corresponds to a ray angle approximately equal to 0 degrees) and be the y-coordinate of the point from, respectively, the reference spectral band and the th spectral band. Then, it turns out from Equation (15) that they may be written as follows:Additionally, a single coordinate of the reference point, denoted as , should be expected with the true parameter in different spectral bands so that the following holds:By subtracting both equations in Equation (24), an estimation of the deviation from the true value of the parameter may be found, i.e.,In order to propose a new value, Equation (25) may be applied once to find the step increment with a single spectral band or in the least squares sense with multiple target bands to fit the best parameter. This new step value may be computed as follows:
5. Corrective Warping of the Datacube
5.1. Building the Set of Matching Pairs
- Identify several feature points in a few regularly spaced spectral layers.
- Predict the position of feature points in each intermediate spectral layer with linear interpolation.
5.2. Fitting the Warping Model
| Algorithm 4 A global scheme to enhance and evaluate the accuracy of the reconstruction. |
|
5.3. Applying the Model and Post-Processing
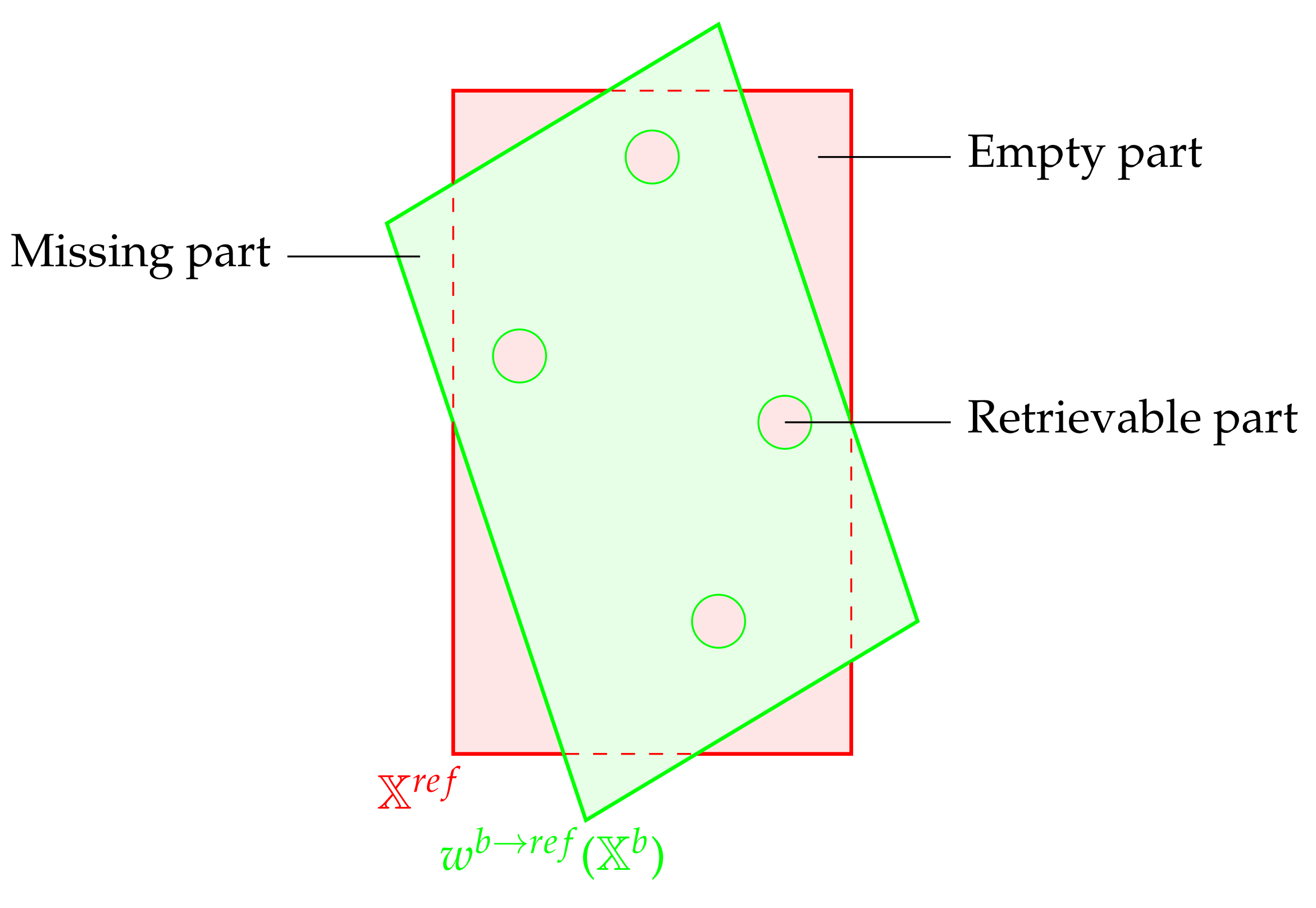
- There may be some empty pixels since the warping model may not be surjective, i.e.,The empty pixels which are surrounded by filled pixels may be spatially interpolated by a post-processing step, as shown in Figure 13. The others are left empty.
- The model may not be injective since two points from the original space point toward the same destination. This property translates mathematically into the following:
- A point from may point outside from . It is represented in Figure 13 as a missing part. In such a case, the corresponding point is not taken into account.
6. Practical Experimentation
6.1. Synthetic Dataset
6.2. Real Dataset
6.3. Evaluation Index
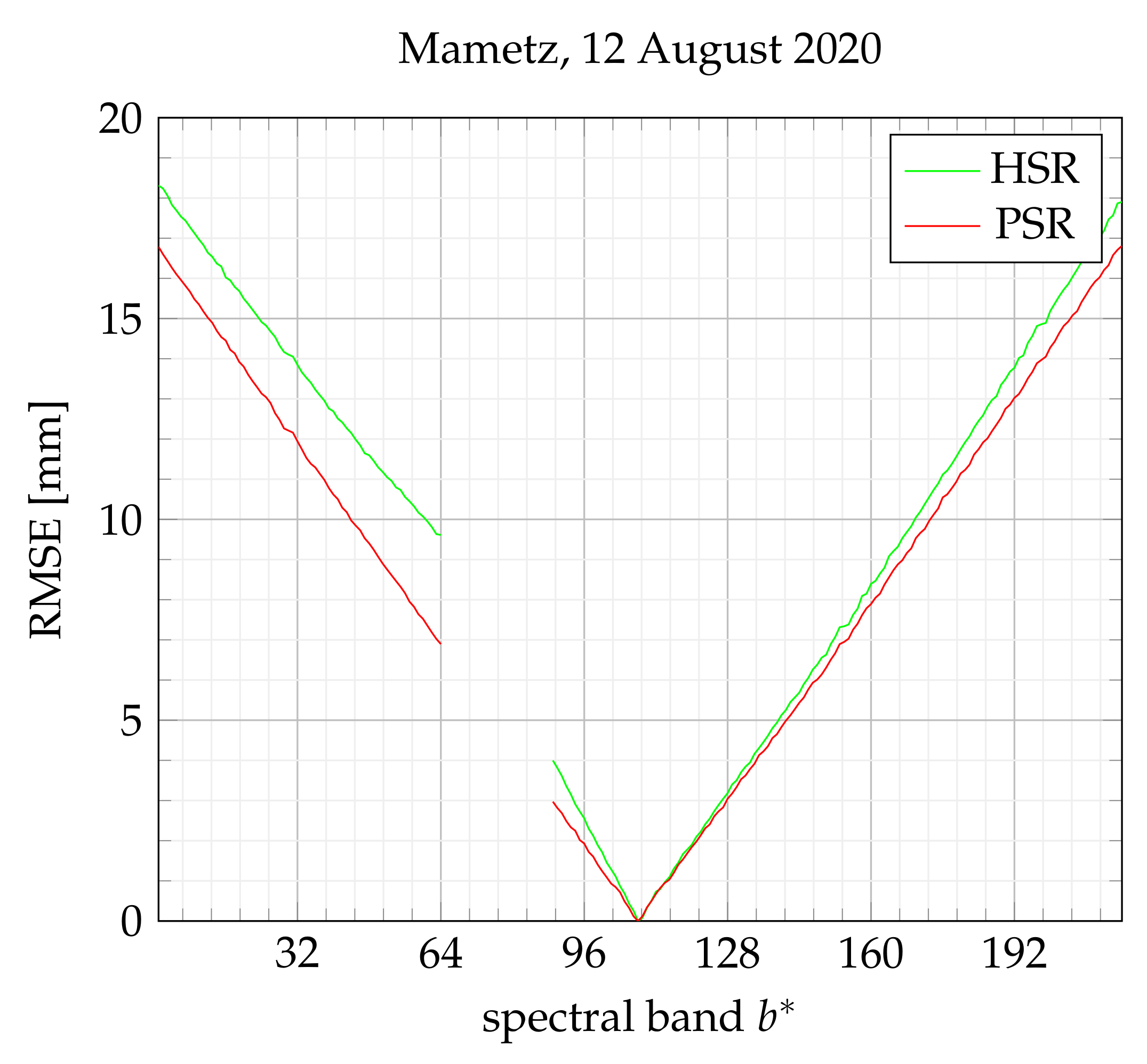
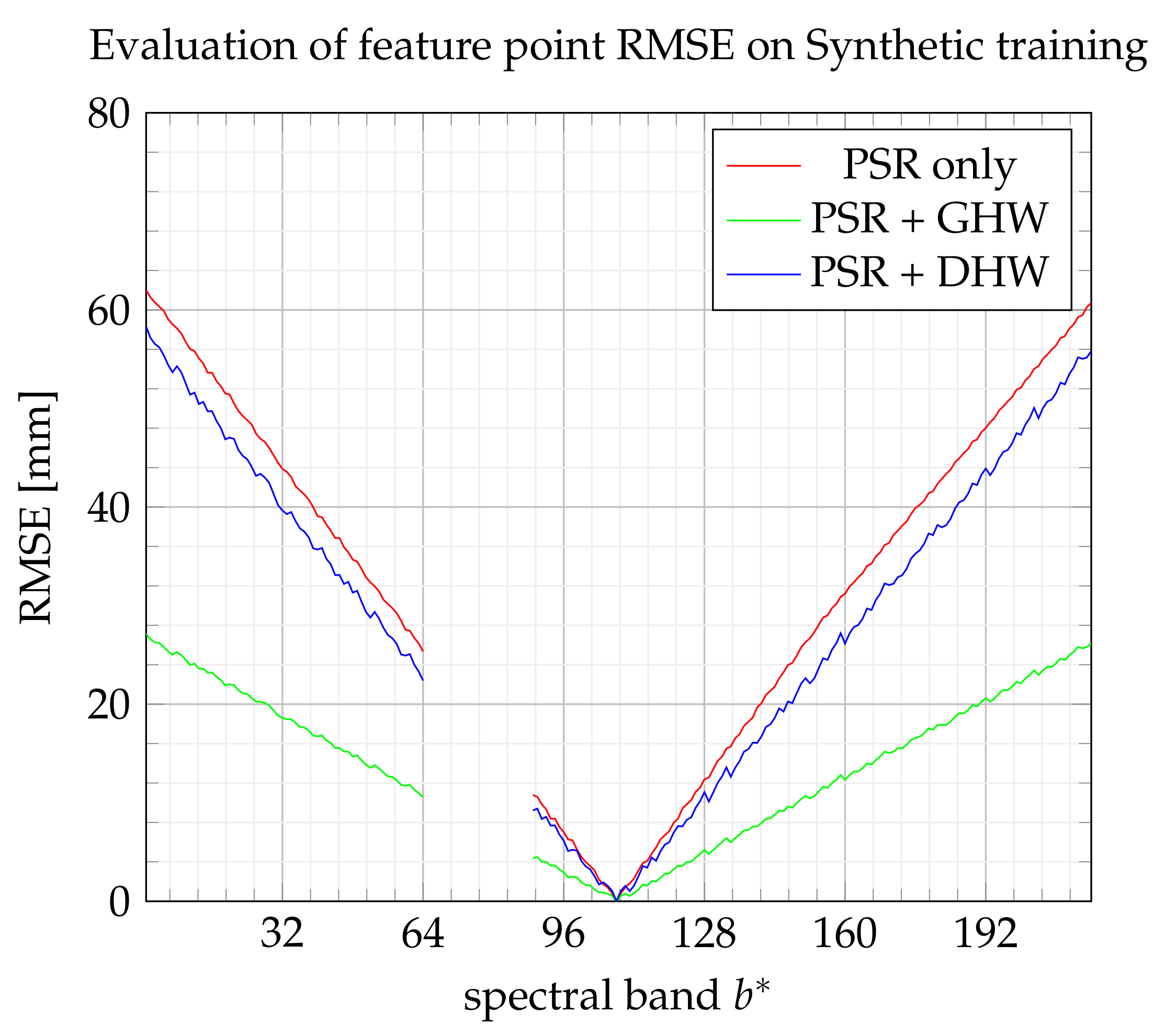
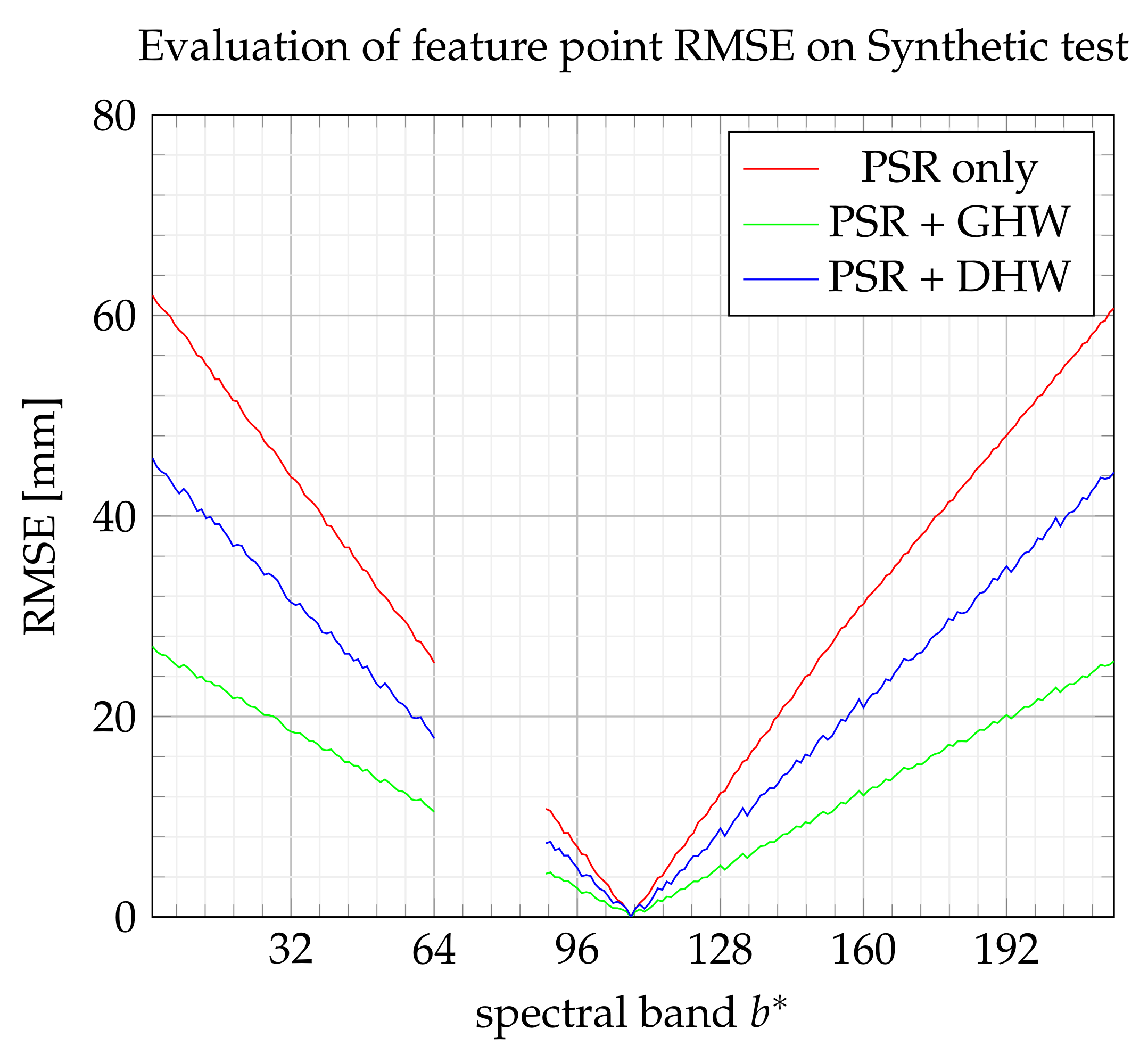
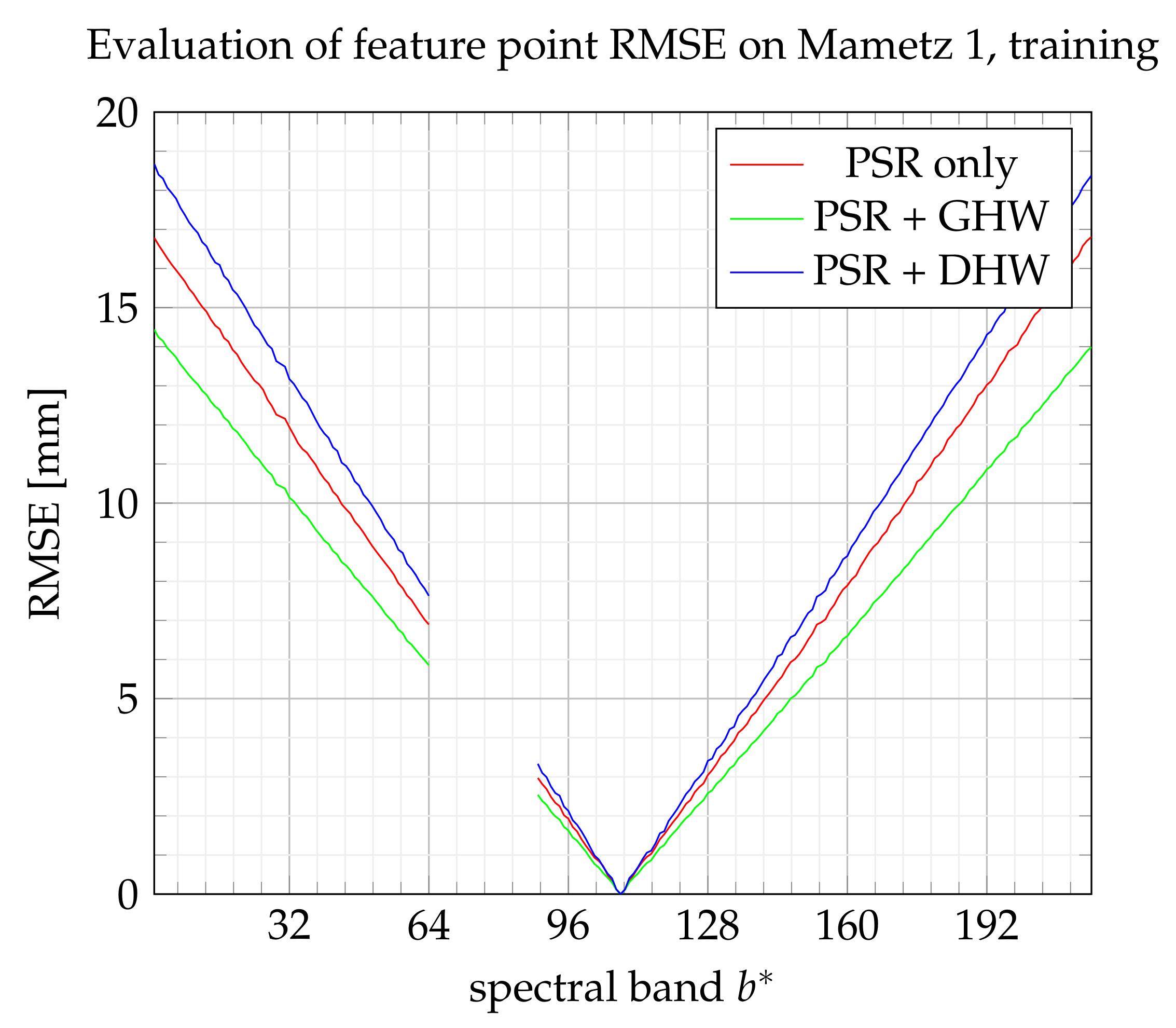
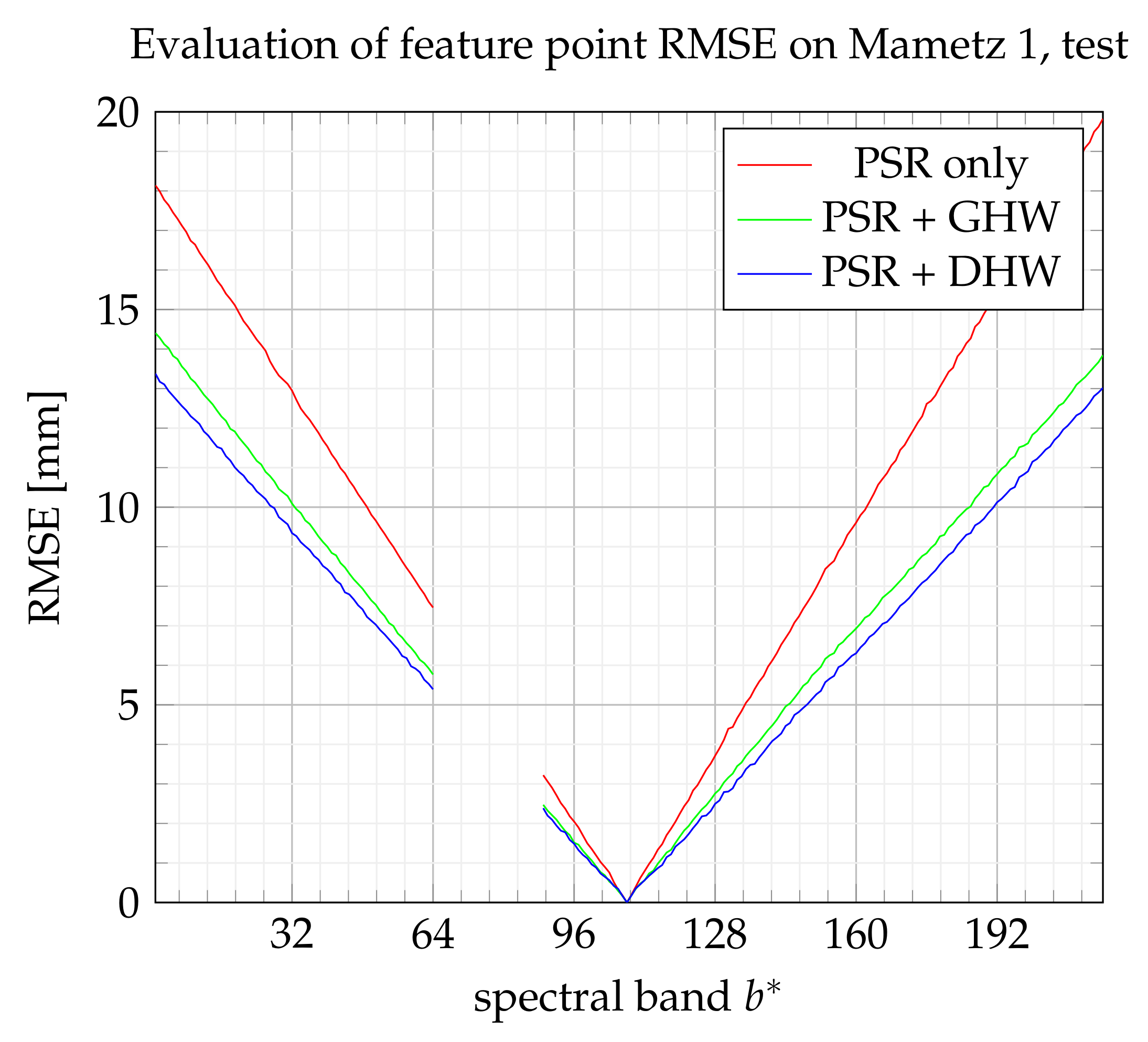
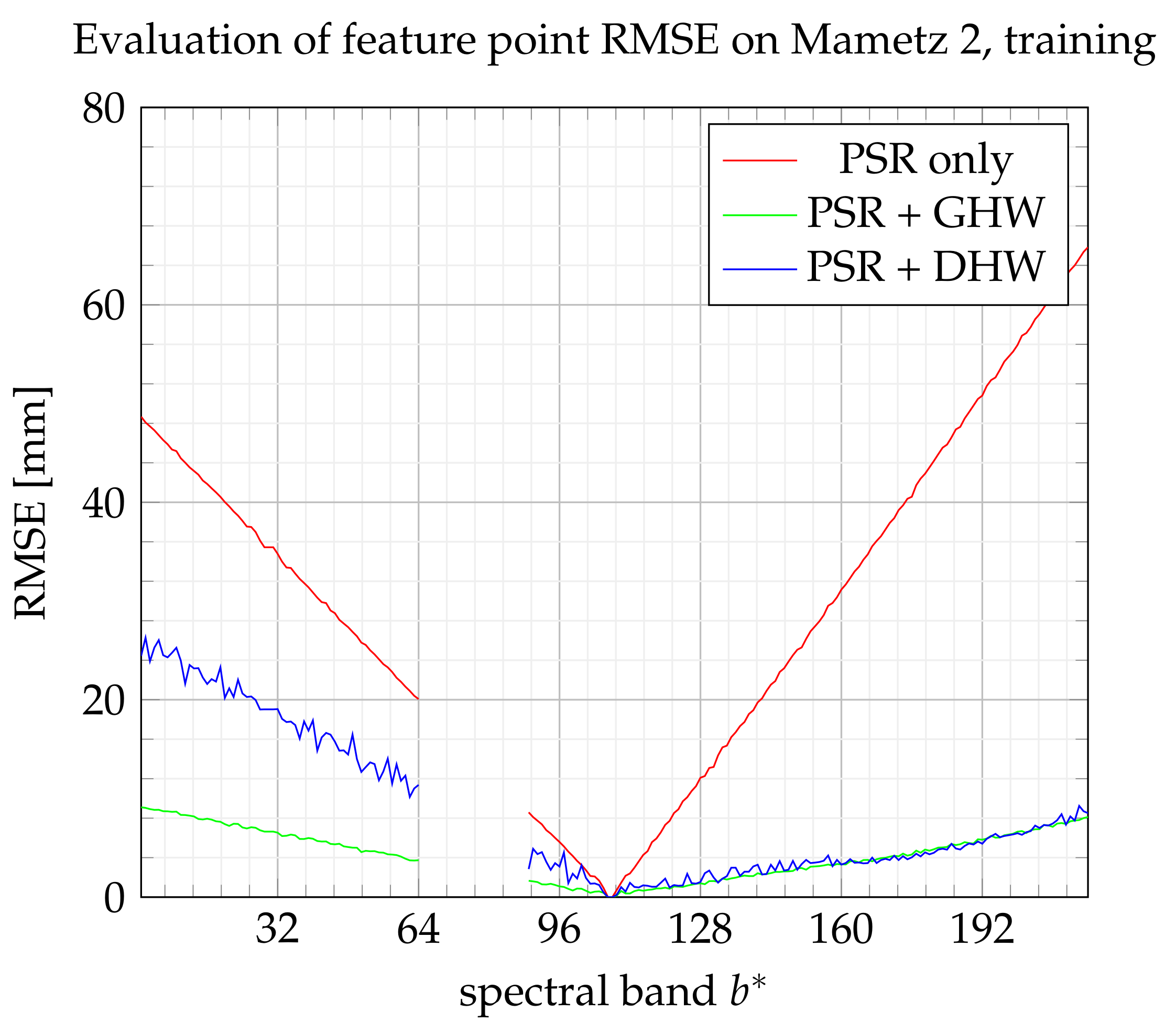
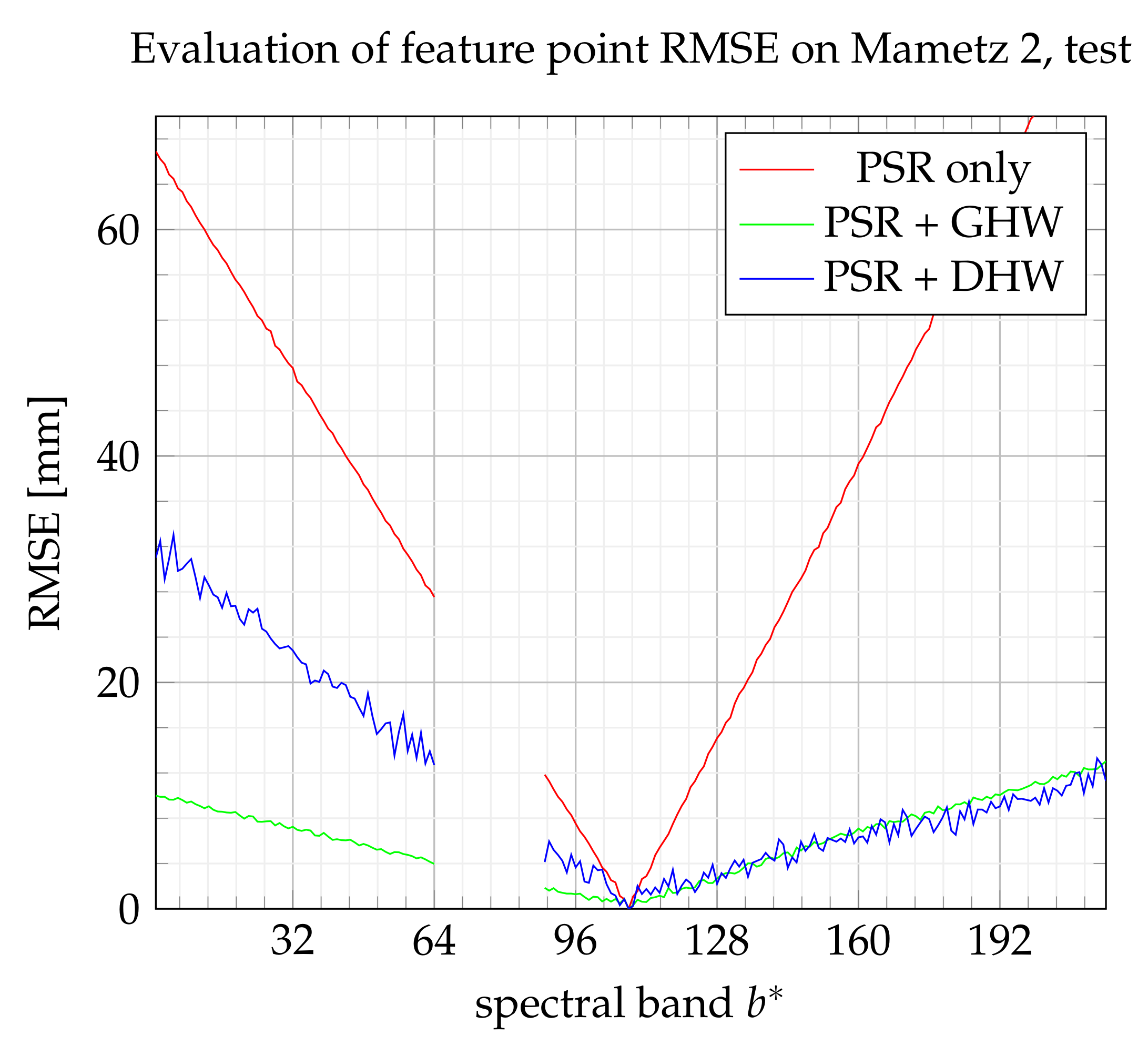
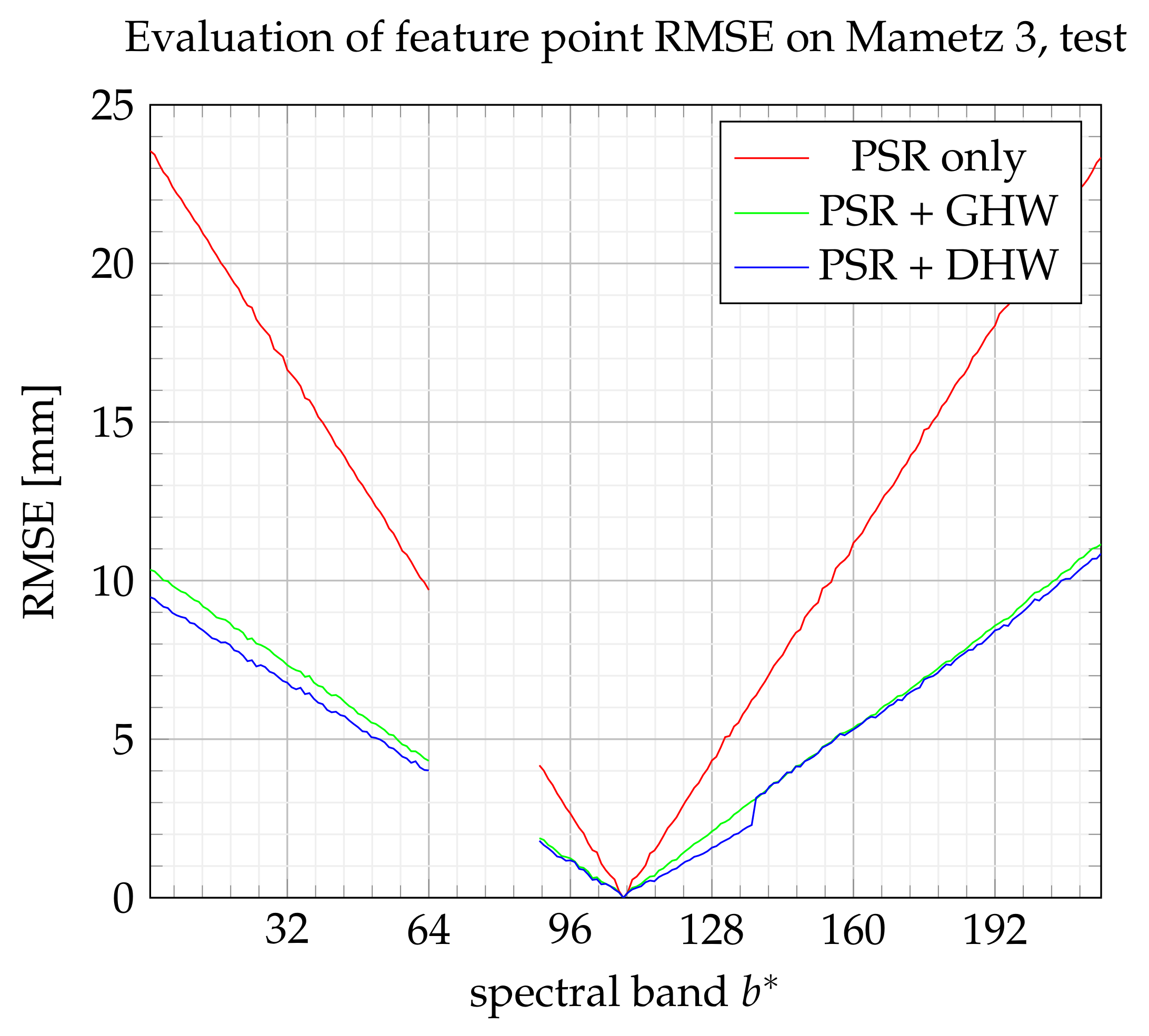
6.4. Results
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhang, J.; Sun, H.; Gao, D.; Qiao, L.; Liu, N.; Li, M.; Zhang, Y. Detection of Canopy Chlorophyll Content of Corn Based on Continuous Wavelet Transform Analysis. Remote Sens. 2020, 12, 2741. [Google Scholar] [CrossRef]
- Liu, L.; Dong, Y.; Huang, W.; Du, X.; Ma, H. Monitoring Wheat Fusarium Head Blight Using Unmanned Aerial Vehicle Hyperspectral Imagery. Remote Sens. 2020, 12, 3811. [Google Scholar] [CrossRef]
- Martín, P.; Zarco-Tejada, P.; González, M.; Berjón, A. Using hyperspectral remote sensing to map grape quality inTempranillo’vineyards affected by iron deficiency chlorosis. Vitis 2007, 46, 7–14. [Google Scholar]
- Appeltans, S.; Guerrero, A.; Nawar, S.; Pieters, J.; Mouazen, A.M. Practical Recommendations for Hyperspectral and Thermal Proximal Disease Sensing in Potato and Leek Fields. Remote Sens. 2020, 12, 1939. [Google Scholar] [CrossRef]
- Lu, B.; Dao, P.D.; Liu, J.; He, Y.; Shang, J. Recent advances of hyperspectral imaging technology and applications in agriculture. Remote Sens. 2020, 12, 2659. [Google Scholar] [CrossRef]
- Tattaris, M.; Reynolds, M.P.; Chapman, S.C. A Direct Comparison of Remote Sensing Approaches for High-Throughput Phenotyping in Plant Breeding. Front. Plant Sci. 2016, 7, 1131. [Google Scholar] [CrossRef]
- Axelsson, C.; Skidmore, A.K.; Schlerf, M.; Fauzi, A.; Verhoef, W. Hyperspectral analysis of mangrove foliar chemistry using PLSR and support vector regression. Int. J. Remote Sens. 2013, 34, 1724–1743. [Google Scholar] [CrossRef]
- Deery, D.; Jimenez-Berni, J.; Jones, H.; Sirault, X.; Furbank, R. Proximal Remote Sensing Buggies and Potential Applications for Field-Based Phenotyping. Agronomy 2014, 4, 349–379. [Google Scholar] [CrossRef] [Green Version]
- Bruning, B.; Liu, H.; Brien, C.; Berger, B.; Lewis, M.; Garnett, T. The Development of Hyperspectral Distribution Maps to Predict the Content and Distribution of Nitrogen and Water in Wheat (Triticum aestivum). Front. Plant Sci. 2019, 10, 1380. [Google Scholar] [CrossRef]
- Amziane, A.; Losson, O.; Mathon, B.; Dumenil, A.; Macaire, L. Reflectance Estimation from Multispectral Linescan Acquisitions under Varying Illumination-Application to Outdoor Weed Identification. Sensors 2021, 21, 3601. [Google Scholar] [CrossRef]
- Livens, S.; Pauly, K.; Baeck, P.; Blommaert, J.; Nuyts, D.; Zender, J.; Delauré, B. A SPATIO-SPECTRAL CAMERA FOR HIGH RESOLUTION HYPERSPECTRAL IMAGING. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2017, 42. [Google Scholar] [CrossRef] [Green Version]
- Sima, A.; Baeck, P.; Nuyts, D.; Delalieux, S.; Livens, S.; Blommaert, J.; Delauré, B.; Boonen, M. Compact hyperspectral imaging system (COSI) for small remotely piloted aircraft systems (RPAS)–system overview and first performance evaluation results. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2016, 41, 1157. [Google Scholar] [CrossRef] [Green Version]
- Ma, J.; Zhou, H.; Zhao, J.; Gao, Y.; Jiang, J.; Tian, J. Robust feature matching for remote sensing image registration via locally linear transforming. IEEE Trans. Geosci. Remote Sens. 2015, 53, 6469–6481. [Google Scholar] [CrossRef]
- Bay, H.; Ess, A.; Tuytelaars, T.; Gool, L.V. Speeded-Up Robust Features (SURF). Comput. Vis. Image Underst. 2008, 110, 346–359. [Google Scholar] [CrossRef]
- Brown, M.; Lowe, D.G. Automatic panoramic image stitching using invariant features. Int. J. Comput. Vis. 2007, 74, 59–73. [Google Scholar] [CrossRef] [Green Version]
- Zaragoza, J.; Chin, T.J.; Brown, M.S.; Suter, D. As-projective-as-possible image stitching with moving DLT. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Portland, OR, USA, 23–28 June 2013; pp. 2339–2346. [Google Scholar]
- Chang, C.H.; Sato, Y.; Chuang, Y.Y. Shape-preserving half-projective warps for image stitching. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 June 2014; pp. 3254–3261. [Google Scholar]
- Zhang, Y.; Wan, Z.; Jiang, X.; Mei, X. Automatic Stitching for Hyperspectral Images Using Robust Feature Matching and Elastic Warp. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 3145–3154. [Google Scholar] [CrossRef]
- Lowe, D.G. Distinctive Image Features from Scale-Invariant Keypoints. Int. J. Comput. Vision 2004, 60, 91–110. [Google Scholar] [CrossRef]
- Fischler, M.A.; Bolles, R.C. Random sample consensus: A paradigm for model fitting with applications to image analysis and automated cartography. Commun. ACM 1981, 24, 381–395. [Google Scholar] [CrossRef]
- Torr, P.H.; Zisserman, A. MLESAC: A new robust estimator with application to estimating image geometry. Comput. Vis. Image Underst. 2000, 78, 138–156. [Google Scholar] [CrossRef] [Green Version]
- Habib, A.; Han, Y.; Xiong, W.; He, F.; Zhang, Z.; Crawford, M. Automated ortho-rectification of UAV-based hyperspectral data over an agricultural field using frame RGB imagery. Remote Sens. 2016, 8, 796. [Google Scholar] [CrossRef] [Green Version]
- Hartley, R.I. In Defense of the Eight-Point Algorithm. IEEE Trans. Pattern Anal. Mach. Intell. 1997, 19, 580–593. [Google Scholar] [CrossRef] [Green Version]
- Gao, J.; Kim, S.J.; Brown, M.S. Constructing image panoramas using dual-homography warping. In Proceedings of the CVPR 2011, Colorado Springs, CO, USA, 20–25 June 2011; pp. 49–56. [Google Scholar]
- Müller-Rowold, M.; Reulke, R. Hyperspectral panoramic imaging. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2018, XLII-1, 323–328. [Google Scholar] [CrossRef] [Green Version]
- Clodius, W.B. Multispectral and Hyperspectral Image Processing, Part 1: Initial Processing; Taylor & Francis: Los Alamos, NM, USA, 2007; pp. 1390–1405. [Google Scholar]
- Lin, W.Y.; Liu, S.; Matsushita, Y.; Ng, T.T.; Cheong, L.F. Smoothly varying affine stitching. In Proceedings of the CVPR 2011, Colorado Springs, CO, USA, 20–25 June 2011; pp. 345–352. [Google Scholar]
- Clevers, J.G.; Gitelson, A.A. Remote estimation of crop and grass chlorophyll and nitrogen content using red-edge bands on Sentinel-2 and-3. Int. J. Appl. Earth Obs. Geoinf. 2013, 23, 344–351. [Google Scholar] [CrossRef]








| Method | Scene Assumption | Pair of RGB Images | Pair of Spectral Datacubes | Pair of Spectral Layers |
|---|---|---|---|---|
| GHW [23] | Objects in the same plane | Fast | X | X |
| APAP [16] | Smooth changes | Slow | X | X |
| DHW [24] | Two distinct planes | Medium | X | X |
| SPHP [17] | Two distinct planes | Slow | X | X |
| Zhang [18] | Smooth changes | X | Fast | X |
| Collection of GHW (ours) | Objects in the same plane | X | X | Medium |
| Collection of DHW (ours) | Two distinct planes | X | X | Slow |
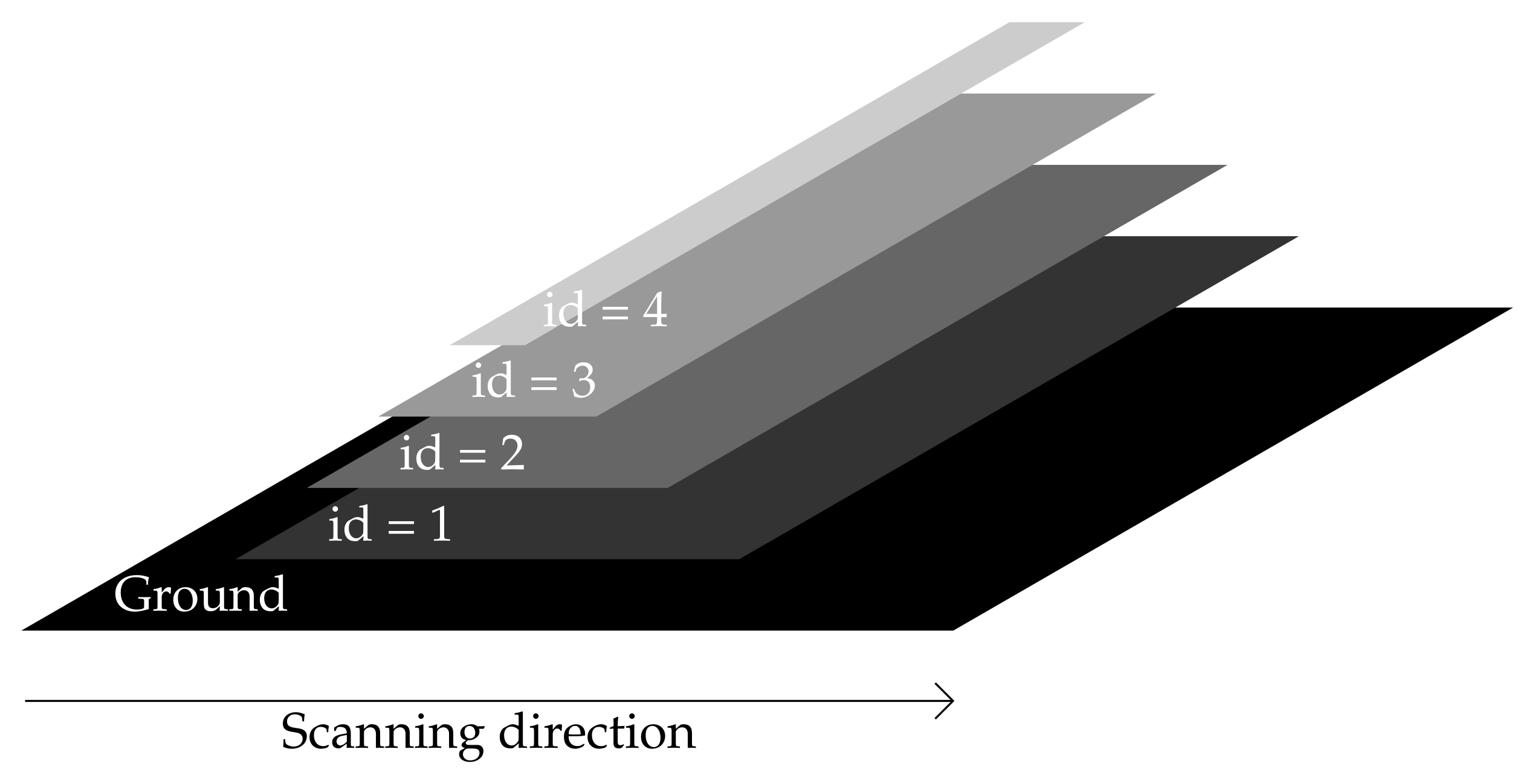
| Id | Position | Height | Width |
|---|---|---|---|
| 1 | 100 mm | 100 mm | 700 mm |
| 2 | 200 mm | 200 mm | 500 mm |
| 3 | 300 mm | 300 mm | 300 mm |
| 4 | 400 mm | 400 mm | 100 mm |
| Dataset | f [mm] | [fps] | Height [m] | GIFOV | Speed | Mode |
|---|---|---|---|---|---|---|
| Mametz 1 | 35 | 10 | ≈2.85 | 0.43 mm/px | ≈2.6 mm/s | open loop |
| Mametz 2 | 12 | 10 | 2.85 | 1.29 mm/px | ≈3.89 mm/s | open loop |
| Mametz 3 | 35 | 10 | 2.85 | 0.43 mm/px | 2.15 mm/s | closed loop |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chatelain, P.; Delmaire, G.; Alboody, A.; Puigt, M.; Roussel, G. Semi-Automatic Spectral Image Stitching for a Compact Hybrid Linescan Hyperspectral Camera towards Near Field Remote Monitoring of Potato Crop Leaves. Sensors 2021, 21, 7616. https://doi.org/10.3390/s21227616
Chatelain P, Delmaire G, Alboody A, Puigt M, Roussel G. Semi-Automatic Spectral Image Stitching for a Compact Hybrid Linescan Hyperspectral Camera towards Near Field Remote Monitoring of Potato Crop Leaves. Sensors. 2021; 21(22):7616. https://doi.org/10.3390/s21227616
Chicago/Turabian StyleChatelain, Pierre, Gilles Delmaire, Ahed Alboody, Matthieu Puigt, and Gilles Roussel. 2021. "Semi-Automatic Spectral Image Stitching for a Compact Hybrid Linescan Hyperspectral Camera towards Near Field Remote Monitoring of Potato Crop Leaves" Sensors 21, no. 22: 7616. https://doi.org/10.3390/s21227616
APA StyleChatelain, P., Delmaire, G., Alboody, A., Puigt, M., & Roussel, G. (2021). Semi-Automatic Spectral Image Stitching for a Compact Hybrid Linescan Hyperspectral Camera towards Near Field Remote Monitoring of Potato Crop Leaves. Sensors, 21(22), 7616. https://doi.org/10.3390/s21227616






