A Low-Power Spiking Neural Network Chip Based on a Compact LIF Neuron and Binary Exponential Charge Injector Synapse Circuits
Abstract
:1. Introduction
2. Architecture and Design
2.1. Spiking Neural Network Model
2.2. Leaky Integrate and Fire Model
3. SNN Implementation and Circuit Design
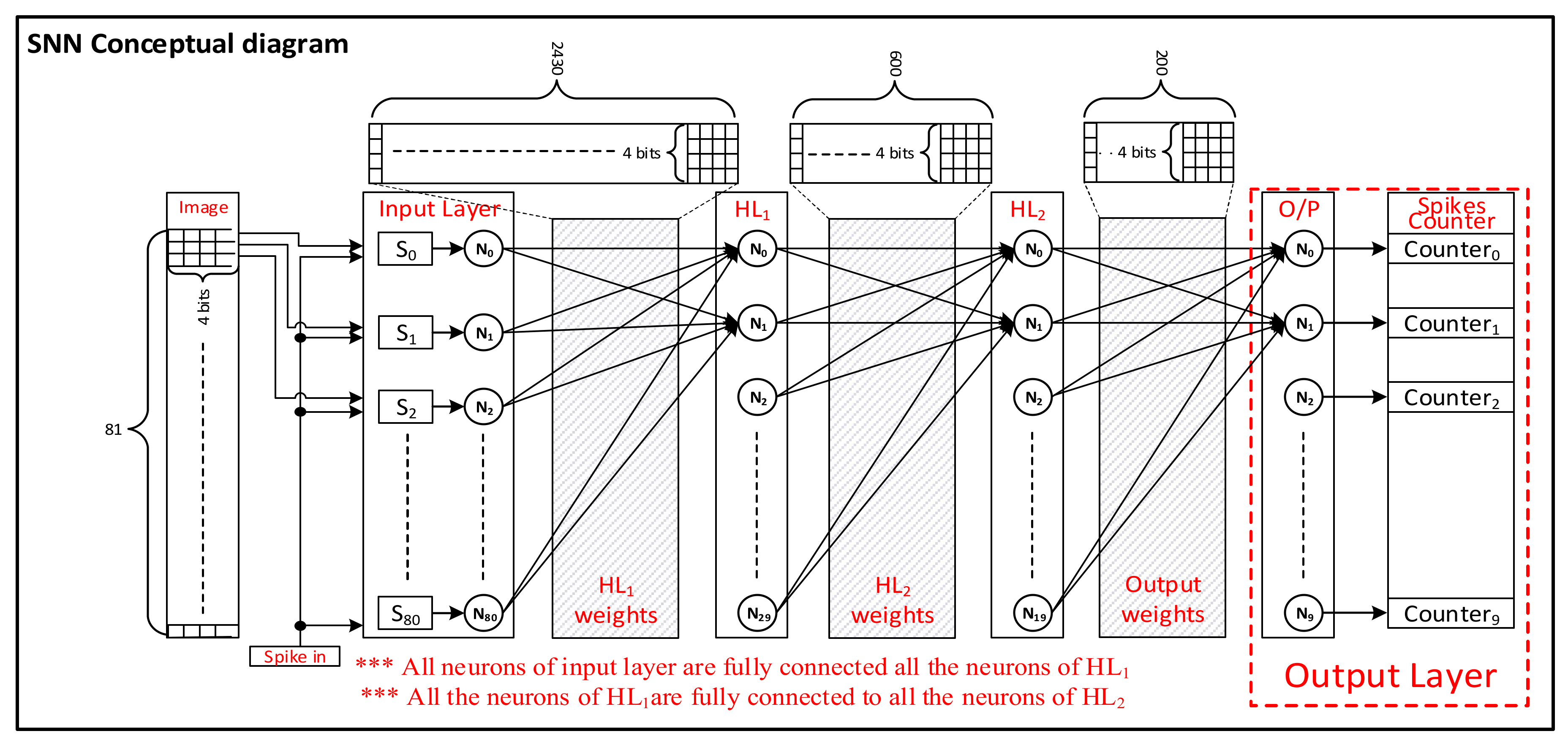
3.1. BSRC-Based SNN Architecture
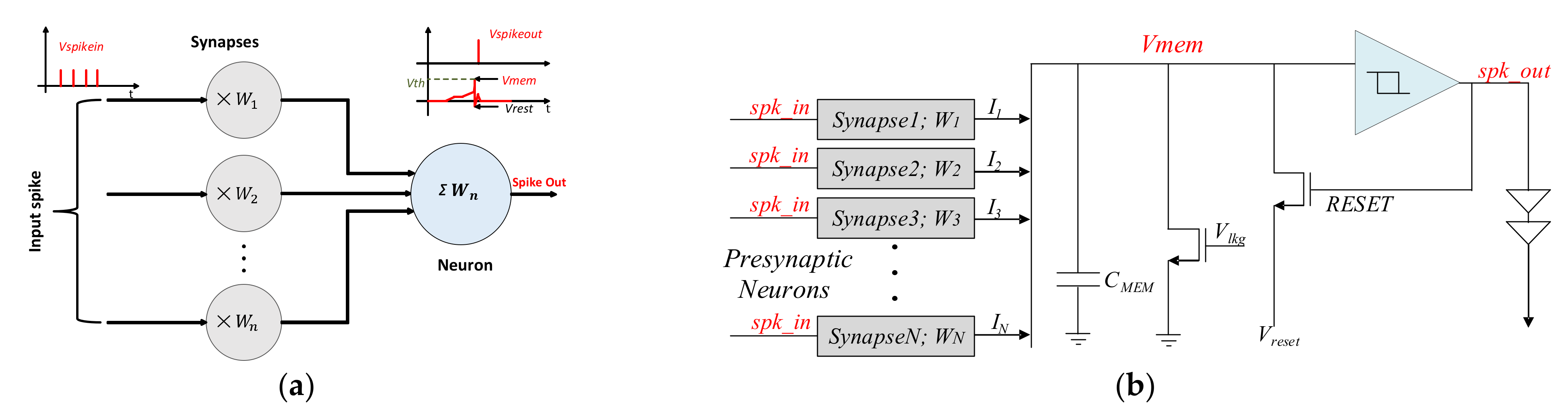
3.2. Analog Spiking Neural Network
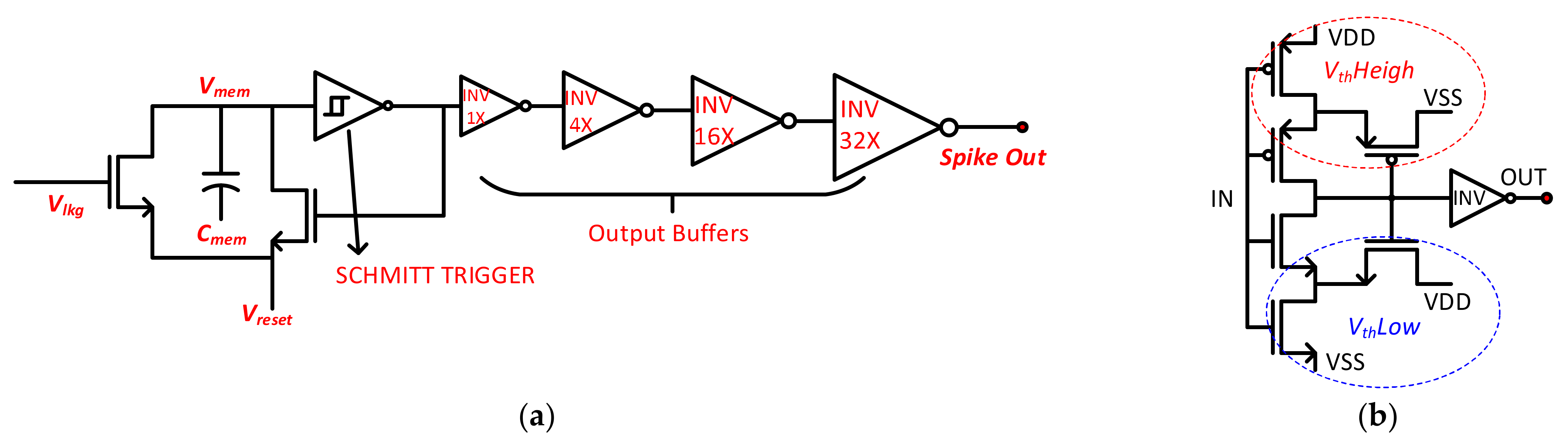
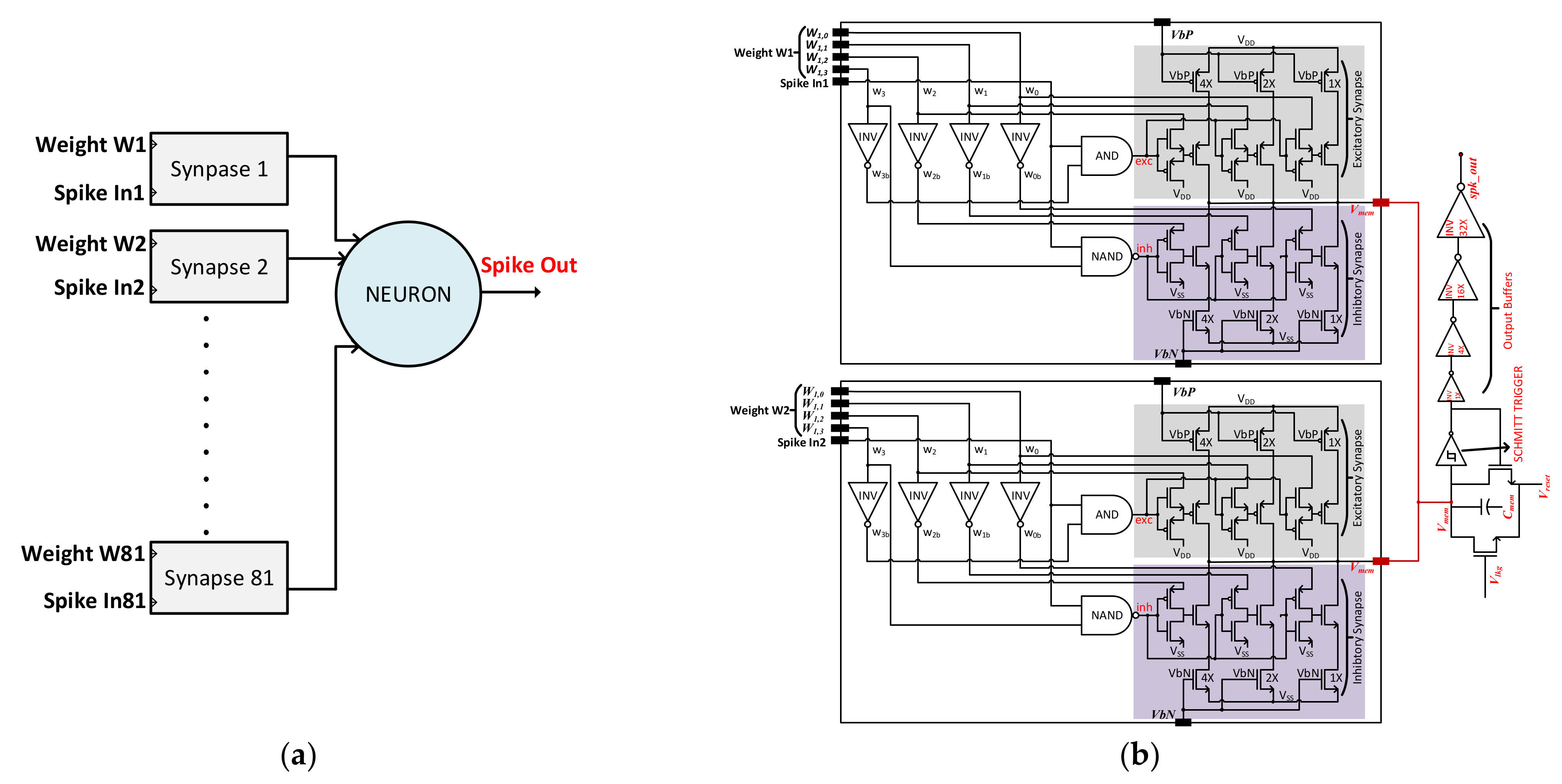
3.2.1. Neuron Circuit
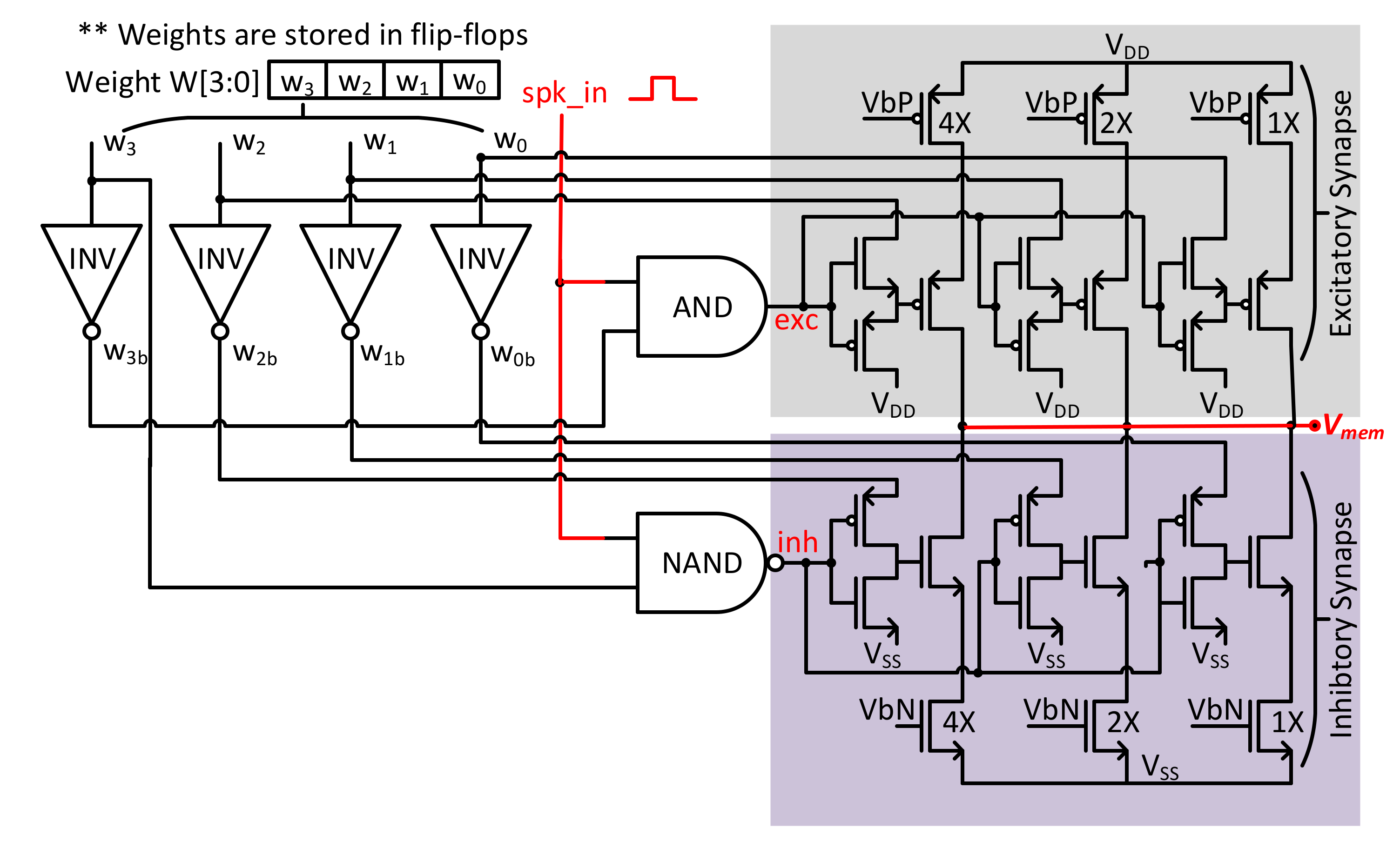
3.2.2. Synapse Circuit
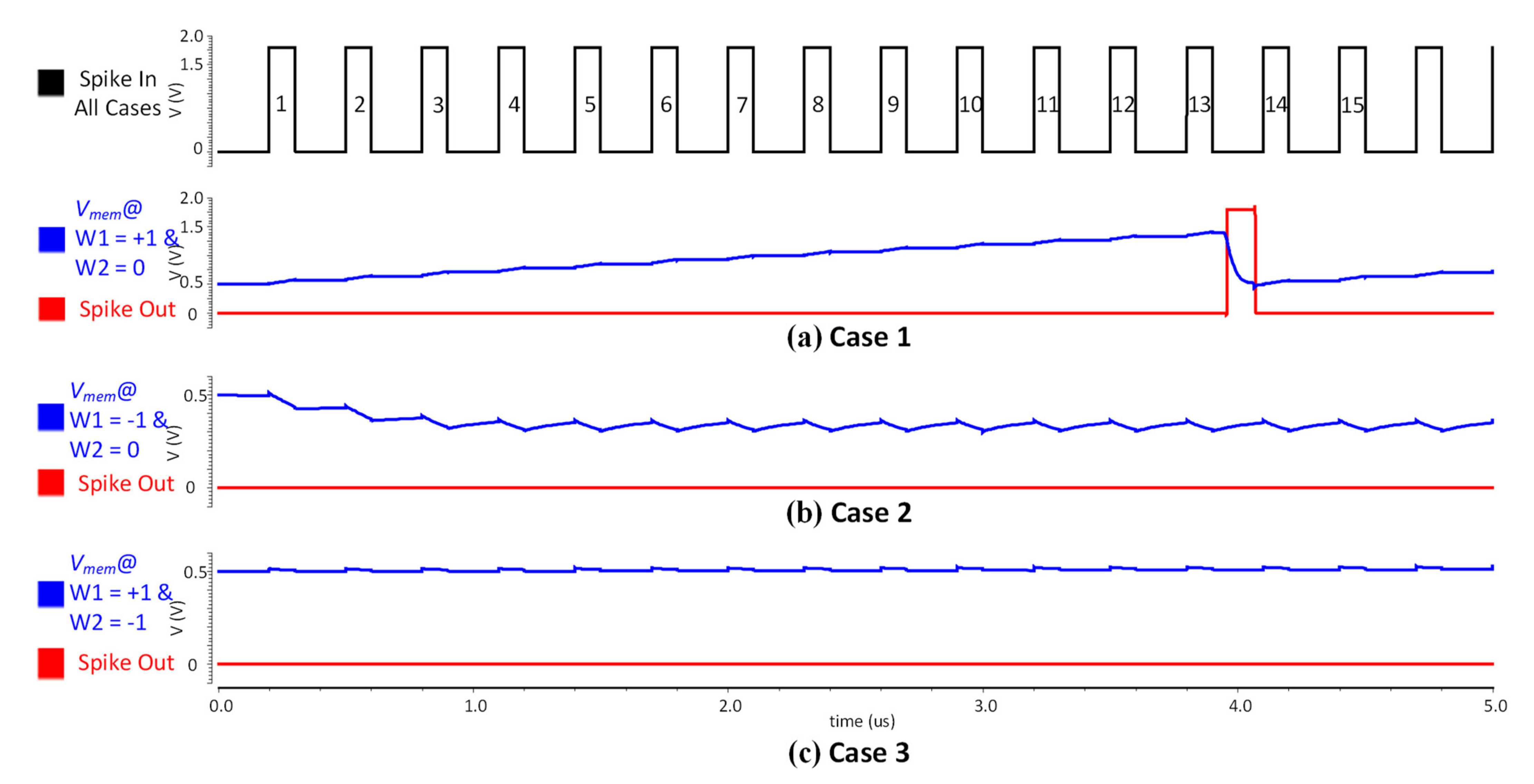
3.2.3. Circuit Simulation
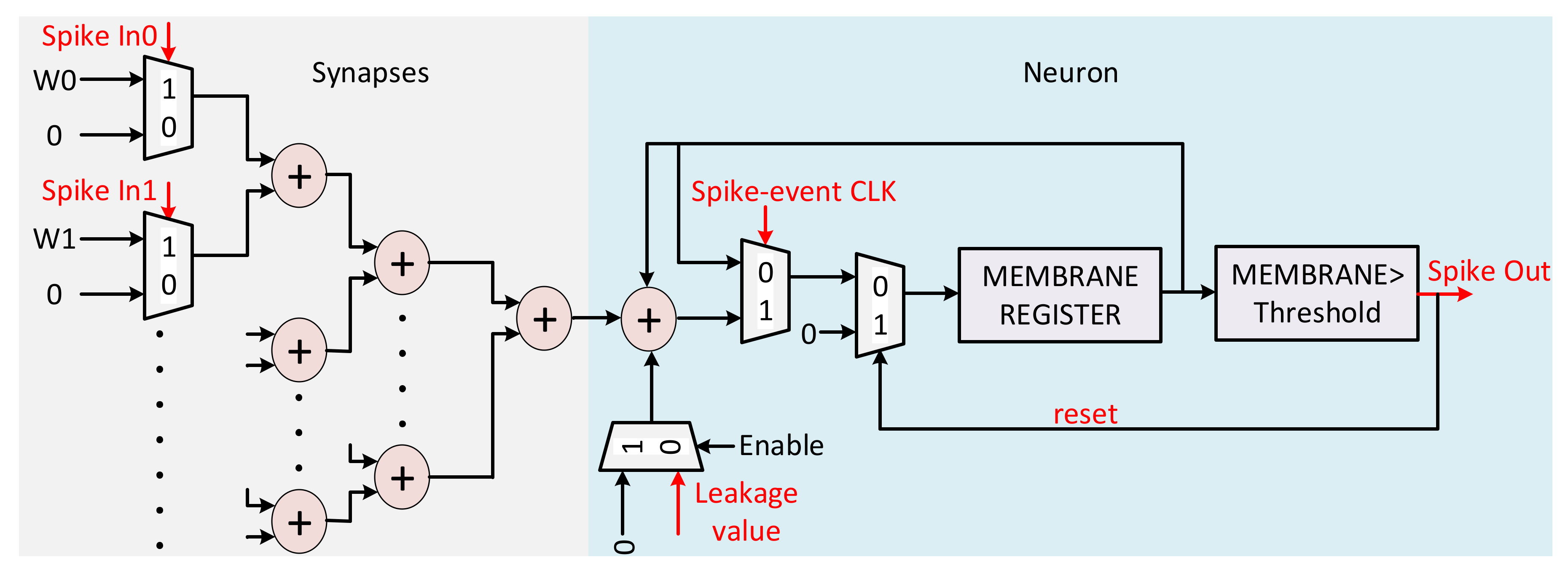
3.3. Fully Digital Implementation of Spiking Neural Network
4. Measurement Results and Analysis
4.1. Implementation of Analog SNN
4.2. Implementation of Digital SNN
5. Performance Analysis
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mead, C. Neuromorphic electronic systems. Proc. IEEE 1990, 78, 1629–1636. [Google Scholar] [CrossRef] [Green Version]
- Prezioso, M.; Merrikh-Bayat, F.; Hoskins, B.D.; Adam, G.C.; Likharev, K.K.; Strukov, D.B. Training and operation of an integrated neuromorphic network based on metal-oxide memristors. Nature 2015, 521, 61–64. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Alex, K.; Ilya, S.; Geoffrey, E.H. ImageNet classification with deep convolutional neural networks. In Proceedings of the 25th International Conference on Neural Information Processing Systems, Lake Tahoe, NV, USA, 3–6 December 2012; pp. 1097–1105. [Google Scholar]
- Lee, J.H.; Delbruck, T.; Pfeiffer, M. Training Deep Spiking Neural Networks Using Backpropagation. Front. Neurosci. 2016, 10, 508. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kyuho, L.; Junyoung, P.; Hoi-Jun, Y. A Low-power, Mixed-mode Neural Network Classifier for Robust Scene Classification. J. Semicond. Technol. Sci. 2019, 19, 129–136. [Google Scholar] [CrossRef]
- Schuman, C.D.; Potok, T.E.; Patton, R.M.; Birdwell, J.D.; Dean, M.E.; Rose, G.S.; Plank, J.S. A Survey of Neuromorphic Computing and Neural Networks in Hardware. Available online: http://arxiv.org/abs/1705.06963 (accessed on 25 January 2021).
- Von Neumann, J. First draft of a report on the EDVAC. IEEE Ann. Hist. Comput. 1993, 15, 27–75. [Google Scholar] [CrossRef]
- Kandel, E.R.; Schwartz, J.H.; Jessell, T.M. Principles of Neural Science, 5th ed.; McGraw-Hill, Health Professions Division: New York, NY, USA, 2012. [Google Scholar]
- Meier, K. Special report: Can we copy the brain?—The brain as computer. IEEE Spectr. 2017, 54, 28–33. [Google Scholar] [CrossRef]
- Mahowald, M.A.; Mead, C. The silicon retina. In Scientific American; Springer Nature: New York, NY, USA, 1991; Volume 264, pp. 76–82. [Google Scholar] [CrossRef]
- Kim, S.; Kim, H.; Hwang, S.; Kim, M.H.; Chang, Y.F.; Park, B.G. Analog synaptic behavior of a silicon nitride memristor. ACS Appl. Mater. Interfaces 2017, 9, 40420–40427. [Google Scholar] [CrossRef]
- Rashvand, P.; Ahmadzadeh, M.R.; Shayegh, F. Design and Implementation of a Spiking Neural Network with Integrate-and-Fire Neuron Model for Pattern Recognition. Int. J. Neural Syst. 2021, 31, 2050073. [Google Scholar] [CrossRef]
- Mead, C. Anlaog VLSI and Neural Systems, 1st ed.; Addison-Wesley: Reading, PA, USA, 1989. [Google Scholar]
- Merolla, P.; Arthur, J.; Akopyan, F.; Imam, N.; Manohar, R.; Modha, D.S. A Digital Neurosynaptic Core Using Embedded Crossbar Memory with 45pJ per Spike in 45 nm. In Proceedings of the IEEE Custom Integrated Circuits Conference, San Jose, CA, USA, 19–21 September 2011; pp. 1–4. [Google Scholar] [CrossRef]
- Islas, C.; Padilla, P.; Prado, M.A. Information Processing in the Brain as Optimal Entropy Transport: A Theoretical Approach. Entropy 2020, 22, 1231. [Google Scholar] [CrossRef]
- Pregowska, A.; Kaplan, E.; Szczepanski, J. How Far can Neural Correlations Reduce Uncertainty? Comparison of Information Transmission Rates for Markov and Bernoulli Processes. Int. J. Neural Syst. 2019, 29, 1950003. [Google Scholar] [CrossRef] [Green Version]
- Crumiller, M.; Knight, B.; Kaplan, E. The Measurement of Information Transmitted by a Neural Population: Promises and Challenges. Entropy 2013, 15, 3507–3527. [Google Scholar] [CrossRef] [Green Version]
- Frenkel, C.; Lefebvre, M.; Legat, J.D.; Bol, D. A 0.086-mm2 12.7-pJ/SOP 64k-Synapse 256-Neuron Online-Learning Digital Spiking Neuromorphic Processor in 28-nm CMOS. IEEE Trans. Biomed. Circuits Syst. 2019, 13, 145–158. [Google Scholar] [CrossRef] [Green Version]
- Miyashita, D.; Kousai, S.; Suzuki, T.; Deguchi, J. Time-Domain Neural Network: A 48.5 TSOp/s/W neuromorphic chip optimized for deep learning and CMOS technology. In Proceedings of the IEEE Asian SSC Conference, Toyama, Japan, 7–9 November 2016; pp. 25–28. [Google Scholar] [CrossRef]
- Harris, J.J.; Jolivet, R.; Engl, E.; Attwell, D. Energy-Efficient Information Transfer by Visual Pathway Synapses. Curr. Biol. 2015, 25, 3151–3160. [Google Scholar] [CrossRef] [Green Version]
- Aamir, S.A.; Stradmann, Y.; Müller, P.; Pehle, C.; Hartel, A.; Grübl, A.; Schemmel, J.; Meier, K. An Accelerated LIF Neuronal Network Array for a Large-Scale Mixed-Signal Neuromorphic Architecture. IEEE Trans. Circuits Syst. I Regul. Pap. 2018, 65, 4299–4312. [Google Scholar] [CrossRef] [Green Version]
- Indiveri, G.; Horiuchi, T. Frontiers in Neuromorphic Engineering. Front. Neurosci. 2011, 5, 118. [Google Scholar] [CrossRef] [Green Version]
- Ebong, I.E.; Mazumder, P. CMOS and memristor-based neural network design for position detection. Proc. IEEE 2012, 100, 2050–2060. [Google Scholar] [CrossRef]
- Chua, L. Memristor-the missing circuit element. IEEE Trans. Circuit Theory 1971, 18, 507–519. [Google Scholar] [CrossRef]
- Li, C.; Belkin, D.; Li, Y.; Yan, P.; Hu, M.; Ge, N.; Jiang, H.; Montgomery, E.; Lin, P.; Wang, Z.; et al. Efficient and self-adaptive in-situ learning in multilayer memristor neural networks. Nat. Commun. 2018, 9, 2385. [Google Scholar] [CrossRef] [Green Version]
- Benjamin, B.V.; Gao, P.; McQuinn, E.; Choudhary, S.; Chandrasekaran, A.R.; Bussat, J.M.; Alvarez-Icaza, R.; Arthur, J.V.; Merolla, P.A.; Boahen, K. Neurogrid: A Mixed-Analog-Digital Multichip System for Large-Scale Neural Simulations. Proc. IEEE 2014, 102, 699–716. [Google Scholar] [CrossRef]
- Park, D.; Lee, J.; Asghar, M.S.; Hong, J.; Arslan, S.; Kim, H. Compact spiking neural network chip design for image classification. J. RICIC 2020, 28, 21–27. [Google Scholar]
- Camuñas-Mesa, L.A.; Linares-Barranco, B.; Serrano-Gotarredona, T. Neuromorphic Spiking Neural Networks and Their Memristor-CMOS Hardware Implementations. Materials 2019, 12, 2745. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ankit, A.; Sengupta, A.; Panda, P.; Roy, K. RESPARC: A Reconfigurable and Energy-Efficient Architecture with Memristive Crossbars for Deep SNN. In Proceedings of the 54th ACM/EDAC/IEEE Design Automation Conference, Austin, TX, USA, 18–22 June 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Jolivet, R.; Rauch, A.; Lüscher, H.R.; Gerstner, W. Integrate-and-fire models with adaptation are good enough: Predicting spike times under random current injection. In Proceedings of the NIPS 18, Vancouver, BC, Canada, 5–8 December 2005; pp. 595–602. [Google Scholar]
- Gerstner, W.; Kistler, W.M.; Naud, R.; Paninski, L. Neuronal Dynamics; Cambridge University Press: Cambridge, UK, 2014. [Google Scholar] [CrossRef]
- Izhikevich, E.M. Simple model of spiking neurons. IEEE Trans. Neural Netw. 2003, 14, 1569–1572. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hodgkin, A.L.; Huxley, A.F. A quantitative description of membrane current and its application to conduction and excitation in nerve. Bull. Math. Biol. 1990, 52, 25–71. [Google Scholar] [CrossRef]
- Diehl, P.U.; Cook, M. Unsupervised learning of digit recognition using spike-timing-dependent plasticity. Front. Comput. Neurosci. 2015, 9, 99. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kim, S.; Choi, B.; Lim, M.; Yoon, J.; Lee, J.; Kim, H.D.; Choi, S.J. Pattern recognition using carbon nanotube synaptic transistors with an adjustable weight update protocol. ACS Nano 2017, 11, 2814–2822. [Google Scholar] [CrossRef]
- Merrikh-Bayat, F.; Guo, X.; Klachko, M.; Prezioso, M.; Likharev, K.K.; Strukov, D.B. High-performance mixed-signal neurocomputing with nanoscale floating-gate memory cell arrays. IEEE Trans. Neural Netw. Learn. Syst. 2018, 29, 4782–4790. [Google Scholar] [CrossRef]
- Woo, J.; Padovani, A.; Moon, K.; Kwak, M.; Larcher, L.; Hwang, H. Linking conductive filament properties and evolution to synaptic behavior of RRAM devices for neuromorphic applications. IEEE Electron. Device Lett. 2017, 38, 1220–1223. [Google Scholar] [CrossRef]
- Kim, H.; Hwang, S.; Park, J.; Yun, S.; Lee, J.H.; Park, B.G. Spiking Neural Network Using Synaptic Transistors and Neuron Circuits for Pattern Recognition with Noisy Images. IEEE Electron. Device Lett. 2018, 39, 630–633. [Google Scholar] [CrossRef]
- O’Connor, P.; Welling, M. Deep Spiking Networks. Available online: https://arxiv.org/abs/1602.08323 (accessed on 20 January 2021).
- Wu, Y.; Deng, L.; Li, G.; Zhu, J.; Shi, L. Spatio-Temporal Backpropagation for Training High-Performance Spiking Neural Networks. Front. Neurosci. 2018, 12, 331. [Google Scholar] [CrossRef]
- Al-Hamid, A.A.; Kim, H. Optimization of Spiking Neural Networks Based on Binary Streamed Rate Coding. Electronics 2020, 9, 1599. [Google Scholar] [CrossRef]
- Asghar, M.S.; Arslan, S.; Kim, H. Low Power Spiking Neural Network Circuit with Compact Synapse and Neuron Cells. In Proceedings of the 2020 International SoC Design Conference, Yeosu, Korea, 21–24 October 2020; pp. 157–158. [Google Scholar] [CrossRef]
- Dutta, S.; Kumar, V.; Shukla, A.; Mohapatra, N.R.; Ganguly, U. Leaky Integrate and Fire Neuron by Charge-Discharge Dynamics in Floating-Body MOSFET. Sci. Rep. 2017, 7, 8257. [Google Scholar] [CrossRef] [Green Version]
- Indiveri, G.; Chicca, E.; Douglas, R. A VLSI Array of Low-Power Spiking Neurons and Bistable Synapses with Spike-Timing Dependent Plasticity. IEEE Trans. Neural Netw. 2006, 17, 211–221. [Google Scholar] [CrossRef] [Green Version]
- Tang, H.; Kim, H.; Cho, D.; Park, J. Spike Counts Based Low Complexity Learning with Binary Synapse. In Proceedings of the 2018 International Joint Conference on Neural Networks, Rio de Janeiro, Brazil, 8–13 July 2018; pp. 1–8. [Google Scholar] [CrossRef]


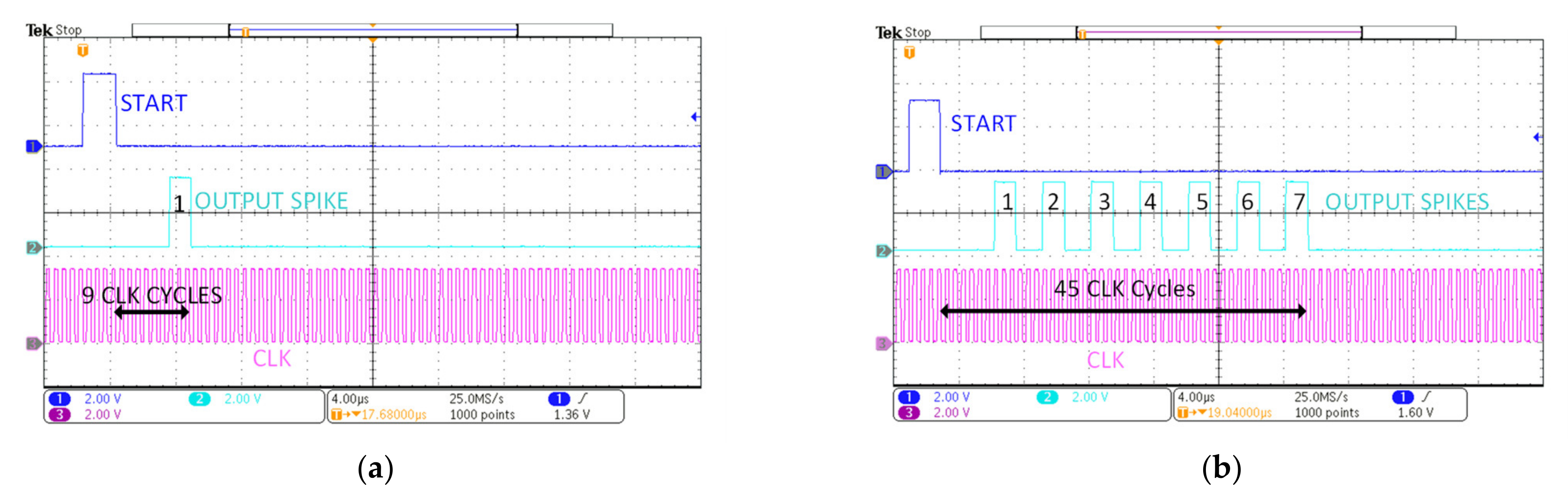
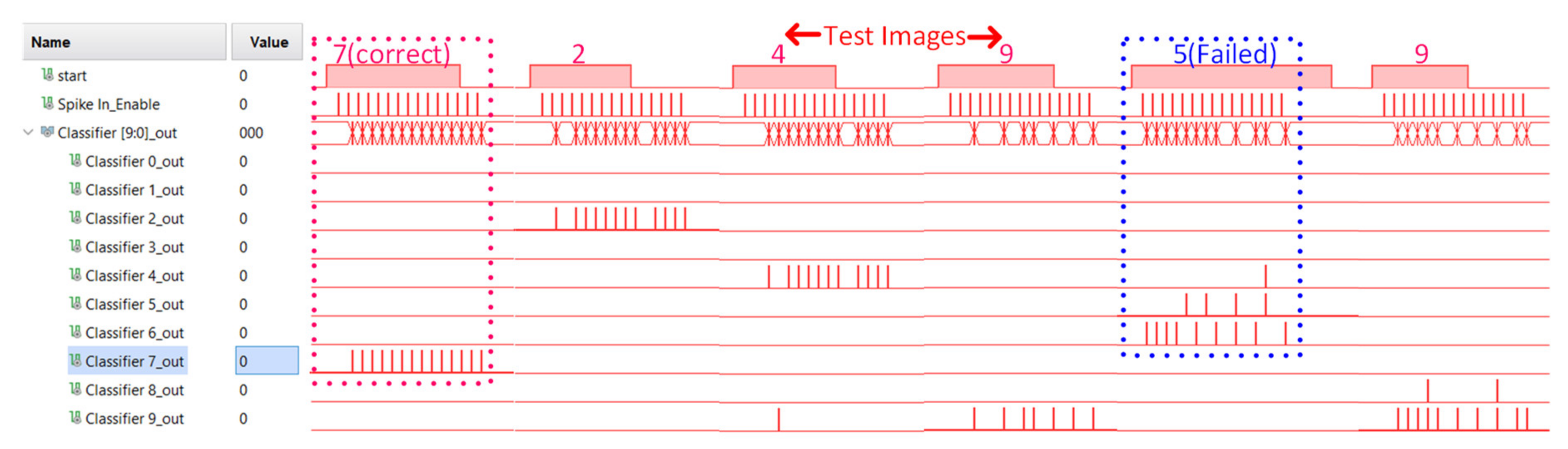
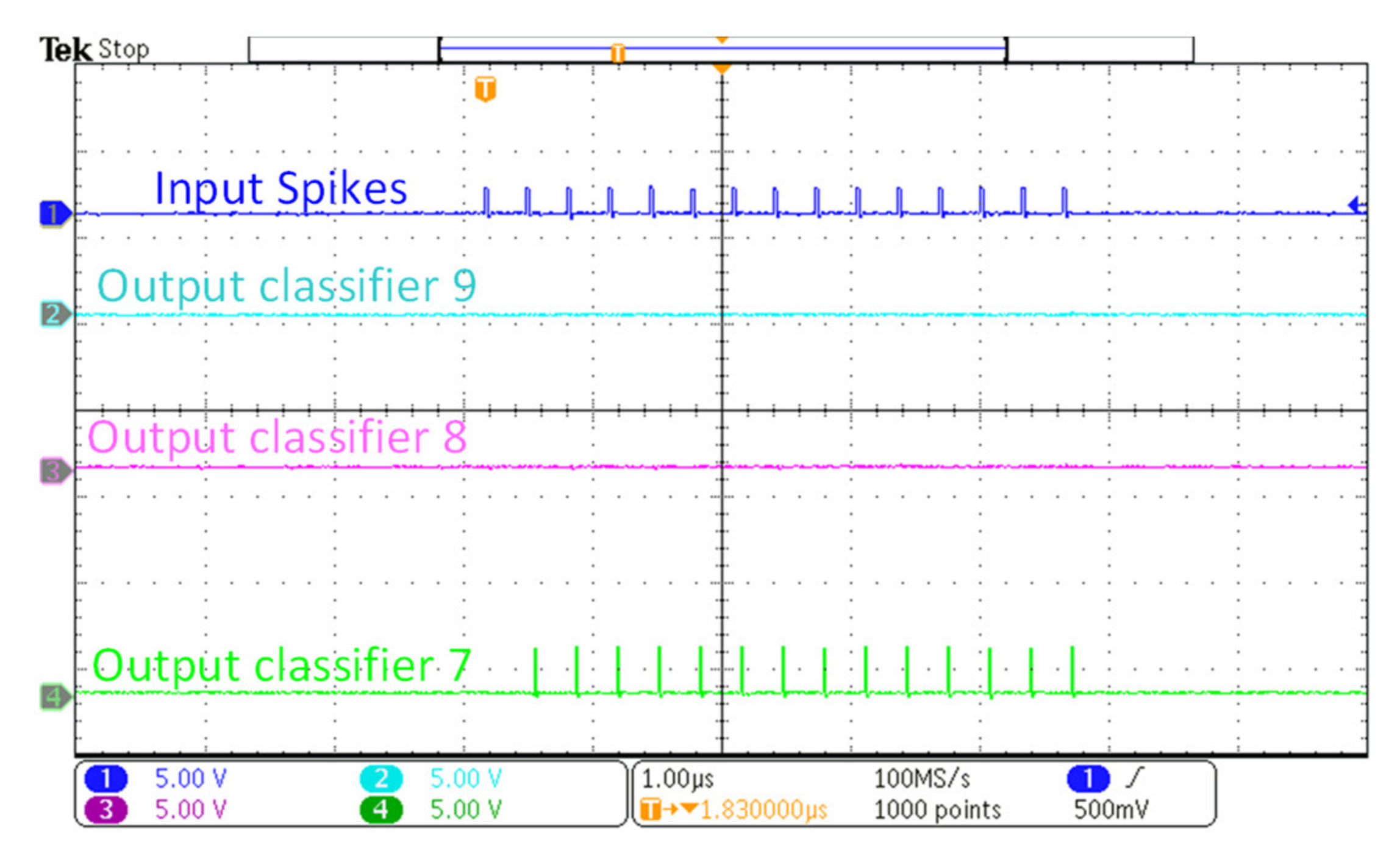
| Parameters | Values |
|---|---|
| Neuron cell Area | 2022.72 μm2 |
| Neuron cell Power Consumption | 25 μW |
| Resting potential | 500 mV |
| Threshold Voltage | 1.4 V |
| Resolution | 4-bit |
| VDD/VSS | 1.8 V/0 V |
| Membrane Capacitance | 35 fF |
| Off-chip Bias voltages | 8 |
| SNN Chip | Area | Power |
|---|---|---|
| Proposed Analog SNN Chip | 3.6 mm2 | 1.06 mW |
| Fully Digital SNN Chip | 3.5 mm2 | 21.2 mW |
| Parameters | [26] | [21] | [5] | [44] | This Work |
|---|---|---|---|---|---|
| CMOS tech. [nm] | 180 | 65 | 130 | 800 | 180 |
| Architecture | Analog | Analog | Mixed-Mode | Mixed-Mode | Analog |
| Classifier type | SNN | SNN | MLP/RBFN | SNN | SNN |
| Neuron Model | Quad. I & F | LIF | Current mode | LIF | LIF |
| Chip Area [mm2] | 168 | 3.6 | 0.140 | 1.6 | 3.6 |
| Power [mW] | 3100 | 48.62 | 2.20 | 40 μ 1 | 1.06 |
| Energy/Spike [pJ] | 941 2 | 790 | - | 900 | 900 |
| Accuracy (%) | - | - | 92 | - | 94.60 |
| Complexity [Total # of weights] | 256 K | 1024 | 750 | 256 | 3311 |
| Area η [Complexity/Area] | 1523 | 284.5 | 5360 | 160 | 920 |
| Power η [Complexity/power] | 82.5 | 21.06 | 341 | - | 3123 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Asghar, M.S.; Arslan, S.; Kim, H. A Low-Power Spiking Neural Network Chip Based on a Compact LIF Neuron and Binary Exponential Charge Injector Synapse Circuits. Sensors 2021, 21, 4462. https://doi.org/10.3390/s21134462
Asghar MS, Arslan S, Kim H. A Low-Power Spiking Neural Network Chip Based on a Compact LIF Neuron and Binary Exponential Charge Injector Synapse Circuits. Sensors. 2021; 21(13):4462. https://doi.org/10.3390/s21134462
Chicago/Turabian StyleAsghar, Malik Summair, Saad Arslan, and Hyungwon Kim. 2021. "A Low-Power Spiking Neural Network Chip Based on a Compact LIF Neuron and Binary Exponential Charge Injector Synapse Circuits" Sensors 21, no. 13: 4462. https://doi.org/10.3390/s21134462
APA StyleAsghar, M. S., Arslan, S., & Kim, H. (2021). A Low-Power Spiking Neural Network Chip Based on a Compact LIF Neuron and Binary Exponential Charge Injector Synapse Circuits. Sensors, 21(13), 4462. https://doi.org/10.3390/s21134462







