Design of a Capacitance-to-Digital Converter Based on Iterative Delay-Chain Discharge in 180 nm CMOS Technology
Abstract
:1. Introduction
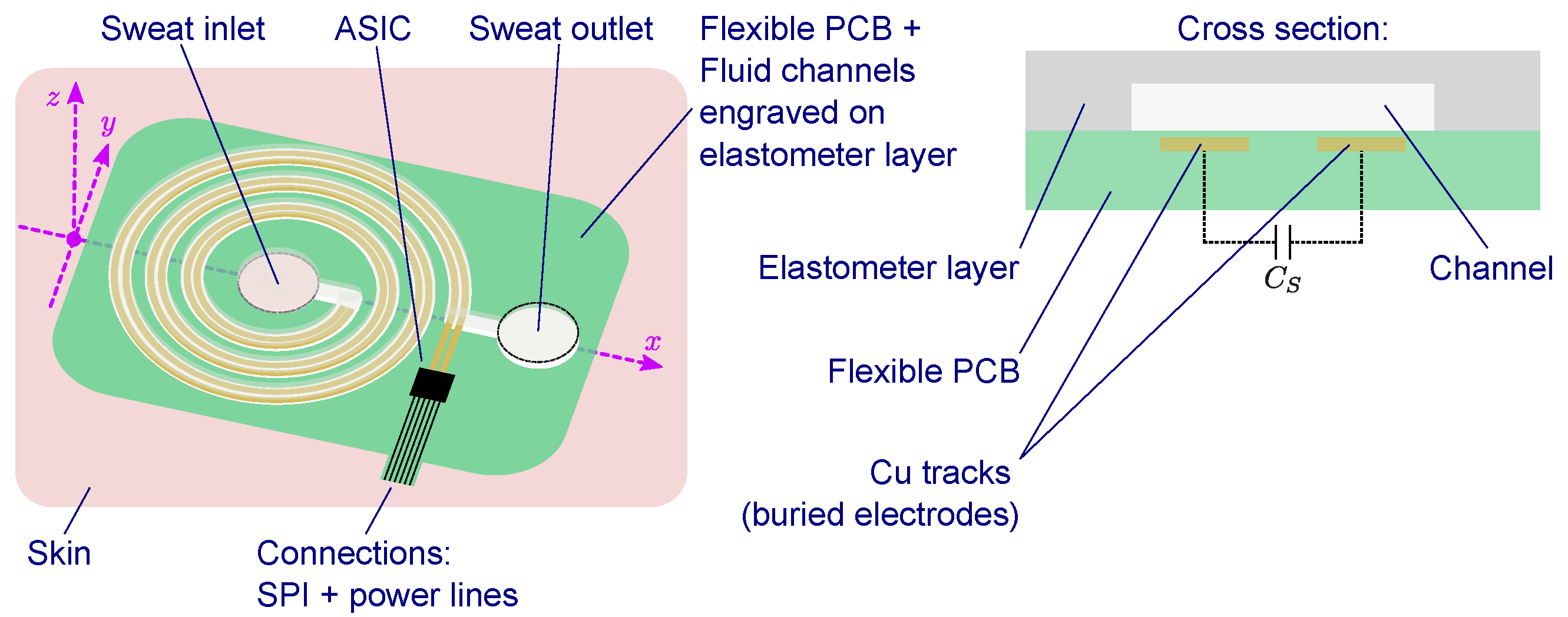
2. Materials and Methods
3. Results
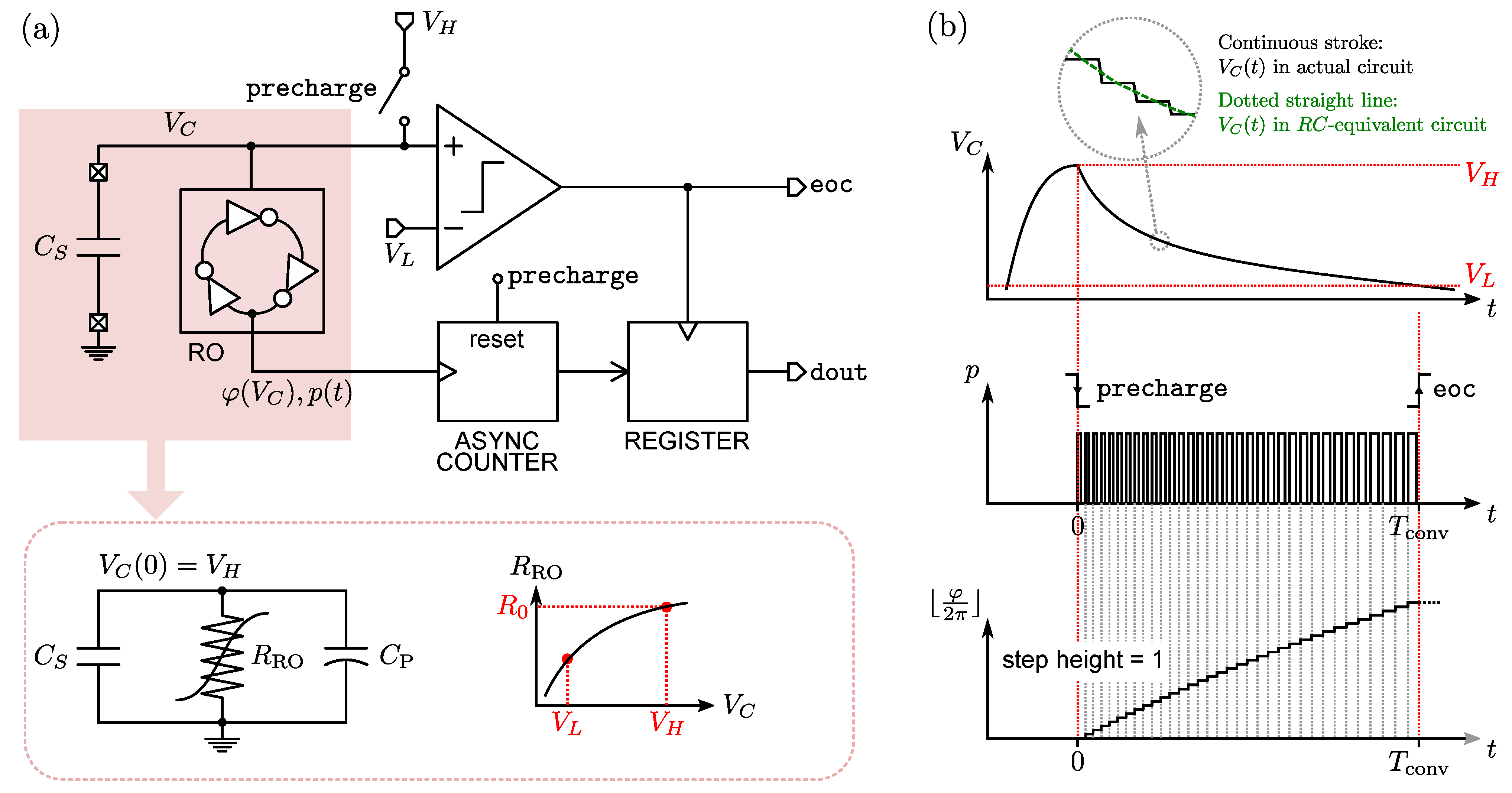
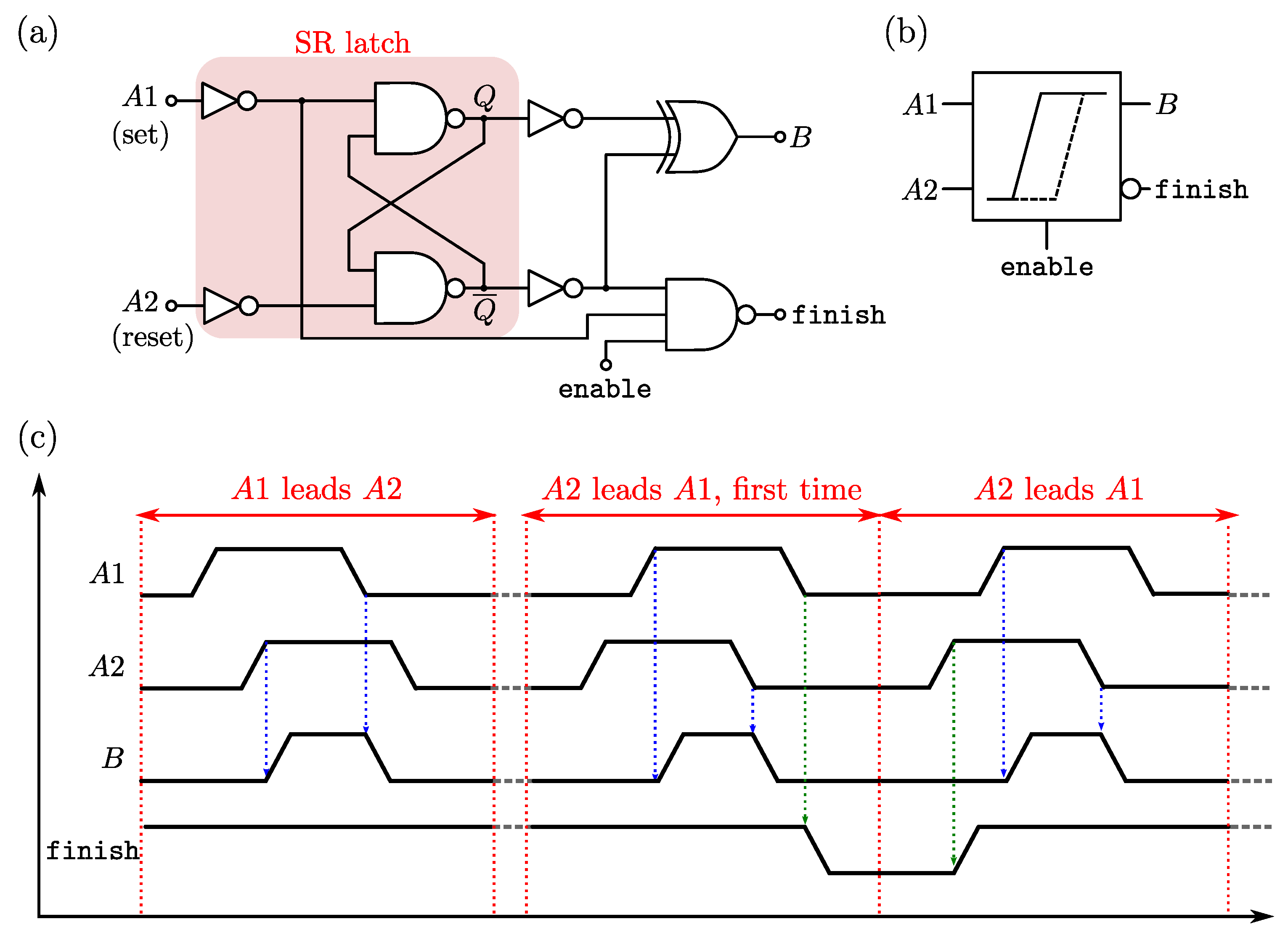
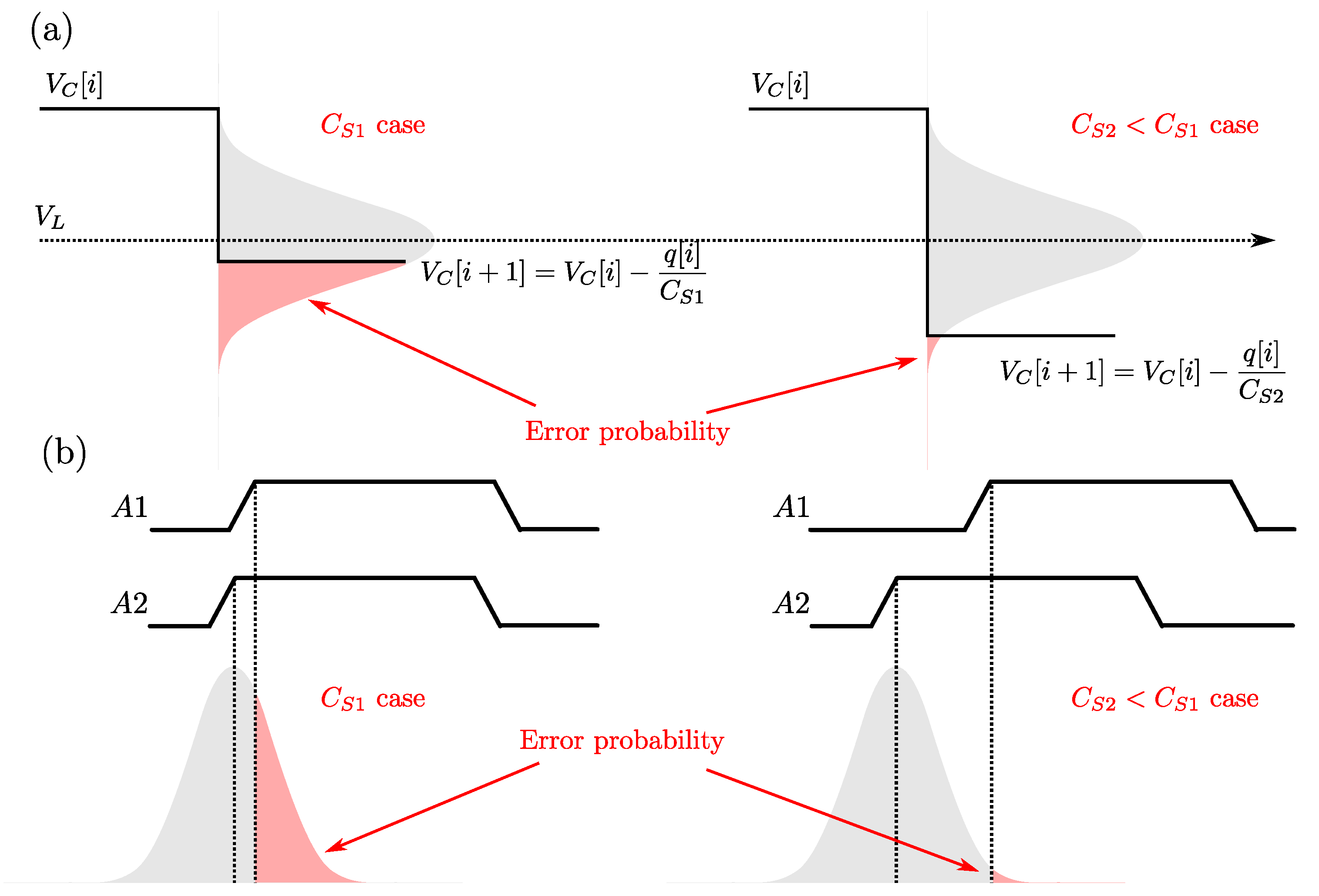
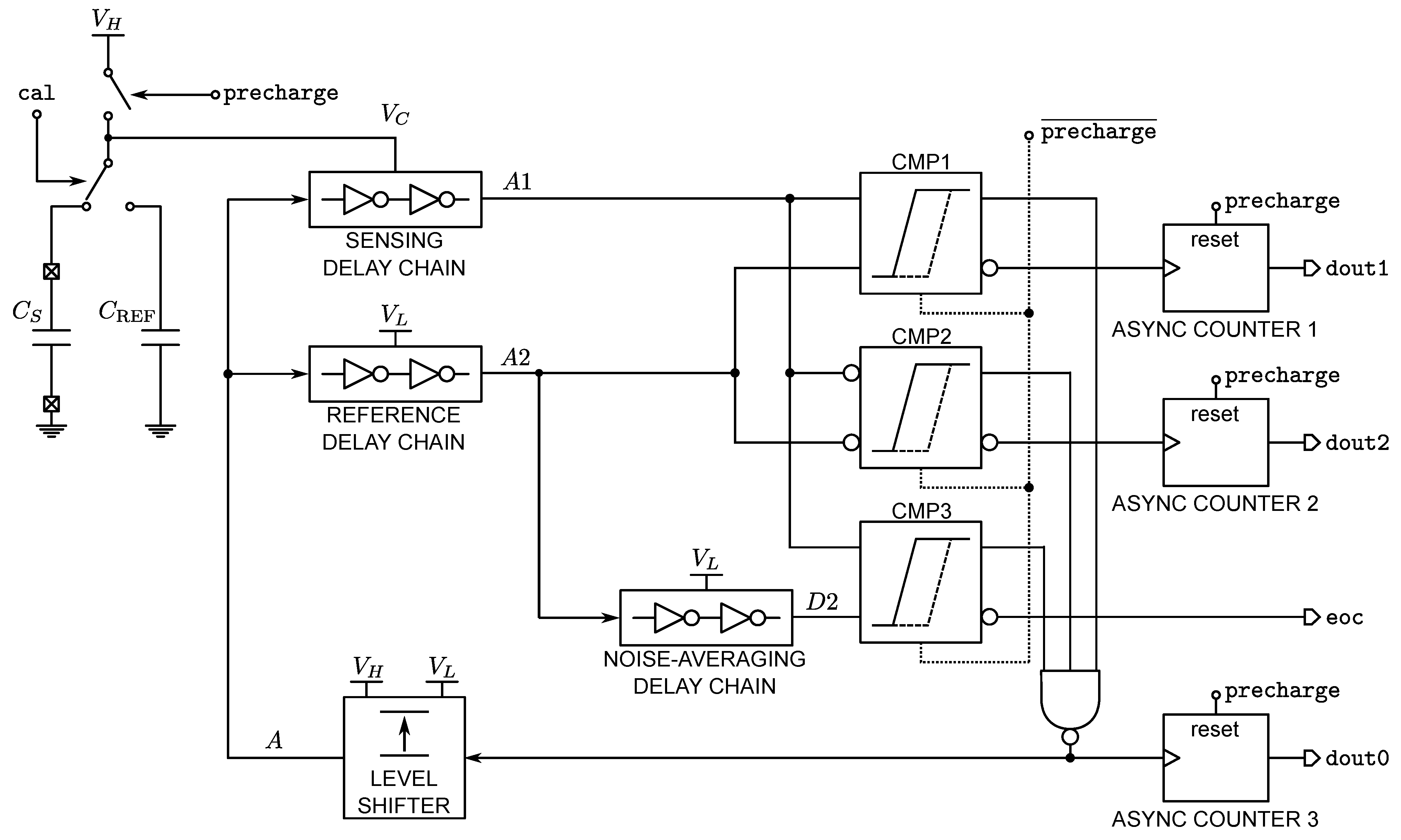
3.1. Principle of Operation
- 1.
- is increased by increasing the term, which is related to both the aspect ratio and the area of the digital ports and the number of delay stages of the inverter-based RO. The short-circuit current, which contributes to , is reduced by increasing L; however, the short-circuit time interval is minimized by reducing the total area. So for a given gate area , it is convenient to reduce the ratio. Clearly, incrementing the number of delay stages increases the discharge rate in each cycle, thus reducing .
- 2.
- is increased by increasing , which can be attained for minimum-sized transistors, i.e., and . The parameter depends on the chosen linearisation point, being strongly dependent on the - range. However, as it will be clear in the following discussion, the fully-digital implementation of the CDC rules out this parameter from the design space. As in point 1, reducing the number of delay stages is beneficial to increase .
- 3.
- is increased by maximizing and minimizing as can be seen in the logarithm argument and in the difference term. is limited by the available supply voltage value, while is limited by the minimum viable supply voltage for the correct operation of the digital gates.
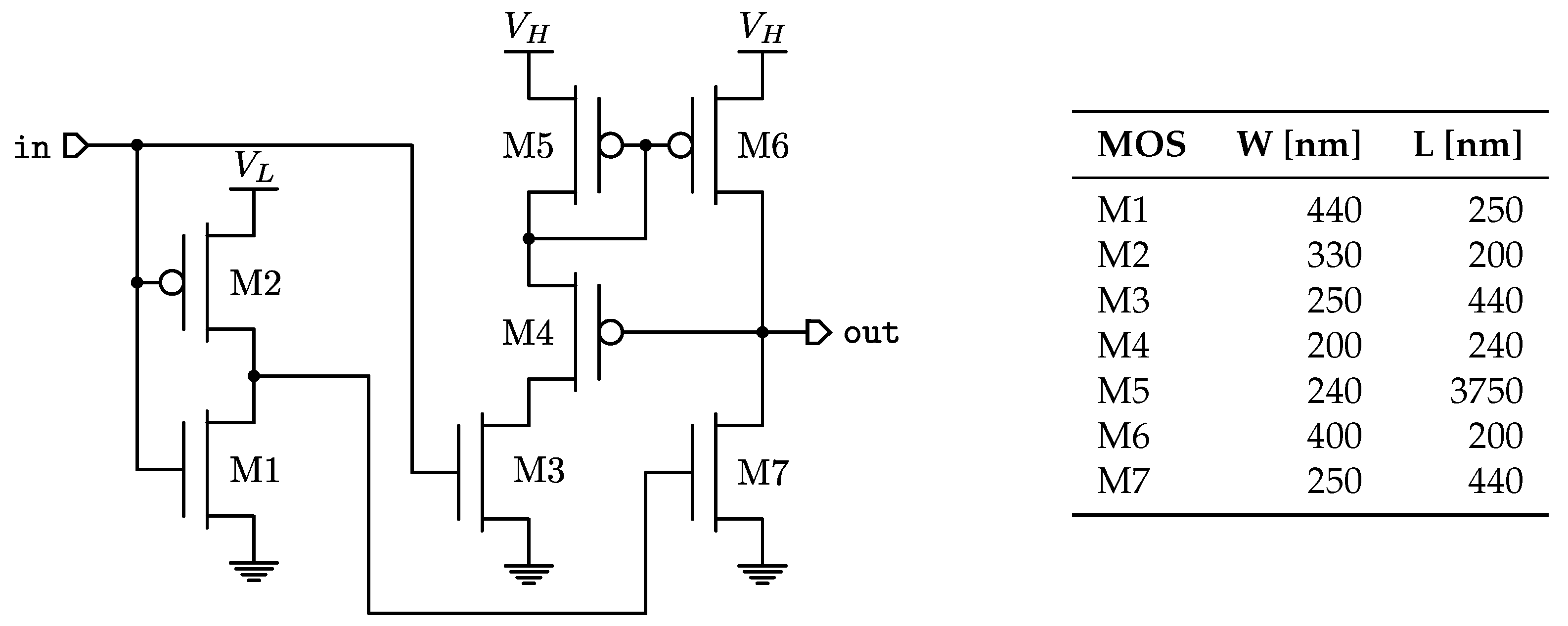
3.2. 180 nm-CMOS Implementation
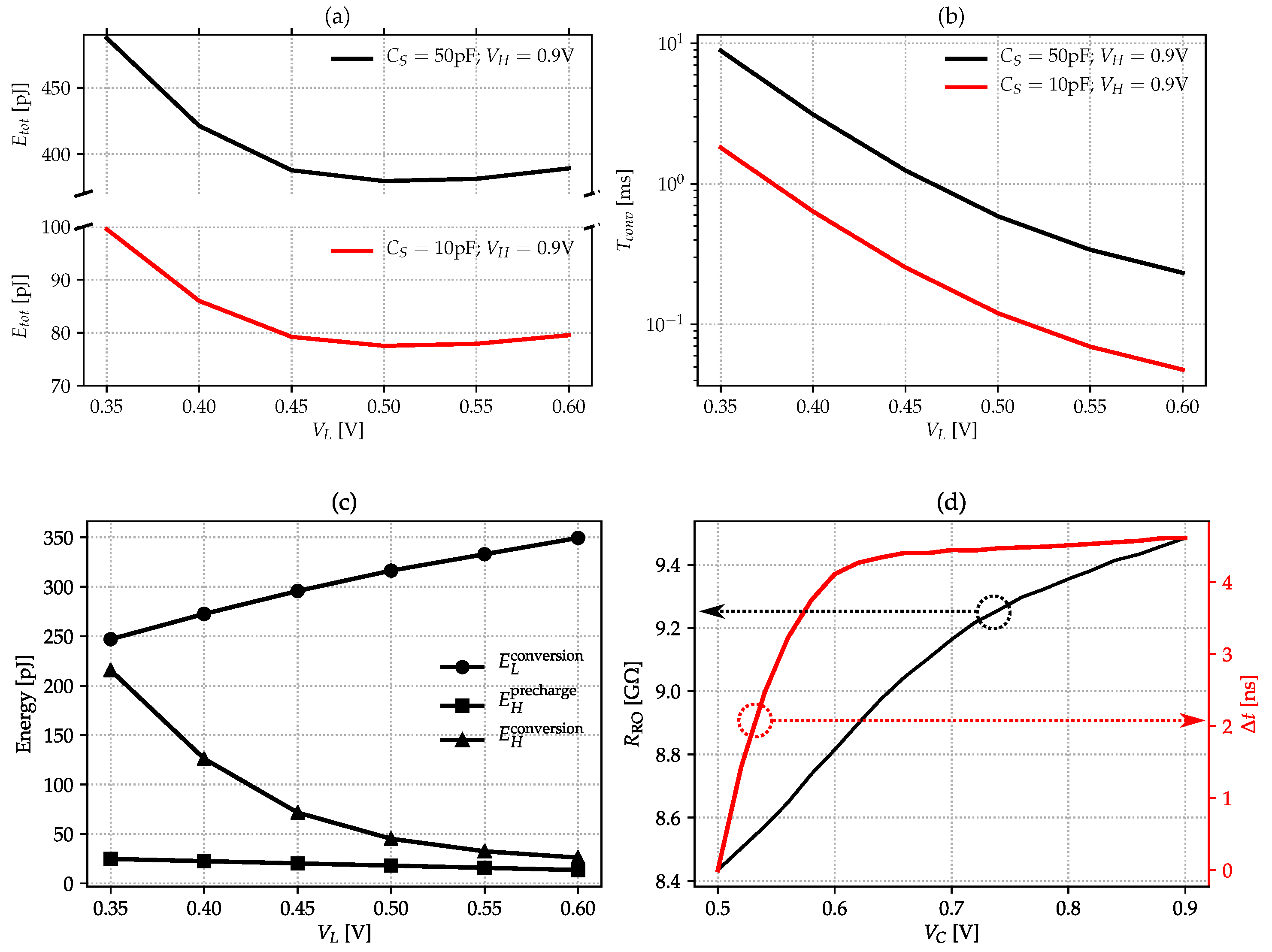
3.3. Prototype Performance
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| CDC | Capacitance-to-Digital Converter |
| PM | Phase/Pulse Modulation |
| M | Modulation |
| CSAR | Capacitive Successive Approximation Register |
| DR | Dynamic Range |
| IDCD | Iterative Delay-Chain Discharge |
| FPCB | Flexible Printed-Circuit Board |
| PDMS | Polydimethylsiloxane |
| ASIC | Application-Specific Integrated Circuit |
| SPI | Serial Peripheral Interface |
| CMOS | Complementary Metal–Oxide–Semiconductor |
| MEMS | Micro-Electro-Mechanical Systems |
| RO | Ring Oscillator |
| VCO | Voltage-Controlled Oscillator |
| MOM | Metal–Oxide–Metal |
| MIM | Metal–Insulator–Metal |
| SNR | Signal-to-Noise Ratio |
| ENOB | Effective Number Of Bits |
| DNL | Differential Non-Linearity |
| LSB | Least-Significant Bit |
| FoM | Figure of Merit |
References
- Baxter Larry, K. Capactive Sensors, Design and Applications; John Wiley & Sons: Hoboken, NJ, USA, 1996. [Google Scholar]
- Ebrahim Ghafar-Zadeh, S.F. Emerging CMOS Capacitive Sensors for Biomedical Applications: A Multidisciplinary Approach; The Institution of Engineering and Technology: London, UK, 2021. [Google Scholar]
- Tan, Z.; Shalmany, S.H.; Meijer, G.C.M.; Pertijs, M.A.P. An Energy-Efficient 15-Bit Capacitive-Sensor Interface Based on Period Modulation. IEEE J. Solid-State Circuits 2012, 47, 1703–1711. [Google Scholar] [CrossRef]
- Nizza, N.; Dei, M.; Butti, F.; Bruschi, P. A Low-Power Interface for Capacitive Sensors with PWM Output and Intrinsic Low Pass Characteristic. IEEE Trans. Circuits Syst. Regul. Pap. 2013, 60, 1419–1431. [Google Scholar] [CrossRef]
- Mohan, R.; Zaliasl, S.; Gielen, G.G.E.; Hoof, C.V.; Yazicioglu, R.F.; Helleputte, N.V. A 0.6-V, 0.015-mm2, Time-Based ECG Readout for Ambulatory Applications in 40-nm CMOS. IEEE J. Solid-State Circuits 2017, 52, 298–308. [Google Scholar] [CrossRef]
- Yang, R.; Pertijs, M.A.P.; Nihtianov, S. A Precision Capacitance-to-Digital Converter with 16.7-bit ENOB and 7.5-ppm/°C Thermal Drift. IEEE J. Solid-State Circuits 2017, 52, 3018–3031. [Google Scholar] [CrossRef]
- Woo, K.C.; Yang, B.D. 0.3-V RC-to-Digital Converter Using a Negative Charge-Pump Switch. IEEE Trans. Circuits Syst. II Express Briefs 2020, 67, 245–249. [Google Scholar] [CrossRef]
- Zhang, T.T.; Law, M.K.; Mak, P.I.; Vai, M.I.; Martins, R.P. Nano-Watt Class Energy-Efficient Capacitive Sensor Interface with On-Chip Temperature Drift Compensation. IEEE Sens. J. 2018, 18, 2870–2882. [Google Scholar] [CrossRef]
- Rogi, C.; Buffa, C.; Milleri, N.D.; Gaggl, R.; Prefasi, E. A Fully-Differential Switched-Capacitor Dual-Slope Capacitance-To-Digital Converter (CDC) for a Capacitive Pressure Sensor. Sensors 2019, 19, 3673. [Google Scholar] [CrossRef] [Green Version]
- Tang, X.; Li, S.; Yang, X.; Shen, L.; Zhao, W.; Williams, R.P.; Liu, J.; Tan, Z.; Hall, N.A.; Pan, D.Z.; et al. An Energy-Efficient Time-Domain Incremental Zoom Capacitance-to-Digital Converter. IEEE J. Solid-State Circuits 2020, 55, 3064–3075. [Google Scholar] [CrossRef]
- Ghanbari, M.M.; Tsai, J.M.; Nirmalathas, A.; Muller, R.; Gambini, S. An Energy-Efficient Miniaturized Intracranial Pressure Monitoring System. IEEE J. Solid-State Circuits 2017, 52, 720–734. [Google Scholar] [CrossRef]
- Alhoshany, A.; Salama, K.N. A Precision, Energy-Efficient, Oversampling, Noise-Shaping Differential SAR Capacitance-to-Digital Converter. IEEE Trans. Instrum. Meas. 2019, 68, 392–401. [Google Scholar] [CrossRef]
- Xin, H.; Andraud, M.; Baltus, P.; Cantatore, E.; Harpe, P. A 0.1-nW−1-μW Energy-Efficient All-Dynamic Versatile Capacitance-to-Digital Converter. IEEE J. Solid-State Circuits 2019, 54, 1841–1851. [Google Scholar] [CrossRef]
- Hussaini, S.; Jiang, H.; Walsh, P.; MacSweeney, D.; Makinwa, K.A.A. A 15-nW per Sensor Interference-Immune Readout IC for Capacitive Touch Sensors. IEEE J. Solid-State Circuits 2019, 54, 1874–1882. [Google Scholar] [CrossRef] [Green Version]
- Narasimman, N.; Nag, D.; Chai, K.T.C.; Kim, T.T.H. A Capacitance to Digital Converter Using Continuous Time ΔΣ Modulator for Microphone-Based Auscultation. IEEE Sens. J. 2021, 21, 13373–13383. [Google Scholar] [CrossRef]
- Tan, Z.; Jiang, H.; Zhang, H.; Tang, X.; Xin, H.; Nihtianov, S. Power-Efficiency Evolution of Capacitive Sensor Interfaces. IEEE Sens. J. 2021, 21, 12457–12468. [Google Scholar] [CrossRef]
- Jung, W.; Jeong, S.; Oh, S.; Sylvester, D.; Blaauw, D. 27.6 A 0.7 pF-to-10 nF fully digital capacitance-to-digital converter using iterative delay-chain discharge. In Proceedings of the 2015 IEEE International Solid-State Circuits Conference-(ISSCC) Digest of Technical Papers, San Francisco, CA, USA, 22–26 February 2015. [Google Scholar] [CrossRef] [Green Version]
- Seshadri, D.R.; Drummond, C.; Craker, J.; Rowbottom, J.R.; Voos, J.E. Wearable Devices for Sports: New Integrated Technologies Allow Coaches, Physicians, and Trainers to Better Understand the Physical Demands of Athletes in Real time. IEEE Pulse 2017, 8, 38–43. [Google Scholar] [CrossRef] [PubMed]
- Dei, M.; Aymerich, J.; Piotto, M.; Bruschi, P.; del Campo, F.; Serra-Graells, F. CMOS Interfaces for Internet-of-Wearables Electrochemical Sensors: Trends and Challenges. Electronics 2019, 8, 150. [Google Scholar] [CrossRef] [Green Version]
- Sharma, A.; Al-Dala’in, T.; Alsadoon, G.; Alwan, A. Use of Wearable Technologies for Analysis of Activity recognition for sports. In Proceedings of the 2020 5th International Conference on Innovative Technologies in Intelligent Systems and Industrial Applications (CITISIA), Sydney, Australia, 23–26 September 2020. [Google Scholar] [CrossRef]
- Nithya, N.; Nallavan, G. Role of Wearables in Sports based on Activity recognition and biometric parameters: A Survey. In Proceedings of the 2021 International Conference on Artificial Intelligence and Smart Systems (ICAIS), Tamilnadu, India, 25–27 March 2021. [Google Scholar] [CrossRef]
- Dobrzynska, J.A.; Gijs, M.A.M. Polymer-based flexible capacitive sensor for three-axial force measurements. J. Micromech. Microeng. 2012, 23, 015009. [Google Scholar] [CrossRef]
- Anandan, N.; George, B. A Wide-Range Capacitive Sensor for Linear and Angular Displacement Measurement. IEEE Trans. Ind. Electron. 2017, 64, 5728–5737. [Google Scholar] [CrossRef]
- Xu, Y.; Shang, D.; Xia, F.; Yakovlev, A. A smart all-digital charge to digital converter. In Proceedings of the 2016 IEEE International Conference on Electronics, Circuits and Systems (ICECS), Monte Carlo, Monaco, 11–14 December 2016. [Google Scholar] [CrossRef] [Green Version]
- Razavi, B. A study of phase noise in CMOS oscillators. IEEE J. Solid-State Circuits 1996, 31, 331–343. [Google Scholar] [CrossRef] [Green Version]
- Cardes, F.; Quintero, A.; Gutierrez, E.; Buffa, C.; Wiesbauer, A.; Hernandez, L. SNDR Limits of Oscillator-Based Sensor Readout Circuits. Sensors 2018, 18, 445. [Google Scholar] [CrossRef] [Green Version]
- Pepe, F.; Andreani, P. An Accurate Analysis of Phase Noise in CMOS Ring Oscillators. IEEE Trans. Circuits Syst. II Express Briefs 2019, 66, 1292–1296. [Google Scholar] [CrossRef]
- Lutkemeier, S.; Ruckert, U. A Subthreshold to Above-Threshold Level Shifter Comprising a Wilson Current Mirror. IEEE Trans. Circuits Syst. II Express Briefs 2010, 57, 721–724. [Google Scholar] [CrossRef]
- Ishihara, F.; Sheikh, F.; Nikolic, B. Level conversion for dual-supply systems. IEEE Trans. Very Large Scale Integr. (VLSI) Syst. 2004, 12, 185–195. [Google Scholar] [CrossRef]
- Chavan, A.; MacDonald, E. Ultra Low Voltage Level Shifters to Interface Sub and Super Threshold Reconfigurable Logic Cells. IEEE Aerosp. Conf. Proc. 2008. [Google Scholar] [CrossRef]
- Kumar, M.; Arya, S.K.; Pandey, S. Level Shifter Design for Low Power Applications. Int. J. Comput. Sci. Inf. Technol. 2010, 2, 124–132. [Google Scholar] [CrossRef]
- Lanuzza, M.; Corsonello, P.; Perri, S. Low-Power Level Shifter for Multi-Supply Voltage Designs. IEEE Trans. Circuits Syst. II Express Briefs 2012, 59, 922–926. [Google Scholar] [CrossRef]



| Process Corner | Uncalibrated [%] | Calibrated [%] | Offset Code |
|---|---|---|---|
| Fast NMOS, Fast PMOS | 59 | ||
| Slow NMOS, Slow PMOS | 67 | ||
| Fast NMOS, Slow PMOS | 62 | ||
| Slow NMOS, Fast PMOS | 62 |
| ISSCC’15 [17] | This Work | |
|---|---|---|
| Technology | 40 nm | 180 nm |
| , | 1.0 V, 0.45 V | 0.9 V, 0.5 V |
| Input range | 0.7 pF to 10 nF | 255.6 fF to 250 pF |
| Linearity error | 1090 ppm | 15.26 ppm |
| Conversion time | 19.06 µs at pF | 132.43 µs at pF 2.93 ms at pF |
| Conversion energy | 35.1 pJ at pF | 85.2 pJ at pF 1884.0 pJ at pF |
| SNR | 53.0 dB | 63.9 dB |
| FoM (Equation (21)) | 141.0 fJ/conversion-step | 99.6 fJ/conversion-step |
| FoM (Equation (22)) | 96.5 fJ/conversion-step | 1.47 pJ/conversion-step |
| Temperature sensitivity | 15.5 ppm/C | 81.9 ppm/C |
| Core size | 42 µm × 40 µm | 160 µm × 120 µm including |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cicalini, M.; Piotto, M.; Bruschi, P.; Dei, M. Design of a Capacitance-to-Digital Converter Based on Iterative Delay-Chain Discharge in 180 nm CMOS Technology. Sensors 2022, 22, 121. https://doi.org/10.3390/s22010121
Cicalini M, Piotto M, Bruschi P, Dei M. Design of a Capacitance-to-Digital Converter Based on Iterative Delay-Chain Discharge in 180 nm CMOS Technology. Sensors. 2022; 22(1):121. https://doi.org/10.3390/s22010121
Chicago/Turabian StyleCicalini, Mattia, Massimo Piotto, Paolo Bruschi, and Michele Dei. 2022. "Design of a Capacitance-to-Digital Converter Based on Iterative Delay-Chain Discharge in 180 nm CMOS Technology" Sensors 22, no. 1: 121. https://doi.org/10.3390/s22010121
APA StyleCicalini, M., Piotto, M., Bruschi, P., & Dei, M. (2022). Design of a Capacitance-to-Digital Converter Based on Iterative Delay-Chain Discharge in 180 nm CMOS Technology. Sensors, 22(1), 121. https://doi.org/10.3390/s22010121








