Monitoring of a Highly Flexible Aircraft Model Wing Using Time-Expanded Phase-Sensitive OTDR
Abstract
1. Introduction
2. Materials and Methods
2.1. Principle of Operation of the TE-ΦOTDR System
2.2. Experimental Setup
2.3. Specimen Description
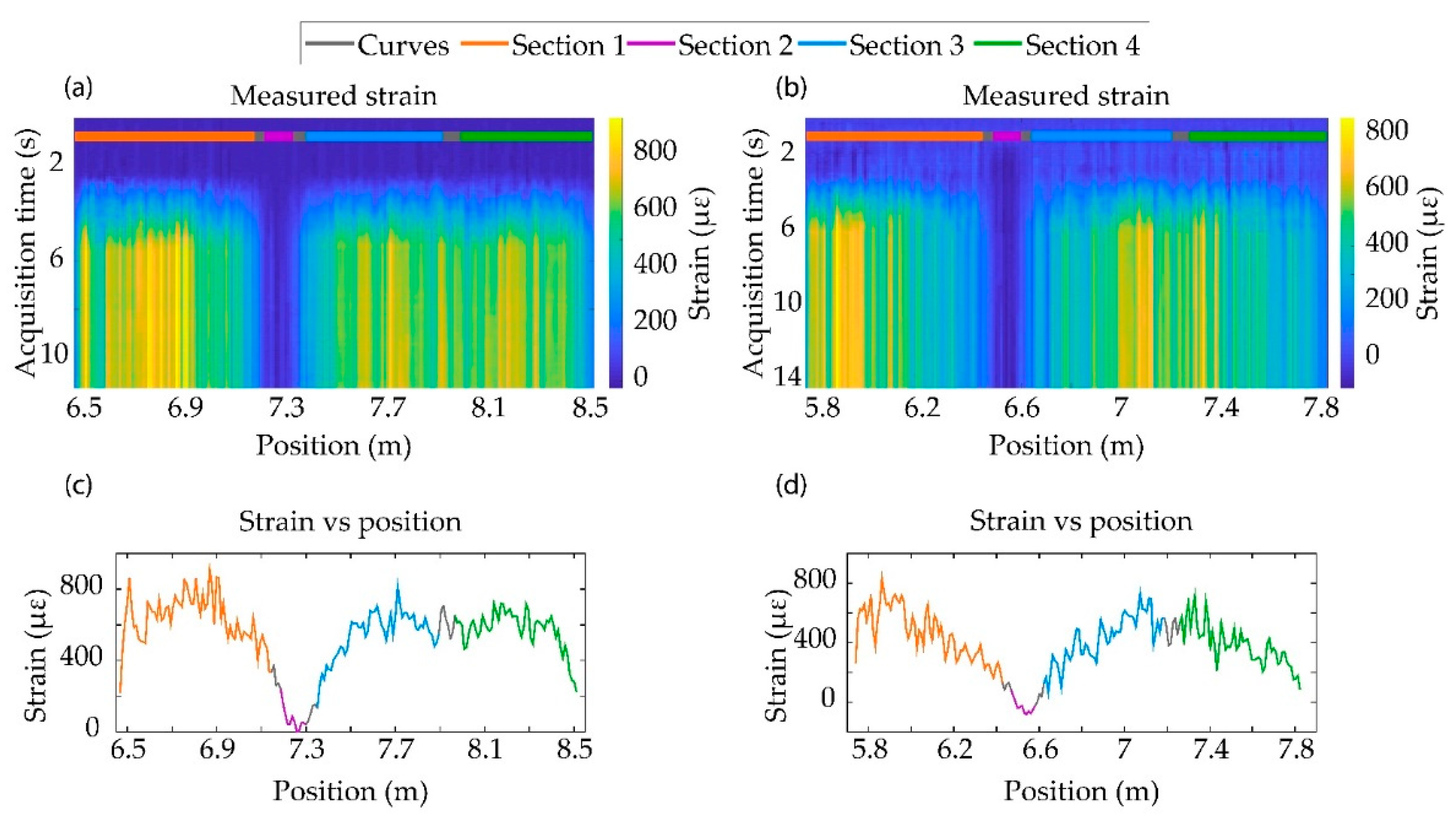
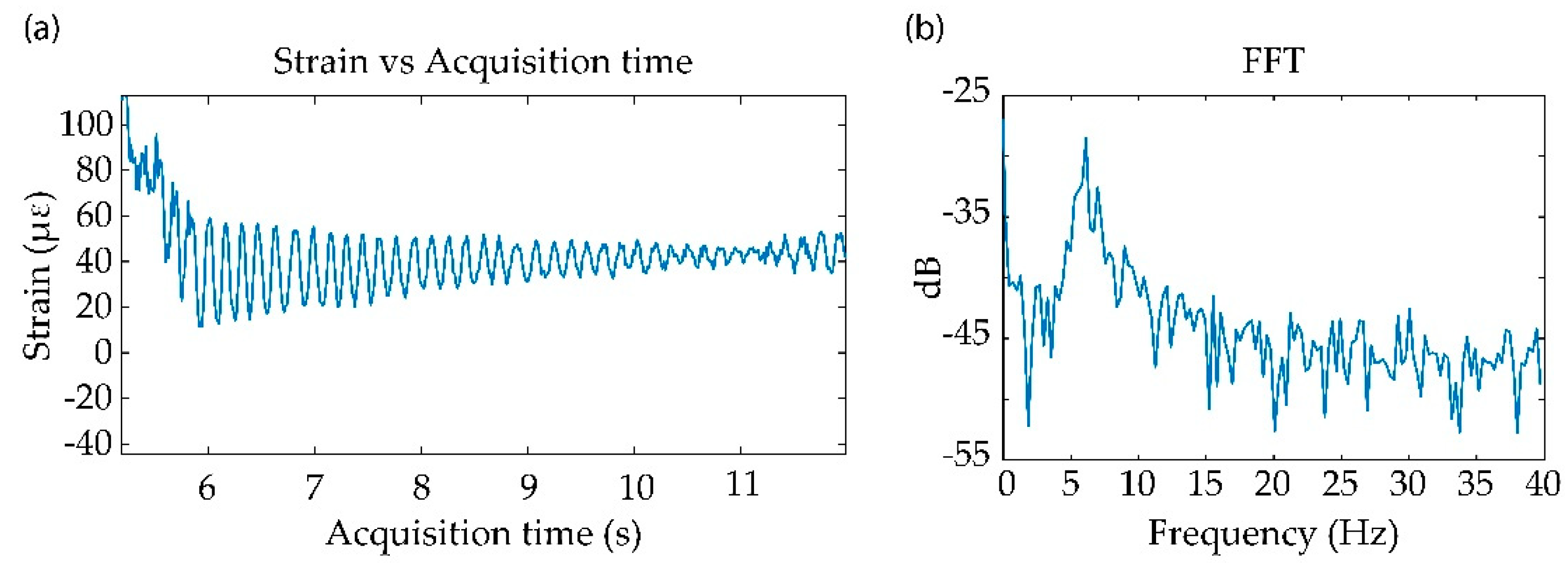
3. Results
3.1. Bending
3.2. Torsion
3.3. Vibration
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Li, H.N.; Li, D.S.; Song, G.B. Recent applications of fiber optic sensors to health monitoring in civil engineering. Eng. Struct. 2004, 26, 1647–1657. [Google Scholar] [CrossRef]
- Ma, Z.; Chen, X. Fiber bragg gratings sensors for aircraft wing shape measurement: Recent applications and technical analysis. Sensors 2019, 19, 55. [Google Scholar] [CrossRef]
- Lee, B. Review of the present status of optical fiber sensors. Opt. Fiber Technol. 2003, 9, 57–79. [Google Scholar] [CrossRef]
- Kersey, A.D.; Davis, M.A.; Patrick, H.J.; LeBlanc, M.; Koo, K.P.; Askins, C.G.; Putnam, M.A.; Friebele, E.J. Fiber grating sensors. J. Light. Technol. 1997, 15, 1442–1463. [Google Scholar] [CrossRef]
- Kinet, D.; Mégret, P.; Goossen, K.W.; Qiu, L.; Heider, D.; Caucheteur, C. Fiber Bragg grating sensors toward structural health monitoring in composite materials: Challenges and solutions. Sensors 2014, 14, 7394–7419. [Google Scholar] [CrossRef] [PubMed]
- Chung, W.H.; Tam, H.Y.; Wai, P.K.A.; Khandelwal, A. Time- and wavelength-division multiplexing of FBG sensors using a semiconductor optical amplifier in ring cavity configuration. IEEE Photonics Technol. Lett. 2005, 17, 2709–2711. [Google Scholar] [CrossRef]
- Cooper, D.J.F.; Coroy, T.; Smith, P.W.E. Time-division multiplexing of large serial fiber-optic Bragg grating sensor arrays. Appl. Opt. 2001, 40, 2643–2654. [Google Scholar] [CrossRef]
- Zhang, M.; Sun, Q.; Wang, Z.; Li, X.; Liu, H.; Liu, D. A large capacity sensing network with identical weak fiber Bragg gratings multiplexing. Opt. Commun. 2012, 285, 3082–3087. [Google Scholar] [CrossRef]
- Mills, J.A.; Hamilton, A.W.; Gillespie, D.I.; Andonovic, I.; Michie, C.; Burnham, K.; Tachtatzis, C. Identifying defects in aerospace composite sandwich panels using high-definition distributed optical fibre sensors. Sensors 2020, 20, 6746. [Google Scholar] [CrossRef]
- Barrias, A.; Casas, J.R.; Villalba, S. A review of distributed optical fiber sensors for civil engineering applications. Sensors 2016, 16, 748. [Google Scholar] [CrossRef]
- Bao, X.; Chen, L. Recent Progress in Distributed Fiber Optic Sensors. Sensors 2012, 12, 8601–8639. [Google Scholar] [CrossRef]
- Thévenaz, L.; Facchini, M.; Fellay, A.; Robert, P.; Inaudi, D.; Dardel, B. Monitoring of large structure using distributed Brillouin fibre sensing. In Proceedings of the 13th International Conference on Optical Fiber Sensors, Kyongju, Korea, 12–16 April 1999; pp. 5–8. [Google Scholar]
- Glišić, B.; Posenato, D.; Inaudi, D. Integrity monitoring of old steel bridge using fiber optic distributed sensors based on Brillouin scattering. In Proceedings of the 14th International Symposium on: Smart Structures and Materials & Nondestructive Evaluation and Health Monitoring, San Diego, CA, USA, 18–22 March 2007; Volume 6531. [Google Scholar]
- Brown, G.A.; Hartog, A. Optical fiber sensors in upstream oil and gas. J. Pet. Technol. 2002, 54, 63–65. [Google Scholar] [CrossRef]
- Inaudi, D.; Glisic, B. Long-range pipeline monitoring by distributed fiber optic sensing. ASME Trans. J. Press. Vessel Technol. 2010, 132, 011701. [Google Scholar] [CrossRef]
- Rahim, N.A.A.; Kutz, J.J.; White, M.M.; Michel, J.; Sang, A.K.; Froggatt, M.E.; Klute, S.M.; Gifford, D.K. Dynamic monitoring of fan blade using high resolution, distributed fiber optic sensing. In Proceedings of the SAMPE Technical Conference, Wichita, KS, USA, 21–24 October 2013. [Google Scholar]
- Klute, S.M.; Sang, A.K.; Gifford, D.K.; Froggatt, M.E. Defect detection during manufacture of composite windturbine blade with embedded fiber optic distributed strain sensor. In Proceedings of the International SAMPETechnical Conference, Long Beach, CA, USA, 23–26 May 2011. [Google Scholar]
- Palmieri, L.; Schenato, L. Distributed Optical Fiber Sensing Based on Rayleigh Scattering. Open Opt. J. 2013, 7, 104–127. [Google Scholar] [CrossRef]
- Li, J.; Gan, J.; Zhang, Z.; Heng, X.; Yang, C.; Qian, Q.; Xu, S.; Yang, Z. High spatial resolution distributed fiber strain sensor based on phase-OFDR. Opt. Express 2017, 25, 27913. [Google Scholar] [CrossRef]
- Wang, Z.N.; Zeng, J.J.; Li, J.; Fan, M.Q.; Wu, H.; Peng, F.; Zhang, L.; Zhou, Y.; Rao, Y.J. Ultra-long phase-sensitive OTDR with hybrid distributed amplification. Opt. Lett. 2014, 39, 5866. [Google Scholar] [CrossRef] [PubMed]
- Martins, H.F.; Martin-Lopez, S.; Corredera, P.; Filograno, M.L.; Frazao, O.; Gonzalez-Herraez, M. Phase-sensitive optical time domain reflectometer assisted by first-order raman amplification for distributed vibration sensing over >100 km. J. Light. Technol. 2014, 32, 1510–1518. [Google Scholar] [CrossRef]
- Zhu, T.; He, Q.; Xiao, X.; Bao, X. Modulated pulses based distributed vibration sensing with high frequency response and spatial resolution. Opt. Express 2013, 21, 2953. [Google Scholar] [CrossRef]
- Martins, H.F.; Shi, K.; Thomsen, B.C.; Martin-Lopez, S.; Gonzalez-Herraez, M.; Savory, S.J. Real time dynamic strain monitoring of optical links using the backreflection of live PSK data. Opt. Express 2016, 24, 22303. [Google Scholar] [CrossRef] [PubMed]
- Soriano-Amat, M.; Martins, H.F.; Durán, V.; Martin-Lopez, S.; Gonzalez-Herraez, M.; Fernández-Ruiz, M.R. Time-expanded phase-sensitive optical time-domain reflectometry. Light Sci. Appl. 2021, 10. [Google Scholar] [CrossRef]
- Coddington, I.; Newbury, N.; Swann, W. Dual-comb spectroscopy. Optica 2016, 3, 414–426. [Google Scholar] [CrossRef]
- Soriano-Amat, M.; Soto, M.A.; Duran, V.; Martins, H.F.; Martin-Lopez, S.; Gonzalez-Herraez, M.; Fernández-Ruiz, M.R. Common-Path Dual-Comb Spectroscopy Using a Single Electro-Optic Modulator. J. Light. Technol. 2020, 38, 5107–5115. [Google Scholar] [CrossRef]
- Vulliez, P. Distributed fiber-optic sensing solves real-world problems. Laser Focus World 2013, 49, 60–67. [Google Scholar]
- Vella, T.; Chadderdon, S.; Selfridge, R.; Schultz, S.; Webb, S.; Park, C.; Peters, K.; Zikry, M. Full-spectrum interrogation of fiber Bragg gratings at 100 kHz for detecion of impact load. Meas. Sci. Technol. 2010, 21, 094009. [Google Scholar] [CrossRef]
- Luna Innovations. Available online: https://www.lunainc.com (accessed on 19 May 2021).
- Zhou, D.P.; Chen, L.; Bao, X.Y. Distributed dynamic strain measurement using optical frequency-domain reflectometry. Appl. Opt. 2016, 55, 6735–6739. [Google Scholar] [CrossRef] [PubMed]
- Li, H.; Liu, Q.; Chen, D.; Deng, Y.; He, Z. High-spatial-resolution fiber-optic distributed acoustic sensor based on Φ-OFDR with enhanced crosstalk suppression. Opt. Lett. 2020, 45, 563–566. [Google Scholar] [CrossRef]


| Technology | Range | Sensitivity | Number of Sensing Points (Spat. Resol.) | Acoustic Samp | BW Photodtector |
|---|---|---|---|---|---|
| FBG (quasi distributed) [27] | 24 m | 1 με | 2000 | 100 Hz | - |
| FBG [28] | - | 75 με | 214 | 200 kHz | - |
| OFDR [30] | 30 m | 200 nε | 150 (20 cm) | 50 Hz | MHz |
| OFDR [31] | 950 m | 100 nε | 9500 (10 cm) | 6.25 kHz | 1 GHz |
| OFDR [29] | 20 m | 2 με | 7700 (2.6 mm) | 50 Hz | - |
| TE-ΦOTDR [24] | 200 m | 490 nε | 10,000 (2 cm) | 20 Hz | <1 MHz |
| TE-ΦOTDR (in this work) | 20 m | 1 με | 1000 (2 cm) | 80 Hz (max. 2.5 kHz) | <1 MHz |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Soriano-Amat, M.; Fragas-Sánchez, D.; Martins, H.F.; Vallespín-Fontcuberta, D.; Preciado-Garbayo, J.; Martin-Lopez, S.; Gonzalez-Herraez, M.; Fernández-Ruiz, M.R. Monitoring of a Highly Flexible Aircraft Model Wing Using Time-Expanded Phase-Sensitive OTDR. Sensors 2021, 21, 3766. https://doi.org/10.3390/s21113766
Soriano-Amat M, Fragas-Sánchez D, Martins HF, Vallespín-Fontcuberta D, Preciado-Garbayo J, Martin-Lopez S, Gonzalez-Herraez M, Fernández-Ruiz MR. Monitoring of a Highly Flexible Aircraft Model Wing Using Time-Expanded Phase-Sensitive OTDR. Sensors. 2021; 21(11):3766. https://doi.org/10.3390/s21113766
Chicago/Turabian StyleSoriano-Amat, Miguel, David Fragas-Sánchez, Hugo F. Martins, David Vallespín-Fontcuberta, Javier Preciado-Garbayo, Sonia Martin-Lopez, Miguel Gonzalez-Herraez, and María R. Fernández-Ruiz. 2021. "Monitoring of a Highly Flexible Aircraft Model Wing Using Time-Expanded Phase-Sensitive OTDR" Sensors 21, no. 11: 3766. https://doi.org/10.3390/s21113766
APA StyleSoriano-Amat, M., Fragas-Sánchez, D., Martins, H. F., Vallespín-Fontcuberta, D., Preciado-Garbayo, J., Martin-Lopez, S., Gonzalez-Herraez, M., & Fernández-Ruiz, M. R. (2021). Monitoring of a Highly Flexible Aircraft Model Wing Using Time-Expanded Phase-Sensitive OTDR. Sensors, 21(11), 3766. https://doi.org/10.3390/s21113766







