Mechanically-Induced Long-Period Fiber Gratings Using Laminated Plates
Abstract
1. Introduction
2. Materials and Methods
2.1. Laminated Plates Construction
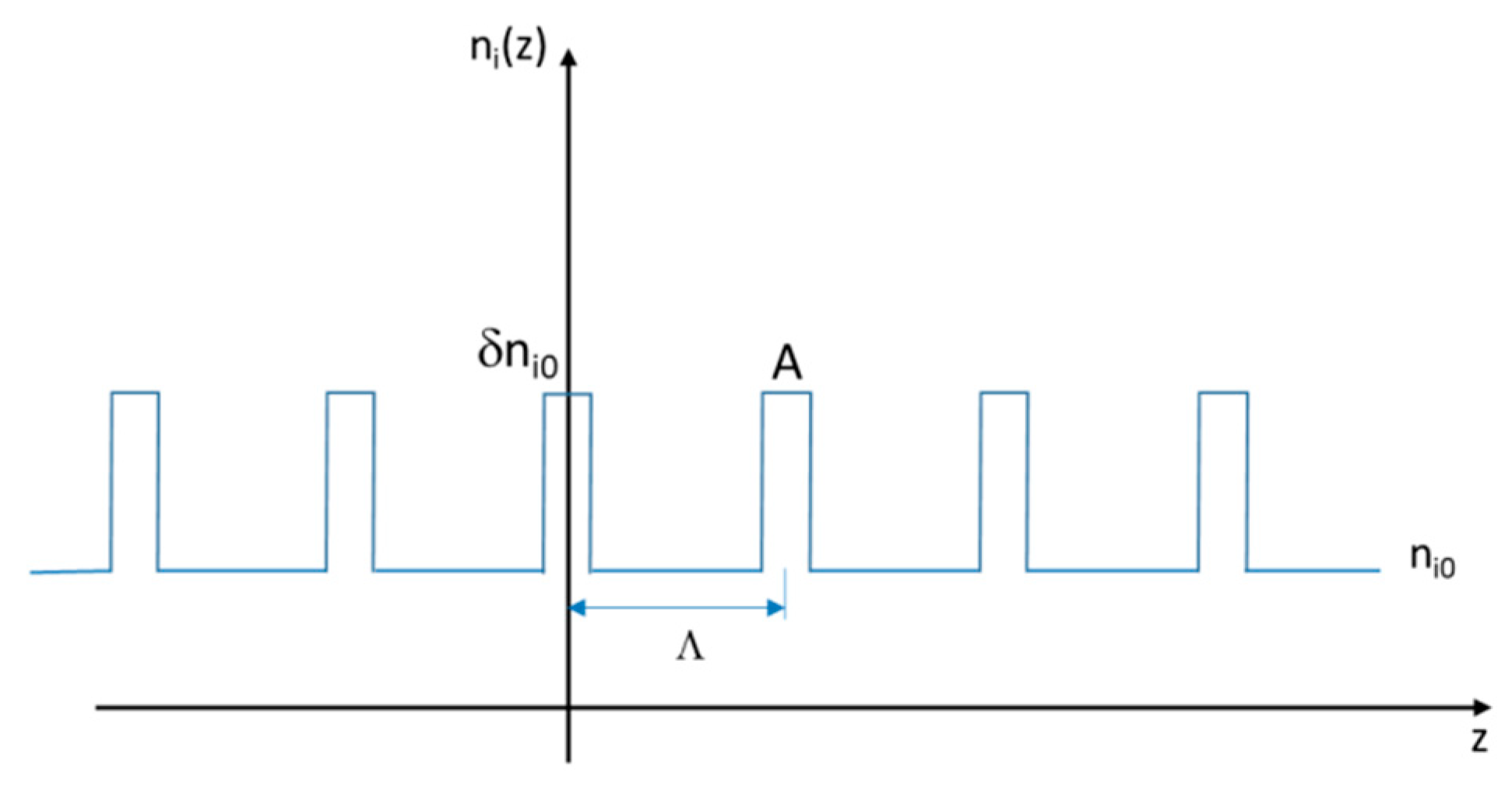
2.2. Refractive Index Modulation by the Laminated Plate
2.3. Experimental Setup
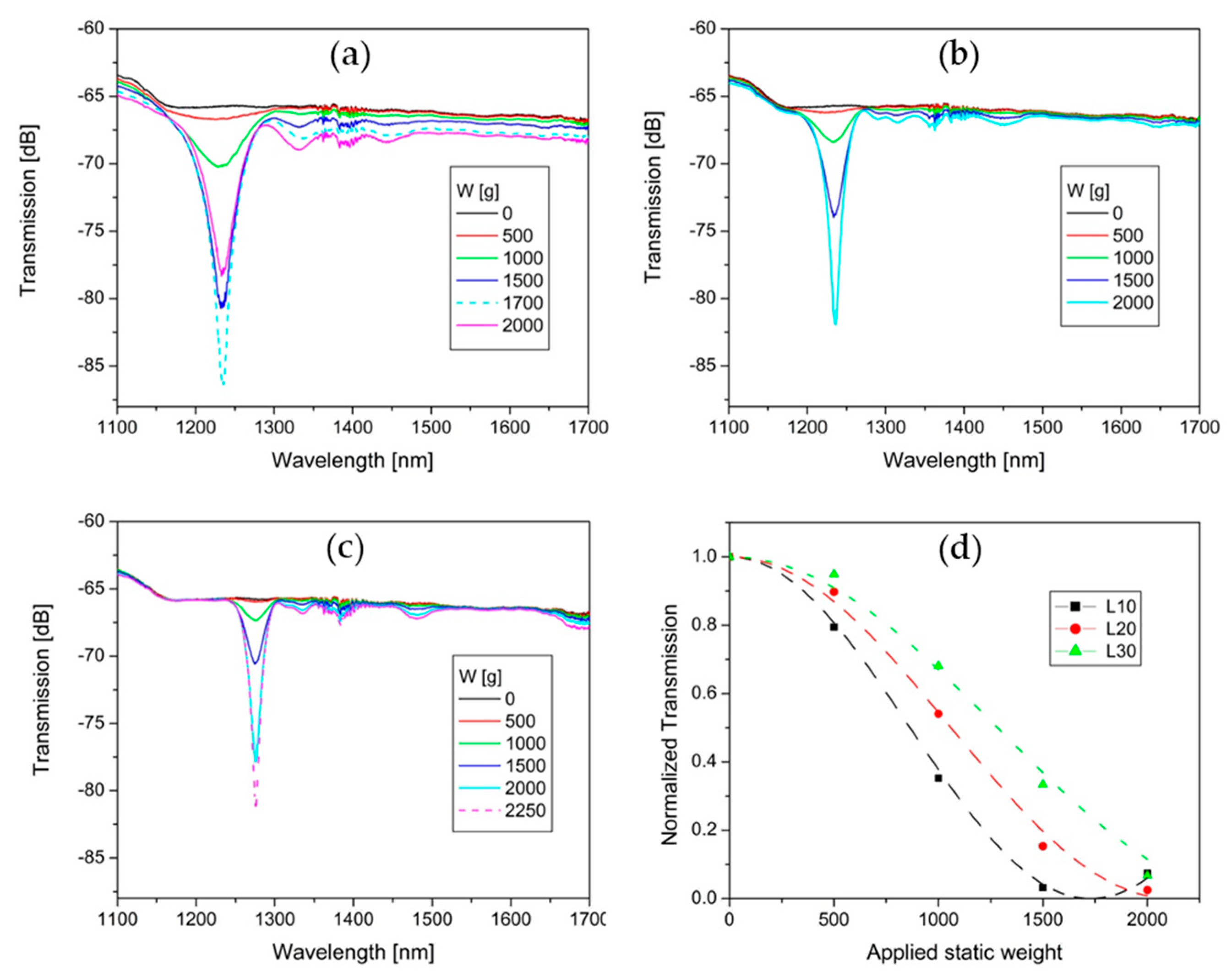
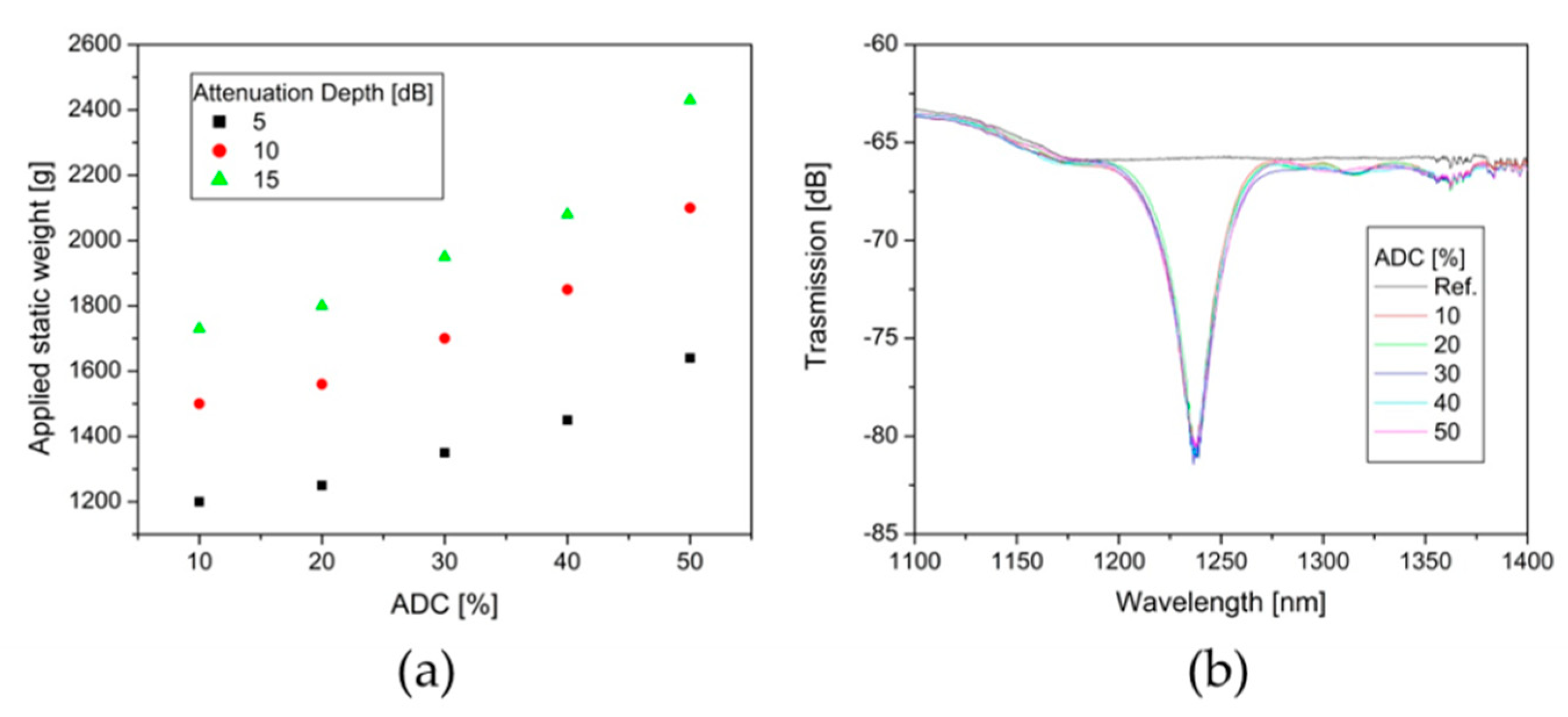
3. Results
4. Analysis of Results
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Vengsarkar, A.M.; Lemaire, P.J.; Judkins, J.B.; Bhatia, V.; Erdogan, T.; Sipe, J.E. Long-period fiber gratings as band-rejection filters. J. Lightware Technol. 1996, 14, 58–65. [Google Scholar] [CrossRef]
- Chiang, K.S.; Liu, Q. Long-period grating devices for application in optical communications. In Proceedings of the 5th ICOCN, Chengdu, China, 23–27 September 2006; pp. 128–133. [Google Scholar]
- Zhao, X.W.; Wang, Q. Mini review: Recent advances in long period fiber grating biological and chemical sensors. Instrum. Sci. Technol. 2019, 47, 40–169. [Google Scholar] [CrossRef]
- Krčmařík, D.; Kulishov, M.; Slavík, R. Long-period fiber gratings in active fibers. In Current Trends in Short- and Long-Period Fiber Gratings; Cuadrado-Laborde, C., Ed.; InTech: Rijeka, Croatia, 2013; pp. 87–104. [Google Scholar]
- Davis, D.D.; Gaylord, T.K.; Glytsis, E.N.; Kosinski, S.G.; Mettler, S.C.; Vengsarkar, A.M. Long-period fibre grating fabrication with focused CO2 laser pulses. Electron. Lett. 1998, 34, 302–303. [Google Scholar] [CrossRef]
- Kondo, Y.; Nouchi, K.; Mitsuyu, T.; Watanabe, M.; Kazansky, P.G.; Hirao, K. Fabrication of long-period fiber gratings by focused irradiation of infrared femtosecond laser pulses. Opt. Lett. 1999, 24, 646–648. [Google Scholar] [CrossRef] [PubMed]
- Enomoto, T.; Shigehara, M.; Ishikawa, S.; Danzuka, T.; Kanamori, H. Long-period fiber grating in a pure-silica-core fiber written by residual stress relaxation. OFC ‘98 Tech. Digest. 1998, 2, 277–278. [Google Scholar]
- Savin, S.; Digonnet, M.J.F.; Kino, G.S.; Shaw, H.J. Tunable mechanically induced long-period fiber gratings. Opt. Lett. 2000, 25, 710–712. [Google Scholar] [CrossRef]
- Dong, X.R.; Sun, X.Y.; Li, H.T.; Hu, Y.W.; Duan, J.A.; Zhou, J.Y.; Wang, C. Femtosecond laser fabrication of long period fiber gratings by a transversal-scanning inscription method and the research of its orientational bending characteristics. Opt. Laser Technol. 2015, 71, 68–72. [Google Scholar] [CrossRef]
- Yin, G.; Wang, Y.; Liao, C.; Zhou, J.; Zhong, X.; Liu, S.; Wang, Q.; Li, Z.; Sun, B.; He, J.; et al. Improved arc discharge technique for inscribing compact long period fiber gratings. In Proceedings of the 23rd International Conference on Optical Fiber Sensors, Santander, Spain, 2–6 June 2014; p. 91577X. [Google Scholar]
- Zhong, X.; Wang, Y.; Liao, C.; Yin, G.; Zhou, J.; Wang, G.; Sun, B.; Tang, J. Long period fiber gratings inscribed with an improved two-dimensional scanning technique. IEEE Photon. J. 2014, 6, 1–8. [Google Scholar] [CrossRef]
- Fu, C.; Wang, Y.; Liu, S.; Bai, Z.; Liao, C.; He, J.; Wang, Y. Recent progress in fabrications and applications of heating-induced long period fiber gratings. Sensors 2019, 19, 4473. [Google Scholar] [CrossRef]
- Heck, M.; Krämer, R.G.; Ullsperger, T.; Goebel, T.A.; Richter, D.; Ünnermann, A.; Nolte, S. Efficient long period fiber gratings inscribed with femtosecond pulses and an amplitude mask. Opt. Lett. 2019, 44, 3980–3983. [Google Scholar] [CrossRef]
- Min, R.; Marques, C.; Nielsen, K.; Bang, O.; Ortega, B. Fast inscription of long period gratings in microstructured polymer optical fibers. IEEE Sens. J. 2018, 18, 1919–1923. [Google Scholar] [CrossRef]
- Liu, W.; Duan, S.; Du, H.; Jiang, H.; Sun, C.; Jin, X.; Zhao, L.; Geng, T.; Tong, C.; Yuan, L. A new ultra long-period fiber grating for measuring torsional characteristics. J. Mod. Opt. 2019, 66, 1215–1218. [Google Scholar] [CrossRef]
- Anzueto-Sánchez, G.; Martínez-Rios, A.; Torres-Gómez, I. Tunable ytterbium-doped fiber laser based on a mechanically induced long period holey fiber grating. Opt. Rev. 2007, 14, 75–77. [Google Scholar] [CrossRef]
- Nair, A.S.; Sudeep Kumar, V.P.; Joe, H. Widely tunable LP11 cladding-mode resonance in a twisted mechanically induced long-period fiber grating. Appl. Opt. 2015, 54, 2007–2010. [Google Scholar] [CrossRef] [PubMed]
- Israelsen, S.M.; Rottwitt, K. Broadband higher order mode conversion using chirped microbend long period gratings. Opt. Express. 2016, 24, 23969–23976. [Google Scholar] [CrossRef]
- Li, S.; Mo, Q.; Hu, X.; Du, C.; Wang, J. Controllable all-fiber orbital angular momentum mode converter. Opt. Lett. 2015, 40, 4376–4379. [Google Scholar] [CrossRef]
- Pradhan, P.; Sengupta, D.; Wang, L.; Tremblay, C.; LaRochelle, S.; Ung, B. The Brillouin gain of vector modes in a few-mode fiber. Sci. Rep. 2017, 7, 1552. [Google Scholar] [CrossRef]
- Statkiewicz-Barabach, G.; Olszewski, J.; Mergo, P.; Urbanczyk, W. Higher-order rocking filters induced mechanically in fibers with different birefringence dispersion. Appl. Opt. 2014, 53, 1258–1267. [Google Scholar] [CrossRef]
- Torres-Gómez, I.; Martínez-Ríos, A.; Ceballos-Herrera, D.E.; Mejía-Beltrán, E.; Selvas-Aguilar, R. Bandpass filter with adjustable bandwidth based on a press-induced long-period twisted holey-fiber grating. Opt. Lett. 2007, 32, 3885–3887. [Google Scholar] [CrossRef]
- Tsutsumi, Y.; Ohashi, M.; Miyoshi, Y. Temperature sensing using an optical time domain reflectometer and mechanical long-period fiber gratings fabricated from a heat-shrinkable tube. IEICE Commun. Express. 2017, 6, 103–108. [Google Scholar] [CrossRef]
- Salas-Alcántara, K.M.; Aparicio-Ixta, L.; Torres-Gómez, I.; Rodríguez, M.; Ramos-Ortíz, G.; Espinosa-Luna, R.; Pichardo-Molina, J.L. Modal interferometer based on a single mechanically induced long-period fiber grating and a nanoparticles-coated film section. Opt. Lett. 2017, 42, 1780–1783. [Google Scholar] [CrossRef] [PubMed]
- Ugale, S.; Mishra, V. Pressure sensor based on mechanically induced LPFG in novel MSM Fiber Structure. Optics Photon. J. 2013, 3, 225–228. [Google Scholar] [CrossRef]
- Liu, H.; Wen, H.; Huang, B.; Amezcua Correa, R.; Sillard, P.; Chen, H.; Li, Z.; Li, G. Reducing group delay spread using uniform long-period gratings. Sci. Rep. 2018, 8, 3882. [Google Scholar] [CrossRef] [PubMed]
- Rego, G.; Fernandes, J.R.A.; Santos, J.L.; Salgado, H.M.; Marques, P.V.S. New technique to mechanically induce long-period fibre gratings. Opt. Commun. 2003, 220, 111–118. [Google Scholar] [CrossRef]
- Yokouchi, T.; Suzaki, Y.; Nakagawa, K.; Yamauchi, M.; Kimura, M.; Mizutani, Y.; Kimura, S.; Ejima, S. Thermal tuning of mechanically induced long-period fiber grating. Appl. Opt. 2005, 44, 5024–5028. [Google Scholar] [CrossRef] [PubMed]
- Tsutsumia, Y.; Hase, T.; Ohashi, M.; Miyoshi, Y.; Kubota, H. Model for estimating the properties of mechanically induced long-period fiber grating based on polarization and applied pressure. IEICE Commun. Express. 2017, 6, 554–559. [Google Scholar] [CrossRef]
- Han, M.; Wang, Y.; Wang, Y.; Wang, A. Fiber-optic physical and biochemical sensing based on transient and traveling long-period gratings. Opt. Lett. 2009, 34, 100–102. [Google Scholar] [CrossRef]
- Chen, C. Foundations for Guided-Wave Optics, 1st ed.; John Wiley & Sons: Danvers, MA, USA, 2007; pp. 285–288. [Google Scholar]
- Okamoto, K.; Hosaka, T.; Edahiro, T. Stress analysis of optical fibers by a finite element Method. IEEE J. Quantum Electron. 1981, 17, 2123–2129. [Google Scholar] [CrossRef]
- Guyard, R.; Leduc, D.; Lupi, C.; Lecieux, Y. Global overview of the sensitivity of long period gratings to strain. Opt. Laser Technol. 2016, 79, 62–73. [Google Scholar] [CrossRef]
- Starodubov, D.S.; Grubsky, V.; Feinberg, J. All-fiber bandpass filter with adjustable transmission using cladding-mode coupling. IEEE Photon. Technol. Lett. 1998, 10, 1590–1592. [Google Scholar] [CrossRef]
- Liu, Z.; Liu, Y.; Mou, C.; Zou, F.; Wang, T. CO2 laser-written long-period fiber grating with a high diffractive order cladding mode near the turning point. Appl. Opt. 2018, 57, 4756–4760. [Google Scholar] [CrossRef] [PubMed]
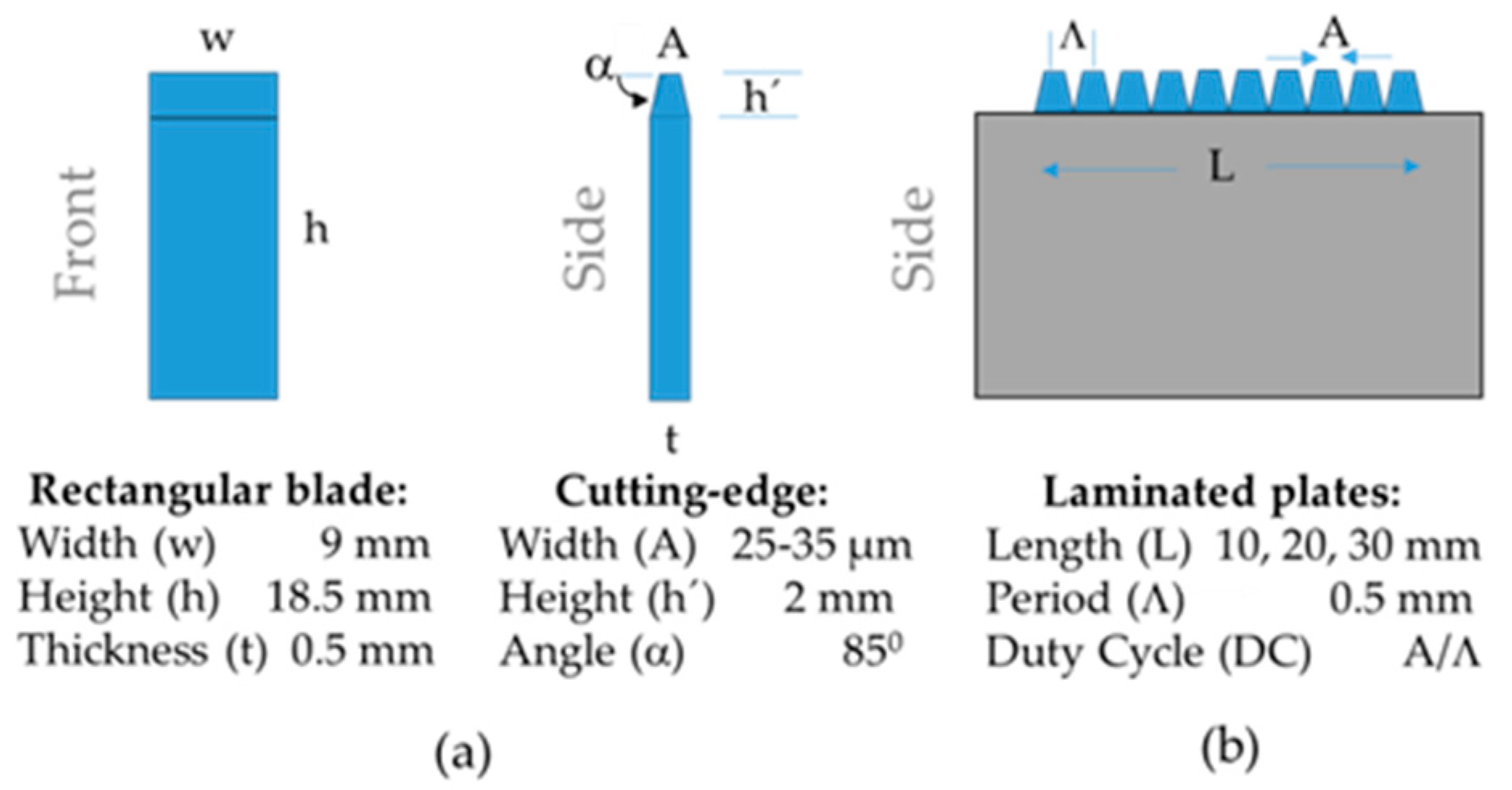


| Laminated Plate | L [mm] | ADC [%] | ||||
|---|---|---|---|---|---|---|
| L10 | 10 | 460 | 94 | 20 | 15 | 20.4 |
| L20 | 20 | 470 | 92 | 18 | 7 | 19.6 |
| L30 | 30 | 490 | 98 | 24 | 16 | 20.0 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Torres-Gómez, I.; Ceballos-Herrera, D.E.; Salas-Alcantara, K.M. Mechanically-Induced Long-Period Fiber Gratings Using Laminated Plates. Sensors 2020, 20, 2582. https://doi.org/10.3390/s20092582
Torres-Gómez I, Ceballos-Herrera DE, Salas-Alcantara KM. Mechanically-Induced Long-Period Fiber Gratings Using Laminated Plates. Sensors. 2020; 20(9):2582. https://doi.org/10.3390/s20092582
Chicago/Turabian StyleTorres-Gómez, Ismael, Daniel E. Ceballos-Herrera, and Karla M. Salas-Alcantara. 2020. "Mechanically-Induced Long-Period Fiber Gratings Using Laminated Plates" Sensors 20, no. 9: 2582. https://doi.org/10.3390/s20092582
APA StyleTorres-Gómez, I., Ceballos-Herrera, D. E., & Salas-Alcantara, K. M. (2020). Mechanically-Induced Long-Period Fiber Gratings Using Laminated Plates. Sensors, 20(9), 2582. https://doi.org/10.3390/s20092582





