Inertial Sensor-Based Motion Tracking in Football with Movement Intensity Quantification
Abstract
1. Introduction
2. Materials and Methods
2.1. System Setup
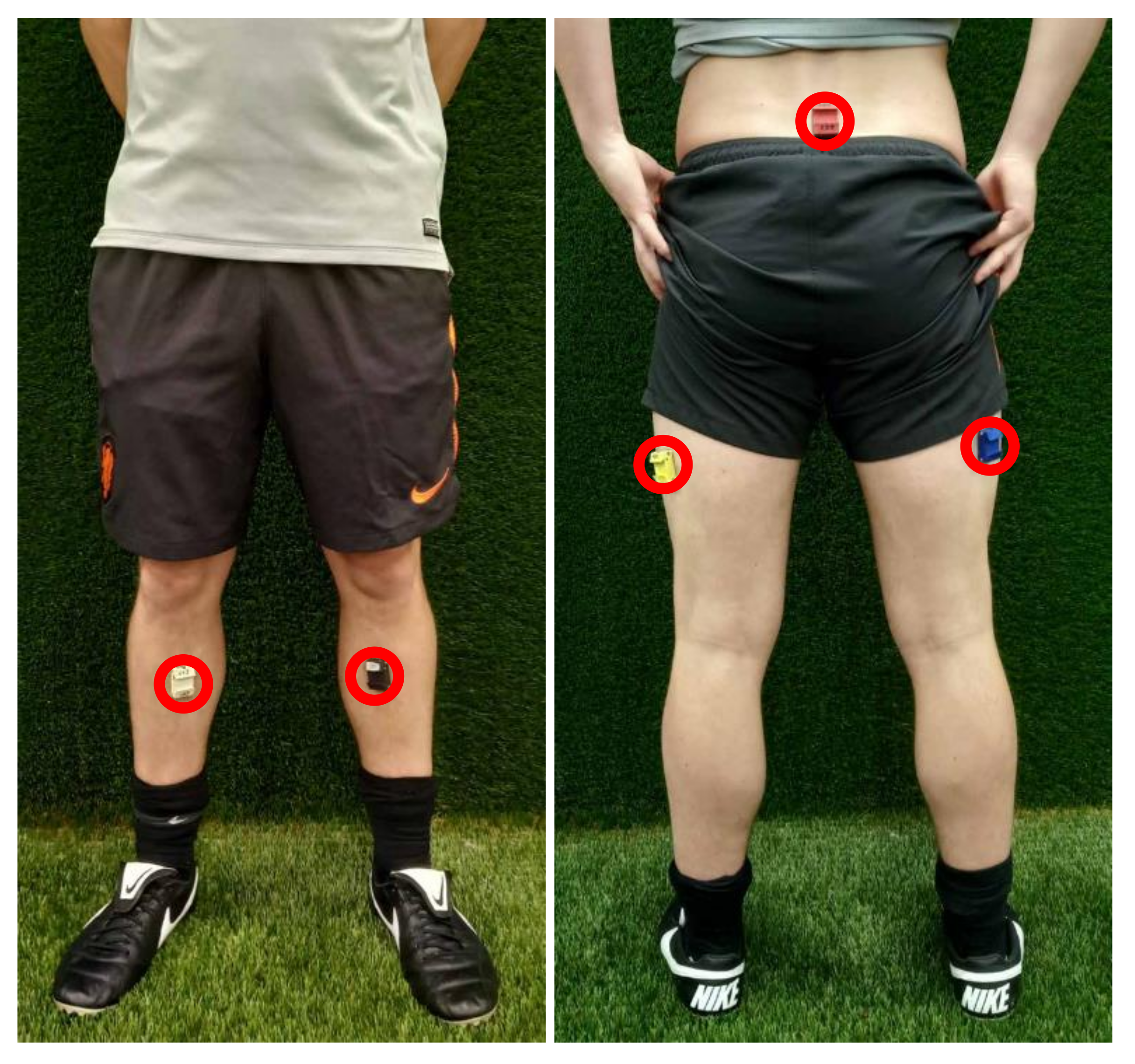
2.1.1. System Hardware
2.1.2. System Calibration
2.1.3. Joint Kinematics
2.2. Experimental Validation
2.2.1. Participants
2.2.2. Equipment
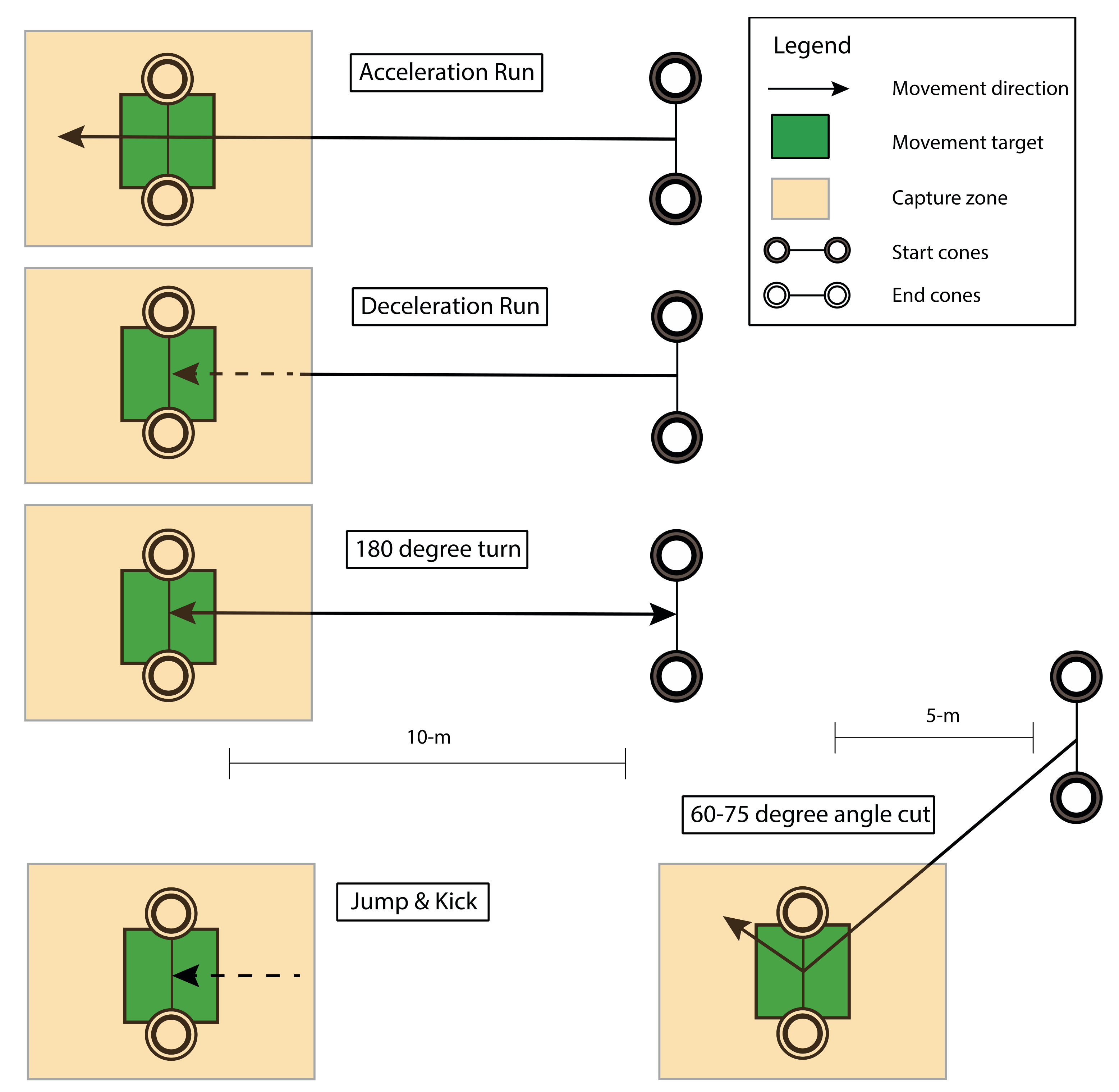
2.2.3. Protocol
2.2.4. Data Processing
2.2.5. Statistical Analysis
3. Results
3.1. Overall
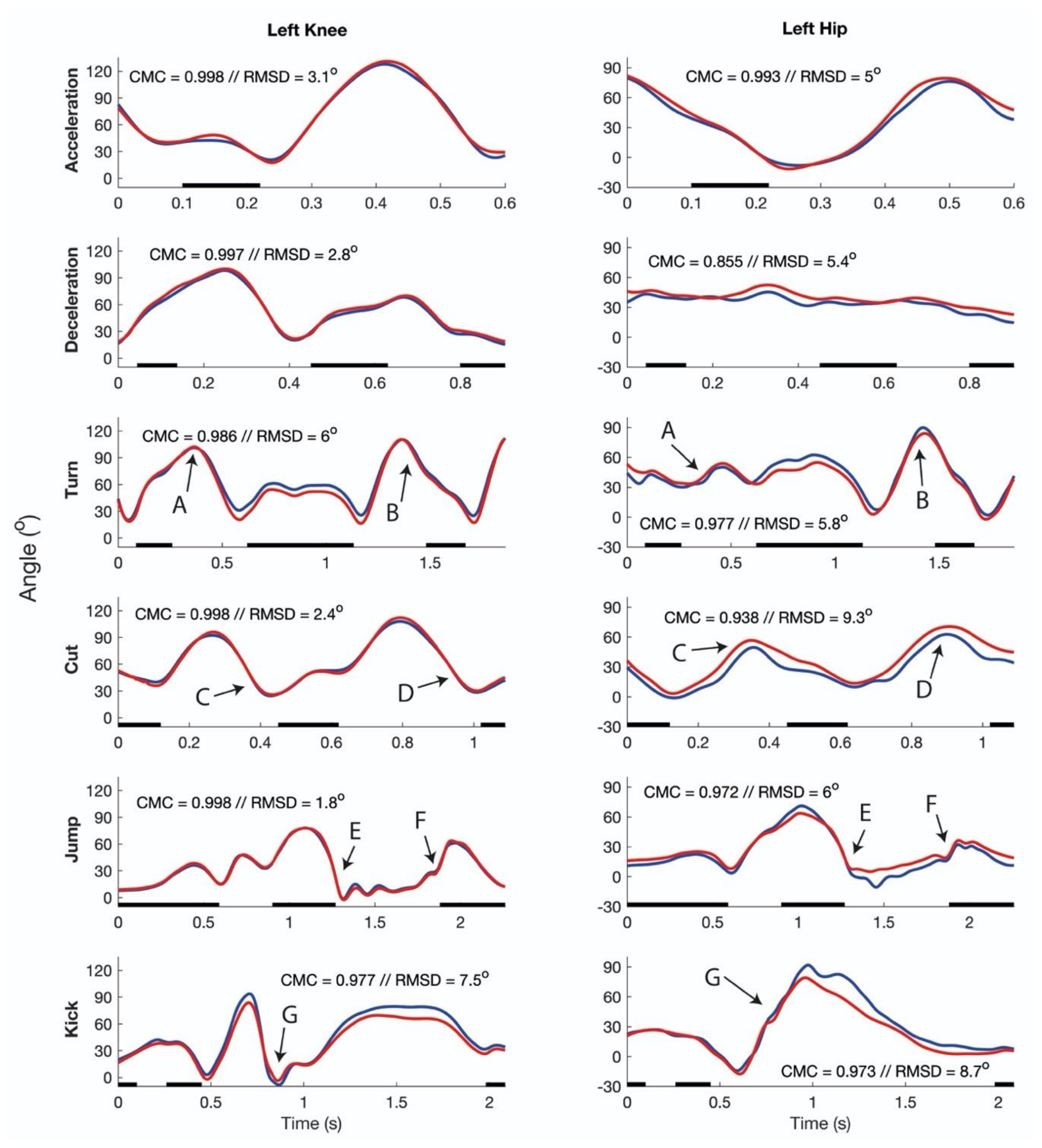
3.2. Running Tasks
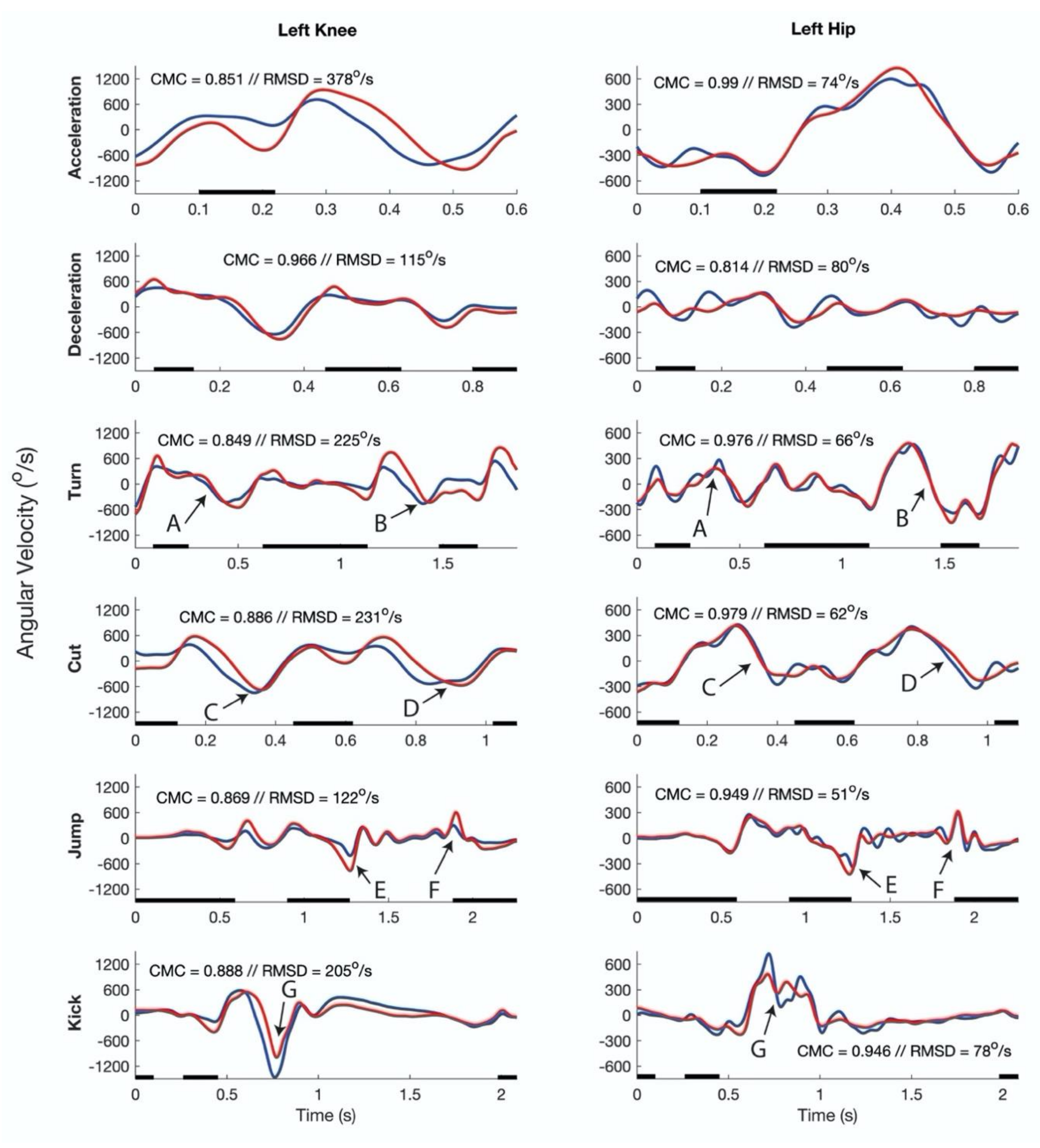
3.3. Jumping and Kicking
3.4. Movement Intensity
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Akenhead, R.; Nassis, G.P. Training Load and Player Monitoring in High-Level Football: Current Practice and Perceptions. Int. J. Sports Physiol. Perf. 2016, 11, 587–593. [Google Scholar] [CrossRef] [PubMed]
- Aughey, R.J. Applications of GPS Technologies to Field Sports. Int. J. Sports Physiol. Perf. 2011, 6, 295–310. [Google Scholar] [CrossRef] [PubMed]
- Vanrenterghem, J.; Nedergaard, N.J.; Robinson, M.A.; Drust, B. Training Load Monitoring in Team Sports: A Novel Framework Separating Physiological and Biomechanical Load-Adaptation Pathways. Sports Med. 2017, 47, 2135–2142. [Google Scholar] [CrossRef] [PubMed]
- Landry, S.C.; McKean, K.A.; Hubley-Kozey, C.L.; Stanish, W.D.; Deluzio, K.J. Neuromuscular and lower limb biomechanical differences exist between male and female elite adolescent soccer players during an unanticipated side-cut maneuver. Am. J. Sports Med. 2007, 35, 1888–1900. [Google Scholar] [CrossRef]
- Lees, A.; Asai, T.; Andersen, T.B.; Nunome, H.; Sterzing, T. The biomechanics of kicking in soccer: A review. J. Sports Sci. 2010, 28, 805–817. [Google Scholar] [CrossRef]
- Van der Worp, H.; de Poel, H.J.; Diercks, R.L.; Van Den Akker-Scheek, I.; Zwerver, J. Jumper’s knee or lander’s knee? A systematic review of the relation between jump biomechanics and patellar tendinopathy. Int. J. Sports Med. 2014, 35, 714–722. [Google Scholar] [CrossRef]
- Stevens, T.G.; de Ruiter, C.J.; Twisk, J.W.; Savelsbergh, G.J.; Beek, P.J. Quantification of in-season training load relative to match load in professional Dutch Eredivisie football players. Sci. Med. Footb. 2017, 1, 117–125. [Google Scholar] [CrossRef]
- Ekstrand, J.; Hägglund, M.; Waldén, M. Epidemiology of muscle injuries in professional football (soccer). Am. J. Sports Med. 2011, 39, 1226–1232. [Google Scholar] [CrossRef]
- Chambers, R.; Gabbett, T.J.; Cole, M.H.; Beard, A. The Use of Wearable Microsensors to Quantify Sport-Specific Movements. Sports Med. 2015, 45, 1065–1081. [Google Scholar] [CrossRef]
- Cuesta-Vargas, A.I.; Galán-Mercant, A.; Williams, J.M. The use of inertial sensors system for human motion analysis. Phys. Ther. Rev. 2010, 15, 462–473. [Google Scholar] [CrossRef]
- Madgwick, S.O.; Harrison, A.J.; Vaidyanathan, A. Estimation of IMU and MARG orientation using a gradient descent algorithm. IEEE Int. Conf. Rehabil. Robot. 2011, 2011, 5975346. [Google Scholar] [CrossRef] [PubMed]
- Luinge, H.J.; Veltink, P.H.; Baten, C.T. Ambulatory measurement of arm orientation. J. Biomech. 2007, 40, 78–85. [Google Scholar] [CrossRef] [PubMed]
- Cooper, G.; Sheret, I.; McMillian, L.; Siliverdis, K.; Sha, N.; Hodgins, D.; Kenney, L.; Howard, D. Inertial sensor-based knee flexion/extension angle estimation. J. Biomech. 2009, 42, 2678–2685. [Google Scholar] [CrossRef] [PubMed]
- Reenalda, J.; Maartens, E.; Homan, L.; Buurke, J.H.J. Continuous three dimensional analysis of running mechanics during a marathon by means of inertial magnetic measurement units to objectify changes in running mechanics. J. Biomech. 2016, 49, 3362–3367. [Google Scholar] [CrossRef] [PubMed]
- Magalhaes, F.A.d.; Vannozzi, G.; Gatta, G.; Fantozzi, S. Wearable inertial sensors in swimming motion analysis: A systematic review. J. Sports Sci. 2015, 33, 732–745. [Google Scholar] [CrossRef] [PubMed]
- Mooney, R.; Corley, G.; Godfrey, A.; Quinlan, L.R.; ÓLaighin, G. Inertial sensor technology for elite swimming performance analysis: A systematic review. Sensors 2016, 16, 18. [Google Scholar] [CrossRef]
- Picerno, P.; Cereatti, A.; Cappozzo, A. Joint kinematics estimate using wearable inertial and magnetic sensing modules. Gait Posture 2008, 28, 588–595. [Google Scholar] [CrossRef]
- Zhang, J.-T.; Novak, A.C.; Brouwer, B.; Li, Q. Concurrent validation of Xsens MVN measurement of lower limb joint angular kinematics. Physiol. Meas. 2013, 34, N63. [Google Scholar] [CrossRef]
- Blair, S.; Duthie, G.; Robertson, S.; Hopkins, W.; Ball, K. Concurrent validation of an inertial measurement system to quantify kicking biomechanics in four football codes. J. Biomech. 2018, 73, 24–32. [Google Scholar] [CrossRef]
- Lebel, K.; Boissy, P.; Nguyen, H.; Duval, C. Inertial measurement systems for segments and joints kinematics assessment: Towards an understanding of the variations in sensors accuracy. Biomed. Eng. Online 2017, 16, 56. [Google Scholar] [CrossRef]
- Wouda, F.J.; Giuberti, M.; Bellusci, G.; Maartens, E.; Reenalda, J.; Van Beijnum, B.-J.F.; Veltink, P.H. Estimation of vertical ground reaction forces and sagittal knee kinematics during running using three inertial sensors. Front. Physiol. 2018, 9, 218. [Google Scholar] [CrossRef] [PubMed]
- Bush, M.; Barnes, C.; Archer, D.T.; Hogg, B.; Bradley, P.S. Evolution of match performance parameters for various playing positions in the English Premier League. Hum. Mov. Sci. 2015, 39, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Chumanov, E.S.; Heiderscheit, B.C.; Thelen, D.G. The effect of speed and influence of individual muscles on hamstring mechanics during the swing phase of sprinting. J. Biomech. 2007, 40, 3555–3562. [Google Scholar] [CrossRef] [PubMed]
- de Ruiter, C.J.; van Dieën, J.H. Stride and Step Length Obtained with Inertial Measurement Units during Maximal Sprint Acceleration. Sports 2019, 7, 202. [Google Scholar] [CrossRef]
- Bastiaansen, B.J.C.; Wilmes, E.; Brink, M.S.; de Ruiter, C.J.; Savelsbergh, G.J.P.; Steijlen, A.; Jansen, K.M.B.; van der Helm, F.C.T.; Goedhart, E.A.; van der Laan, D.; et al. An Inertial Measurement Unit Based Method to Estimate Hip and Knee Joint Kinematics in Team Sport Athletes on the Field. JoVE 2020, in press. [Google Scholar]
- Wu, G.; Cavanagh, P.R. ISB recommendations for standardization in the reporting of kinematic data. J. Biomech. 1995, 28, 1257–1261. [Google Scholar] [CrossRef]
- Kuipers, J.B. Quaternions and Rotation Sequences; Princeton University Press: Princeton, NJ, USA, 1999; Volume 66. [Google Scholar]
- Vicon®. Plug-in-gait modelling instructions. In Vicon® manual. Vicon® 612 Motion Systems; Oxford Metrics Ltd.: Oxford, UK, 2002; pp. 19–22. [Google Scholar]
- Wu, G.; Siegler, S.; Allard, P.; Kirtley, C.; Leardini, A.; Rosenbaum, D.; Whittle, M.; D D’Lima, D.; Cristofolini, L.; Witte, H. ISB recommendation on definitions of joint coordinate system of various joints for the reporting of human joint motion—Part I: Ankle, hip, and spine. J. Biomech. 2002, 35, 543–548. [Google Scholar] [CrossRef]
- Cappozzo, A.; Catani, F.; Della Croce, U.; Leardini, A. Position and orientation in space of bones during movement: Anatomical frame definition and determination. Clin. Biomech 1995, 10, 171–178. [Google Scholar] [CrossRef]
- Ferrari, A.; Cutti, A.G.; Cappello, A. A new formulation of the coefficient of multiple correlation to assess the similarity of waveforms measured synchronously by different motion analysis protocols. Gait Posture 2010, 31, 540–542. [Google Scholar] [CrossRef]
- Ferrari, A.; Cutti, A.G.; Garofalo, P.; Raggi, M.; Heijboer, M.; Cappello, A.; Davalli, A. First in vivo assessment of “Outwalk”: A novel protocol for clinical gait analysis based on inertial and magnetic sensors. Med. Biol. Eng. Comput. 2010, 48, 1–15. [Google Scholar] [CrossRef]
- Favre, J.; Jolles, B.; Aissaoui, R.; Aminian, K. Ambulatory measurement of 3D knee joint angle. J. Biomech. 2008, 41, 1029–1035. [Google Scholar] [CrossRef]
- Nüesch, C.; Roos, E.; Pagenstert, G.; Mündermann, A. Measuring joint kinematics of treadmill walking and running: Comparison between an inertial sensor based system and a camera-based system. J. Biomech. 2017, 57, 32–38. [Google Scholar] [CrossRef] [PubMed]
- Bergamini, E.; Ligorio, G.; Summa, A.; Vannozzi, G.; Cappozzo, A.; Sabatini, A. Estimating orientation using magnetic and inertial sensors and different sensor fusion approaches: Accuracy assessment in manual and locomotion tasks. Sensors 2014, 14, 18625–18649. [Google Scholar] [CrossRef] [PubMed]
| Left Knee | Left Hip | ||||
|---|---|---|---|---|---|
| Movement-type | Intensity | RMSD (o) | CMC | RMSD (o) | CMC |
| Acceleration | low | 4.7 ± 3.2 | 0.992 ± 0.009 | 7.4 ± 2.3 | 0.954 ± 0.047 |
| medium | 5.1 ± 3.2 | 0.993 ± 0.009 | 7.5 ± 2.3 | 0.978 ± 0.014 | |
| high | 6.0 ± 2.7 | 0.990 ± 0.011 | 7.5 ± 2.4 | 0.985 ± 0.011 | |
| Deceleration | low | 4.4 ± 2.7 | 0.991 ± 0.010 | 7.4 ± 2.1 | 0.906 ± 0.063 |
| medium | 4.5 ± 3.1 | 0.992 ± 0.009 | 6.5 ± 3.6 | 0.888 ± 0.155 | |
| high | 5.1 ± 3.5 | 0.987 ± 0.018 | 7.9 ± 3.9 | 0.854 ± 0.184 | |
| Turn | low | 5.1 ± 2.7 | 0.989 ± 0.012 | 8.5 ± 3.3 | 0.951 ± 0.034 |
| medium | 6.2 ± 2.9 | 0.985 ± 0.015 | 10.4 ± 4.0 | 0.928 ± 0.052 | |
| high | 6.4 ± 3.2 | 0.979 ± 0.024 | 10.9 ± 5.9 | 0.913 ± 0.074 | |
| Cut | low | 6.6 ± 3.5 | 0.982 ± 0.014 | 7.6 ± 3.3 | 0.953 ± 0.040 |
| medium | 6.2 ± 2.4 | 0.987 ± 0.007 | 8.5 ± 2.8 | 0.951 ± 0.040 | |
| high | 6.4 ± 3.2 | 0.981 ± 0.018 | 8.6 ± 3.0 | 0.928 ± 0.052 | |
| Jump | low | 3.7 ± 2.9 | 0.994 ± 0.007 | 7.8 ± 3.8 | 0.952 ± 0.045 |
| medium | 3.9 ± 2.5 | 0.992 ± 0.010 | 7.4 ± 3.7 | 0.943 ± 0.054 | |
| high | 4.2 ± 2.6 | 0.990 ± 0.013 | 8.3 ± 4.8 | 0.948 ± 0.058 | |
| Kick | low | 5.3 ± 4.9 | 0.970 ± 0.046 | 7.5 ± 3.7 | 0.957 ± 0.032 |
| medium | 6.0 ± 5.7 | 0.964 ± 0.056 | 6.7 ± 2.6 | 0.971 ± 0.016 | |
| high | 6.2 ± 4.6 | 0.973 ± 0.028 | 7.6 ± 2.5 | 0.965 ± 0.042 | |
| Overall | All | 5.3 ± 3.4 | 0.985 ± 0.022 | 8.0 ± 3.5 | 0.940 ± 0.075 |
| Left Knee | Left Hip | ||||||
|---|---|---|---|---|---|---|---|
| Movement-Type | Intensity | Absolute Angular Velocity (o/s) | RMSD (o/s) | CMC | Absolute Angular Velocity (o/s) | RMSD (o/s) | CMC |
| Acceleration | low | 271 ± 40 | 193 ± 31 | 0.902 ± 0.035 | 147 ± 21 | 67 ± 19 | 0.964 ± 0.019 |
| medium | 394 ± 52 | 278 ± 49 | 0.893 ± 0.028 | 225 ± 40 | 73 ± 17 | 0.981 ± 0.008 | |
| high | 449 ± 43 | 373 ± 48 | 0.858 ± 0.034 | 310 ± 48 | 93 ± 19 | 0.983 ± 0.005 | |
| Deceleration | low | 214 ± 33 | 135 ± 25 | 0.935 ± 0.030 | 104 ± 14 | 58 ± 17 | 0.940 ± 0.037 |
| medium | 264 ± 53 | 165 ± 41 | 0.935 ± 0.023 | 129 ± 27 | 82 ± 28 | 0.918 ± 0.064 | |
| high | 313 ± 101 | 174 ± 63 | 0.945 ± 0.026 | 140 ± 40 | 97 ± 32 | 0.882 ± 0.068 | |
| Turn | low | 187 ± 27 | 158 ± 30 | 0.900 ± 0.038 | 120 ± 22 | 68 ± 12 | 0.942 ± 0.029 |
| medium | 195 ± 45 | 180 ± 21 | 0.836 ± 0.211 | 138 ± 14 | 76 ± 14 | 0.947 ± 0.022 | |
| high | 205 ± 45 | 190 ± 39 | 0.897 ± 0.028 | 154 ± 29 | 94 ± 28 | 0.925 ± 0.050 | |
| Cut | low | 253 ± 48 | 182 ± 27 | 0.896 ± 0.041 | 140 ± 22 | 63 ± 29 | 0.925 ± 0.042 |
| medium | 316 ± 66 | 250 ± 42 | 0.873 ± 0.031 | 191 ± 31 | 85 ± 29 | 0.956 ± 0.028 | |
| high | 339 ± 55 | 253 ± 54 | 0.884 ± 0.042 | 202 ± 31 | 108 ± 36 | 0.958 ± 0.055 | |
| Jump | low | 75 ± 15 | 104 ± 17 | 0.894 ± 0.018 | 75 ± 17 | 56 ± 16 | 0.932 ± 0.025 |
| medium | 106 ± 18 | 119 ± 23 | 0.890 ± 0.030 | 88 ± 19 | 54 ± 10 | 0.939 ± 0.024 | |
| high | 112 ± 20 | 133 ± 15 | 0.878 ± 0.021 | 99 ± 12 | 63 ± 17 | 0.945 ± 0.038 | |
| Kick | low | 124 ± 66 | 116 ± 65 | 0.889 ± 0.084 | 77 ± 50 | 78 ± 29 | 0.814 ± 0.158 |
| medium | 155 ± 69 | 151 ± 79 | 0.887 ± 0.036 | 101 ± 61 | 106 ± 20 | 0.824 ± 0.105 | |
| high | 162 ± 63 | 177 ± 70 | 0.875 ± 0.039 | 116 ± 56 | 121 ± 22 | 0.851 ± 0.089 | |
| Overall | All | 230 ± 113 | 185 ± 81 | 0.893 ± 0.064 | 142 ± 66 | 80 ± 29 | 0.925 ± 0.076 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wilmes, E.; de Ruiter, C.J.; Bastiaansen, B.J.C.; Zon, J.F.J.A.v.; Vegter, R.J.K.; Brink, M.S.; Goedhart, E.A.; Lemmink, K.A.P.M.; Savelsbergh, G.J.P. Inertial Sensor-Based Motion Tracking in Football with Movement Intensity Quantification. Sensors 2020, 20, 2527. https://doi.org/10.3390/s20092527
Wilmes E, de Ruiter CJ, Bastiaansen BJC, Zon JFJAv, Vegter RJK, Brink MS, Goedhart EA, Lemmink KAPM, Savelsbergh GJP. Inertial Sensor-Based Motion Tracking in Football with Movement Intensity Quantification. Sensors. 2020; 20(9):2527. https://doi.org/10.3390/s20092527
Chicago/Turabian StyleWilmes, Erik, Cornelis J. de Ruiter, Bram J. C. Bastiaansen, Jasper F. J. A. van Zon, Riemer J. K. Vegter, Michel S. Brink, Edwin A. Goedhart, Koen A. P. M. Lemmink, and Geert J. P. Savelsbergh. 2020. "Inertial Sensor-Based Motion Tracking in Football with Movement Intensity Quantification" Sensors 20, no. 9: 2527. https://doi.org/10.3390/s20092527
APA StyleWilmes, E., de Ruiter, C. J., Bastiaansen, B. J. C., Zon, J. F. J. A. v., Vegter, R. J. K., Brink, M. S., Goedhart, E. A., Lemmink, K. A. P. M., & Savelsbergh, G. J. P. (2020). Inertial Sensor-Based Motion Tracking in Football with Movement Intensity Quantification. Sensors, 20(9), 2527. https://doi.org/10.3390/s20092527






