Fusion of Mid-Wave Infrared and Long-Wave Infrared Reflectance Spectra for Quantitative Analysis of Minerals
Abstract
1. Introduction
2. Materials and Datasets
2.1. Samples
2.2. Instrumentation and Datasets
2.2.1. Mid-Wave Infrared (MWIR) and Long-Wave Infrared (LWIR) Datasets
2.2.2. Chemical Analysis (XRF)
3. Methodology
3.1. Multivariate Analysis
3.1.1. Principal Component Analysis (PCA)
3.1.2. Partial-Least Squares Regression (PLSR)
3.1.3. Principal Component Regression (PCR)
3.1.4. Support Vector Regression (SVR)
3.2. Model Performance Assessment
3.3. Data Pre-Processing
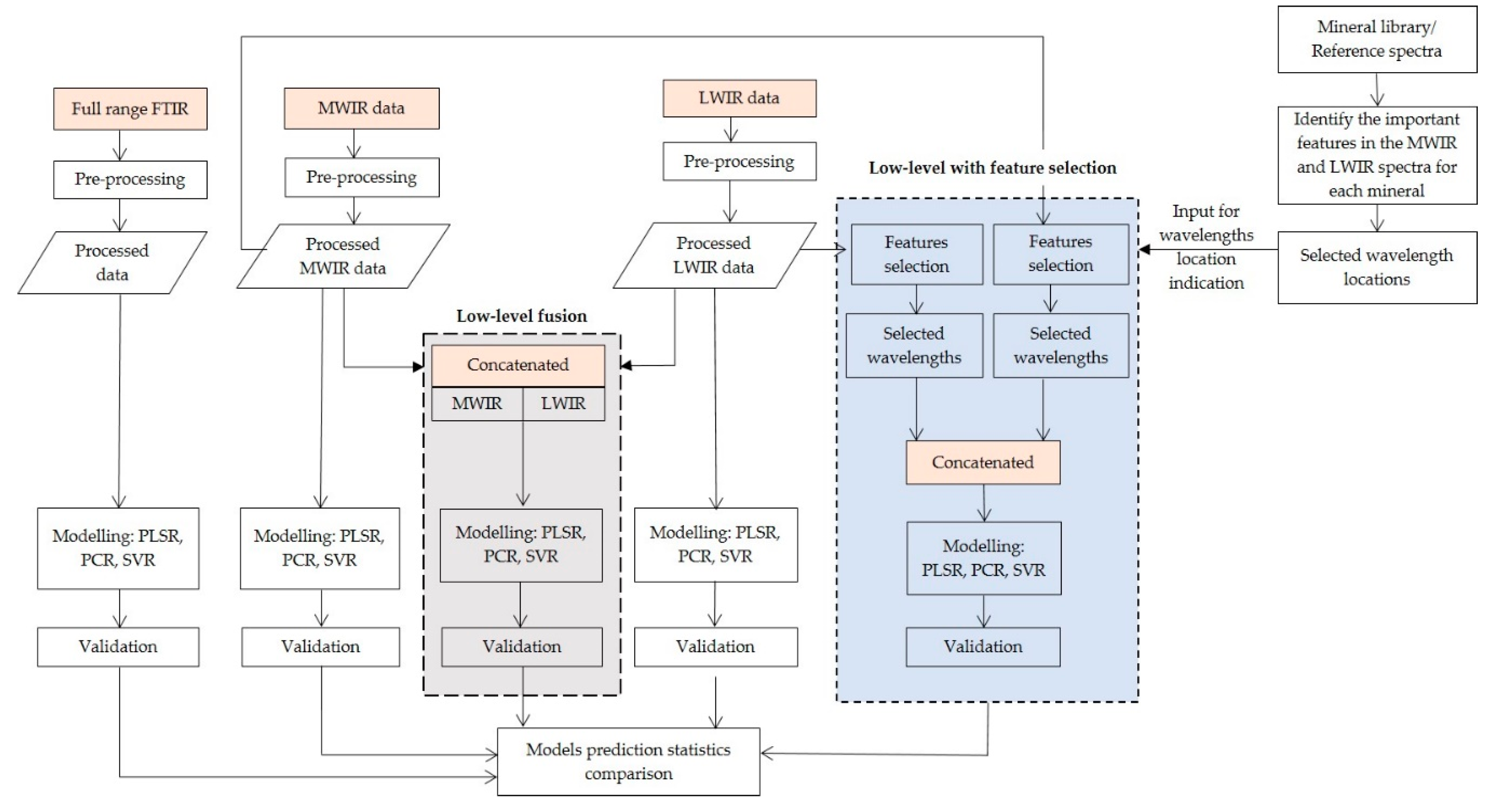
3.4. Data Fusion
3.4.1. Low-Level Data Fusion without Feature Selection
3.4.2. Low-Level Data Fusion with Feature Selection
3.4.3. Individual Datasets
3.5. Calibration and Validation Datasets
4. Results and Discussion
4.1. The Individual Datasets
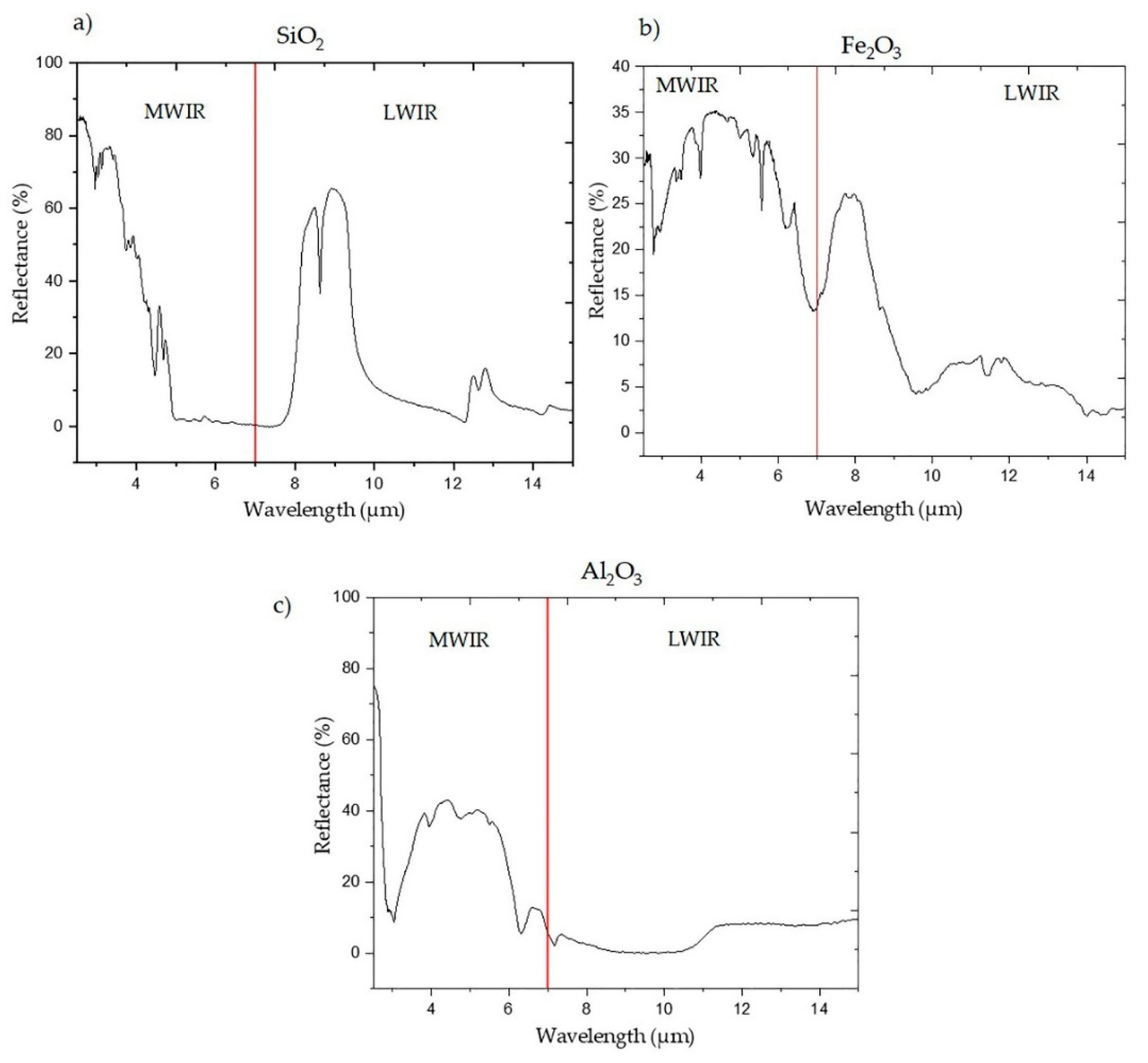
4.1.1. Spectra Features of the Minerals
4.1.2. Exploratory Analysis
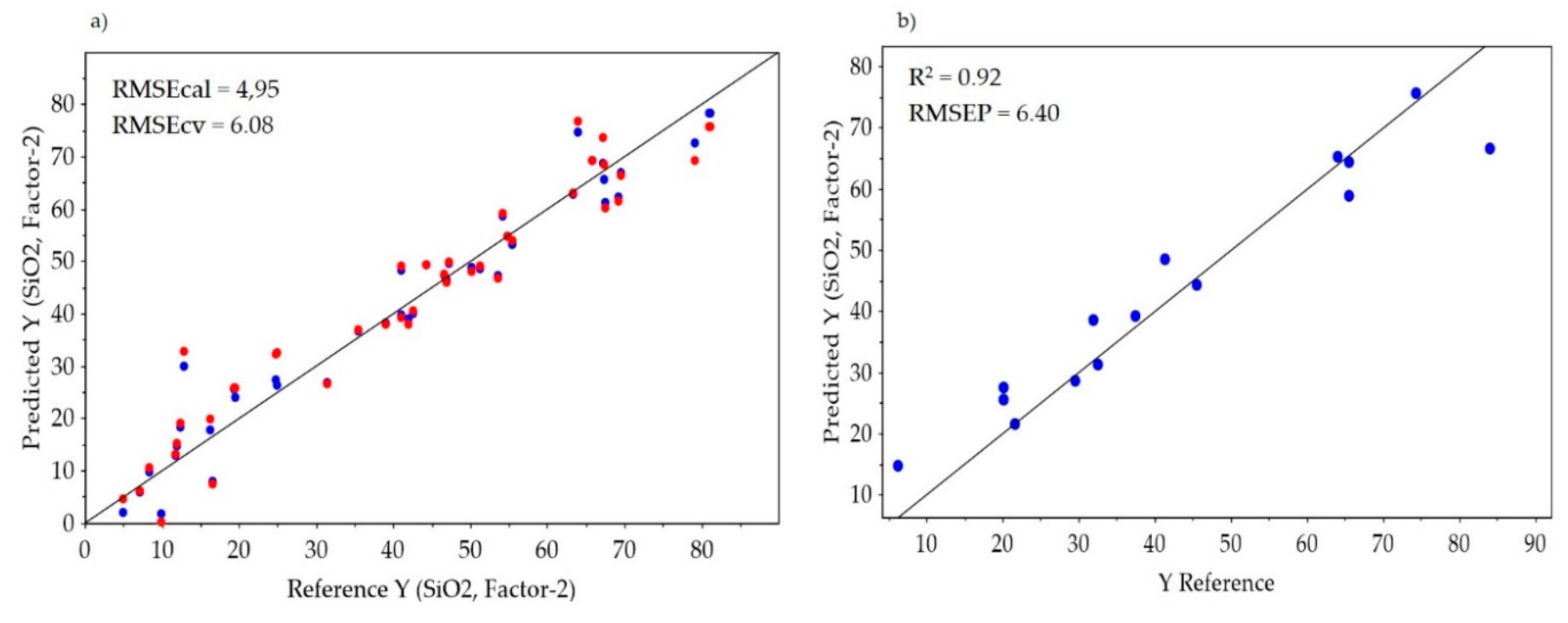
4.1.3. MWIR and LWIR Data Models
4.2. Low-Level Fusion without Feature Selection
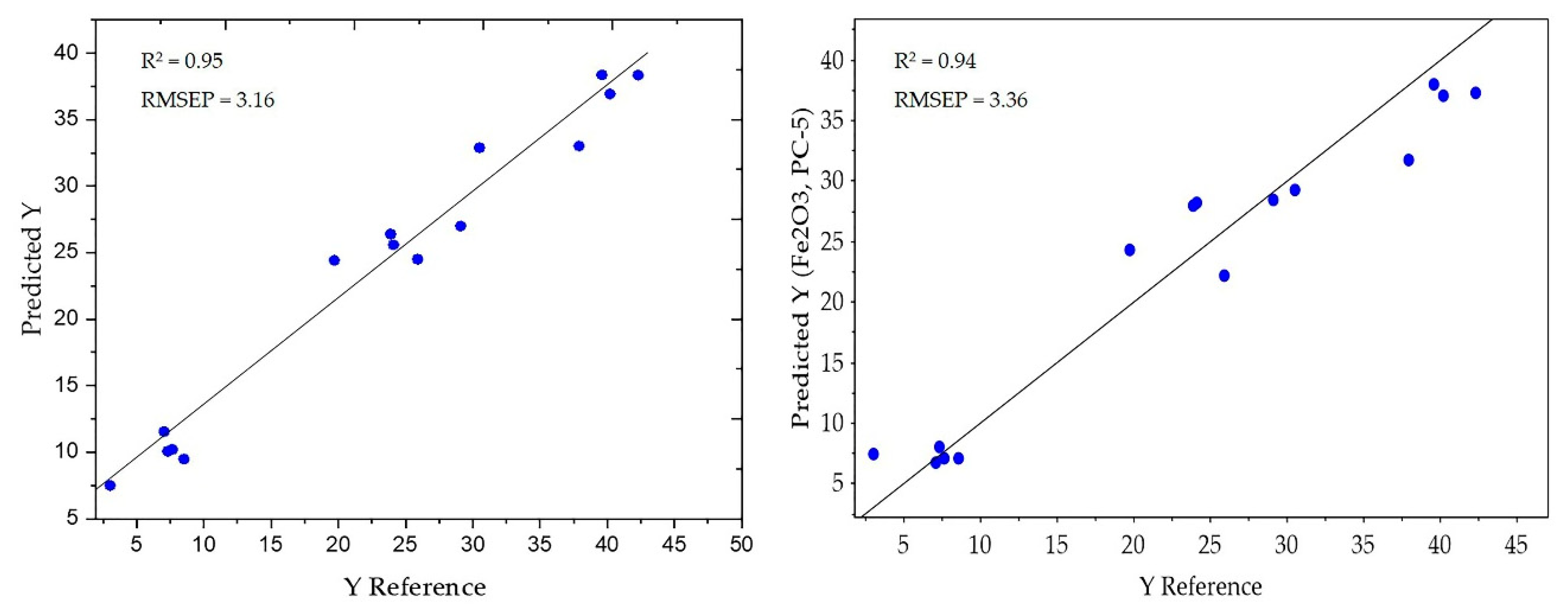
4.3. Low-Level Data Fusion with Feature Selection
4.4. Data Fusion vs. Individual Sensors
4.5. Comparison of the Proposed Models
4.6. Benefits and Limitations of the Proposed Approach for Mining Applications
5. Conclusions
- (1)
- the use of individual spectral regions (MWIR and LWIR);
- (2)
- the effect of different data pre-processing techniques on the prediction performance;
- (3)
- potential for improvement in prediction accuracy by applying low-level and low-level with feature selection data fusion approaches;
- (4)
- comparative benefits of applying linear (PLSR and PCR) and non-linear (SVR) multivariate analysis techniques.
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- David, D. Geometallurgical guidelines for miners, geologists and process engineers—Discovery to design. In Proceedings of the Second AusIMM International Geometallurgy Conference, GeoMet, Melbourne, Australia, 30 September–2 October 2013; pp. 129–132. [Google Scholar]
- Dominy, S.C.; O’Connor, L.; Parbhakar-Fox, A.; Glass, H.J.; Purevgerel, S. Geometallurgy—A Route to More Resilient Mine Operations. Minerals 2018, 8, 560. [Google Scholar] [CrossRef]
- Chukanov, N.V.; Chervonnyi, A.D. Infrared Spectroscopy of Minerals and Related Compounds; Springer: Cham, Switzerland, 2016; p. 1109. [Google Scholar]
- Griffiths, P.R.; Haseth, J.A. Fourier Transform Infrared Spectrometry; John Wiley & Sons: New York, NY, USA, 1986; pp. 51–1047. [Google Scholar]
- Smith, B.C. Introduction to infrared spectroscopy. In Fundamentals of Fourier Transform Infrared Spectroscopy, 2nd ed.; CRC Press: New York, NY, USA, 2011; pp. 1–17. [Google Scholar]
- Agilent-FTIR Compact & Portable Systems. agilent. Available online: http://www.agilent.com/en/products/ftir/ftir-compact-portable-systems/4300-handheld-ftir (accessed on 2 February 2017).
- ASD. Available online: https://www.asdi.com/products-and-services (accessed on 15 September 2019).
- Stuart, B. Infrared Spectroscopy: Fundamentals and Applications; David, J.A., Ed.; John Wiley & Sons: West Sussex, UK, 2004; pp. 1–13. [Google Scholar]
- Rogalski, A.; Chrzanowski, K. Infrared devices and techniques (revision) Metrol. Meas. Syst. 2014, XXI, 565–618. [Google Scholar] [CrossRef]
- Patrice, A.; Stephane, J.; Stephane, R.; Beatrice, V.; Herwig, W. Unexploded Ordnance Detection and Mitigation. In Volatile Compounds Detection by IR Acousto-Optic Detectors; Byrnes, J., Ed.; Springer: Dordrecht, The Netherlands, 2009; pp. 1–10. [Google Scholar]
- Clark, R.N. Spectroscopy of rocks and minerals and principles of spectroscopy. Man. Remote. Sens. 1999, 3, 3–58. [Google Scholar]
- Hollas, J.M. Modern Spectroscopy, 4th ed.; John Wiley & Sons: West Sussex, UK, 2004. [Google Scholar]
- Spectral Evolution. UV-VIS-NIR Spectrometers. Available online: http://www.spectralevolution.com/spectrometers_mining.html (accessed on 12 September 2019).
- Szalai, Z.; Kiss, K.; Jakab, G.; Sipos, P.; Belucz, B.; Németh, T. The use of UV-VIS-NIR reflectance spectroscopy to identify iron minerals. Astron. Nachr. 2013, 334, 940–943. [Google Scholar] [CrossRef]
- Sun, Y.; Seccombe, P.K.; Yang, K. Application of short-wave infrared spectroscopy to define alteration zones associated with the Elura zinc–lead–silver deposit, NSW, Australia. J. Geochem. Explor. 2001, 73, 11–26. [Google Scholar] [CrossRef]
- Dalm, M.; Buxton, M.W.N.; van Ruitenbeek, F.J.A. Ore–Waste Discrimination in Epithermal Deposits Using Near-Infrared to Short-Wavelength Infrared (NIR-SWIR) Hyperspectral Imagery. Math. Geosci. 2018, 51, 849–875. [Google Scholar] [CrossRef]
- Karr, C.; Kovach, J.J. Far-Infrared Spectroscopy of Minerals and Inorganics. Appl. Spectrosc. 1969, 23, 219–223. [Google Scholar] [CrossRef]
- Hecker, C.; Dilles, J.H.; van der Meijde, M.; van der Meer, F.D. Thermal infrared spectroscopy and partial least squares regression to determine mineral modes of granitoid rocks. Geochem. Geophys. Geosyst. 2012, 13. [Google Scholar] [CrossRef]
- Mroczkowska-Szerszeń, M.; Orzechowski, M. Infrared spectroscopy methods in reservoir rocks anaylsis-semiquatitative approch for carbonate rocks. Nafta-Gaz 2018, 11, 1–12. [Google Scholar]
- Palayangoda, S.; Nguyen, Q. An ATR-FTIR procedure for quantitative analysis of mineral constituents and kerogen in oil shale. Oil Shale 2012, 29, 344. [Google Scholar] [CrossRef]
- Guatame-Garcia, A.; Buxton, M. The Use of Infrared Spectroscopy to Determine the Quality of Carbonate-Rich Diatomite Ores. Minerals 2018, 8, 120. [Google Scholar] [CrossRef]
- Kaufhold, S.; Hein, M.; Dohrmann, R.; Ufer, K. Quantification of the mineralogical composition of clays using FTIR spectroscopy. Vib. Spectrosc. 2012, 59, 29–39. [Google Scholar] [CrossRef]
- Cocchi, M. Introduction: Ways and Means to Deal with Data from Multiple Sources. Elsevier 2019, 1–26. [Google Scholar]
- Borràs, E.; Ferré, J.; Boqué, R.; Mestres, M.; Aceña, L.; Busto, O. Data fusion methodologies for food and beverage authentication and quality assessment—A review. Anal. Chim. Acta. 2015, 891, 1–14. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Xiong, Y.; Min, S. Data Fusion Strategy in Quantitative Analysis of Spectroscopy Relevant to Olive oil Adulteration. Vib. Spectrosc. 2019, 101, 20–27. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, J.Y.; Wang, Y.Z. FT-MIR and NIR spectral data fusion: A synergetic strategy for the geographical traceability of Panax notoginseng. Anal. Bioanal. Chem. 2018, 410, 91–103. [Google Scholar] [CrossRef] [PubMed]
- Thrun, S.; Burgard, W.; Fox, D. Probabilistic Robotics; MIT Press: Cambridge, UK, 2005. [Google Scholar]
- Westa, M.S.; Resminib, R.G. Hyperspectral imagery and LiDAR for geological analysis of Cuprite, Nevada. In Proceedings of the Algorithms and Technologies for Multispectral, Hyperspectral, and Ultraspectral Imagery XV, Orlando, FL, USA, 13–16 April 2009. [Google Scholar]
- Biancolillo, A.; Boqué, R.; Cocchi, M.; Marini, F. Chapter 10-Data Fusion Strategies in Food Analysis. Data Handl. Sci. Technol. 2019, 31, 271–310. [Google Scholar]
- Hong, X.; Wang, J. Detection of adulteration in cherry tomato juices based on electronic nose and tongue: comparison of different data fusion approaches. J. Food Eng. 2014, 126, 89–97. [Google Scholar] [CrossRef]
- Khajehzadeh, N.; Haavisto, O.; Koresaar, L. On-stream mineral identification of tailing slurries of an iron ore concentrator using data fusion of LIBS, reflectance spectroscopy and XRF measurement techniques. Miner. Eng. 2017, 113, 83–94. [Google Scholar] [CrossRef]
- Chari, S.K.; Fanning, J.D.; Salem, S.M.; Robinson, A.L.; Halford, C.E. LWIR and MWIR fusion algorithm comparison using image metrics. In Proceedings of the Infrared Imaging Systems: Design, Analysis, Modeling, and Testing XVI, Orlando, FL, USA, 30 March–1 April 2005. [Google Scholar]
- Desta, F.S.; Buxton, M.W.N.; Jansen, J. Data Fusion for the Prediction of Elemental Concentrations in Polymetallic Sulphide Ore using Mid-Wave Infrared and Long-Wave Infrared Reflectance Data. Minerals 2020, 10, 235. [Google Scholar] [CrossRef]
- Seifert, T. Metallogeny and Petrogenesis of Lamprophyres in the Mid-European Variscides—Post-Collisional Magmatism and Its Relationship to Late-Variscan Ore Forming Processes in the Erzgebirge (Bohemian Massif) Germany; IOS Press BV: Amsterdam, The Netherlands, 2008; pp. 1–128. [Google Scholar]
- Benkert, T.; Dietze, A.; Gabriel, P.; Gietzel, J.; Gorz, I.; Grund, K.; Lehmann, H.; Lowe, G.; Mischo, H.; Schaeben, H.; et al. First step towards a virtual mine—Generation of a 3D model of Reiche Zeche in Freiberg. In Proceedings of the 17th Annual Conference of the International Association for Mathematical Geosciences (IAMG), Freiberg, Germany, 5–13 September 2015; pp. 1350–1356. [Google Scholar]
- Desta, F.S.; Buxton, M.W.N. Chemometric Analysis of Mid-Wave Infrared Spectral Reflectance Data for Sulphide Ore Discrimination. Math. Geosci. 2018, 51, 877–903. [Google Scholar] [CrossRef]
- Latan, H.; Noonan, R. Partial Least Squares Path Modelling. Basic Concepts, Methodological Issues and Applications; Springer: Cham, Switzerland, 2017; pp. 3–18. [Google Scholar]
- Zhang, H.; Li, H.; Zhu, H.; Pekárek, J.; Podešva, P.; Chang, H.; Neužil, P. Revealing the secrets of PCR. Sens. Actuators B Chem. 2019, 298. [Google Scholar] [CrossRef]
- Jolliffe, I.T. Principal Component Analysis, 2nd ed.; Springer: New York, NY, USA, 2002. [Google Scholar]
- Weisberg, S. Applied Linear Regression, 2nd ed.; John Wiley & Sons: New York, NY, USA, 1988; p. 324. [Google Scholar]
- Gauthier, T.D.; Hawley, M.E. Introduction to Environmental Forensics. CHAPTER 5-Statistical Methods, 2nd ed.; Murphy, B.L., Morrison, R.D., Eds.; Academic Press: Burlington, MA, USA, 2007; pp. 129–183. [Google Scholar]
- Deris, A.M.; Zain, A.M.; Sallehuddin, R. Overview of Support Vector Machine in Modeling Machining Performances. Procedia Eng. 2011, 24, 308–312. [Google Scholar] [CrossRef]
- Brereton, R.G.; Lloyd, G.R. Support Vector Machines for classification and regression. Analyst 2010, 135, 230–267. [Google Scholar] [CrossRef] [PubMed]
- Alex, J.S.; Bernhard, S. A tutorial on support vector regression. Stat. Comput. 2004, 14, 199–222. [Google Scholar]
- Kecman, V. Support Vector Machines – An Introduction. Stud. Fuzziness Soft Comput. 2005, 177, 1–47. [Google Scholar]
- Roussel, S.; Preys, S.; Chauchard, F.; Lallemand, J. Multivariate data analysis (Chemometrics). Process. Anal. Technol. Food Ind. 2014, 7–59. [Google Scholar]
- Rinnan, Å.; Berg, F.v.d.; Engelsen, S.B. Review of the most common pre-processing techniques for near-infrared spectra. TrAC Trends Anal. Chem. 2009, 28, 1201–1222. [Google Scholar] [CrossRef]
- Bro, R.; Smilde, A.K. Centering and scaling in component analysis. J. Chemom. 2003, 17, 16–33. [Google Scholar] [CrossRef]
- Fearn, T.; Riccioli, C.; Garrido-Varo, A.; Guerrero-Ginel, J.E. On the geometry of SNV and MSC. Chemom. Intell. Lab. Syst. 2009, 96, 22–26. [Google Scholar] [CrossRef]
- NASA. ECOSTRESS Spectral Library. Available online: https://speclib.jpl.nasa.gov (accessed on 1 September 2019).



| Datasets/Fusion Method | Pre-Processing | PLSR | PCR | SVR | |||
|---|---|---|---|---|---|---|---|
| RMSEP | R2 | RMSEP | R2 | RMSEP | R2 | ||
| MWIR | Raw | 6.18 | 0.78 | 7.88 | 0.64 | 5.50 | 0.81 |
| Normalize | 4.53 | 0.88 | 4.97 | 0.86 | 3.95 | 0.90 | |
| Baseline | 5.02 | 0.86 | 4.01 | 0.91 | 6.39 | 0.77 | |
| LWIR | Raw | 7.32 | 0.69 | 5.97 | 0.80 | 4.78 | 0.85 |
| Normalize | 4.51 | 0.88 | 5.34 | 0.84 | 4.57 | 0.87 | |
| Baseline | 7.50 | 0.68 | 5.79 | 0.81 | 5.26 | 0.84 | |
| Full-range | Raw | 6.05 | 0,79 | 5.2 | 0,84 | 4.71 | 0.87 |
| Normalize | 3.68 | 0,92 | 3.95 | 0.91 | 3.40 | 0.93 | |
| Baseline | 4.29 | 0.89 | 4.03 | 0.91 | 4.86 | 0.87 | |
| Low-level | Normalize | 3.30 | 0.94 | 3.36 | 0.94 | 3.16 | 0.95 |
| Baseline | 4.57 | 0.88 | 3.87 | 0.91 | 4.94 | 0.84 | |
| Low-level with the selected features | Normalize | 4.22 | 0.90 | 4.44 | 0.89 | 4.34 | 0.89 |
| Baseline | 5.18 | 0.85 | 5.76 | 0.81 | 7.34 | 0.69 | |
| Datasets/Fusion Method | Pre-Processing | PLSR | PCR | SVR | |||
|---|---|---|---|---|---|---|---|
| RMSEP | R2 | RMSEP | R2 | RMSEP | R2 | ||
| MWIR | Raw | 7.95 | 0.87 | 8.22 | 0.86 | 10.30 | 0.74 |
| Normalize | 7.77 | 0.88 | 8.80 | 0.84 | 8.47 | 0.86 | |
| Baseline | 8.40 | 0.86 | 7.38 | 0.89 | 9.89 | 0.82 | |
| LWIR | Raw | 12.8 | 0.67 | 9.69 | 0.81 | 9.13 | 0.83 |
| Normalize | 6.12 | 0.92 | 6.50 | 0.91 | 6.56 | 0.90 | |
| Baseline | 9.13 | 0.83 | 9.06 | 0.83 | 8.74 | 0.85 | |
| Full-range | Raw | 6.95 | 0.90 | 7.55 | 0.88 | 9.14 | 0.86 |
| Normalize | 6.42 | 0.92 | 7.16 | 0.90 | 7.52 | 0.90 | |
| Baseline | 7.19 | 0.90 | 8.44 | 0.86 | 9.08 | 0.83 | |
| Low-level | Normalize | 5.96 | 0.93 | 7.17 | 0.90 | 6.85 | 0.90 |
| Baseline | 7.66 | 0.88 | 8.56 | 0.85 | 8.69 | 0.89 | |
| Low-level with the selected features | Normalize | 6.40 | 0.92 | 6.06 | 0.93 | 6.77 | 0.91 |
| Baseline | 8.30 | 0.86 | 8.37 | 0.86 | 10.10 | 0.81 | |
| Datasets/Fusion Method | Pre-Processing | PLSR | PCR | SVR | |||
|---|---|---|---|---|---|---|---|
| RMSEP | R2 | RMSEP | R2 | RMSEP | R2 | ||
| MWIR | Raw | 2.16 | 0.79 | 2.05 | 0.81 | 1.69 | 0.86 |
| Normalize | 1.86 | 0.85 | 1.92 | 0.84 | 1.93 | 0.83 | |
| Baseline | 2.11 | 0.80 | 1.99 | 0.82 | 1.68 | 0.88 | |
| LWIR | Raw | 2.47 | 0.73 | 2.59 | 0.70 | 2.3 | 0.77 |
| Normalize | 2.09 | 0.80 | 2.03 | 0.82 | 1.86 | 0.85 | |
| Baseline | 2.29 | 0.76 | 2.71 | 0.75 | 1.83 | 0.84 | |
| Full-range | Raw | 2.02 | 0.82 | 1.99 | 0.82 | 1.75 | 0.87 |
| Normalize | 2.02 | 0.82 | 1.99 | 0.82 | 1.9 | 0.85 | |
| Baseline | 2.15 | 0.79 | 1.82 | 0.85 | 1.69 | 0.87 | |
| Low-level | Normalize | 1.95 | 0.83 | 2.06 | 0.81 | 1.83 | 0.86 |
| Baseline | 2.06 | 0.81 | 2.13 | 0.80 | 1.68 | 0.88 | |
| Low-level with the selected features | Normalize | 1.40 | 0.91 | 1.48 | 0.90 | 1.79 | 0.86 |
| Baseline | 1.82 | 0.85 | 1.77 | 0.86 | 1.59 | 0.89 | |
| Minerals | MWIR Wavelength (µm) | LWIR Wavelength (µm) |
|---|---|---|
| Al2O3 | 2.85–3.10 | 7.00–7.29 |
| 3.83–5.73, 6.20–6.40 | 10.50–11.40 | |
| Fe2O3 | 2.78–2.92, 3.38–3.5, 3.92–4.03, 5.0–5.10 | 7.00–7.20, 7.74–8.05, 9.38–10.00 |
| 5.30–5.39, 5.53–5.69, 6.15–6.31, 6.76–7.00 | 11.30–11.6, 13.90–14.10, 14.40–14.60 | |
| SiO2 | 3.65–4.93 | 8.00–10.00 |
| 12.00–13.00 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Desta, F.; Buxton, M.; Jansen, J. Fusion of Mid-Wave Infrared and Long-Wave Infrared Reflectance Spectra for Quantitative Analysis of Minerals. Sensors 2020, 20, 1472. https://doi.org/10.3390/s20051472
Desta F, Buxton M, Jansen J. Fusion of Mid-Wave Infrared and Long-Wave Infrared Reflectance Spectra for Quantitative Analysis of Minerals. Sensors. 2020; 20(5):1472. https://doi.org/10.3390/s20051472
Chicago/Turabian StyleDesta, Feven, Mike Buxton, and Jeroen Jansen. 2020. "Fusion of Mid-Wave Infrared and Long-Wave Infrared Reflectance Spectra for Quantitative Analysis of Minerals" Sensors 20, no. 5: 1472. https://doi.org/10.3390/s20051472
APA StyleDesta, F., Buxton, M., & Jansen, J. (2020). Fusion of Mid-Wave Infrared and Long-Wave Infrared Reflectance Spectra for Quantitative Analysis of Minerals. Sensors, 20(5), 1472. https://doi.org/10.3390/s20051472






