Dynamic Deformation Measurement of Specular Surface with Deflectometry and Speckle Digital Image Correlation
Abstract
1. Introduction
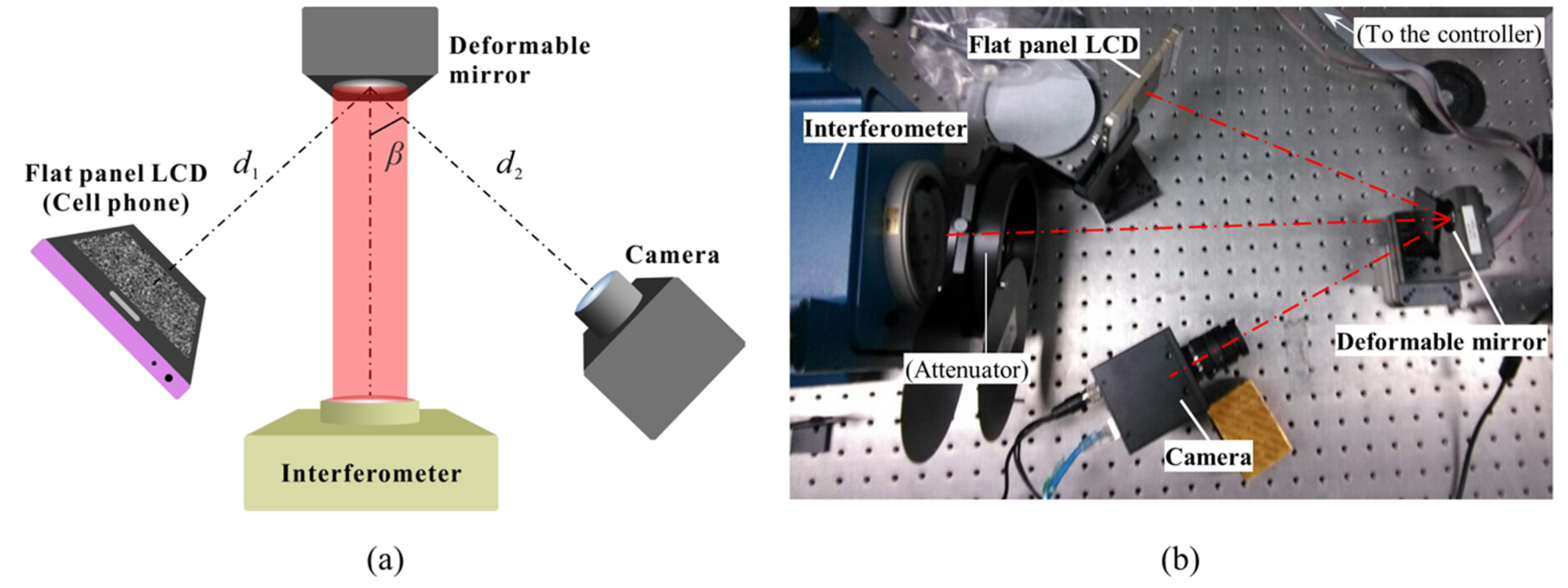
2. Materials and Methods
3. Experiments and Results
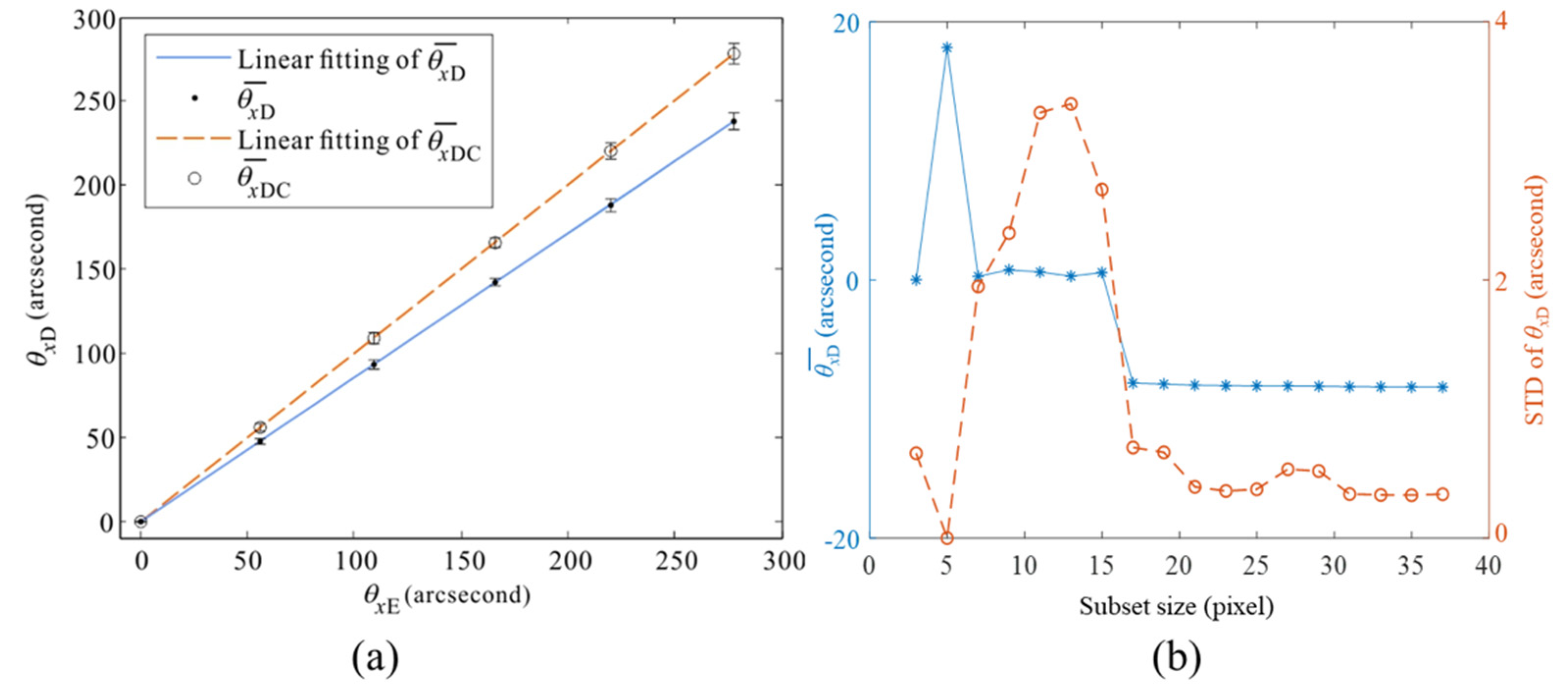
3.1. Calibration of the Linear Coefficient
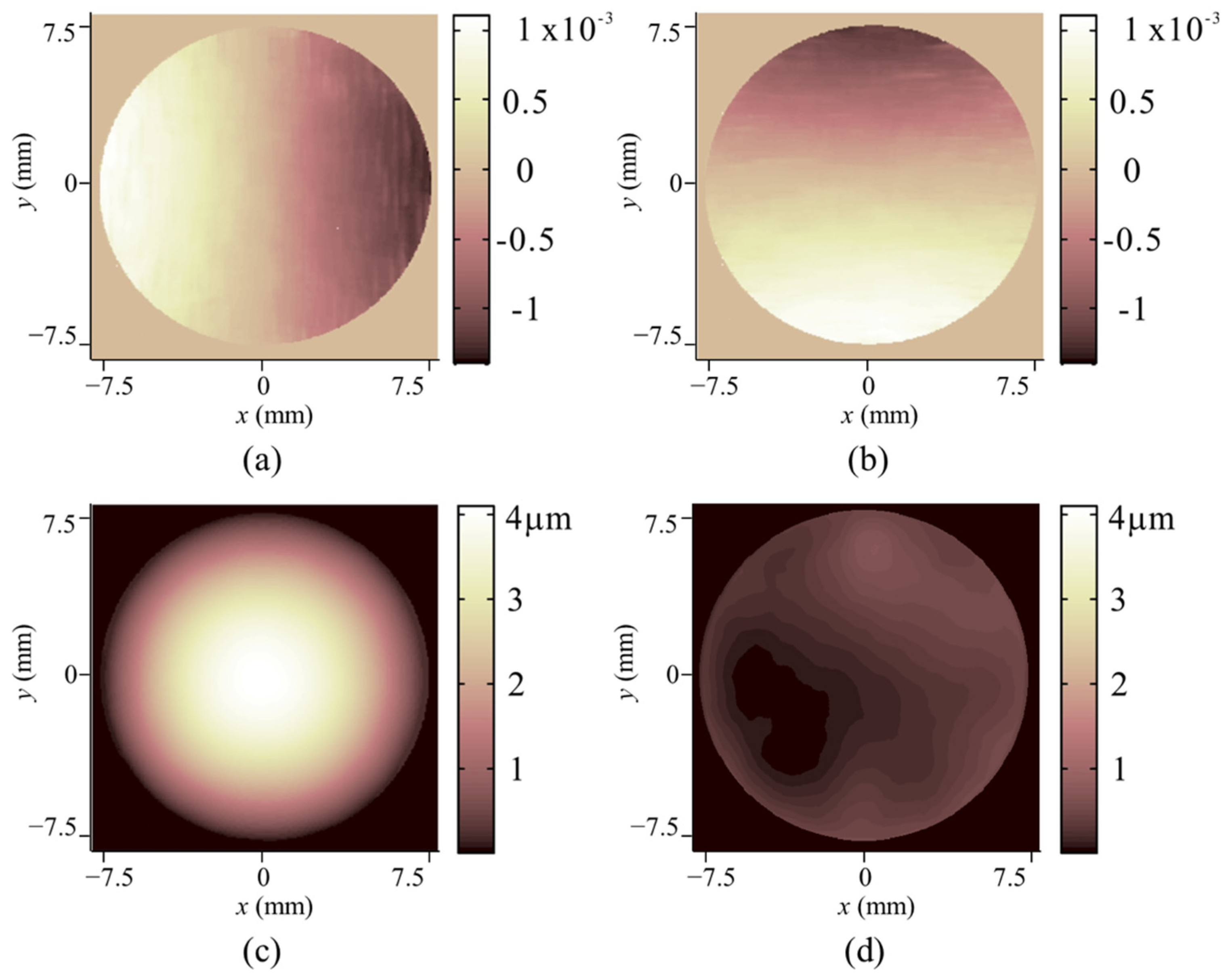
3.2. Deformation Measurement
3.3. Dynamic Measurement
3.4. Error Analysis
4. Conclusions
5. Patents
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Huang, L.; Idir, M.; Zuo, C.; Asundi, A. Review of phase measuring deflectometry. Opt. Laser Eng. 2018, 107, 247–257. [Google Scholar] [CrossRef]
- Knauer, M.; Haulser, G. Phase measuring deflectometry: A new approach to measure specular free-form surfaces. Proc. SPIE 2004, 5457, 366–376. [Google Scholar]
- Tang, Y.; Su, X.; Liu, Y.; Jing, H. 3D shape measurement of the aspheric mirror by advanced phase measuring deflectometry. Opt. Express 2008, 16, 15090–15096. [Google Scholar] [CrossRef] [PubMed]
- Huang, L.; Xue, J.; Gao, B.; McPherson, C.; Beverage, J.; Idir, M. Modal phase measuring deflectometry. Opt. Express 2016, 24, 24649–24664. [Google Scholar] [CrossRef] [PubMed]
- Butel, G.; Smith, G.; Burge, J. Binary pattern deflectometry. Appl. Opt. 2014, 53, 923–930. [Google Scholar] [CrossRef]
- Su, P.; Wang, Y.H.; Burge, J.H.; Kaznatcheev, K.; Idir, M. Non-null full field X-ray metrology using SCOTS: A reflection deflectometry approach. Opt. Express 2012, 20, 12393–12406. [Google Scholar] [CrossRef]
- Huang, R.; Su, P.; Horne, T.; Brusa, G.; Burge, J.H. Optical metrology of a large deformable aspherical mirror using software configurable optical test system. Opt. Eng. 2014, 53, 085106. [Google Scholar] [CrossRef]
- Yang, S.; Shi, X.; Zhang, G.; Lv, C.; Yang, X. Measurement of 3-DOF Planar Motion of the Object Based on Image Segmentation and Matching. Nanomanuf. Metrol. 2019, 2, 124–129. [Google Scholar] [CrossRef]
- Jin, C.; Li, D.; Kewei, E.; Li, M.; Chen, P.; Wang, R.; Xiong, Z. Phase extraction based on iterative algorithm using five-frame crossed fringes in phase measuring deflectometry. Opt. Laser Eng. 2018, 105, 93–100. [Google Scholar] [CrossRef]
- Xiao, Y.; Su, X.; Chen, W. Flexible geometrical calibration for fringe-reflection 3D measurement. Opt. Lett. 2012, 37, 620–622. [Google Scholar] [CrossRef]
- Ren, H.; Gao, F.; Jiang, X. Iterative optimization calibration method for stereo deflectometry. Opt. Express 2015, 23, 22060–22068. [Google Scholar] [CrossRef] [PubMed]
- Kewei, E.; Li, D.; Yang, L.; Yang, L.; Guo, G.; Li, M.; Wang, X.; Zhang, T.; Xiong, Z. Novel method for high accuracy figure measurement of optical flat. Opt. Laser Eng. 2017, 88, 162–166. [Google Scholar]
- Ren, H.; Gao, F.; Jiang, X. Least-squares method for data reconstruction from gradient data in deflectometry. Appl. Opt. 2016, 55, 6052–6059. [Google Scholar] [CrossRef] [PubMed]
- Huang, L.; Idir, M.; Zuo, C.; Kaznatcheev, K.; Zhou, L.; Asundi, A. Comparison of two-dimensional integration methods for shape reconstruction from gradient data. Opt. Laser Eng. 2015, 64, 1–11. [Google Scholar] [CrossRef]
- Li, W.; Huke, P.; Burke, J.; Kopylow, C.; Bergmann, R.B. Measuring deformations with deflectometry. Proc. SPIE 2014, 9203, 92030F. [Google Scholar]
- Liang, H.; Olesch, E.; Yang, Z.; Häusler, G. Single-shot phase-measuring deflectometry for cornea measurement. Adv. Opt. Technol. 2016, 5, 433–438. [Google Scholar] [CrossRef]
- Huang, L.; Ng, C.; Asundi, A. Dynamic three-dimensional sensing for specular surface with monoscopic fringe reflectometry. Opt. Express 2011, 19, 12809–12814. [Google Scholar] [CrossRef]
- Dong, B.; Zeng, F.; Pan, B. A Simple and Practical Single-Camera Stereo-Digital Image Correlation Using a Color Camera and X-Cube Prism. Sensors 2019, 19, 4726. [Google Scholar] [CrossRef]
- Pan, B. Digital image correlation for surface deformation measurement: Historical developments, recent advances and future goals. Meas. Sci. Technol. 2018, 29, 082001. [Google Scholar] [CrossRef]
- Pan, B.; Qian, K.; Xie, H.; Asundi, A. Two-dimensional digital image correlation for in-plane displacement and strain measurement: A review. Meas. Sci. Technol. 2009, 20, 062001. [Google Scholar] [CrossRef]
- Belloni, V.; Ravanelli, R.; Nascetti, A.; Di Rita, M.; Mattei, D.; Crespi, M. py2DIC: A New Free and Open Source Software for Displacement and Strain Measurements in the Field of Experimental Mechanics. Sensors 2019, 19, 3832. [Google Scholar] [CrossRef] [PubMed]
- Yuan, Y.; Huang, J.Y.; Peng, X.L.; Xiong, C.Y.; Fang, J.; Yuan, F. Accurate displacement measurement via a self-adaptive digital image correlation method based on a weighted ZNSSD criterion. Opt. Laser Eng. 2014, 52, 75–85. [Google Scholar] [CrossRef]
- Shi, H.J.; Ji, H.W.; Yang, G.B.; He, X.Y. Shape and deformation measurement system by combining fringe projection and digital image correlation. Opt. Laser Eng. 2013, 51, 47–53. [Google Scholar] [CrossRef]
- Felipe-SeSé, L.; Siegmann, P.; DÍaz, F.A.; Patterson, E.A. Simultaneous in-and-out-of plane displacement measurements using fringe projection and digital image correlation. Opt. Laser Eng. 2013, 52, 66–74. [Google Scholar] [CrossRef]
- Zhong, F.; Kumar, R.; Quan, C. A cost-effective single-shot structured light system for 3D shape measurement. IEEE Sens. J. 2019, 19, 7335–7346. [Google Scholar] [CrossRef]
- Zhong, F.; Kumar, R.; Quan, C. RGB laser speckles based 3D profilometry. Appl. Phys. Lett. 2019, 114, 201104. [Google Scholar] [CrossRef]
- Khan, D.; Shirazi, M.; Kim, M. Single shot laser speckle based 3D acquisition system for medical applications. Opt. Laser Eng. 2018, 105, 43–53. [Google Scholar] [CrossRef]
- Tang, H.; Li, D.; Li, L.; Chen, P.; Wang, R.; Wang, Q. Planar Object Surface Shape Speckle Pattern Deflectometry Based on Digital Image Correlation. Acta Opt. Sin. 2019, 39, 0212006. (In Chinese) [Google Scholar] [CrossRef]
- Zhang, X.; Li, D.; Wang, R.; Tang, H.; Luo, P.; Xu, K. Speckle pattern shifting deflectometry based on digital image correlation. Opt. Express 2019, 27, 25395–25409. [Google Scholar] [CrossRef]
- Zuo, C.; Feng, S.; Huang, L.; Tao, T.; Yin, W.; Chen, Q. Phase shifting algorithms for fringe projection profilometry: A review. Opt. Laser Eng. 2018, 109, 23–59. [Google Scholar] [CrossRef]
- Matczak, M.J.; Sokorowski, A. Computer-aided generation of speckle pattern in digital images. Proc. SPIE 1994, 2340, 158–162. [Google Scholar]
- Tian, L.; Waller, L. Quantitative differential phase contrast imaging in an LED array microscope. Opt. Express 2015, 23, 11394–11403. [Google Scholar] [CrossRef] [PubMed]
- Chen, Z.; Shao, X.; Xu, X.; He, X. Optimized digital speckle patterns for digital image correlation by consideration of both accuracy and efficiency. Appl. Opt. 2018, 57, 884–893. [Google Scholar] [CrossRef] [PubMed]



© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, Y.; Wang, S.; Cheng, X.; Xu, C.; Hao, Q. Dynamic Deformation Measurement of Specular Surface with Deflectometry and Speckle Digital Image Correlation. Sensors 2020, 20, 1278. https://doi.org/10.3390/s20051278
Hu Y, Wang S, Cheng X, Xu C, Hao Q. Dynamic Deformation Measurement of Specular Surface with Deflectometry and Speckle Digital Image Correlation. Sensors. 2020; 20(5):1278. https://doi.org/10.3390/s20051278
Chicago/Turabian StyleHu, Yao, Shaopu Wang, Xuemin Cheng, Chengqiang Xu, and Qun Hao. 2020. "Dynamic Deformation Measurement of Specular Surface with Deflectometry and Speckle Digital Image Correlation" Sensors 20, no. 5: 1278. https://doi.org/10.3390/s20051278
APA StyleHu, Y., Wang, S., Cheng, X., Xu, C., & Hao, Q. (2020). Dynamic Deformation Measurement of Specular Surface with Deflectometry and Speckle Digital Image Correlation. Sensors, 20(5), 1278. https://doi.org/10.3390/s20051278





