Gait Analysis with Wearables Can Accurately Classify Fallers from Non-Fallers: A Step toward Better Management of Neurological Disorders
Abstract
1. Introduction
2. Materials and Methods
2.1. Participants
2.2. Gait Assessment
2.3. Extraction of Gait Characteristics
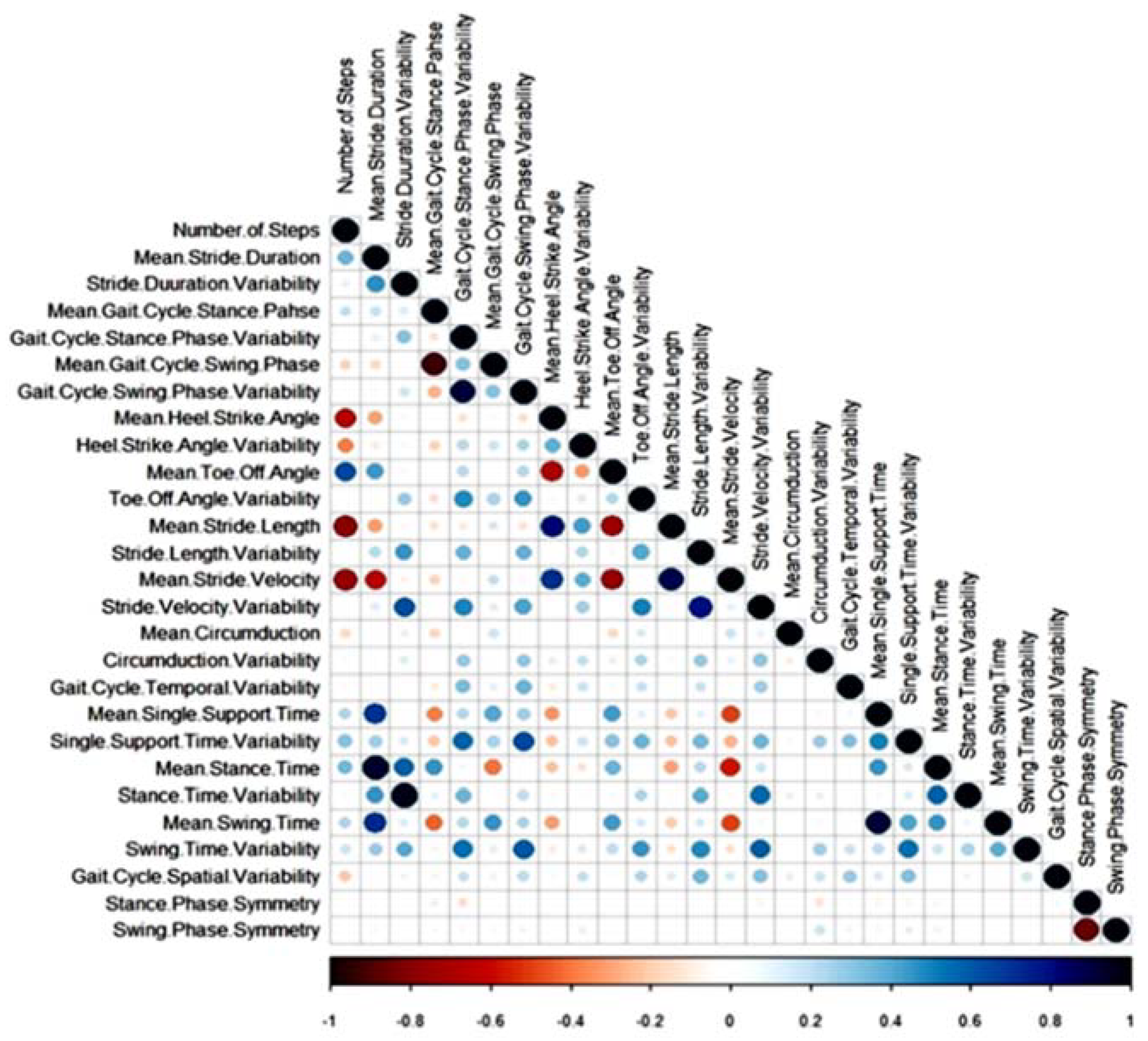
2.4. Statistical Analysis
2.5. Methods of Data Pre-Processing for Machine Learning Models
2.5.1. Standardisation
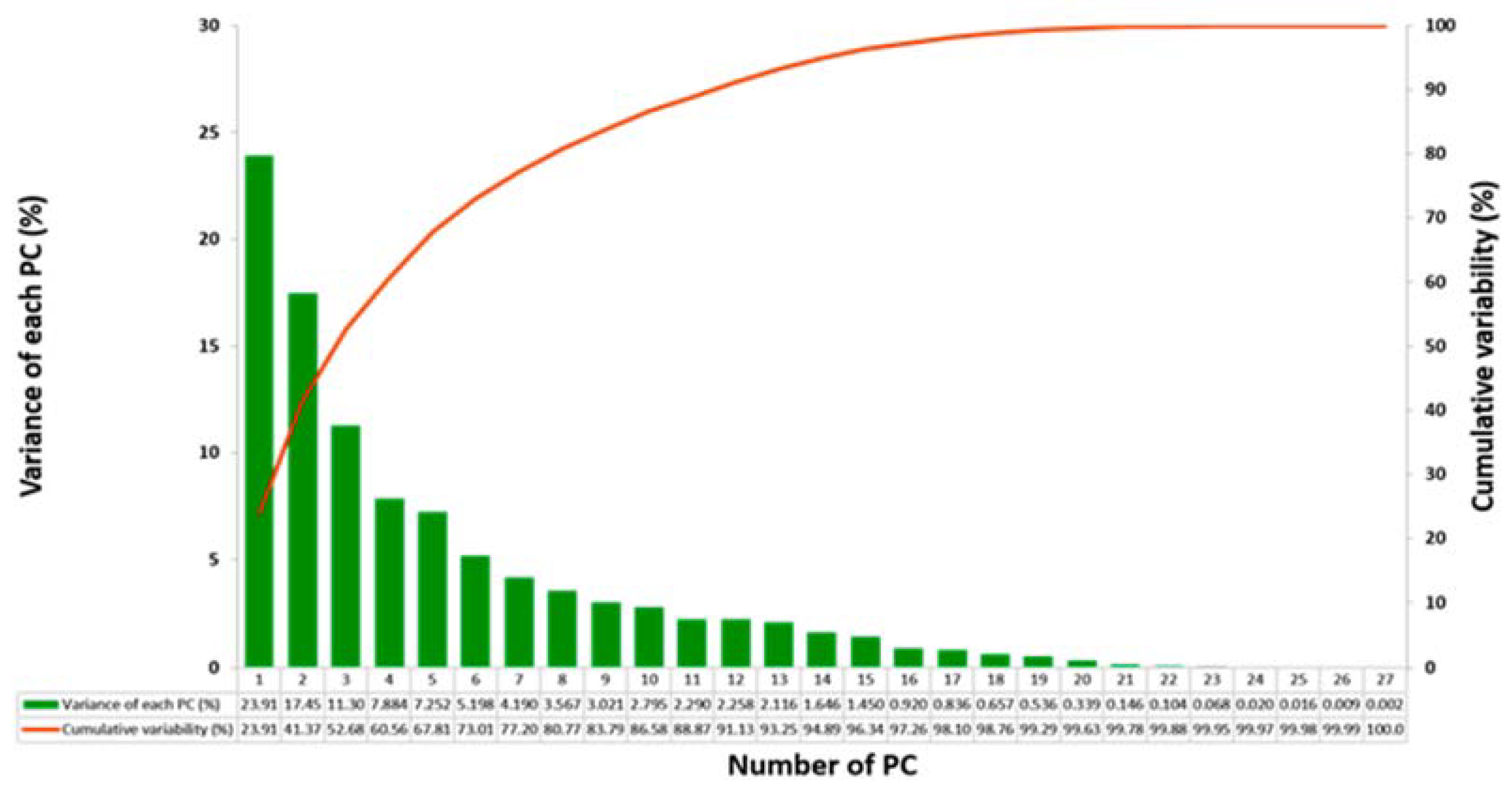
2.5.2. Principal Component Analysis
2.5.3. Path Signature Method
2.6. Classification of Fallers vs. Non-Fallers
3. Results
3.1. Demographics
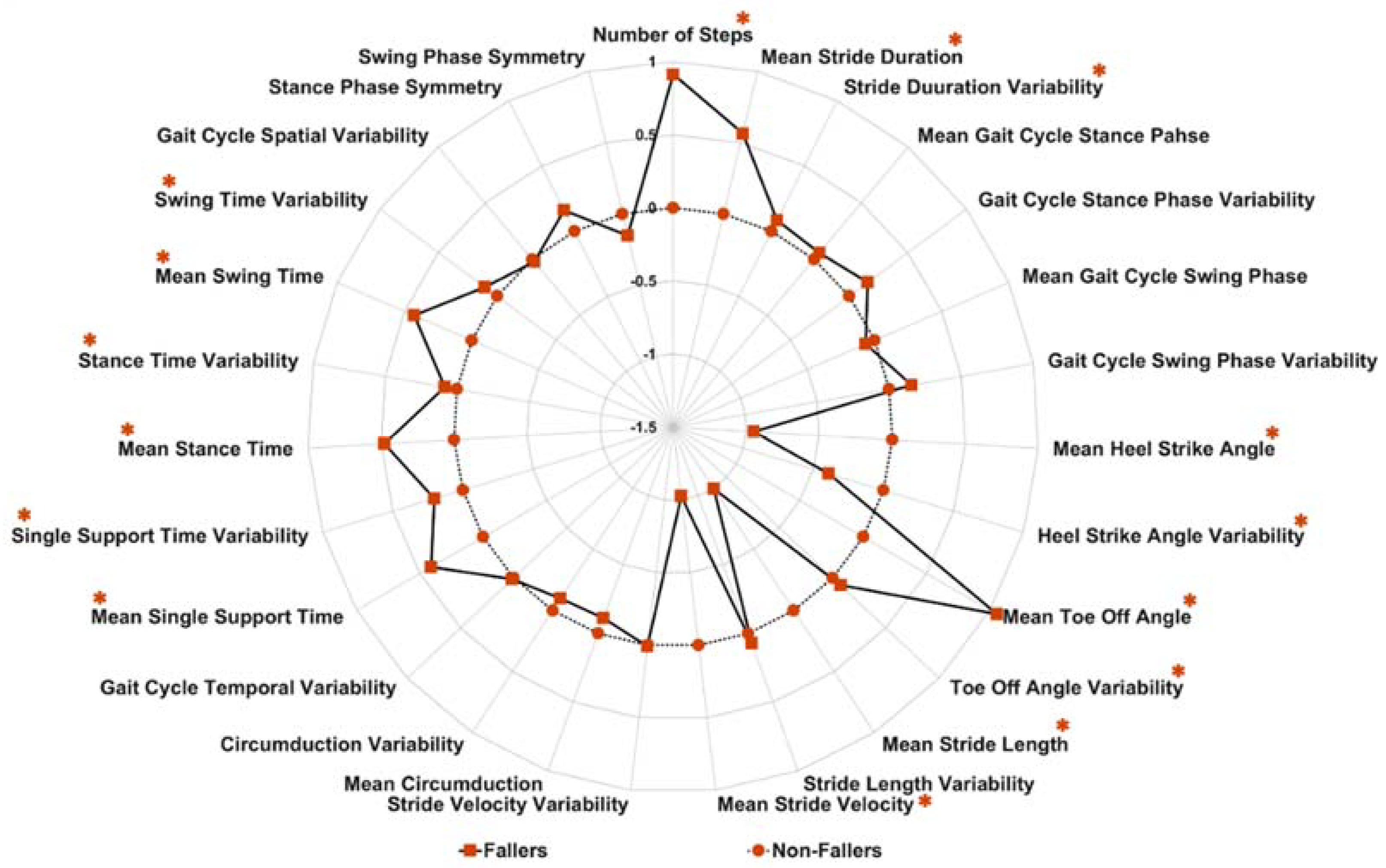
3.2. Differences in Gait Characteristics between Fallers and Non-Fallers
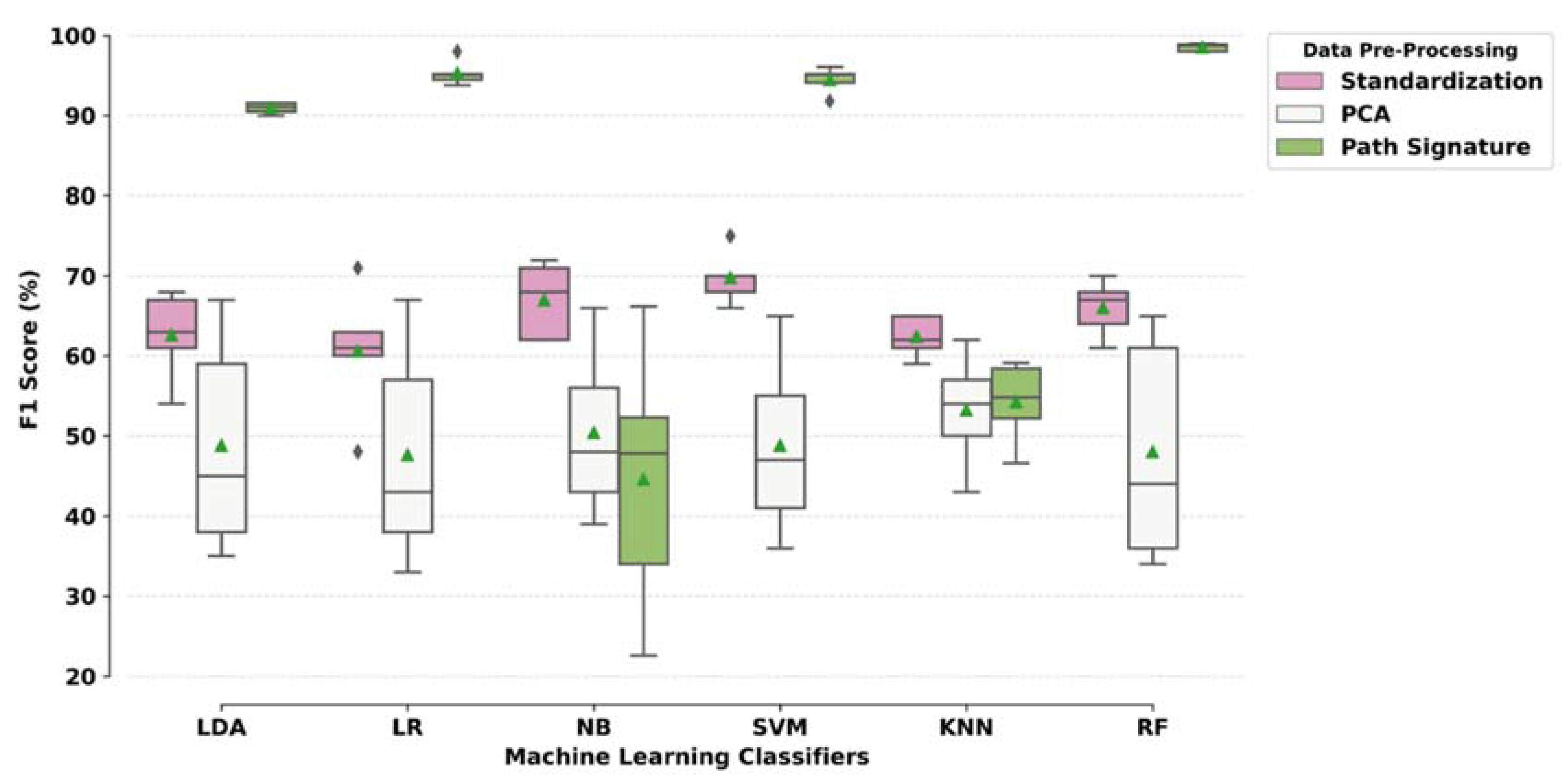
3.3. Classification Modelling Results: Combinations of Pre-Processing Techniques and ML Models
4. Discussion
4.1. Limitations
4.2. Clinical Implications
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
| Results Based on Standardised Spatial-Temporal Features Accuracy (Sen, Spec) | ||||||
| ML Models | Split 1 | Split 2 | Split 3 | Split 4 | Split 5 | Average |
| LDA | 68.57(0.79, 0.56) | 61.9(0.49, 0.73) | 63.81(0.51, 0.76) | 53.33(0.57, 0.51) | 67.9(0.76, 0.55) | 63.10(0.62, 0.62) |
| LR | 71.43(0.79, 0.63) | 63.8(0.49, 0.77) | 61.9(0.51, 0.72) | 47.62(0.54, 0.42) | 59(0.62, 0.55) | 60.75(0.59, 0.62) |
| NB | 62.86(0.76, 0.49) | 71.43(0.55,0.86) | 62.86(0.47, 0.78) | 72.38(0.57, 0.85) | 69.52(0.86, 0.43) | 67.81(0.64, 0.68) |
| SVM | 70.48(0.87, 0.53) | 68.57(0.53,0.82) | 67.62(0.47, 0.87) | 70.48(0.52, 0.85) | 75.24(0.83, 0.63) | 70.48(0.64, 0.74) |
| KNN | 64.76(0.72,0.57) | 60.95(0.59, 0.63) | 61.9(0.55, 0.69) | 64.76(0.54, 0.73) | 59.05(0.63, 0.53) | 62.28(0.61, 0.63) |
| RF | 63.8(0.72,0.55) | 70.48(0.61, 0.79) | 61.9(0.51, 0.72) | 67.62(0.59, 0.75) | 67.62(0.71, 0.63) | 66.284(0.63, 0.69) |
| Results based on PCA Accuracy (Sen, Spec) | ||||||
| ML Models | Split 1 | Split 2 | Split 3 | Split 4 | Split 5 | Average |
| LDA | 60(0.76, 0.43) | 67.62(0.51, 0.82) | 38.1(0.31,0.44) | 44.76(0.35, 0.53) | 34.29(0.32, 0.38) | 48.95(0.45, 0.52) |
| LR | 58.1(0.7, 0.45) | 67.62(0.51, 0.82) | 38.1(0.33, 0.43) | 42.86(0.39, 0.46) | 32.38(0.29, 0.38) | 47.81(0.44, 0.51) |
| NB | 58.1(0.78, 0.37) | 66.67(0.49, 0.82) | 39.05(0.31, 0.46) | 42.86(0.33, 0.51) | 49.52(0.65, 0.25) | 51.24(0.51, 0.48) |
| SVM | 58.1(0.85, 0.29) | 67.62(0.41, 0.91) | 42.86(0.26, 0.59) | 49.52(0.24, 0.7) | 35.24(0.39, 0.3) | 50.67(0.43, 0.56) |
| KNN | 55.24(0.69, 0.41) | 61.9(0.57, 0.66) | 45.7(0.24, 0.67) | 39.05(0.44, 0.36) | 49.52(0.51, 0.48) | 50.28(0.49, 0.52) |
| RF | 60.95(0.69, 0.53) | 64.76(0.59, 0.7) | 36.19(0.41, 0.32) | 43.81(0.52, 0.37) | 35.23(0.25, 0.53) | 48.19(0.49, 0.49) |
| Results based on Path Signature Method Accuracy (Sen, Spec) | ||||||
| ML Models | Split 1 | Split 2 | Split 3 | Split 4 | Split 5 | Average |
| LDA | 91.43(0.961,0.87) | 91.43(0.94, 0.89) | 90.47(0.88, 0.93) | 92.38(0.83, 1) | 93.33(0.95,0.923) | 91.81(0.91, 0.92) |
| LR | 95.24(0.98, 0.93) | 98.095(1,0.96) | 95.2(0.96, 0.94) | 95.24(0.94, 0.97) | 95.24(0.95,0.953) | 95.80(0.97, 0.95) |
| NB | 54.28(0.137,0.93) | 66.67(0.33, 0.96) | 57.14(0.86, 0.29) | 70.47(0.37, 0.97) | 66.67(0.23, 0.94) | 63.05(0.38, 0.82) |
| SVM | 95.24(0.96, 0.94) | 96.19(1, 0.93) | 94.28(0.94, 0.94) | 93.33(0.85, 1) | 96.19(1, 0.94) | 95.05(0.95, 0.95) |
| KNN | 64.76(0.51, 0.78) | 65.71(0.53, 0.77) | 58.09(0.47, 0.69) | 63.810(0.50,0.75) | 62.857(0.43,0.75) | 63.04(0.49, 0.75) |
| RF | 99.05 (1,0.98) | 98.09 (1,0.96) | 98.09 (0.98, 0.98) | 99.05(0.98, 1) | 99.05 (1, 0.98) | 98.67(0.99, 0.98) |
| Results Based on Standardised Spatial-Temporal Features F1 Score (AUC) | ||||||
| ML Models | Split 1 | Split 2 | Split 3 | Split 4 | Split 5 | Average |
| LDA | 0.68(0.71) | 0.61(0.7) | 0.63(0.63) | 0.54(0.54) | 0.67(0.67) | 0.63(0.65) |
| LR | 0.71(0.7) | 0.63(0.69) | 0.61(0.63) | 0.48(0.49) | 0.6(0.63) | 0.61(0.63) |
| NB | 0.62(0.66) | 0.71(0.76) | 0.62(0.65) | 0.72(0.74) | 0.68(0.67) | 0.67(0.7) |
| SVM | 0.7(0.7) | 0.68(0.68) | 0.66(0.67) | 0.7(0.69) | 0.75(0.73) | 0.7(0.7) |
| KNN | 0.65(0.67) | 0.61(0.59) | 0.62(0.65) | 0.65(0.64) | 0.59(0.62) | 0.62(0.63) |
| RF | 0.64(0.7) | 0.7(0.74) | 0.61(0.64) | 0.67(0.72) | 0.68(0.76) | 0.66(0.71) |
| Results based on PCA F1 Score (AUC) | ||||||
| ML Models | Split 1 | Split 2 | Split 3 | Split 4 | Split 5 | Average |
| LDA | 0.59(0.62) | 0.67(0.73) | 0.38(0.34) | 0.45(0.41) | 0.35(0.31) | 0.49(0.48) |
| LR | 0.57(0.62) | 0.67(0.73) | 0.38(0.34) | 0.43(0.41) | 0.33(0.30) | 0.48(0.48) |
| NB | 0.56(0.60) | 0.66(0.71) | 0.39(0.35) | 0.43(0.37) | 0.48(0.39) | 0.50(0.48) |
| SVM | 0.55(0.57) | 0.65(0.66) | 0.41(0.42) | 0.47(0.47) | 0.36(0.34) | 0.49(0.49) |
| KNN | 0.54(0.57) | 0.62(0.65) | 0.43(0.47) | 0.57(0.56) | 0.50(0.50) | 0.53(0.55) |
| RF | 0.61(0.65) | 0.65(0.67) | 0.36(0.35) | 0.44(0.42) | 0.34(0.35) | 0.48(0.49) |
| Results based on Path Signature Method F1 Score (AUC) | ||||||
| ML Models | Split 1 | Split 2 | Split 3 | Split 4 | Split 5 | Average |
| LDA | 0.916(0.916) | 0.911(0.916) | 0.900(0.904) | 0.905(0.913) | 0.916(0.937) | 0.909(0.917) |
| LR | 0.952(0.953) | 0.980(0.982) | 0.951(0.953) | 0.945(0.950) | 0.938(0.952) | 0.953(0.958) |
| NB | 0.226(0.532) | 0.478(0.645) | 0.662(0.580) | 0.523(0.668) | 0.340(0.582) | 0.445(0.601) |
| SVM | 0.951(0.953) | 0.961(0.964) | 0.941(0.943) | 0.918(0.924) | 0.952(0.969) | 0.945(0.951) |
| KNN | 0.584(0.644) | 0.591(0.649) | 0.522(0.578) | 0.548(0.623) | 0.466(0.589) | 0.542(0.616) |
| RF | 0.990(0.991) | 0.980(0.982) | 0.980(0.981) | 0.989(0.989) | 0.988(0.992) | 0.985(0.987) |
Appendix B
- -
- Stride duration: duration of a stride (in seconds)
- -
- Stride length: length of a stride (in meters)
- -
- Stride velocity: velocity of a stride (in meters per second)
- -
- Number of steps: number of steps during the test
- -
- Stance and swing phase duration (as percent of gait cycle)
- -
- Stance and swing time (in seconds)
- -
- Symmetry of stance and swing phases: symmetry calculated based on time differences between the respective left and right phases for a given outcome
- -
- Single support time: time at which only one foot is on the floor (in seconds)
- -
- Heel-strike angle and toe-off angle: angle of the forefoot during the specific time points (in °)
- -
- Foot circumduction: foot circumduction describes the swing width (distance between an imaginary straight walking line of foot and the point of maximum actual deflection of the respective foot during the swing phase) of the respective leg (in meters)
Appendix C
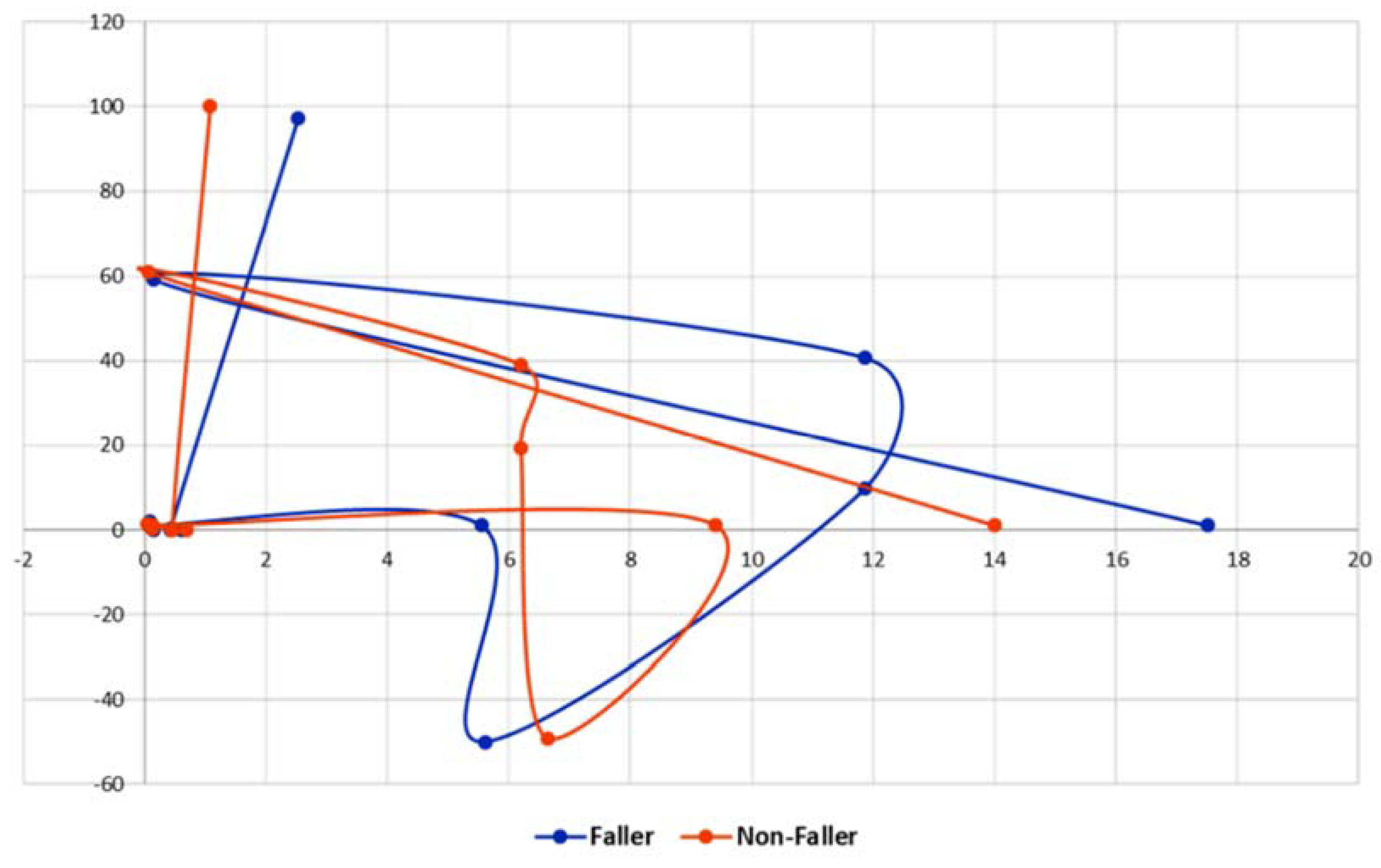
References
- Rubenstein, L.Z. Falls in older people: Epidemiology, risk factors and strategies for prevention. Age Ageing 2006, 35, ii37–ii41. [Google Scholar] [CrossRef]
- Rantz, M.; Skubic, M.; Abbott, C.; Galambos, C.; Popescu, M.; Keller, J.; Stone, E.; Back, J.; Miller, S.J.; Petroski, G.F. Automated in-home fall risk assessment and detection sensor system for elders. Gerontologist 2015, 55, S78–S87. [Google Scholar] [CrossRef] [PubMed]
- Blake, A.; Morgan, K.; Bendall, M.; Dallosso, H.; Ebrahim, S.; Arie, T.a.; Fentem, P.; Bassey, E. Falls by elderly people at home: Prevalence and associated factors. Age Ageing 1988, 17, 365–372. [Google Scholar] [CrossRef] [PubMed]
- Hunter, H.; Rochester, L.; Morris, R.; Lord, S. Longitudinal falls data in parkinson’s disease: Feasibility of fall diaries and effect of attrition. Disabil. Rehabil. 2018, 40, 2236–2241. [Google Scholar] [CrossRef] [PubMed]
- Sattin, R.W. Falls among older persons: A public health perspective. Annu. Rev. Public Health 1992, 13, 489–508. [Google Scholar] [CrossRef]
- Zampogna, A.; Mileti, I.; Palermo, E.; Celletti, C.; Paoloni, M.; Manoni, A.; Mazzetta, I.; Dalla Costa, G.; Pérez-López, C.; Camerota, F. Fifteen years of wireless sensors for balance assessment in neurological disorders. Sensors 2020, 20, 3247. [Google Scholar] [CrossRef]
- Murray, C.J.; Lopez, A.D. Global mortality, disability, and the contribution of risk factors: Global burden of disease study. Lancet 1997, 349, 1436–1442. [Google Scholar] [CrossRef]
- Ambrose, A.F.; Paul, G.; Hausdorff, J.M. Risk factors for falls among older adults: A review of the literature. Maturitas 2013, 75, 51–61. [Google Scholar] [CrossRef]
- Nishtala, P.S.; Narayan, S.W.; Wang, T.; Hilmer, S.N. Associations of drug burden index with falls, general practitioner visits, and mortality in older people. Pharmacoepidemiol. Drug Saf. 2014, 23, 753–758. [Google Scholar] [CrossRef]
- Gleason, C.E.; Gangnon, R.E.; Fischer, B.L.; Mahoney, J.E. Increased risk for falling associated with subtle cognitive impairment: Secondary analysis of a randomized clinical trial. Dement. Geriatr. Cogn. Disord. 2009, 27, 557–563. [Google Scholar] [CrossRef]
- Gillespie, L.D.; Gillespie, W.J.; Robertson, M.C.; Lamb, S.E.; Cumming, R.G.; Rowe, B.H. Interventions for preventing falls in elderly people. Cochrane Database Syst. Rev. 2003. [Google Scholar] [CrossRef]
- Deandrea, S.; Lucenteforte, E.; Bravi, F.; Foschi, R.; La Vecchia, C.; Negri, E. Risk factors for falls in community-dwelling older people: “A systematic review and meta-analysis”. Epidemiology 2010, 21, 658–668. [Google Scholar] [CrossRef] [PubMed]
- Tinetti, M.E.; Kumar, C. The patient who falls: “It’s always a trade-off”. JAMA 2010, 303, 258–266. [Google Scholar] [CrossRef] [PubMed]
- Bell, A.J.; Talbot-Stern, J.K.; Hennessy, A. Characteristics and outcomes of older patients presenting to the emergency department after a fall: A retrospective analysis. Med. J. Aust. 2000, 173, 179–182. [Google Scholar] [CrossRef]
- Roudsari, B.S.; Ebel, B.E.; Corso, P.S.; Molinari, N.A.M.; Koepsell, T.D. The acute medical care costs of fall-related injuries among the us older adults. Injury 2005, 36, 1316–1322. [Google Scholar] [CrossRef]
- Ganz, D.A.; Bao, Y.; Shekelle, P.G.; Rubenstein, L.Z. Will my patient fall? JAMA 2007, 297, 77–86. [Google Scholar] [CrossRef]
- Lord, S.; Galna, B.; Rochester, L. Moving forward on gait measurement: Toward a more refined approach. Mov. Disord. 2013, 28, 1534–1543. [Google Scholar] [CrossRef]
- Kikkert, L.H.; De Groot, M.H.; van Campen, J.P.; Beijnen, J.H.; Hortobágyi, T.; Vuillerme, N.; Lamoth, C.C. Gait dynamics to optimize fall risk assessment in geriatric patients admitted to an outpatient diagnostic clinic. PLoS ONE 2017, 12, e0178615. [Google Scholar] [CrossRef]
- Podsiadlo, D.; Richardson, S. The timed “up & go”: A test of basic functional mobility for frail elderly persons. J. Am. Geriatr. Soc. 1991, 39, 142–148. [Google Scholar]
- Berg, K.O.; Wood-Dauphinee, S.L.; Williams, J.I.; Maki, B. Measuring balance in the elderly: Validation of an instrument. Can. J. Public Health 1992, 83, S7–S11. [Google Scholar]
- Barry, E.; Galvin, R.; Keogh, C.; Horgan, F.; Fahey, T. Is the timed up and go test a useful predictor of risk of falls in community dwelling older adults: A systematic review and meta-analysis. BMC Geriatr. 2014, 14, 14. [Google Scholar] [CrossRef] [PubMed]
- Hamacher, D.; Singh, N.; Van Dieen, J.; Heller, M.; Taylor, W. Kinematic measures for assessing gait stability in elderly individuals: A systematic review. J. R. Soc. Interface 2011, 8, 1682–1698. [Google Scholar] [CrossRef] [PubMed]
- Del Din, S.; Godfrey, A.; Rochester, L. Validation of an accelerometer to quantify a comprehensive battery of gait characteristics in healthy older adults and parkinson’s disease: Toward clinical and at home use. IEEE J. Biomed. Health Inform. 2015, 20, 838–847. [Google Scholar] [CrossRef] [PubMed]
- Del Din, S.; Godfrey, A.; Galna, B.; Lord, S.; Rochester, L. Free-living gait characteristics in ageing and parkinson’s disease: Impact of environment and ambulatory bout length. J. Neuroeng. Rehabil. 2016, 13, 46. [Google Scholar] [CrossRef]
- Pol, M.; van Nes, F.; van Hartingsveldt, M.; Buurman, B.; de Rooij, S.; Kröse, B. Older people’s perspectives regarding the use of sensor monitoring in their home. Gerontologist 2016, 56, 485–493. [Google Scholar] [CrossRef]
- Leach, J.M.; Mellone, S.; Palumbo, P.; Bandinelli, S.; Chiari, L. Natural turn measures predict recurrent falls in community-dwelling older adults: A longitudinal cohort study. Sci. Rep. 2018, 8, 4316. [Google Scholar] [CrossRef]
- Qiu, H.; Rehman, R.Z.U.; Yu, X.; Xiong, S. Application of wearable inertial sensors and a new test battery for distinguishing retrospective fallers from non-fallers among community-dwelling older people. Sci. Rep. 2018, 8, 16349. [Google Scholar] [CrossRef]
- Zhou, Y.; Zia Ur Rehman, R.; Hansen, C.; Maetzler, W.; Del Din, S.; Rochester, L.; Hortobágyi, T.; Lamoth, C.J. Classification of neurological patients to identify fallers based on spatial-temporal gait characteristics measured by a wearable device. Sensors 2020, 20, 4098. [Google Scholar] [CrossRef]
- Rehman, R.Z.U.; Klocke, P.; Hryniv, S.; Galna, B.; Rochester, L.; Del Din, S.; Alcock, L. Turning detection during gait: Algorithm validation and influence of sensor location and turning characteristics in the classification of parkinson’s disease. Sensors 2020, 20, 5377. [Google Scholar] [CrossRef]
- Weinstein, M.; Booth, J. Preventing falls in older adults: A multifactorial approach. Home Health Care Manag. Pract. 2006, 19, 45–50. [Google Scholar] [CrossRef]
- Del Din, S.; Galna, B.; Godfrey, A.; Bekkers, E.M.; Pelosin, E.; Nieuwhof, F.; Mirelman, A.; Hausdorff, J.M.; Rochester, L. Analysis of free-living gait in older adults with and without parkinson’s disease and with and without a history of falls: Identifying generic and disease-specific characteristics. J. Gerontol. Ser. A 2019, 74, 500–506. [Google Scholar] [CrossRef] [PubMed]
- Hausdorff, J.M.; Edelberg, H.K.; Mitchell, S.L.; Goldberger, A.L.; Wei, J.Y. Increased gait unsteadiness in community-dwelling elderly fallers. Arch. Phys. Med. Rehabil. 1997, 78, 278–283. [Google Scholar] [CrossRef]
- Chelli, A.; Pätzold, M. A machine learning approach for fall detection and daily living activity recognition. IEEE Access 2019, 7, 38670–38687. [Google Scholar] [CrossRef]
- Liang, S.; Ning, Y.; Li, H.; Wang, L.; Mei, Z.; Ma, Y.; Zhao, G. Feature selection and predictors of falls with foot force sensors using knn-based algorithms. Sensors 2015, 15, 29393–29407. [Google Scholar] [CrossRef]
- Bet, P.; Castro, P.C.; Ponti, M.A. Fall detection and fall risk assessment in older person using wearable sensors: A systematic review. Int. J. Med. Inform. 2019, 130, 103946. [Google Scholar] [CrossRef]
- Hsu, W.C.; Sugiarto, T.; Lin, Y.J.; Yang, F.C.; Lin, Z.Y.; Sun, C.T.; Hsu, C.L.; Chou, K.N. Multiple-wearable-sensor-based gait classification and analysis in patients with neurological disorders. Sensors 2018, 18, 3397. [Google Scholar] [CrossRef]
- Massart, D. Data handling in science and technology. In Chemometrics: A Textbook; Elsevier Science B.V.: Amsterdam, The Netherlands, 1988; Volume 2. [Google Scholar]
- Balakrishnama, S.; Ganapathiraju, A. Linear Discriminant Analysis-A Brief Tutorial; Institute for Signal and information Processing, Department of Electrical and Computer Engineering, Mississippi State University: Starkville, MS, USA, 1998; pp. 1–8. [Google Scholar]
- Figueiredo, J.; Santos, C.P.; Moreno, J.C. Automatic recognition of gait patterns in human motor disorders using machine learning: A review. Med. Eng. Phys. 2018, 53, 1–12. [Google Scholar] [CrossRef]
- Moore, P.; Lyons, T.; Gallacher, J.; Initiative, A.s.D.N. Using path signatures to predict a diagnosis of alzheimer’s disease. PLoS ONE 2019, 14, e0222212. [Google Scholar] [CrossRef]
- Reizenstein, J.; Graham, B. The iisignature library: Efficient calculation of iterated-integral signatures and log signatures. arXiv 2018, arXiv:1802.08252. [Google Scholar]
- Rehman, R.Z.U.; Del Din, S.; Shi, J.Q.; Galna, B.; Lord, S.; Yarnall, A.J.; Guan, Y.; Rochester, L. Comparison of walking protocols and gait assessment systems for machine learning-based classification of parkinson’s disease. Sensors 2019, 19, 5363. [Google Scholar] [CrossRef]
- Wahid, F.; Begg, R.K.; Hass, C.J.; Halgamuge, S.; Ackland, D.C. Classification of parkinson’s disease gait using spatial-temporal gait features. IEEE J. Biomed. Health Inform. 2015, 19, 1794–1802. [Google Scholar] [CrossRef]
- Bernhard, F.P.; Sartor, J.; Bettecken, K.; Hobert, M.A.; Arnold, C.; Weber, Y.G.; Poli, S.; Margraf, N.G.; Schlenstedt, C.; Hansen, C. Wearables for gait and balance assessment in the neurological ward-study design and first results of a prospective cross-sectional feasibility study with 384 inpatients. BMC Neurol. 2018, 18, 114. [Google Scholar] [CrossRef]
- Donath, L.; Faude, O.; Lichtenstein, E.; Nüesch, C.; Mündermann, A. Validity and reliability of a portable gait analysis system for measuring spatiotemporal gait characteristics: Comparison to an instrumented treadmill. J. Neuroeng. Rehabil. 2016, 13, 6. [Google Scholar] [CrossRef]
- Stolze, H.; Klebe, S.; Zechlin, C.; Baecker, C.; Friege, L.; Deuschl, G. Falls in frequent neurological diseases. J. Neurol. 2004, 251, 79–84. [Google Scholar] [CrossRef] [PubMed]
- Doi, T.; Hirata, S.; Ono, R.; Tsutsumimoto, K.; Misu, S.; Ando, H. The harmonic ratio of trunk acceleration predicts falling among older people: Results of a 1-year prospective study. J. Neuroeng. Rehabil. 2013, 10, 7. [Google Scholar] [CrossRef]
- König, N.; Taylor, W.; Armbrecht, G.; Dietzel, R.; Singh, N.B. Identification of functional parameters for the classification of older female fallers and prediction of ‘first-time’fallers. J. R. Soc. Interface 2014, 11, 20140353. [Google Scholar] [CrossRef] [PubMed]
- Rehman, R.Z.U.; Buckley, C.; Micó-Amigo, M.E.; Kirk, C.; Dunne-Willows, M.; Mazzà, C.; Shi, J.Q.; Alcock, L.; Rochester, L.; Del Din, S. Accelerometry-based digital gait characteristics for classification of parkinson’s disease: What counts? IEEE Open J. Eng. Med. Biol. 2020, 1, 65–73. [Google Scholar] [CrossRef]
- Mohamad, I.B.; Usman, D. Standardization and its effects on k-means clustering algorithm. Res. J. Appl. Sci. Eng. Technol. 2013, 6, 3299–3303. [Google Scholar] [CrossRef]
- Reid, S.M.; Graham, R.B.; Costigan, P.A. Differentiation of young and older adult stair climbing gait using principal component analysis. Gait Posture 2010, 31, 197–203. [Google Scholar] [CrossRef] [PubMed]
- Daffertshofer, A.; Lamoth, C.J.; Meijer, O.G.; Beek, P.J. Pca in studying coordination and variability: A tutorial. Clin. Biomech. 2004, 19, 415–428. [Google Scholar] [CrossRef] [PubMed]
- Lyons, T. Rough paths, signatures and the modelling of functions on streams. arXiv 2014, arXiv:1405.4537. [Google Scholar]
- Xie, Z.; Sun, Z.; Jin, L.; Ni, H.; Lyons, T. Learning spatial-semantic context with fully convolutional recurrent network for online handwritten chinese text recognition. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 40, 1903–1917. [Google Scholar] [CrossRef] [PubMed]
- Levin, D.; Lyons, T.; Ni, H. Learning from the past, predicting the statistics for the future, learning an evolving system. arXiv 2013, arXiv:1309.0260. [Google Scholar]
- Chevyrev, I.; Kormilitzin, A. A primer on the signature method in machine learning. arXiv 2016, arXiv:1603.03788. [Google Scholar]
- Flint, G.; Hambly, B.; Lyons, T. Discretely sampled signals and the rough hoff process. Stoch. Process. Appl. 2016, 126, 2593–2614. [Google Scholar] [CrossRef]
- Yang, W.; Lyons, T.; Ni, H.; Schmid, C.; Jin, L.; Chang, J. Leveraging the path signature for skeleton-based human action recognition. arXiv 2017, arXiv:1707.03993. [Google Scholar]
- Chen, K.T. Integration of paths--a faithful representation of paths by noncommutative formal power series. Trans. Am. Math. Soc. 1958, 89, 395–407. [Google Scholar] [CrossRef]
- Arribas, I.P.; Goodwin, G.M.; Geddes, J.R.; Lyons, T.; Saunders, K.E. A signature-based machine learning model for distinguishing bipolar disorder and borderline personality disorder. Transl. Psychiatry 2018, 8, 274. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V. Scikit-learn: Machine learning in python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Matykiewicz, P.; Pestian, J. Effect of Small Sample Size on Text Categorization with Support Vector Machines. In Proceedings of the 2012 Workshop on Biomedical Natural Language Processing, Montreal, QC, Canada, 3–8 June 2012; pp. 193–201. [Google Scholar]
- Halilaj, E.; Rajagopal, A.; Fiterau, M.; Hicks, J.L.; Hastie, T.J.; Delp, S.L. Machine learning in human movement biomechanics: Best practices, common pitfalls, and new opportunities. J. Biomech. 2018, 81, 1–11. [Google Scholar] [CrossRef]
- Dinov, I.D. Black box machine-learning methods: Neural networks and support vector machines. In Data Science and Predictive Analytics; Springer: Berlin/Heidelberg, Germany, 2018; pp. 383–422. [Google Scholar]
- Loh, W.Y. Variable selection for classification and regression in large p, small n problems. In Probability Approximations and Beyond; Springer: Berlin/Heidelberg, Germany, 2012; pp. 135–159. [Google Scholar]
- Genuer, R.; Poggi, J.M.; Tuleau, C. Random forests: Some methodological insights. arXiv 2008, arXiv:0811.3619. [Google Scholar]
- Ayer, T.; Chhatwal, J.; Alagoz, O.; Kahn Jr, C.E.; Woods, R.W.; Burnside, E.S. Comparison of logistic regression and artificial neural network models in breast cancer risk estimation. Radiographics 2010, 30, 13–22. [Google Scholar] [CrossRef] [PubMed]
- Rish, I. An empirical study of the naive bayes classifier. In Proceedings of the IJCAI 2001 Workshop on Empirical Methods in Artificial Intelligence, Seattle, WA, USA, 4–10 August 2001; pp. 41–46. [Google Scholar]
- Cunningham, P.; Delany, S.J. K-nearest neighbour classifiers. arXiv 2020, arXiv:2004.04523. [Google Scholar]
- Gao, C.; Sun, H.; Wang, T.; Tang, M.; Bohnen, N.I.; Müller, M.L.T.M.; Herman, T.; Giladi, N.; Kalinin, A.; Spino, C.; et al. Model-based and model-free machine learning techniques for diagnostic prediction and classification of clinical outcomes in parkinson’s disease. Sci. Rep. 2018, 8, 7129. [Google Scholar] [CrossRef]
- Paul, S.S.; Canning, C.G.; Sherrington, C.; Lord, S.R.; Close, J.C.; Fung, V.S. Three simple clinical tests to accurately predict falls in people with parkinson’s disease. Mov. Disord. 2013, 28, 655–662. [Google Scholar] [CrossRef]
- Gyamfi, K.S.; Brusey, J.; Hunt, A.; Gaura, E. Linear classifier design under heteroscedasticity in linear discriminant analysis. Expert Syst. Appl. 2017, 79, 44–52. [Google Scholar] [CrossRef]
- Juszczak, P.; Tax, D.; Duin, R.P. Feature Scaling in Support Vector Data Description; Citeseer: Delft University of Technology, Delft, The Netherlands, 2002; pp. 95–102. [Google Scholar]
- Strobl, C.; Boulesteix, A.L.; Zeileis, A.; Hothorn, T. Bias in random forest variable importance measures: Illustrations, sources and a solution. BMC Bioinform. 2007, 8, 25. [Google Scholar] [CrossRef]
- Jolliffe, I.T.; Cadima, J. Principal component analysis: A review and recent developments. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2016, 374, 20150202. [Google Scholar] [CrossRef]
- Echambadi, R.; Hess, J.D. Mean-centering does not alleviate collinearity problems in moderated multiple regression models. Mark. Sci. 2007, 26, 438–445. [Google Scholar] [CrossRef]
- Miesch, A. Scaling variables and interpretation of eigenvalues in principal component analysis of geologic data. J. Int. Assoc. Math. Geol. 1980, 12, 523–538. [Google Scholar] [CrossRef]
- O’Malley, N.; Clifford, A.M.; Comber, L.; Coote, S. Fall definitions, faller classifications and outcomes used in falls research among people with multiple sclerosis: A systematic review. Disabil. Rehabil. 2020, 1–8. [Google Scholar] [CrossRef]
- Hua, A.; Quicksall, Z.; Di, C.; Motl, R.; LaCroix, A.Z.; Schatz, B.; Buchner, D.M. Accelerometer-based predictive models of fall risk in older women: A pilot study. NPJ Digit. Med. 2018, 1, 25. [Google Scholar] [CrossRef] [PubMed]
- O’Loughlin, J.L.; Robitaille, Y.; Boivin, J.F.; Suissa, S. Incidence of and risk factors for falls and injurious falls among the community-dwelling elderly. Am. J. Epidemiol. 1993, 137, 342–354. [Google Scholar] [CrossRef] [PubMed]
- Kerr, G.K.; Worringham, C.J.; Cole, M.H.; Lacherez, P.F.; Wood, J.M.; Silburn, P. Predictors of future falls in parkinson disease. Neurology 2010, 75, 116–124. [Google Scholar] [CrossRef] [PubMed]
- Mactier, K.; Lord, S.; Godfrey, A.; Burn, D.; Rochester, L. The relationship between real world ambulatory activity and falls in incident parkinson’s disease: Influence of classification scheme. Parkinsonism Relat. Disord. 2015, 21, 236–242. [Google Scholar] [CrossRef] [PubMed]

| Demographics | Non-Fallers (n = 190) Mean ± SD | Fallers (n = 159) Mean ± SD | p-Value |
|---|---|---|---|
| M/F | 115/75 | 88/71 | 0.330 |
| Age (year) | 61.6 ± 12.2 | 65.0 ± 12.7 | 0.009 |
| Height (m) | 1.73 ± 0.1 | 1.70 ± 0.1 | 0.021 |
| Mass (kg) | 81.89 ± 16.35 | 76.31 ± 14.87 | 0.002 |
| BMI (kg/m2) | 27.22 ± 4.76 | 26.08 ± 4.34 | 0.027 |
| ML Models | Data Pre-Processing Methods Accuracy (Sensitivity, Specificity)% | ||
|---|---|---|---|
| Standardisation | PCA | Path Signature | |
| Linear Discriminant Analysis (LDA) | 63.10(62, 62) | 48.95(45, 52) | 91.81(91, 92) |
| Logistic Regression (LR) | 60.75(59, 62) | 47.81(44, 51) | 95.80(97, 95) |
| Naïve Bayes (NB) | 67.81(64, 68) | 51.24(51, 48) | 63.05(38, 82) |
| Support Vector Machine (SVM-linear) | 70.48(64, 74) | 50.67(43, 56) | 95.05(95, 95) |
| K-Nearest Neighbour (KNN) | 62.28(61, 63) | 50.28(49, 52) | 63.04(49, 75) |
| Random Forest (RF) | 66.28(63, 69) | 48.19(49, 49) | 98.67(99, 98) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rehman, R.Z.U.; Zhou, Y.; Del Din, S.; Alcock, L.; Hansen, C.; Guan, Y.; Hortobágyi, T.; Maetzler, W.; Rochester, L.; Lamoth, C.J.C. Gait Analysis with Wearables Can Accurately Classify Fallers from Non-Fallers: A Step toward Better Management of Neurological Disorders. Sensors 2020, 20, 6992. https://doi.org/10.3390/s20236992
Rehman RZU, Zhou Y, Del Din S, Alcock L, Hansen C, Guan Y, Hortobágyi T, Maetzler W, Rochester L, Lamoth CJC. Gait Analysis with Wearables Can Accurately Classify Fallers from Non-Fallers: A Step toward Better Management of Neurological Disorders. Sensors. 2020; 20(23):6992. https://doi.org/10.3390/s20236992
Chicago/Turabian StyleRehman, Rana Zia Ur, Yuhan Zhou, Silvia Del Din, Lisa Alcock, Clint Hansen, Yu Guan, Tibor Hortobágyi, Walter Maetzler, Lynn Rochester, and Claudine J. C. Lamoth. 2020. "Gait Analysis with Wearables Can Accurately Classify Fallers from Non-Fallers: A Step toward Better Management of Neurological Disorders" Sensors 20, no. 23: 6992. https://doi.org/10.3390/s20236992
APA StyleRehman, R. Z. U., Zhou, Y., Del Din, S., Alcock, L., Hansen, C., Guan, Y., Hortobágyi, T., Maetzler, W., Rochester, L., & Lamoth, C. J. C. (2020). Gait Analysis with Wearables Can Accurately Classify Fallers from Non-Fallers: A Step toward Better Management of Neurological Disorders. Sensors, 20(23), 6992. https://doi.org/10.3390/s20236992











