A Personalized Diagnosis Method to Detect Faults in a Bearing Based on Acceleration Sensors and an FEM Simulation Driving Support Vector Machine
Abstract
1. Introduction
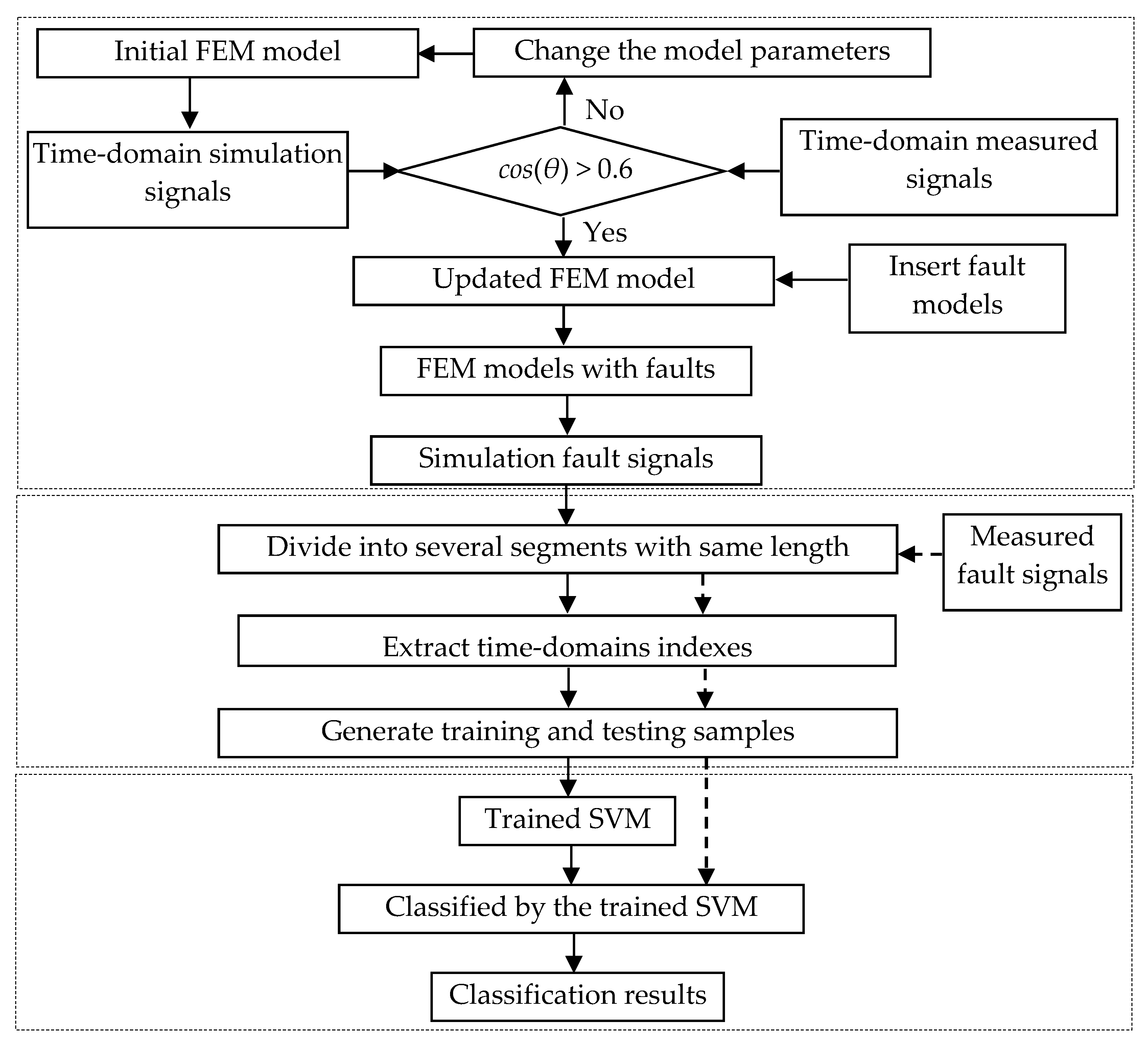
2. The Basic Principle of Personalized Diagnosis Method
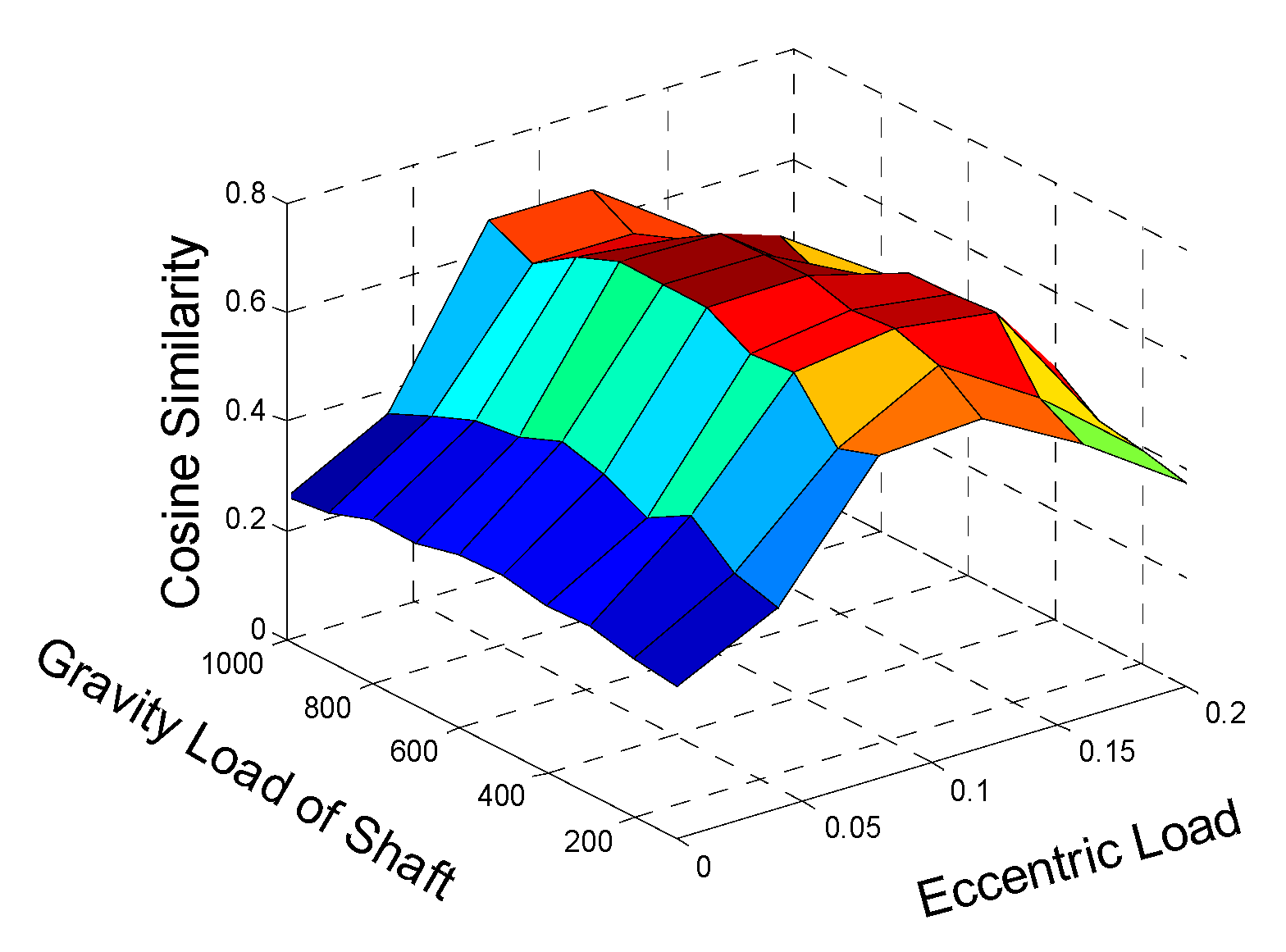
2.1. Cosine Similarity-Based FEM Model Updating Technique
2.2. A Brief Review of SVM
2.3. The Personalized Diagnosis Method by Using FEM Simulation and SVM
2.3.1. Construct and Update the FEM Model for a Mechanical System
2.3.2. Obtain the Faulty Training Samples
2.3.3. Fault Classification Using SVM
3. Experimental Investigations
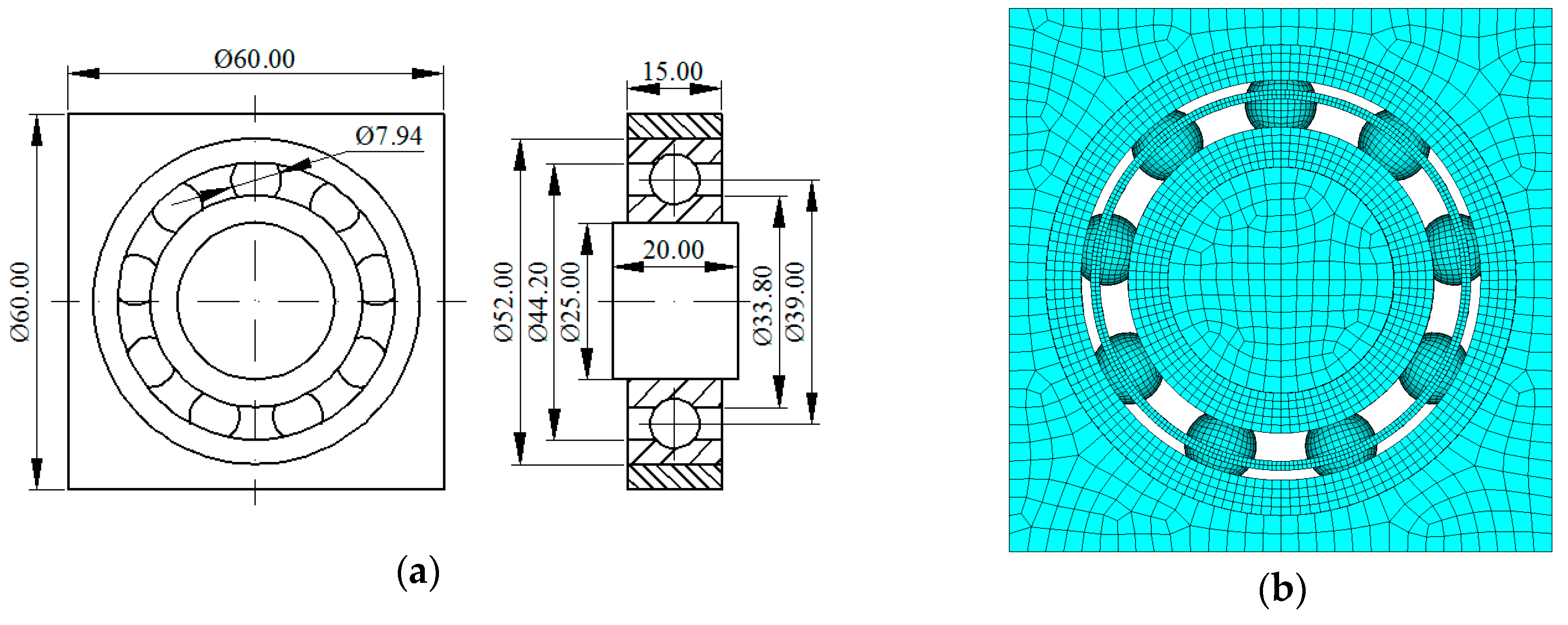
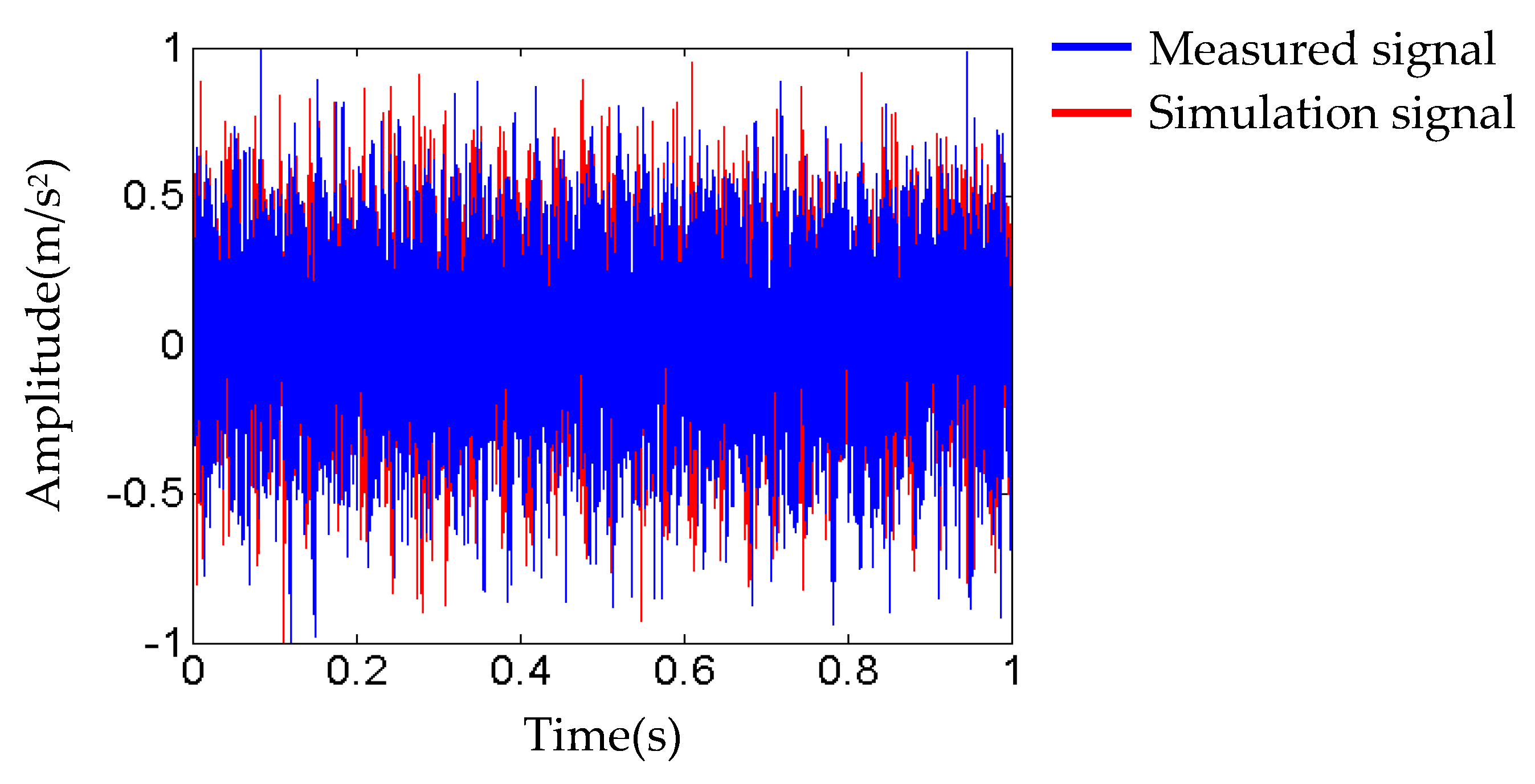
3.1. Construction and Updating of Bearing FEM Model
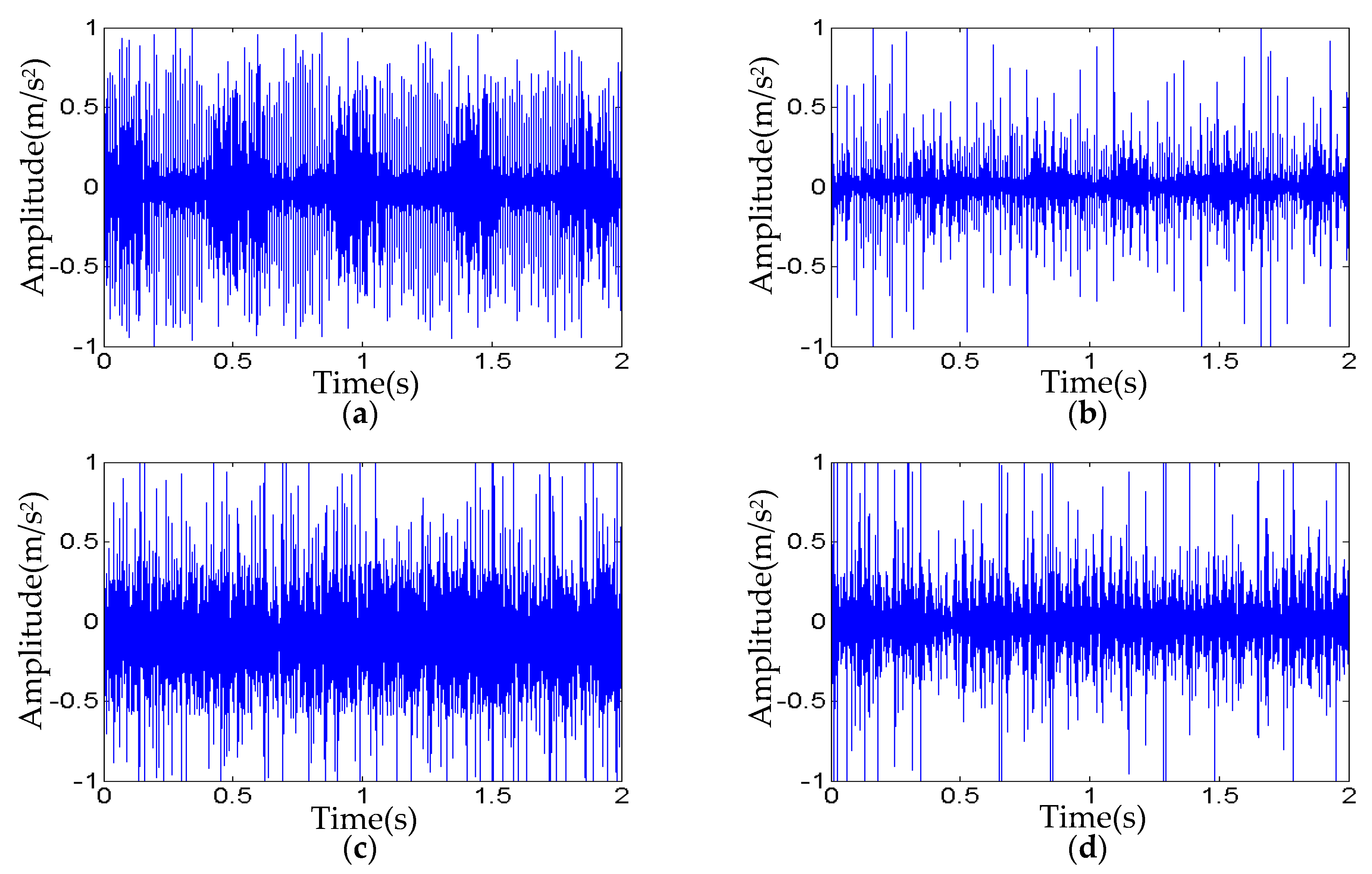
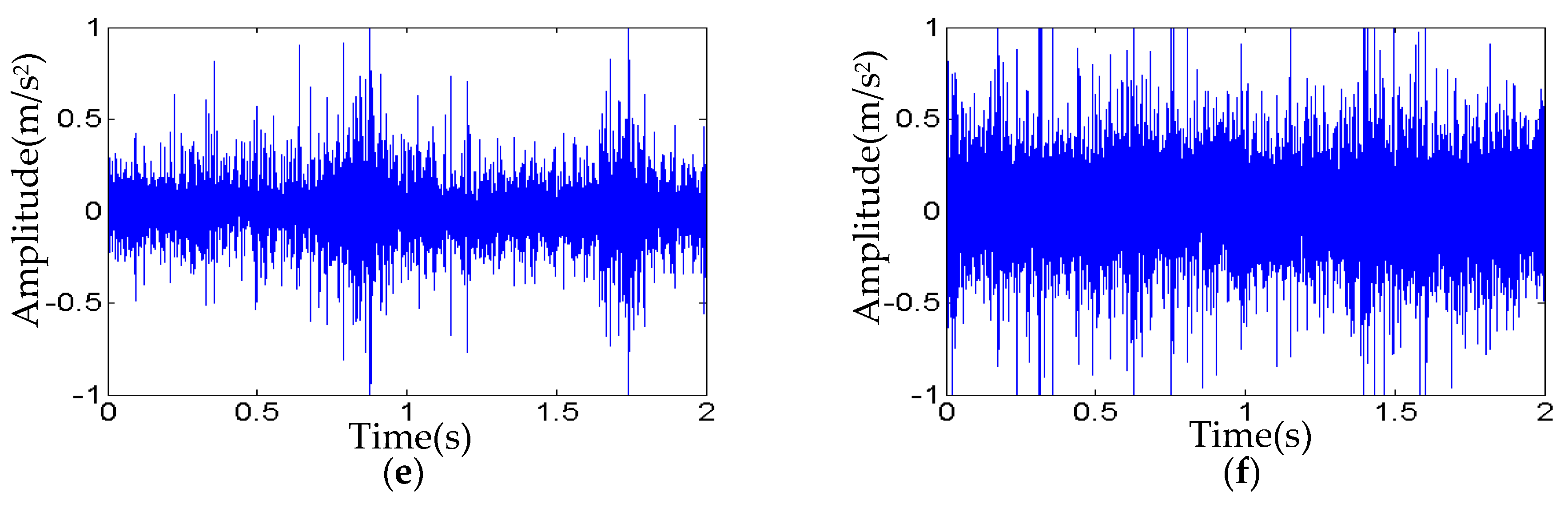
3.2. Generation of Simulation Fault Training Samples
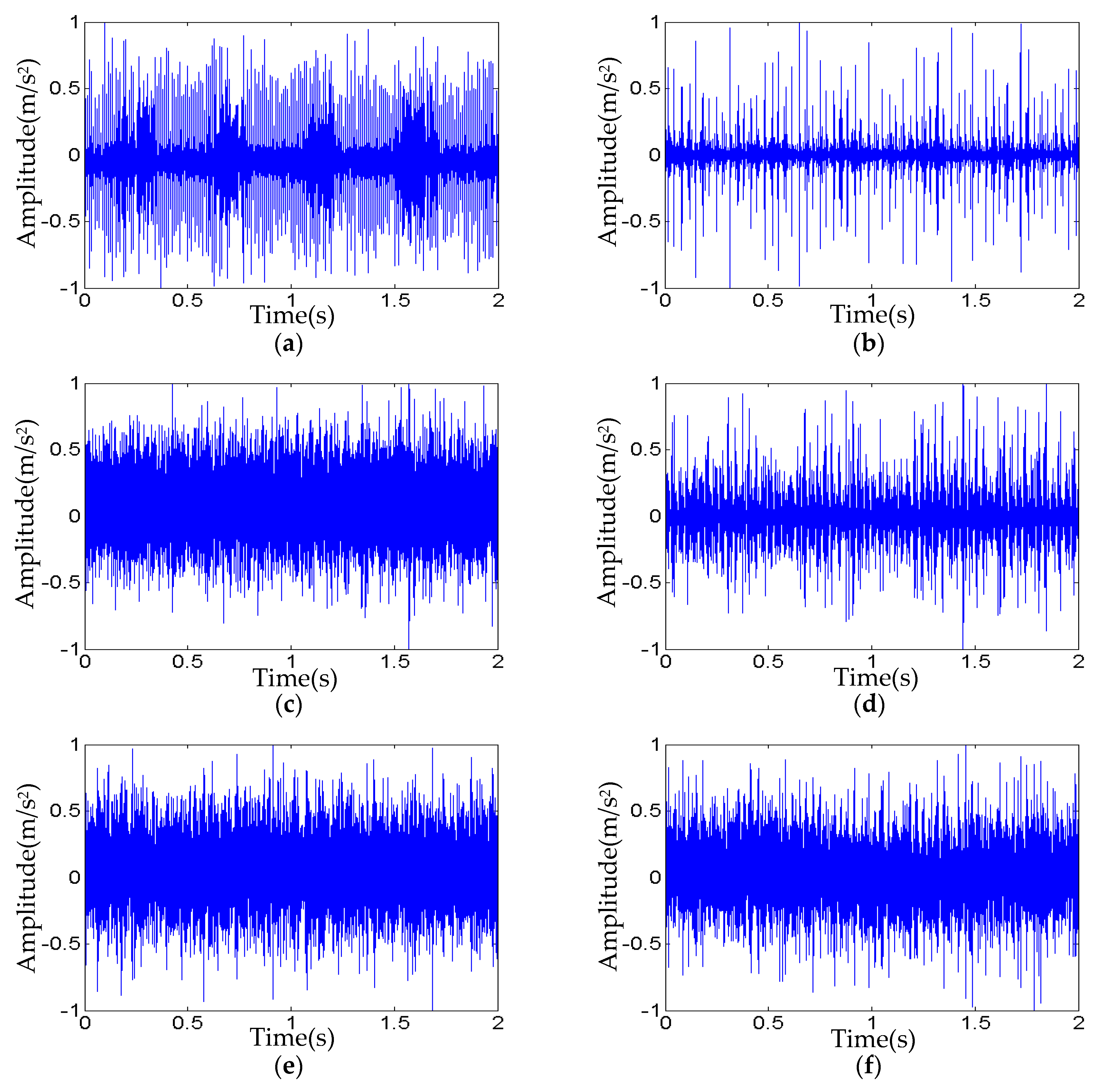
3.3. Experimental Investigations Using a Public Bearing Dataset Based on SVM
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Wang, D.; Miao, Q. Smoothness index-guided Bayesian inference for determining joint posterior probability distributions of anti-symmetric real Laplace wavelet parameters for identification of different bearing faults. J. Sound. Vib. 2015, 345, 250–266. [Google Scholar] [CrossRef]
- Zhao, R.; Yan, R.; Chen, Z.; Mao, K.; Wang, P.; Gao, R. Deep learning and its applications to machine health monitoring. Mech. Syst. Signal Pr. 2019, 115, 213–237. [Google Scholar] [CrossRef]
- Qin, Y.; Wang, X.; Zou, J.Q. The optimized deep belief networks with improved logistic Sigmoid units and their application in fault diagnosis for planetary gearboxes of wind turbines. IEEE T. Ind. Electron. 2019, 66, 3814–3824. [Google Scholar] [CrossRef]
- Wang, S.H.; Xiang, J.W.; Zhong, Y.T.; Zhou, Y.Q. Convolutional Neural Network-based Hidden Markov Models for Rolling Element Bearing Fault Identification. Knowl.-Based Syst. 2017, 144, 65–76. [Google Scholar] [CrossRef]
- Yang, B.; Lei, Y.G.; Jia, F.; Xing, S.B. An intelligent fault diagnosis approach based on transfer learning from laboratory bearings to locomotive bearings. Mech. Syst. Signal Pr. 2019, 122, 692–706. [Google Scholar] [CrossRef]
- Kumar, A.; Kumar, R. Time-frequency analysis and support vector machine in automatic detection of defect from vibration signal of centrifugal pump. Measurement 2017, 108, 119–133. [Google Scholar] [CrossRef]
- Wang, S.H.; Xiang, J.W.; Zhong, Y.T.; Tang, H.S. A data indicator-based deep belief networks to detect multiple faults in axial piston pumps. Mech. Syst. Signal Pr. 2018, 112, 154–170. [Google Scholar] [CrossRef]
- Wang, S.H.; Xiang, J.W. A minimum entropy deconvolution-enhanced convolutional neural networks for fault diagnosis of axial piston pumps. Soft Comput 2019, 1–15. [Google Scholar] [CrossRef]
- Kumar, A.; Kumar, R. Adaptive artificial intelligence for automatic identification of defect in the angular contact bearing. Neural. Comput. Appl. 2018, 29, 277–287. [Google Scholar] [CrossRef]
- Bregon, A.; Alonso-González, C.J.; Pulido, B. Integration of simulation and state observers for online fault detection of nonlinear continuous systems. IEEE Trans. Syst. Man Cy.-S. 2014, 44, 1553–1568. [Google Scholar] [CrossRef]
- Xiang, J.W.; Jiang, Z.S.; Chen, X.F. A class of wavelet-based Rayleigh-Euler beam element for analyzing rotating shafts. Shock Vib. 2011, 18, 447–458. [Google Scholar] [CrossRef]
- Xiang, J.W.; Long, J.Q.; Jiang, Z.S. A numerical study using Hermitian cubic spline wavelets for the analysis of shafts. Proc. Inst. Mech. Eng. 2010, 224, 1843–1851. [Google Scholar] [CrossRef]
- Xiang, J.W.; Zhong, Y.T. A novel personalized diagnosis methodology using numerical simulation and an intelligent method to detect faults in a shaft. Appl. Sci-Basel. 2016, 6, 414. [Google Scholar] [CrossRef]
- Wang, S.H.; Xiang, J.W.; Tang, H.S.; Liu, X.Y.; Zhong, Y.T. Minium entropy deconvolution based on simulation determined band pass fiter to detect faults in bearings of axial piston pumps. ISA Transaction 2018, 50, 599–608. [Google Scholar]
- Ren, W.X.; Chen, H.B. Finite element model updating in structural dynamics by using the response surface method. Eng. Struct. 2010, 32, 2455–2465. [Google Scholar] [CrossRef]
- Liu, B.; Ling, S.F. On the selection of informative wavelets for machinery diagnosis. Mech. Syst. Signal Pr. 1999, 13, 145–162. [Google Scholar] [CrossRef]
- Biswas, S.K.; Milanfar, P. One shot detection with laplacian object and fast matrix cosine similarity. IEEE T. Pattern Anal. 2016, 38, 546–562. [Google Scholar] [CrossRef]
- Chen, F.F.; Tang, B.P.; Song, T. Multi-fault diagnosis study on roller bearing based on multi-kernel support vector machine with chaotic particle swarm optimization. Measurement 2014, 47, 576–590. [Google Scholar] [CrossRef]
- Liu, W.Y.; Han, J.G.; Lu, X.N. A new gear fault feature extraction method based on hybrid time-frequency analysis. Neural Comput. Appl. 2014, 25, 387–392. [Google Scholar] [CrossRef]
- Liu, Z.; Cao, H.; Chen, X. Multi-fault classification based on wavelet SVM with PSO algorithm to analyze vibration signals from rolling element bearings. Neurocomputing 2013, 99, 399–410. [Google Scholar] [CrossRef]
- Hemez, F.M.; Doebling, S.W. Test-analysis correlation and finite element model updating for nonlinear transient dynamics. In Proceedings of the 17th International Modal Analysis Conference, Kissimmee, FL, USA, 1999; 3727, p. 1501. [Google Scholar]
- Link, M.; Weiland, M. Damage Identification by Multi-Model Updating in the Modal and in the Time Domain. Mech. Syst. Signal Process 2009, 23, 1734–1746. [Google Scholar] [CrossRef]
- Hasselman, T.K.; Anderson, M.C.; Gan, W.S. Principal components analysis for nonlinear model correlation, updating and uncertainty evaluation. In Proceedings of the 16th International Modal Analysis Conference, Santa Barbara, CA, USA, 1998; 3243, pp. 644–651. [Google Scholar]
- Sarin, H.; Kokkolaras, M.; Hulbert, G.; Papalambros, P. Comparing Time Histories for Validation of Simulation Models: Error Measures and Metrics. J. Dyn. Syst. 2010, 132, 173–179. [Google Scholar] [CrossRef]
- Zapico-Valle, J.L.; Alonso-Camblor, R. A new method for finite element model updating in structural dynamics. Mech. Syst. Signal Pr. 2010, 24, 2137–2159. [Google Scholar] [CrossRef]
- Kheir, N.A.; Holmes, W.M. Modeling and credibility of random ensembles. Simulation 1982, 38, 93–103. [Google Scholar] [CrossRef]
- Xiang, J.W.; Liang, M.; He, Y.M. Experimental investigation of frequency-based multi-damage detection for beams using support vector regression. Eng. Fract. Mech. 2014, 131, 257–268. [Google Scholar] [CrossRef]
- Case Western Reserve University. Bearing Data Center. Available online: http://csegroups.case.edu/bearingdatacenter/home (accessed on 26 October 2019).
- Hamrock, B.J.; Dowson, D. Ball bearing lubrication: The Elastohydrodynamics of Elliptical Contacts; Wiley & Sons: New York, NY, USA, 1982; pp. 279–281. [Google Scholar]
- Gupta, P.K. Advanced Dynamics of Rolling Elements; Springer: New York, NY, USA, 1986; pp. 203–209. [Google Scholar]
- Zhao, C.; Yu, X.; Huang, Q.; Ge, S.; Gao, X. Analysis on the load characteristics and coefficient of friction of angular contact ball bearing at high speed. Tribol. Int. 2015, 87, 50–56. [Google Scholar]
- Wei, J.; Gao, P.; Hu, X.L.; Sun, W. Effects of dynamic transmission errors and vibration stability in helical gears. J. Mech. Sci. Technol. 2014, 28, 2253–2262. [Google Scholar] [CrossRef]
- Zhao, M.M.; Ji, J.C. Dynamic analysis of wind turbine gearbox components. Energies 2016, 9, 110. [Google Scholar] [CrossRef]
- Al-Shyyab, A.; Kahraman, A. Non-linear dynamic analysis of a multi-mesh gear train using multi-term harmonic balance method: period-one motions. J. Sound Vib. 2005, 284, 151–172. [Google Scholar] [CrossRef]
- Chen, B.; Li, S.S.; Chen, J.; Lu, Y.X. The sources of damping in rolling element bearings under oscillating conditions. Lubr. Eng. 2013, 38, 62–66. [Google Scholar]
- Chen, S.Y.; Kung, C.; Liao, T.T. Dynamic analysis of a rotary hollow shaft with hot-fit part using contact elements with friction. T. Can. Soc. Mech. Eng. 2011, 35, 461–474. [Google Scholar] [CrossRef]
- Harris, T.A. Rolling Bearing Analysis, 3rd ed.; Wiley & Sons: London, UK, 1991. [Google Scholar]
- Franc, V.; Hlavác, V. Statistical Pattern Recognition Toolbox for Matlab; Center for Machine Perception, Czech Technical University: Prague, Czech Republic, 2004. [Google Scholar]
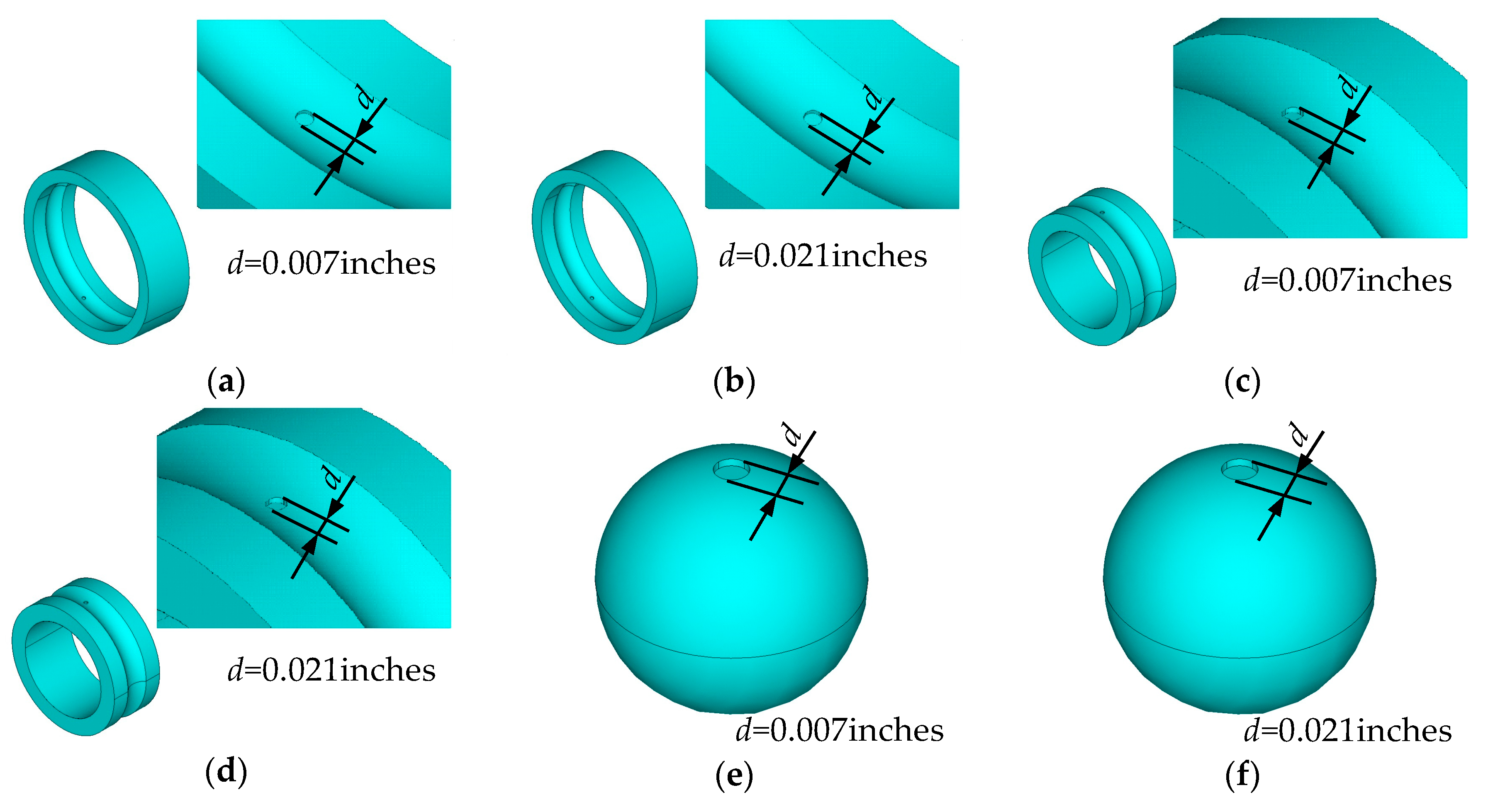
| Index | Equation | Index | Equation |
|---|---|---|---|
| Mean | Average amplitude | ||
| Standard deviation | Square root amplitude | ||
| Variance | Skewness | ||
| Peak | Kurtosis | ||
| Maximum | Shape factor | ||
| Minimum | Impulse factor | ||
| Peak to peak | Peak factor | ||
| Root mean square | Clearance indicator |
| Component | Element Size (mm) |
|---|---|
| Outer ring | 1 |
| Inner ring | 1 |
| Ball | 1 |
| Cage | 0.5 |
| Shaft | 2 |
| Bearing seat | 2 |
| Contact Parameters | Value | Loading Parameters | Value |
|---|---|---|---|
| FKN | 0.12 | Fg | 500 N |
| f1 | 0.02 | Fe | 0.12 MPa |
| f2 | 0.016 | n | 1797 rpm |
| 0.02 | Fro | 0.5 MPa |
| cos(θ). | Fe (MPa) | ||||||
|---|---|---|---|---|---|---|---|
| 0 | 0.04 | 0.08 | 0.12 | 0.16 | 0.2 | ||
| Fg (N) | 100 | 0.202 | 0.268 | 0.394 | 0.505 | 0.403 | 0.374 |
| 200 | 0.193 | 0.292 | 0.463 | 0.559 | 0.446 | 0.351 | |
| 300 | 0.151 | 0.255 | 0.412 | 0.498 | 0.501 | 0.306 | |
| 400 | 0.206 | 0.311 | 0.455 | 0.581 | 0.455 | 0.364 | |
| 500 | 0.223 | 0.351 | 0.501 | 0.618 | 0.451 | 0.411 | |
| 600 | 0.169 | 0.271 | 0.504 | 0.601 | 0.507 | 0.403 | |
| 700 | 0.201 | 0.336 | 0.503 | 0.499 | 0.473 | 0.418 | |
| 800 | 0.203 | 0.227 | 0.472 | 0.549 | 0.437 | 0.372 | |
| 900 | 0.174 | 0.294 | 0.418 | 0.517 | 0.422 | 0.393 | |
| 1000 | 0.161 | 0.258 | 0.358 | 0.458 | 0.428 | 0.358 | |
| Fault Type | Training Samples | Testing Samples | Faults Labels | Classification Accuracy Using the Present Method (%) | Classification Accuracy Using the Measured Signals Alone (%) | Relative Error (%) |
|---|---|---|---|---|---|---|
| T1 | 40 | 40 | 1 | 90% | 92% | 2.2 |
| T2 | 40 | 40 | 2 | 92.5% | 95% | 2.6 |
| T3 | 40 | 40 | 3 | 87.5% | 95% | 7.9 |
| T4 | 40 | 40 | 4 | 87.5% | 90% | 7.9 |
| T5 | 40 | 40 | 5 | 85% | 97.5% | 12.8 |
| T6 | 40 | 40 | 6 | 82.5% | 87.5% | 5.7 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, X.; Huang, H.; Xiang, J. A Personalized Diagnosis Method to Detect Faults in a Bearing Based on Acceleration Sensors and an FEM Simulation Driving Support Vector Machine. Sensors 2020, 20, 420. https://doi.org/10.3390/s20020420
Liu X, Huang H, Xiang J. A Personalized Diagnosis Method to Detect Faults in a Bearing Based on Acceleration Sensors and an FEM Simulation Driving Support Vector Machine. Sensors. 2020; 20(2):420. https://doi.org/10.3390/s20020420
Chicago/Turabian StyleLiu, Xiaoyang, Haizhou Huang, and Jiawei Xiang. 2020. "A Personalized Diagnosis Method to Detect Faults in a Bearing Based on Acceleration Sensors and an FEM Simulation Driving Support Vector Machine" Sensors 20, no. 2: 420. https://doi.org/10.3390/s20020420
APA StyleLiu, X., Huang, H., & Xiang, J. (2020). A Personalized Diagnosis Method to Detect Faults in a Bearing Based on Acceleration Sensors and an FEM Simulation Driving Support Vector Machine. Sensors, 20(2), 420. https://doi.org/10.3390/s20020420






