An Analytical Conductance Model for Gas Detection Based on a Zigzag Carbon Nanotube Sensor
Abstract
1. Introduction
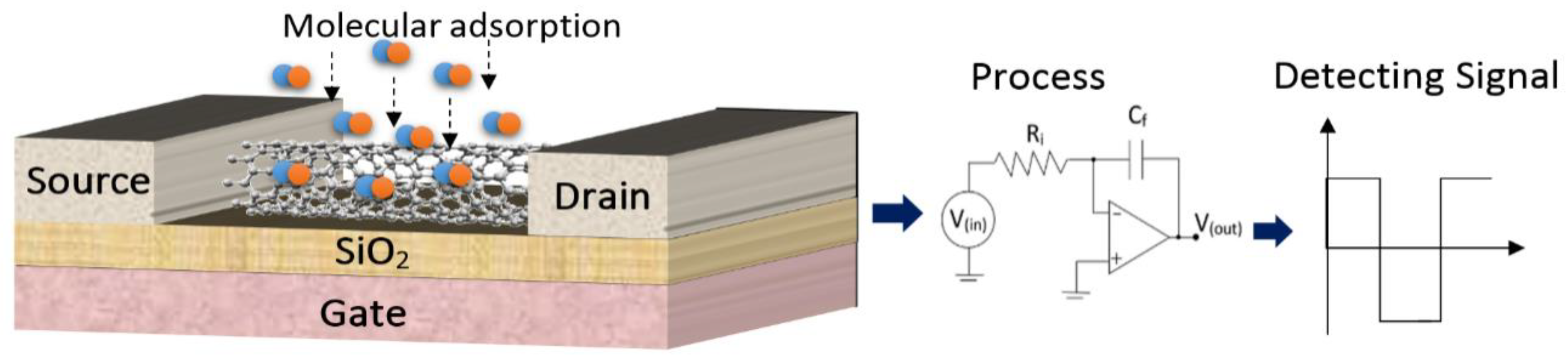
2. Materials and Methods
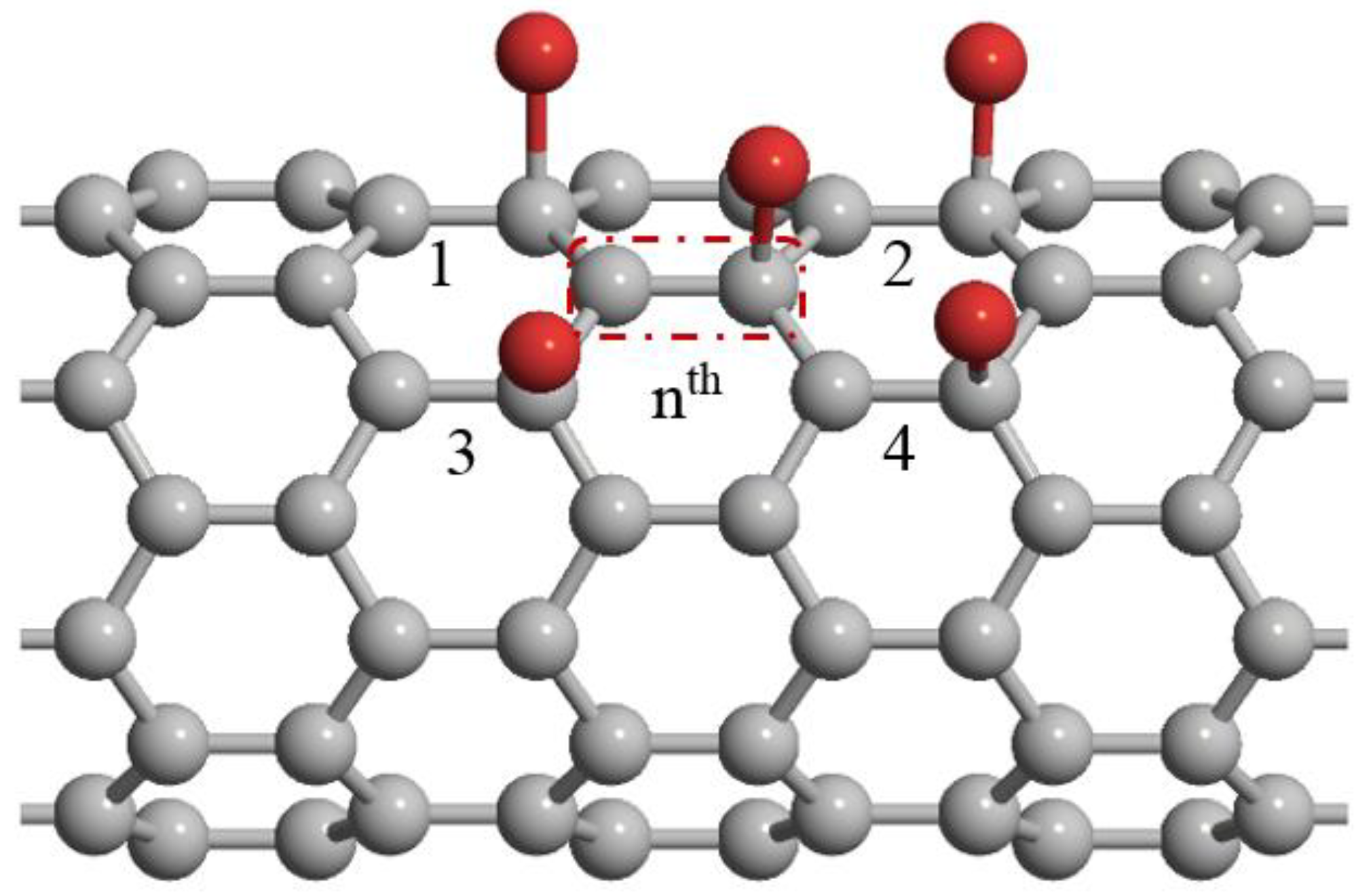
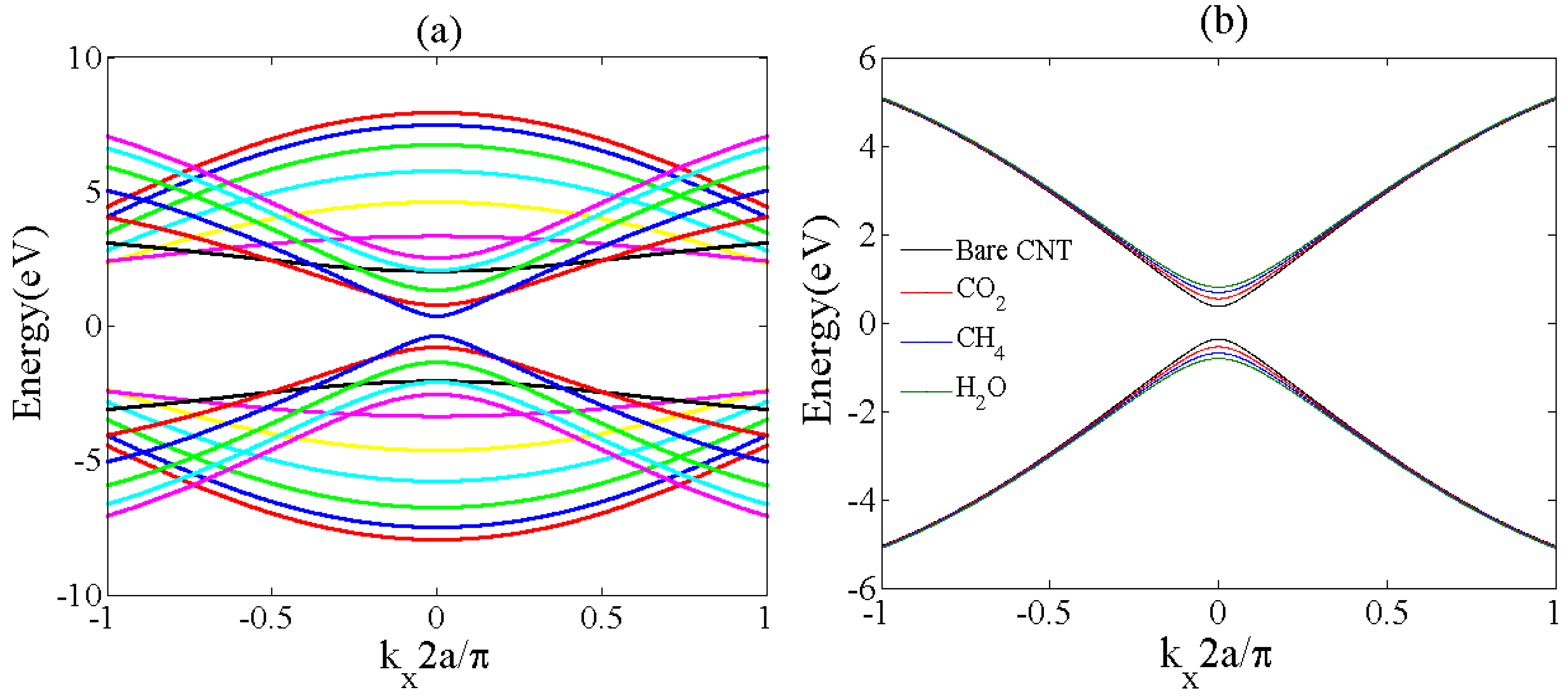
2.1. Energy Band Structure Modeling
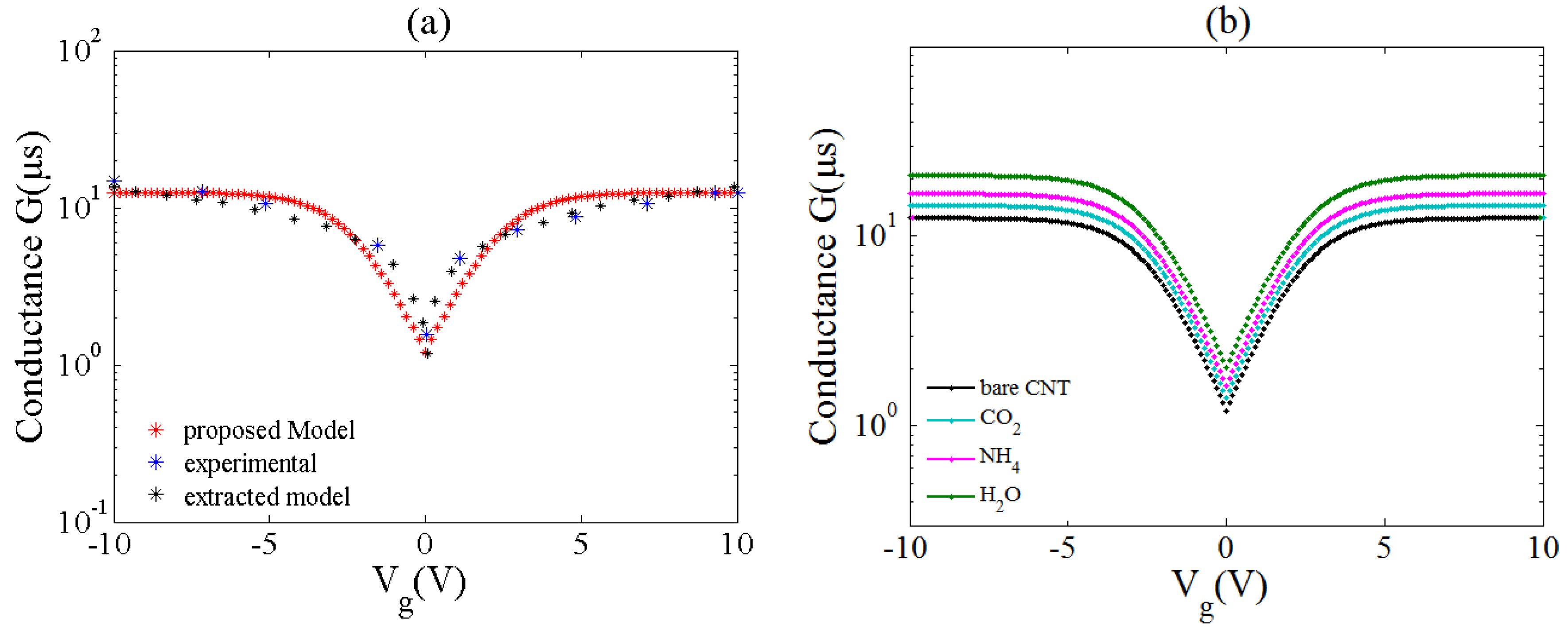
2.2. Conductance Model By Considering Gas Adsorption Effect
3. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Akbari, E.; Afroozeh, A.; Tan, M.L.P.; Arora, V.K.; Ghadiry, M. Analytical Assessment of Carbon allotropes for Gas Sensor Applications. Measurement 2016, 92, 295–302. [Google Scholar] [CrossRef]
- Ellis, J.E.; Star, A. Carbon nanotube based gas sensors toward breath analysis. ChemPlusChem 2016, 81, 1248–1265. [Google Scholar] [CrossRef]
- Drewniak, S.; Muzyka, R.; Stolarczyk, A.; Pustelny, T.; Kotyczka-Morańska, M.; Setkiewicz, M. Studies of reduced graphene oxide and graphite oxide in the aspect of their possible application in gas sensors. Sensors 2016, 16, 103. [Google Scholar] [CrossRef] [PubMed]
- Karimi, F.; Ahmadi, M.; Rahmani, M.; Akbari, E.; Kiani, M.J.; Khalid, M. Analytical modeling of graphene-based DNA sensor. Sci. Adv. Mater. 2012, 4, 1142–1147. [Google Scholar] [CrossRef]
- Pourasl, A.; Ahmadi, M.T.; Rahmani, M.; Ismail, R. Graphene Based Biosensor Model for Escherichia Coli Bacteria Detection. J. Nanosci. Nanotechnol. 2017, 17, 601–605. [Google Scholar] [CrossRef]
- Veigas, B.; Fortunato, E.; Baptista, P.V. Field effect sensors for nucleic acid detection: Recent advances and future perspectives. Sensors 2015, 15, 10380–10398. [Google Scholar] [CrossRef]
- Sangtarash, S.; Sadeghi, H.; Ahmadi, M.; Ghadiry, M.; Anwar, S.; Ismail, R. Schottky current in carbon nanotube-metal contact. J. Comput. Theor. Nanosci. 2012, 9, 1554–1557. [Google Scholar] [CrossRef]
- Pourasl, A.H.; Ahmadi, M.T.; Rahmani, M.; Ismail, R.; Tan, M.L.P. Graphene and CNT Field Effect Transistors Based Biosensor Models. In Handbook of Research on Nanoelectronic Sensor Modeling and Applications; Ahmadi, M.T., Ismail, R., Anwar, S., Eds.; IGI Global: Hershey, PA, USA, 2016; pp. 294–333. [Google Scholar]
- Meyyappan, M. Carbon Nanotube-Based Chemical Sensors. Small 2016, 12, 2118–2129. [Google Scholar] [CrossRef]
- Chen, J.; Kumar, S. Variability in Output Characteristics of Single-Walled Carbon Nanotube Thin-Film Transistors. IEEE Trans. Nanotechnol. 2018, 17, 353–361. [Google Scholar]
- Salvato, M.; Scagliotti, M.; De Crescenzi, M.; Crivellari, M.; Messi, R.; Castrucci, P. Increasing Efficiency in Single-Walled Carbon Nanotube/n-Si Photodetectors by Voltage Doping. IEEE Trans. Nanotechnol. 2018, 17, 837–840. [Google Scholar]
- Datta, S. Quantum Transport: Atom to Transistor; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Marconcini, P.; Macucci, M. The kp method and its application to graphene, carbon nanotubes and graphene nanoribbons: The Dirac equation. arXiv 2011, arXiv:1105.1351. [Google Scholar]
- Saito, R.; Fujita, M.; Dresselhaus, G.; Dresselhaus, M.S. Electronic structure of graphene tubules based on C 60. Phys. Rev. B 1992, 46, 1804. [Google Scholar] [CrossRef] [PubMed]
- Lee, C.Y.; Strano, M.S. Understanding the Dynamics of Signal Transduction for Adsorption of Gases and Vapors on Carbon Nanotube Sensors. Langmuir 2005, 21, 5192–5196. [Google Scholar] [CrossRef]
- Guo, S.Y.; Hou, P.X.; Wang, H.X.; Shi, C.; Fang, H.T.; Liu, C. Transparent and flexible hydrogen sensor based on semiconducting single-wall carbon nanotube networks. Carbon 2019, 151, 156–159. [Google Scholar] [CrossRef]
- Sinha, N.; Ma, J.; Yeow, J.T. Carbon nanotube-based sensors. J. Nanosci. Nanotechnol. 2006, 6, 573–590. [Google Scholar] [CrossRef] [PubMed]
- Pourasl, A.H.; Ahmadi, M.T.; Rahmani, M.; Chin, H.C.; Lim, C.S.; Ismail, R.; Tan, M.L.P. Analytical modeling of glucose biosensors based on carbon nanotubes. Nanoscale Res. Lett. 2014, 9, 33. [Google Scholar] [CrossRef]
- Wang, Q.; Arash, B. A review on applications of carbon nanotubes and graphenes as nano-resonator sensors. Comput. Mater. Sci. 2014, 82, 350–360. [Google Scholar] [CrossRef]
- Lee, S.W.; Lee, W.; Hong, Y.; Lee, G.; Yoon, D.S. Recent advances in carbon material-based NO2 gas sensors. Sens. Actuators B Chem. 2018, 255, 1788–1804. [Google Scholar] [CrossRef]
- Yu, X.; Chen, X.; Li, H.; Ding, X. A high-stability QCM Humidity sensor coated with nanodiamond/multiwalled carbon nanotubes nanocomposite. IEEE Trans. Nanotechnol. 2018, 17, 506–512. [Google Scholar] [CrossRef]
- Kuo, C.Y.; Chan, C.L.; Gau, C.; Liu, C.; Shiau, S.H.; Ting, J. Nano Temperature Sensor Using Selective Lateral Growth of Carbon Nanotube Between Electrodes. IEEE Trans. Nanotechnol. 2007, 6, 63–69. [Google Scholar] [CrossRef]
- Camilli, L.; Passacantando, M. Advances on sensors based on carbon nanotubes. Chemosensors 2018, 6, 62. [Google Scholar] [CrossRef]
- Li, J.; Lu, Y.; Ye, Q.; Cinke, M.; Han, J.; Meyyappan, M. Carbon nanotube sensors for gas and organic vapor detection. Nano Lett. 2003, 3, 929–933. [Google Scholar] [CrossRef]
- Young, S.; Lin, Z. Ethanol gas sensors based on multi-wall carbon nanotubes on oxidized Si substrate. Microsyst. Technol. 2018, 24, 55–58. [Google Scholar] [CrossRef]
- da Silva, L.B.; Fagan, S.B.; Mota, R. Ab Initio Study of Deformed Carbon Nanotube Sensors for Carbon Monoxide Molecules. Nano Lett. 2004, 4, 65–67. [Google Scholar] [CrossRef]
- Wu, R.J.; Huang, Y.C.; Yu, M.R.; Lin, T.H.; Hung, S.L. Application of m-CNTs/NaClO4/Ppy to a fast response, room working temperature ethanol sensor. Sens. Actuators B Chem. 2008, 134, 213–218. [Google Scholar] [CrossRef]
- Nguyen, L.; Phan, P.; Duong, H.; Nguyen, C.; Nguyen, L. Enhancement of NH3 gas sensitivity at room temperature by carbon nanotube-based sensor coated with Co nanoparticles. Sensors 2013, 13, 1754–1762. [Google Scholar] [CrossRef]
- Joshi, K.A.; Prouza, M.; Kum, M.; Wang, J.; Tang, J.; Haddon, R.; Chen, W.; Mulchandani, A. V-type nerve agent detection using a carbon nanotube-based amperometric enzyme electrode. Anal. Chem. 2006, 78, 331–336. [Google Scholar] [CrossRef]
- Akbari, E.; Ahmadi, M.; Kiani, M.; Feizabadi, H.K.; Rahmani, M.; Khalid, M. Monolayer graphene based CO2 gas sensor analytical model. J. Comput. Theor. Nanosci. 2013, 10, 1301–1304. [Google Scholar] [CrossRef]
- Akbari, E.; Arora, V.K.; Enzevaee, A.; Ahmadi, M.T.; Saeidmanesh, M.; Khaledian, M.; Karimi, H.; Yusof, R. An analytical approach to evaluate the performance of graphene and carbon nanotubes for NH3 gas sensor applications. Beilstein J. Nanotechnol. 2014, 5, 726–734. [Google Scholar] [CrossRef]
- Rahmani, M.; Ahmadi, M.; Karimi, H.; Kiani, M.; Akbari, E.; Ismail, R. Analytical modeling of monolayer graphene-based NO2 sensor. Sensor Lett. 2013, 11, 270–275. [Google Scholar] [CrossRef]
- Akbari, E.; Ahmadi, M.; Yusof, R.; Ghadiry, M.; Saeidmanesh, M. Gas concentration effect on channel capacitance in graphene based sensors. J. Comput. Theor. Nanosci. 2013, 10, 2449–2452. [Google Scholar] [CrossRef]
- Moradian, R.; Mohammadi, Y.; Ghobadi, N. Investigation of gas sensing properties of armchair graphene nanoribbons. J. Phys. Condens. Matter 2008, 20, 425211. [Google Scholar] [CrossRef]
- Tien, H.M.; Chau, N.H.; Loan, P.T.K. Tight-binding calculations of band structure and conductance in graphene nano-ribbons. Commun. Phys. 2009, 19, 1–8. [Google Scholar] [CrossRef][Green Version]
- Zhao, K.; Zhao, M.; Wang, Z.; Fan, Y. Tight-binding model for the electronic structures of SiC and BN nanoribbons. Phys. E Low-Dimens. Syst. Nanostruct. 2010, 43, 440–445. [Google Scholar] [CrossRef]
- Modarresi, M.; Roknabadi, M.; Shahtahmasbi, N. Transport properties of an armchair boron-nitride nanoribbon embedded between two graphene electrodes. Phys. E Low-Dimens. Syst. Nanostruct. 2011, 43, 1751–1754. [Google Scholar] [CrossRef]
- Saffarzadeh, A. Modeling of gas adsorption on graphene nanoribbons. J. Appl. Phys. 2010, 107, 114309. [Google Scholar] [CrossRef]
- Zhang, D.; Liu, J.; Jiang, C.; Liu, A.; Xia, B. Quantitative detection of formaldehyde and ammonia gas via metal oxide-modified graphene-based sensor array combining with neural network model. Sens. Actuators B Chem. 2017, 240, 55–65. [Google Scholar] [CrossRef]
- Bejaoui, A.; Guerin, J.; Aguir, K. Modeling of a p-type resistive gas sensor in the presence of a reducing gas. Sens. Actuators B Chem. 2013, 181, 340–347. [Google Scholar] [CrossRef]
- Jeon, J.Y.; Kang, B.C.; Byun, Y.T.; Ha, T.J. High-performance gas sensors based on single-wall carbon nanotube random networks for the detection of nitric oxide down to the ppb-level. Nanoscale 2019, 11, 1587–1594. [Google Scholar] [CrossRef]
- Zheng, H.; Wang, Z.; Luo, T.; Shi, Q.; Chen, J. Analytical study of electronic structure in armchair graphene nanoribbons. Phys. Rev. B 2007, 75, 165414. [Google Scholar] [CrossRef]
- Ezawa, M. Peculiar width dependence of the electronic properties of carbon nanoribbons. Phys. Rev. B 2006, 73, 45432. [Google Scholar] [CrossRef]
- Harrison, W.A. Electronic Structure and the Properties of Solids: The Physics of the Chemical Bond; Courier Corporation: Chelmsford, MA, USA, 2012. [Google Scholar]
- Zhao, J.; Buldum, A.; Han, J.; Lu, J.P. Gas molecule adsorption in carbon nanotubes and nanotube bundles. Nanotechnology 2002, 13, 195. [Google Scholar] [CrossRef]
- Wong, H.S.P.; Akinwande, D. Carbon Nanotube and Graphene Device Physics; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Ahmadi, M.T.; Johari, Z.; Amin, N.A.; Mousavi, S.M.; Ismail, R. Carbon nanotube conductance model in parabolic band structure. In Proceedings of the 2010 IEEE International Conference on Semiconductor Electronics (ICSE2010), Malacca, Malaysia, 28–30 June 2010. [Google Scholar]
- Anantram, M.; Leonard, F. Physics of carbon nanotube electronic devices. Rep. Prog. Phys. 2006, 69, 507. [Google Scholar] [CrossRef]

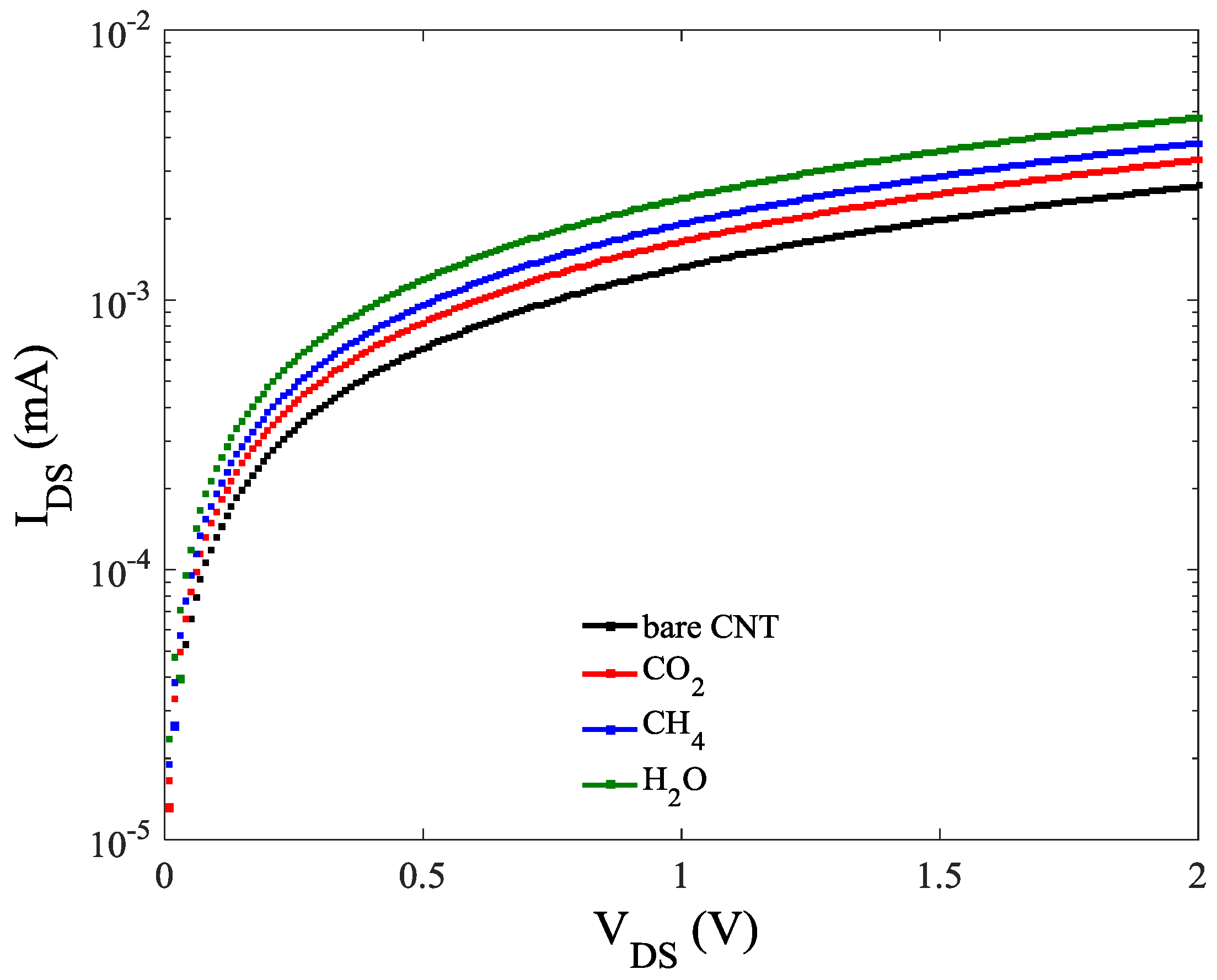
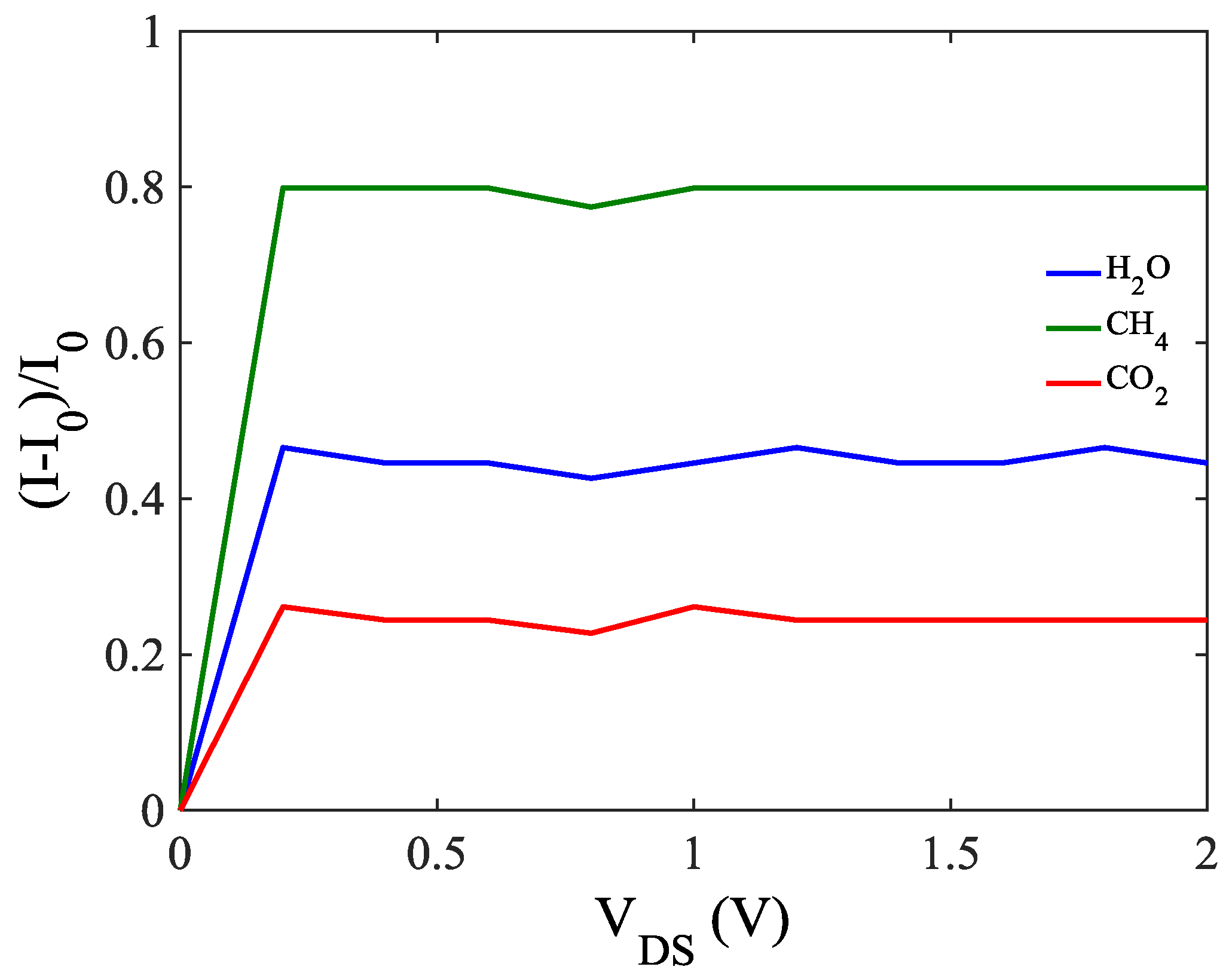
| Adsorption Type | Distance from ZCNT Surface (Å) | Hopping Parameter |
|---|---|---|
| CH4 | tC-CH4 = 0.445tR | |
| CO2 | tC-CO2 = 0.43tR | |
| H2O | tC-H2O = 0.528tR |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hosseingholipourasl, A.; Hafizah Syed Ariffin, S.; Ahmadi, M.T.; Rahimian Koloor, S.S.; Petrů, M.; Hamzah, A. An Analytical Conductance Model for Gas Detection Based on a Zigzag Carbon Nanotube Sensor. Sensors 2020, 20, 357. https://doi.org/10.3390/s20020357
Hosseingholipourasl A, Hafizah Syed Ariffin S, Ahmadi MT, Rahimian Koloor SS, Petrů M, Hamzah A. An Analytical Conductance Model for Gas Detection Based on a Zigzag Carbon Nanotube Sensor. Sensors. 2020; 20(2):357. https://doi.org/10.3390/s20020357
Chicago/Turabian StyleHosseingholipourasl, Ali, Sharifah Hafizah Syed Ariffin, Mohammad Taghi Ahmadi, Seyed Saeid Rahimian Koloor, Michal Petrů, and Afiq Hamzah. 2020. "An Analytical Conductance Model for Gas Detection Based on a Zigzag Carbon Nanotube Sensor" Sensors 20, no. 2: 357. https://doi.org/10.3390/s20020357
APA StyleHosseingholipourasl, A., Hafizah Syed Ariffin, S., Ahmadi, M. T., Rahimian Koloor, S. S., Petrů, M., & Hamzah, A. (2020). An Analytical Conductance Model for Gas Detection Based on a Zigzag Carbon Nanotube Sensor. Sensors, 20(2), 357. https://doi.org/10.3390/s20020357







