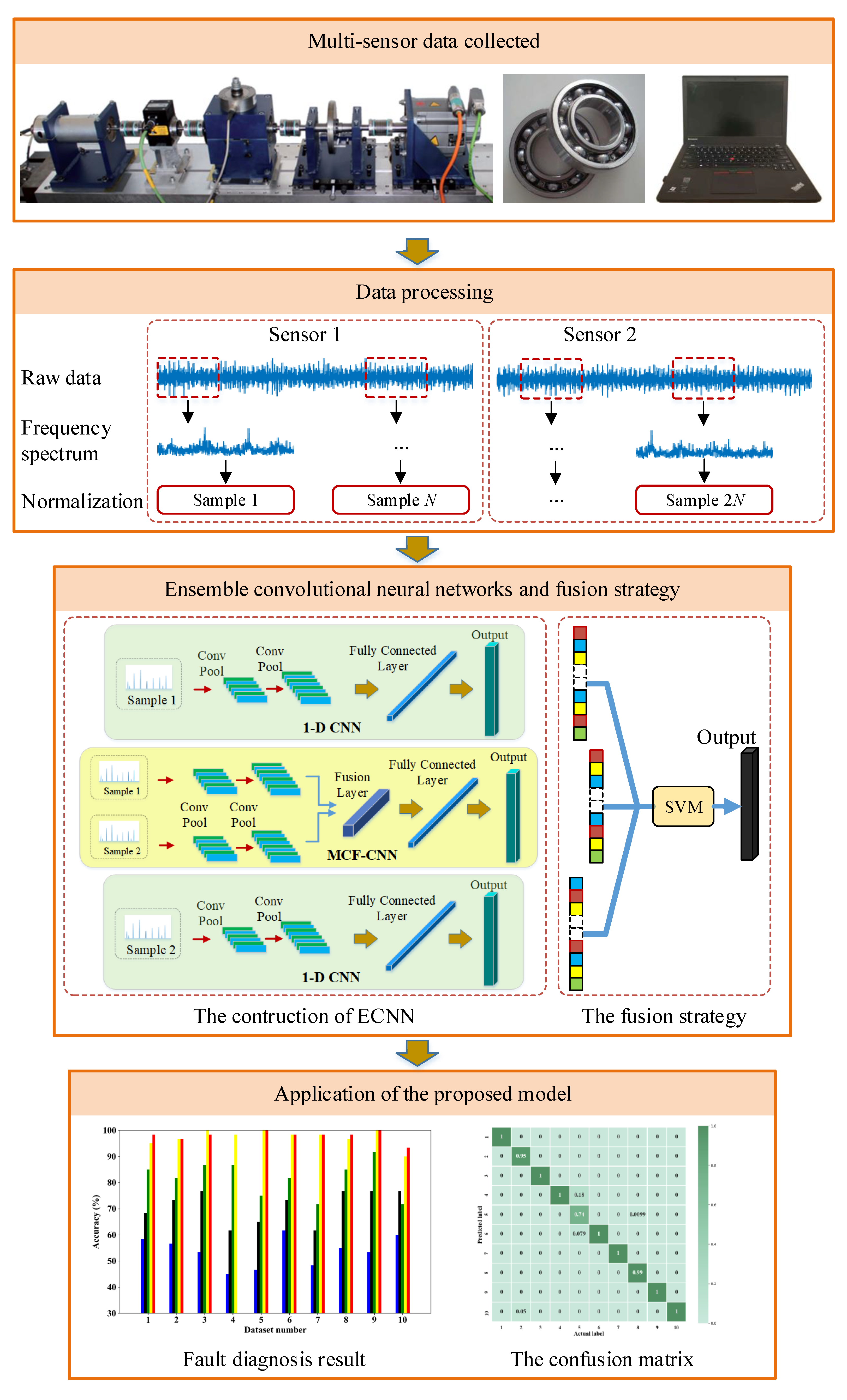
1. Introduction
Rotating machinery is widely used in modern industry. Due to long-time running under complicated conditions such as high speed, heavy load and strong impact, rotating machinery will inevitably have some faults, which can result in enormous losses and serious casualties [
1]. Therefore, the fault diagnosis of rotating machinery is necessary to ensure the safe and efficient operation of machinery [
2,
3].
Traditional fault diagnosis methods are mainly based on model analysis or signal processing techniques. The model-based diagnosis methods emphasize the deep understanding of the dynamic characteristics of rotating machinery. Immovilli et al. [
4] conduct a theoretical analysis based on the vibration and current signals. Kerschen et al. [
5] provide extensive reviews on model-based analysis of vibrating systems. These methods usually require the design of the explicit mathematical model to simulate the behavior of the machine, while the development of the mathematical model is almost impossible when dealing with modern machines with very complex structures. The methods based on signal processing techniques often utilize signal models, such as power spectrum [
6], high order spectrum [
6,
7,
8], composite spectrum [
9,
10,
11], to directly extract the fault features from the measured signals for the classification. Among the various measured signals, vibration signals [
12,
13] are most popular due to the inclusion of more fault information. In addition to the vibration signals, magnetic flux signals [
14] are also used to fault diagnosis. Besides, some researchers have also applied these methods for machine condition monitoring [
15,
16,
17]. However, these methods still rely on the analysis of the mechanical structure and extracting effective fault features is blind and difficult.
Different from traditional diagnosis methods, Intelligent fault diagnosis aims to effectively analyze massive data and automatically provide diagnosis results, which has become a new trend in the field of equipment condition monitoring [
18]. Generally, traditional intelligent fault diagnosis of rotating machinery can be regarded as a pattern recognition problem. It can be divided into two steps: feature extraction and pattern classification [
19], which can result in two inherent shortcomings—(1) The feature extraction process is difficult in that it relies on advanced signal processing technology and extensive engineering experience [
20]. Moreover, the extracted features often do not fully reflect the fault characteristics which limits the application. (2) Current pattern recognition methods in the fault classification, such as artificial neural network (ANN) [
21,
22] and support vector machine (SVM) [
23], belong to the shallow learning model. Such model has no more than one nonlinear transformation [
24]. Due to the complex non-linear characteristics of fault signals, the shallow learning model is difficult to effectively learn representative features for fault diagnosis [
25,
26]. Consequently, it is necessary to build deep-architecture learning model to achieve more efficient and automatic fault diagnosis.
In recent years, deep learning provides a new research hotspot for analyzing and processing the big data, which has made great achievements in the fields of image, finance, meteorology, and natural language [
27]. As a typical model of deep learning, a convolutional neural network (CNN) [
28] can automatically learn more representative characteristics for fault diagnosis, thus overcoming the inherent shortcomings of traditional intelligent diagnosis methods. CNN has been widely applied in the field of fault diagnosis. However, in most studies [
29,
30,
31,
32], the input is only limited to the single-sensor data, which greatly limits the further performance improvement of the CNN fault diagnosis model. To overcome these drawbacks, a feasible method is using the information provided by multi-sensor data.
According to the literature [
33], multi-sensor data fusion of fault diagnosis can be divided into three levels: data-level fusion, feature-level fusion and decision-level fusion. Data-level fusion is the lowest level, including Kalman filtering [
34], principal component analysis (PCA) [
35] and independent component analysis (ICA) [
36], and so forth. This fusion methods directly takes data from different sensors as new data sources, which ignores the inner relationship of different sensors [
37]. For the feature-level fusion, features from different sensors are extracted and selected by signal processing techniques. The more abundant data from multiple sensors makes the selection of sensitive features more difficult [
38]. Decision-level fusion fuses the results of different classifiers to achieve a better decision. Common fusion algorithms include the majority voting [
39], SVM [
40,
41], dempster-shafer (DS) evidence theory [
42], random forest (RF) [
43] and Bayesian estimation [
44]. However, these studies for different levels of fusion generally ignore the coupling relationship between multi-sensor data, which causes information losses [
37].
Recently, the CNN models based on multi-sensor data have been used for fault diagnosis. Generally, multi-sensor signals are connected into long signals [
38] or arranged into 2-D images [
45] as the input of CNN. Furthermore, Gong et al. [
46] propose an improved CNN-SVM model by usage of the 2-D signals from multi-sensor data. Chen et al. [
47] compare different fusion methods at the input layer of CNN by taking horizontal and vertical vibration signals. These models can effectively extract the coupling features between different sensors, thus achieving better performance than traditional methods based on multi-sensor data. However, on the one hand, they ignore the inherent information of the single-sensor data and fail to effectively fuse the inherent information with the coupling information acquired by the multi-sensor data, resulting in information losses. On the other hand, the generalization of the model is important due to the large inter-class divergence and small divergence between classes of the collected signals. But current research mainly focuses on the optimization of individual network, which limits the generalization of the model. In addition, the splicing or arranging of massive time-domain data may lead to the problem of over-fitting.
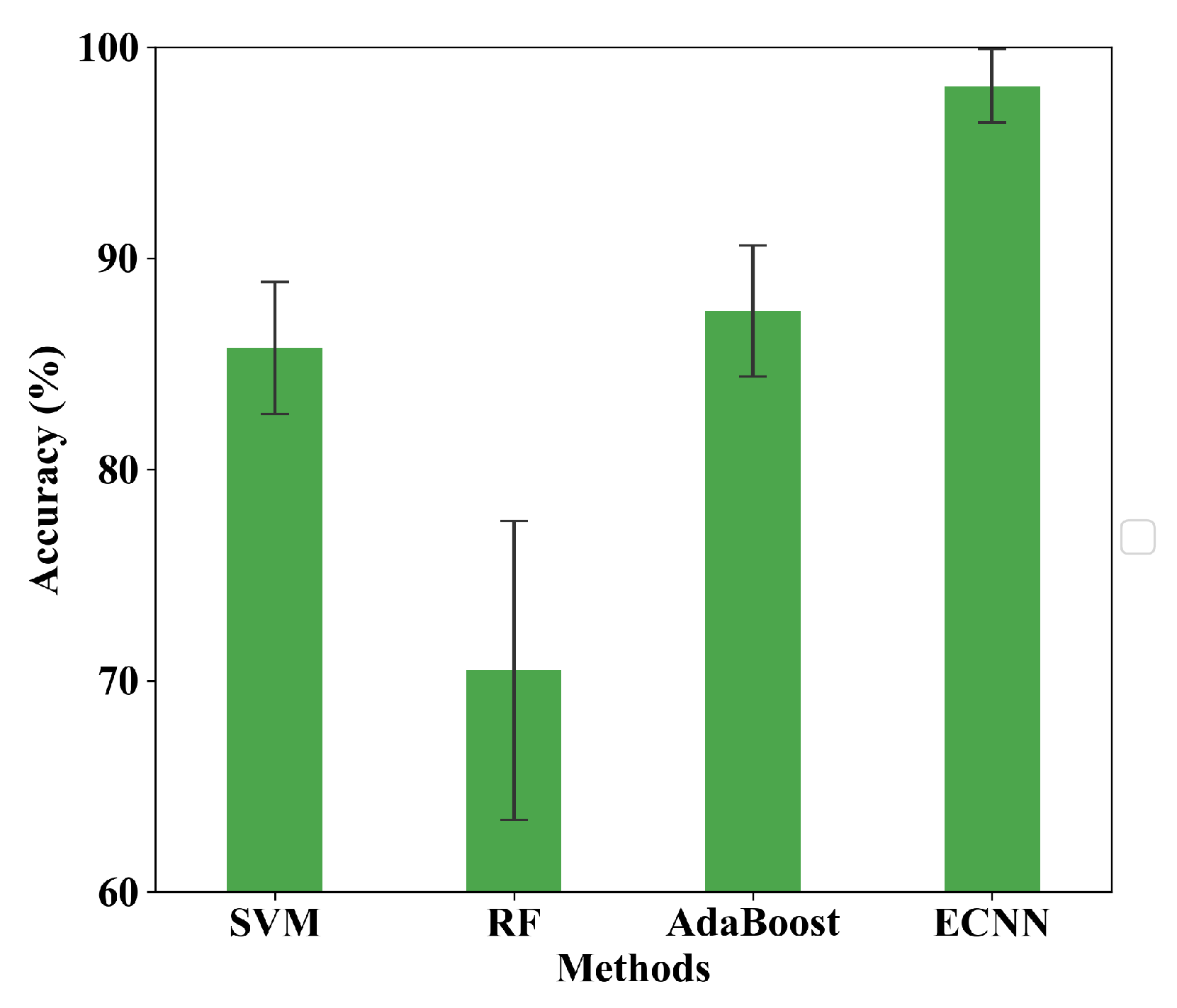
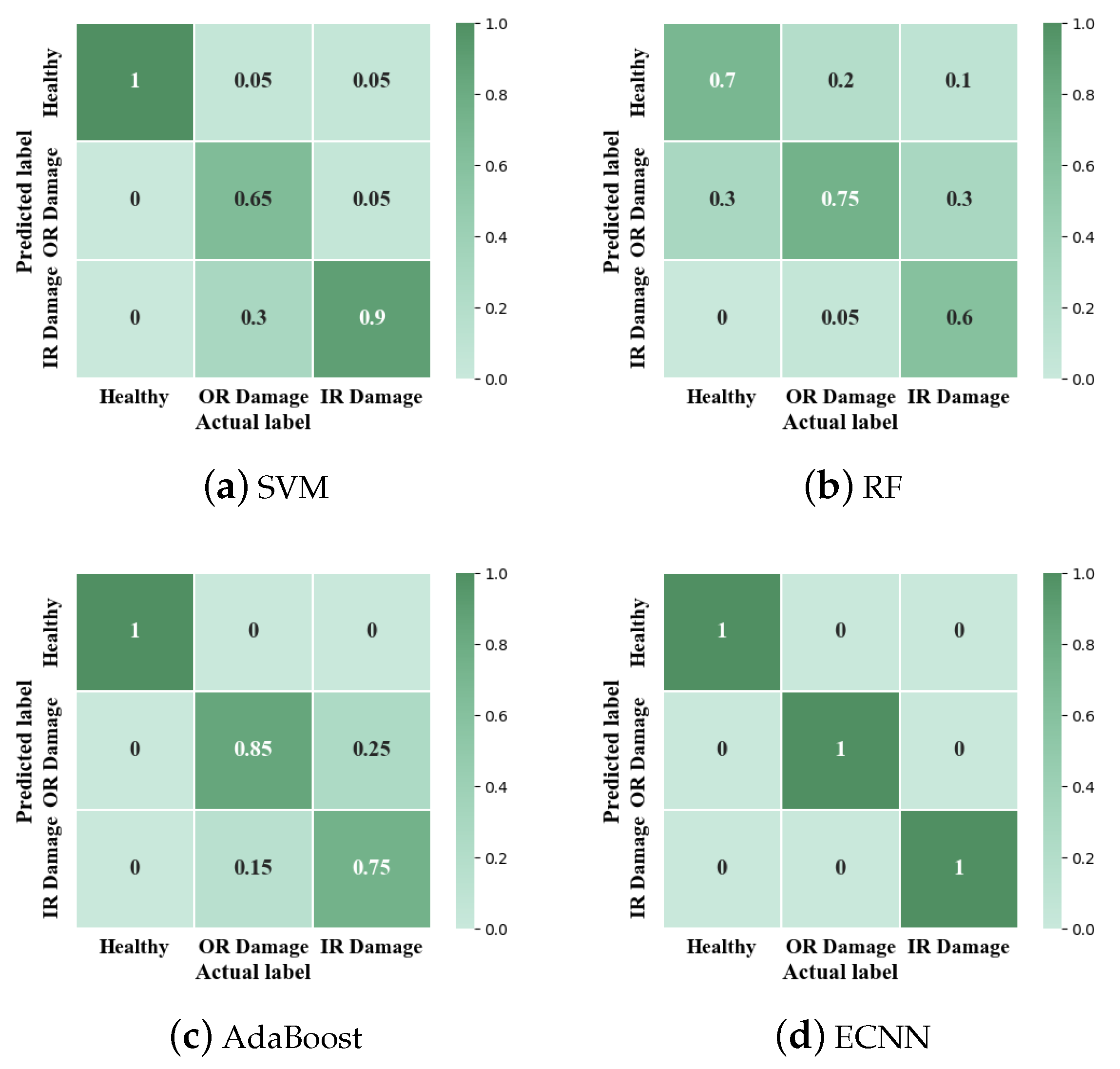
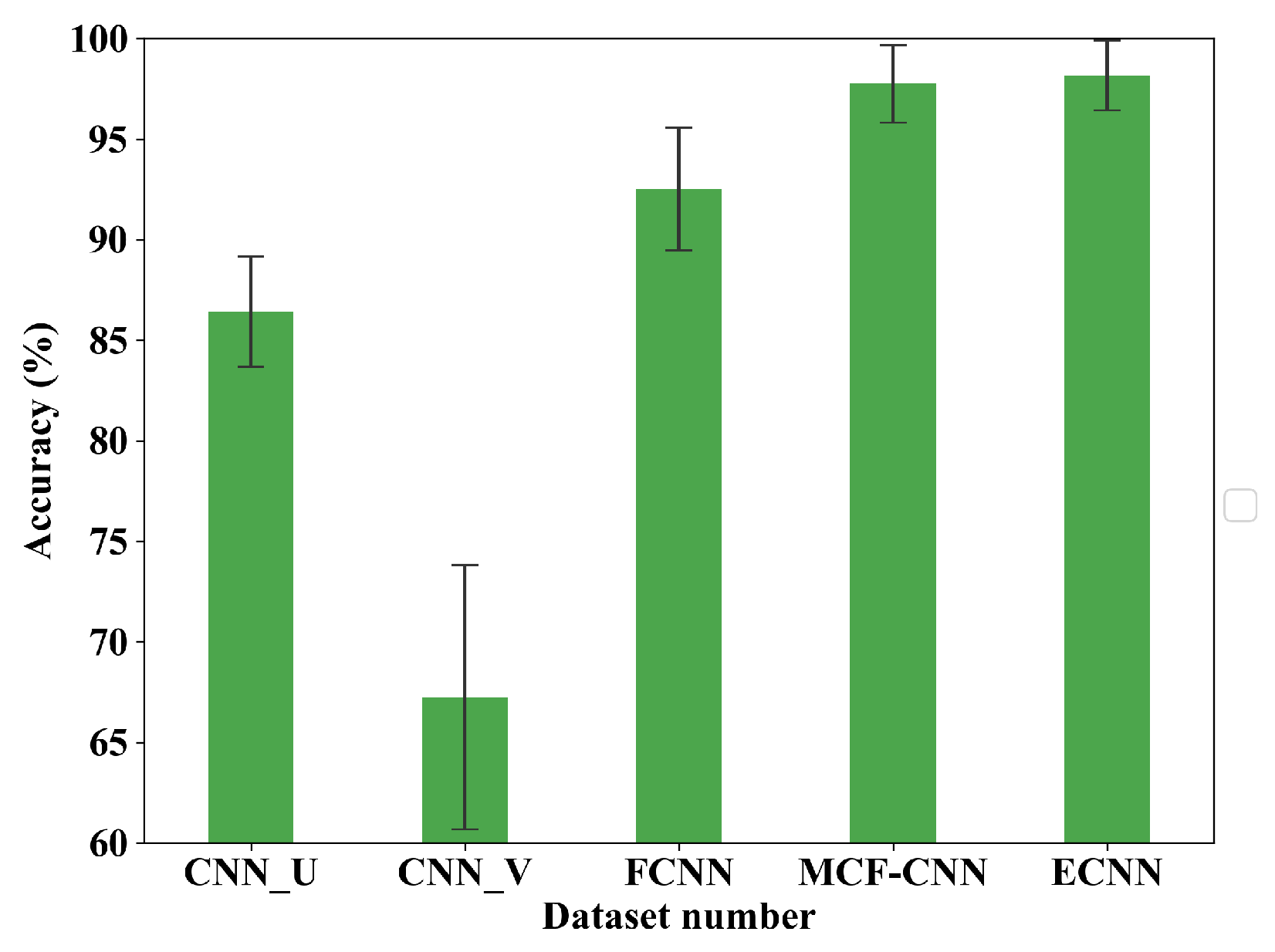
To solve the above problems, a novel model named ensemble convolutional neural networks (ECNN) using multi-sensor data is proposed for bearing fault diagnosis in this manuscript. The proposed model, ECNN, can automatically and effectively extract features for classification that gets rid of the dependence on signal processing techniques and diagnosis experience. Besides, a multi-channel fusion convolutional neural network (MCF-CNN) and two 1-D CNNs are designed to construct ensemble model. The coupling features between multi-sensor data are extracted by the MCF-CNN model and the inherent features of the single-sensor data are extracted by 1-D CNN model, overcoming the problem of information losses. Furthermore, to improve the generalization and robustness of the proposed model, the SVM combination strategy is employed to integrate the result of multiple CNN models. The proposed model uses frequency spectrum as the input of CNN, verified based on two typical rolling bearing fault databases.
In
Section 2, a brief theory of CNN is introduced.
Section 3 describes the main framework of ECNN in detail. In
Section 4, the experimental results are analyzed and discussed based on the CWRU database and the Paderborn University database. Finally, the conclusions and outlook are given in
Section 5.
2. The Standard Convolutional Neural Network
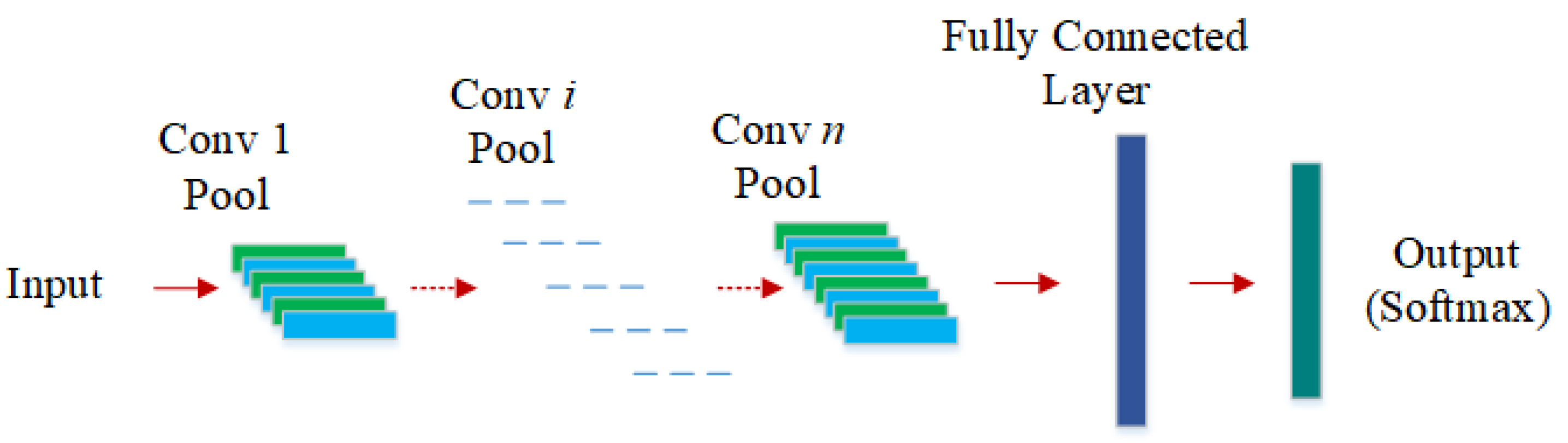
CNN is one of the most prevalent deep learning models in recent years. As shown in
Figure 1, CNN processes the input samples through multiple convolutional layers and pooling layers to obtain a series of deep feature maps. Suppose the input of
lth convolutional layer is
, which belongs to
and
A and
B are the dimensions of the input data. Then the output of the convolutional layer can be calculated as follows:
where
is the linear activation,
is a set of kernels of
lth convolutional layer, * represents the convolutional operation,
represents the feature maps in the previous layer
,
is the bias vector and
f is the Relu activation function. The output
is conducted by the max pooling operation:
where
is the output feature maps of pooling layer and
represents the up-sampling function of max pooling.
After several operations of convolution and pooling, deep feature maps are expanded into fully connected layer:
where
is the fully connected layer,
is the weight,
represents the feature vector in the previous layer
,
is the bias vector.
For the output
of last fully connected layer, softmax function achieves the mapping between the fully connected layer and the target output:
where
is the predicted probability belonging to the
ith class,
is the
ith output neuron of last fully connected layer.
3. The Proposed Model
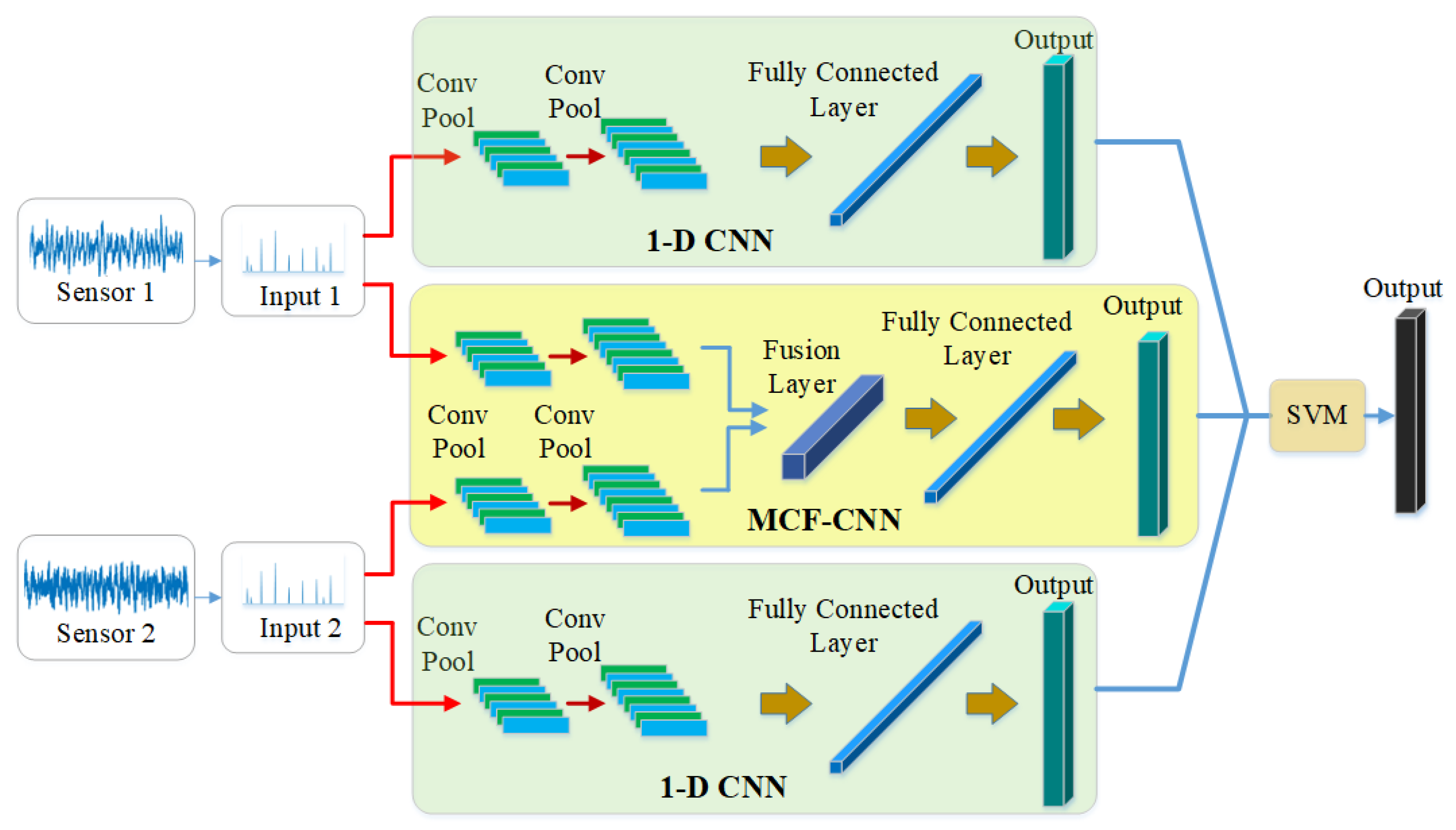
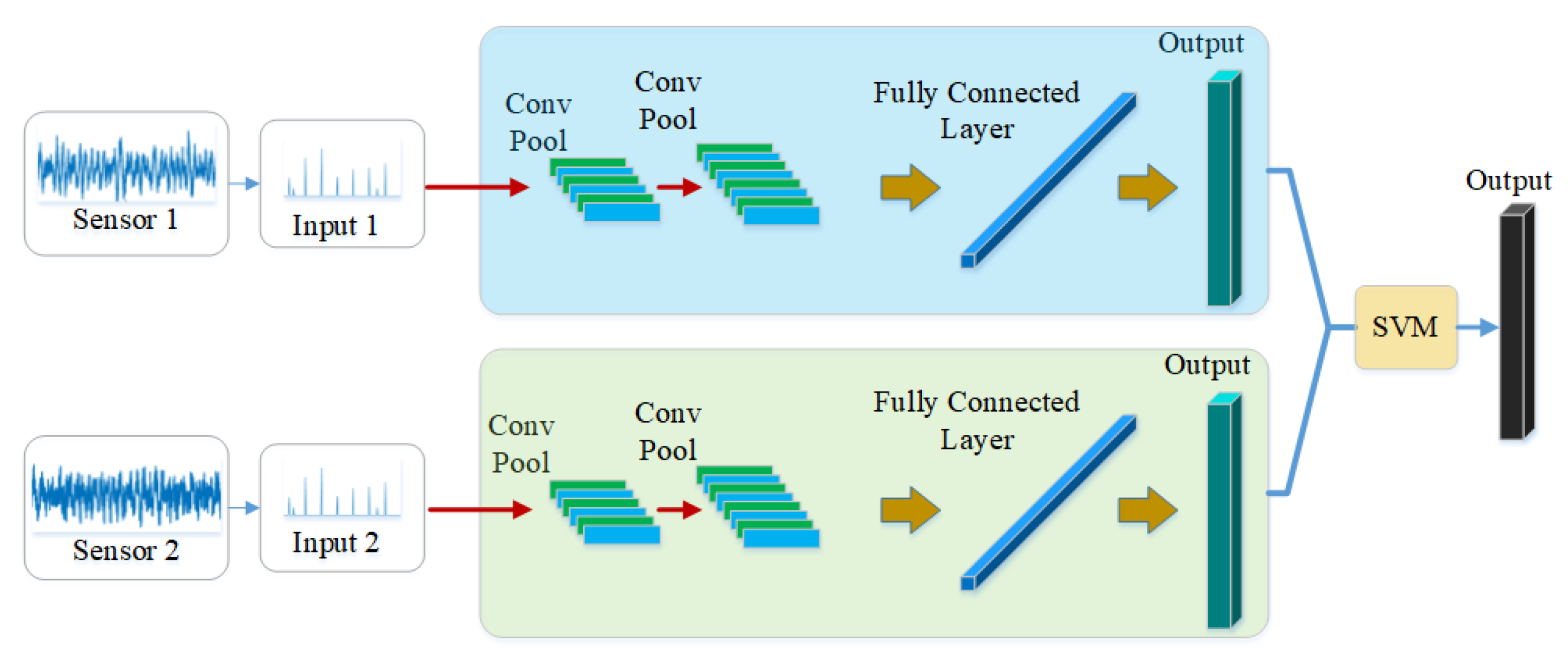
In this manuscript, a novel model, ECNN, is developed for bearing fault diagnosis. The input of the model is the frequency spectrum of the collected signals so that we select the one-dimensional convolutional neural network (1-D CNN) with the one-dimensional filter as the kernel of CNN. It is clearly seen that the framework contains three CNN branches based on two-sensor data.
Figure 2 shows the overall framework of the proposed model. The MCF-CNN branch is used to extract the coupling features between the two-sensor data and the two 1-D CNN branches focus on the contribution of the single-sensor data. Thus, more comprehensive fault information can be collected for fault diagnosis, overcoming the problem of information losses. The SVM combination strategy is employed to give the final results by fusing three CNN branches. More details of the proposed model are described in the following subsection.
3.1. Multi-Channels Fusion Convolutional Neural Network
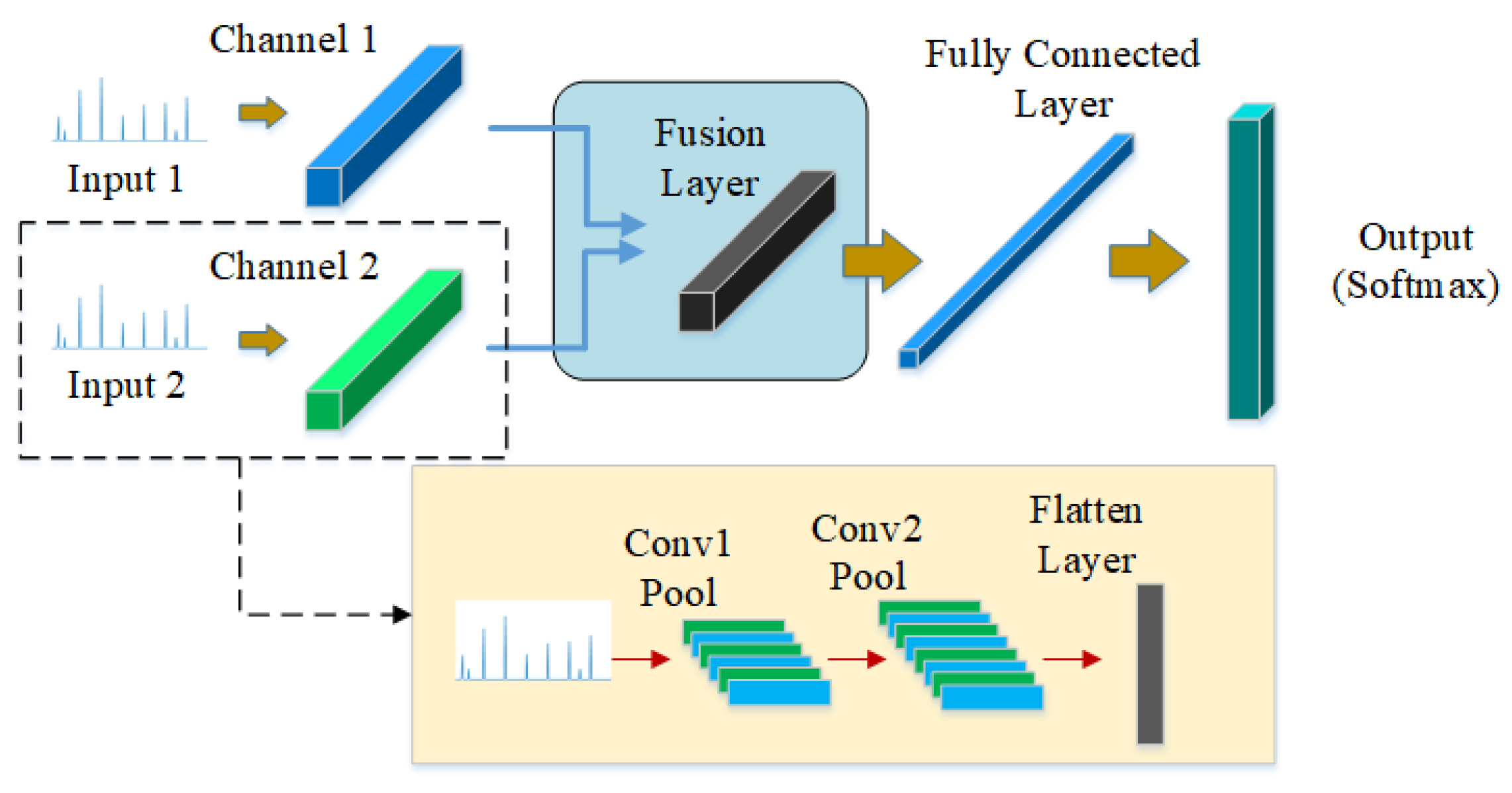
As shown in
Figure 3, MCF-CNN has two independent channels at the input layer which process multi-channel data separately. After multiple convolution and pooling operations, the deep features from multi-sensor data are fused at the fully connected layer. The main idea is that the two independent channels based on different sensors can extract the coupling features. Then the two channels are fused to enhance the fault information that facilitates classification. Finally, the classification is accomplished at the end of the network. It can be assumed that the MCF-CNN has better performance than the CNN with single-channel input because the multi-channel inputs are simultaneously trained under the same learning framework and the parameters of different channels can be jointly optimized during the training process.
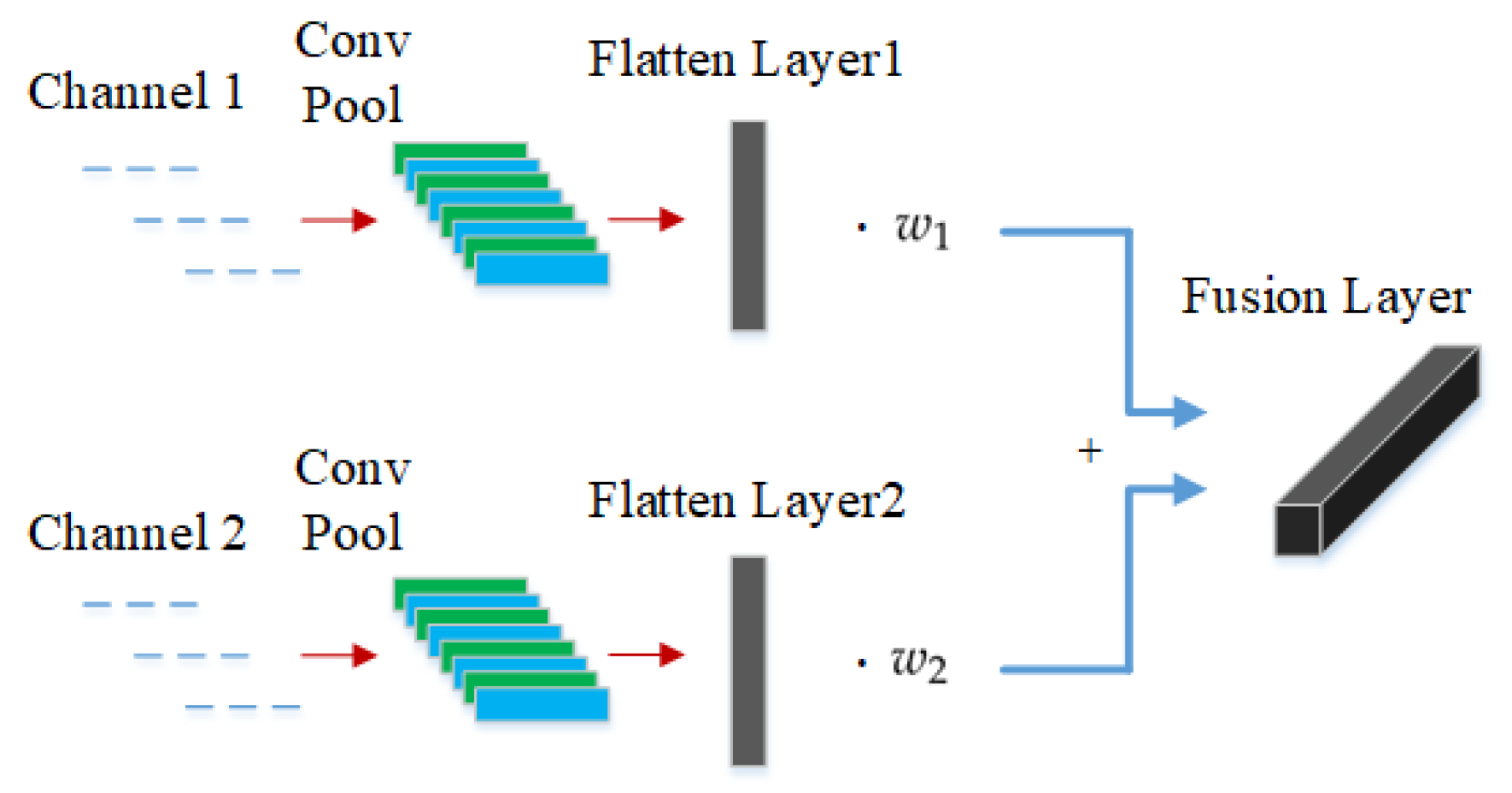
Figure 4 shows the fusion layer of MCF-CNN. Each input channel of MCF-CNN processes the input data through the convolution and pooling operations, calculating a number of feature maps. The two channels are set at the same network structure. The number of convolutional layers, the size of the kernel and the activation function are identical. At the end of each channel, the extracted feature maps are expanded into a one-dimensional feature vector, which is flatten layer. Next, the fusion layer combines the 1-D feature vector of the two channels. Denote the two feature vectors as
and
. The dimensions of
and
should be equal, then the fused feature vector
can be obtained
where
and
are the fusion weight of the feature vectors
and
, respectively, which are learned during the training process. The dimension of the fusion weight is consistent with the dimension of the feature vector. The relationship can be determined by the two weights, which is beneficial to extract the coupling features.
After the fusion layer, two fully connected layers are used to classify the input signals. The first fully connected layer has hundreds of neurons and the number of neurons in the last fully connected layer corresponds to the categories of classification tasks. The softmax function is used to convert the vector of the last fully connected layer into a probability distribution form.
3.2. The Construction of Ensemble Convlutional Neural Networks
The traditional fault diagnosis methods based on multi-sensor data ignore the coupling information between signals. The CNN fault diagnosis models based on multi-sensor data focuses on the coupling information between the signals and ignores the inherent information of the single-channel sensor. These methods all result in information losses. In addition, the performance of CNN fault diagnosis model is often limited due to single network framework. Ensemble learning is a new technique, which uses multiple individual learners and a certain combination strategy to get better results than each individual learner. Recently, a lot of ensemble learning methods have been applied for machinery fault diagnosis. Thus, ensemble learning of ECNN is constructed for fault diagnosis.
To collect more comprehensive fault information, the 1-D CNN model and the MCF-CNN model are used to construct ECNN. Since the databases contain the data from two sensors, two 1-D CNN models and one MCF-CNN model can be obtained. The input of the 1-D CNN is single sensor data, while the input of the MCF-CNN is the data from two sensors which are accepted by the two channel of MCF-CNN respectively.
3.3. The Fusion Strategy
The next step is to design a fusion strategy to combine the results of three CNN branches. Among the common fusion strategies, the majority voting is a widely used fusion method for ease of execution. However, the majority voting treats each classifier equally, resulting in poor performance when there are fewer classifiers. Obviously, it is not appropriate to use this method here because there are only three classifiers. The SVM is a popular machine learning method for classification, regression because of the small structural risk. In addition, the SVM model with kernel function can also learn the non-learning relationship of the input data. Thus, The SVM model with RBF kernel is chosen as the ensemble learning algorithm to fuse the results of three CNN branches.
For the
nth samples, define the predicted probability that belong to the
ith class of the
mth CNN as
and
, which can also be regarded as deep feature representations of the input sample. The deep feature representations of
,
and
are employed as the input of the SVM ensemble learning algorithm. The input can be expressed as follow:
where
,
N represents the number of the train samples. On the training set, we use the deep feature representations
of the
nth training sample as the input and the real label
of the samples as the output to learn the SVM ensemble learning algorithm. On the testing set, the deep feature representations
are used as the input of the SVM ensemble learning algorithm and then the prediction
of the samples can be obtained. The accuracy of the classifier is can be expressed:
where
represents the real label of the
n sample on the testing set and
(·) represents the indicator function.
3.4. The General Procedure of the Proposed Model
This manuscript develops a new model called ECNN for bearing fault diagnosis.
Figure 5 gives the flowchart illustrating of the proposed model and the general procedure can be summarized:
Step 1: The signal acquisition devices collect data from multiple sensors.
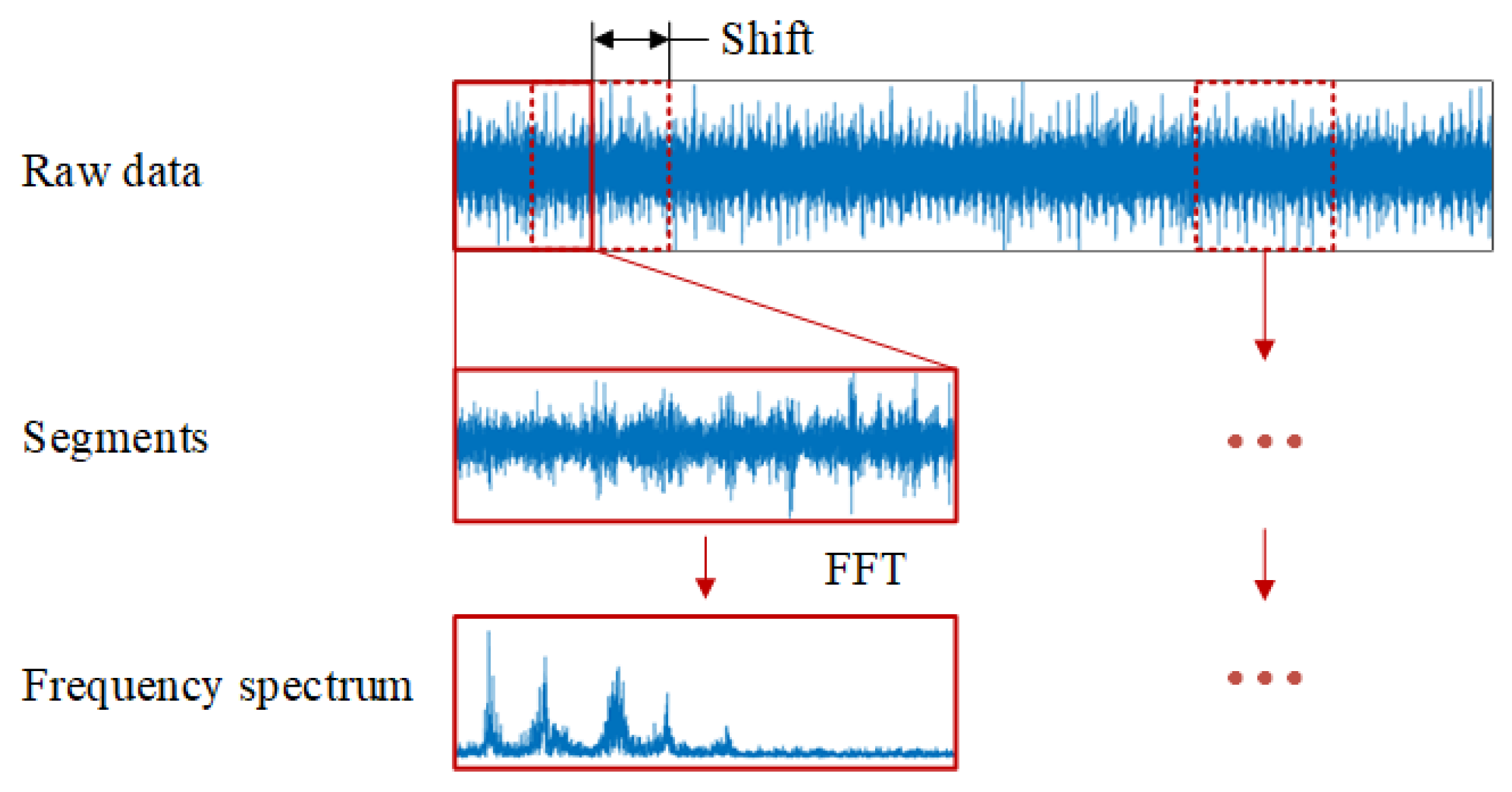
Step 2: The collected data are divided into training and testing set and the raw signals are divided into a series of segments. The frequency spectrum of the segment is used as the input of the CNN model.
Step 3: The MCF-CNN based on multi-sensor data and two 1-D CNNs based on single-sensor data are designed to construct ECNN based on training set.
Step 4: The SVM ensemble algorithm is employed to combine the results of three CNN branches.
Step 5: Validate the performance of the ECNN based on the testing set.
3.5. Discussion of the Proposed Model
Based on the typical model of deep learning, convolutional neural network, the proposed model fuses the multi-sensors data as two level. The advantage of the proposed model is can be summarized as follows:
The proposed model does not require complex mathematical models and does not rely on signal processing techniques and expert experience compared with the traditional fault diagnosis methods.
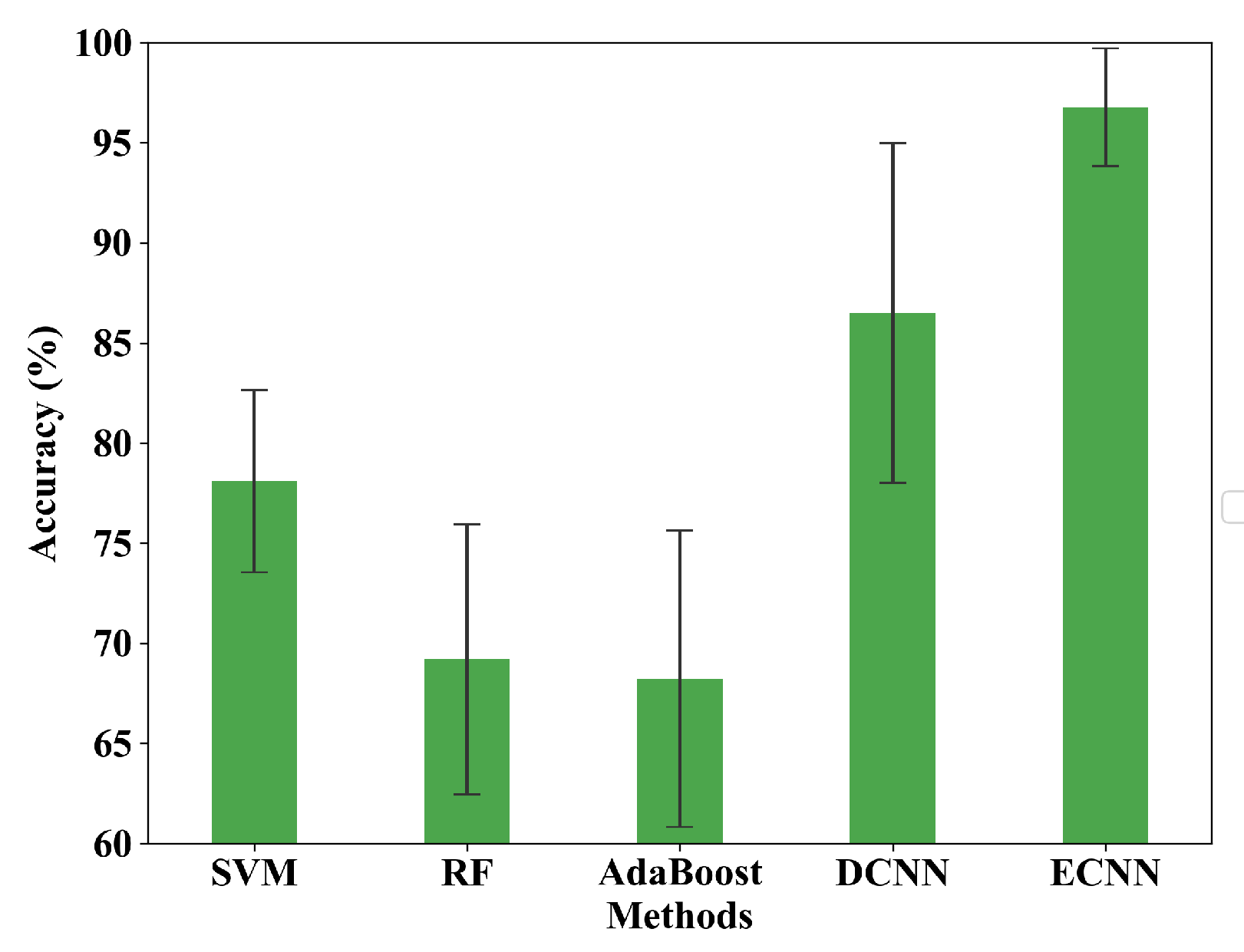
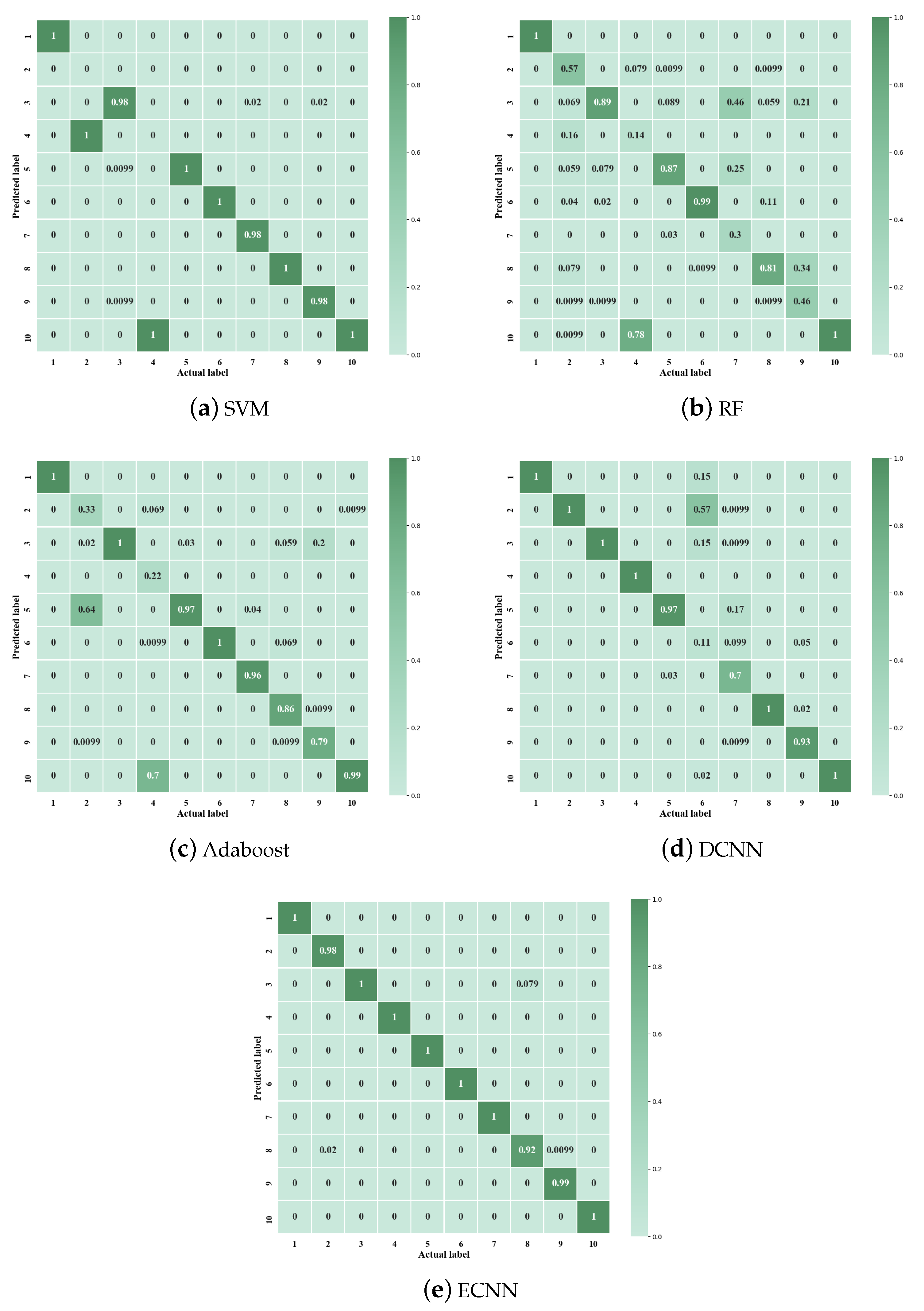
Compared with intelligent diagnosis methods, the proposed model does not require the process of complex feature extraction and feature selection. Besides, the deep learning framework can effectively extract more useful fault information for classification, which can further improve the diagnostic accuracy. Similarly, the new network structure, MCF-CNN, has the better ability to extract features.
The MCF-CNN model fuses multi-sensor data at the feature level and ECNN fuses the results of three CNN branches at decision level, effectively overcoming the problem of information losses during the fusion process.