Optical Sensors for Multi-Axis Angle and Displacement Measurement Using Grating Reflectors
Abstract
1. Introduction
2. Multi-Axis Optical Angle Sensors
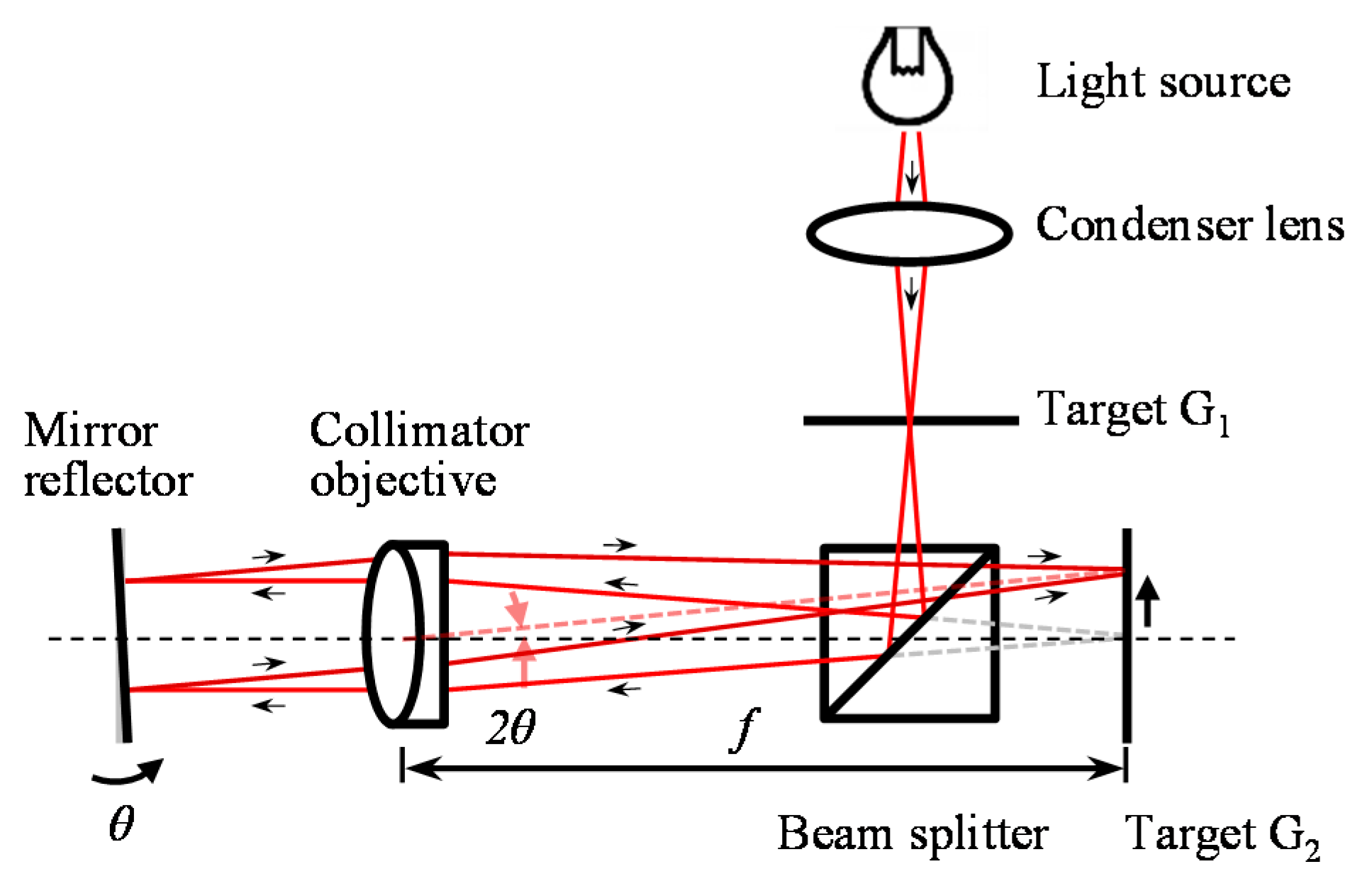
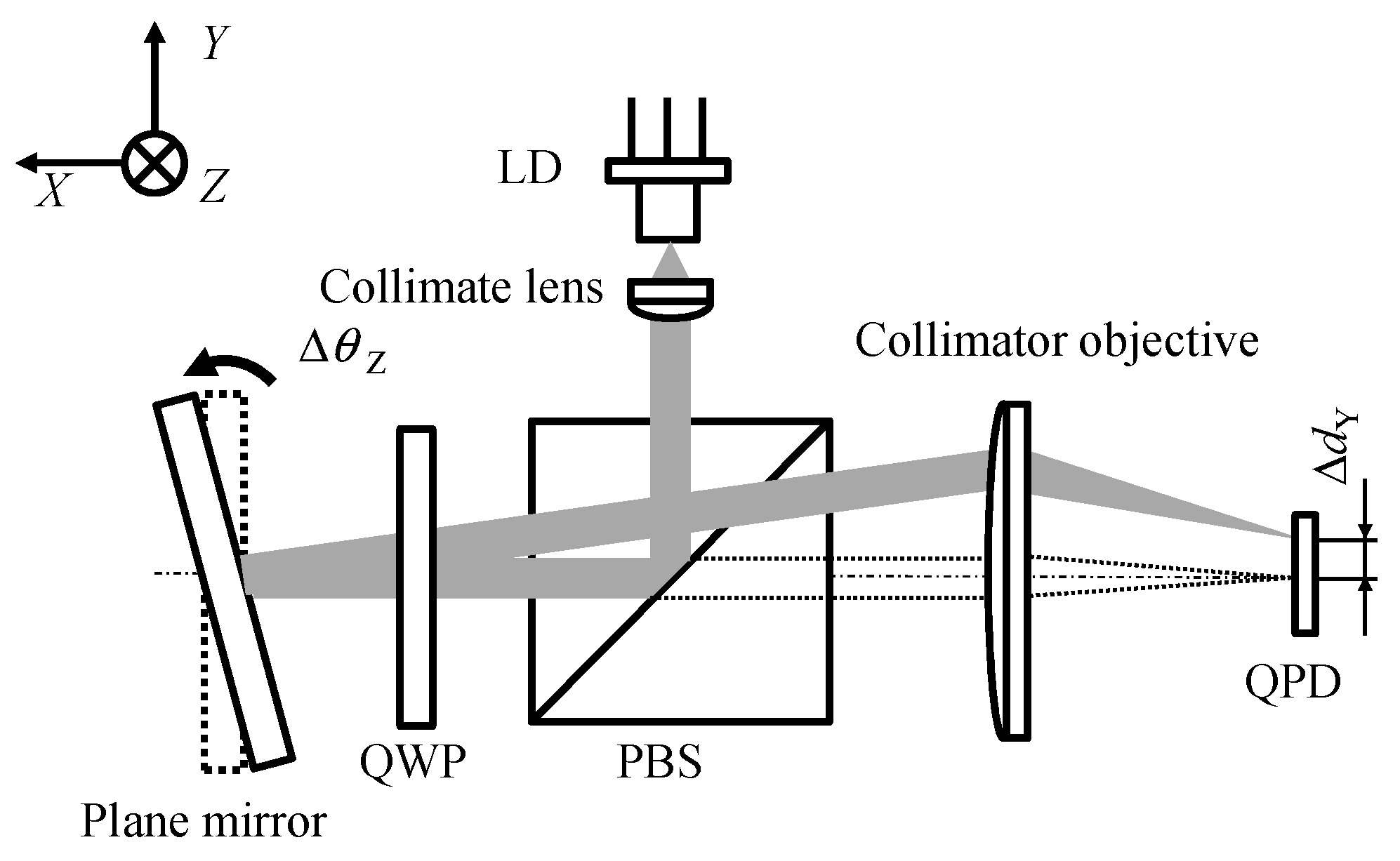
2.1. Conventional Optical Sensors for Multi-Axis Angle Measurement
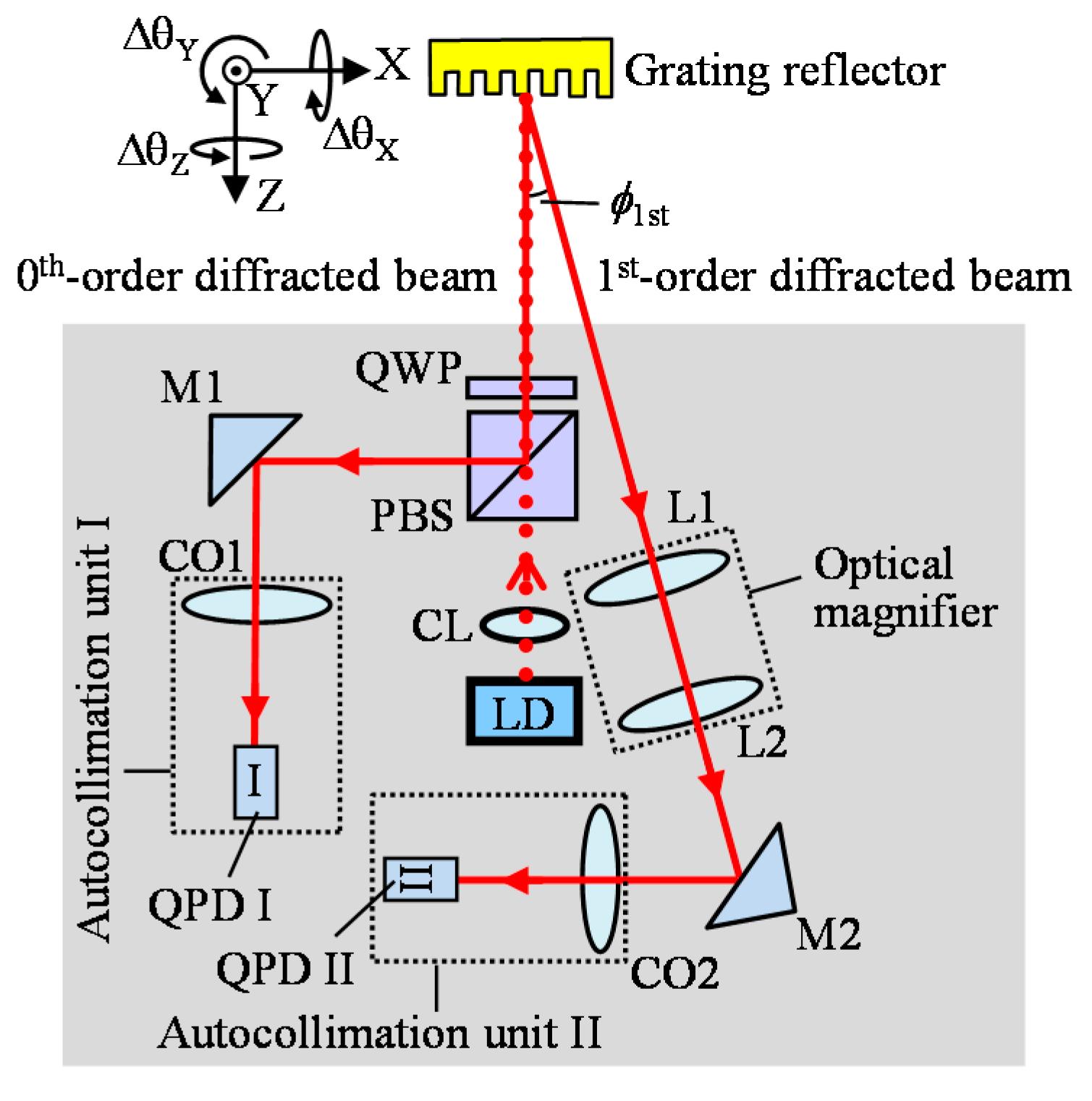
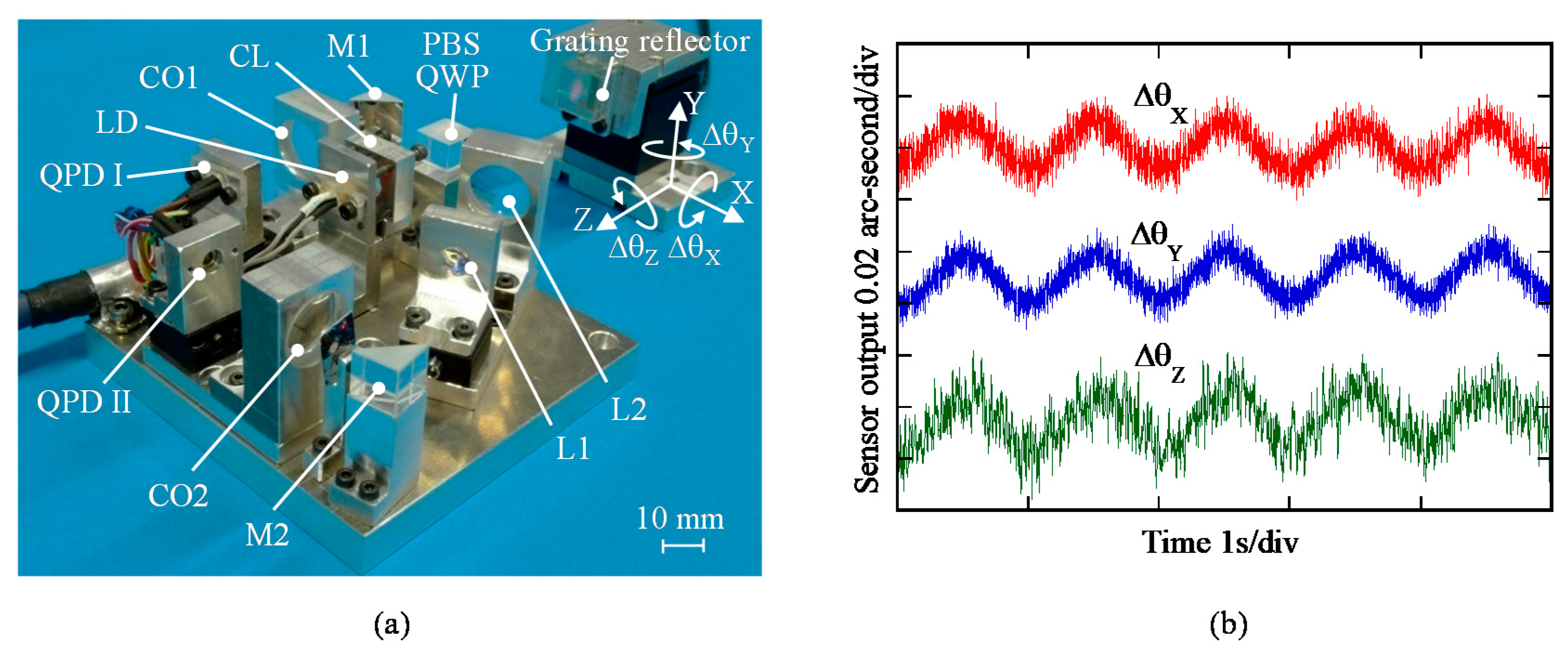
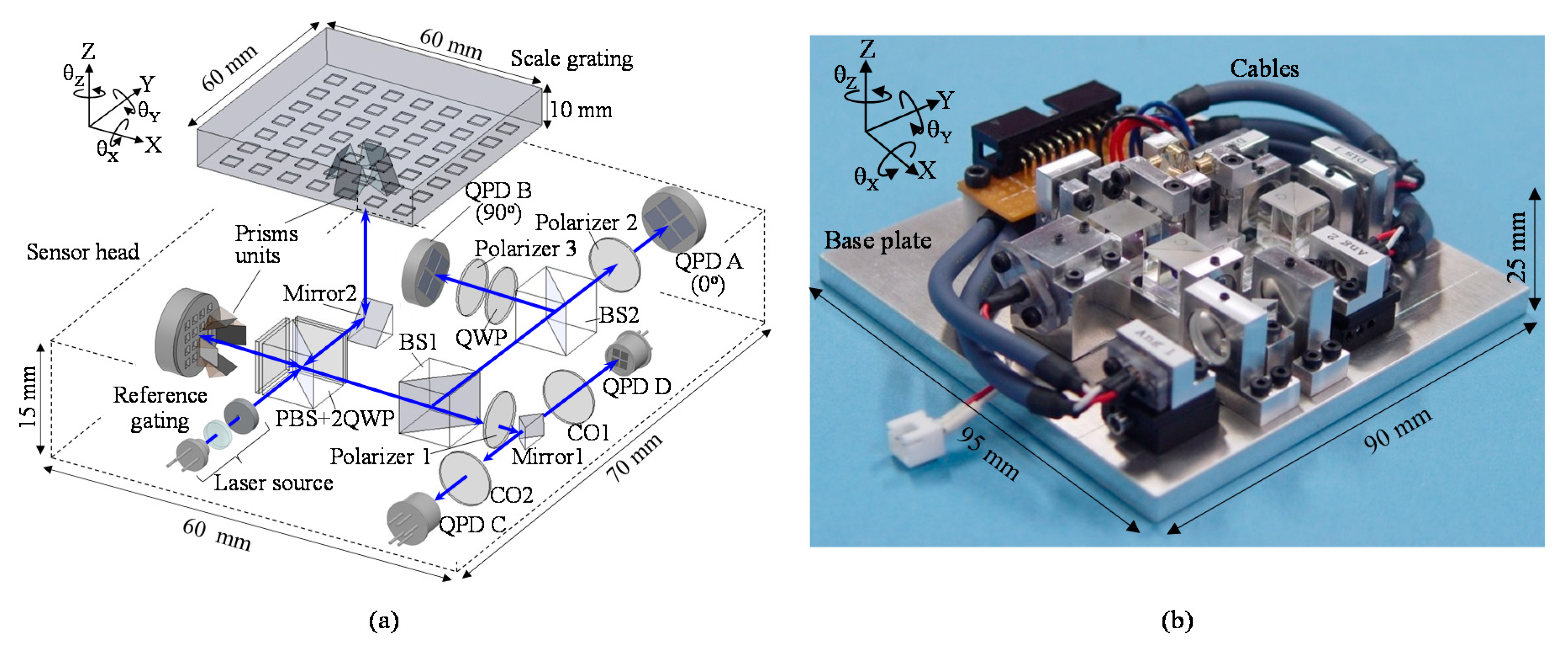
2.2. Three-Axis Autocollimator Using Diffraction Grating Reflector
3. Multi-Axis Optical Displacement Sensors
3.1. Conventional Optical Sensors for Multi-Axis Displacement Measurement
3.2. Two-Axis Planar Encoder Using Two-Dimensional Scale Grating
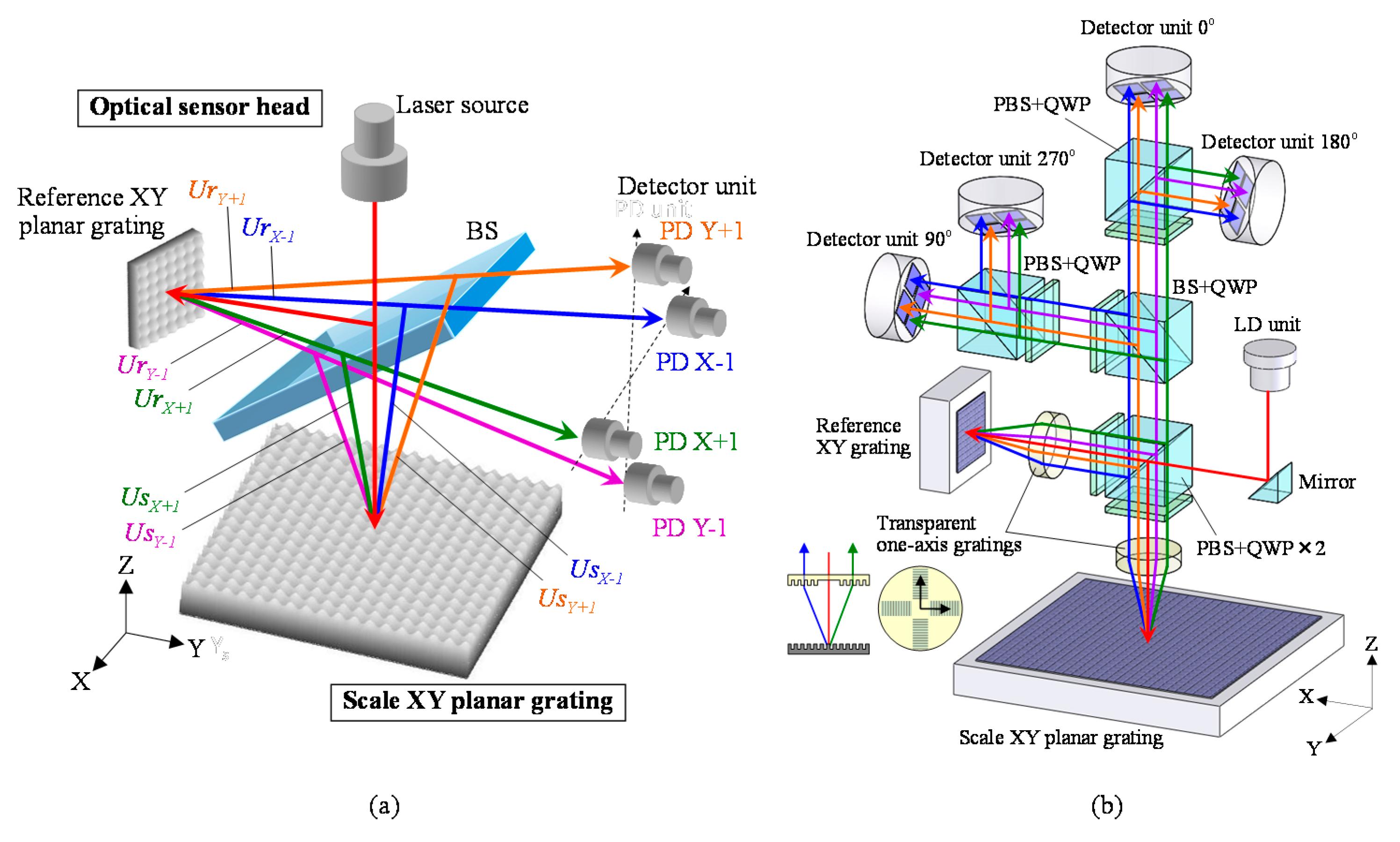
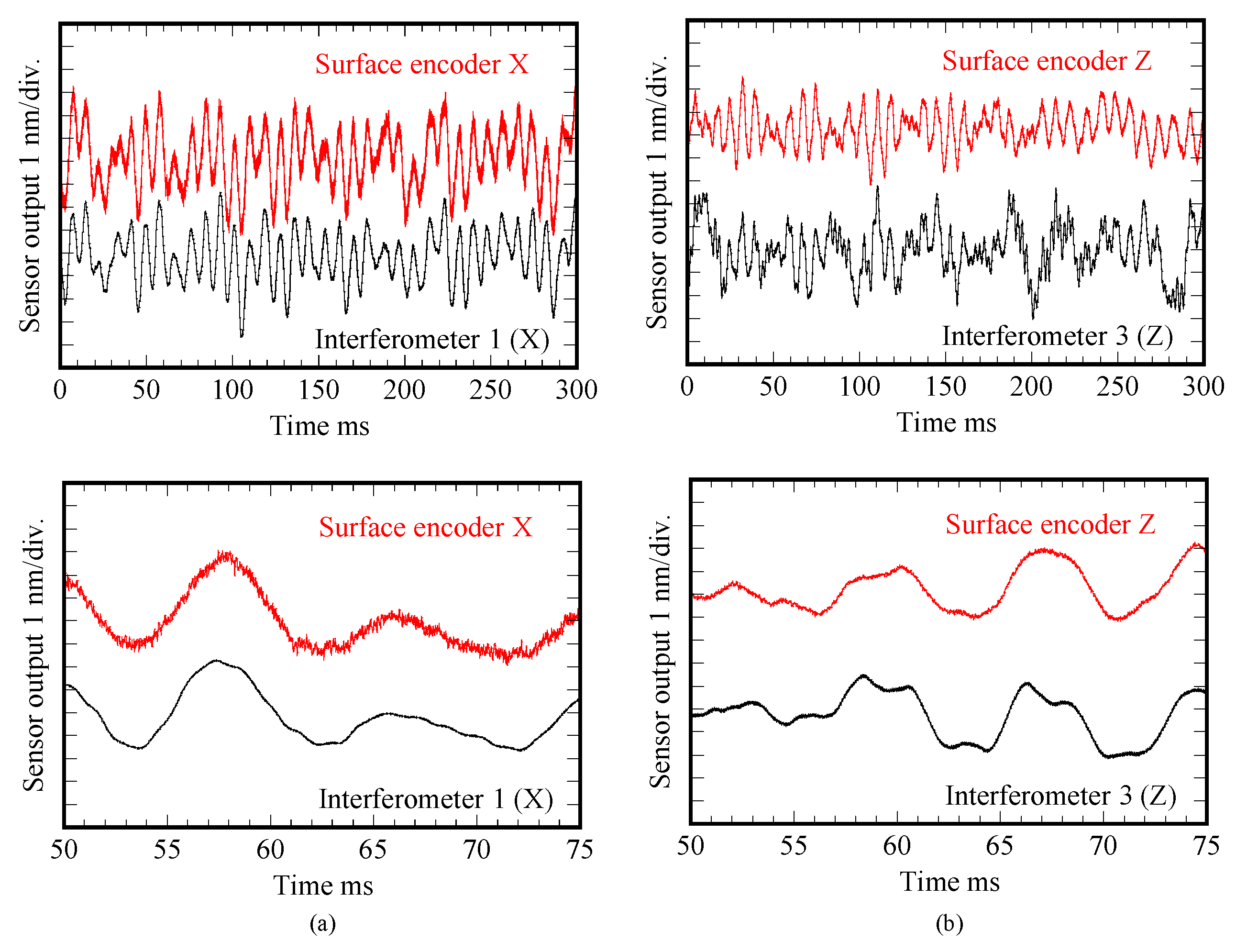
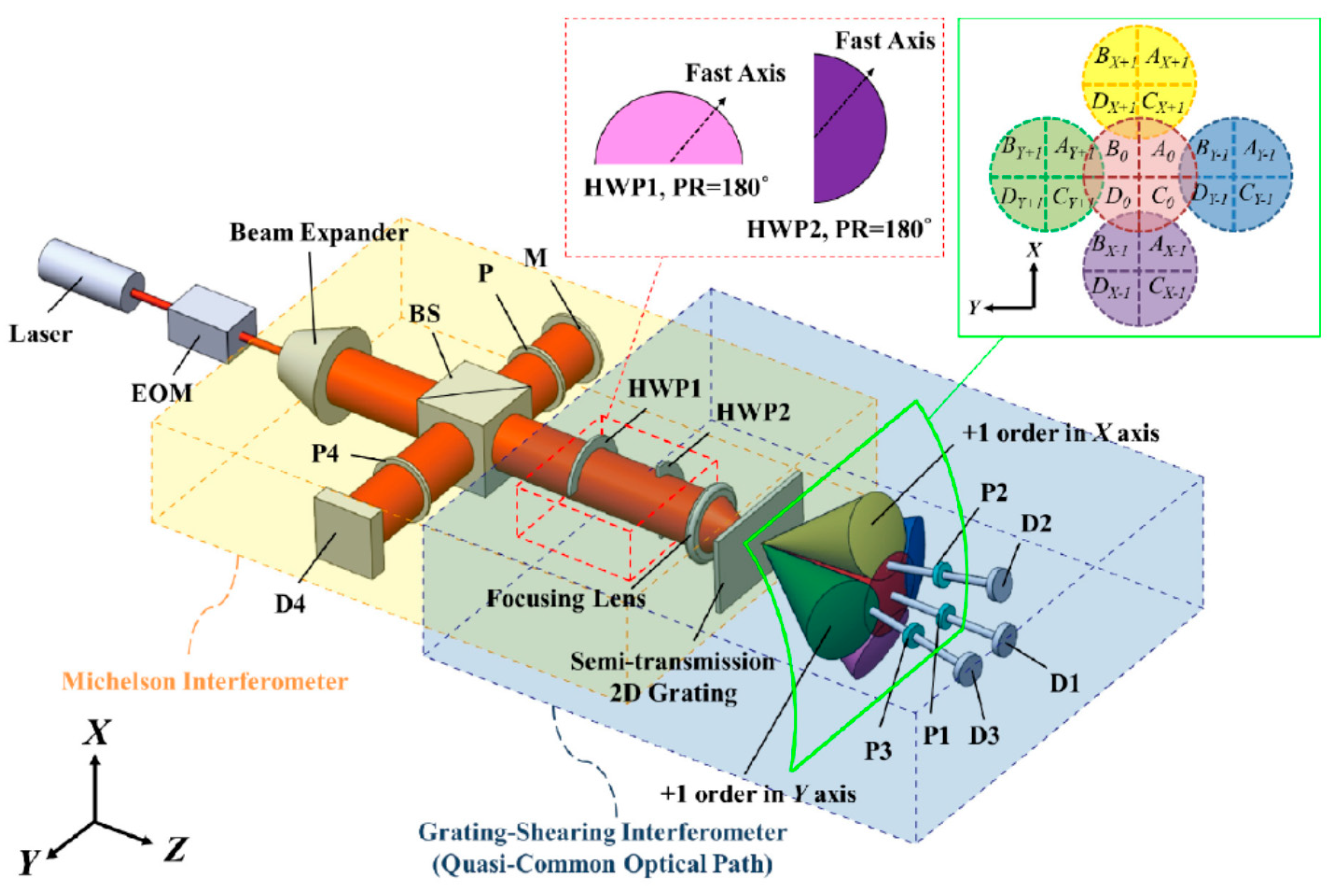
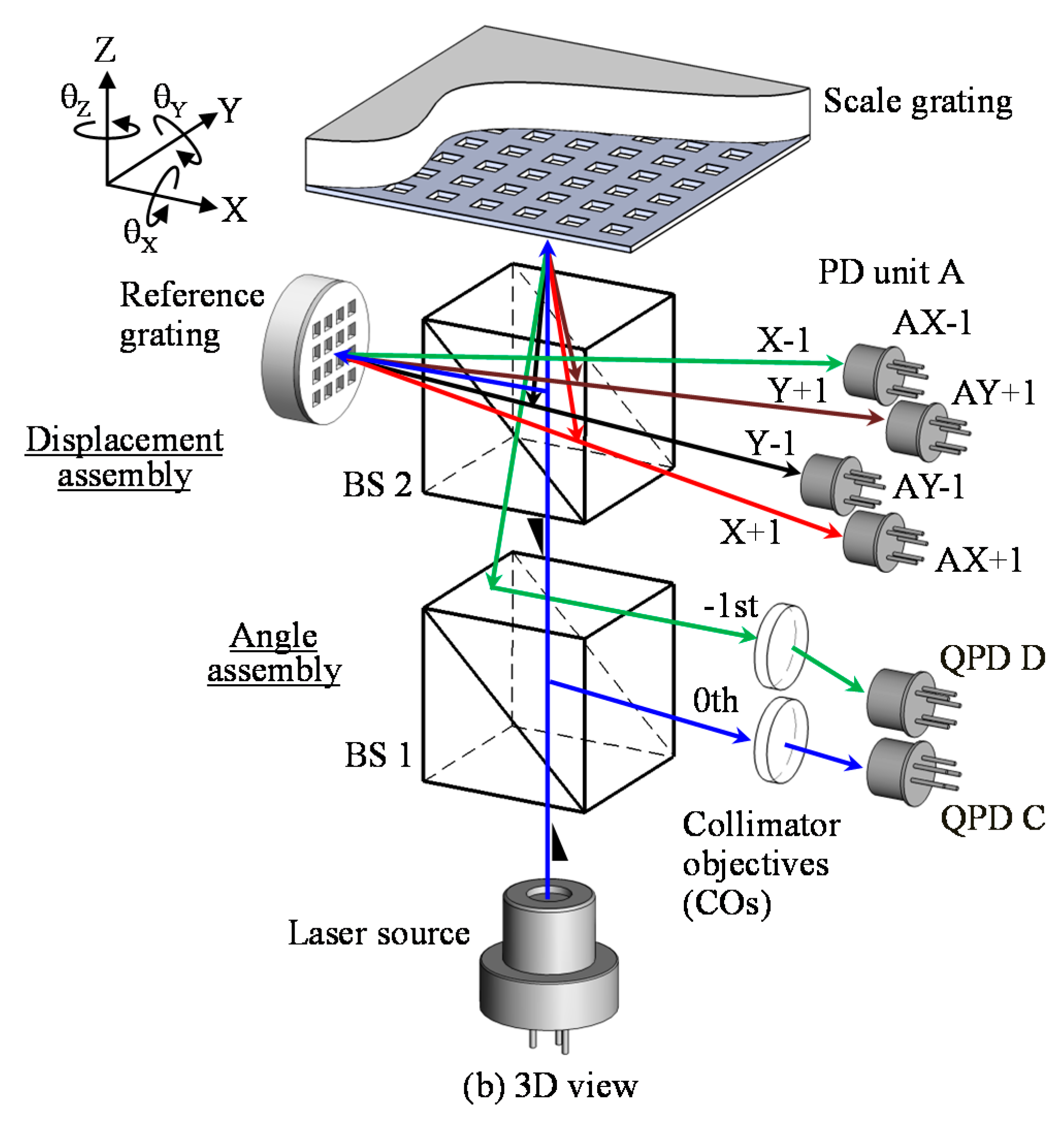
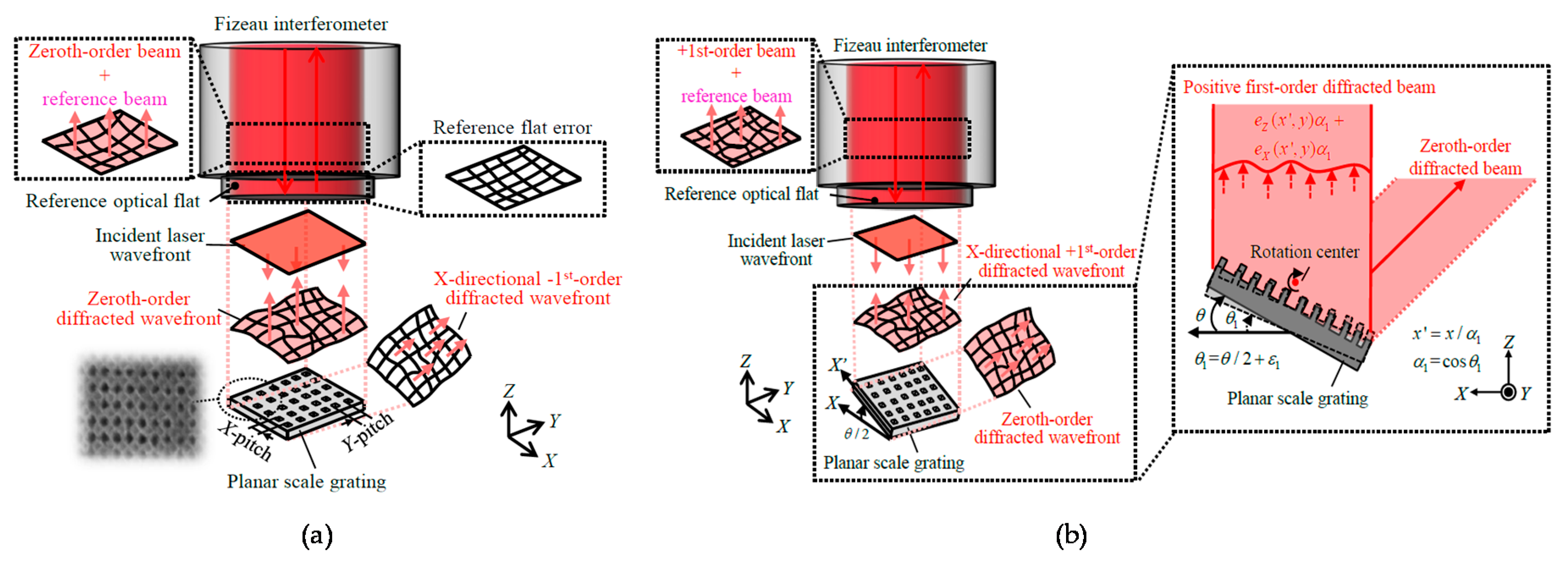
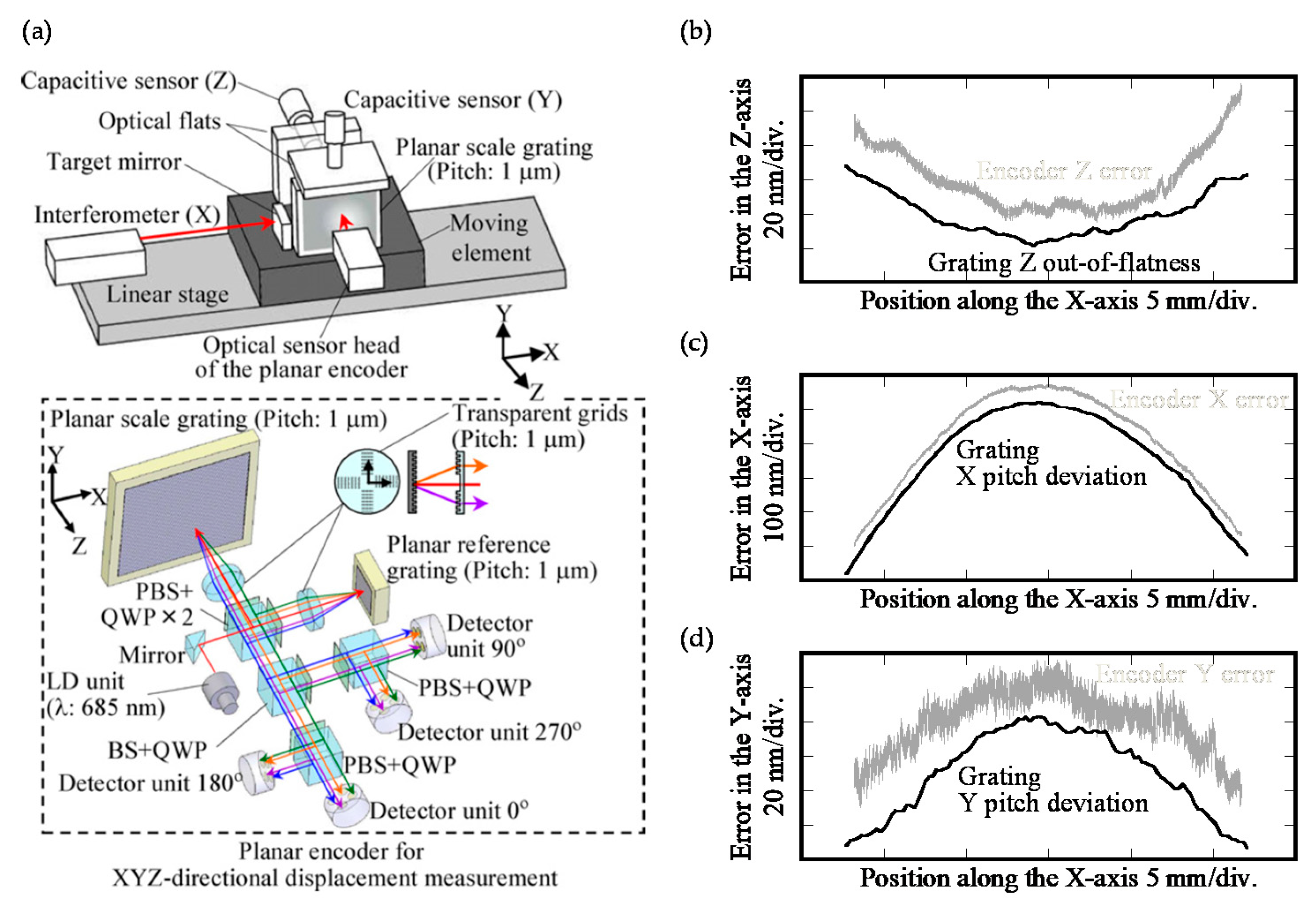
3.3. Three-Axis Planar Encoder Using Diffraction Scale Grating
3.3.1. Principle of the Three-Axis Planar Encoder
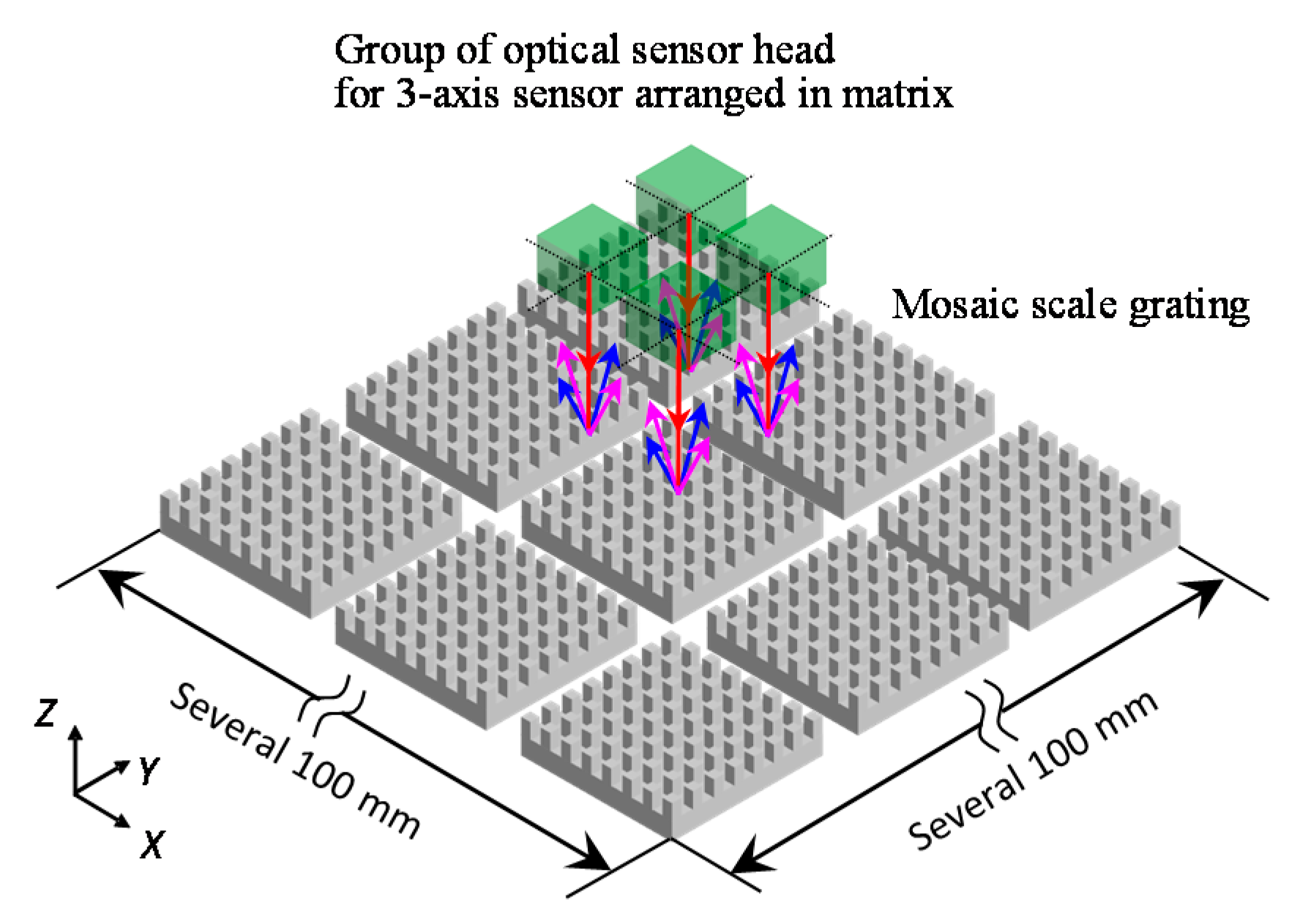
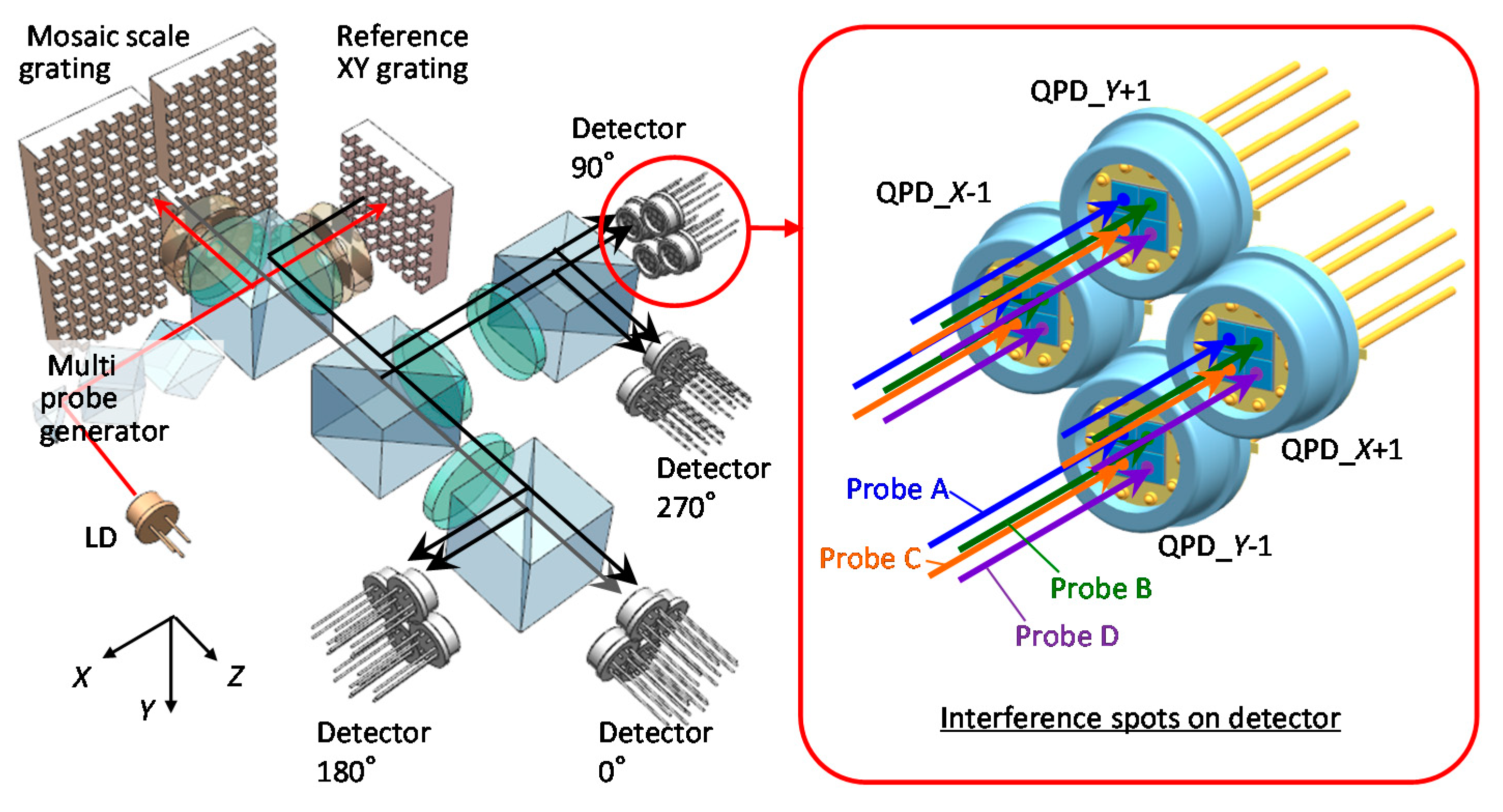
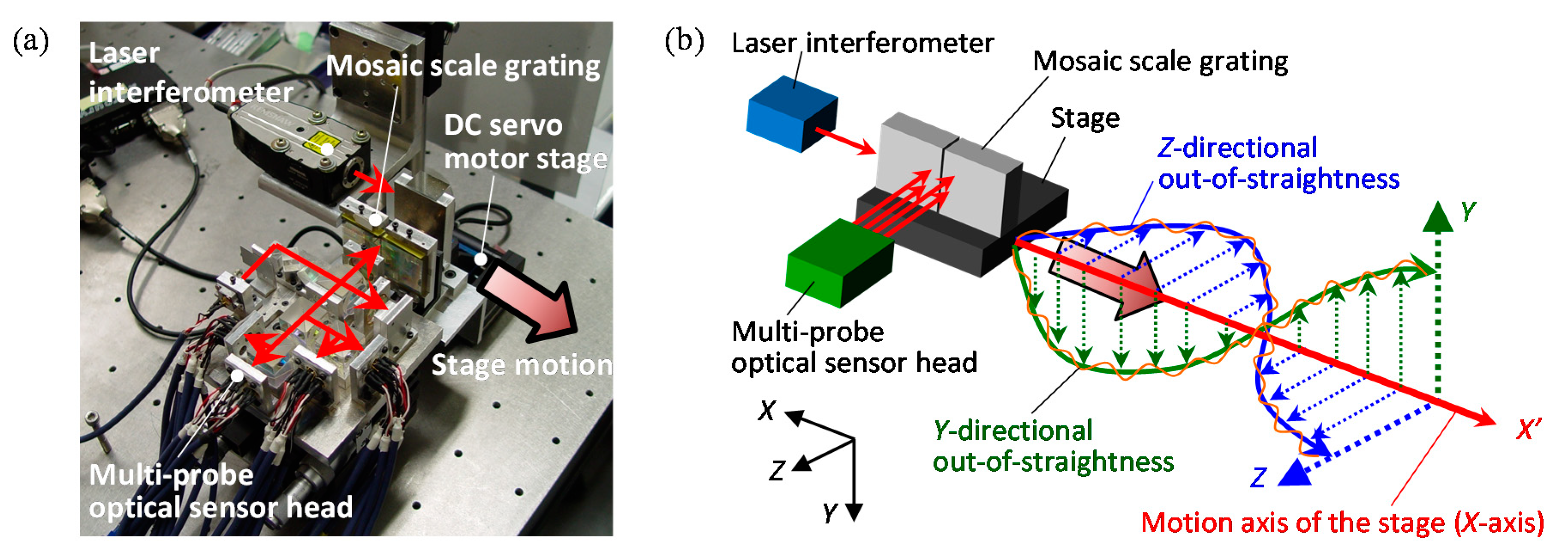
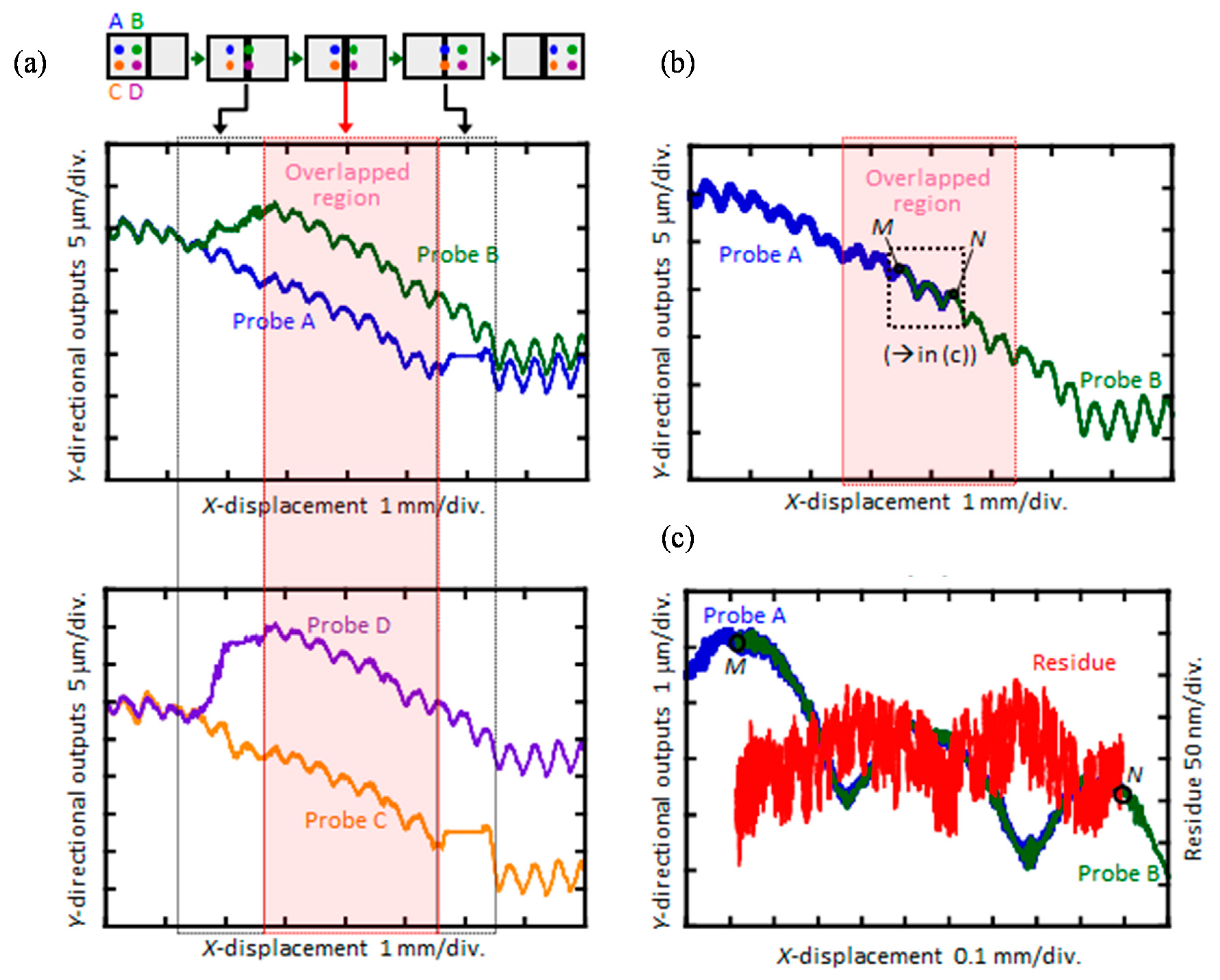
3.3.2. Multi-Beam Planar Encoder with a Mosaic Scale Grating
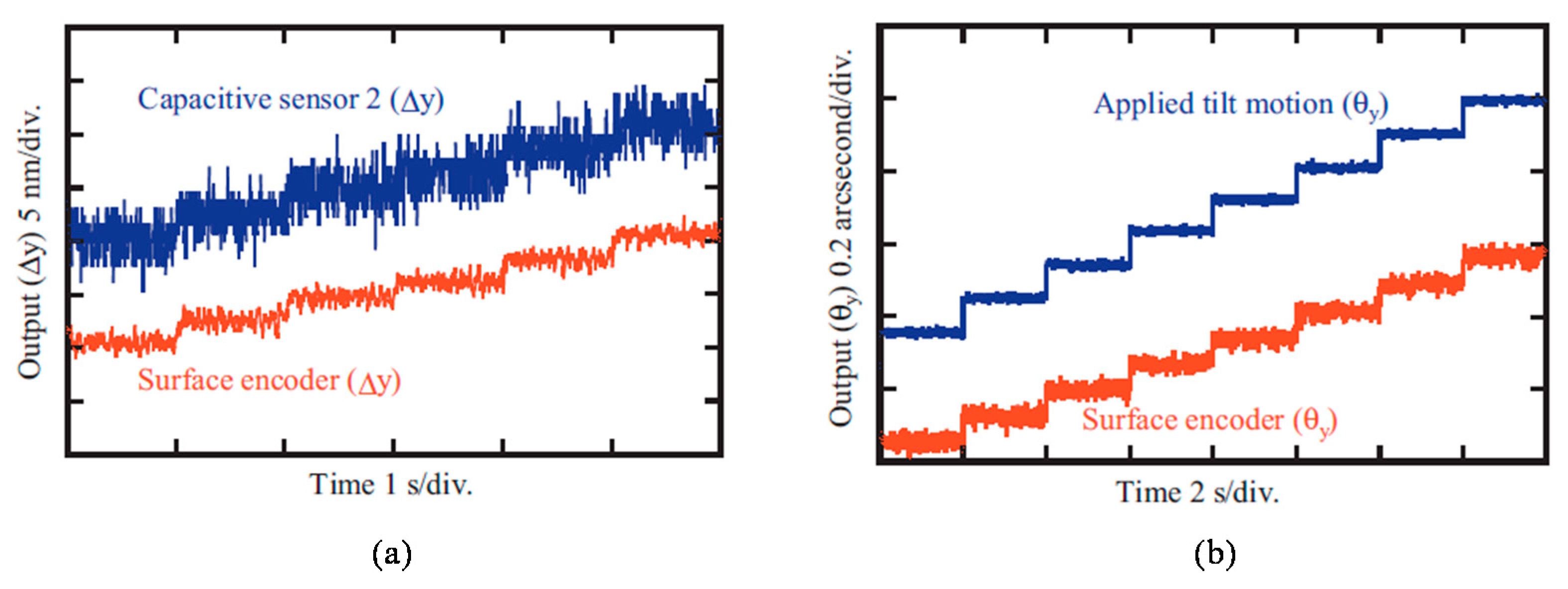
3.3.3. A Six-Degree-Of-Freedom Planar Encoder
4. Fabrication and Verification of Scale Grating
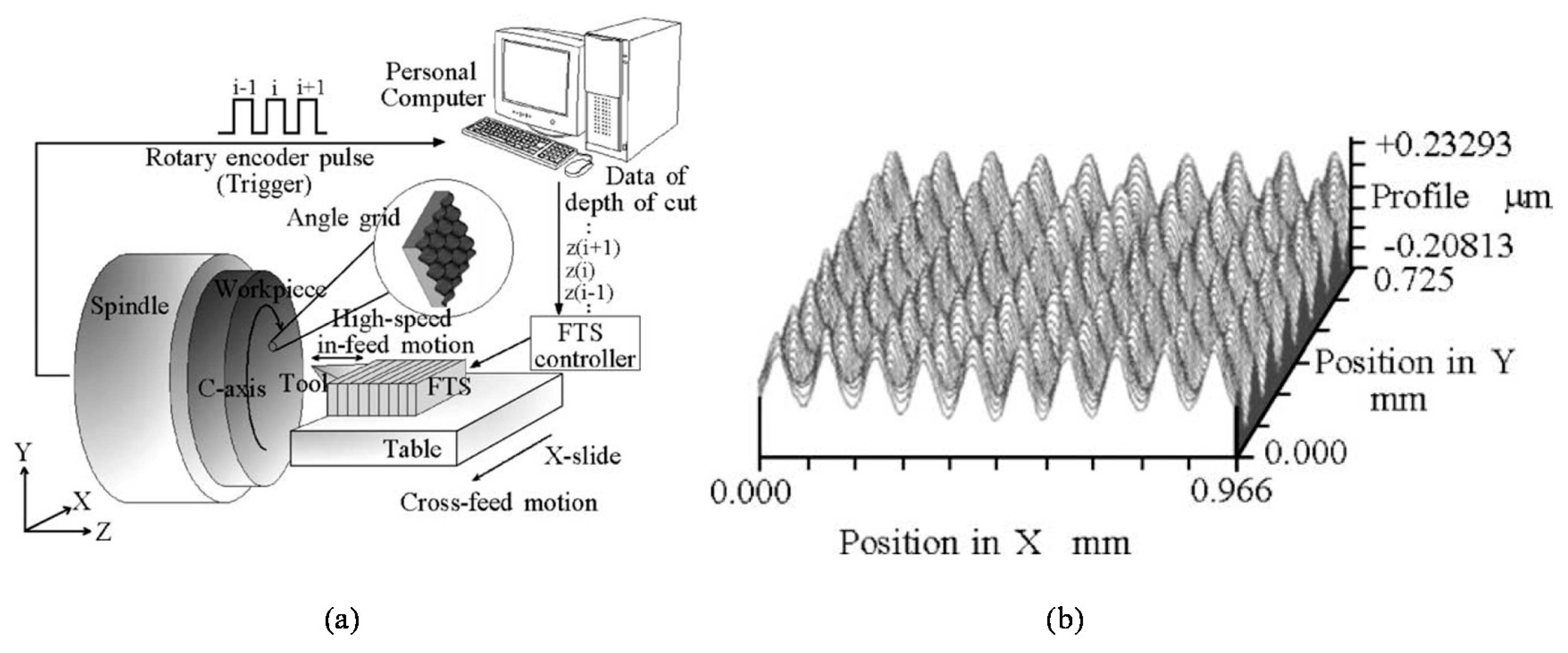
4.1. Fast-Tool-Servo Cutting of Angular Scale Gratings
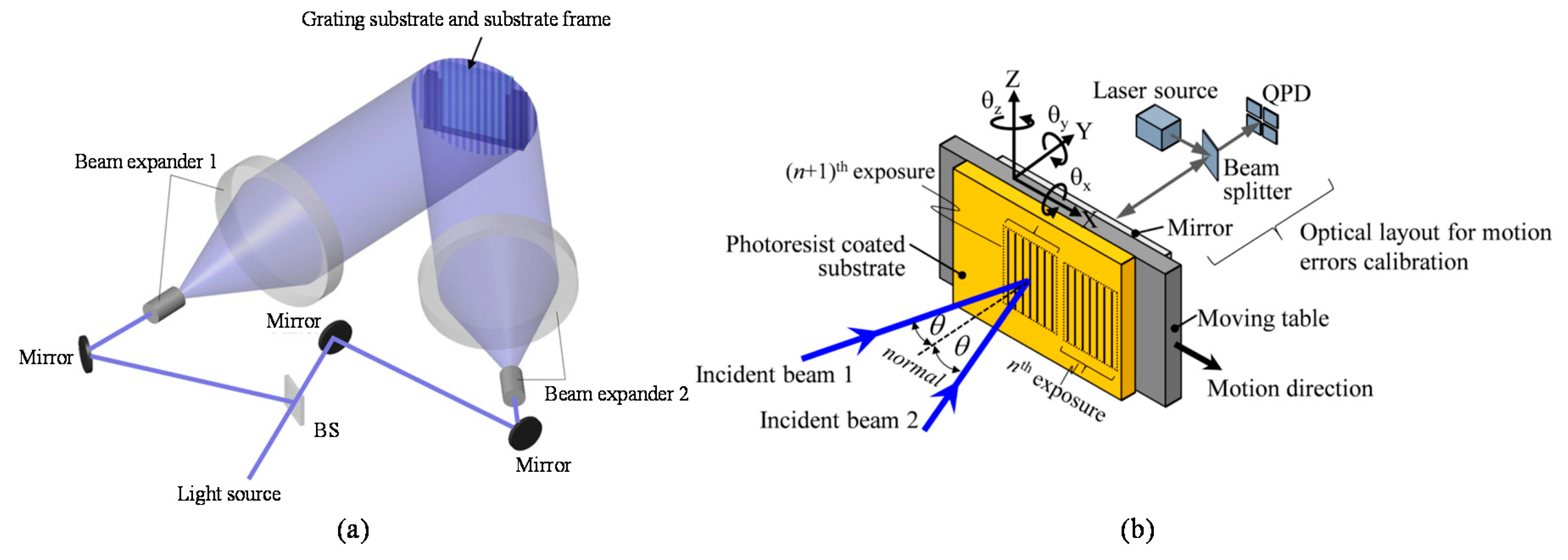
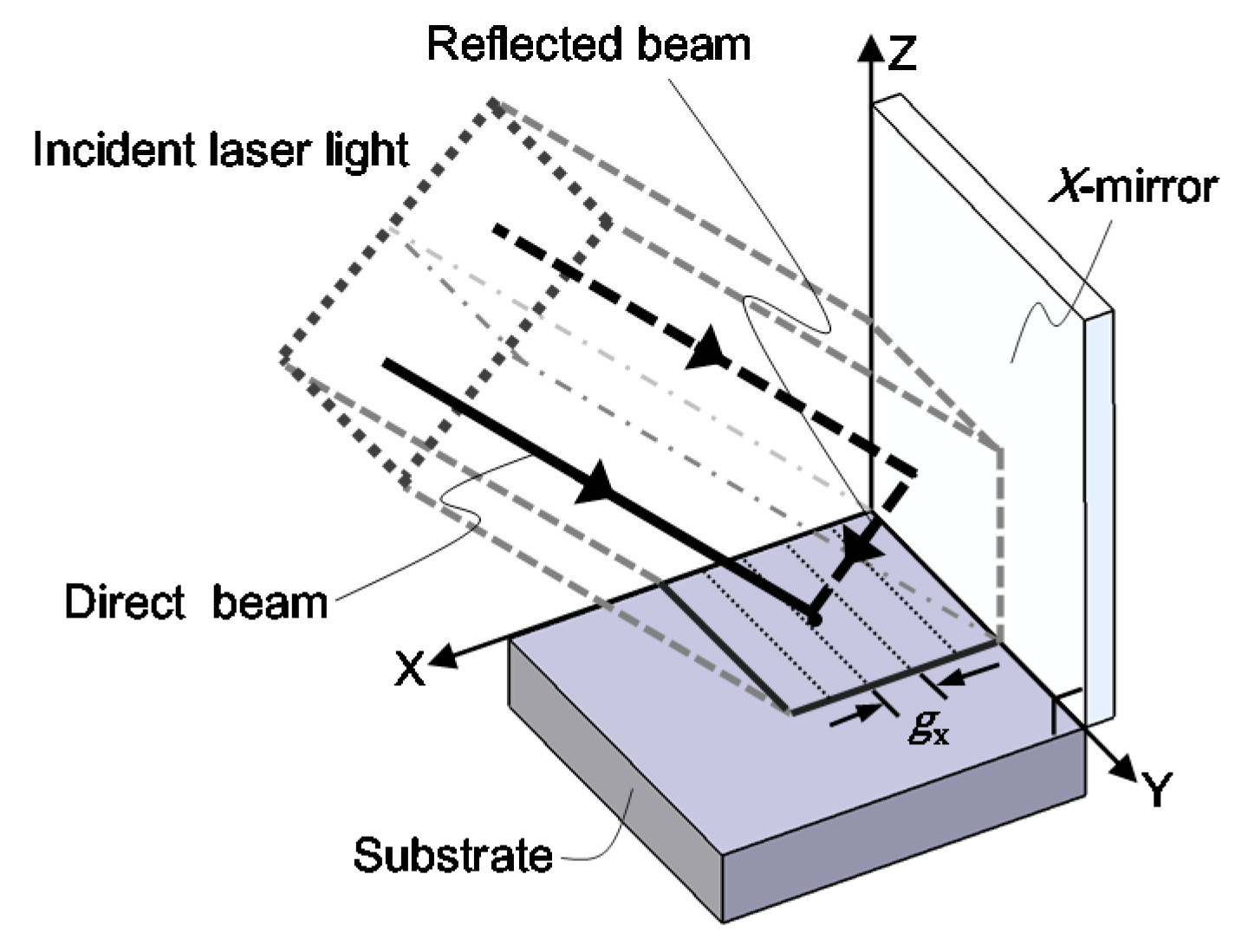
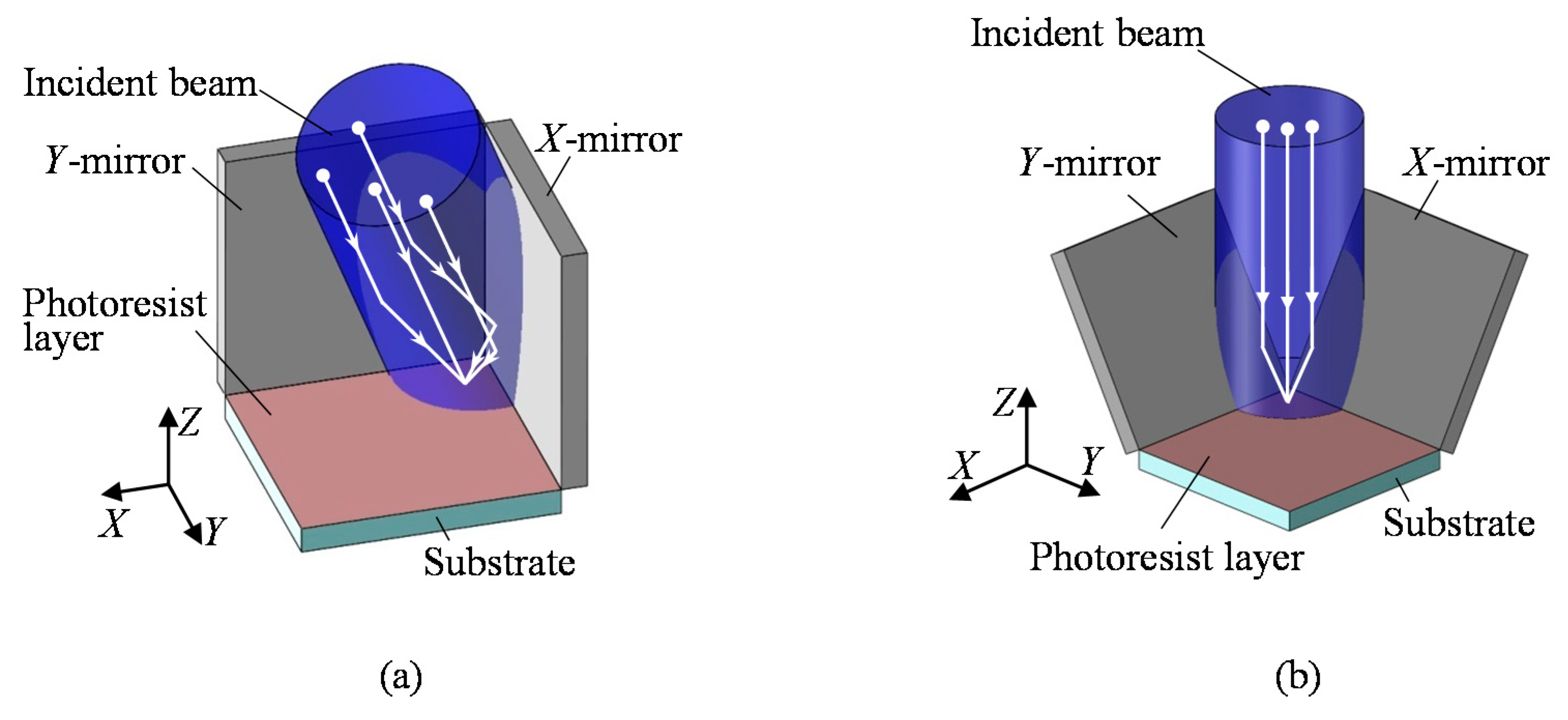
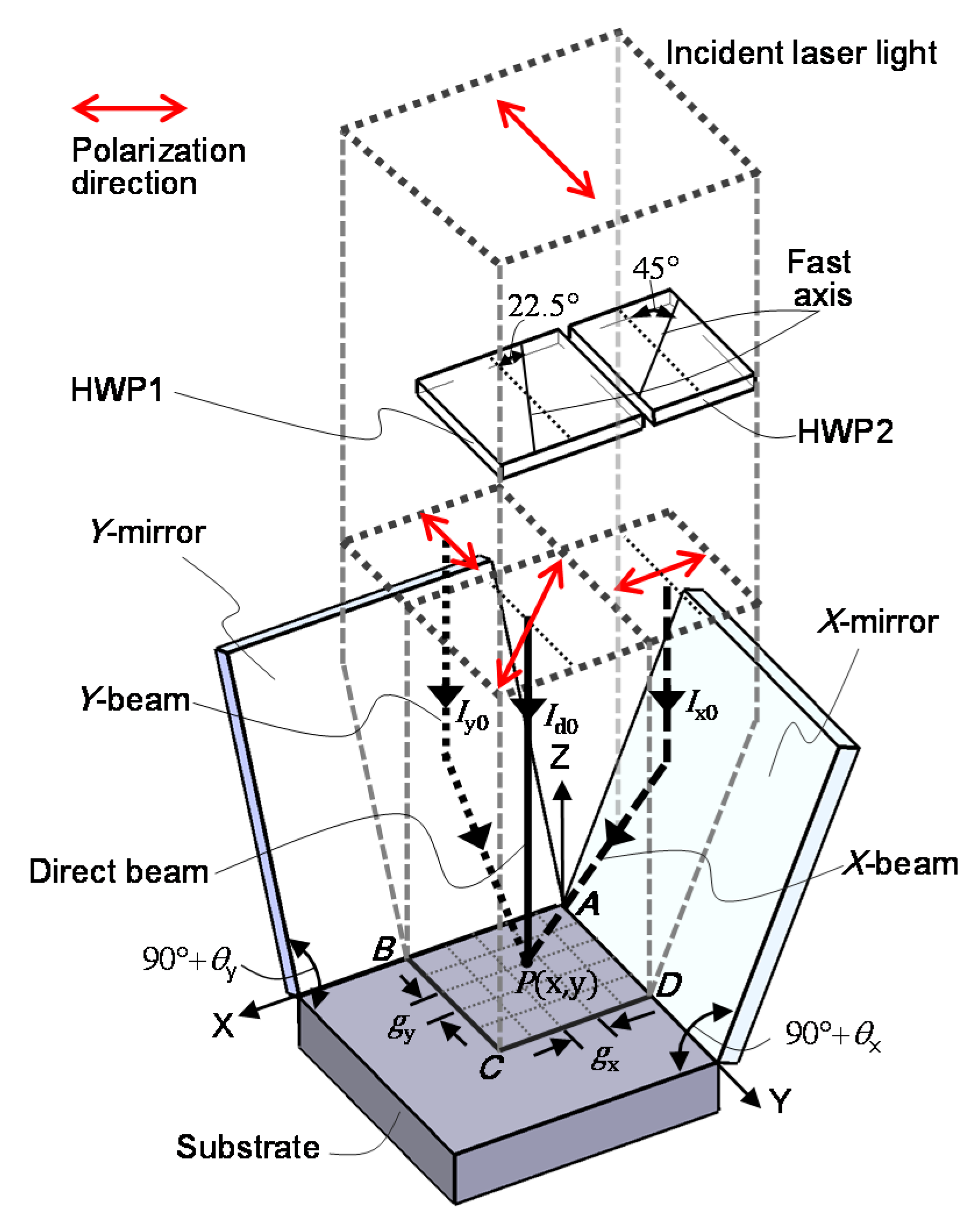
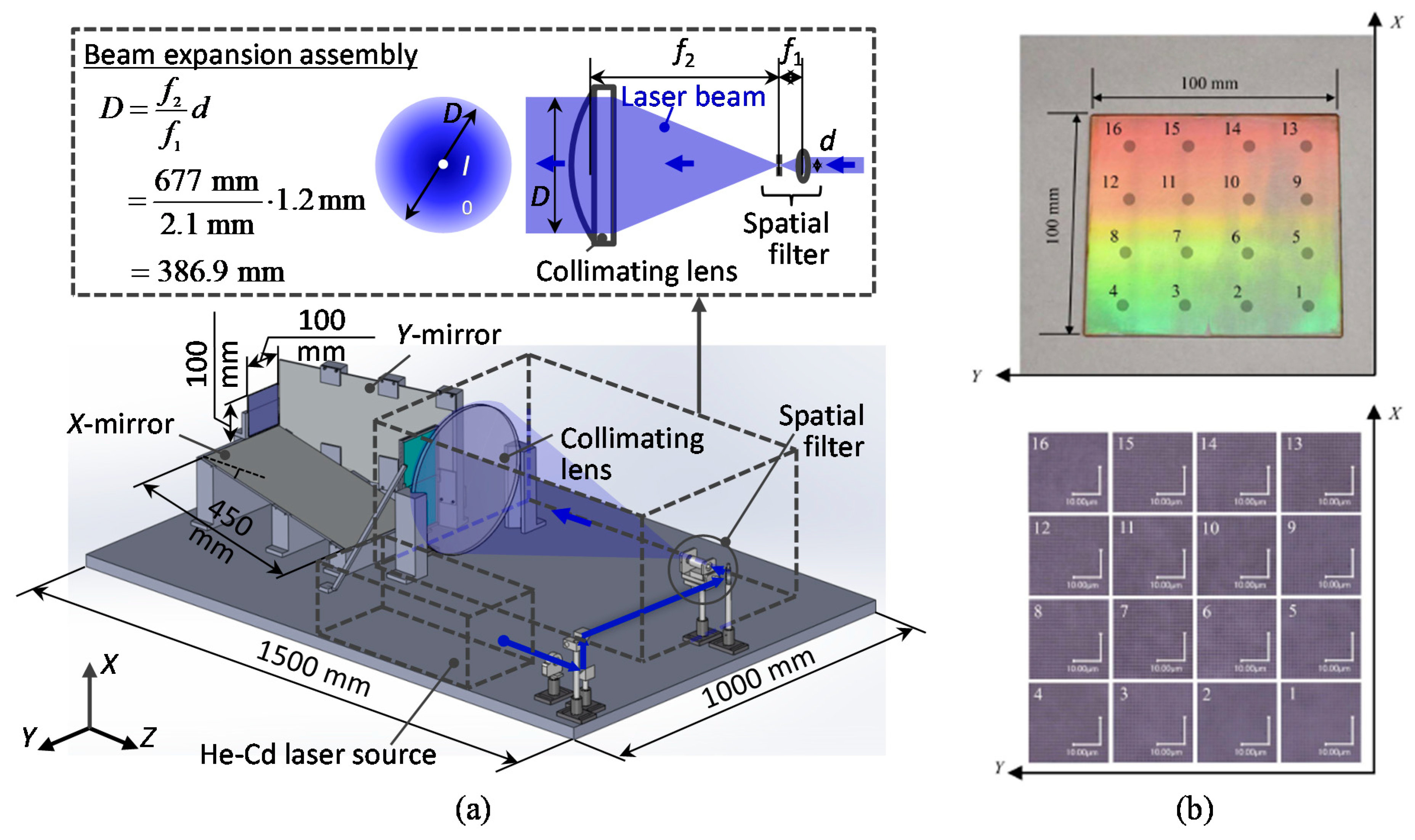
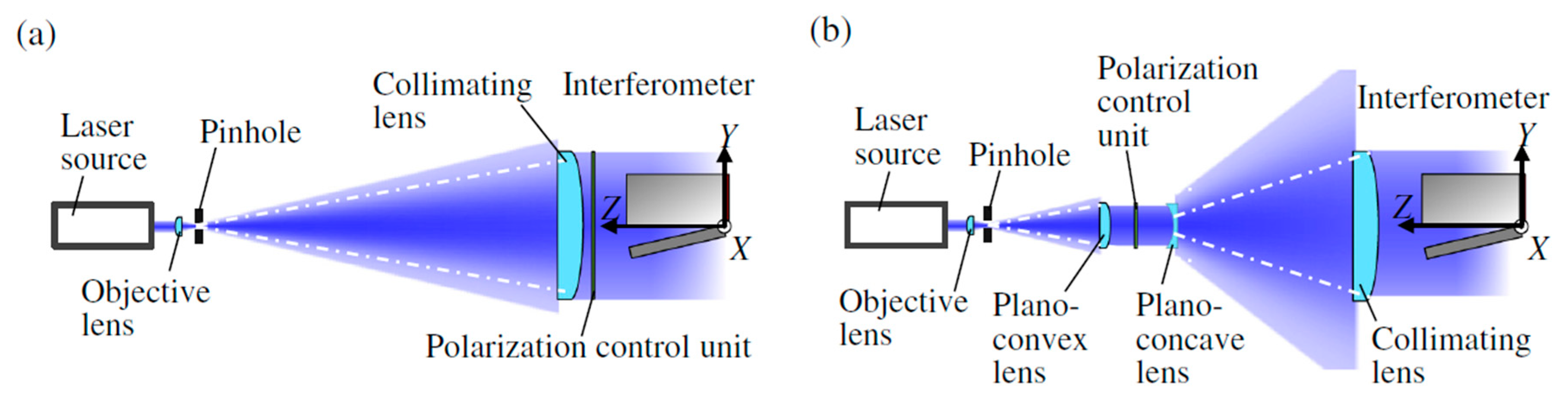
4.2. Interference Lithography of Diffraction Scale Gratings
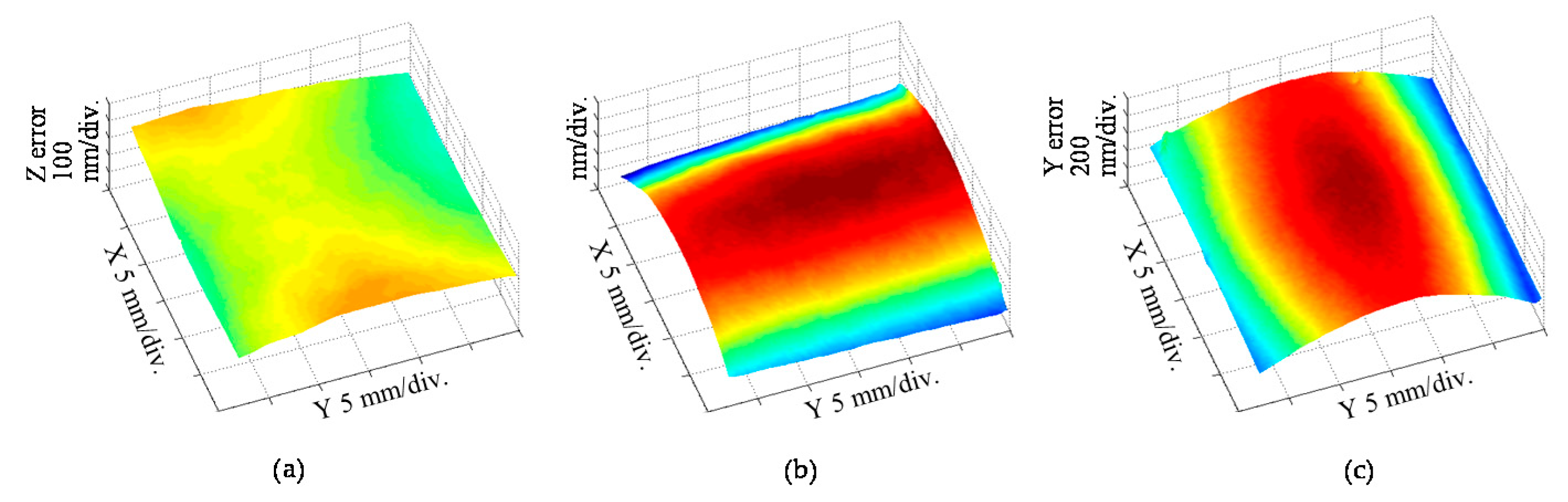
4.3. Evaluation of Pitch Deviations of a Two-Dimensional Scale Grating
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Gao, W.; Haitjema, H.; Fang, F.Z.; Leach, R.K.; Cheung, C.F.; Savio, E.; Linares, J.M. On-machine and in-process surface metrology for precision manufacturing. Cirp Ann.-Manuf. Technol. 2019, 68, 843–866. [Google Scholar] [CrossRef]
- Gao, W. Precision Nanometrology-Sensors and Measuring Systems for Nanomanufacturing; Springer: London, UK, 2010. [Google Scholar]
- Farago, F.T.; Curtis, M.A. Handbook of Dimensional Measurement; Industrial Press Inc.: New York, NY, USA, 1994. [Google Scholar]
- Gao, W.; Kim, S.W.; Bosse, H.; Haitjema, H.; Chen, Y.L.; Lu, X.D.; Knapp, W.; Weckenmann, A.; Estler, W.T.; Kunzmann, H. Measurement technologies for precision positioning. Cirp Ann.-Manuf. Technol. 2015, 64, 773–796. [Google Scholar] [CrossRef]
- Acosta, D.; Albajez, J.A.; Yagüe-Fabra, J.A.; Velázquez, J.V. Verification of Machine Tools Using Multilateration and a Geometrical Approach. Nanomanuf. Metrol. 2018, 1, 39–44. [Google Scholar] [CrossRef]
- Keysight Technologies Technical Overview. Optics and Laser Heads for Laser-Interferometer Positioning Systems; Keysight Technologies: Santa Rosa, CA, USA, 2017. [Google Scholar]
- Steinmetz, C.R. Sub-micron position measurement and control on precision machine tools with laser interferometry. Precis. Eng. 1990, 12, 12–24. [Google Scholar] [CrossRef]
- HEIDENHAIN. Catalogue. Exposed Linear Encoders, AKLIP21. 2014. Available online: https://www.heidenhain.com/fileadmin/pdb/media/img/208960-2F_Exposed_Linear_Encoders_en.pdf (accessed on 30 November 2019).
- Renishaw plc, Catalogue. ResoluteTM Absolute Optical Encoder with BiSS Serial Communications. 2014. Available online: https://resources.renishaw.com/en/details/data-sheet-resolute-absolute-optical-encoder-with-biss-serial-communications--111510 (accessed on 27 November 2019).
- Capacitive Sensors; Physik Instrumente GmbH & Co.KG: Karlsruhe, Germany. Available online: https://www.physikinstrumente.com (accessed on 10 September 2019).
- Peng, Y.; Ito, S.; Shimizu, Y.; Azuma, T.; Gao, W.; Niwa, E. A Cr-N thin film displacement sensor for precision positioning of a micro-stage. Sens. Actuators A Phys. 2014, 11, 89–97. [Google Scholar] [CrossRef]
- Adachi, K.; Matsukuma, H.; Sugawara, T.; Shimizu, Y.; Gao, W.; Niwa, E.; Sasaki, Y. Integration of a Cr–N Thin-Film Displacement Sensor into an XY Micro-stage for Closed-Loop Nano-positioning. Nanomanuf. Metrol. 2019, 2, 131–139. [Google Scholar] [CrossRef]
- Mehta, A.; Mohammed, W.; Johnson, E.G. Multimode Interference-Based Fiber-Optic Displacement sensor. IEEE Photonics Technol. Lett. 2003, 15, 1129–1131. [Google Scholar] [CrossRef]
- Gao, Z.; Hu, J.; Zhu, Y.; Duan, G. A new 6-degree-of-freedom measurement method of X-Y stages based on additional information. Precis. Eng. 2013, 37, 606–620. [Google Scholar] [CrossRef]
- Fan, K.C.; Chen., M.J. A 6-degree-of-freedom Measurement System for the Accuracy of X–Y Stages. Precis. Eng. 2000, 24, 15–23. [Google Scholar] [CrossRef]
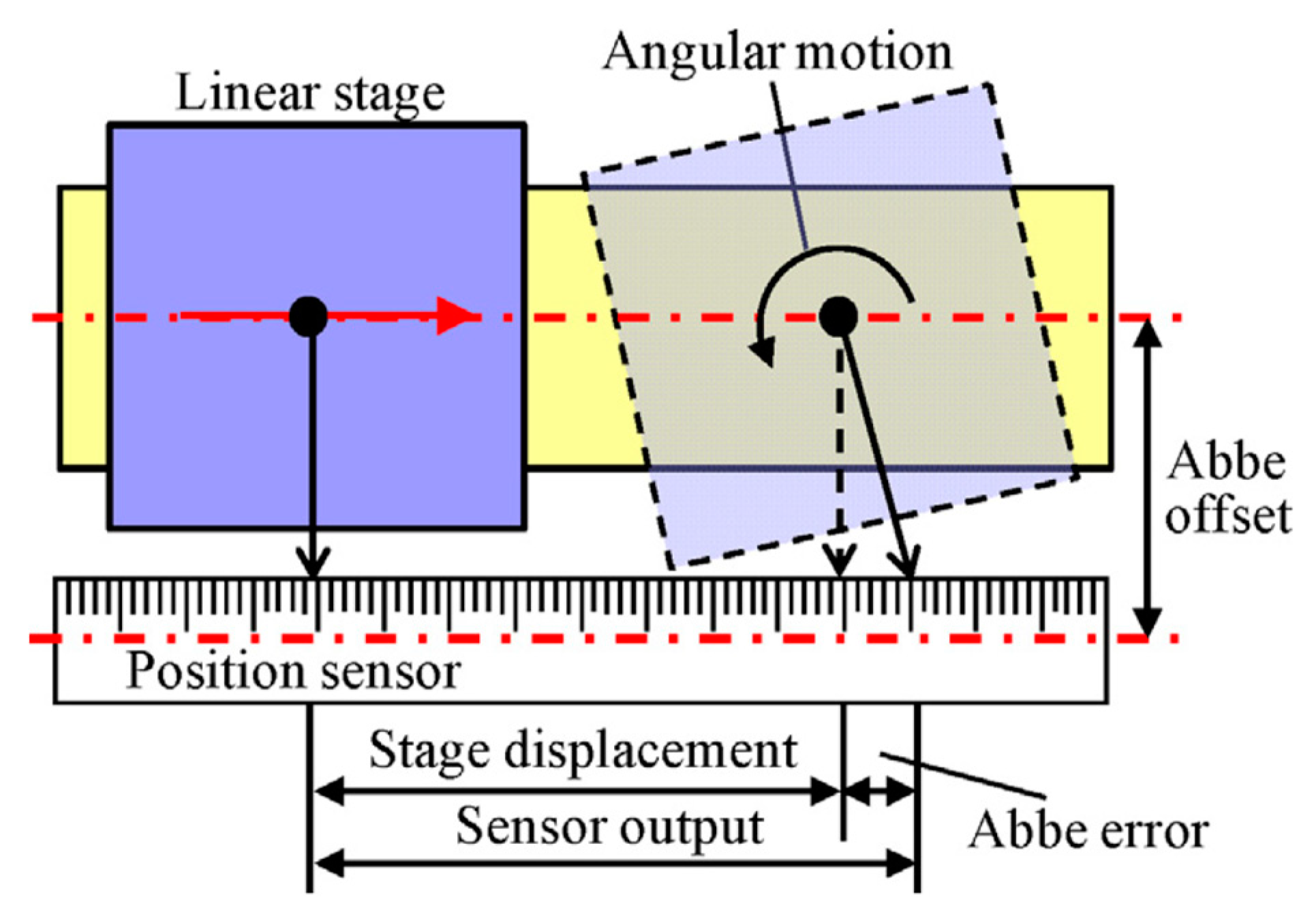
- Abbe, E. Measuring instruments for physicists. J. Sci. Instrum. 1890, 10, 446–448. (In Germany) [Google Scholar]
- Bryan, J.B. The Abbé principle revisited: An updated interpretation. Precis. Eng. 1979, 1, 129–132. [Google Scholar] [CrossRef]
- Tam, R. Ultra-Precision Coordinate Measuring Machine—Design, Calibration and Error Compensation. Ph.D. Thesis, Technische Universiteit Delft, Eindhoven, The Netherlands, 2001. [Google Scholar]
- Leach, R. Abbe Error/Offset. In CIRP Encyclopedia of Production Engineering; Chatti, S., Laperrière, L., Reinhart, G., Tolio, T., The International Academy for Production, Eds.; Springer: Berlin/Heidelberg, Germany, 2018. [Google Scholar]
- Manske, E.; Jäger, G.; Hausotte, T.; Füßl, R. Recent Developments and Challenges of Nanopositioning and Nanomeasuring Technology. Meas. Sci. Technol. 2012, 23, 074001. [Google Scholar] [CrossRef]
- Kunzmann, H.; Pfeifer, T.; Flügge, J. Scales vs Laser Interferometers. Performance and Comparison of Two Measuring Systems. Cirp Ann.-Manuf. Technol. 1993, 42, 753–767. [Google Scholar] [CrossRef]
- Haitjema, H. Achieving traceability and sub-nanometer uncertainty using interferometric techniques. Meas. Sci. Technol. 2008, 19, 084002. [Google Scholar] [CrossRef]
- Haitjema, H.; Cosijns, S.J.; Roset, N.J.J.; Jansen, M.J. Improving a commercially available heterodyne laser interferometer to subnm uncertainty. In Proceedings of the SPIE, Eindhoven, The Netherlands, 20 November 2003; p. 5190. [Google Scholar] [CrossRef]
- Meiners-Hagen, K.; Meyer, T.; Prellinger, G.; Pöschel, W.; Dontsov, D.; Pollinger, F. Overcoming the refractivity limit in manufacturing environment. Opt. Express 2016, 24, 24092–24104. [Google Scholar] [CrossRef]
- Pollinger, F.; Meyer, T.; Beyer, J.; Doloca, N.R.; Schellin, W.; Niemeier, W.; Jokela, J.; Hakli, P.; Abou-Zeid, A.; Meiners-Hagen, K. The upgraded PTB 600 m baseline: A high-accuracy reference for the calibration and the development of long distance measurement devices. Meas. Sci. Technol. 2012, 23, 094018. [Google Scholar] [CrossRef]
- Pollinger, F.; Meiners-Hagen, K.; Wedde, M.; Abou-Zeid, A. Diode-laser based High-precision Absolute Distance Interferometer of 20 m Range. Appl. Opt. 2009, 48, 6188–6194. [Google Scholar] [CrossRef]
- Schödel, R. Ultra-High Accuracy Thermal Expansion Measurements with PTB’s Precision Interferometer. Meas. Sci. Technol. 2008, 19, 084003. [Google Scholar] [CrossRef]
- Teimel, A. Technology and application of grating interferometers in high-precision measurement. Precis. Eng. 1992, 14, 147–154. [Google Scholar] [CrossRef]
- Rieger, G.; Ludwig, K.; Hauch, J.; Clemens, W. GMR sensors for contactless position detection. Sens. Actuators A Phys. 2001, 91, 7–11. [Google Scholar] [CrossRef]
- Chen, Z.; Pu, H.; Liu, X.; Peng, D.; Yu, Z. A time-grating sensor for displacement measurement with long range and nanometer accuracy. IEEE Trans. Instrum. Meas. 2015, 64, 3105–3115. [Google Scholar] [CrossRef]
- Shimizu, Y.; Ishida, A.; Matsuno, Y.; Matsukuma, H.; Gao, W. A Design Study of a Heat Flow-Type Reading Head for a Linear Encoder Based on a Micro Thermal Sensor. Nanomanuf. Metrol. 2019, 2, 100–110. [Google Scholar] [CrossRef]
- Lin, C.; Yan, S.; Du, Z.; Wang, G.; Wei, C. Symmetrical short-period and high signal-to-noise ratio heterodyne grating interferometer. Chin. Opt. Lett. 2015, 13, 100501. [Google Scholar]
- Zherdev, A.Y.; Odinokov, S.B.; Lushnikov, D.S. Optical position encoder on four-section diffraction grating. In Proceedings of the SPIE, Prague, Czech Republic, 15 May 2017; Volume 10233, p. 102331I. [Google Scholar]
- Williams, R.P.; Hord, S.K.; Hall, N.A. Optically read displacement detection using phase-modulated diffraction gratings with reduced zeroth-order reflections. Appl. Phys. Lett. 2017, 110, 151104. [Google Scholar] [CrossRef]
- Lv, Q.; Liu, Z.; Wang, W.; Li, X.; Li, S.; Song, Y.; Yu, H.; Li, W. Simple and compact grating-based heterodyne interferometer with the Littrow configuration for high-accuracy and long-range measurement of two-dimensional displacement. Appl. Opt. 2018, 57, 9455–9463. [Google Scholar] [CrossRef] [PubMed]
- Shin, D.; Kim, B. A laser interferometer encoder with two micromachined gratings generating phase-shifted quadrature. J. Micromech. Microeng. 2011, 21, 085036. [Google Scholar] [CrossRef]
- Fan, K.C.; Zhang, Y.L.; Miao, J.W. Error compensation of grating interferometer due to angular error of linear stage. In Proceedings of the IEEE/ASME International Conference on Advanced Intelligent Mechatronics, Kachsiung, Taiwan, 11–14 July 2012; pp. 428–431. [Google Scholar]
- Wu, C.C.; Hsu, C.C.; Lee, J.Y.; Chen, Y.Z.; Yang, J.S. Littrow-type self-aligned laser encoder with high tolerance using double diffractions. Opt. Commun. 2013, 297, 89–97. [Google Scholar] [CrossRef]
- Wu, C.C.; Chen, Y.Z.; Liao, C.H. Common-path laser planar encoder. Opt. Exp. 2013, 21, 18872–18883. [Google Scholar] [CrossRef]
- Tiemann, I.; Spaeth, C.; Wallner, G.; Metz, G.; Israel, W.; Yamaryo, Y.; Shimomura, T.; Kubo, T.; Wakasa, T.; Morosawa, T.; et al. An International Length Comparison Using Vacuum Comparators and a Photoelectric Incremental Encoder as Transfer Standard. Precis. Eng. 2008, 32, 1–6. [Google Scholar] [CrossRef]
- Tamiya, H.; Taniguchi, K.; Yamazaki, K.; Aoyama, H. Detection principle and verification of non-contact displacement meter with pico-meter resolution. J. Adv. Mech. Des. Syst. Manuf. 2018, 12. [Google Scholar] [CrossRef]
- Guan, J.; Köchert, P.; Weichert, C.; Köning, R.; Siaudinyte, L.; Flügge, J. A differential interferometric heterodyne encoder with 30 picometer periodic nonlinearity and sub-nanometer stability. Precis. Eng. 2017, 50, 114–118. [Google Scholar] [CrossRef]
- Magnescale. Self-Compensating Absolute Laserscale. Available online: http://www.mgscale.com/mgs/language/english/news/20141020-1.html (accessed on 12 September 2019).
- Oiwa, T.; Katsuki, M.; Karita, M.; Gao, W.; Makinouchi, S.; Sato, K.; Oohashi., Y. Report of Questionnaire Survey on Ultra-Precision Positioning; Technical Committee of Ultra-Precision Positioning, Japan Society for Precision Engineering (JSPE): Tokyo, Japan, 2015. [Google Scholar]
- Köning, R.; Flügge, J.; Bosse, H. A Method for the in situ Determination of Abbe Errors and Their Correction. Meas. Sci. Technol. 2007, 18, 476–481. [Google Scholar] [CrossRef]
- Gao, W.; Saito, Y.; Sato, H.; Kiyono, S.; Shimizu, H.; Hirose, J. Development of a Sensitive Two-Axis Micro-Angle Sensor. J. Jpn. Soc. Precis. Eng. 2006, 72, 1174–1178. [Google Scholar] [CrossRef][Green Version]
- Shimizu, Y.; Tan, S.L.; Murata, D.; Maruyama, T.; Ito, S.; Chen, Y.L.; Gao, W. Ultra-sensitive angle sensor based on laser autocollimation for measurement of stage tilt motions. Opt. Express 2016, 24, 2788–2805. [Google Scholar] [CrossRef] [PubMed]
- Möller-Wedel Optical GmbH. Catalogue 2014, Electronic Autocollimators ELCOMAT HR. Available online: https://www.haag-streit.com/moeller-wedel-optical/products/electronic-autocollimators/elcomat-product-line/elcomat-hr/ (accessed on 27 November 2019).
- Gao, W.; Ohnuma, H.; Shimizu, H.; Kiyono, S. A Precision Angle Sensor Using a Multi-Cell Photodiode Array. Ann. Cirp 2004, 53, 425–428. [Google Scholar] [CrossRef]
- Gao, W.; Kiyono, S.; Satoh, E. Precision Measurement of Multi-Degree-Of-Freedom Spindle Errors Using Two-Dimensional Slope Sensors. Cirp Ann.-Manuf. Technol. 2002, 51, 447–450. [Google Scholar] [CrossRef]
- Ennos, A.E.; Virdee, M.S. High Accuracy Profile Measurement of Quasi-Conical Mirror Surfaces by Laser Autocollimation. Precis. Eng. 1982, 4, 5–8. [Google Scholar] [CrossRef]
- Gao, W.; Saito, Y.; Muto, H.; Arai, Y.; Shimizu, Y. A Three-Axis Autocollimator for Detection of Angular Error Motions of a Precision Stage. Cirp Ann.-Manuf. Technol. 2011, 60, 515–518. [Google Scholar] [CrossRef]
- Li, X.; Shimizu, Y.; Ito, T.; Cai, Y.; Ito, S.; Gao, W. Measurement of six-degree-of-freedom planar motions by using a multiprobe surface encoder. Opt. Eng. 2014, 53. Paper No.122405. [Google Scholar] [CrossRef]
- Li, X.; Gao, W.; Muto, H.; Shimizu, Y.; Ito, S.; Dian, S. A Six-Degree-Of-Freedom Surface Encoder for Precision Positioning of a Planar Motion Stage. Precis. Eng. 2013, 37, 771–781. [Google Scholar] [CrossRef]
- Matsukuma, H.; Ishizuka, R.; Furuta, M.; Li, X.; Shimizu, Y.; Gao, W. Reduction in Cross-Talk Errors in a Six-Degree-of-Freedom Surface Encoder. Nanomanuf. Metrol. 2019, 2, 111–123. [Google Scholar] [CrossRef]
- Gao, W.; Dejima, S.; Shimizu, Y.; Kiyono, S. Precision Measurement of Two-Axis Positions and Tilt Motions Using a Surface Encoder. Cirp Ann.-Manuf. Technol. 2003, 52, 435–438. [Google Scholar] [CrossRef]
- Kimura, A.; Gao, W.; Zeng, L. Position and Out-of-Straightness Measurement of a Precision Linear Air-Bearing Stage by Using a Two-Degree-Of-Freedom Linear Encoder. Meas. Sci. Technol. 2010, 21, 054005. [Google Scholar] [CrossRef]
- Gao, W.; Kimura, A. A Three-Axis Displacement Sensor with Nanometric Resolution. Ann. Cirp 2007, 56, 529–532. [Google Scholar] [CrossRef]
- Kimura, A.; Gao, W.; Kim, W.; Hosono, K.; Shimizu, Y.; Shi, L.; Zeng, L. A Sub-Nanometric Three-Axis Surface Encoder with Short-Period Planar Gratings for Stage Motion Measurement. Precis. Eng. 2012, 36, 576–585. [Google Scholar] [CrossRef]
- Gao, W.; Dejima, S.; Yanai, H.; Katakura, K.; Kiyono, S.; Tomita, Y. A Surface Motor-Driven Planar Motion Stage Integrated with an XYθZ Surface Encoder for Precision Positioning. Precis. Eng. 2004, 28, 329–337. [Google Scholar] [CrossRef]
- Shimizu, Y.; Ito, T.; Li, X.; Kim, W.J.; Gao, W. Design and Testing of a Four-probe Optical Sensor Head for Three-axis Surface Encoder with a Mosaic Scale Grating. Meas. Sci. Technol. 2014, 25, 09402. [Google Scholar] [CrossRef]
- Hsu, C.C.; Wu, C.C.; Lee, J.Y.; Chen, H.Y.; Weng, H.F. Reflection type heterodyne grating interferometry for in-plane displacement measurement. Opt. Commun. 2008, 281, 2582–2589. [Google Scholar] [CrossRef]
- Lin, C.B.; Yan, S.H.; Ding, D.; Wang, G. Two-dimensional diagonal-based heterodyne grating interferometer with enhanced signal-to-noise ratio and optical subdivision. Opt. Eng. 2018, 57, 064102. [Google Scholar] [CrossRef]
- Lee, J.Y.; Hsieh, H.L.; Lerondel, G.; Deturche, R.; Lu, M.P.; Chen, J.C. Heterodyne grating interferometer based on a quasi-common-optical path configuration for a two-degrees-of-freedom straightness measurement. Appl. Opt. 2011, 50, 1272–1279. [Google Scholar] [CrossRef]
- Wu, C.C.; Hsu, C.C.; Lee, J.Y.; Liu, C.Y. Optical heterodyne laser encoder for in-plane nanopositioning. In Proceedings of the SPIE, San Diego, CA, USA, 11 August 2008; Volume 7063, p. 70631A. [Google Scholar]
- Chung, Y.C.; Fan, K.C.; Lee, B.C. Development of a novel planar encoder for 2D displacement measurement in nanometer resolution and accuracy. In Proceedings of the 9th World Congress on Intelligent Control and Automation, Taipei, Taiwan, 21–25 June 2011; pp. 449–453. [Google Scholar]
- Wei, P.P.; Lu, X.; Qiao, D.; Zou, L.; Huang, X.; Tan, J.; Lua, Z. Two-dimensional displacement measurement based on two parallel gratings. Rev. Sci. Instrum. 2018, 89, 065105. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.Z.; Dong, X.H.; Guo, J.; Xie, T. Two-dimensional displacement sensing using a cross diffraction grating scheme. J. Opt. A Pure Appl. Opt. 2004, 6, 106–111. [Google Scholar] [CrossRef]
- Lin, C.B.; Yan, S.H.; Du, Z.G.; Wei, C.; Wang, G. High-efficiency gold-coated cross-grating for heterodyne grating interferometer with improved signal contrast and optical subdivision. Opt. Commun. 2015, 339, 86–93. [Google Scholar] [CrossRef]
- Feng, C.; Zeng, L.J.; Wang, S.W. Heterodyne planar grating encoder with high alignment tolerance, especially insensitivity to grating tilts. In Proceedings of the SPIE, Chengdu, China, 31 January 2013; Volume 8759, p. 85793L. [Google Scholar]
- Fan, K.C.; Liao, B.H.; Chung, Y.C.; Chung, T.T. Displacement measurement of planar stage by diffraction planar encoder in nanometer resolution. In Proceedings of the EEE International Instrumentation and Measurement Technology Conference Proceedings, Graz, Austria, 13–16 May 2012; pp. 894–897. [Google Scholar]
- Fan, K.C.; Lee, B.C.; Chung, Y.C. A planar laser diffraction encoder in Littrow configuration for 2D nanometric positioning. Int. J. Autom. Smart Technol. 2011, 1, 93–99. [Google Scholar] [CrossRef]
- Wu, C.C.; Chang, C.C.; Kao, C.F.; Peng, G.S. Novel planar laser encoder system for two-dimensional positioning with ultra high head-to-scale alignment tolerance. In Proceedings of the SPIE, San Diego, CA, USA, 3 November 2003; Volume 5173, pp. 55–63. [Google Scholar]
- Hsieh, H.L.; Chen, J.C.; Lerondel, G.; Lee, J.Y. Two dimensional displacement measurement by quasicommon-optical-path heterodyne grating interferometer. Opt. Express 2011, 19, 9770–9782. [Google Scholar] [CrossRef] [PubMed]
- Lin, J.; Guan, J.; Wen, F.; Tan, J. High-resolution and wide range displacement measurement based on planar grating. Opt. Commun. 2017, 404, 132–138. [Google Scholar] [CrossRef]
- Li, X.; Shi, Y.; Xiao, X.; Zhou, Q.; Wu, G.; Lu, H.; Ni, K. Design and Testing of a Compact Optical Prism Module for Multi-Degree-of-Freedom Grating Interferometry Application. Appl. Sci. 2018, 8, 2495. [Google Scholar] [CrossRef]
- Pan, S.W.; Hsieh, H.L.; Wang, W.C. 6-DOF displacement and angle measurements using heterodyne laser encoder. In Proceedings of the SPIE, San Diego, CA, USA, 20 September 2013; Volume 8819, p. 881909. [Google Scholar]
- Hsieh, H.L.; Pan, S.W. Development of a grating-based interferometer for six-degree-of-freedom displacement and angle measurements. Opt. Express 2015, 23, 2451–2465. [Google Scholar] [CrossRef]
- Liu, C.H.; Cheng, C.H. Development of a grating based multi-degree-of-freedom laser linear encoder using diffracted light. Sens. Actuators A Phys. 2012, 181, 87–93. [Google Scholar] [CrossRef]
- Gao, W.; Takeshi, A.; Satoshi, K.; Yuichi, O.; Masashi, Y. Precision Nanofabrication and Evaluation of a Large Area Sinusoidal Grid Surface for a Surface Encoder. Precis. Eng. 2003, 27, 289–298. [Google Scholar] [CrossRef]
- Kimura, A.; Gao, W.; Kiyono, S. Design and Construction of a Surface Encoder with Dual Sine-Grids. Int. J. Precis. Eng. Manuf. 2007, 8, 20–25. [Google Scholar]
- Li, X.; Gao, W.; Shimizu, Y.; Ito, S. A Two-Axis Lloyd’s Mirror Interferometer for Fabrication of Two Dimensional Diffraction Gratings. Cirp Ann.-Manuf. Technol. 2014, 63, 435–438. [Google Scholar] [CrossRef]
- Shimizu, Y.; Aihara, R.; Mano, K.; Chen, C.; Chen, Y.L.; Chen, X.; Gao, W. Design and testing of a compact non-orthogonal two-axis Lloyd’s mirror interferometer for fabrication of large-area two-dimensional scale gratings. Precis. Eng. 2018, 52, 138–151. [Google Scholar] [CrossRef]
- Shimizu, Y.; Mano, K.; Zhang, K.; Matsukuma, H.; Gao, W. Accurate polarization control in a non-orthogonal two-axis Lloyd’s mirror interferometer for fabrication of two-dimensional scale gratings. Opt. Eng. 2019, 58, 092611. [Google Scholar] [CrossRef]
- Shimizu, Y.; Mano, K.; Murakami, H.; Hirota, S.; Matsukuma, H.; Gao, W. Design optimization of a non-orthogonal two-axis Lloyd’s mirror interferometer for fabrication of large-area two-dimensional scale gratings. Precis. Eng. 2019, 60, 280–290. [Google Scholar] [CrossRef]
- Gao, W.; Kimura, A. A Fast Evaluation Method for Pitch Deviation and Out-of-Flatness of a Planar Scale Grating. Ann. Cirp 2010, 59, 505–508. [Google Scholar] [CrossRef]
- Chen, X.; Shimizu, Y.; Xiong, X.; Chen, Y.L.; Gao, W. Self-calibration of Fizeau interferometer and planar scale gratings in Littrow setup. Opt. Express 2017, 25, 21567. [Google Scholar] [CrossRef]
- Xiong, X.; Shimizu, Y.; Chen, X.; Matsukuma, H.; Gao, W. Uncertainty Evaluation for Measurements of Pitch Deviation and Out-of-Flatness of Planar Scale Gratings by a Fizeau Interferometer in Littrow Configuration. Appl. Sci. 2018, 8, 2539. [Google Scholar] [CrossRef]
- Schwenke, H.; Knapp, W.; Haitjema, H.; Weckenmann, A.; Schmitt, R.; Delbressine, F. Geometric error measurement and compensation of machines-An update. Cirp Ann.-Manuf. Technol. 2008, 57, 660–675. [Google Scholar] [CrossRef]
- Meyer, G.; Amer, M. Novel optical approach to atomic force microscopy. Appl. Phys. Lett. 1988, 53, 1045–1047. [Google Scholar] [CrossRef]
- Huang, P.S.; Kiyono., S.; Kamada, O. Angle measurement based on the internal-reflection effect: A new method. Appl. Opt. 1992, 31, 6047–6055. [Google Scholar] [CrossRef] [PubMed]
- Shan, M.; Min, R.; Zhong, Z.; Wang, Y.; Zhang, Y. Differential reflective fiber-optic angular displacement sensor. Opt. Laser Technol. 2015, 68, 124–128. [Google Scholar] [CrossRef]
- Ralf, D.G.; Ingolf, W.; Andreas, J.; Reinhard, P. Use and treaceable calibration of autocollimators for ultra-precise measurement of slope and topography. In Proceedings of the SPIE, Munich, Germany, 22 October 2001; Volume 4401. [Google Scholar] [CrossRef]
- Autocollimator. Available online: http://www.precipedia.jspe.or.jp (accessed on 10 September 2019).
- Fan, K.C.; Li, R.J.; Xu, P. Design and Verification of Micro/Nano-Probes for Coordinate Measuring Machines. Nanomanuf. Metrol. 2019, 2, 1–15. [Google Scholar] [CrossRef]
- Gao, W.; Huang, P.S.; Yamada, T.; Kiyono, S. A compact and sensitive two-dimensional angle probe for flatness measurement of large silicon wafers. Precis. Eng. 2002, 26, 396–404. [Google Scholar] [CrossRef]
- Graves, L.R.; Smith, G.A.; Apai, D.; Kim, D.W. Precision Optics Manufacturing and Control for Next-Generation Large Telescopes. Nanomanuf. Metrol. 2019, 2, 65–90. [Google Scholar] [CrossRef]
- Tanimura, Y.; Kato, T. Reflection Device of Autocollimator for Measuring Three Components of Angular Alignment. Jpn. J. Precis. Eng. 1987, 53, 896–901. (In Japanese) [Google Scholar] [CrossRef][Green Version]
- Liu, C.H.; Jywe, W.Y.; Tzeng, S.C. Simple three-dimensional laser angle sensor for three-dimensional small-angle measurement. Appl. Opt. 2004, 43, 2840–2845. [Google Scholar] [CrossRef]
- Shimizu, Y.; Maruyama, T.; Ito, S.; Gao, W. A Three-Axis Angle Sensor with a Linear Encoder Scale Reflector. Appl. Mech. Mater. 2017, 870, 141–146. [Google Scholar] [CrossRef]
- Schwenke, H.; Neuschaefer-Rube, U.; Pfeifer, T.; Kunzmann, H. Optical methods for dimensional metrology in production engineering. Cirp Ann.-Manuf. Technol. 2002, 51, 685–699. [Google Scholar] [CrossRef]
- Weichert, C.; Köchert, P.; Köning, R.; Flügge, J.; Andreas, B.; Kuetgens, U.; Yacoot, A. A Heterodyne Interferometer with Periodic Nonlinearities Smaller than 10 pm. Meas. Sci. Technol. 2012, 23, 094005. [Google Scholar] [CrossRef]
- Yacoot, A.; Cross, N. Measurement of Picometer Non-linearity in an Optical Grating Encoder Using X-ray Interferometry. Meas. Sci. Technol. 2003, 14, 148–152. [Google Scholar] [CrossRef]
- Fan, K.C.; Miao, J.W.; Gong, W.; Zhang, Y.L. High precision measurement system based on coplanar XY-stage. In Proceedings of the SPIE, Yunnan, China, 15 November 2011; Volume 8321, p. 832119. [Google Scholar]
- Bernhardt, R. Temperature Robust Structure of a Coordinate Measuring Machine. In Proceedings of the Euspen Special Interest Group Meeting, Thermal Issues, Zurich, Switzerland, 2014. [Google Scholar]
- Zygo Corp. Heterodyne Laser Interferometers. Available online: http://www.zygo.com (accessed on 27 November 2019).
- Donker, R.L.; Widdershoven, I.; Brouns, D.; Spaan, H.A.M. Realization of Isara400: A Large Measurement Volume Ultra-Precision CMM. In Proceedings of the ASPE Annual Meeting, Monterey, CA, USA, 4–9 October 2009; pp. 35–38. [Google Scholar]
- Jäger, G.; Manske, E.; Hausotte, T.; Büchner, H.J. The Metrological Basis and Operation of Nanopositioning and Nanomeasuring Machine NMM-1. Tech. Mess. 2009, 76, 227–234. [Google Scholar] [CrossRef]
- Sternkopf, C.; Manske, E. Digital frequency offset-locked He–Ne laser system with high beat frequency stability, narrow optical linewidth and optical fibre output. Meas. Sci. Technol. 2018, 29, 06413. [Google Scholar] [CrossRef]
- Heidenhain. Encoders for Machine Tool Inspection and Acceptance Testing. Available online: https://www.heidenhain.com/fileadmin/pdb/media/img/208871-29_Measuring_Devices_For_Machine_Tool_Inspection_and_Acceptance_Testing_01.pdf (accessed on 9 September 2019).
- Castenmiller, T.; Van de Mast, F.; De Kort, T.; Van de Vin, C.; De Wit, M.; Stegen, R.; Van Cleef, S. Towards Ultimate Optical Lithography with Nxt: 1950i Dual Stage Immersion Platform. In Proceedings of the SPIE, San Jose, CA, USA, 12 March 2010; Volume 7640, p. 76401N. [Google Scholar]
- Schmidt, R.M.H. Ultra-Precision Engineering in Lithographic Exposure Equipment for the Semiconductor Industry. Philos. Trans. R. Soc. A—Math. Phys. Eng. Sci. 2012, 370, 3950–3972. [Google Scholar] [CrossRef] [PubMed]
- Gao, W.; Tano, M.; Sato, S.; Kiyono, S. On-machine measurement of a cylindrical surface with sinusoidal micro-structures by an optical slope sensor. Precis. Eng. 2006, 30, 274–279. [Google Scholar] [CrossRef]
- Gao, W. Precision Nanometrology and its Applications to Precision Nanosystems. Int. J. Precis. Eng. Manuf. 2005, 6, 14–20. [Google Scholar]
- Fang, F.Z.; Xu, F. Recent Advances in Micro/Nano-cutting: Effect of Tool Edge and Material Properties. Nanomanuf. Metrol. 2018, 1, 4–31. [Google Scholar] [CrossRef]
- Zhao, S.S.; Hou, C.L.; Bai, J.; Yang, G.; Tian, F. Nanometer-scale displacement sensor based on phase-sensitive diffraction grating. Appl. Opt. 2011, 50, 1413–1416. [Google Scholar] [CrossRef]
- ITRS2013 Executive Summary. Available online: http://www.itrs2.net (accessed on 9 September 2019).
- JHoose, J.; Loewen, E.; Wiley, R.; Bzasiak, T.; Zheleznyak, S.; Sroda, T. Grand gratings: Bigger is better, thanks to mosaic technology-today’s larger telescopes’ unprecedented challenge. Photon. Spectra 1995, 29, 118–136. [Google Scholar]
- Blasiak, T.; Zheleznyak, S. History and construction of large mosaic diffraction gratings. In Proceedings of the International Symposium on Optical Science and Technology, San Diego, CA, USA, 11–13 September 2002; pp. 370–377. [Google Scholar]
- Evans, C. Design and Construction of a Large Grating Ruling Engine. Precis. Eng. 1981, 3, 193–200. [Google Scholar] [CrossRef]
- Harrison, G.R. The Production of Diffraction Gratings; I. Development of The Ruling Art. J. Opt. Soc. Am. 1949, 39, 413–426. [Google Scholar] [CrossRef]
- Harrison, G.R.; Stroke, G.W. Interferometric Control of Grating Ruling with Continuous Carriage Advance. J. Opt. Soc. Am. 1955, 45, 112–121. [Google Scholar] [CrossRef]
- David, C.; Bruder, J.; Rohbeck, T.; Grünzweig, C.; Kottler, C.; Diaz, A.; Bunk, O.; Pfeiffer, F. Fabrication of diffraction gratings for hard X-ray phase contrast imaging. Microelectron. Eng. 2007, 84, 1172–1177. [Google Scholar] [CrossRef]
- Brueck, S.R.J. Optical and Interferometric Lithography-Nanotechnology Enablers. Proc. IEEE 2005, 93, 1704–1721. [Google Scholar] [CrossRef]
- Konkola, P.T.; Chen, C.G.; Heilmann, R.K.; Joo, C.; Montoya, J.C.; Chang, C.H.; Schattenburg, M.L. Nanometer-level repeatable metrology using the Nanoruler. J. Vac. Sci. Technol. B Microelectron. Nanometer Struct. Process. Meas. Phenom. 2003, 21, 3097–3101. [Google Scholar] [CrossRef]
- Chua, J.K.; Murkeshan, V.M. Patterning of Two-Dimensional Nanoscale Features Using Grating-Based Multiple Beams Interference Lithography. Phys. Scr. 2009, 80, 015401. [Google Scholar] [CrossRef]
- Ma, D.; Zhao, Y.; Zeng, L. Achieving unlimited recording length in interference lithography via broad-beam scanning exposure with self-referencing alignment. Sci. Rep. 2017, 7, 926. [Google Scholar] [CrossRef]
- Heilmann, R.K.; Konkola, P.T.; Chen, C.G.; Pati, G.S.; Schattenburg, M.L. Digital heterodyne interference fringe control system. J. Vac. Sci. Technol. B 2001, 19, 2342–2346. [Google Scholar] [CrossRef]
- Li, X.; Zhou, Q.; Zhu, X.; Lu, H.; Yang, L.; Ma, D.; Sun, J.; Ni, K.; Wang, X. Holographic fabrication of an arrayed one-axis scale grating for a two-probe optical linear encoder. Opt. Express 2017, 25, 16028. [Google Scholar] [CrossRef]
- Boor, J.; Geyer, N.; Gösele, U.; Schmidt, V. Three-beam interference lithography: Upgrading a Lloyd’s interferometer for single-exposure hexagonal patterning. Opt. Lett. 2009, 34, 1783–1785. [Google Scholar] [CrossRef]
- Vala, M.; Homola, J. Flexible method based on four-beam interference lithography for fabrication of large areas of perfectly periodic plasmonic arrays. Opt. Express 2014, 22, 18778–19789. [Google Scholar] [CrossRef] [PubMed]
- Shimizu, Y.; Aihara, R.; Zongwei, R.; Chen, Y.L.; Ito, S.; Gao, W. Influences of misalignment errors of optical components in an orthogonal two-axis Lloyd’s mirror interferometer. Opt. Express 2016, 24, 17521–27535. [Google Scholar] [CrossRef] [PubMed]
- Byun, I.; Kim, J. Cost-effective laser interferometer lithography using a 405 nm AlInGaN semiconductor laser. J. Micromech. Microeng. 2010, 20, 055024. [Google Scholar] [CrossRef]
- Chen, X.; Ren, Z.; Shimizu, Y.; Chen, Y.L.; Gao, W. Optimal polarization modulation for orthogonal two-axis Lloyd’s mirror interference lithography. Opt. Express 2017, 25, 22238. [Google Scholar] [CrossRef] [PubMed]
- Hung, Y.J.; Chang, H.J.; Chang, P.C.; Lin, J.J.; Kao, T.C. Employing refractive beam shaping in a Lloyd’s interference lithography system for uniform periodic nanostructure formation. J. Vac. Sci. Technol. B 2017, 35, 030601. [Google Scholar] [CrossRef]
- Chen, X.; Shimizu, Y.; Chen, C.; Chen, Y.L.; Gao, W. Generalized method for probing ideal initial polarization states in multibeam Lloyd’s mirror interference lithography of 2D scale gratings. J. Vac. Sci. Technol. B 2018, 36, 021601. [Google Scholar] [CrossRef]
- Gonda, S.; Doi, T.; Kurosawa, T.; Tanimura, Y.; Hisata, N.; Yamagishi, T.; Fujimoto, H.; Yukawa, H. Real-time, interferometrically measuring atomic force microscope for direct calibration of standards. Rev. Sci. Instrum. 1999, 70, 3362–3368. [Google Scholar] [CrossRef]
- Misumi, I.; Gonda, S.; Kurosawa, T.; Takamasu, K. Uncertainty in pitch measurements of one-dimensional grating standards using a nanometrological atomic force microscope. Meas. Sci. Technol. 2003, 14, 463–471. [Google Scholar] [CrossRef]
- Dai, G.; Pohlenz, F.; Xu, M.; Koenders, L.; Danzebrink, H.U.; Wilkening, G. Accurate and Traceable Measurement of Nano- and Micro-structures. Meas. Sci. Technol. 2006, 17, 545–552. [Google Scholar] [CrossRef]
- Eves, B.J. Design of a Large Measurement-Volume Metrological Atomic Force Microscope (AFM). Meas. Sci. Technol. 2009, 20, 084003. [Google Scholar] [CrossRef]
- Buhr, E.; Michaelis, W.; Diener, A.; Mirandé, W. Multi-wavelength VIS/UV, Optical Diffractometer for High-accuracy Calibration of Nano-Scale Pitch Standards. Meas. Sci. Technol. 2007, 18, 667–674. [Google Scholar] [CrossRef]
- Shimizu, Y.; Uehara, K.; Matsukuma, H.; Gao, W. Evaluation of the grating period based on laser diffraction by using a mode-locked femtosecond laser beam. J. Adv. Mech. Des. Syst. Manuf. 2018, 12, 18–00173. [Google Scholar] [CrossRef]
- Sawabe, M.; Maeda, F.; Yamaryo, Y.; Simomura, Y.; Saruki, Y.; Kubo, T.; Sakai, H.; Aoyagi, S. A New Vacuum Interferometric Comparator for Calibrating the Fine Linear Encoders and Scales. Precis. Eng. 2004, 28, 320–328. [Google Scholar] [CrossRef]
- Takahashi, A.; Miwa, N. An Experimental Verification of the Compensation of Length Change of Line Scales Caused by Ambient Air Pressure. Meas. Sci. Technol. 2010, 21, 045305. [Google Scholar] [CrossRef]
- Yu, H.Y.; Liu, H.Z.; Li, X.; Ye, G.; Shi, Y.; Yin, L.; Jiang, W.; Chen, B.; Liu, X. Calibration of non-contact incremental linear encoders using a macro–micro dual-drive high-precision comparator. Meas. Sci. Technol. 2015, 26, 095103. [Google Scholar] [CrossRef]
- Shimizu, Y.; Kudo, Y.; Chen, Y.L.; Ito, S.; Gao, W. An optical lever by using a mode-locked laser for angle measurement. Precis. Eng. 2017, 47, 72–80. [Google Scholar] [CrossRef]
- Jang, Y.S.; Kim, S.W. Distance Measurements Using Mode-Locked Lasers: A Review. Nanomanuf. Metrol. 2018, 1, 131–147. [Google Scholar] [CrossRef]
- Chen, Y.L.; Shimizu, Y.; Tamada, J.; Kudo, Y.; Madokoro, S.; Nakamura, K.; Gao, W. Optical frequency domain angle measurement in a femtosecond laser autocollimator. Opt. Express 2017, 25, 16725. [Google Scholar] [CrossRef]
- Chen, Y.L.; Shimizu, Y.; Kudo, Y.; Ito, S.; Gao, W. Mode-locked laser autocollimator with an expanded measurement range. Opt. Express 2016, 24, 15554–15569. [Google Scholar] [CrossRef]


© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shimizu, Y.; Matsukuma, H.; Gao, W. Optical Sensors for Multi-Axis Angle and Displacement Measurement Using Grating Reflectors. Sensors 2019, 19, 5289. https://doi.org/10.3390/s19235289
Shimizu Y, Matsukuma H, Gao W. Optical Sensors for Multi-Axis Angle and Displacement Measurement Using Grating Reflectors. Sensors. 2019; 19(23):5289. https://doi.org/10.3390/s19235289
Chicago/Turabian StyleShimizu, Yuki, Hiraku Matsukuma, and Wei Gao. 2019. "Optical Sensors for Multi-Axis Angle and Displacement Measurement Using Grating Reflectors" Sensors 19, no. 23: 5289. https://doi.org/10.3390/s19235289
APA StyleShimizu, Y., Matsukuma, H., & Gao, W. (2019). Optical Sensors for Multi-Axis Angle and Displacement Measurement Using Grating Reflectors. Sensors, 19(23), 5289. https://doi.org/10.3390/s19235289






