1. Introduction
Synthesis of microscale particles capable of drug transportation and/or active manipulations with cells is one of the most actively developing trends in modern biomedicine [
1]. A promising class of such objects, well tunable and controllable, are polymersomes: vesicle-like submicron capsules whose walls are formed by a bilayer membrane built of an amphiphilic block copolymer [
2,
3,
4,
5,
6,
7]. The polymersome might be loaded with biomedical substances (cargo) whereas the membrane might be functionalized to be stimuli-sensitive to a number of factors: pH, temperature, oxidation/reduction, electric/magnetic fields, light, ultrasound, etc. Chemical versatility and stability of polymersomes ensure a variety of their foreseen applications: biosensing systems, nanoreactors, drug carriers with externally activated release, imaging, and even prototypes of artificial cell organelles.
The objects of current study are magnetosensitive polymersomes (magnetopolymersomes, MPSs) whose membrane is modified by introducing inside it magnetic (e.g., maghemite) nanoparticles (MNPs) [
8,
9,
10,
11]. Due to the hydrophilic/hydrophobic interplay, the MNPs are confined inside the sandwich structure formed by the inner and outer amphiphilic polymer layers (shells); the width of the intershell gap is adjusted in such a way that it just a bit exceeds the MNP size. With such a construction, magnetodeformational susceptibility of MPSs comes out several orders of magnitude higher than that of any other types of microcapsules.
Nowadays, chemical synthesis of various modifications of MPSs is rapidly developing, and they are available in different shapes and morphologies [
12,
13]. In [
14], membranes of poly(trimethylene carbonate)-
b-poly(L-glutamic acid) (PTMC-
b-PGA) with incorporated maghemite (
) nanoparticles are reported. The monolayer, double-layer and multilayer vesicles with poly(styrene)-
b-poly(acrylic acid) (PS-
b-PAA) membranes of tuned thickness and stuffed with MNPs are obtained in [
15]. The tests demonstrate that the polymersomes with thicker membrane and higher MNP density display enhanced MRI contrast, higher magnetization and better release profile of their drug cargo. In structure investigations, it is found that larger MNPs drift closer to the inner membrane boundary that leads to larger curvature of the latter [
16]. Besides dilute systems, preparation of size-controlled assemblies of densely packed submicron PS-
b-PAA polymersomes is also possible [
16].
Now a commonly established fact is that under an applied external field, MPSs notably stretch along the field direction. Moreover, as revealed by small-angle neutron scattering (SANS), the field causes changes in the membrane structure making it anisotropic, and this anisotropy increases with the applied field. The evaluated scattering anisotropy factor is also found to be dependent on the MNP content, size and curvature of the membrane. According to the SANS observations, the field strength at which the field-dependence of the anisotropy factor attains a plateau coincides with that saturating the MNP magnetic moments [
14].
The granted biocompatibility of MPSs and experimentally proven opportunity to magnetically control their shape as well as the changes of MNP distribution inside the membrane, commend them as really smart micro-objects for biomedical use. For further progress, one needs a valid concept of complex magnetomechanical and magnetostructural properties of MPSs that, as for now, is virtually nonexistent. A promising, if not the only, way to fill in this gap, i.e., to study and predict the deformational and structure responses of MPSs, is an extensive use of computer simulations. In what follows, we describe a flexible computational model of an MPS and use it to analyze the field-induced shape and volume effects.
2. Model and Simulations
A coarse-grained molecular dynamics description of a magnetic polymersome was developed in [
17]. Here, we use it to investigate the dependence of magnetodeformational behavior of an MPS on the overall size of the latter.
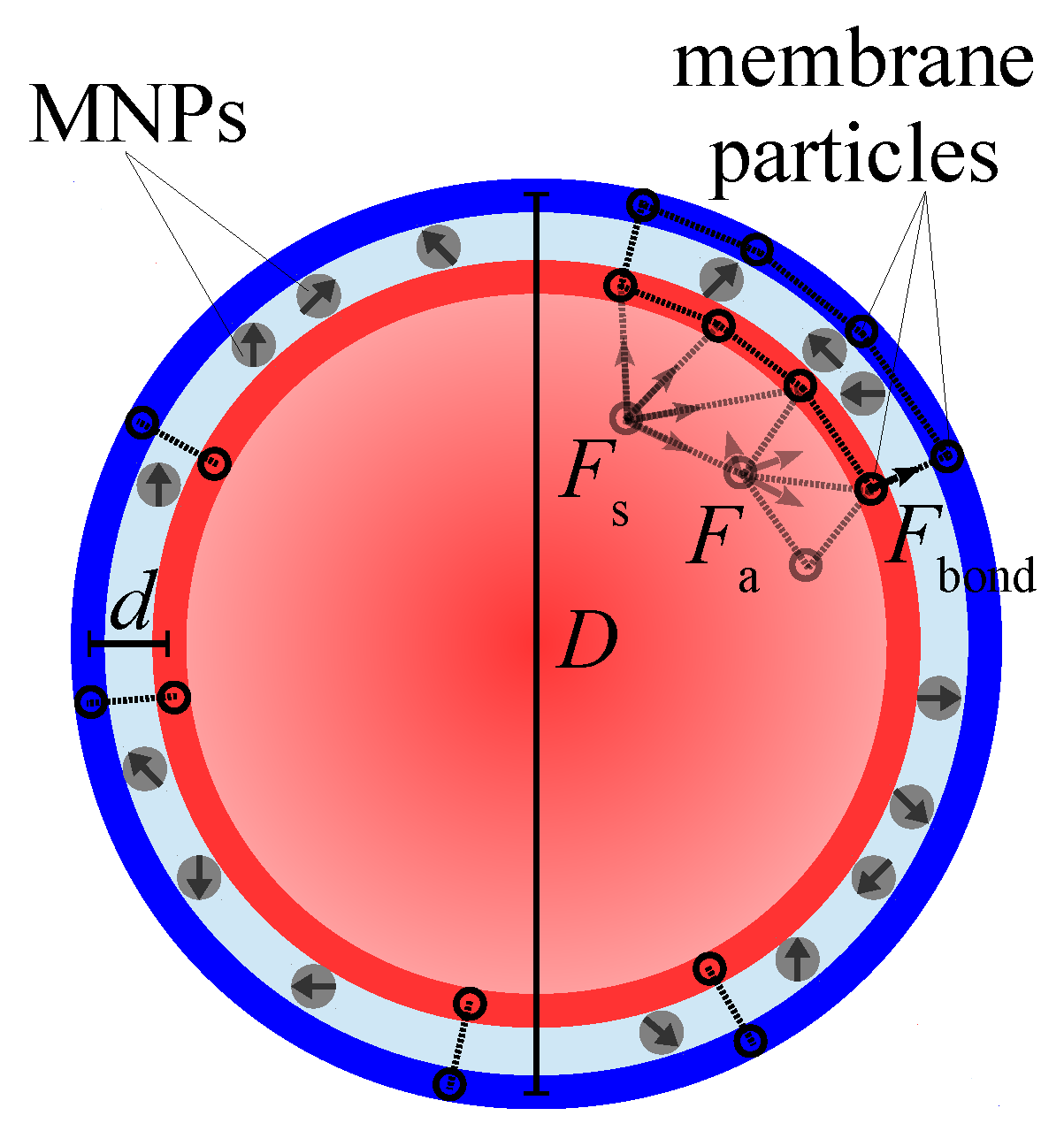
The model MPS is built of the particles of two types: non-magnetic polymer ones (beads) and MNPs. The sandwiched amphiphilic membrane, within which the MNPs are confined, is presented as two nested spherical shells, the inner and outer ones, see
Figure 1. Each shell consists of an equal number of beads arranged in a quasi-2D triangular mesh, so that the centers of beads are the mesh nodes; the diameters of the beads are denoted as
and
, respectively, where the subscript indicates the shell.
Inside each shell the bead centers are connected with stiff springs to ensure virtual constancy of the inter-bead distances and, thus, the area of the triangle built of any three neighboring beads. At the surface organized in such a way, any pair of side-abutting triangles is, however, free to fold along their mutual border. In other words, the overall surface area of the shell is conserved but the shell bending elasticity is negligible.
Inside this double-shell membrane, in a number of points uniformly distributed over its surface, the subtending beads (nodes) of the shells are linked with identical linear elastic springs; the stress-free length h of the spring defines the equilibrium thickness of the intershell layer. Given that the total membrane thickness is , whereas the gap accessible for the MNPs is . The connectivity parameter of the membrane is defined as the ratio of the number of spring-bonded pairs to the whole number of particles in the shell; evidently, diminution of enhances the extent of the layer thickness fluctuations.
Inside the MPS membrane, a certain number of monodisperse spherical magnetic nanoparticles is confined, thus making a kind of quasi-2D magnetic fluid. The volume fraction of the MNPs is defined with respect to the volume of the intershell space where they are allowed to move. From the calculation viewpoint, each MNP is treated as a structureless bead of diameter with a built-in magnetic (dipole) moment fixed at its center. The intershell gap but slightly exceeds , so that the intershell layer might accommodate only a monolayer of MNPs. In magnetic aspect, the MNPs are coupled with each other as point dipoles; in steric aspect, they interact as soft spheres. The diameters and of the shell beads are chosen is such a way that the shells are impenetrable for the MNPs.
To commence simulation, first, under the above-presented conditions a multi-element object (a model MPS) is constructed as a hollow sphere of outer diameter D with a double-shell wall, within which a given number of MNPs is uniformly distributed; the number of the beads in the shells is chosen accordingly. Then all the interparticle interactions are “switched on”, and the model MPS is set in contact with Langevin thermostat that induces Brownian motion of all the elements of the system. Therefore, the thermostat imitates the presence of isothermal solvent (consisting of light-weight molecules) which uniformly fills in all the space outside and inside the MPS.
From this instant the coarse-grained molecular dynamics calculation starts and is carried out until the system comes to equilibrium; the criterion for the latter is stabilization of the overall energy value. This stage yields the basic (field-free) state of the MPS and enables one to obtain its characteristics. Then a uniform magnetic field is imposed, i.e., the Zeeman energy is added to the energy of each magnetic element, and the calculation process is run anew.
Technically, each calculation implies the numerical solution of the set of coupled equations of motion for all the center-of-mass position vectors
where subscript
i enumerates all the elements of the model MPS, beads or magnetic particles:
here
is the element mass,
the force derived from the total potential energy. The second term in the right-hand side of Equation (
1) is the dissipative force with translational friction coefficient
, and
is the random force generated by Langevin thermostat.
The force experienced by each bead of any shell is
with
being the total stretching/compression force on the part of neighboring mesh nodes,
a sum of forces depending on relative change of the areas of the mesh triangles which have the
i-th node as a common vertex,
an elastic force entailed by the presence of the bonds connecting the
i-th node of one shell with the subtending node of another one,
a total force of soft mutual repulsion between the
i-th and all the other MNPs, this set of forces is defined by pairwise Weeks-Chandler-Andersen (truncated Lennard-Jones) potential [
18].
The force acting on each MNP is
Here
is the sum of pairwise forces derived from the dipolar magnetic interaction of the
i-th MNP that bears magnetic moment
directed along unit vector
with all the others located at the intercenter distances
. This force has the form
here
is vacuum permeability. The second and third terms in the right-hand part of Equation (
2) are the soft repulsion forces between MNPs and between MNPs and the confining shells, respectively.
Note that for MNPs, besides translational degrees of freedom, the rotational ones matter as well, since the magnetic moment orientations enter the interparticle forces, see Equation (
3). The pertinent equations of rotary dynamics with the corresponding torques induced both by the local fields and external field
are included in the whole set of equation as well.
All computer simulations were performed with the aid of ESPResSo code [
19], the shells were implemented following the scheme proposed in [
20]. The computational experiments included preliminary steps to obtain equilibrium distribution of MNPs inside the MPS membrane under zero external field (basic state) and magnetization steps to obtain the changes induced by the applied field. For every MPS size and for every value of the field strength, the calculations were carried out on 10 copies of the model MPS which differed only in initial orientational distribution of the MNP magnetic moments.
The nondimensional parameters which characterize the system under study are as follows. The intensity of the magnetic dipolar interaction
is defined as the ratio of energy of magnetic dipolar interaction of two identical MNPs placed at the closest possible distance, i.e.,
, to thermal energy with
being the Boltzmann constant and
T temperature.
The second parameter is the reference Zeeman energy of an MNP in the field of strength
scaled with thermal one:
Let us clarify the relations between the dimensional parameters of the problem and their nondimensional counterparts used in the calculations. The nanoparticle diameter
is set to 15 nm that with the typical magnetization of a ferrite (magnetite or maghemite)
emu yields for the MNP magnetic moment
emu. Then, assuming room temperature that is the only choice for aqueous solutions, for the dipole interaction parameter (
4) one gets
.
The Langevin argument evaluated for the same conditions comes out is related to dimensional field strength as , so that corresponds to kOe that is completely feasible value.
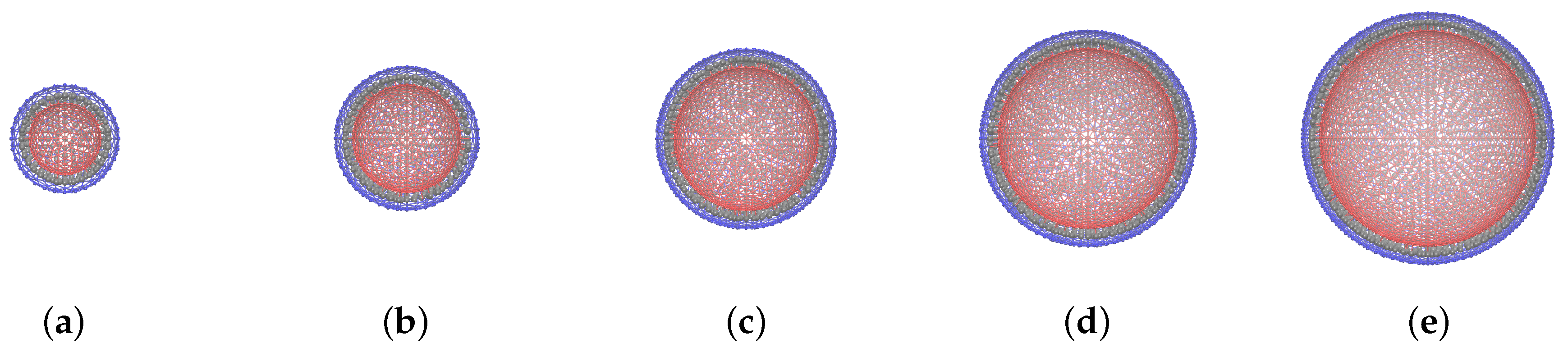
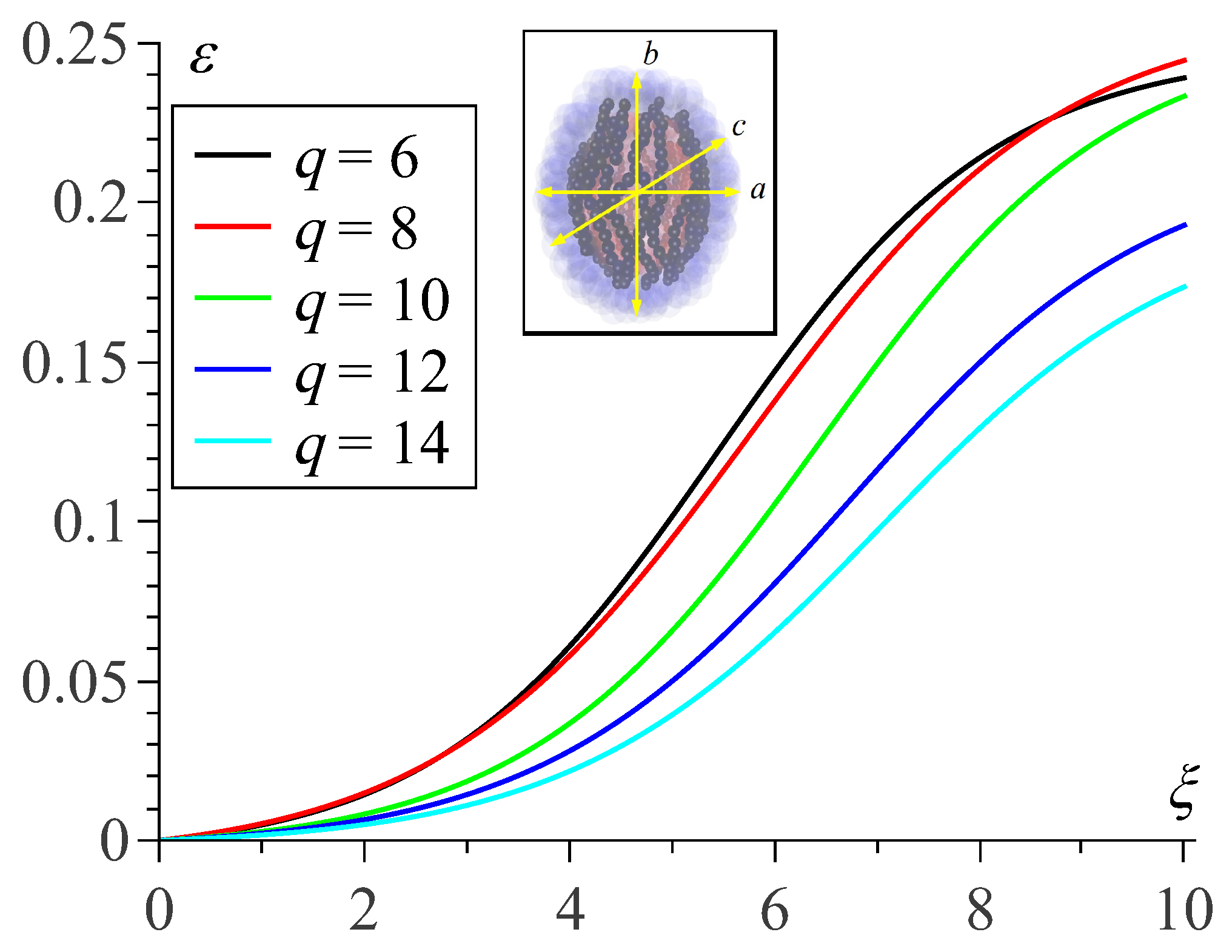
The intershell distance h is taken as the length unit; in this scale, and . With the above-introduced value of the MNP diameter nm, for the MPS parameters one finds: nm and nm. The size of simulated MPSs varies from to that makes 2.3 time difference; the value of D refers to the initial geometry of the MPS, i.e., a sphere. Taking the above-given value of h, one finds that the dimensional size of the tested MPS spans from 300 to 700 nm. In the membranes of all the samples, the volume content of MNPs is constant and equal vol.%, and the connectivity of the MPS shells is set to .
Keeping the MNP size , dipole parameter , layer thickness , volume content and connectivity constant, we ensure that the “quality” of the MPS membranes is the same (at least, before the field is applied). The next section presents the results of simulating the field-induced responses of such MPSs under variation of their overall sizes D.
4. Discussion
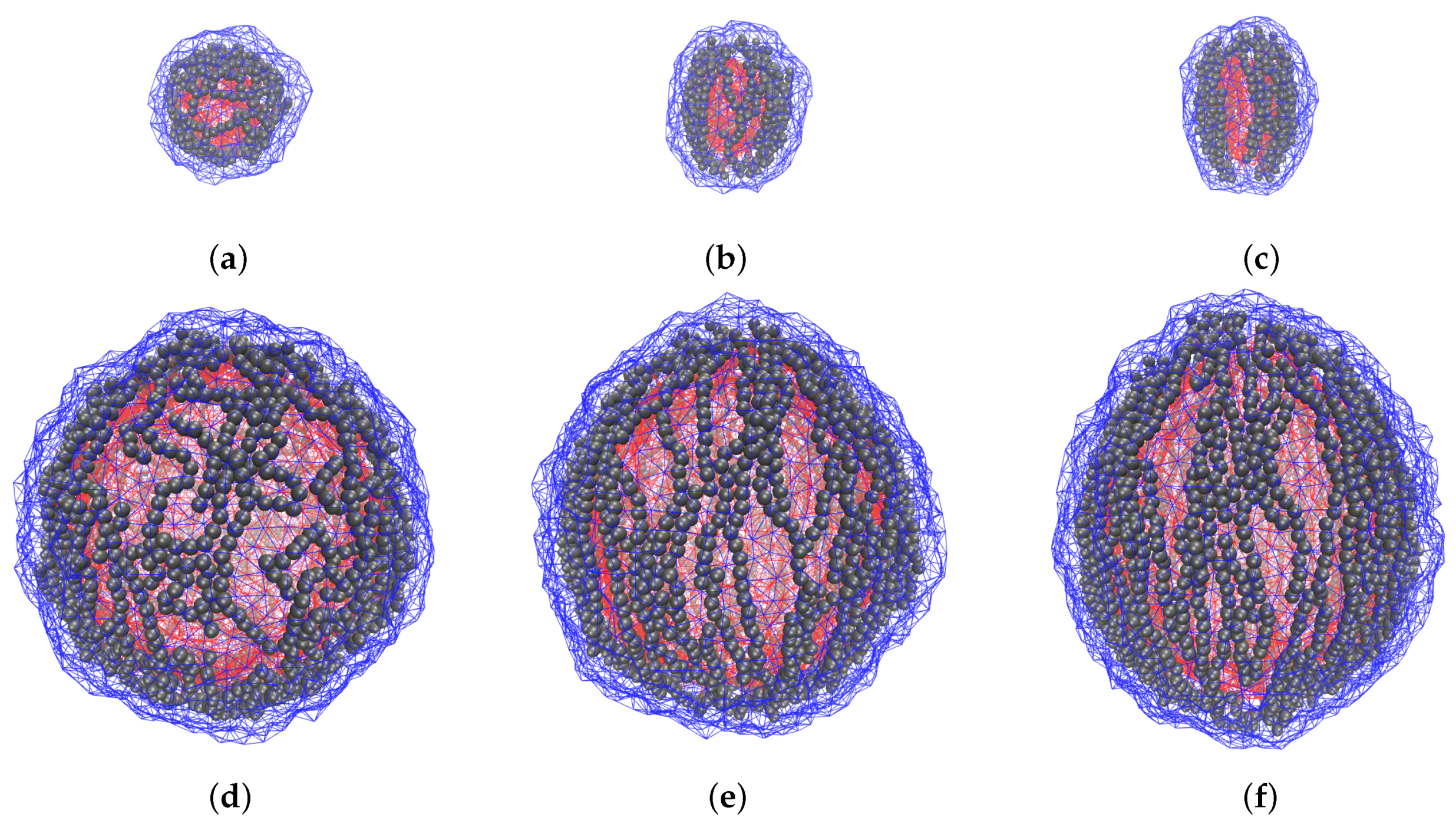
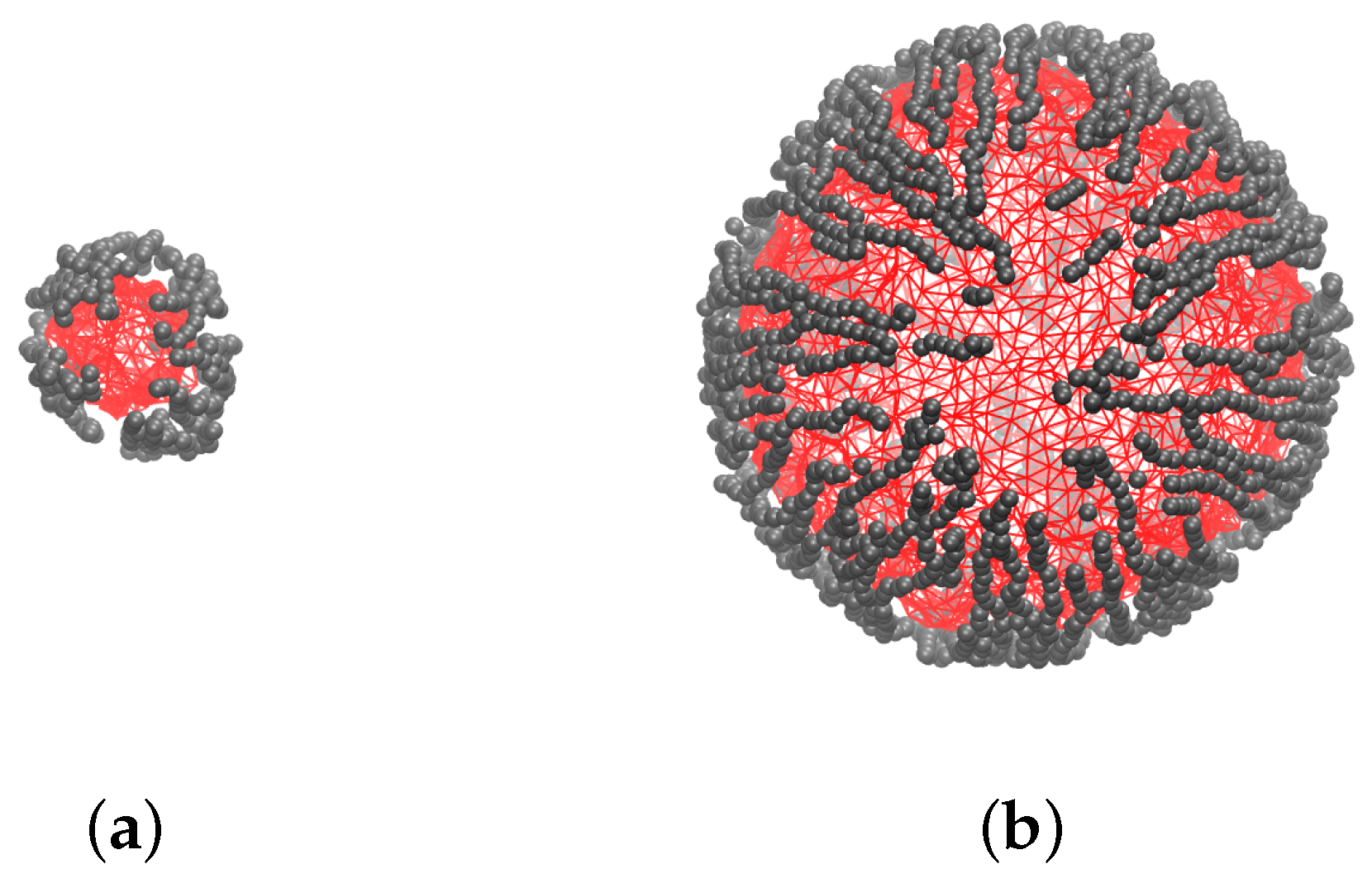
The coarse-grained molecular dynamics model is applied to investigate the field-induced overall deformation of an MPS and the internal restructuring accompanying it. This enables one to understand the dimension effect: the influence of the size factor on the polymersomes with the same properties of their membranes. The obtained results point out that in these objects the overall changes (shape anisotropy, volume defect) are essentially determined by the structure rearrangements which take place in the magnetically active membrane. As the snapshots of
Figure 3 show, the MNPs, formerly dwelling in randomly oriented loose aggregates, re-group and unite in well-formed chains fairly well aligned with the direction of the imposed field; the increase of the field enhances the straightness of the chains. Therefore, one comes to a conclusion that the field-induced chaining of the particles is the main mechanism of MPS elongation. Moreover, it is clear that the equilibrium shape of an MPS is established as a result of interplay between the magnetostatic forces which group the particles and align the chains, and the steric forces which maintain the MNPs confinement in the intra-membrane space.
At a first sight, in the membrane of a larger polymersome (lower curvature), the nanoparticles are more free to align, and, thus, in such an object the conditions for the field-induced elongation are more favorable. However, as the simulation results presented in
Figure 4 show, our modelling points out the opposite tendency. To explain this, in below we present qualitative considerations which, if not being exhaustive, should be an important part of the effect.
In our view, the found dependence is a manifestation of the anisotropic character of the dipole-dipole interaction in a confined geometry of a spherical layer. As known, the dipolar particles with parallel orientation of their magnetic moments attract each other if positioned in a “head-to-tail” pattern and experience mutual repulsion in “side-by-side” configuration. More broadly, the particles repel each other if their center-to-center vector is inclined to the field under the angles and are mutually attracted in all the other positions.
When such particles are enclosed in a spherical layer, which is the case of an MPS subjected to a strong field, the situations in the “equatorial” and “polar” zones of the membrane are qualitatively different. (For convenience, we liken an MPS to a globe whose poles are at the points where the direction of external field is parallel to the surface normal.) Indeed, as long as the MPS is sufficiently large , those MNPs that inhabit the equatorial zone, are in quite favorable situation for building meridional chains of the “head-to-tail” structure. Meanwhile, for those which at zero field occupied the near-polar zone, the situation strongly depends on the curvature of the layer.
At high curvature (small MPS), virtually all feasible center-to-center vectors fall outside the
interval. This implies that the formerly “polar” particles are attracted by the ends of the meridional chains, drift in their directions, and, thus, deplete the polar zone. At low curvature (large MPS), for a notable number of particles in the near-polar zone have their center-to-center vectors inside the
interval and, thus, experience mutual repulsion. Instead of joining long meridional chains, those MNPs would be repelled by their ends and would stably dwell in the polar zone as single entities or very short weakly linked aggregates. An illustration for this conclusion is given by snapshots in
Figure 6.
Evidently, those non-chained particles do not contribute to the stretching effect and by that reduce to some extent the number and/or length of the formed chains. Moreover, the repulsion exerted by those “polar” particles on the nearly-situated chains should extend the MPS in the direction transverse to the field direction and, albeit weakly, but also contribute to diminution of the field-induced stretching of larger MPSs. In
Appendix A we propose a “toy” model that justifies the effect of this chain-length reduction on the size-dependent magnetic deformation of MPSs.
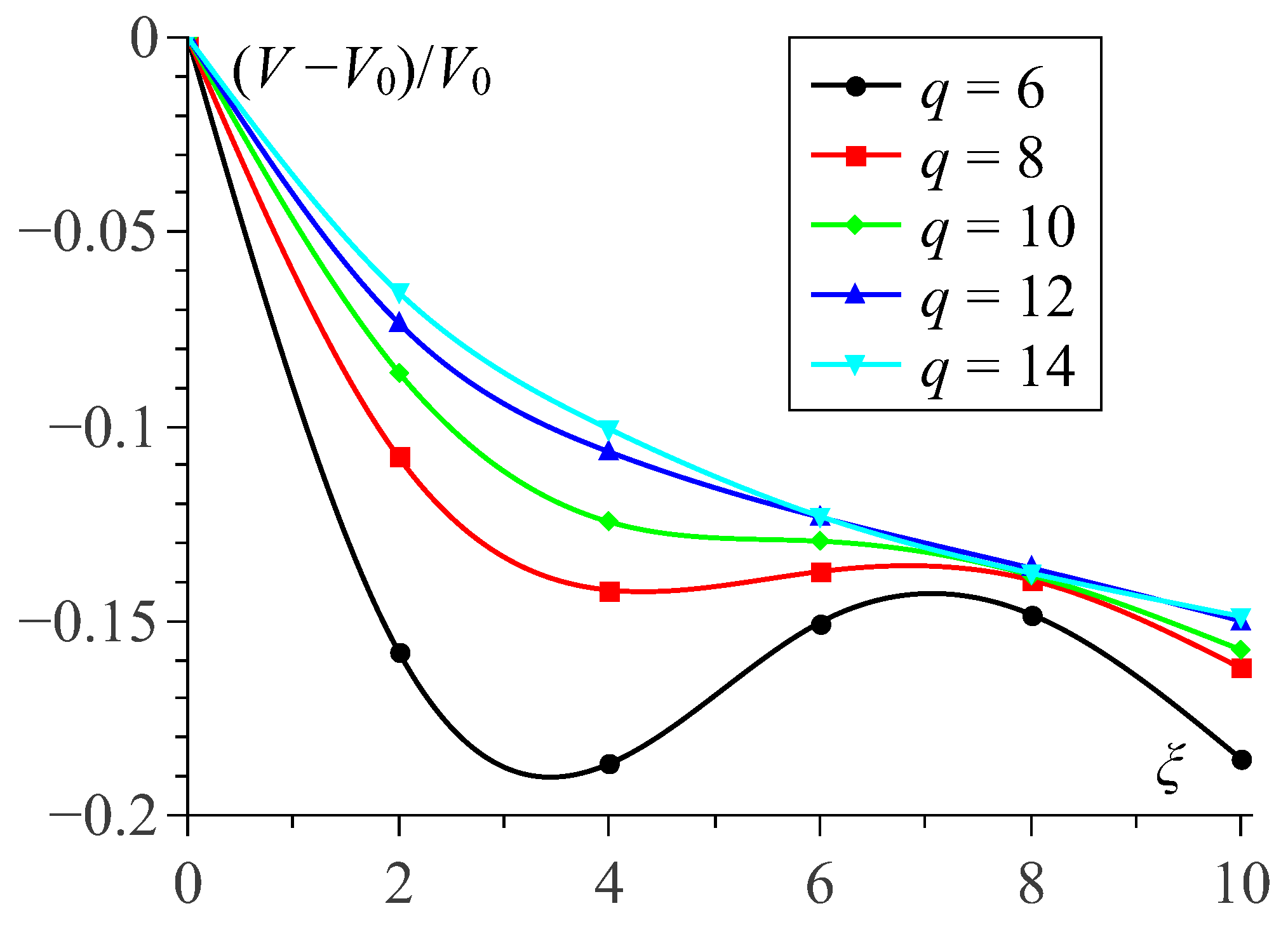
Another effect that is worth of discussion is the non-monotonic field dependence of the inner volume of small polymersomes, see
Figure 5. In general, as it is could be shown analytically, when a sphere is deformed to spheroid under condition of constancy of its lateral area, the “volume defect” is always negative. Therefore, the found negative volume change, see
Figure 5, confirms the assumption of high surface tension of the membrane shells. Looking to details, we surmise that the initial stretching of the MPS in the low field range (
to
), see
Figure 3 (
a), where the chains are very curvilinear, is due to orientation of some chain fragments without breaking their overall structure arrangement.
In small polymersomes, on further growth of the field (
to
), the structure rearrangement requires numerous breaks of the formerly existing chains. When the extensive chain rupture takes place, the particle structure becomes more loose, and this transformation, although not completely (see curve for
in
Figure 5), but to some extent reduces the volume defect. As soon as the chain fragments unite in a new conformations which are plausible for making quasi-meridional lines, the diminution of
V resumes. Finally, the field-induced restructuring results in building up inside the membrane a barrel-like superstructure (we remind of the afore-mentioned effect of depleting the polar zones) that makes a small MPS to efficiently stretch along the field direction, see
Figure 3c. In large polymersomes, the already existing chains have much more freedom for their conformational changes and perform them with almost no breaks. Therefore the initially formed aggregates gradually reorganize in long-chain patterns; because of that, in such an MPS compression of the inner cavity goes in monotonic way, see plots for
and
in
Figure 5 and
Figure 3d–f.