Coherent Optical Transduction of Suspended Microcapillary Resonators for Multi-Parameter Sensing Applications
Abstract
1. Introduction
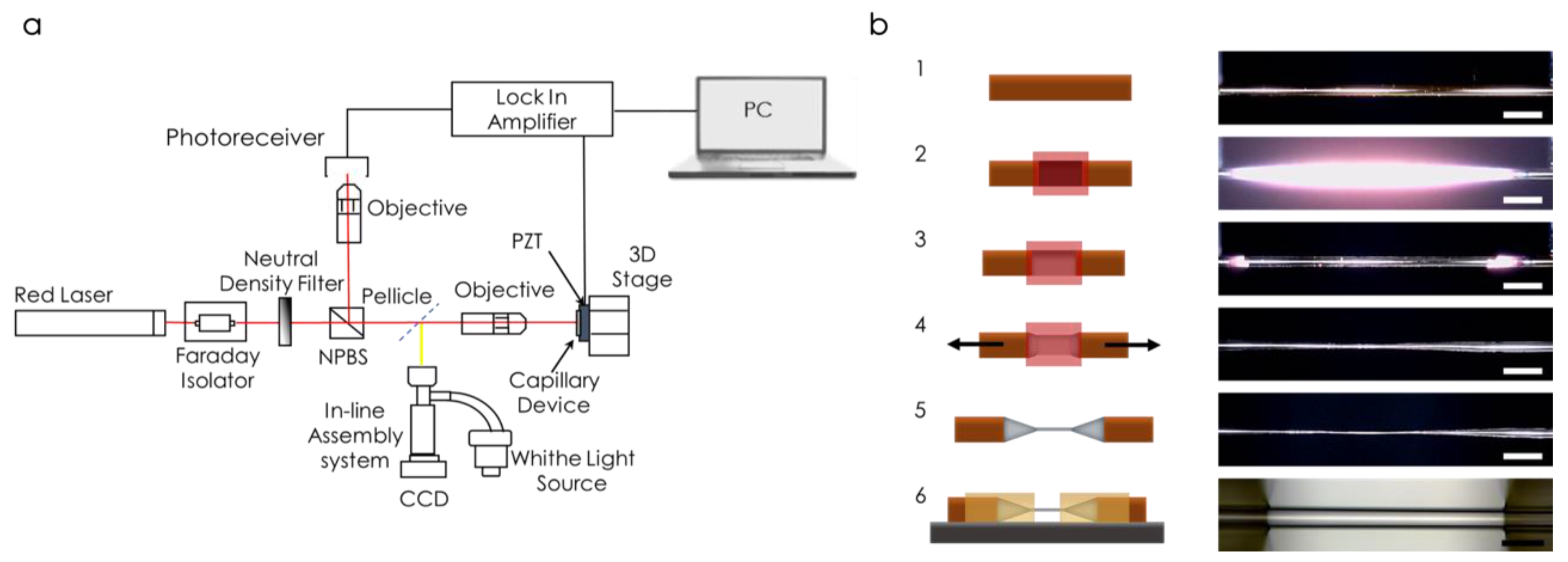
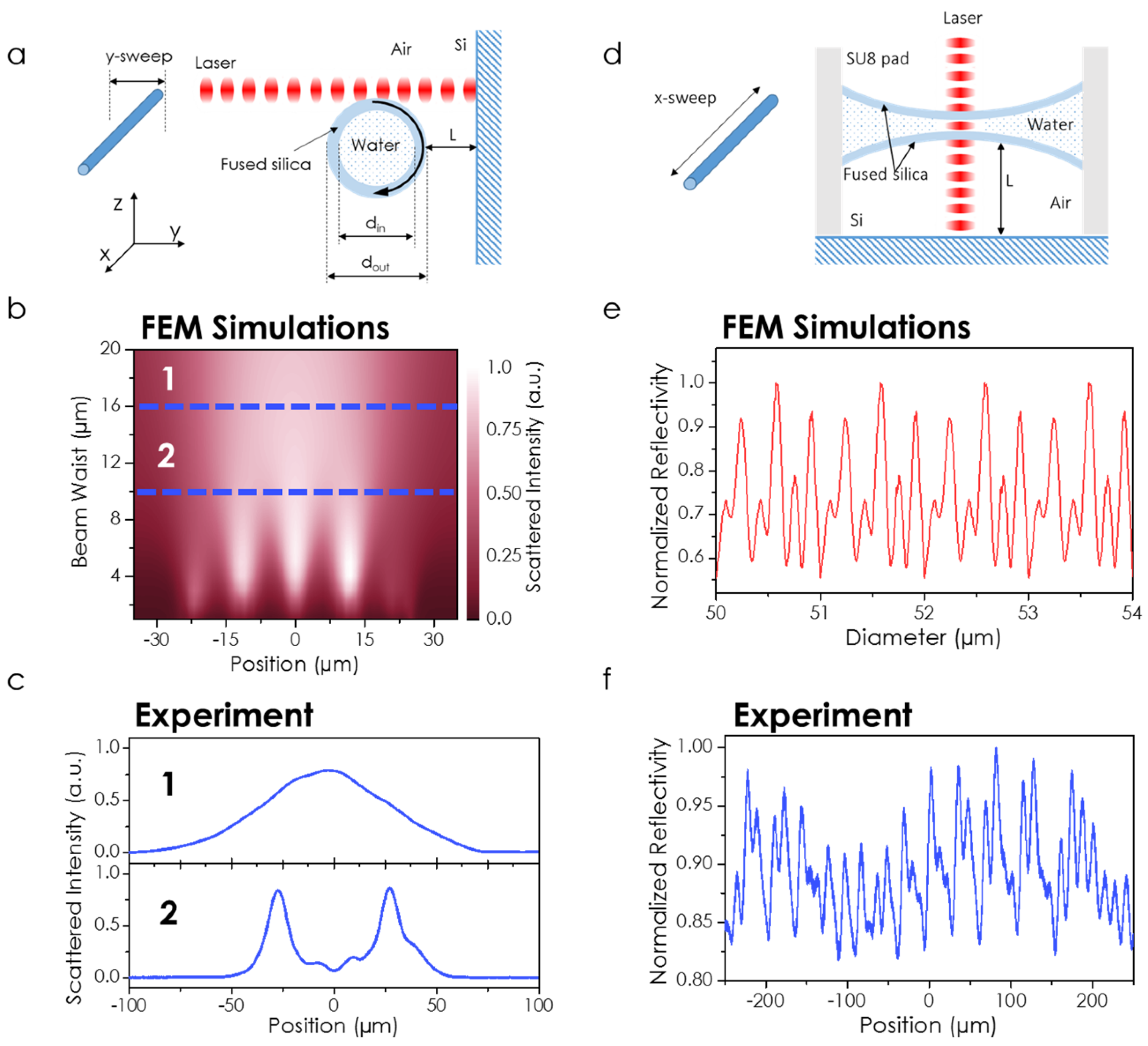
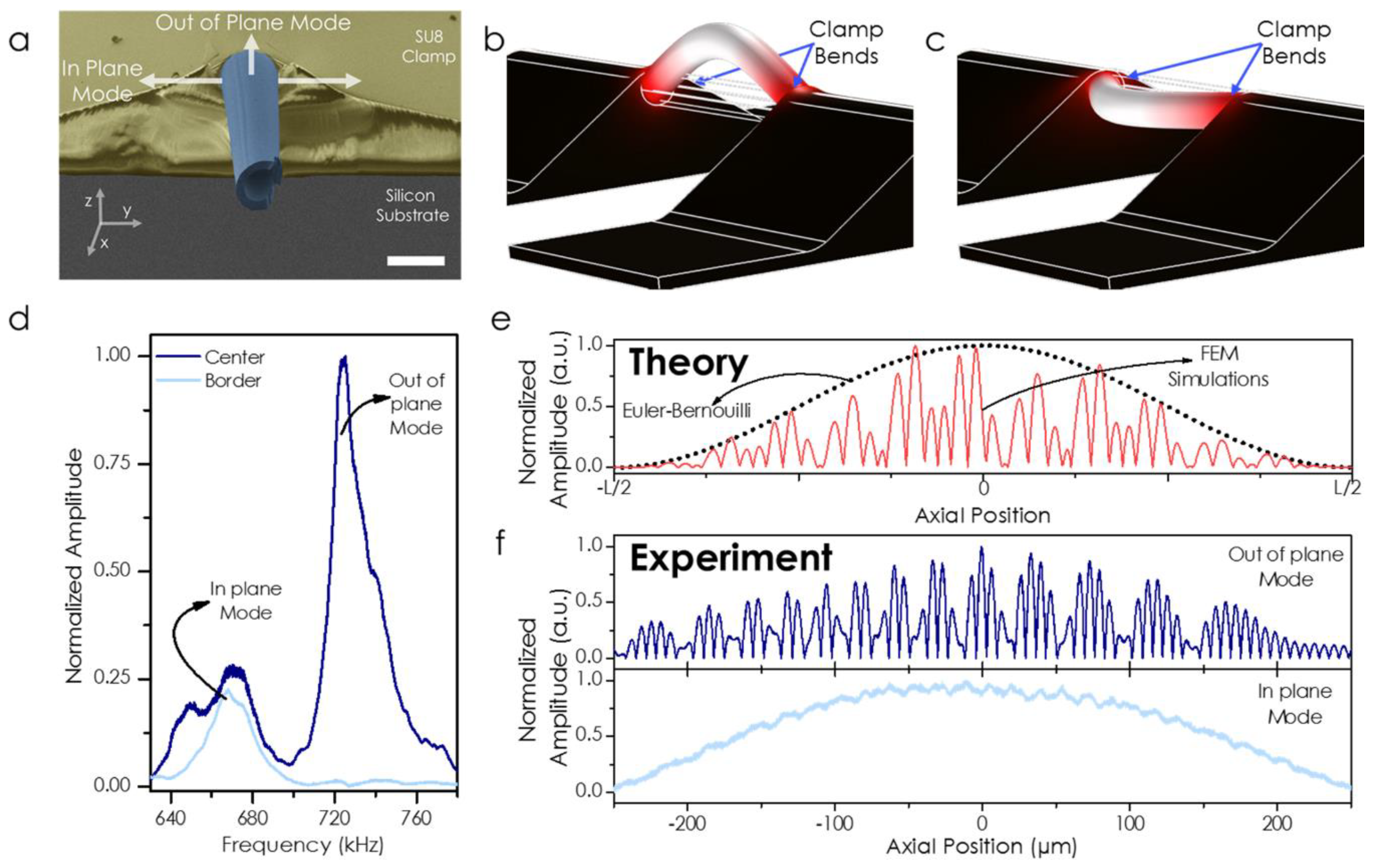
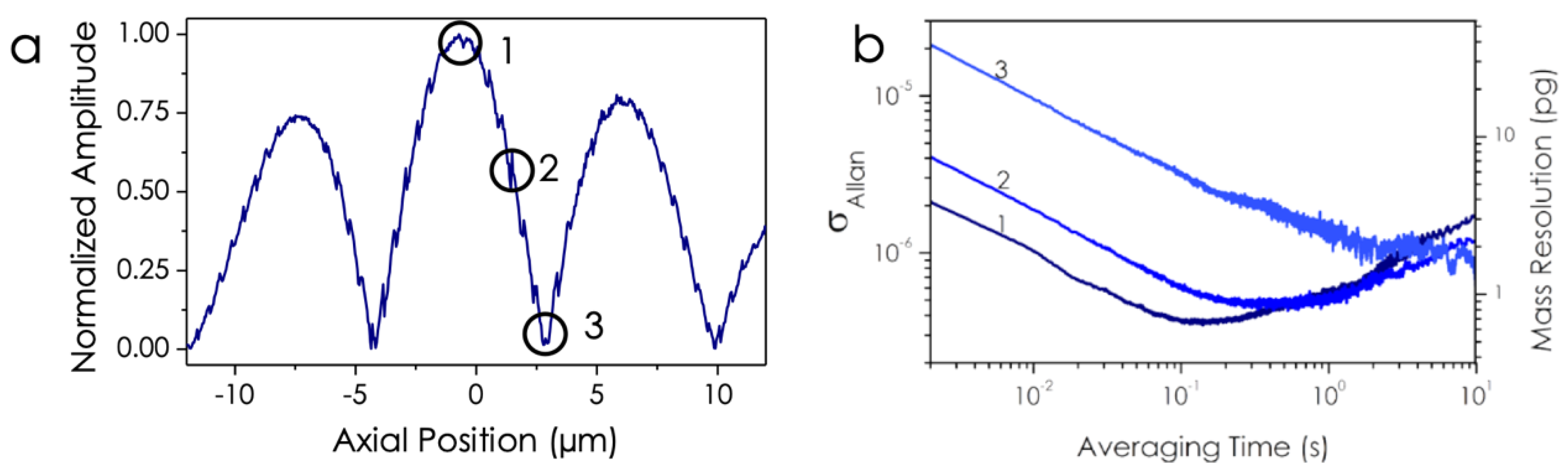
2. Results and Discussion
3. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Giraldo, J.P.; Wu, H.; Newkirk, G.M.; Kruss, S. Nanobiotechnology approaches for engineering smart plant sensors. Nat. Nanotechnol. 2019, 14, 541–553. [Google Scholar] [CrossRef] [PubMed]
- Vikesland, P.J. Nanosensors for water quality monitoring. Nat. Nanotechnol. 2018, 13, 651–660. [Google Scholar] [CrossRef] [PubMed]
- Srinivas, P.R.; Barker, P.; Srivastava, S. Nanotechnology in Early Detection of Cancer. Lab. Investig. 2002, 82, 657–662. [Google Scholar] [CrossRef] [PubMed]
- Kosaka, P.M.; Pini, V.; Ruz, J.J.; da Silva, R.A.; Gonzalez, M.U.; Ramos, D.; Calleja, M.; Tamayo, J. Detection of cancer biomarkers in serum using a hybrid mechanical and optoplasmonic nanosensor. Nat. Nanotechnol. 2014, 9, 1047–1053. [Google Scholar] [CrossRef]
- Barry, R.C.; Lin, Y.; Wang, J.; Liu, G.; Timchalk, C.A. Nanotechnology-based electrochemical sensors for biomonitoring chemical exposures. J. Expo. Sci. Environ. Epidemiol. 2009, 19, 1–18. [Google Scholar] [CrossRef]
- Rugar, D.; Budakian, R.; Mamin, H.J.; Chui, B.W. Single spin detection by magnetic resonance force microscopy. Nature 2004, 430, 329. [Google Scholar] [CrossRef]
- Li, M.; Tang, H.X.; Roukes, M.L. Ultra-sensitive NEMS-based cantilevers for sensing, scanned probe and very high-frequency applications. Nat. Nanotechnol. 2007, 2, 114–120. [Google Scholar] [CrossRef]
- Garcia-Sanchez, D.; van der Zande, A.M.; Paulo, A.S.; Lassagne, B.; McEuen, P.L.; Bachtold, A. Imaging mechanical vibrations in suspended graphene sheets. Nano Lett. 2008, 8, 1399–1403. [Google Scholar] [CrossRef]
- Ramos, D.; Gil-Santos, E.; Malvar, O.; Llorens, J.M.; Pini, V.; San Paulo, A.; Calleja, M.; Tamayo, J. Silicon nanowires: Where mechanics and optics meet at the nanoscale. Sci. Rep. 2013, 3, 3445. [Google Scholar] [CrossRef] [PubMed]
- Binnig, G.; Quate, C.F.; Gerber, C. Atomic force microscope. Phys. Rev. Lett. 1986, 56, 930–933. [Google Scholar] [CrossRef] [PubMed]
- Collaboration, L.S.; Virgo, C.; Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abernathy, M.R.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; et al. Observation of gravitational waves from a binary black hole merger. Phys. Rev. Lett. 2016, 116, 061102. [Google Scholar] [CrossRef]
- Ramos, D.; Tamayo, J.; Mertens, J.; Calleja, M. Photothermal excitation of microcantilevers in liquids. J. Appl. Phys. 2006, 99, 124904. [Google Scholar] [CrossRef]
- Ramos, D.; Mertens, J.; Calleja, M.; Tamayo, J. Phototermal self-excitation of nanomechanical resonators in liquids. Appl. Phys. Lett. 2008, 92, 173108. [Google Scholar] [CrossRef]
- Chan, J.; Alegre, T.P.M.; Safavi-Naeini, A.H.; Hill, J.T.; Krause, A.; Gröblacher, S.; Aspelmeyer, M.; Painter, O. Laser cooling of a nanomechanical oscillator into its quantum ground state. Nature 2011, 478, 89–92. [Google Scholar] [CrossRef]
- Metzger, C.H.; Karrai, K. Cavity cooling of a microlever. Nature 2004, 432, 1002–1005. [Google Scholar] [CrossRef]
- Eichenfield, M.; Chan, J.; Camacho, R.M.; Vahala, K.J.; Painter, O. Optomechanical crystals. Nature 2009, 462, 78–82. [Google Scholar] [CrossRef]
- Aspelmeyer, M.; Kippenberg, T.J.; Marquardt, F. Cavity optomechanics. Rev. Mod. Phys. 2014, 86, 1391–1452. [Google Scholar] [CrossRef]
- Kippenberg, T.J.; Vahala, K.J. Cavity optomechanics: Back-action at the mesoscale. Science 2008, 321, 1172. [Google Scholar] [CrossRef]
- Cleland, A. Photons refrigerating phonons. Nat. Phys. 2009, 5, 458–460. [Google Scholar] [CrossRef]
- O’Connell, A.D.; Hofheinz, M.; Ansmann, M.; Bialczak, R.C.; Lenander, M.; Lucero, E.; Neeley, M.; Sank, D.; Wang, H.; Weides, M.; et al. Quantum ground state and single-phonon control of a mechanical resonator. Nature 2010, 464, 697–703. [Google Scholar] [CrossRef]
- Ramos, D.; Frank, I.W.; Deotare, P.B.; Bulu, I.; Lončar, M. Non-linear mixing in coupled photonic crystal nanobeam cavities due to cross-coupling opto-mechanical mechanisms. Appl. Phys. Lett. 2014, 105, 181121. [Google Scholar] [CrossRef]
- Gil-Santos, E.; Baker, C.; Nguyen, D.T.; Hease, W.; Gomez, C.; Lemaître, A.; Ducci, S.; Leo, G.; Favero, I. High-frequency nano-optomechanical disk resonators in liquids. Nat. Nanotechnol. 2015, 10, 810. [Google Scholar] [CrossRef] [PubMed]
- Armani, D.K.; Kippenberg, T.J.; Spillane, S.M.; Vahala, K.J. Ultra-high-Q toroid microcavity on a chip. Nature 2003, 421, 925–928. [Google Scholar] [CrossRef] [PubMed]
- Thompson, J.D.; Zwickl, B.M.; Jayich, A.M.; Marquardt, F.; Girvin, S.M.; Harris, J.G.E. Strong dispersive coupling of a high-finesse cavity to a micromechanical membrane. Nature 2008, 452, 72–75. [Google Scholar] [CrossRef] [PubMed]
- Ramos, D.; Gil-Santos, E.; Pini, V.; Llorens, J.M.; Fernández-Regúlez, M.; San Paulo, Á.; Calleja, M.; Tamayo, J. Optomechanics with silicon nanowires by harnessing confined electromagnetic modes. Nano Lett. 2012, 12, 932–937. [Google Scholar] [CrossRef] [PubMed]
- Ramos, D.; Malvar, O.; Davis, Z.J.; Tamayo, J.; Calleja, M. Nanomechanical plasmon spectroscopy of single gold nanoparticles. Nano Lett. 2018, 18, 7165–7170. [Google Scholar] [CrossRef] [PubMed]
- Chien, M.-H.; Brameshuber, M.; Rossboth, B.K.; Schütz, G.J.; Schmid, S. Single-molecule optical absorption imaging by nanomechanical photothermal sensing. Proc. Natl. Acad. Sci. USA 2018, 115, 11150. [Google Scholar] [CrossRef] [PubMed]
- Kosaka, P.M.; Calleja, M.; Tamayo, J. Optomechanical devices for deep plasma cancer proteomics. Semin. Cancer Biol. 2018, 52, 26–38. [Google Scholar] [CrossRef]
- Hyun Kim, K.; Bahl, G.; Lee, W.; Liu, J.; Tomes, M.; Fan, X.; Carmon, T. Cavity optomechanics on a microfluidic resonator with water and viscous liquids. Light Sci. Appl. 2013, 2, e110. [Google Scholar] [CrossRef]
- Pang, L.; Chen, H.M.; Freeman, L.M.; Fainman, Y. Optofluidic devices and applications in photonics, sensing and imaging. Lab Chip 2012, 12, 3543–3551. [Google Scholar] [CrossRef]
- Burg, T.P.; Godin, M.; Knudsen, S.M.; Shen, W.; Carlson, G.; Foster, J.S.; Babcock, K.; Manalis, S.R. Weighing of biomolecules, single cells and single nanoparticles in fluid. Nature 2007, 446, 1066–1069. [Google Scholar] [CrossRef] [PubMed]
- Burg, T.P.; Manalis, S.R. Suspended microchannel resonators for biomolecular detection. Appl. Phys. Lett. 2003, 83, 2698–2700. [Google Scholar] [CrossRef]
- Bahl, G.; Kim, K.H.; Lee, W.; Liu, J.; Fan, X.; Carmon, T. Brillouin cavity optomechanics with microfluidic devices. Nat. Commun. 2013, 4, 1994. [Google Scholar] [CrossRef]
- Suh, J.; Han, K.; Bahl, G. Imaging of acoustic pressure modes in opto-mechano-fluidic resonators with a single particle probe. Appl. Phys. Lett. 2018, 112, 071106. [Google Scholar] [CrossRef]
- Malvar, O.; Ramos, D.; Martínez, C.; Kosaka, P.; Tamayo, J.; Calleja, M. Highly sensitive measurement of liquid density in air using suspended microcapillary resonators. Sensors 2015, 15, 7650–7657. [Google Scholar] [CrossRef]
- Lee, D.; Kim, J.; Cho, N.-J.; Kang, T.; Kauh, S.; Lee, J. Pulled microcapillary tube resonators with electrical readout for mass sensing applications. Sci. Rep. 2016, 6, 33799. [Google Scholar] [CrossRef]
- Martín-Pérez, A.; Ramos, D.; Tamayo, J.; Calleja, M. Real-time particle spectrometry in liquid environment using microfluidic-nanomechanical resonators. In Proceedings of the 2019 20th International Conference on Solid-State Sensors, Actuators and Microsystems & Eurosensors XXXIII (TRANSDUCERS & EUROSENSORS XXXIII), Berlin, Germany, 23–27 June 2019; pp. 2146–2149. [Google Scholar]
- Pini, V.; Ramos, D.; Dominguez, C.M.; Ruz, J.J.; Malvar, O.; Kosaka, P.M.; Davis, Z.J.; Tamayo, J.; Calleja, M. Optimization of the readout of microdrum optomechanical resonators. Microelectron. Eng. 2017, 183–184, 37–41. [Google Scholar] [CrossRef]
- Tamayo, J.; Kosaka, P.M.; Ruz, J.J.; San Paulo, Á.; Calleja, M. Biosensors based on nanomechanical systems. Chem. Soc. Rev. 2013, 42, 1287–1311. [Google Scholar] [CrossRef]
- Sansa, M.; Sage, E.; Bullard, E.C.; Gély, M.; Alava, T.; Colinet, E.; Naik, A.K.; Villanueva, L.G.; Duraffourg, L.; Roukes, M.L.; et al. Frequency fluctuations in silicon nanoresonators. Nat. Nanotechnol. 2016, 11, 552. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Martín-Pérez, A.; Ramos, D.; Tamayo, J.; Calleja, M. Coherent Optical Transduction of Suspended Microcapillary Resonators for Multi-Parameter Sensing Applications. Sensors 2019, 19, 5069. https://doi.org/10.3390/s19235069
Martín-Pérez A, Ramos D, Tamayo J, Calleja M. Coherent Optical Transduction of Suspended Microcapillary Resonators for Multi-Parameter Sensing Applications. Sensors. 2019; 19(23):5069. https://doi.org/10.3390/s19235069
Chicago/Turabian StyleMartín-Pérez, Alberto, Daniel Ramos, Javier Tamayo, and Montserrat Calleja. 2019. "Coherent Optical Transduction of Suspended Microcapillary Resonators for Multi-Parameter Sensing Applications" Sensors 19, no. 23: 5069. https://doi.org/10.3390/s19235069
APA StyleMartín-Pérez, A., Ramos, D., Tamayo, J., & Calleja, M. (2019). Coherent Optical Transduction of Suspended Microcapillary Resonators for Multi-Parameter Sensing Applications. Sensors, 19(23), 5069. https://doi.org/10.3390/s19235069







