A New Design of an MOEMS Gyroscope Based on a WGM Microdisk Resonator
Abstract
1. Introduction
2. Structure of the MOEMS Gyroscope and Operational Principle of the MEMS Disk Resonator
2.1. Structure of the New MOEMS Gyroscope
2.2. Operational Principle of the MEMS Disk Resonator
3. Analysis and Simulation of the WGM Resonator
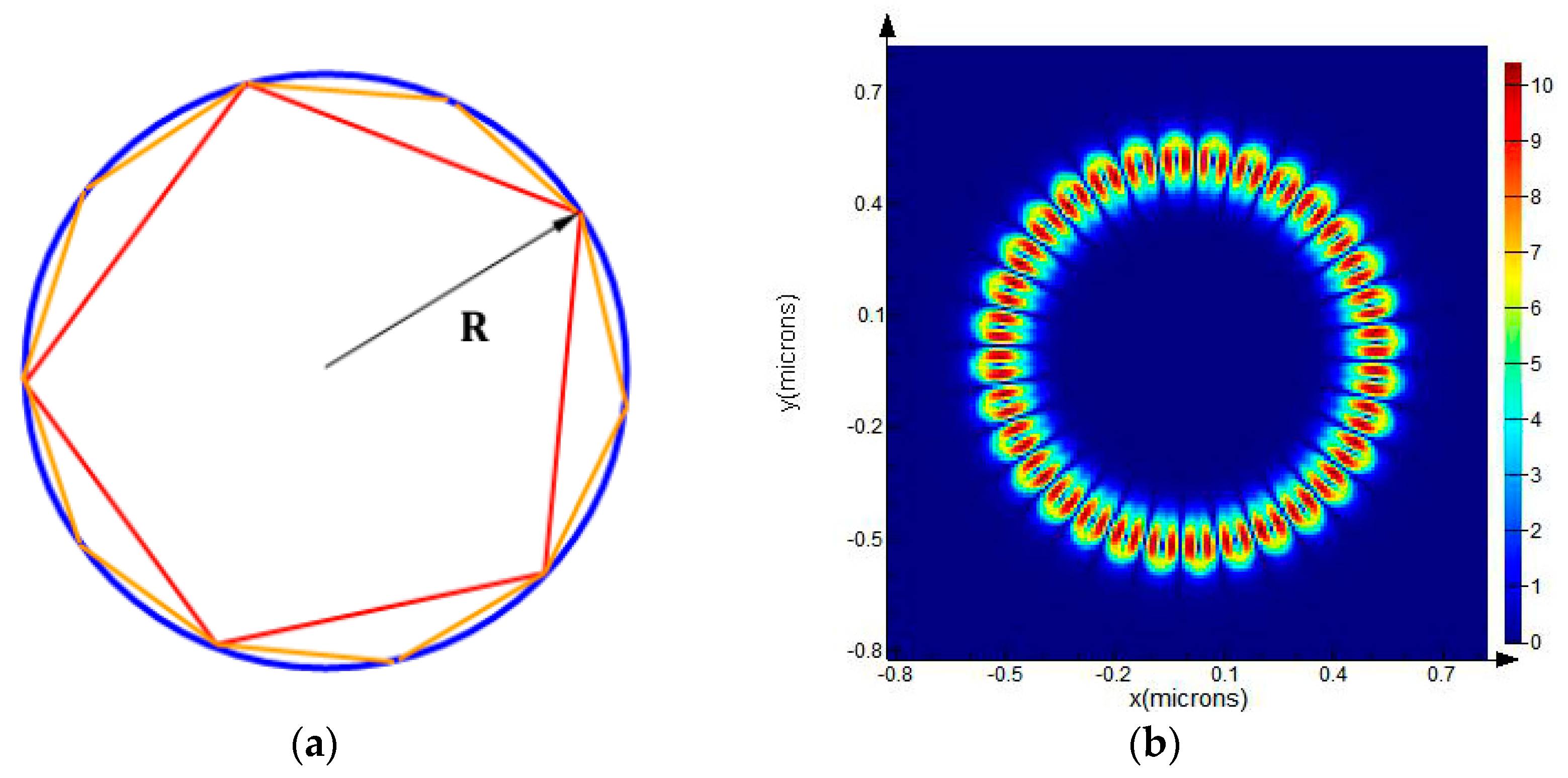
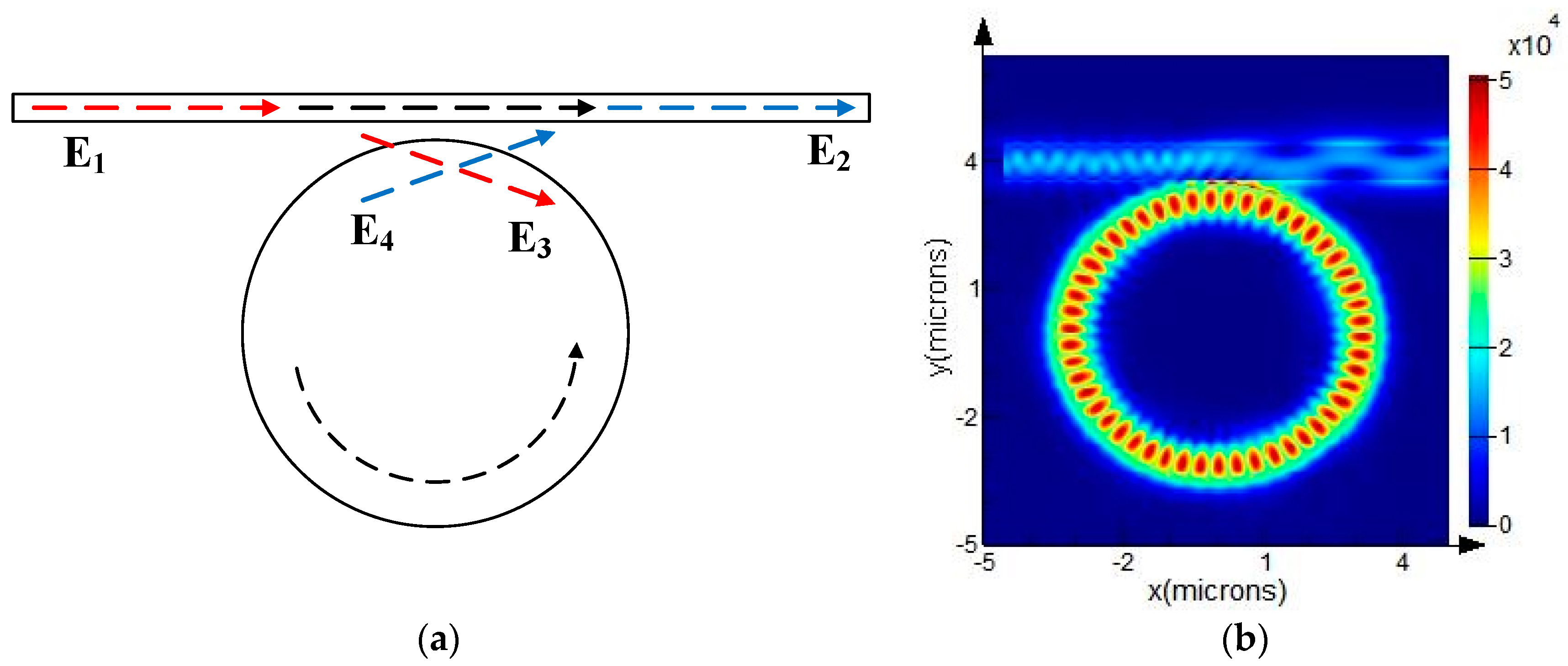
3.1. Operational Principle of the WGM Resonator
3.2. Approximation of the Modes in a WGM Disk Resonator
3.3. Quality Factor Q of the WGM Resonator
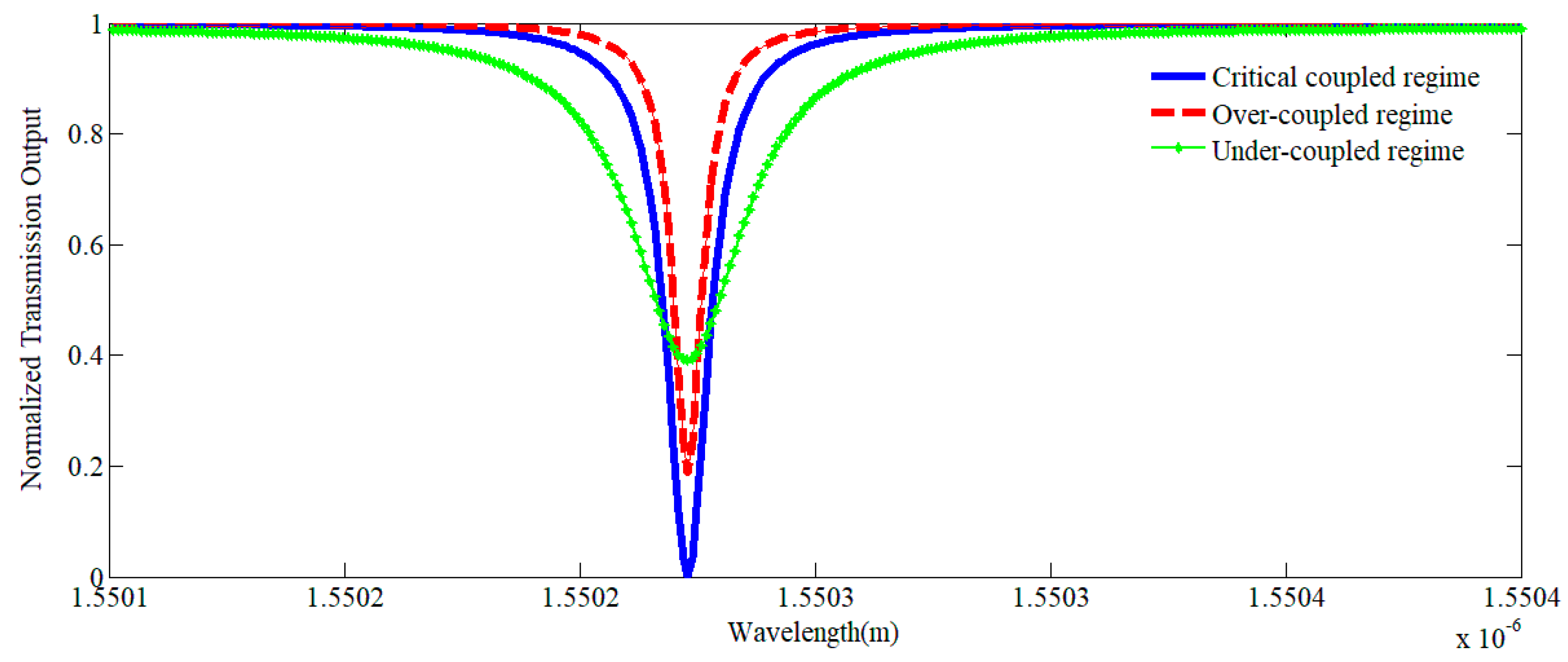
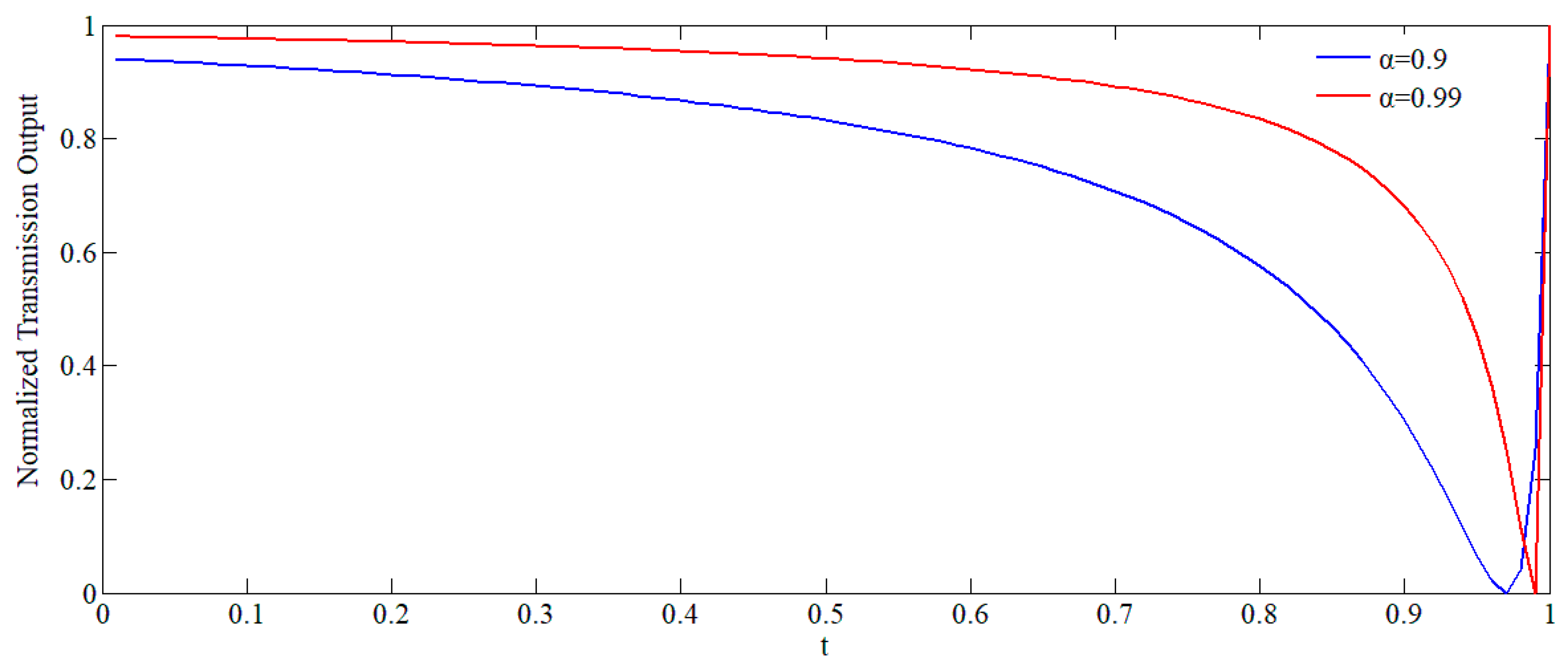
3.4. The Model of the Theoretical Approach of Single Waveguides Coupled to WGM Resonators
- (1)
- Under-coupled regime: When the waveguide is far from the resonator, the coupling is very weak. When the waveguide moves close to the resonator, the overlap of the waveguide mode and WGMs will increase. However, when |t| > α, the transmission T decreases continuously from unity and approaches zero.
- (2)
- Critical coupled regime: When the waveguide gets closer to the resonator such that |t| = α, the normalized transmission T is zero, which means that all of the input power is coupled to the resonator.
- (3)
- Over-coupled regime: When the gap between the waveguide and the resonator is further decreased, the overlap of the modes becomes larger and the normalized transmission T becomes greater than 0 again; this is called the over-coupled regime.
4. Analysis and Simulation of the MOEMS Gyroscope
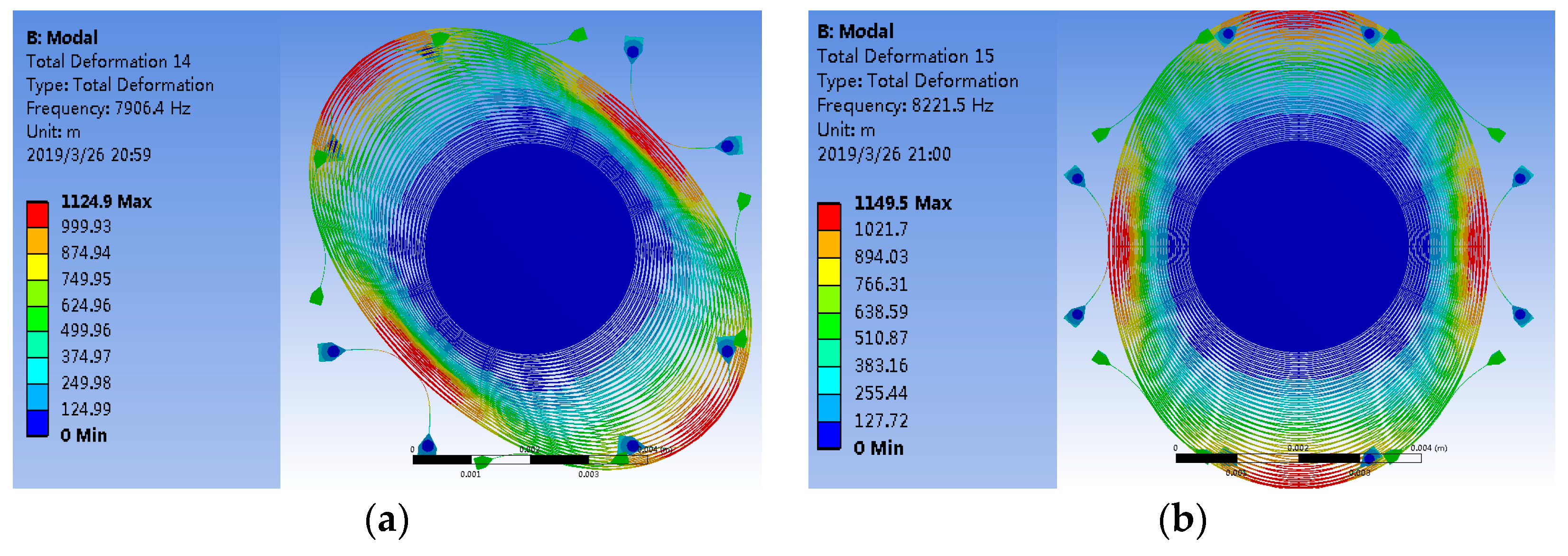
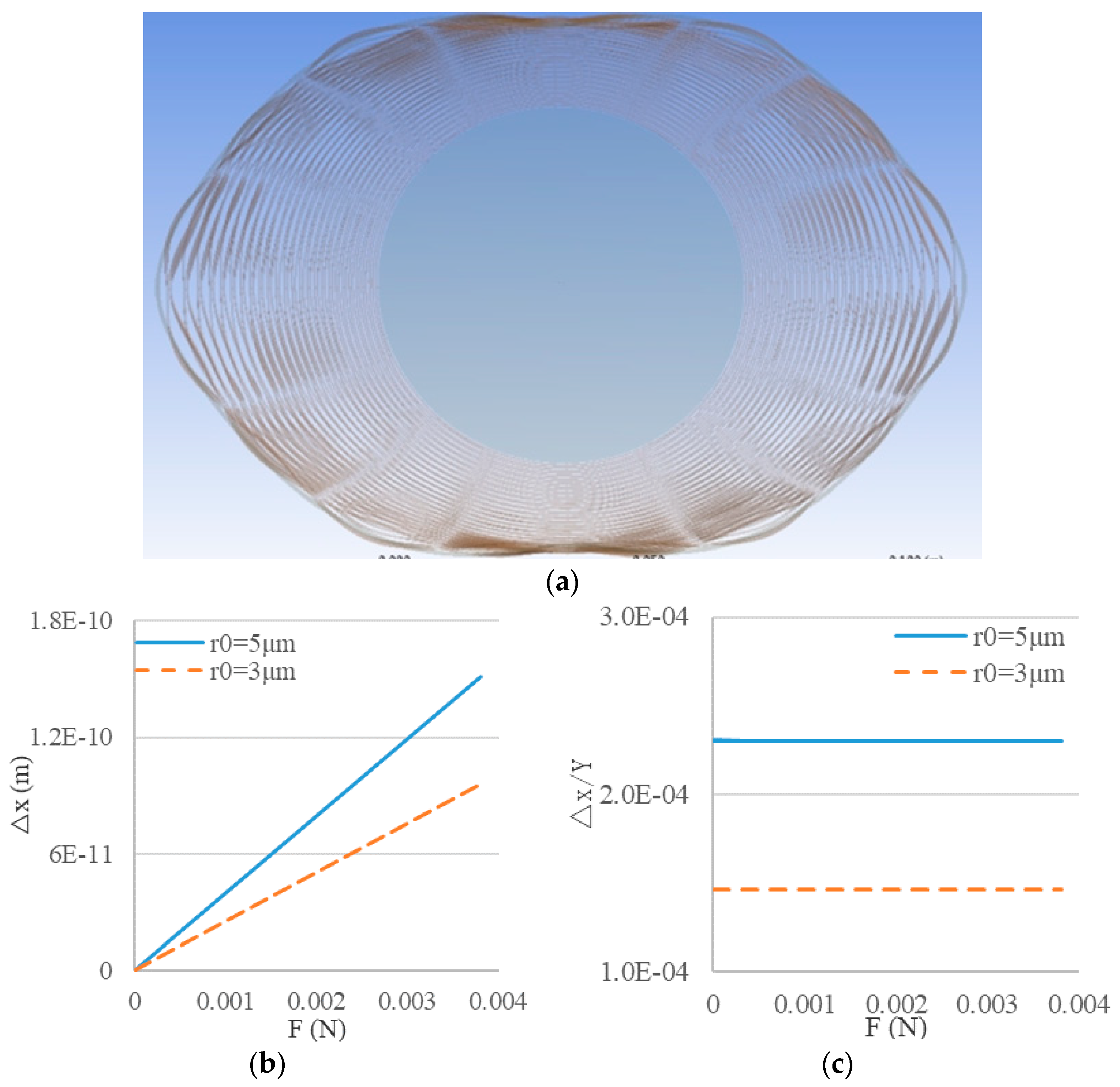
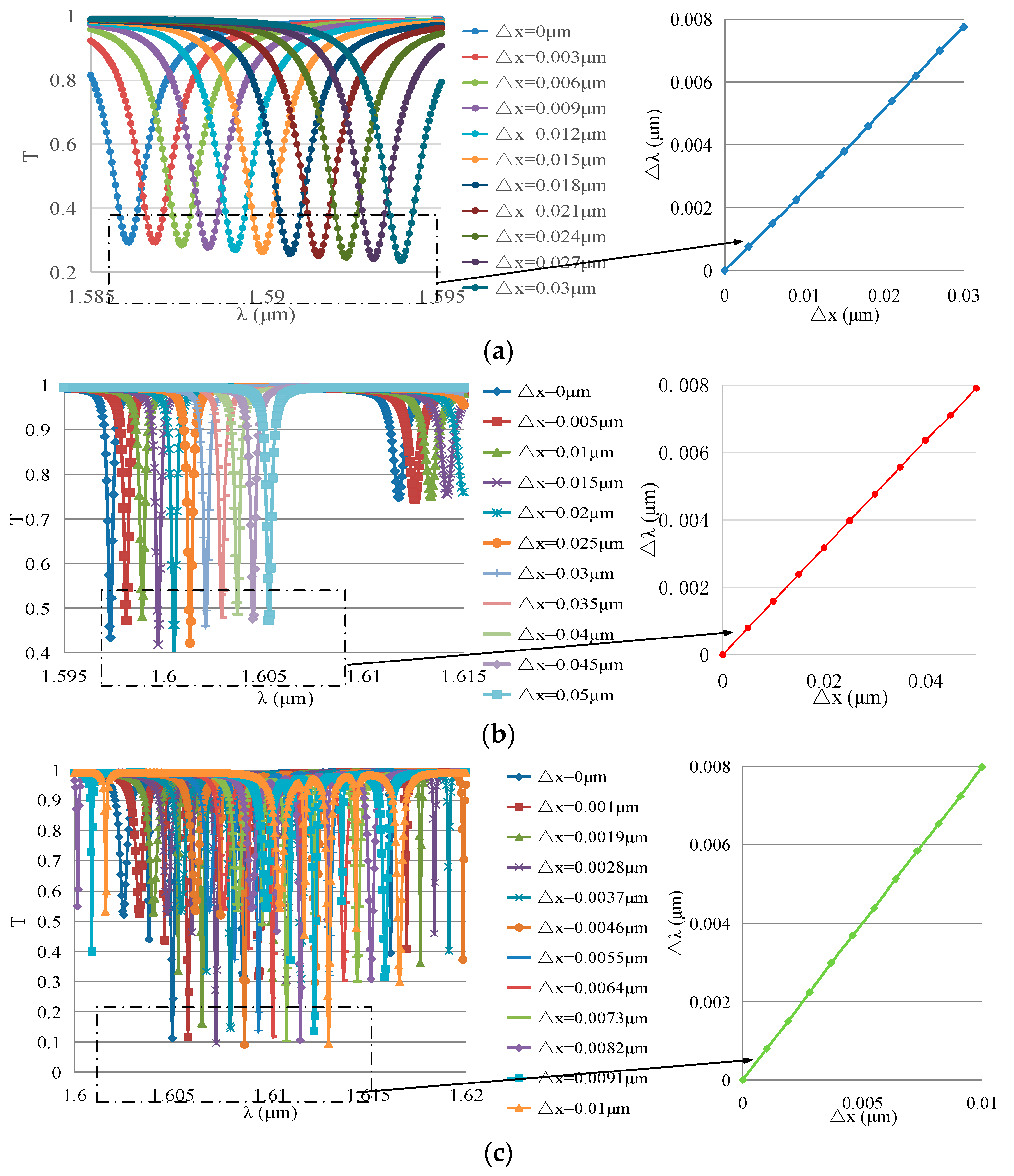
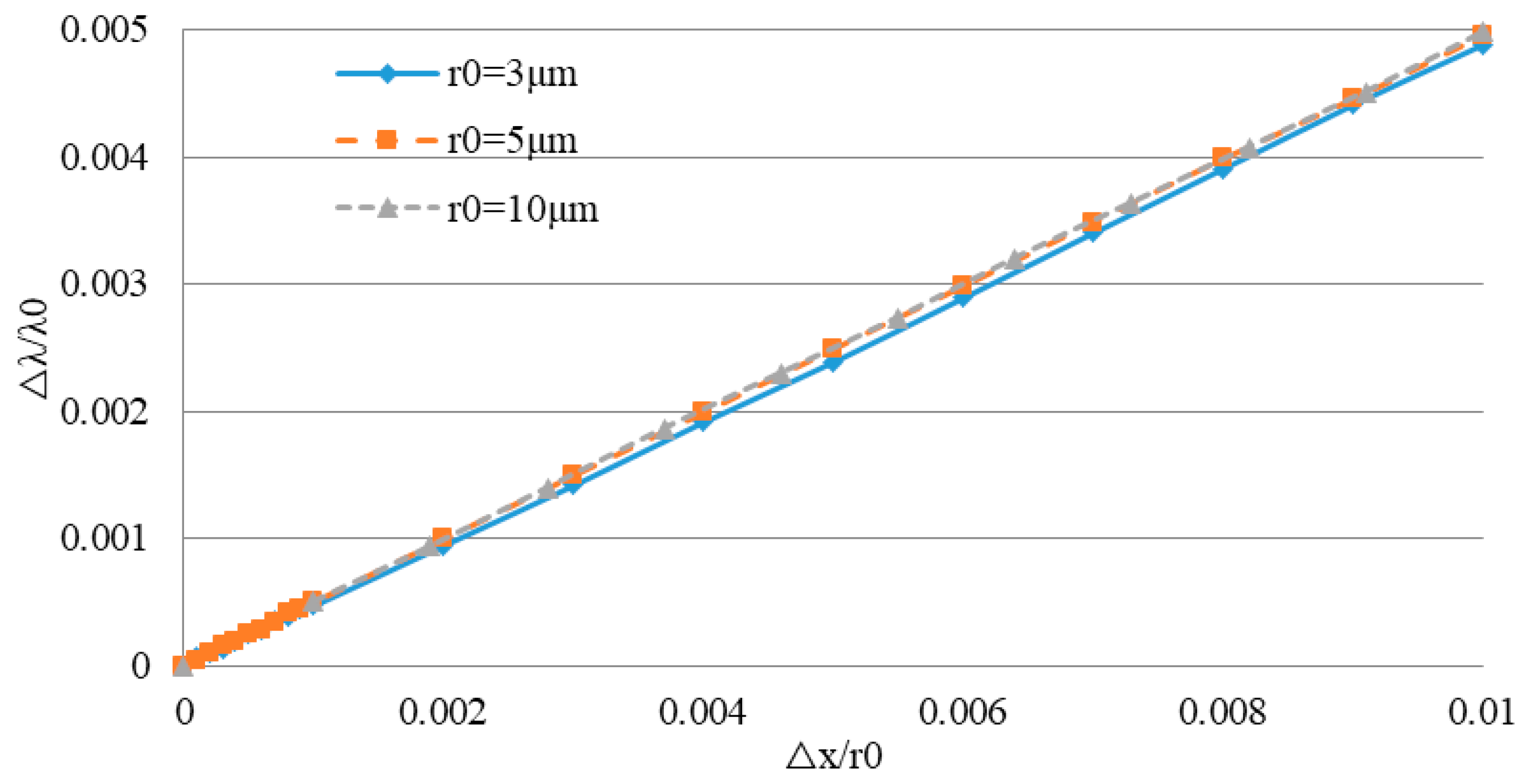
4.1. The Relationship between Frequency Shift and Deformation of the WGM Resonator
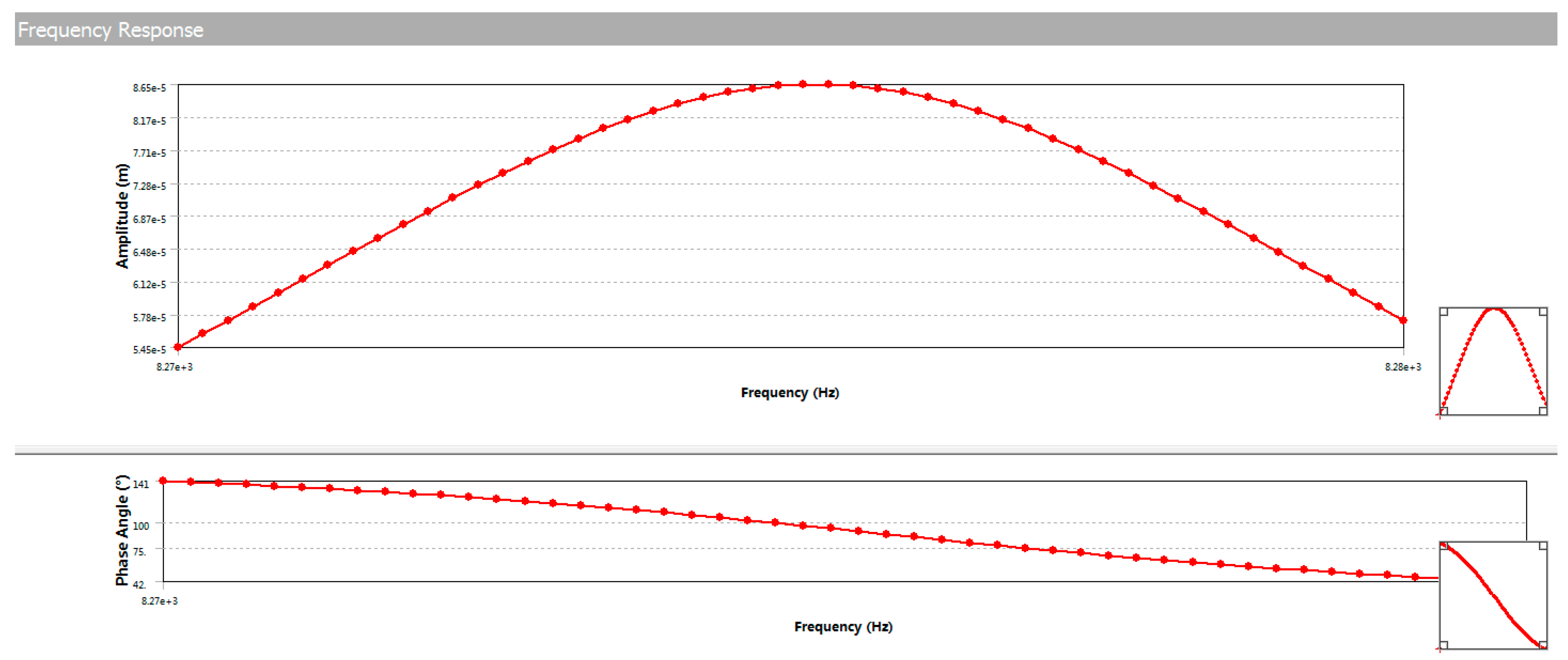
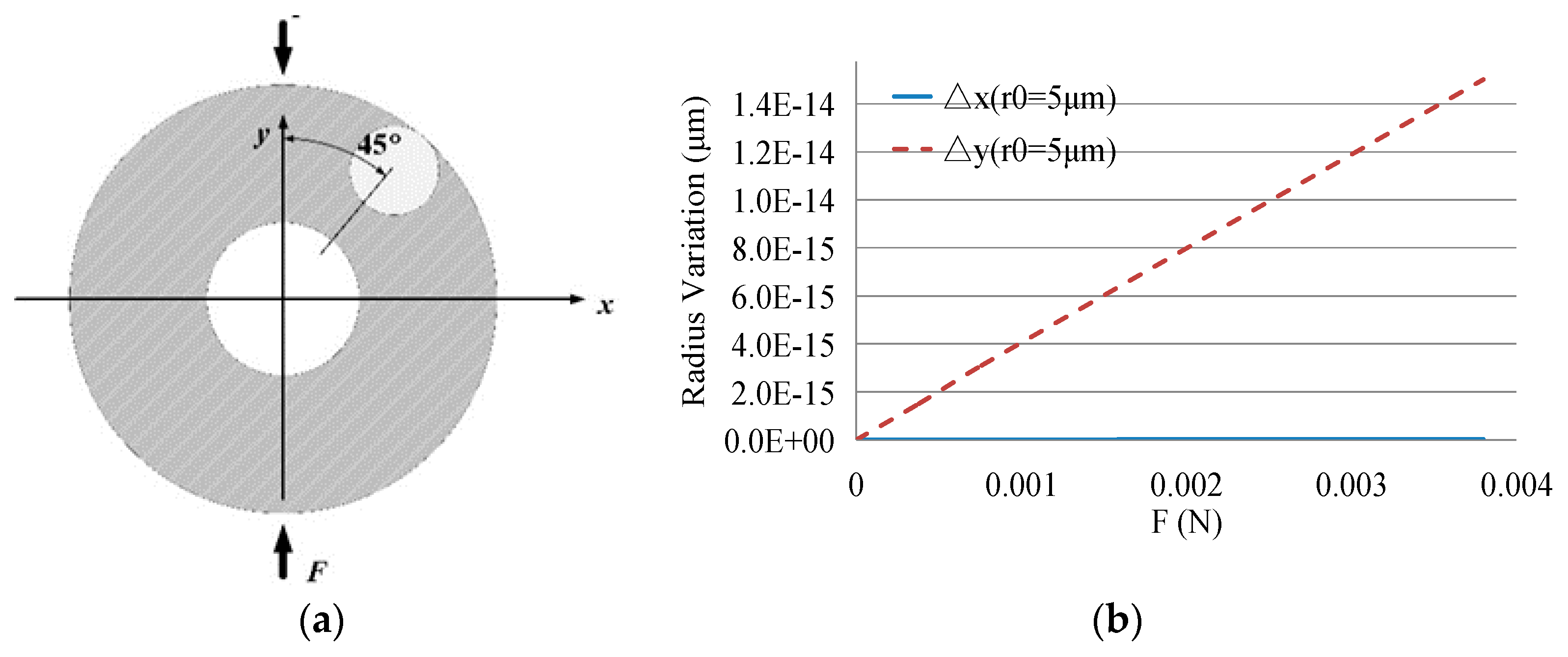
4.2. The Relationship between Deformation of the WGM Resonator and Stress on the MEMS Resonator
5. Simulation of the MOEMS Gyroscope
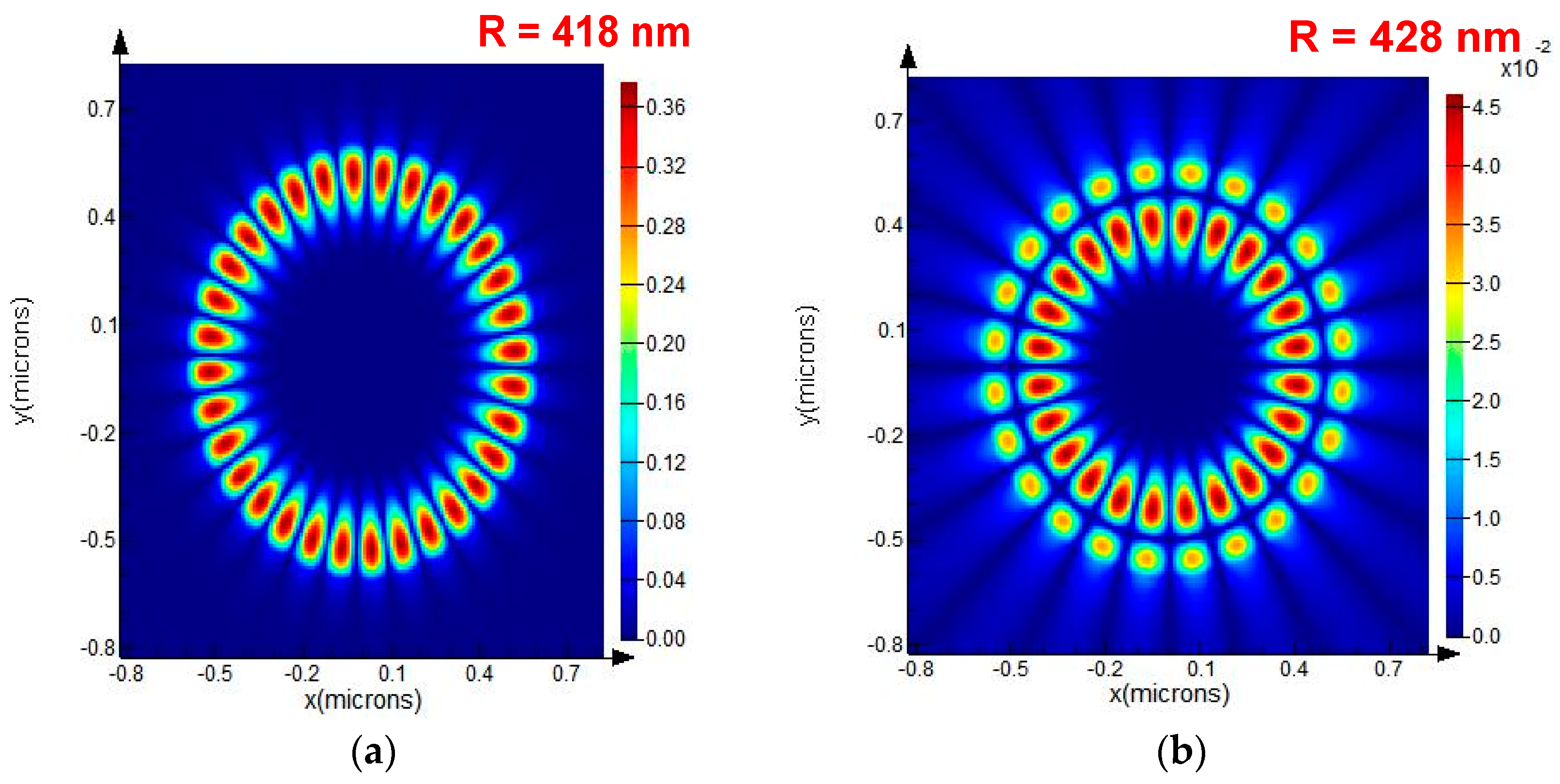
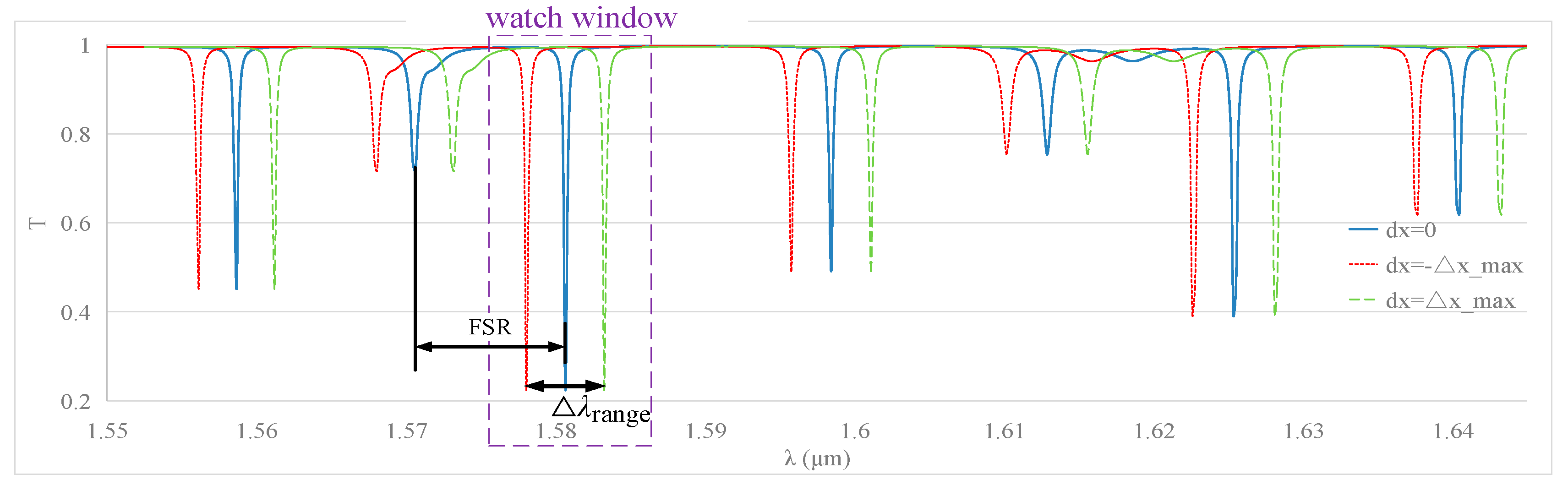
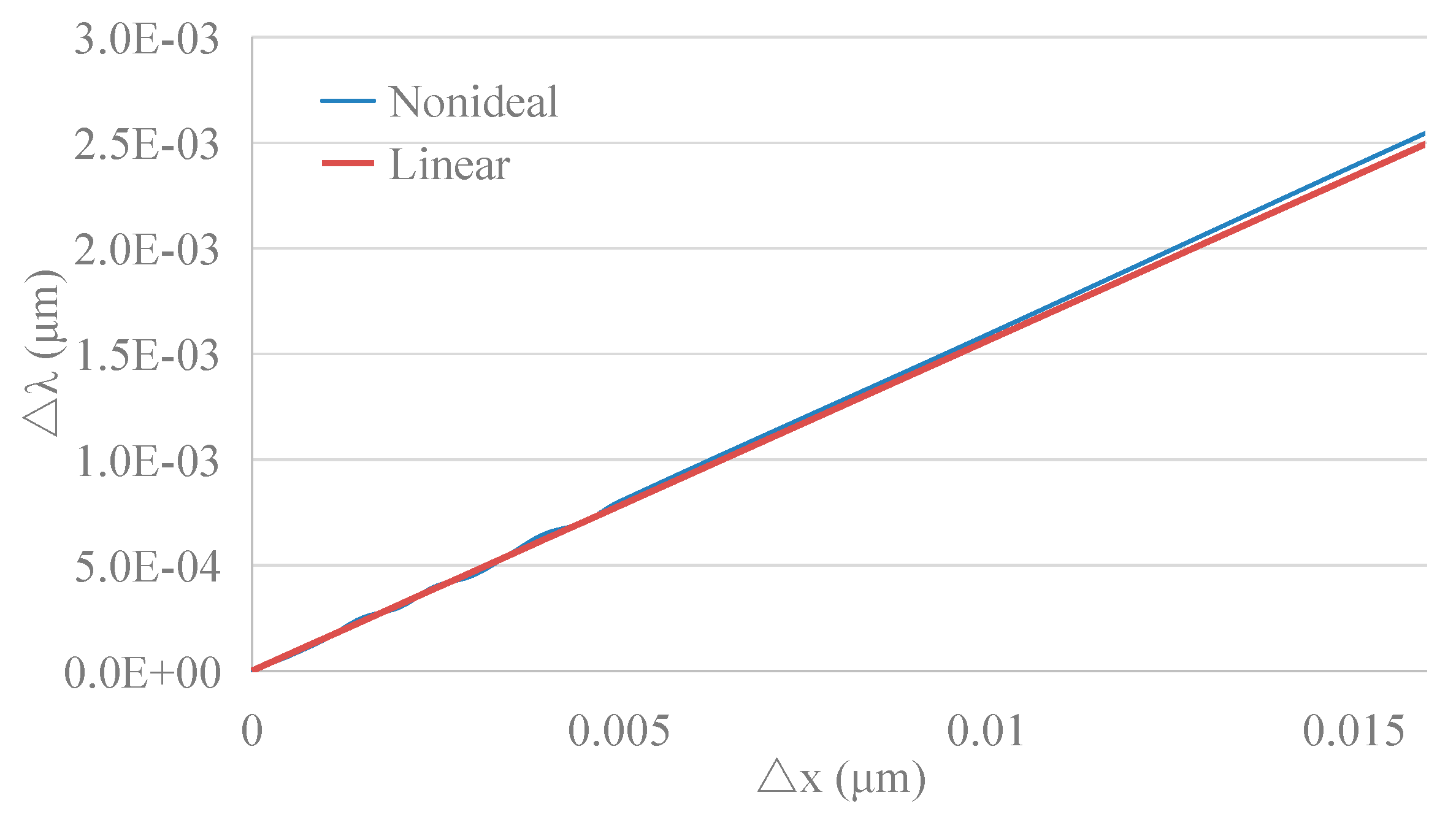
5.1. Simulation Analysis of the Resonant Wavelength Shift of a Deformed WGM Resonator
5.2. Key Specifications of the MOEMS Gyroscope
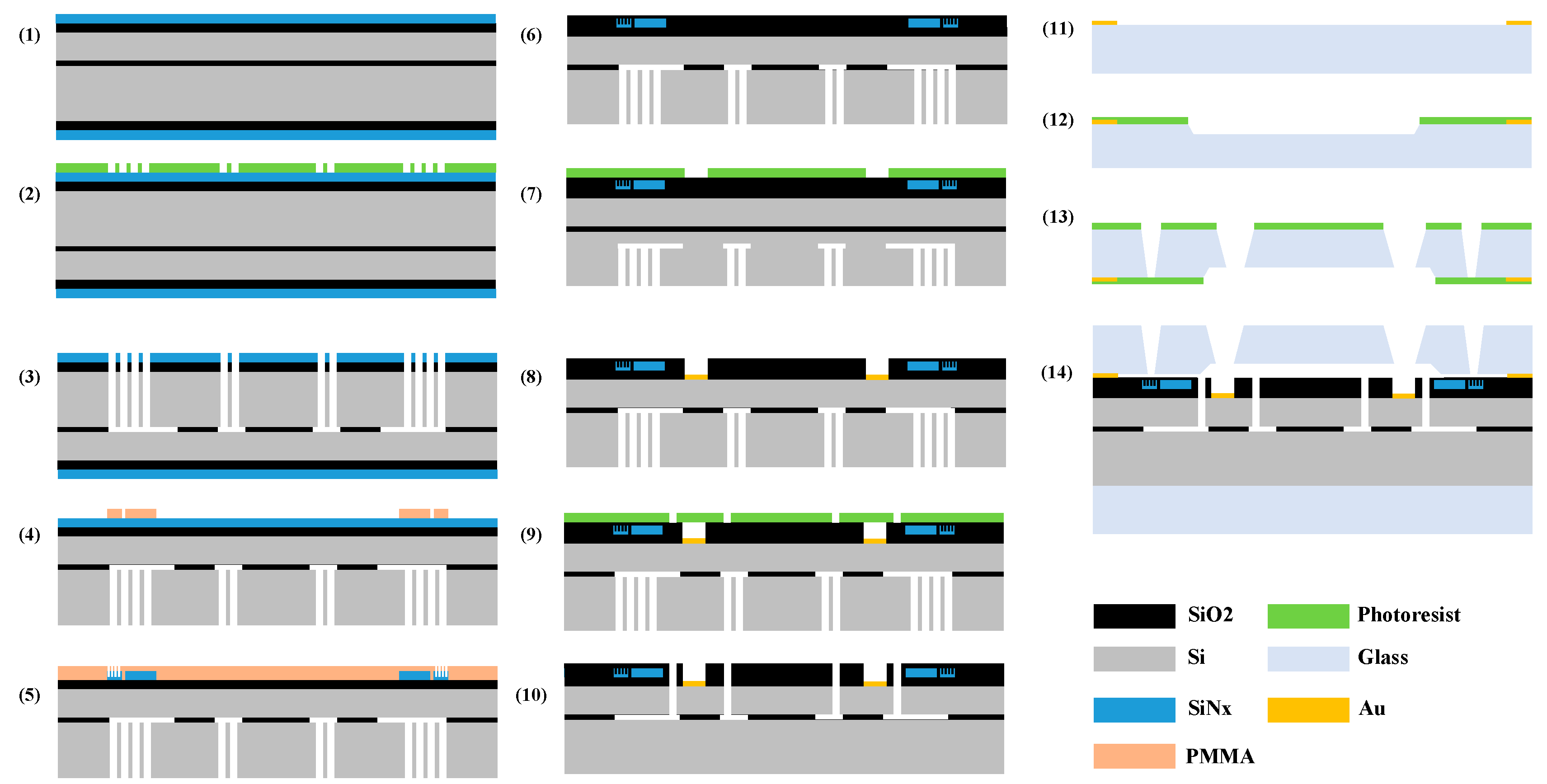
6. Process and Result of Fabrication
- (1)
- A 2 µm plasma-enhanced chemical vapor deposition (PECVD) silicon nitride (SiNx) layer was deposited on the top and bottom sides of the SOI wafer.
- (2)
- The photoresist was put on the bottom side of the wafer through spin coating and patterned by mask1 to define the holes in the handle layer.
- (3)
- The through-holes in the handle layer were formed through deep reactive ion etching (DRIE), and then part of the buried oxide layer was etched by the input KOH vapor from the holes.
- (4)
- The bottom SiO2 layer and SiNx layer were polished after Step (3), then a layer of PMMA was applied on the top SiNx layer. After that, the pattern of the optical disk resonator and the wave guide was defined using e-beam lithography.
- (5)
- The remaining PMMA was washed off after the WGM resonator and the wave guide were created through reactive ion etching (RIE), and then a new PMMA layer was applied on the same side. Next, the pattern of the grating coupler was defined on the PMMA using e-beam lithography, and the coupler was made with the help of inductively coupled plasma (ICP) etching.
- (6)
- The PMMA was cleaned off after Step (5), and then another SiO2 layer was deposited on the front of the wafer to protect the optical devices made in the last step.
- (7)
- The photoresist was spun on the deposited SiO2 layer, and then the pattern of metal pads was defined on the photoresist using mask2.
- (8)
- With the pattern from Step (7), the position of the pad in the device layer was exposed after wet etching, and then 30/300 nm thick Cr/Au was deposited in the pattern to form the pads through a lift-off process. After that, the remaining photoresist was cleaned off the wafer.
- (9)
- We spun the photoresist again and defined the pattern of the MEMS disk resonator in the photoresist using mask3.
- (10)
- The resonator structure and the electrodes were simultaneously released using the Bosch ICP.
- (11)
- The pattern of the bonding point and the metal envelope wall in the glass, which would be used for gold silicon bonding, was created. As in Steps (7) and (8), the pattern was defined using mask4 and the object was formed through a lift-off process.
- (12)
- We spun the photoresist on the glass and then defined the pattern of the cavity using mask5, then wet etched the cavity in the glass.
- (13)
- We spun the photoresist on another side of the glass and defined the pattern of the through holes using mask6, then wet etched the holes in the glass.
- (14)
- The glass cap was bonded with the SOI through gold–silicon bonding with the bonding point and the metal envelope wall. Then, another glass wafer was bonded on the bottom of the SOI wafer using the anodic bonding method.
7. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Krishnamoorthy, U.; Olsson, R.H.; Bogart, G.R.; Baker, M.S.; Carr, D.W.; Swiler, T.P.; Clews, P.J. In-plane MEMS-based nano-g accelerometer with sub-wavelength optical resonant sensor. Sens. Actuators A Phys. 2008, 145–146, 283–290. [Google Scholar] [CrossRef]
- Krause, A.G.; Winger, M.; Blasius, T.D.; Lin, Q.; Painter, O. A high-resolution microchip optomechanical accelerometer. Nat. Photonics 2012, 6, 768–772. [Google Scholar] [CrossRef]
- Soltani, M.; Yegnanarayanan, S.; Adibi, A. Ultra-high Q planar silicon microdisk resonators for chip-scale silicon photonics. Opt. Express 2007, 15, 4694–4704. [Google Scholar] [CrossRef] [PubMed]
- Barclay, P.E.; Srinivasan, K.; Painter, O.; Lev, B.; Mabuchi, H. Integration of fiber-coupled high-Q SiNx microdisks with atom chips. Appl. Phys. Lett. 2006, 89, 131108. [Google Scholar] [CrossRef]
- Niehusmann, J.; Vörckel, A.; Bolivar, P.H.; Wahlbrink, T.; Henschel, W.; Kurz, H. Ultrahigh-quality-factor silicon-on-insulator microring resonator. Opt. Lett. 2004, 29, 2861–2863. [Google Scholar] [CrossRef] [PubMed]
- Li, J.J.; Zhu, K.D. All-optical mass sensing with coupled mechanical resonator systems. Phys. Rep. 2013, 525, 223–254. [Google Scholar] [CrossRef]
- Bhola, B.; Steier, W.H. A Novel Optical Microring Resonator Accelerometer. IEEE Sens. J. 2007, 7, 1759–1766. [Google Scholar] [CrossRef]
- Chao, C.Y.; Guo, L.J. Design and optimization of microring resonators in biochemical sensing applications. J. Lightwave Technol. 2006, 24, 1395–1402. [Google Scholar] [CrossRef]
- Cho, S.Y.; Jokerst, N.M. A Polymer Microdisk Photonic Sensor Integrated onto Silicon. IEEE Photonic Technol. Lett. 2006, 18, 2096–2098. [Google Scholar] [CrossRef]
- Morand, A.; Zhang, Y.; Martin, B.; Phan Huy, K.; Amans, D.; Benech, P.; Verbert, J.; Hadji, E.; Fédéli, J. Ultra-compact microdisk resonator filters on SOI substrate. Opt. Express 2006, 14, 12814–12821. [Google Scholar] [CrossRef] [PubMed]
- Kiyat, I.; Kocabas, C.; Aydinli, A. Integrated micro ring resonator displacement sensor for scanning probe microscopies. J. Micromech. Microeng. 2004, 14, 374. [Google Scholar] [CrossRef]
- Fang, W.; Buchholz, D.B.; Bailey, R.C.; Hupp, J.T.; Chang, R.P.H.; Cao, H. Detection of chemical species using ultraviolet microdisk lasers. Appl. Phys. Lett. 2004, 85, 3666–3668. [Google Scholar] [CrossRef]
- Krioukov, E.; Klunder, D.J.; Driessen, A.; Greve, J.; Otto, C. Sensor based on an integrated optical microcavity. Opt. Lett. 2002, 27, 512–514. [Google Scholar] [CrossRef] [PubMed]
- Xia, D.; Huang, L.; Xu, L.; Gao, H. Structural Analysis of Disk Resonance Gyroscope. Micromachines 2017, 8, 296. [Google Scholar] [CrossRef] [PubMed]
- Xia, D.; Hu, Y.; Kong, L.; Chang, C. Design of a Digitalized Microgyroscope System Using ΣΔ Modulation Technology. IEEE Sens. J. 2015, 15, 3793–3806. [Google Scholar] [CrossRef]
- Le, T.M. Integration of Practical High Sensitivity Whispering Gallery Mode Resonator Sensors. Bachelor’s Thesis, USC, Los Angeles, CA, USA, 2012. [Google Scholar]
- Yariv, A. Critical coupling and its control in optical waveguide-ring resonator systems. IEEE Photonic Technol. Lett. 2002, 14, 483–485. [Google Scholar] [CrossRef]
- Chianese, R.B.; Erdlac, R.J. The general solution to the distribution of stresses in a circular ring compressed by two forces acting along a diameter. Q. J. Mech. Appl. Math. 1988, 41, 239–247. [Google Scholar] [CrossRef]
- Muskhelishvili, N.I. Some Basic Problems of the Mathematical Theory of Elasticity; Springer: Dordrecht, The Netherlands, 1977. [Google Scholar]
- Painter, C.C.; Shkel, A.M. Identification of anisoelasticity for electrostatic trimming of rate-integrating gyroscopes. In Proceedings of the Smart Structures and Materials 2002: Smart Electronics, MEMS, and Nanotechnology, San Diego, CA, USA, 11 July 2002; SPIE: New York, NY, USA, 2002; pp. 157–168. [Google Scholar]
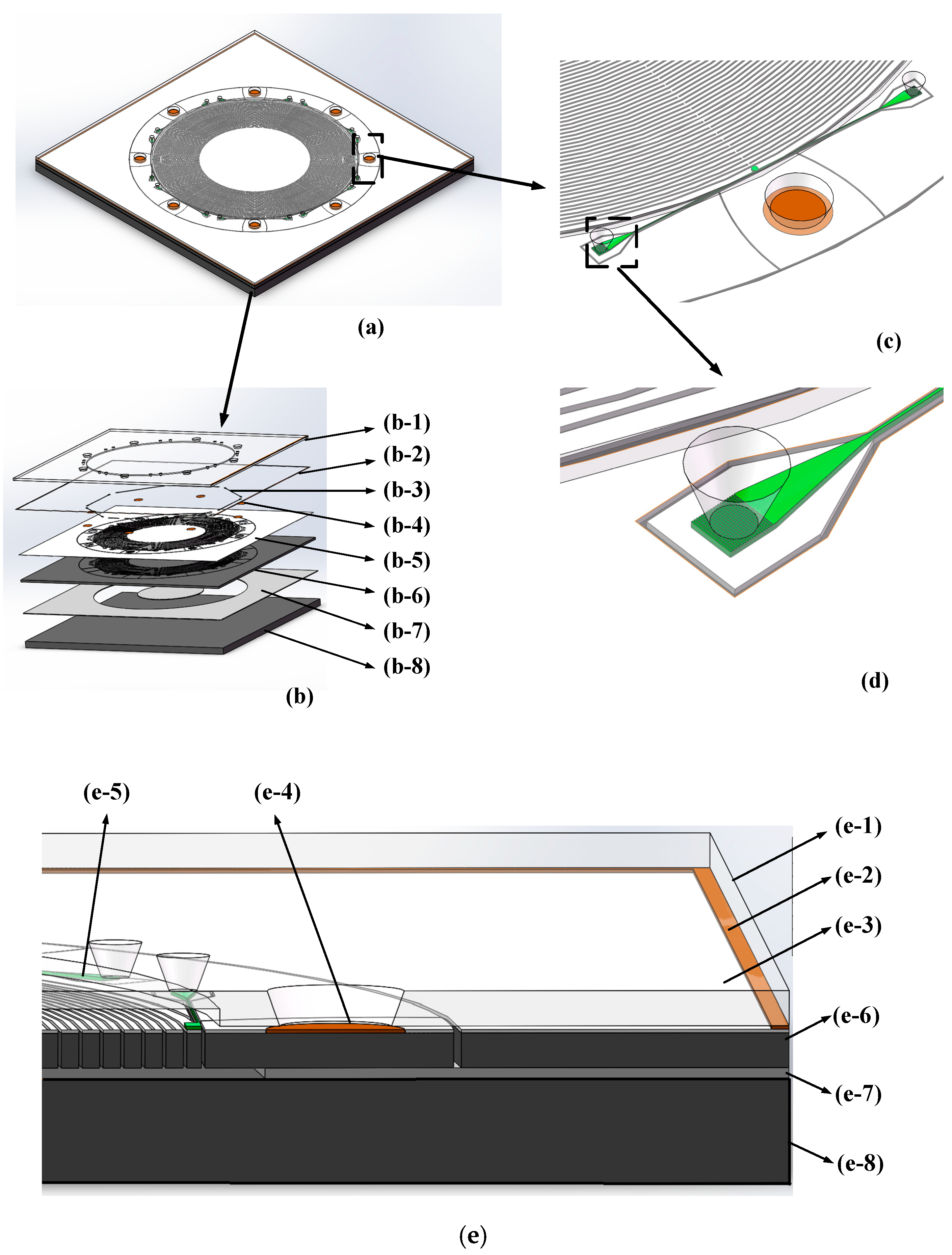

| No. | Name | Material | Thickness(µm) |
|---|---|---|---|
| e-1 | Gap layer | Glass | 100 |
| e-2 | Sealing layer | Au/Cr/Sn | 1 |
| e-3 | Optical components layer | SiNx | 0.35 |
| e-4 | Metal pads layer | Au/Cr | 0.3 |
| e-5 | Optical substrate layer | SiO2 | 2 |
| e-6 | Device layer | Doped silicon | 60 |
| e-7 | Buried oxide layer | SiO2 | 2 |
| e-8 | Handle layer | Monocrystalline silicon | 500 |
| Parameter | Value |
|---|---|
| Spoke number | 16 |
| Ring number | 60 |
| Spoke width | 20 µm |
| Spoke length | 10 µm |
| Ring width | 20 µm |
| Electrode gap | 1.5 µm |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xia, D.; Huang, L.; Zhao, L. A New Design of an MOEMS Gyroscope Based on a WGM Microdisk Resonator. Sensors 2019, 19, 2798. https://doi.org/10.3390/s19122798
Xia D, Huang L, Zhao L. A New Design of an MOEMS Gyroscope Based on a WGM Microdisk Resonator. Sensors. 2019; 19(12):2798. https://doi.org/10.3390/s19122798
Chicago/Turabian StyleXia, Dunzhu, Lingchao Huang, and Liye Zhao. 2019. "A New Design of an MOEMS Gyroscope Based on a WGM Microdisk Resonator" Sensors 19, no. 12: 2798. https://doi.org/10.3390/s19122798
APA StyleXia, D., Huang, L., & Zhao, L. (2019). A New Design of an MOEMS Gyroscope Based on a WGM Microdisk Resonator. Sensors, 19(12), 2798. https://doi.org/10.3390/s19122798




