EEG-Based Emotion Recognition Using Quadratic Time-Frequency Distribution
Abstract
1. Introduction
2. Materials and Methods
2.1. The DEAP Dataset
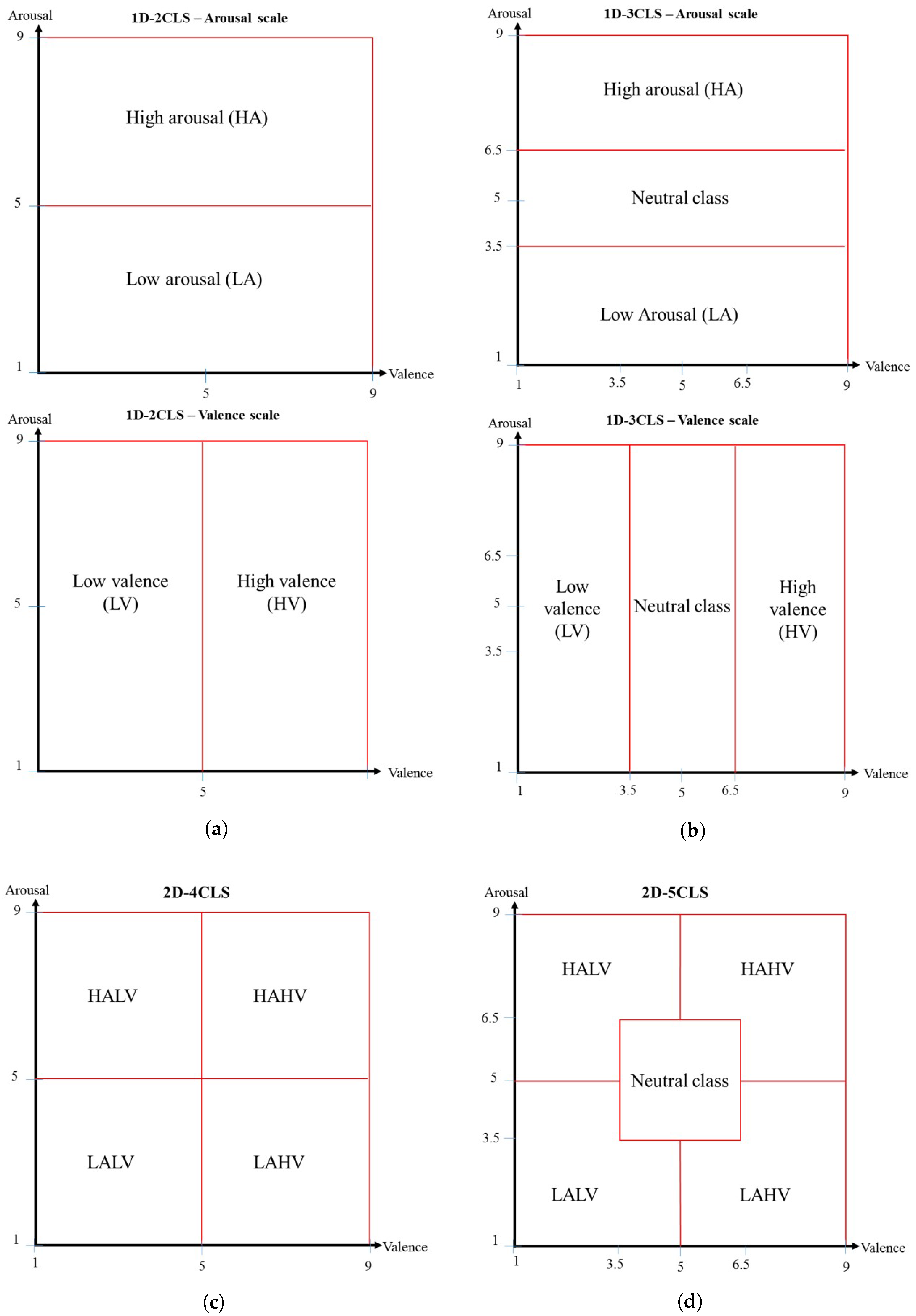
2.2. Emotion Labeling Schemes
- (A)
- In this labeling scheme, the arousal and valence scales are used independently to define two emotion classes for each scale. Specifically, for each trial in the DEAP dataset, if the associated arousal value is greater than five, then the trial is assigned to the high arousal (HA) emotion class. Otherwise, the trial is assigned to the low arousal (LA) emotion class. Similarly, for each trial in the DEAP dataset, if the associated valence value is greater than five, then the trial is assigned to the high valence (HV) emotion class. Otherwise, the trial is assigned to the low valence (LV) emotion class. Figure 1a illustrates the emotion classes defined based on the 1D-2CLS.
- (B)
- This emotion labeling scheme utilizes the arousal and valence scales independently to define three emotion classes for each scale. In particular, using the arousal scale, a trial is assigned to the high arousal (HA) emotion class, the neutral emotion class or the low arousal (LA) emotion class depending on whether the associated arousal value is within the interval [6.5–9], (3.5–6.5) or [1–3.5], respectively. Similarly, using the valence scale, a trial is assigned to the high valence (HV) emotion class, the neutral emotion class or the low valence (LV) emotion class depending on whether the associated valence value is within the interval [6.5–9], (3.5–6.5) or [1–3.5], respectively. Figure 1b illustrates the emotion classes defined based on the 2D-3CLS.
- (C)
- This emotion labeling scheme utilizes the 2D arousal-valence plane, which was proposed by Russell [23], to describe and quantify various emotional states. In particular, using the 2D arousal-valence plane, an emotional state can be viewed as a point in the 2D plane defined by the axes of the valence scale and the arousal scale, such that the arousal and valence scales are represented by the vertical and horizontal axes, respectively, of the 2D plane. Therefore, the 2D arousal-valence plane can be divided into four quadrants, where each quadrant represents a specific emotion class. The emotion classes defined based on the 2D-4CLS are: the high arousal/high valence (HAHV), low arousal/high valence (LAHV), low arousal/low valence (LALV) and high arousal/low valence (HALV) emotion classes. The term “low” in each of the four defined emotion classes indicates that the arousal value or the valence value is less than five, while the term “high” indicates that the arousal value or the valence value is greater than five. Figure 1c illustrates the emotion classes defined based on the 2D-4CLS.
- (D)
- The two-dimensional five-class labeling scheme (2D-5CLS):In this labeling scheme, we extend the 2D-4CLS to include the neutral emotion class, which represents the no-emotion state. In particular, we divide the 2D arousal-valence plane into five regions, where each region represents a specific emotion class. The emotion classes defined based on the 2D-5CLS are: the HAHV, LAHV, LALV, HALV and neutral emotion classes. The neutral emotion class is employed to represent the trials in which the arousal and valence values fall within the interval (3.5–6.5). Figure 1d illustrates the emotion classes defined based on the 2D-5CLS.
2.3. EEG Signals Acquisition and Preprocessing
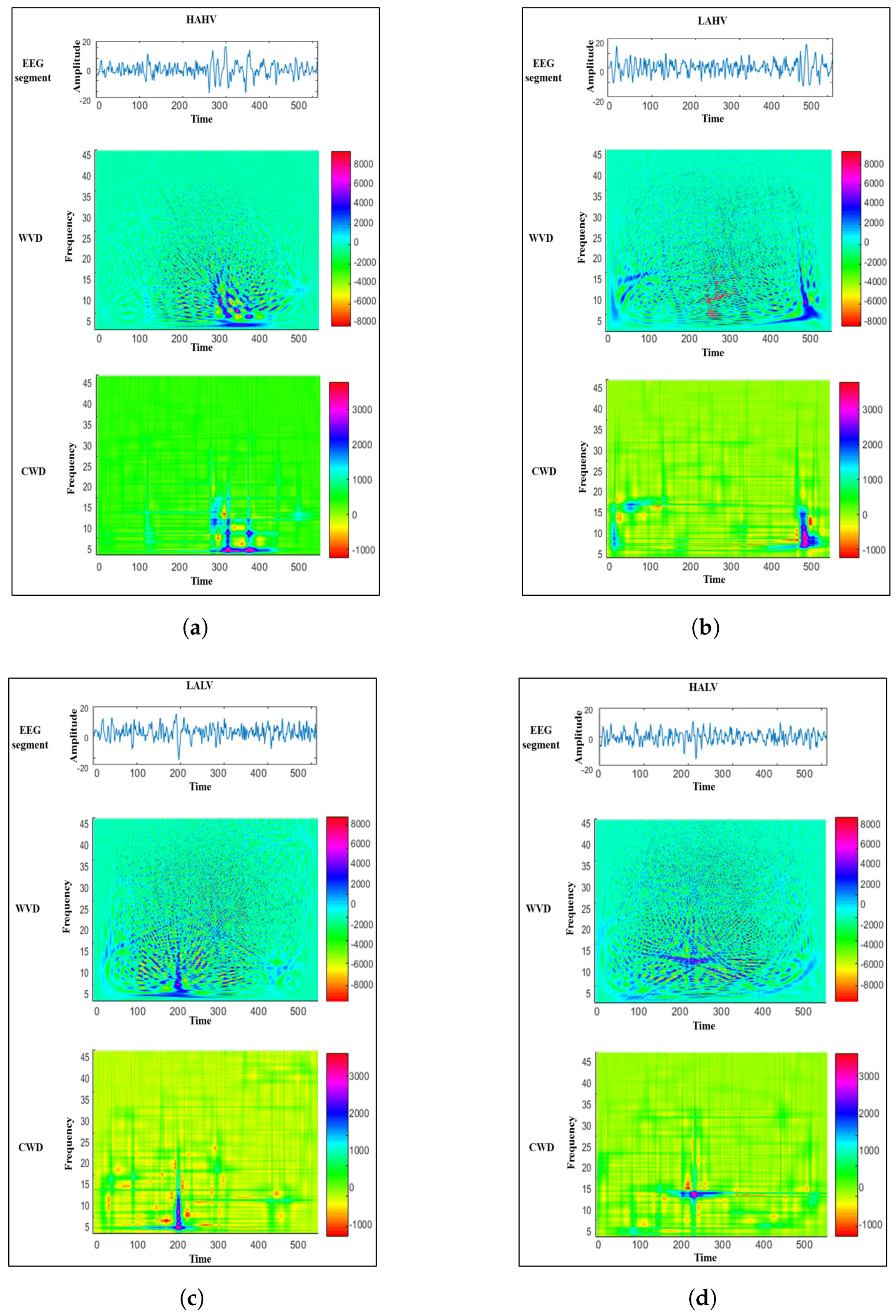
2.4. Time-Frequency Analysis of EEG Signals
- I
- Compute the analytic signal, , of the real-valued signal, , as follows:where is the Hilbert transform [42].
- II
- Calculate the Wigner–Ville distribution (WVD) of as follows:where and represent the WVD and the complex conjugate of , respectively.
- III
- Convolve the obtained with a time-frequency smoothing kernel, , as follows:where represents the QTFD of . In fact, the type of constructed QTFD is determined based on the utilized time-frequency kernel. For example, the time-frequency kernel is used to construct the WVD, which is considered a QTFD [36]. The WVD produces a TFR that has an excellent resolution in the time- and frequency-domain. Nonetheless, the WVD-based TFR contains cross-terms that may distort the signal components [18,35,41] and, hence, increases the difficulty to interpret the obtained TFR visually. Therefore, in this study, we employ an exponential time-frequency kernel to reduce the effect of the cross-terms and maintain an adequate resolution in both the time- and frequency-domain. The employed exponential kernel is defined as follows:where is a parameter that controls the suppression of the cross-terms, and its value is experimentally selected to be . The QTFD constructed using the kernel defined in Equation (4) is known as the Choi–Williams distribution (CWD) [43].
2.5. CWD-Based Time-Frequency Features
2.6. Emotion Classification
2.7. Evaluation Analyses and Metrics
- A
- Channel-based analysis:In this analysis, we investigate the effect of utilizing various groups of EEG channels, which cover different regions of the brain, on the accuracy of recognizing the emotion classes defined based on the four emotion labeling schemes. Recently, several studies have indicated that the frontal, prefrontal, temporal, parietal and occipital regions of the brain are involved in emotional responses [25,32,51,52,53,54,55,56,57,58]. In particular, Mohammadi et al. [58] utilized five pairs of electrodes that cover the frontal and frontal parietal regions of the brain, where these pairs are F3-F4, F7-F8, FC1-FC2, FC5-FC6 and FP1-FP2, to recognize emotional states defined based on the 2D arousal-valence plane. In another study by Zhuang et al. [25], the prefrontal, parietal, occipital and temporal regions were found to have an important role in emotion recognition. These regions of the brain are covered by the following pairs of electrodes: AF3-AF4, P3-P4, P7-P8, CP5-CP6, O1-O2, and T7-T8. Therefore, in this study, we have selected 11 symmetrical pairs of EEG channels out of the 16 pairs of EEG channels provided in the DEAP dataset. The selected pairs of electrodes cover the parietal region (P3-P4, P7-P8 and CP5-CP6), frontal region (F3-F4, F7-F8, FC1-FC2, FC5-FC6, AF3-AF4 and FP1-FP2), temporal region (T7-T8) and occipital region (O1-O2). Table 4 presents the brain regions covered by the selected 11 pairs of EEG channels.To study the effect of the utilized different EEG channels on the accuracy of decoding emotion classes, the selected 11 pairs of EEG channels were organized into four different configurations to perform the analysis. Specifically, in the first configuration, denoted by , we investigate the effect of utilizing each symmetrical pair of EEG channels independently on the accuracy of decoding the emotion classes defined in each emotion labeling scheme. In the second configuration, denoted by , we study the effect of utilizing 12 EEG channels that are located in the frontal and temporal regions of the brain on the accuracy of recognizing the emotion classes of each emotion labeling scheme. In the third configuration, denoted by , we explore the effect of utilizing eight EEG channels that are located in the parietal and occipital regions of the brain on the accuracy of recognizing the emotion classes of each emotion labeling scheme. Finally, in the fourth configuration, denoted by , we study the effect of utilizing all the selected 22 EEG channels on the accuracy of recognizing the emotion classes of each emotion labeling scheme. Table 5 summarizes the aforementioned four configurations and shows the EEG channels comprised within each configuration.To implement this evaluation analysis, for each subject, we built an SVM classifier to perform the classification analysis associated with each emotion labeling scheme using the time-frequency features extracted from the EEG channels in each configuration. Specifically, for each symmetrical pair of EEG channels in , we build a SVM model for each emotion labeling scheme. The dimensionality of the feature vectors extracted from each symmetrical pair of EEG channels in is equal to 26 . Similarly, for each group of EEG channels defined in , and , we built an SVM model for each emotion labeling scheme. The dimensionality of the feature vectors extracted from the EEG channels in , and is 156 , 104 and 286 , respectively.
- B
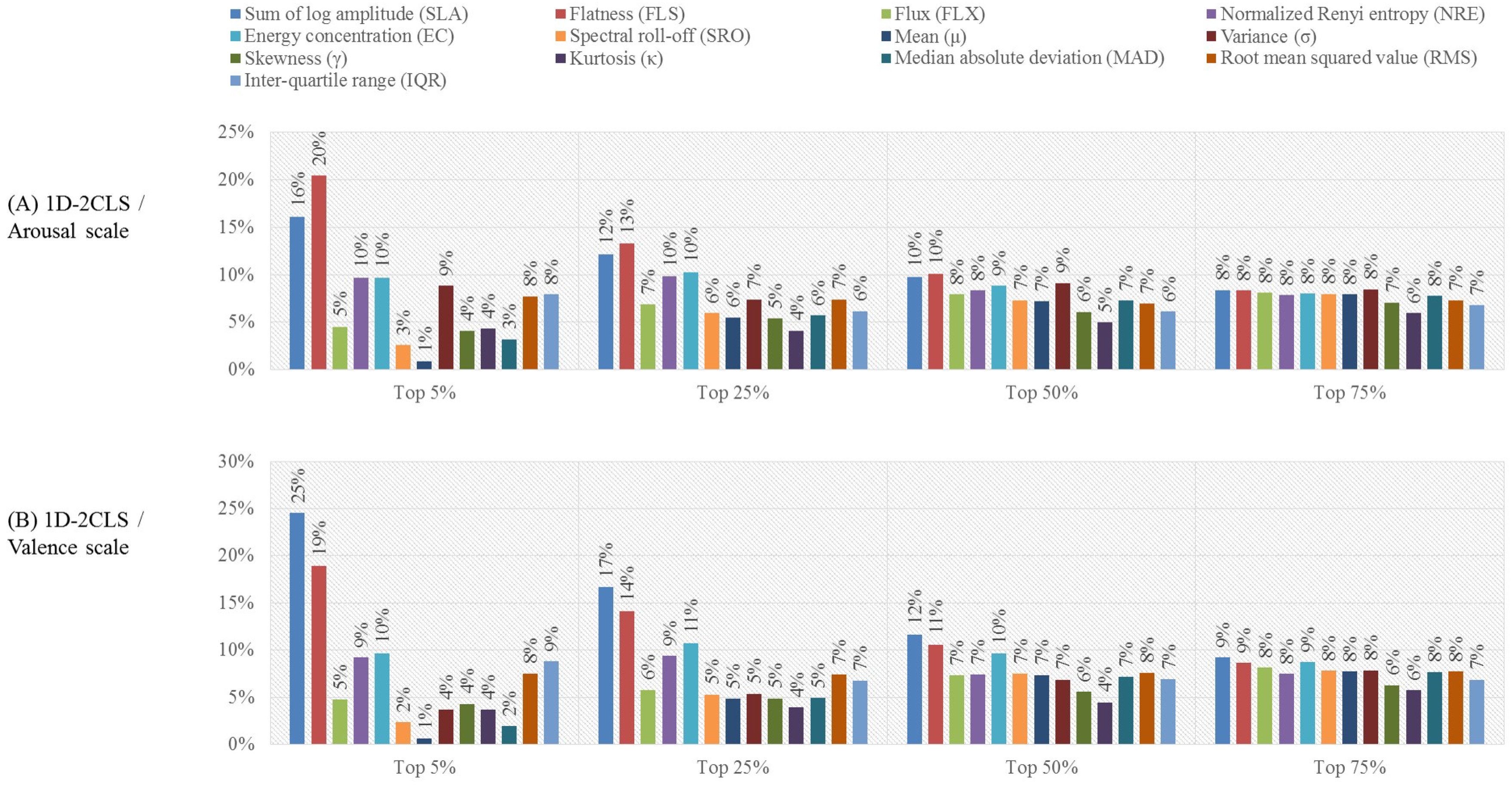
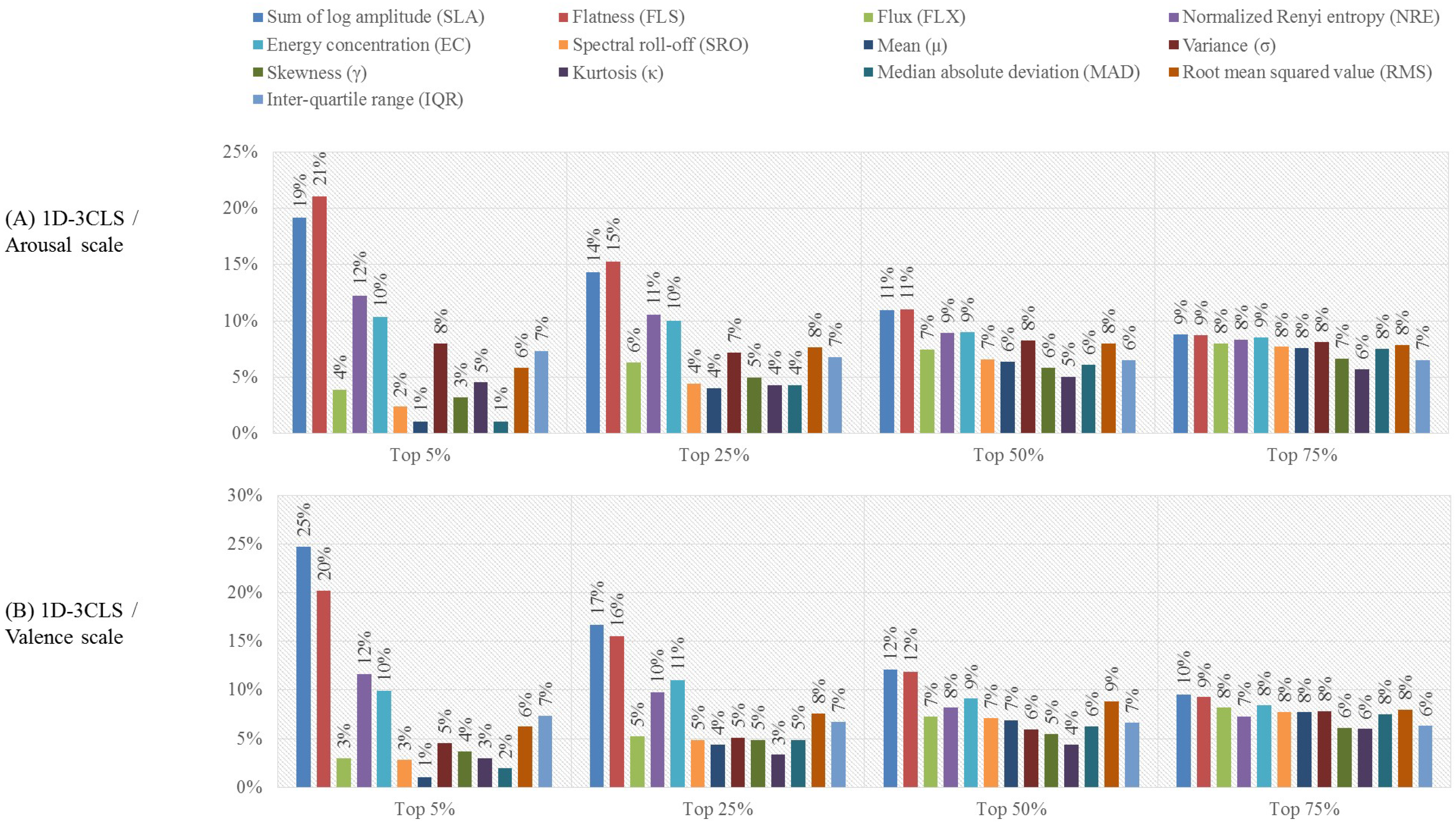
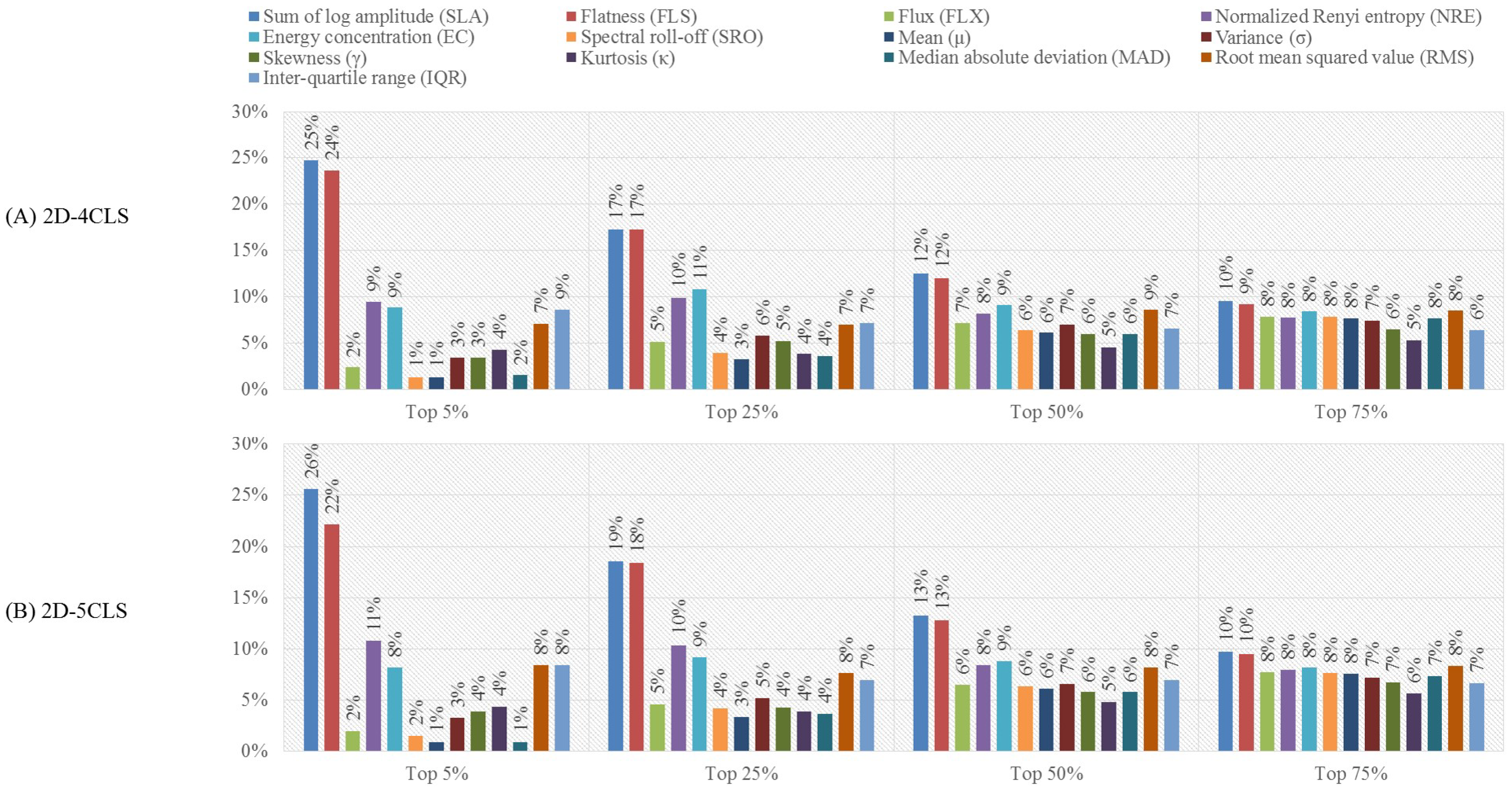
- Feature-based analysis:In this analysis, we investigate the effect of reducing the dimensionality of the extracted feature vectors on the accuracy of recognizing the emotion classes defined based on the four emotion labeling schemes. In particular, we utilize the minimal redundancy maximum relevance (mRMR) [59] algorithm to reduce the dimensionality of the constructed feature vectors. The mRMR algorithm utilizes the mutual information to select a subset of features that has the maximum correlation with a specific emotion class and the minimum correlation between the selected features [59,60]. The selected subset of features is ranked according to the minimal-redundancy-maximal-relevance criterion. Previous studies [61,62] indicated that using the mRMR algorithm to select features for emotion classification applications can outperform other feature selection algorithms, such as the ReliefFfeature selection algorithm [63]. In this work, we employ the mRMR algorithm to construct four feature selection scenarios, namely the top , , and scenarios. In particular, the mRMR algorithm is used to reduce the size of the extracted feature vectors by selecting the top , , and of the features that satisfy the minimal-redundancy-maximal-relevance criterion [62]. Then, we study the effect of utilizing the features obtained using each of the feature selection scenarios on the accuracy of recognizing the emotion classes of each emotion labeling scheme. For the purpose of this evaluation analysis, we utilize the results obtained from the channel-based evaluation analysis to apply the mRMR feature selection algorithm on the feature vectors extracted from the EEG channels associated with the EEG channel configuration that achieves the best classification performance.
- C
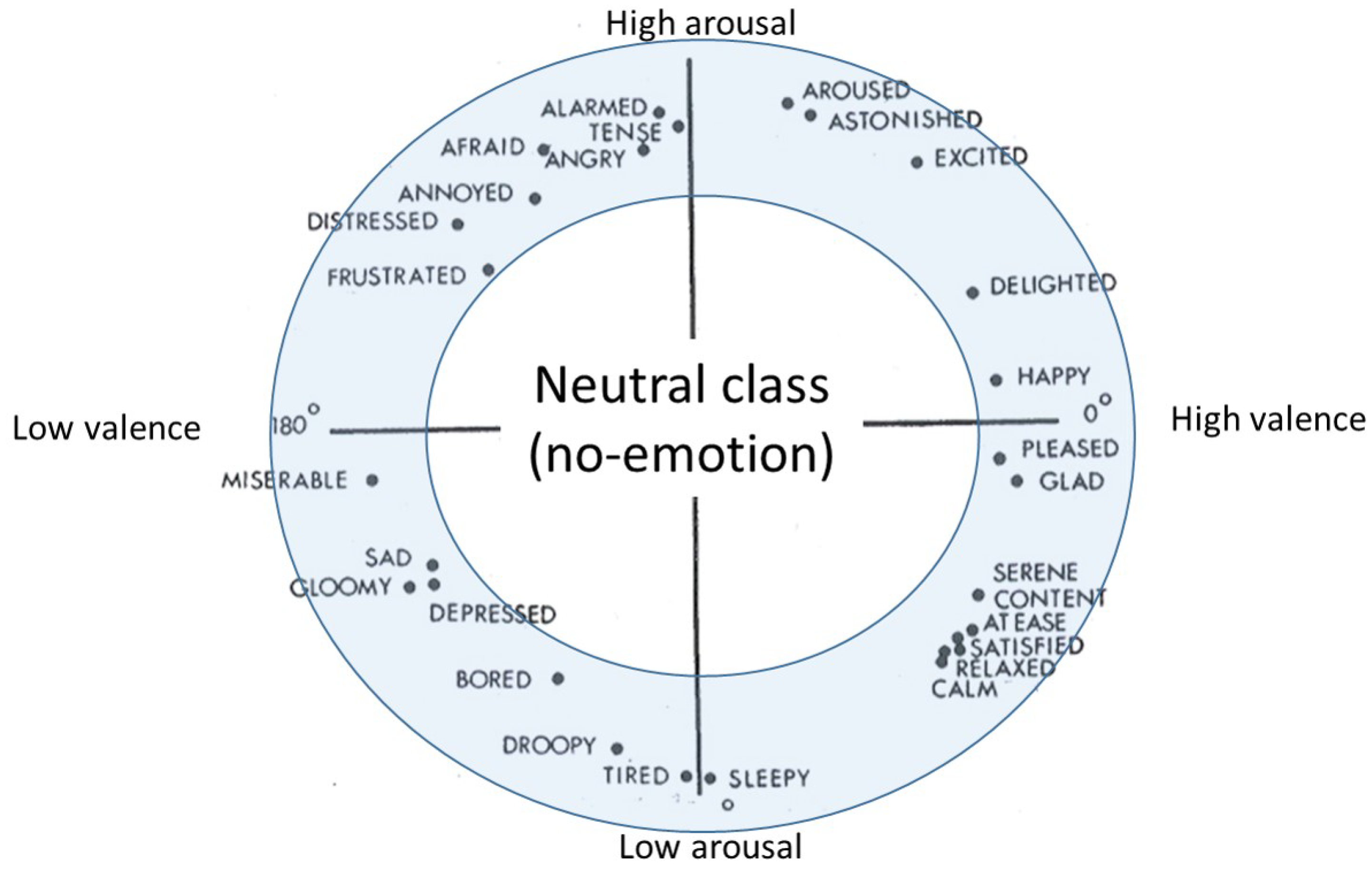
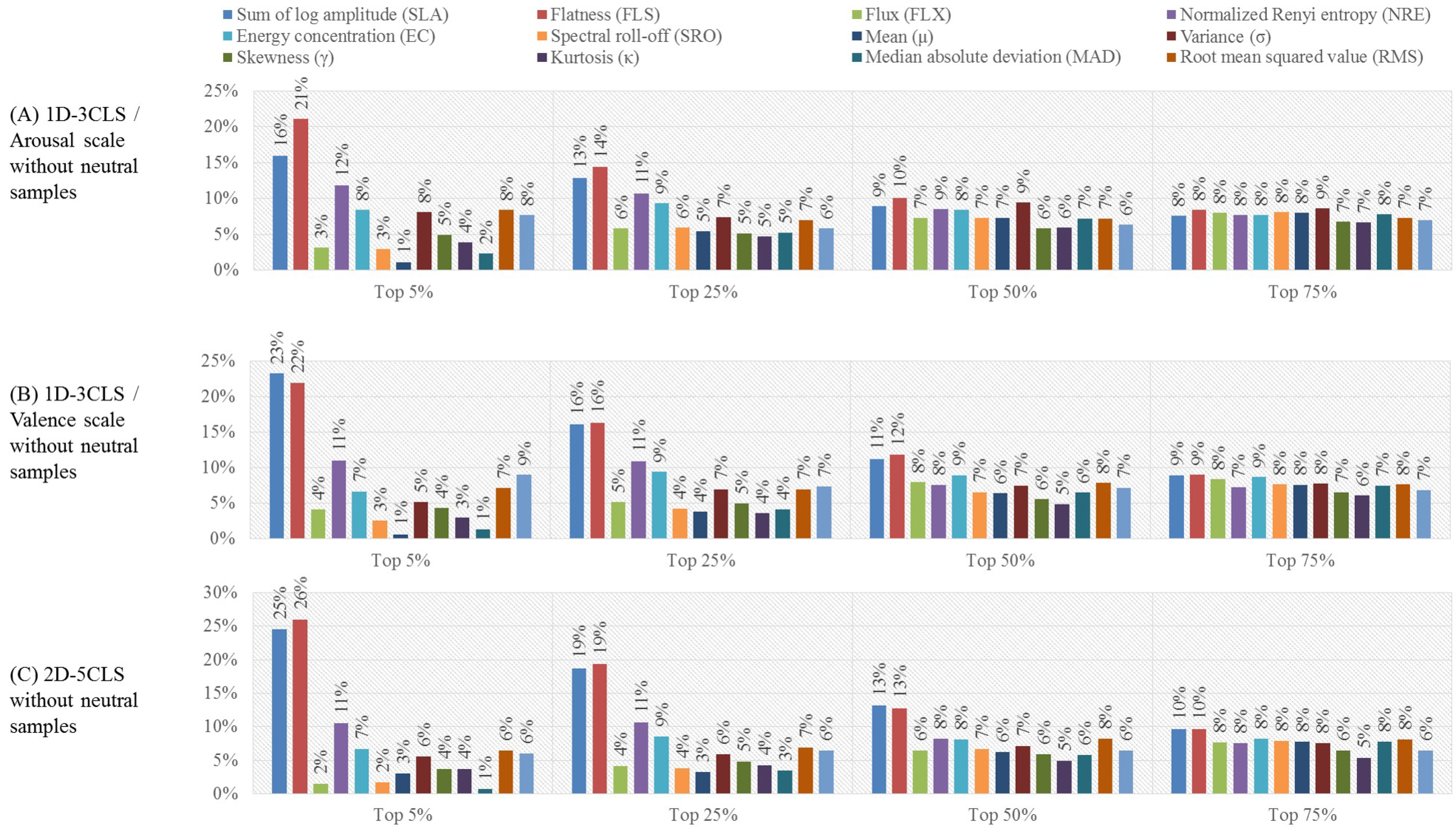
- Neutral class exclusion analysis:In this evaluation analysis, we study the effect of excluding the samples that correspond to the neutral class, which are defined in the 1D-3CLS and 2D-5CLS, on the accuracy of decoding the remaining non-neutral emotion classes. According to Russell [23], emotional states are organized in a circular configuration around the circumference of the 2D arousal-valence plane, as depicted in Figure 3. This implies that the region corresponding to the neutral class, which is the area bounded by the interval (3.5–6.5) on the arousal scale and the interval (3.5–6.5) on the valence scale, does not describe emotional states effectively [4]. Therefore, in this evaluation analysis, we exclude the feature vectors extracted from the trials that are falling within the region that represents the neutral class on the 2D arousal-valence plane. To implement this evaluation analysis, we re-perform the previous two evaluation analyses, namely the channel- and feature-based analyses, after excluding the feature vectors that belong to the neutral class.
3. Results
3.1. Results of the Channel-Based Evaluation Analysis
3.2. Results of the Feature-Based Evaluation Analysis
3.3. Results of the Neutral Class Exclusion Analysis
4. Discussion
4.1. Channel-Based Evaluation Analysis
4.2. Feature-Based Evaluation Analysis
4.3. Neutral Class Exclusion Analysis
4.4. Comparison with Other Studies
4.5. Limitations and Future Work
- Firstly, in this study, we have utilized SVM classifiers to decode various emotion classes. In fact, the selection of the SVM classifier was based on the fact that SVM classifiers have been employed in the vast majority of the existing EEG-based emotion recognition studies, which in turn simplifies the comparison between the performance of our proposed approach and previous approaches. In addition, the SVM classifier has been reported in many previous studies to achieve good classification performance compared with other classifiers. Nonetheless, motivated by the recent promising results attained in analyzing physiological signals using deep learning approaches [75], we are planning to investigate the use of deep learning approaches, such as convolutional neural network (CNN), to extract time-frequency features from the constructed QTFD-based representation. Moreover, we intend to utilize the learned CNN-based time-frequency features with other types of classifiers, such as long short-term memory (LSTM) networks, which may provide a better description of how emotional states evolve over time. In addition, the promising results reported in [12] that were obtained by analyzing multi-modality emotion-related acquisition signals, such as visual, speech and text signals, using a deep learning technique, such as CNN, suggest that utilizing different emotion-related input modalities might improve the emotion classification performance. Therefore, in the future, we intend to employ deep learning techniques to enhance the performance of our approach by analyzing different emotion-related signals acquired using different modalities, including EEG signals, speech and visual cues.
- Secondly, the nonstationary nature of the EEG signals and the inter- and inter-personal variations in emotion responses impose the need to construct a large-scale and well-balanced dataset to avoid classification bias and overfitting problems. Moreover, the recorded physiological responses to stimuli in real-world applications may differ from the responses recorded in a well-controlled environment. This implies that the results presented in this study may overestimate the performance in real-world applications. Therefore, in the near future, we plan to acquire a large-scale EEG dataset under realistic recording conditions to evaluate the effectiveness of our proposed QTFD-based emotion recognition approach in real-world applications.
- Thirdly, our proposed approach, including the computation of the QTFD and the extraction of the thirteen time-frequency features, was implemented using MATLAB (The MathWorks Inc., Natick, MA, USA). The QTFD and the feature extraction routines were executed on a computer workstation with a -GHz Intel Xeon Processor (Intel Corporation, Santa Clara, CA, USA) and 8 GB memory. The average ± standard deviation time required to compute the QTFD for an EEG segment of length 512 samples is ms ± ms, and the average ± standard deviation time required to extract the thirteen time-frequency features from the computed QTFD is ms ± ms. Therefore, the average time required to compute the QTFD for the 22 EEG channels in is approximately ms, while the average time required to compute the thirteen time-frequency features for the 22 EEG channels in is approximately ms. Thus, the total time required to compute the QTFD and extract the thirteen time-frequency features for the 22 EEG channels is approximately ms, which is less than the duration of the utilized sliding window (i.e., 4 s). This implies that our proposed approach can be used in real-world applications. Nonetheless, we believe that there is still a room to improve the run-time of the proposed approach using parallel computing technology, which allows the utilization of our approach in various clinical applications.
- Fourthly, we are also planning to customize our proposed approach to target specific clinical applications, such as pain detection. In particular, rather than classifying the emotion classes into high versus low arousal/valence levels, which is the main goal of the current study, we plan in the near future to extend our work by utilizing the extracted time-frequency features to estimate the values of the arousal and valence scales associated with various emotional states. Such an extension can be of great benefit for estimating the level of pain a patient is feeling, especially for patients who are unable to verbally communicate their feelings.
- Finally, we plan to extend the analyses conducted in the current study from subject-dependent analyses to subject-independent analyses. Such an extension can provide insight regarding the ability of the proposed QTFD-based approach to recognize emotion classes for new subjects that were not part of the training set, which can be of great benefit for several real-world applications.
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Doukas, C.; Maglogiannis, I. Intelligent pervasive healthcare systems. In Advanced Computational Intelligence Paradigms in Healthcare-3; Springer: New York, NY, USA, 2008; pp. 95–115. [Google Scholar]
- Petrantonakis, P.C.; Hadjileontiadis, L.J. Emotion Recognition From EEG Using Higher Order Crossings. IEEE Trans. Inf. Technol. Biomed. 2010, 14, 186–197. [Google Scholar] [CrossRef] [PubMed]
- Purnamasari, P.D.; Ratna, A.A.P.; Kusumoputro, B. Development of Filtered Bispectrum for EEG Signal Feature Extraction in Automatic Emotion Recognition Using Artificial Neural Networks. Algorithms 2017, 10, 63. [Google Scholar] [CrossRef]
- Menezes, M.L.R.; Samara, A.; Galway, L.; Sant’Anna, A.; Verikas, A.; Alonso-Fernandez, F.; Wang, H.; Bond, R. Towards emotion recognition for virtual environments: an evaluation of eeg features on benchmark dataset. Pers. Ubiquitous Comput. 2017, 21, 1003–1013. [Google Scholar] [CrossRef]
- Chen, J.; Hu, B.; Moore, P.; Zhang, X.; Ma, X. Electroencephalogram-based emotion assessment system using ontology and data mining techniques. Appl. Soft Comput. 2015, 30, 663–674. [Google Scholar] [CrossRef]
- Bourel, F.; Chibelushi, C.C.; Low, A.A. Robust facial expression recognition using a state-based model of spatially-localised facial dynamics. In Proceedings of the Fifth IEEE International Conference on Automatic Face and Gesture Recognition, Washington, DC, USA, 20–21 May 2002; pp. 113–118. [Google Scholar]
- Cohen, I.; Sebe, N.; Garg, A.; Chen, L.S.; Huang, T.S. Facial expression recognition from video sequences: Temporal and static modeling. Comput. Vis. Image Underst. 2003, 91, 160–187. [Google Scholar] [CrossRef]
- Alazrai, R.; Lee, C.G. Real-time emotion identification for socially intelligent robots. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Saint Paul, MN, USA, 14–18 May 2012; pp. 4106–4111. [Google Scholar]
- Alazrai, R.; Lee, C.G. An narx-based approach for human emotion identification. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Vilamoura, Portugal, 7–12 October 2012; pp. 4571–4576. [Google Scholar]
- Schuller, B.; Reiter, S.; Muller, R.; Al-Hames, M.; Lang, M.; Rigoll, G. Speaker independent speech emotion recognition by ensemble classification. In Proceedings of the IEEE International Conference on Multimedia and Expo, Amsterdam, The Netherlands, 6 July 2005; pp. 864–867. [Google Scholar]
- Yu, F.; Chang, E.; Xu, Y.Q.; Shum, H.Y. Emotion detection from speech to enrich multimedia content. In Pacific-Rim Conference on Multimedia; Springer: Berlin/Heidelberg, Germany, 2001; pp. 550–557. [Google Scholar]
- Poria, S.; Chaturvedi, I.; Cambria, E.; Hussain, A. Convolutional MKL based multimodal emotion recognition and sentiment analysis. In Proceedings of the IEEE 16th International Conference on Data Mining (ICDM), Barcelona, Spain, 12–15 December 2016; pp. 439–448. [Google Scholar]
- Picard, R.W.; Vyzas, E.; Healey, J. Toward machine emotional intelligence: Analysis of affective physiological state. IEEE Trans. Pattern Anal. Mach. Intell. 2001, 23, 1175–1191. [Google Scholar] [CrossRef]
- Nasoz, F.; Alvarez, K.; Lisetti, C.L.; Finkelstein, N. Emotion recognition from physiological signals for user modeling of affect. In Proceedings of the UM 2003, 9th International Conference on User Model, Pittsburg, PA, USA, 22–26 June 2003. [Google Scholar]
- Nie, D.; Wang, X.W.; Shi, L.C.; Lu, B.L. EEG-based emotion recognition during watching movies. In Proceedings of the 5th International IEEE/EMBS Conference on Neural Engineering (NER), Cancun, Mexico, 27 April–1 May 2011; pp. 667–670. [Google Scholar]
- Martini, N.; Menicucci, D.; Sebastiani, L.; Bedini, R.; Pingitore, A.; Vanello, N.; Milanesi, M.; Landini, L.; Gemignani, A. The dynamics of EEG gamma responses to unpleasant visual stimuli: From local activity to functional connectivity. NeuroImage 2012, 60, 922–932. [Google Scholar] [CrossRef] [PubMed]
- Yin, Z.; Zhao, M.; Wang, Y.; Yang, J.; Zhang, J. Recognition of Emotions Using Multimodal Physiological Signals and an Ensemble Deep Learning Model. Comput. Methods Prog. Biomed. 2017, 140, 93–110. [Google Scholar] [CrossRef] [PubMed]
- Alazrai, R.; Alwanni, H.; Baslan, Y.; Alnuman, N.; Daoud, M.I. EEG-Based Brain-Computer Interface for Decoding Motor Imagery Tasks within the Same Hand Using Choi-Williams Time-Frequency Distribution. Sensors 2017, 17, 1937. [Google Scholar] [CrossRef] [PubMed]
- Nicolas-Alonso, L.F.; Gomez-Gil, J. Brain computer interfaces, a review. Sensors 2012, 12, 1211–1279. [Google Scholar] [CrossRef] [PubMed]
- Castiglioni, P. Choi-Williams Distribution. In Encyclopedia of Biostatistics; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2005. [Google Scholar]
- Boubchir, L.; Al-Maadeed, S.; Bouridane, A. On the use of time-frequency features for detecting and classifying epileptic seizure activities in non-stationary EEG signals. In Proceedings of the 2014 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Florence, Italy, 4–9 May 2014; pp. 5889–5893. [Google Scholar]
- Tzallas, A.T.; Tsipouras, M.G.; Fotiadis, D.I. Epileptic seizure detection in EEGs using time-frequency analysis. IEEE Trans. Inf. Technol. Biomed. 2009, 13, 703–710. [Google Scholar] [CrossRef] [PubMed]
- Russell, J.A. A circumplex model of affect. J. Personal. Soc. Psychol. 1980, 39, 11–61. [Google Scholar] [CrossRef]
- Koelstra, S.; Muhl, C.; Soleymani, M.; Lee, J.S.; Yazdani, A.; Ebrahimi, T.; Pun, T.; Nijholt, A.; Patras, I. DEAP: A Database for Emotion Analysis; Using Physiological Signals. IEEE Trans. Affect. Comput. 2012, 3, 18–31. [Google Scholar] [CrossRef]
- Zhuang, N.; Zeng, Y.; Tong, L.; Zhang, C.; Zhang, H.; Yan, B. Emotion Recognition from EEG Signals Using Multidimensional Information in EMD Domain. BioMed Res. Int. 2017, 2017. [Google Scholar] [CrossRef] [PubMed]
- Liu, W.; Zheng, W.L.; Lu, B.L. Multimodal emotion recognition using multimodal deep learning. arXiv, 2016; arXiv:1602.08225. [Google Scholar]
- Rozgic, V.; Vitaladevuni, S.N.; Prasad, R. Robust EEG emotion classification using segment level decision fusion. In Proceedings of the 2013 IEEE International Conference on Acoustics, Speech and Signal Processing, Vancouver, BC, Canada, 26–31 May 2013; pp. 1286–1290. [Google Scholar]
- Chung, S.Y.; Yoon, H.J. Affective classification using Bayesian classifier and supervised learning. In Proceedings of the 2012 12th International Conference on Control, Automation and Systems, JeJu Island, Korea, 17–21 October 2012; pp. 1768–1771. [Google Scholar]
- Tripathi, S.; Acharya, S.; Sharma, R.D.; Mittal, S.; Bhattacharya, S. Using Deep and Convolutional Neural Networks for Accurate Emotion Classification on DEAP Dataset. In Proceedings of the Twenty-Ninth AAAI Conference on Innovative Applications, San Francisco, CA, USA, 6–9 February 2017; pp. 4746–4752. [Google Scholar]
- Jirayucharoensak, S.; Pan-Ngum, S.; Israsena, P. EEG-based emotion recognition using deep learning network with principal component based covariate shift adaptation. Sci. World J. 2014, 2014, 627892. [Google Scholar] [CrossRef] [PubMed]
- Atkinson, J.; Campos, D. Improving BCI-based emotion recognition by combining EEG feature selection and kernel classifiers. Expert Syst. Appl. 2016, 47, 35–41. [Google Scholar] [CrossRef]
- Zheng, W.L.; Zhu, J.Y.; Lu, B.L. Identifying Stable Patterns over Time for Emotion Recognition from EEG. IEEE Trans. Affect. Comput. 2017. [Google Scholar] [CrossRef]
- Zubair, M.; Yoon, C. EEG Based Classification of Human Emotions Using Discrete Wavelet Transform. In IT Convergence and Security 2017; Kim, K.J., Kim, H., Baek, N., Eds.; Springer: Singapore, 2018; pp. 21–28. [Google Scholar]
- Niedermeyer, E.; da Silva, F.L. Electroencephalography: Basic Principles, Clinical Applications, and Related Fields; Lippincott Williams & Wilkins: Philadelphia, PA, USA, 2005. [Google Scholar]
- Toole, J.M.O. Discrete Quadratic Time-Frequency Distributions: Definition, Computation, and a Newborn Electroencephalogram Application. Ph.D. Thesis, School of Medicine, The University of Queensland, Brisbane, Australia, 2009. [Google Scholar]
- Boashash, B. Time-Frequency Signal Analysis and Processing: A Comprehensive Reference; Academic Press: Cambridge, MA, USA, 2015. [Google Scholar]
- Alazrai, R.; Aburub, S.; Fallouh, F.; Daoud, M.I. EEG-based BCI system for classifying motor imagery tasks of the same hand using empirical mode decomposition. In Proceedings of the 10th IEEE International Conference on Electrical and Electronics Engineering (ELECO), Bursa, Turkey, 30 November–2 December 2017; pp. 615–619. [Google Scholar]
- Koenig, W.; Dunn, H.K.; Lacy, L.Y. The Sound Spectrograph. J. Acoust. Soc. Am. 1946, 18, 19–49. [Google Scholar] [CrossRef]
- Mallat, S. A Wavelet Tour of Signal Processing: The Sparse Way; Academic Press: Cambridge, MA, USA, 2008. [Google Scholar]
- Boashash, B.; Ouelha, S. Automatic signal abnormality detection using time-frequency features and machine learning: A newborn EEG seizure case study. Knowl. Based Syst. 2016, 106, 38–50. [Google Scholar] [CrossRef]
- Boashash, B.; Azemi, G.; O’Toole, J.M. Time-Frequency Processing of Nonstationary Signals: Advanced TFD Design to Aid Diagnosis with Highlights from Medical Applications. IEEE Signal Process. Mag. 2013, 30, 108–119. [Google Scholar] [CrossRef]
- Hahn, S.L. Hilbert Transforms in Signal Processing; Artech House: Boston, MA, USA, 1996; Volume 2. [Google Scholar]
- Choi, H.I.; Williams, W.J. Improved time-frequency representation of multicomponent signals using exponential kernels. IEEE Trans. Acoust. Speech Signal Process. 1989, 37, 862–871. [Google Scholar] [CrossRef]
- Swami, A.; Mendel, J.; Nikias, C. Higher-Order Spectra Analysis (HOSA) Toolbox, Version 2.0.3; Signals & Systems, Inc.: Culver City, CA, USA, 2000. [Google Scholar]
- Zheng, W.L.; Lu, B.L. Investigating Critical Frequency Bands and Channels for EEG-Based Emotion Recognition with Deep Neural Networks. IEEE Trans. Auton. Ment. Dev. 2015, 7, 162–175. [Google Scholar] [CrossRef]
- Boashash, B.; Boubchir, L.; Azemi, G. A methodology for time-frequency image processing applied to the classification of non-stationary multichannel signals using instantaneous frequency descriptors with application to newborn EEG signals. EURASIP J. Adv. Signal Process. 2012, 2012, 117. [Google Scholar] [CrossRef]
- Qian, H.; Mao, Y.; Xiang, W.; Wang, Z. Recognition of human activities using SVM multi-class classifier. Pattern Recognit. Lett. 2010, 31, 100–111. [Google Scholar] [CrossRef]
- Kreßel, U.H.G. Pairwise classification and support vector machines. In Advances in Kernel Methods; MIT Press: Cambridge, MA, USA, 1999; pp. 255–268. [Google Scholar]
- Hsu, C.W.; Lin, C.J. A comparison of methods for multiclass support vector machines. IEEE Trans. Neural Netw. 2002, 13, 415–425. [Google Scholar] [PubMed]
- Chang, C.C.; Lin, C.J. LIBSVM: A library for support vector machines. ACM Trans. Intell. Syst. Technol. 2011, 2, 27. [Google Scholar] [CrossRef]
- Zhang, J.; Zhao, S.; Huang, W.; Hu, S. Brain Effective Connectivity Analysis from EEG for Positive and Negative Emotion. In Neural Information Processing; Liu, D., Xie, S., Li, Y., Zhao, D., El-Alfy, E.S.M., Eds.; Springer International Publishing: New York, NY, USA, 2017; pp. 851–857. [Google Scholar]
- Li, X.; Yan, J.Z.; Chen, J.H. Channel Division Based Multiple Classifiers Fusion for Emotion Recognition Using EEG Signals. In Proceedings of the 2017 International Conference on Information Science and Technology, Wuhan, China, 24–26 March 2017; Volume 11, p. 07006. [Google Scholar]
- Petrantonakis, P.C.; Hadjileontiadis, L.J. A Novel Emotion Elicitation Index Using Frontal Brain Asymmetry for Enhanced EEG-Based Emotion Recognition. IEEE Trans. Inf. Technol. Biomed. 2011, 15, 737–746. [Google Scholar] [CrossRef] [PubMed]
- Coan, J.A.; Allen, J.J.; Harmon-Jones, E. Voluntary facial expression and hemispheric asymmetry over the frontal cortex. Psychophysiology 2001, 38, 912–925. [Google Scholar] [CrossRef] [PubMed]
- Khezri, M.; Firoozabadi, M.; Sharafat, A.R. Reliable emotion recognition system based on dynamic adaptive fusion of forehead biopotentials and physiological signals. Comput. Methods Programs Biomed. 2015, 122, 149–164. [Google Scholar] [CrossRef] [PubMed]
- Niemic, C.P.; Warren, K. Studies of Emotion; A Theoretical and Empirical Review of Psychophysiological Studies of Emotion; JUR: Rochester, NY, USA, 2002; Volume 1, pp. 15–19. [Google Scholar]
- Lin, Y.P.; Wang, C.H.; Jung, T.P.; Wu, T.L.; Jeng, S.K.; Duann, J.R.; Chen, J.H. EEG-Based Emotion Recognition in Music Listening. IEEE Trans. Biomed. Eng. 2010, 57, 1798–1806. [Google Scholar] [PubMed]
- Mohammadi, Z.; Frounchi, J.; Amiri, M. Wavelet-based emotion recognition system using EEG signal. Neural Comput. Appl. 2017, 28, 1985–1990. [Google Scholar] [CrossRef]
- Ding, C.; Peng, H. Minimum redundancy feature selection from microarray gene expression data. J. Bioinform. Comput. Biol. 2005, 3, 185–205. [Google Scholar] [CrossRef] [PubMed]
- Radovic, M.; Ghalwash, M.; Filipovic, N.; Obradovic, Z. Minimum redundancy maximum relevance feature selection approach for temporal gene expression data. BMC Bioinform. 2017, 18, 9. [Google Scholar] [CrossRef] [PubMed]
- Jenke, R.; Peer, A.; Buss, M. Feature Extraction and Selection for Emotion Recognition from EEG. IEEE Trans. Affect. Comput. 2014, 5, 327–339. [Google Scholar] [CrossRef]
- Zhuang, N.; Zeng, Y.; Yang, K.; Zhang, C.; Tong, L.; Yan, B. Investigating Patterns for Self-Induced Emotion Recognition from EEG Signals. Sensors 2018, 18, 841. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Chen, M.; Zhao, S.; Hu, S.; Shi, Z.; Cao, Y. Relieff-based EEG sensor selection methods for emotion recognition. Sensors 2016, 16, 1558. [Google Scholar] [CrossRef] [PubMed]
- Alazrai, R.; Momani, M.; Daoud, M.I. Fall Detection for Elderly from Partially Observed Depth-Map Video Sequences Based on View-Invariant Human Activity Representation. Appl. Sci. 2017, 7, 316. [Google Scholar] [CrossRef]
- Alazrai, R.; Momani, M.; Khudair, H.A.; Daoud, M.I. EEG-based tonic cold pain recognition system using wavelet transform. Neural Comput. Appl. 2017. [Google Scholar] [CrossRef]
- Yoon, H.J.; Chung, S.Y. EEG-based emotion estimation using Bayesian weighted-log-posterior function and perceptron convergence algorithm. Comput. Biol. Med. 2013, 43, 2230–2237. [Google Scholar] [CrossRef] [PubMed]
- Van den Broek, S.P.; Reinders, F.; Donderwinkel, M.; Peters, M. Volume conduction effects in EEG and MEG. Electroencephalogr. Clin. Neurophysiol. 1998, 106, 522–534. [Google Scholar] [CrossRef]
- Liao, K.; Xiao, R.; Gonzalez, J.; Ding, L. Decoding individual finger movements from one hand using human EEG signals. PLoS ONE 2014, 9, e85192. [Google Scholar] [CrossRef] [PubMed]
- Verma, G.K.; Tiwary, U.S. Affect representation and recognition in 3D continuous valence-arousal-dominance space. Multimed. Tools Appl. 2016, 76, 2159–2183. [Google Scholar] [CrossRef]
- Zhou, S.M.; Gan, J.Q.; Sepulveda, F. Classifying mental tasks based on features of higher-order statistics from EEG signals in brain-computer interface. Inf. Sci. 2008, 178, 1629–1640. [Google Scholar] [CrossRef]
- Boashash, B.; Azemi, G.; Khan, N.A. Principles of time-frequency feature extraction for change detection in non-stationary signals: Applications to newborn EEG abnormality detection. Pattern Recognit. 2015, 48, 616–627. [Google Scholar] [CrossRef]
- Stanković, L. A measure of some time-frequency distributions concentration. Signal Process. 2001, 81, 621–631. [Google Scholar] [CrossRef]
- Acharya, U.R.; Fujita, H.; Sudarshan, V.K.; Bhat, S.; Koh, J.E. Application of entropies for automated diagnosis of epilepsy using EEG signals: A review. Knowl. Based Syst. 2015, 88, 85–96. [Google Scholar] [CrossRef]
- Acharya, U.R.; Fujita, H.; Sudarshan, V.K.; Oh, S.L.; Adam, M.; Koh, J.E.; Tan, J.H.; Ghista, D.N.; Martis, R.J.; Chua, C.K.; et al. Automated detection and localization of myocardial infarction using electrocardiogram: A comparative study of different leads. Knowl. Based Syst. 2016, 99, 146–156. [Google Scholar] [CrossRef]
- Faust, O.; Hagiwara, Y.; Hong, T.J.; Lih, O.S.; Acharya, U.R. Deep learning for healthcare applications based on physiological signals: A review. Comput. Methods Programs Biomed. 2018, 161, 1–13. [Google Scholar] [CrossRef] [PubMed]
| Emotion Labeling Scheme | Emotion Description Scale | Emotion Class | Number of Trials | Number of Feature Vectors for the 32 Subjects | The Mean Number of Feature Vectors for Each Individual Subject |
|---|---|---|---|---|---|
| 1D-2CLS | Arousal | Low arousal (LA) | 543 | 15,747 | 492 |
| High arousal (HA) | 737 | 21,373 | 668 | ||
| Valence | Low valence (LV) | 572 | 16,588 | 518 | |
| High valence (HV) | 708 | 20,532 | 518 | ||
| 1D-3CLS | Arousal | Low arousal (LA) | 304 | 8816 | 276 |
| Neutral | 607 | 17,603 | 334 | ||
| High arousal (HA) | 369 | 10,701 | 550 | ||
| Valence | Low valence (LV) | 297 | 8613 | 269 | |
| Neutral | 537 | 15,573 | 404 | ||
| High valence (HV) | 446 | 12,934 | 487 | ||
| 2D-4CLS | 2D arousal-valence plane | HAHV | 439 | 12,731 | 398 |
| LAHV | 269 | 7801 | 244 | ||
| LALV | 274 | 7946 | 248 | ||
| HALV | 298 | 8642 | 270 | ||
| 2D-5CLS | 2D arousal-valence plane | HAHV | 368 | 10,672 | 334 |
| LAHV | 198 | 5742 | 179 | ||
| LALV | 208 | 6032 | 189 | ||
| HALV | 220 | 6380 | 199 | ||
| Neutral | 286 | 8294 | 259 |
| Description of the Time-Frequency Features | Mathematical Formulation of the Extracted Time-Frequency Features |
|---|---|
| The mean of the CWD () | |
| The variance of the CWD () | |
| The skewness of the CWD () | |
| The kurtosis of the CWD () | |
| Sum of the logarithmic amplitudes of the CWD (SLA) | |
| Median absolute deviation of the CWD (MAD) | |
| Root mean square value of the CWD (RMS) | |
| Inter-quartile range of the CWD (IQR) |
| Description of the Time-Frequency Features | Mathematical Formulation of the Extracted Time-Frequency Features |
|---|---|
| The flatness of the CWD (FLS) | |
| The flux of the CWD (FLX) | |
| The spectral roll-off of the CWD (SRO) | |
| The normalized Renyi entropy of the CWD (NRE) | |
| The energy concentration of the CWD (EC) |
| Brain Region | Selected Pairs of EEG Channels |
|---|---|
| Parietal region | P3-P4, P7-P8 and CP5-CP6 |
| Frontal region | F3-F4, F7-F8, FC1-FC2, FC5-FC6, AF3-AF4 and FP1-FP2 |
| Temporal region | T7-T8 |
| Occipital region | O1-O2 |
| Configuration | Description | EEG Channels |
|---|---|---|
| Configuration 1 () | This configuration includes 11 independent pairs of symmetric EEG channels. | P3-P4, P7-P8, CP5-CP6, F3-F4, F7-F8, FC1-FC2, FC5-FC6, AF3-AF4, FP1-FP2, T7-T8, and O1-O2 |
| Configuration 2 () | This configuration includes 12 EEG channels located in the frontal and temporal areas of the brain. | FP1, FP2, F3, F4, F7, F8, FC1, FC2, T7, T8, FC5, and FC6 |
| Configuration 3 () | This configuration includes eight EEG channels located in the parietal and occipital areas of the brain. | P3, P4, CP5, CP6, P7, P8, O1, and O2 |
| Configuration 4 () | This configuration includes all the selected EEG channels. | P3, P4, P7, P8, CP5, CP6, F3, F4, F7, F8, FC1, FC2, FC5, FC6, AF3, AF4, FP1, FP2, T7, T8, O1, and O2 |
| Configuration | 1D-2CLS | 1D-3CLS | 2D-4CLS | 2D-5CLS | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Arousal | Valence | Arousal | Valence | ||||||||||
| C1 | AF3-AF4 | 72.5 | 62.3 | 73.9 | 69.7 | 65.2 | 41.2 | 64.0 | 49.2 | 58.4 | 45.9 | 56.4 | 42.0 |
| CP5-CP6 | 74.4 | 63.1 | 71.7 | 66.6 | 65.4 | 41.8 | 64.0 | 49.8 | 58.1 | 44.5 | 55.5 | 40.5 | |
| F3-F4 | 73.7 | 63.0 | 71.6 | 67.0 | 65.1 | 39.6 | 63.0 | 48.3 | 57.1 | 45.4 | 55.0 | 41.0 | |
| F7-F8 | 74.3 | 64.1 | 72.8 | 68.4 | 65.8 | 41.2 | 64.3 | 48.9 | 58.9 | 46.8 | 56.9 | 42.8 | |
| FC1-FC2 | 73.0 | 61.7 | 72.1 | 66.4 | 64.6 | 40.1 | 62.4 | 46.9 | 57.1 | 44.8 | 54.9 | 40.4 | |
| FC5-FC6 | 74.7 | 65.1 | 73.5 | 68.7 | 66.2 | 42.0 | 64.7 | 51.3 | 59.5 | 46.4 | 57.2 | 43.1 | |
| FP1-FP2 | 74.3 | 64.1 | 71.6 | 66.7 | 65.9 | 42.0 | 63.1 | 49.6 | 58.0 | 48.1 | 55.5 | 41.8 | |
| O1-O2 | 75.9 | 66.7 | 72.8 | 67.4 | 65.9 | 42.1 | 63.2 | 49.8 | 58.7 | 45.9 | 56.1 | 40.1 | |
| P3-P4 | 74.7 | 64.6 | 72.4 | 67.3 | 65.6 | 41.3 | 64.1 | 48.9 | 58.7 | 45.5 | 55.8 | 41.4 | |
| P7-P8 | 75.2 | 64.7 | 72.0 | 66.6 | 66.0 | 43.0 | 64.4 | 50.6 | 58.6 | 46.9 | 57.1 | 41.3 | |
| T7-T8 | 74.5 | 64.6 | 73.5 | 69.0 | 67.0 | 44.9 | 65.6 | 51.6 | 60.5 | 49.4 | 57.9 | 45.3 | |
| C2 | 81.0 | 75.1 | 79.6 | 77.3 | 74.7 | 60.4 | 73.4 | 65.3 | 70.6 | 62.5 | 68.8 | 56.6 | |
| C3 | 80.1 | 74.4 | 77.1 | 73.9 | 72.1 | 55.4 | 70.2 | 61.2 | 66.1 | 56.9 | 64.9 | 51.4 | |
| C4 | 83.1 | 78.5 | 80.7 | 78.5 | 76.0 | 62.2 | 75.6 | 68.1 | 72.5 | 65.0 | 71.1 | 59.7 | |
| Labeling Scheme | Top 5% | Top 25% | Top 50% | Top 75% | |||||
|---|---|---|---|---|---|---|---|---|---|
| 1D-2CLS | Arousal | 80.5 | 73.6 | 86.6 | 83.8 | 83.7 | 79.5 | 83.5 | 78.7 |
| Valence | 78.7 | 76.1 | 85.8 | 82.4 | 82.1 | 80.6 | 81.0 | 79.3 | |
| 1D-3CLS | Arousal | 75.4 | 58.9 | 78.8 | 65.8 | 78.4 | 65.5 | 77.9 | 65.0 |
| Valence | 73.7 | 66.1 | 77.8 | 70.6 | 76.5 | 69.4 | 75.9 | 68.9 | |
| 2D-4CLS | 69.5 | 60.9 | 75.1 | 68.8 | 73.9 | 66.7 | 73.0 | 65.5 | |
| 2D-5CLS | 69.9 | 57.8 | 73.8 | 61.9 | 73.1 | 61.0 | 72.0 | 60.0 | |
| Subject | 1D-2CLS | 1D-3CLS | 2D-4CLS | 2D-5CLS | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Arousal | Valence | Arousal | Valence | |||||||||
| Acc | STD | Acc | STD | Acc | STD | Acc | STD | Acc | STD | Acc | STD | |
| S1 | 84.9 | 2.4 | 83.7 | 2.6 | 78.4 | 2.5 | 77.3 | 2.5 | 76.2 | 3.1 | 75.7 | 4.7 |
| S2 | 82.3 | 2.2 | 81.7 | 2.9 | 77.6 | 1.0 | 75.8 | 4.4 | 73.1 | 3.0 | 72.5 | 2.4 |
| S3 | 87.9 | 1.5 | 86.3 | 3.4 | 83.4 | 2.4 | 81.2 | 2.1 | 78.4 | 3.1 | 76.4 | 1.2 |
| S4 | 85.3 | 4.2 | 84.6 | 1.5 | 76.0 | 4.4 | 77.9 | 2.0 | 75.2 | 3.2 | 73.8 | 3.9 |
| S5 | 90.4 | 2.2 | 91.0 | 3.2 | 77.6 | 1.8 | 78.6 | 0.4 | 74.0 | 3.5 | 72.9 | 3.1 |
| S6 | 82.4 | 1.7 | 81.9 | 1.4 | 78.0 | 2.4 | 77.0 | 2.1 | 74.2 | 4.2 | 72.8 | 1.1 |
| S7 | 87.5 | 1.4 | 88.7 | 2.1 | 86.6 | 2.5 | 86.1 | 1.2 | 84.3 | 1.4 | 82.3 | 1.5 |
| S8 | 88.8 | 0.8 | 87.3 | 2.0 | 75.0 | 1.9 | 73.8 | 0.9 | 71.5 | 4.7 | 70.7 | 1.5 |
| S9 | 85.3 | 1.0 | 86.2 | 2.7 | 84.0 | 2.6 | 83.2 | 1.6 | 81.0 | 2.3 | 80.9 | 2.0 |
| S10 | 88.6 | 1.6 | 87.2 | 2.1 | 85.6 | 1.9 | 83.4 | 1.5 | 78.4 | 3.1 | 76.6 | 2.9 |
| S11 | 86.0 | 1.8 | 84.3 | 2.2 | 72.3 | 3.3 | 71.0 | 2.3 | 67.7 | 2.1 | 65.7 | 2.7 |
| S12 | 84.5 | 1.8 | 82.7 | 2.2 | 75.4 | 2.3 | 73.5 | 3.0 | 68.1 | 2.0 | 66.8 | 1.7 |
| S13 | 92.2 | 0.9 | 91.8 | 2.8 | 82.4 | 2.8 | 81.9 | 4.3 | 77.4 | 2.4 | 75.8 | 1.9 |
| S14 | 86.3 | 2.7 | 85.5 | 1.0 | 75.5 | 3.2 | 74.1 | 2.5 | 70.1 | 2.2 | 69.7 | 2.0 |
| S15 | 84.8 | 1.7 | 83.1 | 1.3 | 80.9 | 1.8 | 81.3 | 2.0 | 79.1 | 2.7 | 77.9 | 2.7 |
| S16 | 92.7 | 5.0 | 91.4 | 2.4 | 86.6 | 2.2 | 84.9 | 1.8 | 82.3 | 3.5 | 81.7 | 1.3 |
| S17 | 86.5 | 3.1 | 85.0 | 3.8 | 83.5 | 1.7 | 82.3 | 1.8 | 80.0 | 1.6 | 78.0 | 1.6 |
| S18 | 84.4 | 4.3 | 86.1 | 2.6 | 81.6 | 2.7 | 83.6 | 2.8 | 80.2 | 1.5 | 78.4 | 2.7 |
| S19 | 82.6 | 3.2 | 82.8 | 2.7 | 74.6 | 2.7 | 74.1 | 3.7 | 72.2 | 2.0 | 70.9 | 1.9 |
| S20 | 85.8 | 3.2 | 83.2 | 3.7 | 75.9 | 1.4 | 73.3 | 2.8 | 71.3 | 1.7 | 69.1 | 5.0 |
| S21 | 86.2 | 2.7 | 85.2 | 4.4 | 72.4 | 2.2 | 71.4 | 1.5 | 69.1 | 2.5 | 67.9 | 1.9 |
| S22 | 85.4 | 1.2 | 84.6 | 2.0 | 75.1 | 2.5 | 73.4 | 3.5 | 70.2 | 6.6 | 68.9 | 4.1 |
| S23 | 91.8 | 1.5 | 90.5 | 2.3 | 86.2 | 2.6 | 87.9 | 1.0 | 83.6 | 3.3 | 81.6 | 2.2 |
| S24 | 87.9 | 3.5 | 85.4 | 3.3 | 76.4 | 2.6 | 75.3 | 2.7 | 73.2 | 1.3 | 71.8 | 1.7 |
| S25 | 84.6 | 3.1 | 83.6 | 2.5 | 74.3 | 2.1 | 72.8 | 2.7 | 69.2 | 3.7 | 68.3 | 3.7 |
| S26 | 87.7 | 2.4 | 86.6 | 2.3 | 78.8 | 2.0 | 73.2 | 4.1 | 70.2 | 2.1 | 69.2 | 4.0 |
| S27 | 83.8 | 1.3 | 82.3 | 1.9 | 76.6 | 4.7 | 72.4 | 1.9 | 78.2 | 3.2 | 76.3 | 2.3 |
| S28 | 92.7 | 2.9 | 91.7 | 3.3 | 79.9 | 2.0 | 79.8 | 2.1 | 77.2 | 2.7 | 73.9 | 2.0 |
| S29 | 84.3 | 2.7 | 84.0 | 2.7 | 80.1 | 1.6 | 78.1 | 2.8 | 74.2 | 1.9 | 72.8 | 2.3 |
| S30 | 86.6 | 3.2 | 85.9 | 2.4 | 82.7 | 1.2 | 81.5 | 2.7 | 79.0 | 2.4 | 77.6 | 3.0 |
| S31 | 84.2 | 0.8 | 83.7 | 3.5 | 75.1 | 3.1 | 73.7 | 1.1 | 72.1 | 2.1 | 70.9 | 4.4 |
| S32 | 88.0 | 2.2 | 87.6 | 1.0 | 73.3 | 1.2 | 75.0 | 2.4 | 73.3 | 4.3 | 72.0 | 2.8 |
| Overall average | 86.6 | 2.3 | 85.8 | 2.5 | 78.8 | 2.4 | 77.8 | 2.3 | 75.1 | 2.8 | 73.7 | 2.6 |
| Configuration | 1D-3CLS | 2D-5CLS | |||||
|---|---|---|---|---|---|---|---|
| Arousal | Valence | ||||||
| C1 | AF3-AF4 | 81.5 | 70.7 | 79.5 | 71.5 | 64.2 | 49.2 |
| CP5-CP6 | 79.7 | 67.5 | 79.4 | 70.1 | 63.8 | 47.3 | |
| F3-F4 | 79.7 | 67.6 | 78.2 | 68.5 | 62.3 | 47.2 | |
| F7-F8 | 80.6 | 69.9 | 79.0 | 70.9 | 64.4 | 49.5 | |
| FC1-FC2 | 80.7 | 68.9 | 78.5 | 68.6 | 63.5 | 47.2 | |
| FC5-FC6 | 80.4 | 68.7 | 79.7 | 70.7 | 64.3 | 50.0 | |
| FP1-FP2 | 81.4 | 69.9 | 79.1 | 70.7 | 63.2 | 48.1 | |
| O1-O2 | 80.1 | 68.2 | 79.2 | 71.1 | 63.7 | 46.6 | |
| P3-P4 | 81.3 | 69.4 | 78.8 | 70.0 | 63.9 | 47.8 | |
| P7-P8 | 80.4 | 69.6 | 79.4 | 69.1 | 64.4 | 49.1 | |
| T7-T8 | 82.2 | 71.4 | 80.1 | 72.2 | 65.4 | 50.1 | |
| C2 | 87.4 | 78.6 | 85.6 | 79.8 | 74.0 | 60.3 | |
| C3 | 85.2 | 76.1 | 83.5 | 76.5 | 70.5 | 56.8 | |
| C4 | 88.4 | 80.2 | 87.0 | 81.9 | 77.0 | 63.8 | |
| Labeling Scheme | Top 5% | Top 25% | Top 50% | Top 75% | |||||
|---|---|---|---|---|---|---|---|---|---|
| 1D-3CLS | Arousal | 84.6 | 78.4 | 89.8 | 81.8 | 88.6 | 80.8 | 88.5 | 80.5 |
| Valence | 85.9 | 80.1 | 88.9 | 83.1 | 87.7 | 82.4 | 87.0 | 81.9 | |
| 2D-5CLS | 74.2 | 60.4 | 79.3 | 66.7 | 78.9 | 66.3 | 77.9 | 65.1 | |
| Method | Features and Classifier | Number of EEG Channels | Labeling Scheme | Accuracy (%) | |
|---|---|---|---|---|---|
| Arousal | Valence | ||||
| Koelstra et al. [24], 2012 | Power spectral features, Gaussian naive Bayes classifier | 32 | 1D-2CLS | 62.0 | 57.6 |
| Chung and Yoon [28], 2012 | Power spectral features, Bayes classifier | 32 | 1D-2CLS | 66.4 | 66.6 |
| Rozgic et al. [27], 2013 | Power spectral features, SVM | 32 | 1D-2CLS | 69.1 | 76.9 |
| Liu et al. [26], 2016 | Deep belief network-based features, SVM | 32 | 1D-2CLS | 80.5 | 85.2 |
| Atkinson and Campos [31], 2016 | Statistical, fractal dimension and band power features, SVM | 14 | 1D-2CLS | 73.0 | 73.1 |
| Tripathi et al. [29], 2017 | Statistical time-domain features, neural networks | 32 | 1D-2CLS | 73.3 | 81.4 |
| Zhuang et al. [25], 2017 | EMD-based features, SVM | 8 | 1D-2CLS | 71.9 | 69.1 |
| Li et al. [52], 2017 | Time, frequency and nonlinear dynamic features, SVM | 8 | 1D-2CLS | 83.7 | 80.7 |
| Yin et al. [17], 2017 | Statistical and power spectral features, neural networks | 32 | 1D-2CLS | 77.1 | 76.1 |
| Our approach | QTFD-based features, SVM | 22 | 1D-2CLS | 86.6 | 85.8 |
| Menezes et al. [4], 2017 | Statistical, Power spectral and HOC features, SVM | 4 | 1D-3CLS after excluding the neutral samples | 74 | 88.4 |
| Our approach | QTFD-based features, SVM | 22 | 1D-3CLS after excluding the neutral samples | 89.8 | 88.9 |
| Chung and Yoon [28], 2012 | Power spectral, Bayes classifier | 32 | 1D-3CLS | 51.0 | 53.4 |
| Jirayucharoensak et al. [30], 2014 | Principle component analysis, deep leaning network | 32 | 1D-3CLS | 52.0 | 53.4 |
| Atkinson and Campos [31], 2016 | Statistical, fractal dimension and band power features, SVM | 14 | 1D-3CLS | 60.7 | 62.3 |
| Menezes et al. [4], 2017 | Statistical, power spectral and HOC features, SVM | 4 | 1D-3CLS | 63.1 | 58.8 |
| Tripathi et al. [29], 2017 | Statistical time-domain features, neural networks | 32 | 1D-3CLS | 57.5 | 66.7 |
| Our approach | QTFD-based features, SVM | 22 | 1D-3CLS | 78.8 | 77.8 |
| Zheng et al. [32], 2017 | STFT-based features, SVM | 32 | 2D-4CLS | 69.6 | |
| Zubair and Yoon [33], 2018 | Statistical and wavelet-based features, SVM | 32 | 2D-4CLS | 49.7 | |
| Our approach | QTFD-based features, SVM | 22 | 2D-4CLS | 75.1 | |
| Our approach | QTFD-based features, SVM | 22 | 2D-5CLS after excluding the neutral samples | 79.3 | |
| Our approach | QTFD-based features, SVM | 22 | 2D-5CLS | 73.8 | |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alazrai, R.; Homoud, R.; Alwanni, H.; Daoud, M.I. EEG-Based Emotion Recognition Using Quadratic Time-Frequency Distribution. Sensors 2018, 18, 2739. https://doi.org/10.3390/s18082739
Alazrai R, Homoud R, Alwanni H, Daoud MI. EEG-Based Emotion Recognition Using Quadratic Time-Frequency Distribution. Sensors. 2018; 18(8):2739. https://doi.org/10.3390/s18082739
Chicago/Turabian StyleAlazrai, Rami, Rasha Homoud, Hisham Alwanni, and Mohammad I. Daoud. 2018. "EEG-Based Emotion Recognition Using Quadratic Time-Frequency Distribution" Sensors 18, no. 8: 2739. https://doi.org/10.3390/s18082739
APA StyleAlazrai, R., Homoud, R., Alwanni, H., & Daoud, M. I. (2018). EEG-Based Emotion Recognition Using Quadratic Time-Frequency Distribution. Sensors, 18(8), 2739. https://doi.org/10.3390/s18082739





