A Novel Certificateless Signature Scheme for Smart Objects in the Internet-of-Things
Abstract
:1. Introduction
2. Preliminary
- The ECDLP is defined as follows: Let the notation denotes an elliptic curve over a prime finite field , defined by an equation: , where are constants such that . All points Pi = (xi, yi) on E and the infinity point O form a cyclic group G under the operation of point addition R = P + Q defined based on the chord-and-tangent rule. In addition, t · P = P + P + … + P (t times) is defined as a scalar multiplication, where P is a generator of G with order n. The ECDLP is that given a group G of elliptic curve points with prime order n, a generator P of G and a point x · P, it is computationally infeasible to derive x, where .
- Step 1 (Setup phase): A trusted KGC (key generation center) generates a master secret key , a corresponding master public key and a set of public parameters, i.e., .
- Step 2 (PartialPrivateKeyExtract phase): With the master secret key , and the user i’s identity , KGC generates a partial secret key for the user i.
- Step 3: KGC sends to the user i.
- Step 4 (SetSecretValue phase): Upon receiving , the user i examine the correctness of . If it holds, the user i randomly selects a value as his/her secret. Otherwise, the session is terminated.
- Step 5 (SetPublicKey phase): With and , the user i generates and outputs his/her public key .
- Step 6 (Sign phase): With the message m, this phase outputs a signature which is based on m, and .
- Step 7: the user i sends to the verifier.
- Step 8 (Verify phase): With the signature of the message m, the verifier examine the correctness of . If the examination holds, the signature is valid. Otherwise, the session is terminated.
3. The Proposed Certificateless Signature Scheme for IoT-Based Smart Objects
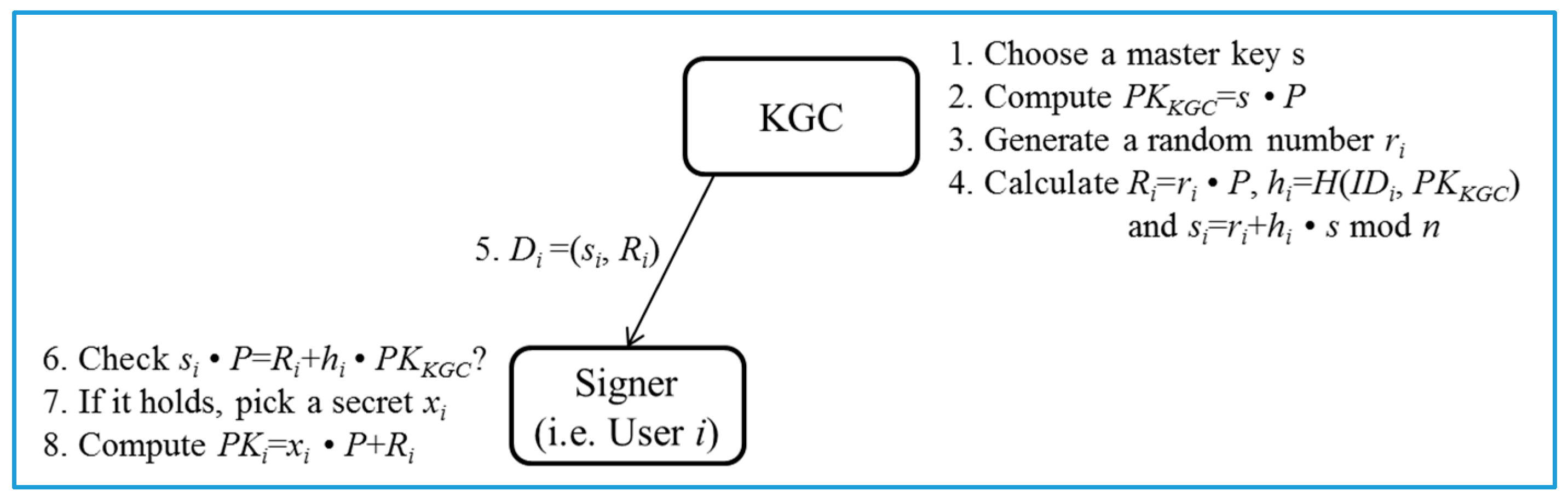
- Pre-processing phase (Figure 2):
- ○
- Steps 1–4: KGC generates a group G of elliptic curve points with prime order n and determines a generator P of G. Then, KGC chooses a master key and a secure hash function . Next, KGC calculates a master public key . Eventually, KGC publishes and keeps securely. Next, given , and the identity of user i, KGC generates a random number , and calculates , and mod n.
- ○
- Steps 5–6: KGC returns a partial private key to the user i who checks the validity of via whether the equation mod n holds or not. The correctness of is presented as follows:
- ○
- Steps 7–8: If it holds, the user i picks a random number as his/her own secret value. Otherwise, the session is terminated. Then, given and , the user i computes as his/her public key.
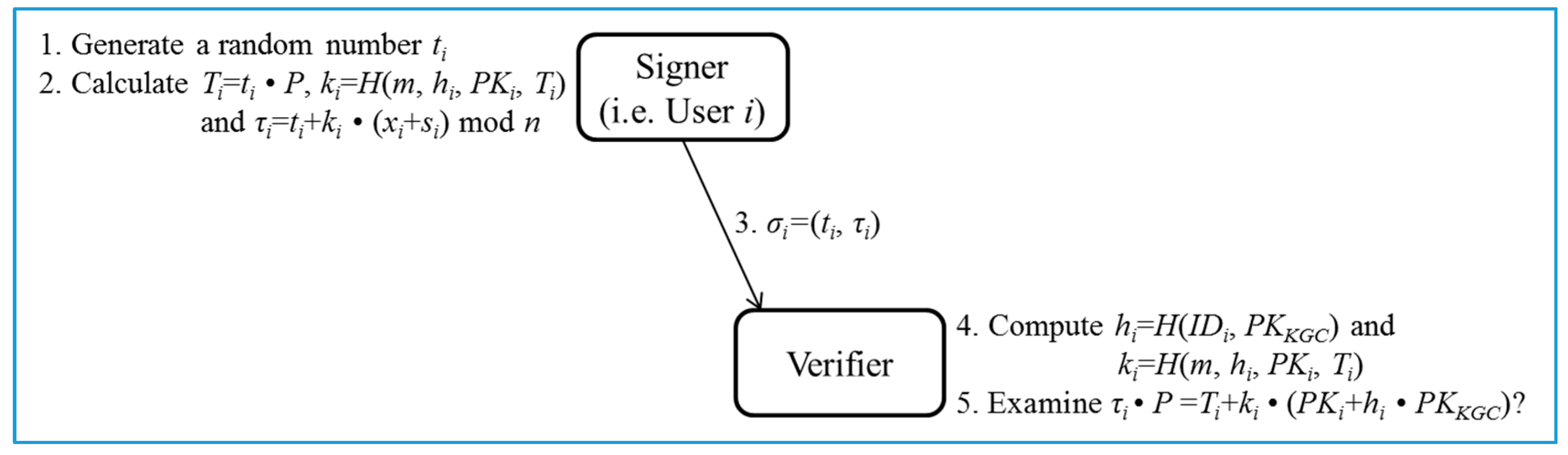
- Sign/Verify phase (Figure 3):
- ○
- Steps 1–3 (Sign): Given , , and a message m, the user i first chooses a random number . Then, the user i computes , and mod n. Note that the computation of is performed at the Pre-processing phase and thus the cost can be removed. Finally, the user i outputs as the signature of the message m.
- ○
- Steps 4–5 (Verify): Given , , , and , the verifier first computes and . Next, the verifier examines if holds. The signature is accepted if the equation holds. The correctness of the signature is presented as follows:
4. Security Analysis
4.1. Adversary Model for Certificateless Signature
- : The oracle takes as input a query , where is the party ’s identity, and then runs algorithms PartialPrivateKeyExtract, SetSecretValue, and SetPublicKey to obtain the partial private key , the secret value , and the public key .
- : The oracle takes as input a query . It browses the list and returns the party ’s public key .
- : The oracle takes as input a query . This oracle replaces the party ’s public key with and updates the corresponding information in the list .
- : The oracle takes as input a query . It browses the list and returns the secret values . However, if the party has been asked the query, it returns .
- : The oracle takes as input a query . It then browses the list L and returns the partial private key .
- : The oracle takes as input a query , where denotes the message to be signed. This oracle outputs a signature such that . If the public key has not been replaced, i.e., , is the public key returned from the oracle . Otherwise, , where is the latest public key value submitted to the oracle .
- (1)
- has never queried the oracle .
- (2)
- has never queried the oracle .
- (3)
- true ← Verify(mt, σt, params, IDt, PKt) where PKt is the current public key of party t and it may be replaced by SA1.
- (1)
- has never queried the oracle .
- (2)
- has never queried the oracle .
- (3)
- true ← Verify(mt, σt, params, IDt, PKt), where is the original public key of party.
4.2. Formal Analysis
- Initialization phase: picks an identity as the challenged identity in Game 1, sets and sends to .
- Query phase:
- ➢
- : The oracle takes as input a query . If has been created, nothing happens. Otherwise, runs algorithms PartialPrivateKeyExtract, SetSecretValue, and SetPublicKey to obtain the partial private key , the secret value and the public key . Next, returns to .
- ➢
- query:
- (1)
- When accesses a hash query on , if the list contains , returns to . Otherwise, picks a random number , returns to , and adds to .
- (2)
- When accesses a hash query on , if the list contains , returns to . Otherwise, picks a random number , returns to , and adds to .
- ➢
- : Upon receiving a query with an identity from , performs the following steps.
- (1)
- If , selects three random numbers , and performs , , , and . Then, adds to list , and and to list , respectively. Finally, returns to .
- (2)
- Otherwise, generates three random numbers , and sets , , and . Then, adds to list , and and to list , respectively. Finally, returns to .
- ➢
- : Upon receiving an query for an identity from , performs the following steps.
- (1)
- If , stops the session.
- (2)
- Otherwise, looks at for . If there exists a record of such a tuple, returns to ; otherwise, makes a query with and returns to accordingly.
- ➢
- : When receives an query for an identity from , looks for in the list . If there is such a tuple, returns to . Otherwise, makes a query and returns to .
- ➢
- : Once receives a query for some from , looks for in the list . If there exists such a record, sets and . Otherwise, makes a query with and then sets and .
- ➢
- : Upon receiving a query with from , looks for and in the lists . Next, generates a random number , and computes and . After that, returns to .
- : does not abort in all of the queries.
- : successfully forges a valid signature .
- : The forged signature satisfies .
- ➢
- : When makes this query with an identity , acts as follows:
- (1)
- If , generates two random numbers , and computes , , mod n and . Then, adds , and to the lists and , respectively. Finally, returns to .
- (2)
- Otherwise, selects a random value , and sets , , mod n and . Then, adds , and to the lists and respectively. Finally, returns to .
- ➢
- : When makes this query with an identity , looks for in . If there exists a record of such a tuple, returns to ; otherwise, makes a query with and returns to accordingly.
- ➢
- : When makes this query with an identity , acts as follows:
- (1)
- If , terminates the session.
- (2)
- Otherwise, looks for in . If there is such a record, returns to ; otherwise, makes a query with and then returns to .
- : does not abort in all of the queries.
- : successfully forges a valid signature .
- : The forged signature satisfies .
5. System Implementation and Performance Evaluation
- (1)
- Condition (1). For the Arduino Uno, we adopt elliptic curve points over a prime field with a 192-bit prime , a random number generator with a 96-bit output sequence and a secure one-way hash function, i.e., SHA-3 (512-bit) [22] as the underlying crypto-modules in our proposed certificateless scheme.
- (2)
- Condition (2). For the Raspberry PI 2 platform, the elliptic curve is with a 384-bit prime and the random number generator is with 96-bit output sequence. In addition, SHA-3 (512-bit) is implemented as the one-way hash function.
6. Related Work
6.1. Review of Certificateless Signature Schemes
6.2. Previously Unknown Weakness in Wang et al’s (2015) CLS Scheme
- Revisiting the scheme:
- ➢
- In the Setup phase, KGC generates a group G of elliptic curve points with prime order n and determines a generator P of G, prior to randomly selecting a master secret key and computing the master public key . Then, KGC chooses two secure hash functions and , and publishes a set of system parameters, i.e., .
- ➢
- In the PartialPrivateKeyExtract phase, given , and the user i’s identity , KGC selects a random number , and computes , and mod n. Next, KGC returns the partial private key to the user i. Upon receiving , i is able to verify by examining whether two values, i.e., and , are identical or not since .
- ➢
- In the SetSecretValue phase, given , the user i randomly selects as his/her secret value.
- ➢
- In the SetPublicKey phase, given and , the user i computes his/her public key as .
- ➢
- In the Sign phase, given , , and a message m, the user i selects a random value , and outputs a signature with a series of computed values , and mod n.
- ➢
- In the Verify phase, Given , , , m and , the verifier computes and , and then checks whether the equation holds. Note that is accepted if the equation holds. That is, .
- Cryptanalysis
- ➢
- Suppose there exists a malicious super type I adversary j which seeks to forge a valid signature on a message m' chosen by the adversary j. The adversary j eavesdrops a valid signature with message m issued by the user i from any previous session, where , , , , , , mod n, and mod n.
- ➢
- Since the adversary j is a super type I adversary, j is able to issue an oracle query of ExtractSecretValue(i) and replace any entity’s public key including KGC’s public key. With the eavesdropped values, i.e., , and , and public values, i.e., and , the adversary j chooses a random number , and derives , , and mod n. Note that the secret is retrieved via ExtractSecretValue(i) oracle query.
- ➢
- So far, the adversary j can forge a valid signature on the chosen message m'. It is obvious that the equation holds. Therefore, the resistance to signature forgery attack cannot be guaranteed under the assumption of existing a malicious super type I adversary.
6.3. Security and Performance Comparative Summary
7. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Yang, Y.; Lu, J.; Choo, K.K.R.; Liu, J. On Lightweight Security Enforcement in Cyber-physical Systems. In Proceedings of the International Workshop on Lightweight Cryptography for Security & Privacy (LightSec 2015), Bochum, Germany, 10–11 September 2015. [Google Scholar]
- D'Orazio, C.; Choo, K.-K.R. Circumventing iOS Security Mechanisms for APT Forensic Investigations: A Security Taxonomy for Cloud Apps. Future Gener. Comput. Syst. 2016. [Google Scholar] [CrossRef]
- D'Orazio, C.; Choo, K.-K.R. A Technique to Circumvent SSL/TLS Validations on iOS Devices. Future Gener. Comput. Syst. 2016. [Google Scholar] [CrossRef]
- D'Orazio, C.; Choo, K.-K.R.; Yang, L.T. Data Exfiltration from Internet of Things Devices: iOS Devices as Case Studies. IEEE Internet Things J. 2017, 4, 524–535. [Google Scholar] [CrossRef]
- Yao, X.; Han, X.; Du, X.; Zhou, X. A lightweight multicast authentication mechanism for small scale IoT applications. IEEE Sens. J. 2013, 13, 3696–3701. [Google Scholar] [CrossRef]
- Kawamoto, Y.; Nishiyama, H.; Kato, N.; Shimizu, Y.; Takahara, A.; Jiang, T. Effectively collecting data for the location-based authentication in the Internet of Things. IEEE Sens. J. 2015. [Google Scholar] [CrossRef]
- Hernandez-Ramos, J.L.; Pawlowski, M.P.; Jara, A.J.; Skarmeta, A.F.; Ladid, L. Toward a lightweight authentication and authorization framework for smart objects. IEEE J. Sel. Areas Commun. 2015, 33, 690–702. [Google Scholar] [CrossRef]
- Gope, P.; Hwang, T. BSN-Care: A Secure IoT-based modern healthcare system using body sensor network. IEEE Sens. J. 2016, 16, 1368–1376. [Google Scholar] [CrossRef]
- Yang, Y.; Cai, H.; Wei, Z.; Lu, H.; Choo, K.-K.R. Towards Lightweight Anonymous Entity Authentication for IoT Applications. In Proceedings of the 21st Australasian Conference on Information Security and Privacy-CISP 2016, Melbourne, Australia, 4–6 July 2016; pp. 265–280. [Google Scholar]
- Nguyen, K.; Ouahla, N.; Laurent, M. Lightweight Certificateless and Provably-Secure Signcryptosystem for the Internet of Things. In Proceedings of the 14th IEEE International Conference on Trust, Security and Privacy in Computing and Communications (IEEE TrustCom-15), Helsinki, Finland, 20–22 August 2015. [Google Scholar]
- Toorani, M.; Beheshti, A.A. An elliptic curve-based signcryption scheme with forward secrecy. J. Appl. Sci. 2009, 9, 1025–1035. [Google Scholar] [CrossRef]
- Dutta, M.; Singh, A.K.; Kumar, A. An Efficient Signcryption Scheme based on ECC with Forward Secrecy and Encrypted Message Authentication. In Proceedings of the IEEE 3rd International Advance Computing Conference (IACC), Ghaziabad, India, 22–23 February 2013. [Google Scholar]
- Yu, G.; Yang, H.; Fan, S.; Han, W. Efficient Certificateless Signcryption Scheme from Weil Pairing. J. Netw. 2011, 6, 1280–1287. [Google Scholar] [CrossRef]
- Singh, J.; Kumar, V.; Kumar, R. An RSA based Certificateless Signature Scheme for Wireless Sensor Networks. In Proceedings of the 2015 International Conference on Green Computing and Internet of Things (ICGCIoT), Noida, India, 8–10 October 2016. [Google Scholar]
- Sharma, G.; Bala, S.; Verma, A.K. An improved RSA Based Certificateless Signature Scheme for Wireless Sensor Networks. Int. J. Network Secur. 2016, 18, 82–89. [Google Scholar]
- Tsai, J.-L. A New Efficient Certificateless Short Signature Scheme Using Bilinear Pairings. IEEE Syst. J. 2015. [Google Scholar] [CrossRef]
- Huang, X.; Mu, Y.; Susilo, W.; Wong, D.S.; Wu, W. Certificateless signature revisited. In Proceedings of the 12th Australasian Conference on Information Security and Privacy (ACISP), Townsville, Australia, 2–4 July 2007; pp. 308–322. [Google Scholar]
- Al-Riyami, S.; Paterson, K. Certificateless public key cryptography. In Proceedings of the International Conference on the Theory and Application of Cryptology and Information Security (ASIACRYPT), Taipei, Taiwan, 30 November–4 December 2003; pp. 452–473. [Google Scholar]
- Huang, X.; Mu, Y.; Susilo, W.; Wong, D.S.; Wu, W. Certificateless Signatures: New Schemes and Security Models. Comput. J. 2012, 55, 457–474. [Google Scholar] [CrossRef]
- Pointcheval, D.; Stern, J. Security Proofs for Signature Schemes. In Proceedings of the International Conference on the Theory and Applications of Cryptographic Techniques (EUROCRYPT), Saragossa, Spain, 12–16 May 1996; pp. 387–398. [Google Scholar]
- FIPS PUB 186–4, Digital Signature Standard (DSS), National Institute of Standards and Technology, June 2009. Available online: http://nvlpubs.nist.gov/nistpubs/FIPS/NIST.FIPS.186-4.pdf (accessed on 1 May 2017).
- Dworkin, M.J. SHA-3 Standard: Permutation-Based Hash and Extendable-Output Functions, NIST FIPS-202. August 2015. Available online: http://nvlpubs.nist.gov/nistpubs/FIPS/NIST.FIPS.202.pdf (accessed on 24 December 2016).
- The Bouncy Castle Crypto APIs. 2016. Available online: https://www.bouncycastle.org/ (accessed on 24 December 2016).
- Fackelmann/SHA3. Available online: https://github.com/Fackelmann/SHA3 (accessed on 20 March 2017).
- Kmackay/micro-ecc. Available online: https://github.com/kmackay/micro-ecc (accessed on 20 March 2017).
- AESLib. Available online: https://github.com/DavyLandman/AESLib (accessed on 21 April 2017).
- Maletsky, K. RSA vs ECC Comparison for Embedded Systems (White Paper), Atmel. Available online: http://www.atmel.com/Images/Atmel-8951-CryptoAuth-RSA-ECC-Comparison-Embedded-Systems-WhitePaper.pdf (accessed on 18 January 2017).
- Wang, L.; Chen, K.; Long, Y.; Mao, X.; Wang, H. A Modified Efficient Certificateless Signature Scheme without Bilinear Pairings. In Proceedings of the 2015 International Conference on Intelligent Networking and Collaborative Systems (INCOS), Taipei, Taiwan, 2–4 September 2015. [Google Scholar] [CrossRef]
- Gong, P.; Li, P. Further Improvement of a Certificateless Signature Scheme without Pairing. Int. J. Commun. Syst. 2014, 27, 2083–2091. [Google Scholar] [CrossRef]
- Yeh, K.-H.; Tsai, K.-Y.; Kuok, R.-Z.; Wu, T.-C. Robust Certificateless Signature Scheme without Bilinear Pairings. In Proceedings of the International Conference on IT Convergence and Security (ICITCS 2013), Macau, China, 16–18 December 2013. [Google Scholar]
- Yeh, K.-H.; Tsai, K.-Y.; Fan, C.-Y. An Efficient Certificateless Signature Scheme without Bilinear Pairings. Multimed. Tools Appl. 2015, 74, 6519–6530. [Google Scholar] [CrossRef]
- Shi, W.; Kumar, N.; Gong, P.; Zhang, Z. Cryptanalysis and Improvement of a Certificateless Signcryption Scheme without Bilinear Pairing. Front. Comput. Sci. 2014, 8, 656–666. [Google Scholar] [CrossRef]
- Pang, L.; Hu, Y.; Liu, Y.; Xu, K.; Li, H. Efficient and Secure Certificateless Signature Scheme in the Standard Model. Int. J. Commun. Syst. 2017, 30. [Google Scholar] [CrossRef]

| Environment | Description |
|---|---|
| Arduino Uno | Atmel ATmega328P 8-Bit 16MHz AVR Architecture Memory 2 KB RAM/32 KB EEPROM |
| Raspberry PI 2 | Broadcom BCM2836 @ 1 GHz Quad-Core ARM Cortex-A7 Architecture with 1 GB DDR2 RAM and SanDisk 16 GB Class 10 SD Card |
| Programming Language | (For Raspberry PI 2) Eclipse 3.8 with Oracle Java 8 ARM (For Arduino Uno) ANSI C |
| Crypto API | (For Raspberry PI 2) The Bouncy Castle Crypto APIs [23] (For Arduino Uno) Fackelmann/SHA3 [24], Kmackay/micro-ecc [25], AESLib [26] |
| Phase | Computation Cost | Execution Time | Total |
|---|---|---|---|
| Pre-processing | Generate , , , (96-bit) | 4.414 ms | 23.044 s |
| Compute (SHA-3 with 288 bit input sequence) | 0.2 ms | ||
| Compute , , , (ECC 192-bit) | 14.4 s | ||
| Verify (ECC 192-bit) | 8.64 s | ||
| Sign | Generate (96-bit) | 1.104 ms | 11.537 s |
| Compute (SHA-3 with 1408-bit input sequence) 1 | 16.2 ms | ||
| Compute (ECC with 192-bit) | 2.88 s | ||
| Compute (ECC 192-bit) | 8.64 s | ||
| Verify | Compute (SHA-3 with 288-bit input sequence) | 0.2 ms | 14.416 s |
| Compute (SHA-3 with 1408-bit input sequence) 1 | 16.2 ms | ||
| Verify (ECC 192-bit) | 14.4 s |
| Phases of the Proposed Scheme | Total Execution Time |
|---|---|
| Pre-processing phase | 10.812 s |
| Sign phase | 5.421 s |
| Verify phase | 6.771 s |
| Input Sequence of AES | Encryption/Decryption |
|---|---|
| AES-128 with 32/64/128/256 Bytes Input Sequence | 0.63 ms |
| AES-256 with 32/64/128/256 Bytes Input Sequence | 0.87 ms |
| Phase | Computation Cost | Execution Time | Total |
|---|---|---|---|
| Pre-processing | Generate , , , (96-bit) | 0.276 ms | 0.895 ms |
| Compute (SHA-3 with 480-bit input sequence) | 0.0051 ms | ||
| Compute , , , (ECC 384-bit) | 0.355 ms | ||
| Verify (ECC 384-bit) | 0.213 ms | ||
| Sign | Generate (96-bit) | 0.069 ms | 1.549 ms |
| Compute (SHA-3 with 1792-bit input sequence) 1 | 1.196 ms | ||
| Compute (ECC with 384-bit) | 0.071 ms | ||
| Compute (ECC 384-bit) | 0.213 ms | ||
| Verify | Compute (SHA-3 with 480-bit input sequence) | 0.0051 ms | 1.556 ms |
| Compute (SHA-3 with 1792-bit input sequence) 1 | 1.196 ms | ||
| Verify (ECC 384-bit) | 0.355 ms |
| SHA-3 Operation | Execution Time |
|---|---|
| SHA-3 with 576-bit input sequence | 0.412 ms |
| SHA-3 with 1152-bit input sequence | 0.939 ms |
| SHA-3 with 1728-bit input sequence | 1.194 ms |
| SHA-3 with 2304-bit input sequence | 1.726 ms |
| SHA-3 with 2880-bit input sequence | 2.260 ms |
| SHA-3 with 3456-bit input sequence | 2.407 ms |
| SHA-3 with 4032-bit input sequence | 2.807 ms |
| SHA-3 with 4608-bit input sequence | 3.215 ms |
| SHA-3 with 5184-bit input sequence | 4.084 ms |
| SHA-3 with 5760-bit input sequence | 4.430 ms |
| Gong & Li’s Scheme [29] | Wang et al’s Scheme [28] | Tsai’s Scheme [16] | Our proposed Scheme | |
|---|---|---|---|---|
| Resistance to Super Type I Adversary | No | No | Yes | Yes |
| Resistance to Super Type II Adversary | Yes | Yes | Yes | Yes |
| Sign Phase | Verify Phase | In Total | |
|---|---|---|---|
| Gong & Li’s scheme [29] | 1Tem + 2Tm + 2Tadd + 2Th + 1Tg | 4Tem + 3Teadd + 3Th | 5Tem + 2Tm + 3Teadd + 2Tadd + 5Th + 1Tg |
| Wang et al’s scheme [28] | 1Tem + 1Tm + 2Tadd + 1Th + 1Tg | 3Tem + 3Teadd + 2Th | 4Tem + 1Tm + 3Teadd + 2Tadd + 3Th + 1Tg |
| Tsai’s scheme [16] | 1Tinv + 1Tem + 1Tm + 1Tadd + 1Th | 2Tbp + 2Tem + 2Teadd + 2Th | 1Tinv + 2Tbp + 3Tem + 1Tm + 2Teadd + 1Tadd + 3Th |
| Our proposed scheme | 1Tem + 1Tm + 2Tadd + 1Th + 1Tg | 3Tem + 2Teadd + 2Th | 4Tem + 1Tm + 2Teadd + 2Tadd + 3Th + 1Tg |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yeh, K.-H.; Su, C.; Choo, K.-K.R.; Chiu, W. A Novel Certificateless Signature Scheme for Smart Objects in the Internet-of-Things. Sensors 2017, 17, 1001. https://doi.org/10.3390/s17051001
Yeh K-H, Su C, Choo K-KR, Chiu W. A Novel Certificateless Signature Scheme for Smart Objects in the Internet-of-Things. Sensors. 2017; 17(5):1001. https://doi.org/10.3390/s17051001
Chicago/Turabian StyleYeh, Kuo-Hui, Chunhua Su, Kim-Kwang Raymond Choo, and Wayne Chiu. 2017. "A Novel Certificateless Signature Scheme for Smart Objects in the Internet-of-Things" Sensors 17, no. 5: 1001. https://doi.org/10.3390/s17051001
APA StyleYeh, K.-H., Su, C., Choo, K.-K. R., & Chiu, W. (2017). A Novel Certificateless Signature Scheme for Smart Objects in the Internet-of-Things. Sensors, 17(5), 1001. https://doi.org/10.3390/s17051001







