1. Introduction
Robotics has received notoriety in our society mainly due to the wide use of manipulators. However, recent advances on the research of autonomous vehicles have shown a much more vast range of applications, such as exploration, surveillance and environmental monitoring. In this sense, the use of aerial robots have a clear advantage over other kind of robots, since they are able to navigate over large areas faster and with a privileged view from above.
Autonomous mapping in Robotics could be defined as the task of acquiring models of the environment using autonomous mobile robots [
1]. One of the most versatile type of mapping is the aerial one. Aerial surveys can use a great variety of sensors such as cameras, lasers, radio receptors, barometers, magnetometers, etc. Currently, most aerial surveys are created using a manned aircraft with expensive and special equipment, and therefore it is a high cost and time consuming task, as it generally must be done on large areas. In this context, autonomous aerial robots can bring many benefits to the workers and companies. Mapping with autonomous robots can reduce the risk of endangering human lives, and it can also reduce the economic costs of the task.
In this context, geophysical maps such as magnetic, gravitational and textured digital elevation maps can be used in different situations. Some practical applications that benefit from such maps are: (i) in geology it is possible to use a coverage strategy to detect minerals of commercial interest beneath the ground; (ii) in the military, to find unexploded ordnance (UXOs), sunken ships and submarines at sea; (iii) in archeology, they are used to create maps of subsurface buried artifacts; among others.
One of the main aspects that must be considered before executing a mapping is which type of information must be acquired, and consequently the sensors that will be used. In geophysical surveys, magnetometers are among the most widely used ones, allowing for the evaluation of the magnetic field at a certain region.
The fluxgate magnetometer is a traditional and well known instrument that have been used in geophysical exploration for decades, mostly due to its small size, good sensitivity, low noise and relatively low power consumption. This low noise characteristic is however directly related to a strong limit on its frequency response.
Fluxgate sensors are built using materials of high magnetic permeability that are excited up to the saturation limits by a source with periodic current. A significant part of this noise is due to magnetic properties of the sensor core. The right choice of materials and special thermal treatment can produce sensors with very low noise figures. The characteristics of the core material are also fundamental to improve the intensity of the induced signal in the sense coil [
2]. There are several new amorphous and crystaline (nanocrystaline) materials available [
3,
4,
5], and deeper investigation would be necessary to see if this class of material has the potential to be used in fluxgate applications.
In most uses as in geomagnetic stations, the fluxgate integration filter is set to frequencies usually below 1 Hz, with 0.1 Hz being typical [
6], which is not adequate for moving platform applications. To increase the sensor frequency response, a higher frequency is also necessary for the core excitation, consequently affecting the core material choice. Cobalt based amorphous alloys are among the best for fluxgate sensor due to its lower intrinsic noise and lower conductivity which result in smaller eddy currents, favoring its use at higher frequencies [
7].
In this work, we discuss the development of a state-of-the-art three-axis fluxgate magnetometer to be used in aeromagnetic surveys. The proposed sensor is specially designed for small rotary-wing UAVs, considering possible applications in the mining industry such as prospection of ferromagnetic minerals beneath the ground.
The magnetometer uses two ring-cores with CoFeSiB amorphous ribbon developed for the detection of small ferrous minerals concentration. Due to UAV restricted resources, the electronic design aims to reduce its size and power consumption. The sensor housing is assembled far from the electronics, in order to allow enough distance from the UAV’s motors, a substantial source of magnetic noise.
The remainder of this paper is structured as follows:
Section 2 presents the details regarding the magnetometer development. The coverage path planning strategy for autonomous mapping is proposed in
Section 3, followed by
Section 4 in which we describe the methodology for data acquisition and map generation. The experiments and analysis about the results are presented in
Section 5 and finally in
Section 6 we draw the conclusions and discuss paths for future investigation.
2. Magnetometer Development
Detailed geophysical surveys need accurate sensor information. These mapping executions with aerial techniques are very restricted. In most cases, such missions are done manually using a manned aircraft, which increases the survey duration, as well as the economical costs, whilst the quality of data is not necessarily improved. Other types of magnetic surveys can be done by foot or by ground vehicles, thus augmenting the survey time.
On the other hand, mapping with autonomous robots can reduce risks and costs related to the task. Due to the UAV’s potential to increase productivity while mitigating safety hazards, mining companies already benefit from such equipment integrated into their operations.
The sensor described here is designed specifically for mining applications, focusing on aeromagnetic surveys for prospection of ferromagnetic minerals beneath the ground. The instrument is capable to detect small ferrous minerals concentration, and suitable for installation in moving platforms. Considering the UAV restrictions, the developed magnetometer presents particular characteristics, including reduced weight, dimensions, and power consumption. We also decrease costs greatly by considering the use of small and inexpensive robots. The proposed sensor is at par with other fluxgate magnetometers on the market with a similar scale range and sensitivity [
8,
9] but with an increased data rate of ≈4–5 Hz and smaller size.
Table 1 presents a summary of the three-axis fluxgate magnetometer proposed to be used in autonomous aeromagnetic surveys.
Figure 1 shows the complete sensor mounting.
2.1. Materials
In this work, we used a
composition melted by melt-spinner method [
10] and after submitted to a convenient stress-annealing technique [
11] increasing its sensibility and reducing its noise level.
As shown in the literature, there is a dependence between the magnetization process of the amorphous ribbon and the induced effects when an external load (“stress”) is applied on the ribbon during the adjustment process in the core [
12]. So to reduce them is convenient to use the ring-core geometry as applied in this experiment.
The ribbon was improved using an adequate stress-annealing that is fundamental to induce the appearance of transverse magnetic anisotropy causing rotation of the spontaneous domains of magnetization. A domain study of magnetization processes in a stress-annealed metallic glass ribbon for fluxgate sensors [
12] confirms the importance of the longitudinal axis of the amorphous ribbon to be an easy magnetization axis, as well as the need of a convenient rotation of the domain walls, to obtain low levels of noises in fluxgate sensors. When the ribbon is accurately thermally annealed, it makes possible to obtain a fluxgate sensor with low level of noise, with a performance superior to the commercial crystalline materials [
13].
2.2. Instrument Construction
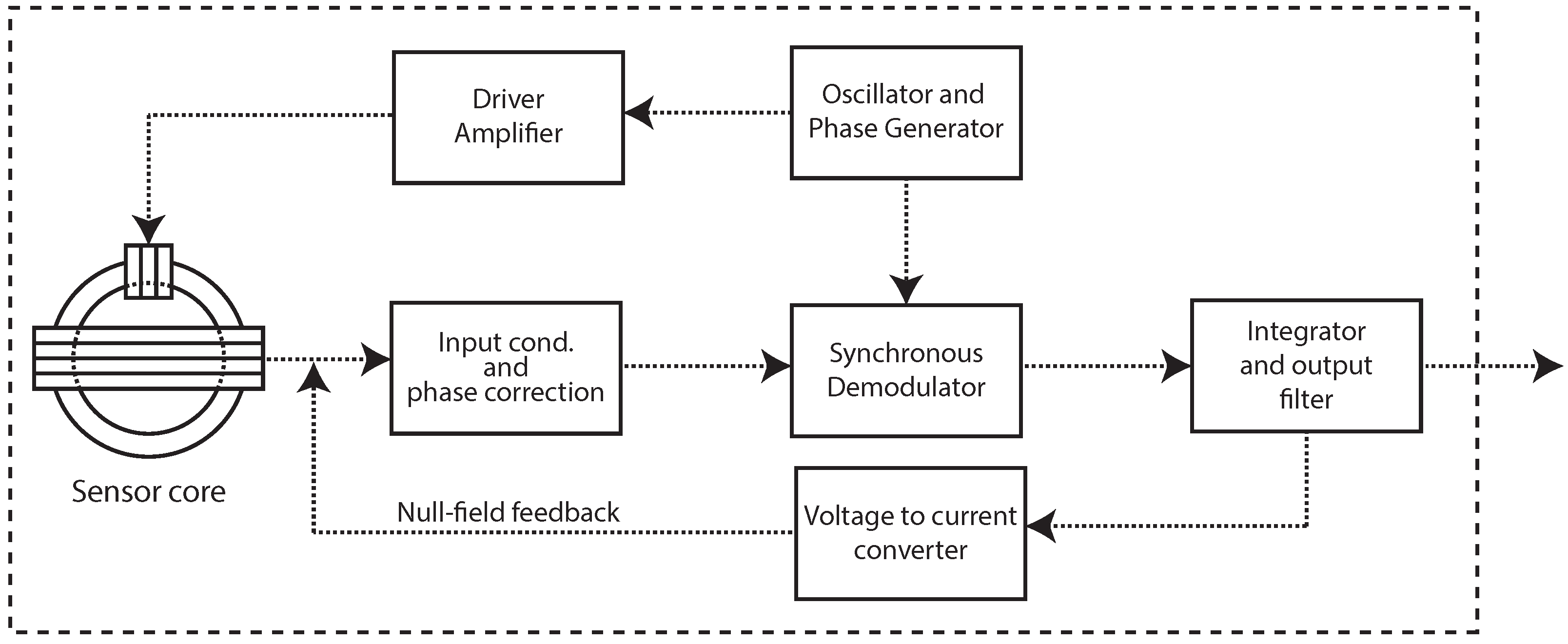
The electronic circuit devised for this application is based on the traditional topology of second harmonic synchronous demodulation with current feedback, with the sensor operating in a null field condition [
14]. This arrangement allows for a large dynamic range and great stability, reducing the circuit sensitivity to core parameter variations. A simplified block diagram for the sensor processing circuitry is shown on
Figure 2.
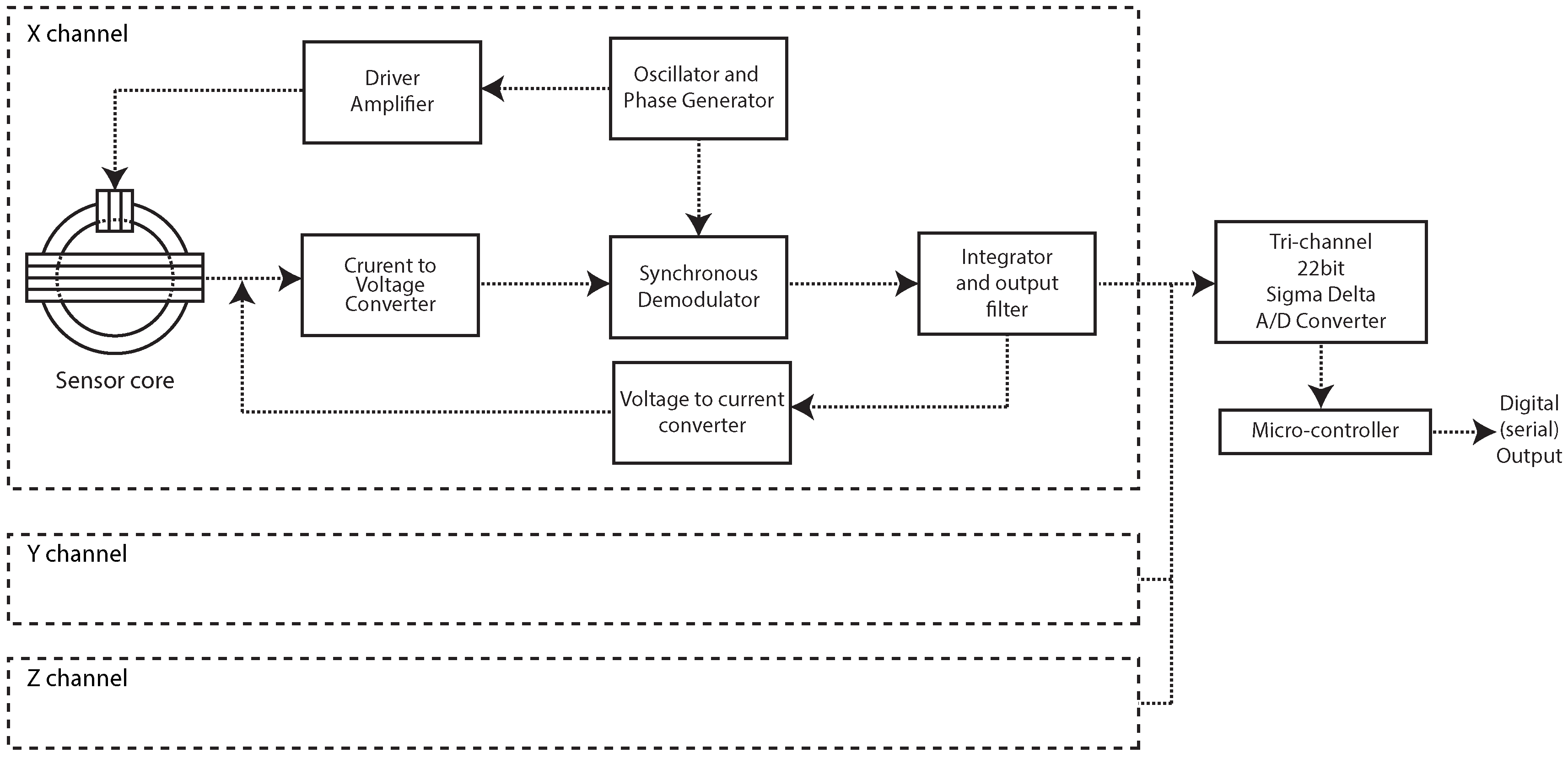
Although based on a traditional configuration, some minor changes were made to assure a good performance under fast changing field conditions as faced on a moving platform. No resonant filter was used at the sensor secondary winding and a special capacitive sampling and hold acted as a synchronous demodulator. All control pulses were produced by a small micro controller embedded in the oscillator and phase generation stage, conferring also great flexibility during the adjustment and calibration tasks. In order to reduce overall sensor size, two axes were wounded over one single core. This arrangement additionally saves 30% of drive power when compared to traditional three ring cores topology.
After demodulation and integration, the analog signal from each axis is carried to a three channel 22 bit sigma-delta A/D converter, controlled by a small micro-controller responsible for taking the measurements, apply calibration coefficients and transmit the resultant information throughout a serial communication port as in
Figure 3.
5. Experimental Evaluation
Additional to the standard testing and calibration protocols, the magnetometer was subject to a few characterization procedures in order to confirm its specifications as required for this unique application.
5.1. Noise and Sensitivity
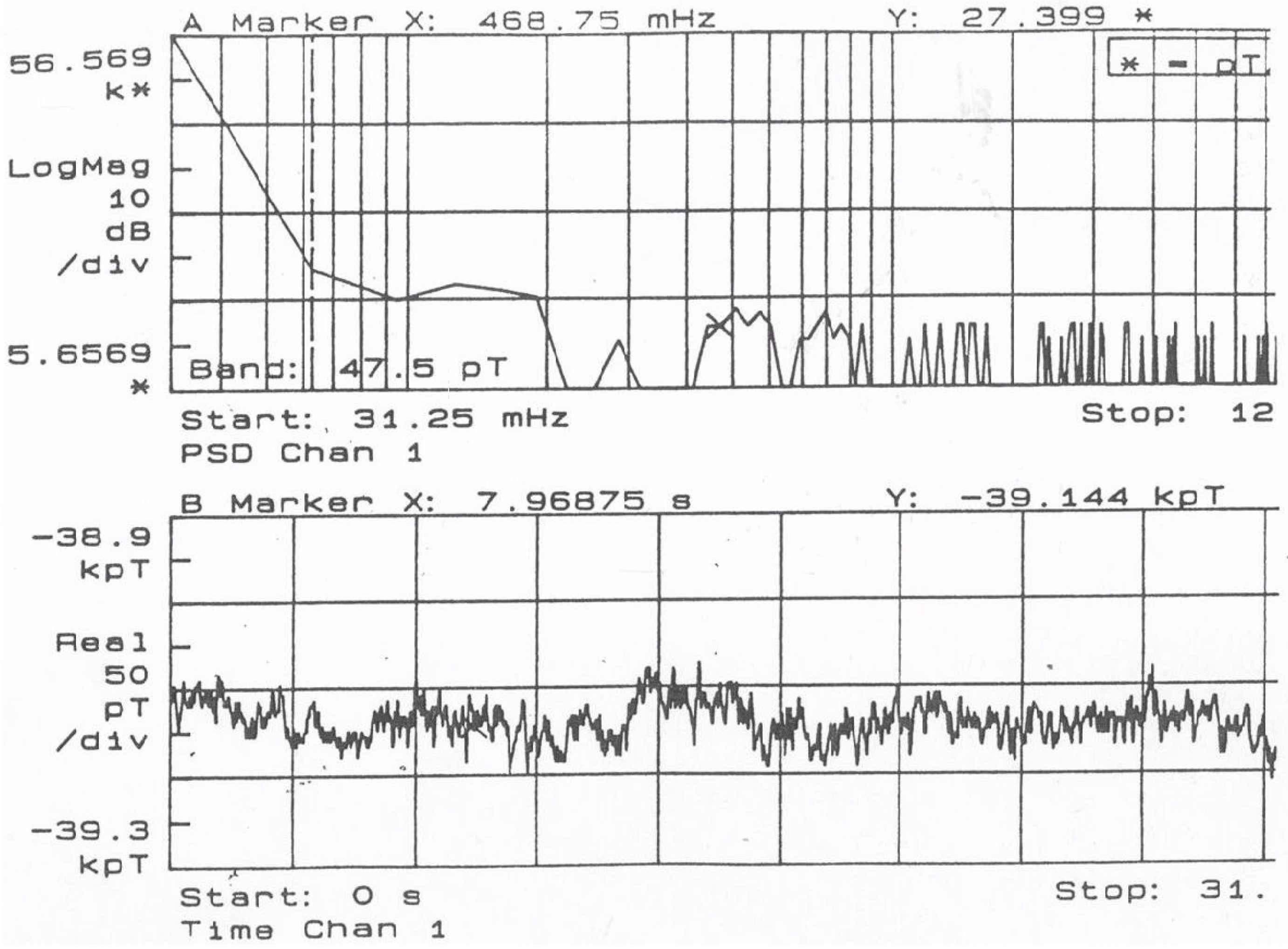
While typical commercial sensor cores present noise level of 100
rms in the interval of 0.1
to 10
, the sensor used in this experiment presents—in the same level—noise value below 47.5
rms (
Figure 9). The sensor output (before data conversion) was measured by a digital Spectrum Analyzer (SR850, Stanford Research Systems/CA-USA). During this analysis the sensor elements were kept inside a demagnetized mu-metal shield with five layers.
For sensitivity characterization a 0.1 square wave current driving a 100 cm wide triaxial Helmholtz coil was used. The current square wave was obtained from a computer controlled source calibrator (2400 SourceMeter, Keithley Tektronix/OR-USA) and a lab current amplifier with current sensors inline. A set of three 6 1/2 digit voltmeters (8846A 6.5 Digit Precision Multimeter, Fluke/WA-USA) were used to compare each channel reading. Signals as low as 0.5 were detected showing excellent sensitivity for the instrument.
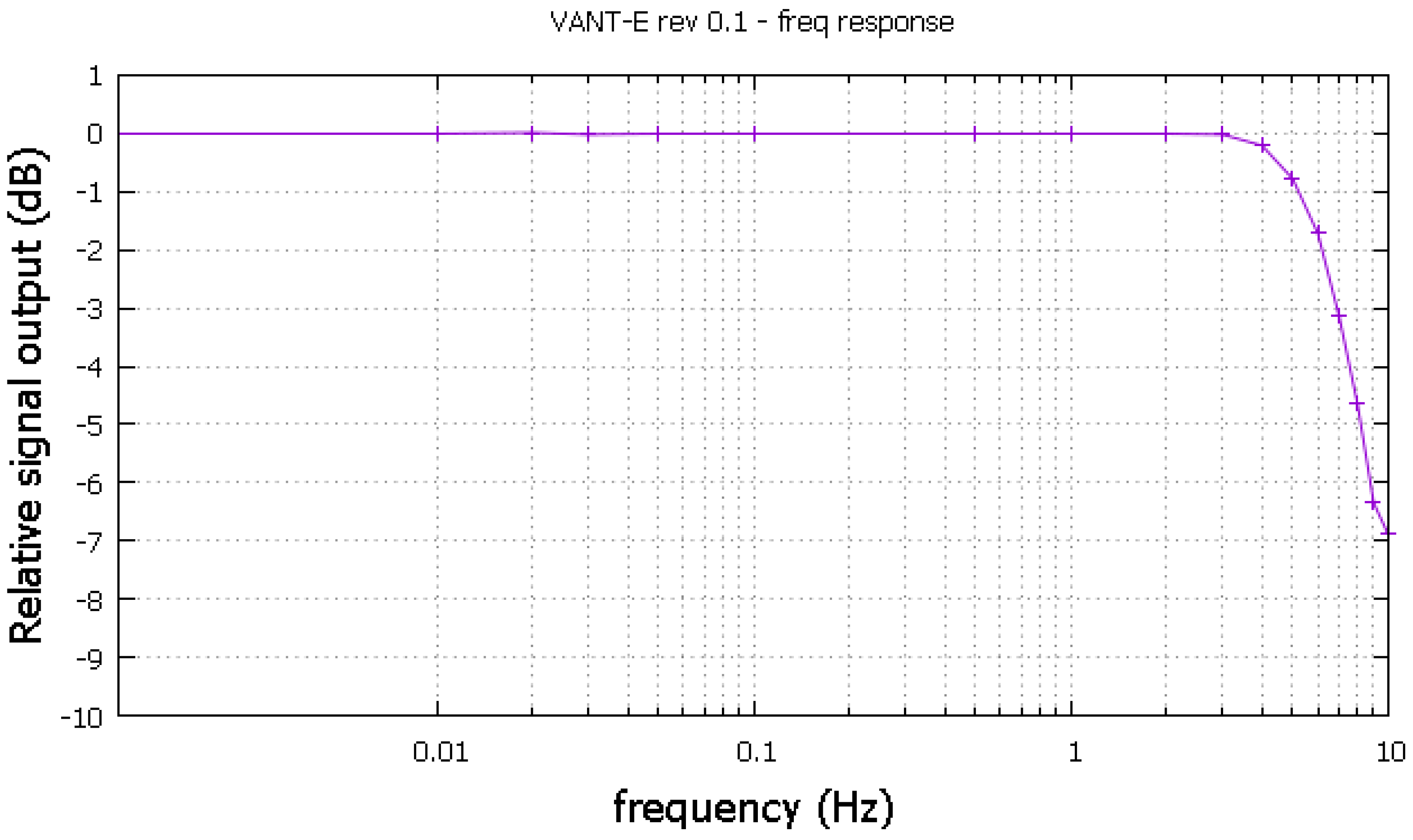
5.2. Frequency Response
To test the magnetometer frequency response, a sinusoidal current sweep ranging from a few milihertz to 10
was applied to the Helmholtz coil (single axis at a time). For these low frequencies direct AC rms readings are not possible due to voltmeter low band limitations. A fast DC sampling with instantaneous normalization was used instead. After some adjustments the magnetometer achieved a −3 dB cutting just above 7
as shown in the
Figure 10.
5.3. Sensor Behavior Characterization
Using a magnetometer sensor in proximity with an electrically motorized drone requires special considerations. The motor iron components and its strong operational current represent a significant source of noise, capable to disturb and even impair the intended magnetic survey. Under normal operation, the drone internal computer supplies the motor with a wide range of power levels, depending on the flight profile and attitude.
In order to empirically estimate the UAV intrinsic magnetic noise and avoid as much as possible its disturbance, a set of measures were taken around the vehicle with the help of a GSM-19T proton magnetometer. The GSM-19T is an instrument of regular use for geophysical surveys, showing great sensitivity and precision more than adequate for our noise investigation. To map all possible situations, we tested the drone at different distances from the GSM-19T exercising motor current levels ranging from off state to full power, searching for a minimum possible distance for the magnetometer to be installed where no interference could be detected. Since this is a much more sensitive base magnetometer, we found safe distances of aproximately 3 .
We have also conducted an experiment with the developed fluxgate magnetometer. The experiment is composed by three tests, each one consisted in a mapping profile containing a single line of 6 m long aligned to the magnetic north, at a place free of sources of strong magnetic interference. Each measurement was obtained every m along the line, where for each measurement we collected the mean norm of 10 readings from the sensor, in order to remove the high frequency noise. In all tests, the drone was positioned in the middle of the line.
The goal for this analysis was to reduce as much as possible the distance between drone and sensor, considering that a sensor hanging in a long cable can pose limitations on flight control and generate safety issues. Below a distance of one meter the disturbance was such that in some events the magnetometer was unable to provide any readings even for the lowest power levels applied. We found that distances starting from 2 m can be used depending on the drone size and motor power required for a given flight profile. Our conclusion is that beyond 3 m of separation between sensor and drone no significant change on readings was present at any power level.
In the first test, the drone was turned off and the battery cable was disconnected. The second test consisted in powering the drone, excepting the motors. Finally, in the third test, the motors were rotating at moderate speed, without taking off the ground.
By analyzing the results, we observed a peak at approximately the 1.0
mark. So we safely assume the distance of the next stable measurement, as a minimum distance to locate the sensor. Finally we decided to add 10 cm extra for cautiousness, ending up with the sensor being located at 1.1
of the drone. Based on this simple (and conservative) approach, our observations have shown that the impact of the drone’s airframe, electronics and power levels were negligible at the chosen distance and position. Others works in the literature, for example [
34], report on the use of booms of similar size (considering the distance to the motors).
This distance is very important because the magnetic field of the robot will change depending on payload and thrust applied to motors, so incorrectly setting this distance will interfere directly with the measurements in a non-predictable way. We have not conducted an exhaustive characterization of the setup, as at this moment the focus was to find a compromise solution that would guarantee the system operation, allowing us to demonstrate the feasibility of the concept. Nevertheless, measuring the sensitivity of the complete setup is part of a future work.
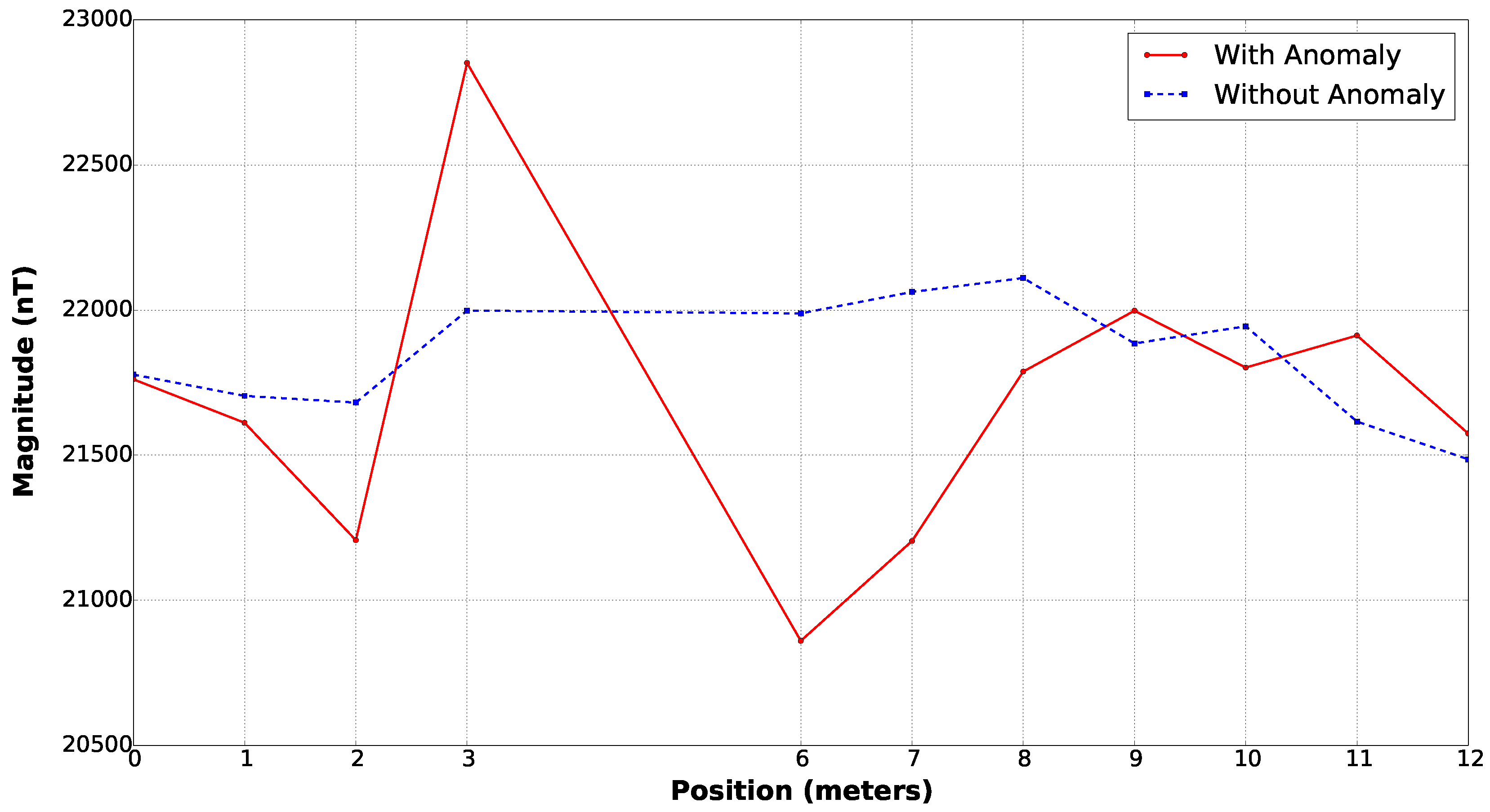
Finally, the last evaluation applied was a small survey over a controlled site submitting the sensor to real environment conditions of local noise and gradients. A 12 m profile where a ferromagnetic container of half cubic meters and 300
was placed over the magnetometer path as depicted on
Figure 11. The results for this survey (
Figure 12) exhibit an anomaly having an amplitude of approximately 2000
next to the position the container was placed.
5.4. UAV Sensor Mounting
Small aerial robots have serious payload limitations, and their small size also creates a challenge to accommodate a large number of sensors and payload. The developed magnetometer has a weight of 89 (head) and 174 (PCB with case). Due the light weight nature of this sensor, typical pendulum carrying wasn’t possible: small wind perturbations greatly alter the sensor position and angle, thus decreasing sensor accuracy.
The way the sensor is mounted on the drone is key to having correct measurements. We tested different mountings such as pendulum and vertical mountings. Despite the pendulum mounting don’t had any serious impact in aircraft mobility, wind and even the normal movement of the drone generated a unpredictable motions on the sensor, thus generating extra noise. A vertical mounting do not prove to be robust enough on this type of drone due the expected distance between the sensor and the drone body.
Given those limitations we proposed a “boom” mounting. A 1.1
lightweight
aluminum bar pointing at the front of the robot was the more stable mounting. The magnetic permeability of aluminum is known to be close to
, making it a good material for the magnetometer mounting. This mounting can be seen on
Figure 13 on a X8+ drone from 3DR. Also a companion computer and extra batteries needed to be added to acquire and process the sensor data accurately. A Raspberry Pi 2 computer was connected to the
Pixhawk control board to process sensor information when a survey point was reached.
All the weight on the aircraft needed to be balanced before flight to avoid misbehavior and control problems during flight. This balancing was done on the X and Y axes of the aircraft, carefully moving all components of the system until the drone stays still on his center of gravity.
5.5. UAV Field Experiment
In order to validate our technique, we performed a complete survey using the proposed methodology. All the steps required for the mapping and data processing phases were performed automatically by the robot and processing software with little to no human interaction.
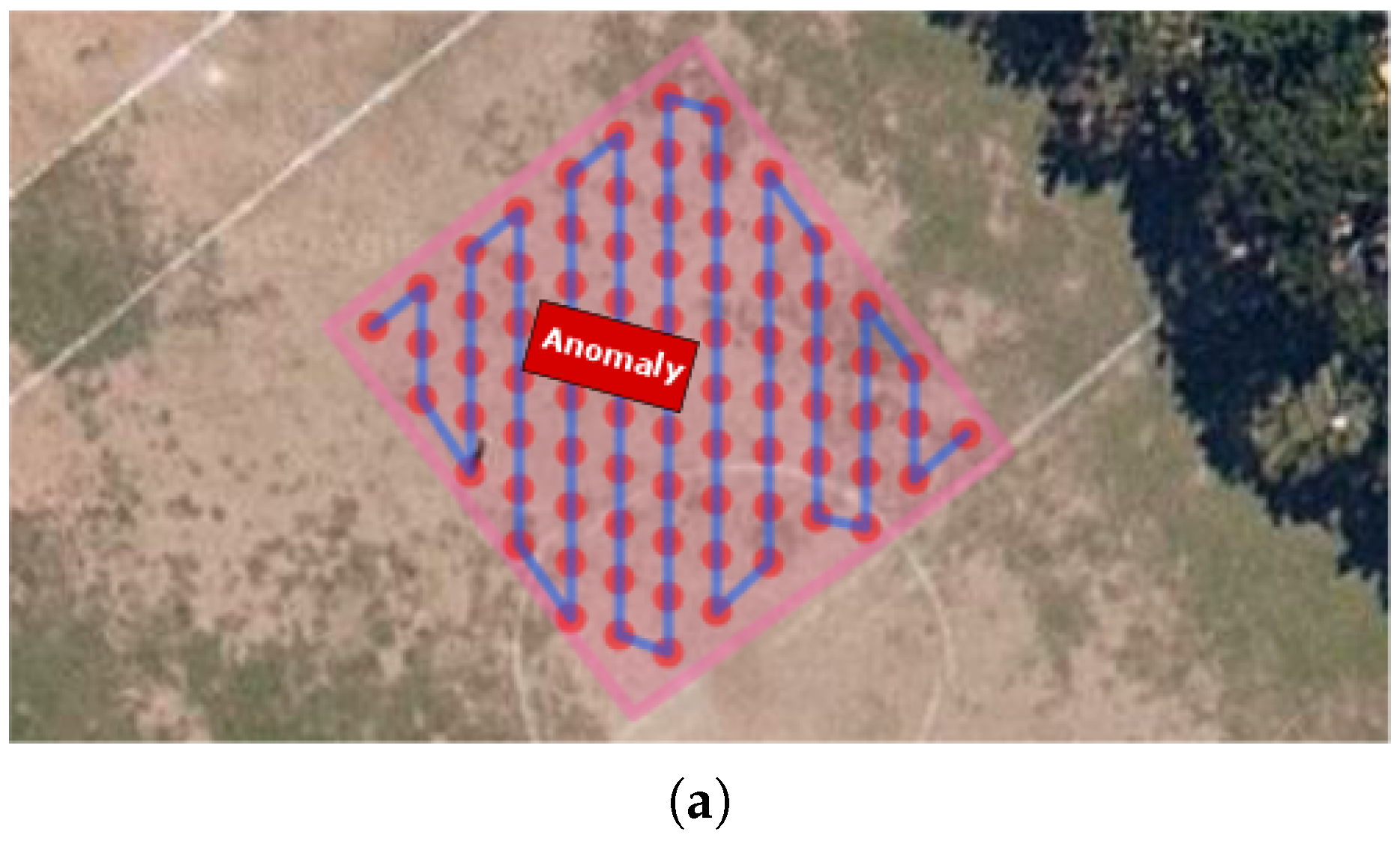
The objective of this experiment was to generate consistent maps, where one is able to identify an artificial anomaly caused by a metallic structure placed at a known position. A 2.10 m × 3.00 m car was used as an anomaly. The chosen location for the survey was the middle of a soccer field, far away from other sources of magnetic interference such as power lines or big metal structures.
Figure 14 depicts the experiment setup. A video illustrating the complete execution of a survey campaign is available at [
35].
The mapping profile created for this experiment has a 2 m of separation between survey points, and 7 s hover time over an area of 381 m
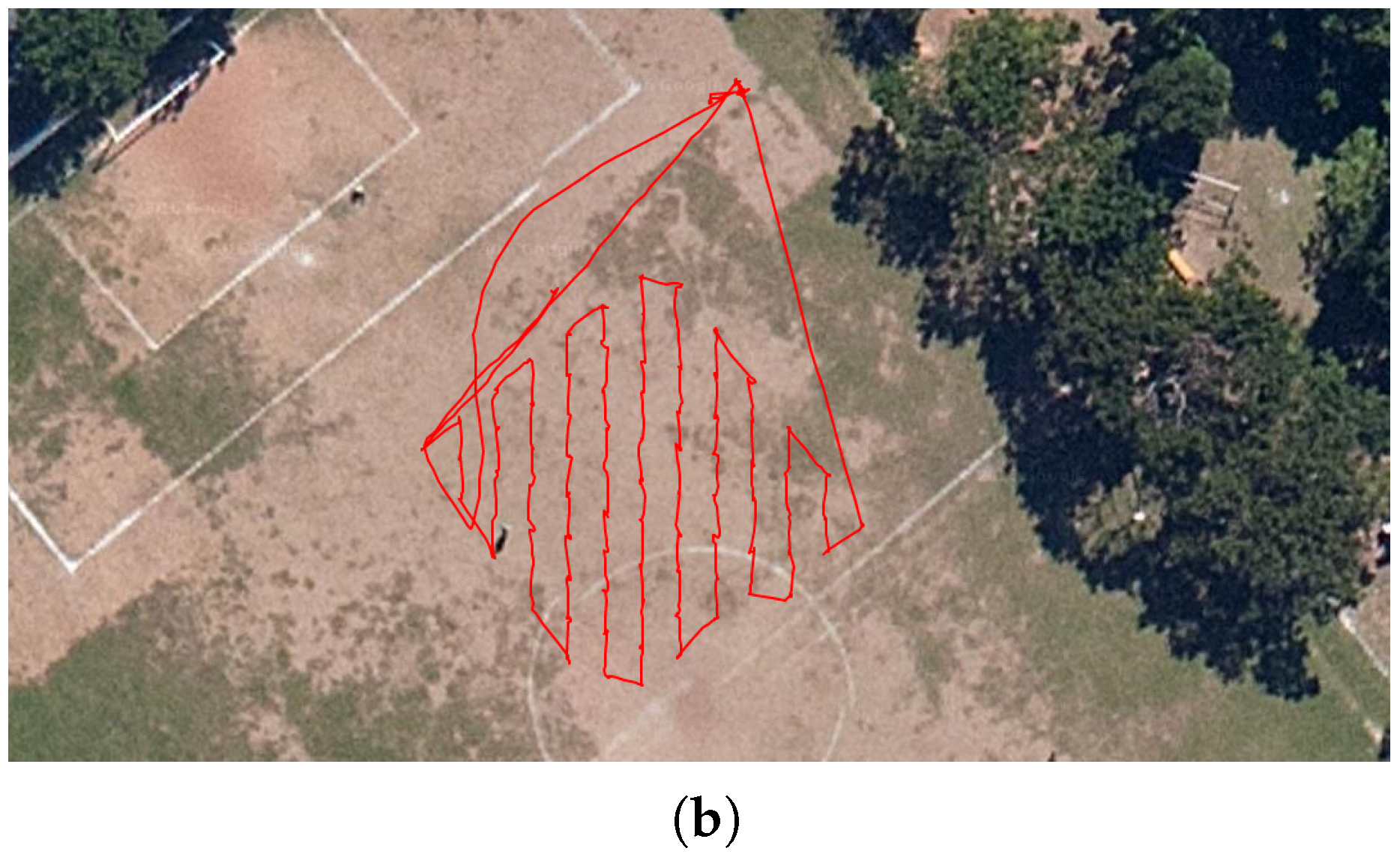
2. The survey length was 181 m. At every survey point the robot faced the sensor to the magnetic north. The planned survey path and the executed one can be seen on
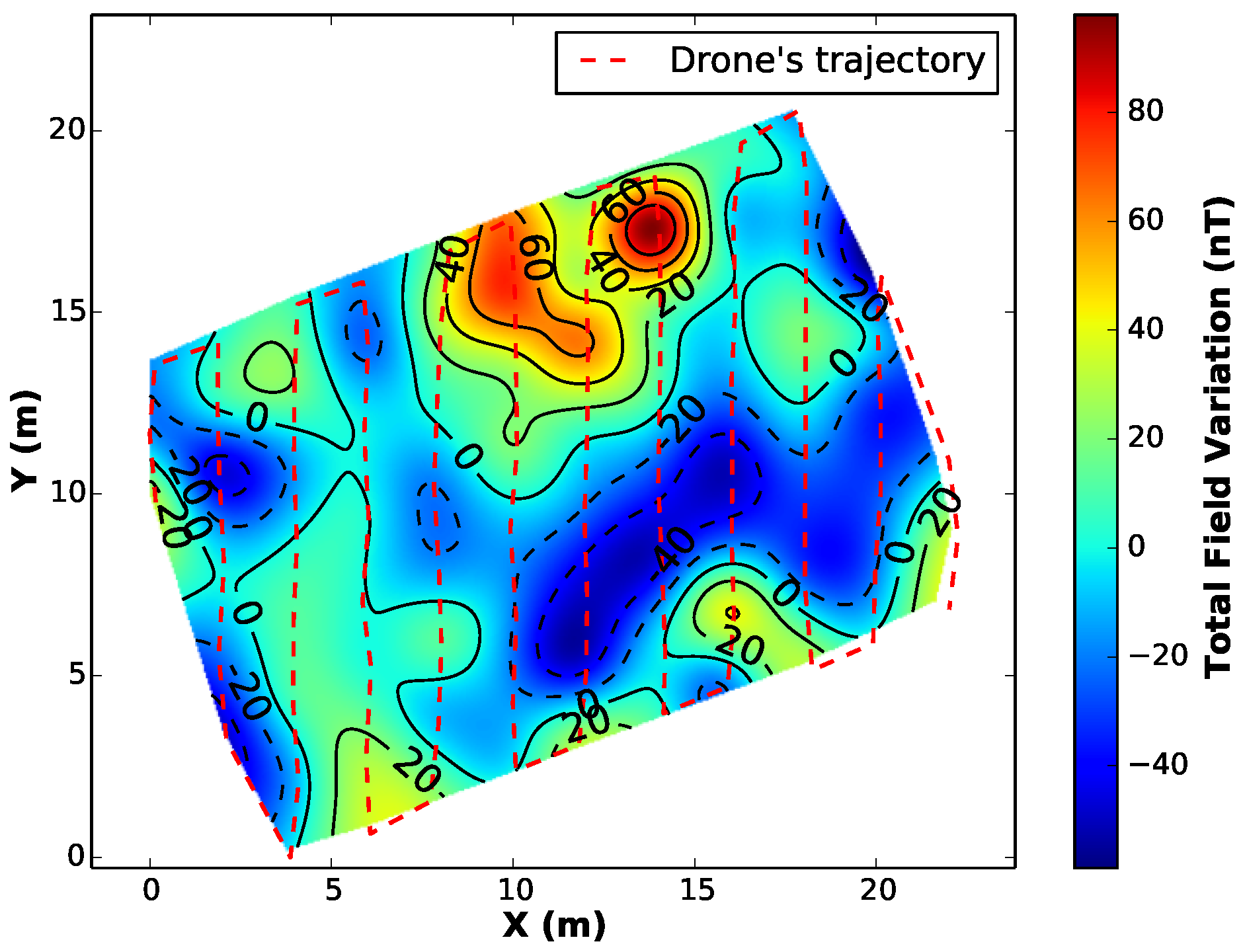
Figure 15.
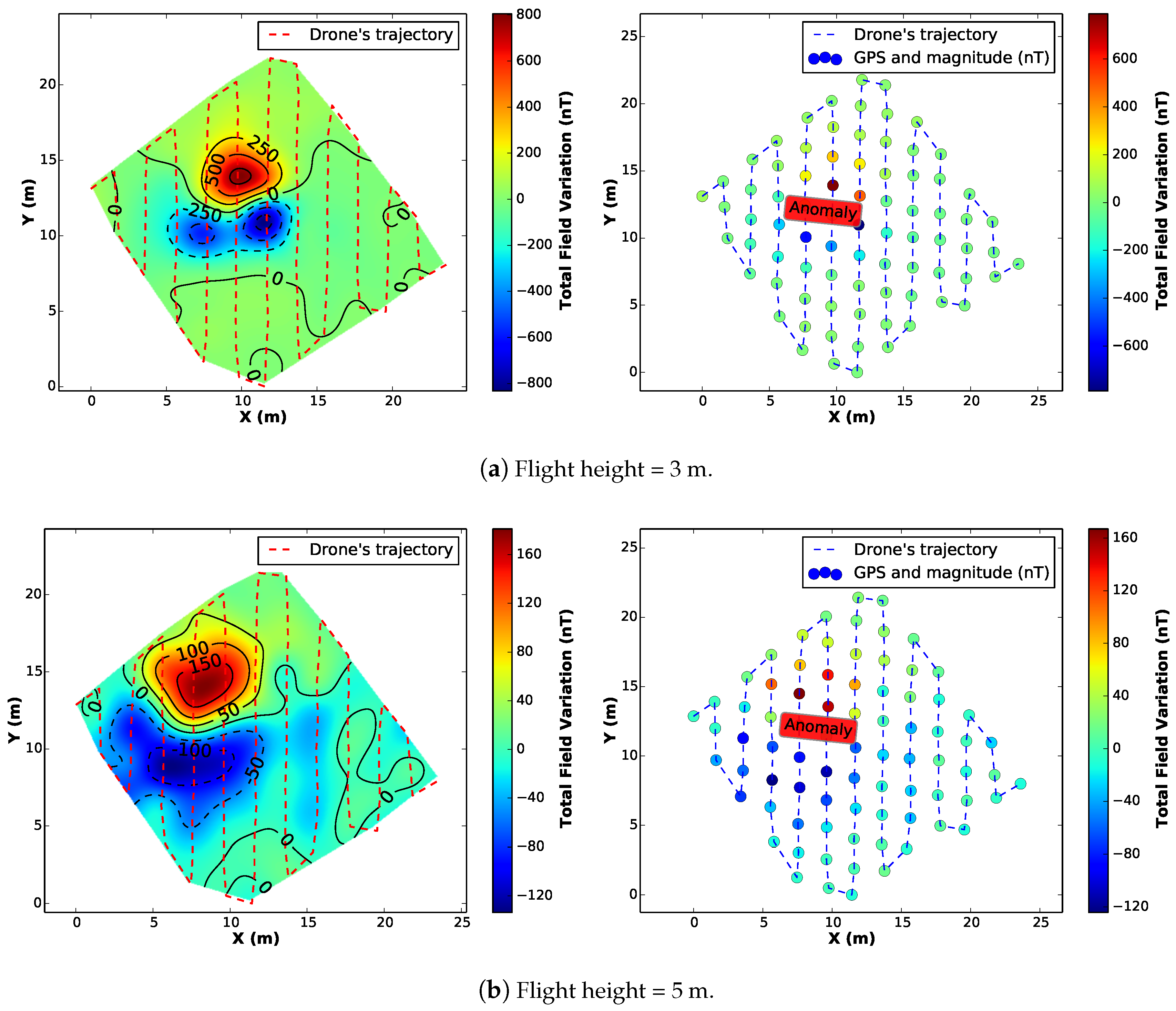
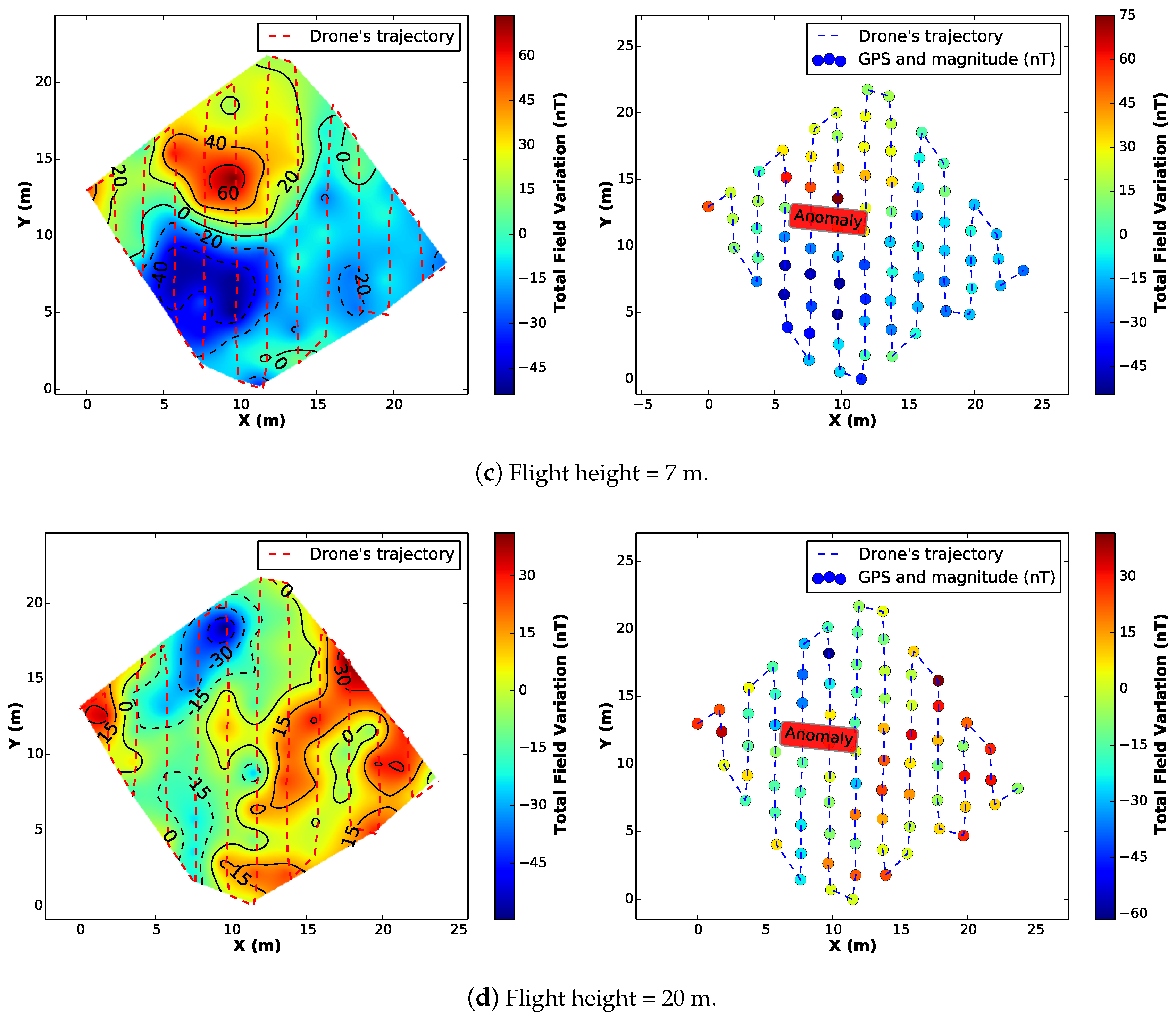
We executed the same profile configuration for 4 different surveys at 3, 5, 7 and 20 m of height above the ground.
Figure 16 presents the results of the aeromagnetic maps.
By comparing the interpolated maps from all the surveys, it is clear that the magnetometer was able to detect the variation of the magnetic field in the vehicle’s surroundings, leaving an expected dipolar magnetic signature on the generated map, specially for the first case (flight height = 3 m). However, as expected, with a greater distance between the sensor and the anomaly (flight height = 20 m), the map looses quality/resolution and the anomaly is undetectable.
6. Conclusions and Future Work
6.1. Conclusions
The interest and research in UAVs has been increasingly growing, specially due to the decrease in cost, weight, size and performance of actuators, sensors and processors. These type of vehicles clearly have their niche of applications, being one of their main advantages a privileged view from above. Considering the mining industry, it is possible to use such vehicles in the prospection of minerals of commercial interest beneath the ground.
In this context, we discussed the development of a state-of-the-art three-axis fluxgate magnetometer to be used in autonomous aeromagnetic surveys. The electronic was built aiming to reduce its size and power consumption, and the sensor housing was assembled far from the electronics in order to allow enough distance from important sources of magnetic noise, such as the vehicle’s motors. Due to the sensor small size and weight, it is very sensitive to noise generated from fast rotational movements and vibration. We proposed the use of rotary-wing autonomous aerial robots that can hover over survey points. This limitation makes it impractical for mounting this sensor on other types of aircraft such as fixed-wing aircrafts.
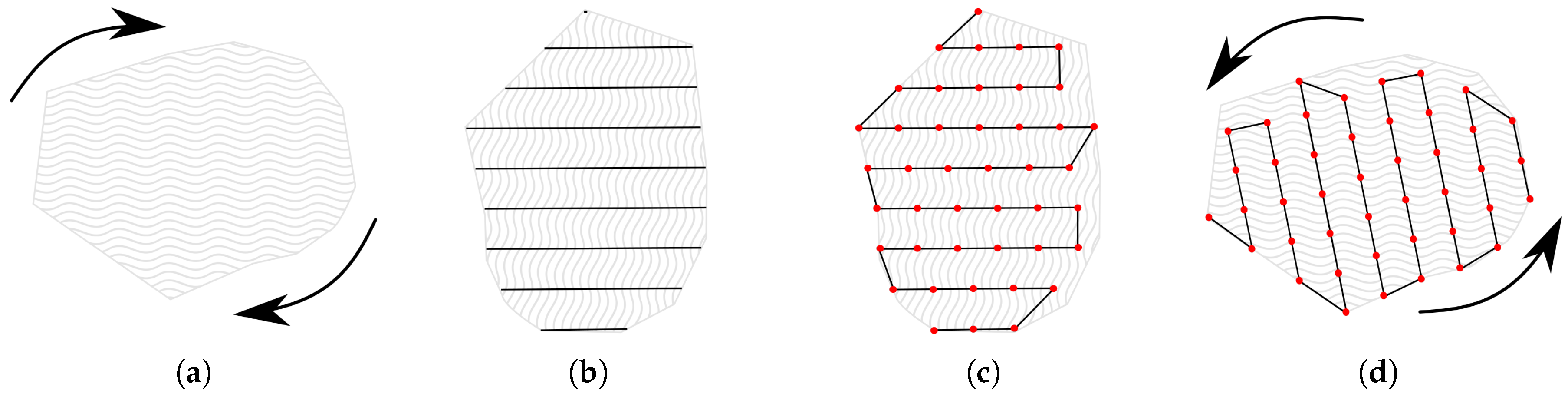
For the particular task of aeromagnetic surveys, we have proposed the use of modified version of the Maza et al. [
22] path planning algorithm, which is based on the lawnmower coverage pattern. It was modified to subdivide the path on several small size segments and to customize survey angle to match the magnetic north or another arbitrary angle. Also we proposed a method to overcome GPS accuracy on surveys, changing the visiting sequence of those survey points.
Through an extensive set of experiments performed to determine the mapping profile parameters, map generation methodology and adequate vehicle’s mounting configuration, we were able to successfully generate meaningful magnetic maps. Our method is highly automated, and the system is easily reproducible and scalable to multiple drones with small addition in costs.
6.2. Future Work
The work has several future directions that can be pursued in order to improve the methodology, which includes the extension of the proposed technique to multi-robot ensembles and to environments with obstacles, both providing better representations of real-world scenarios.
Furthermore, every survey campaign has unique characteristics, in this sense, on future work we aim to improve the parameter selection for surveys such as hover time, sample size and distance between survey points. We also intend to evaluate how the influence of different sensor mounting positions affect accuracy of data acquisition.
Future work will also involve the application of the proposed methodology on a prospective mining scenario, comparing results to known previous generated maps with conventional methods.