Towards Camera-LIDAR Fusion-Based Terrain Modelling for Planetary Surfaces: Review and Analysis
Abstract
:1. Introduction
2. Terrain Perception Onboard Planetary Rovers
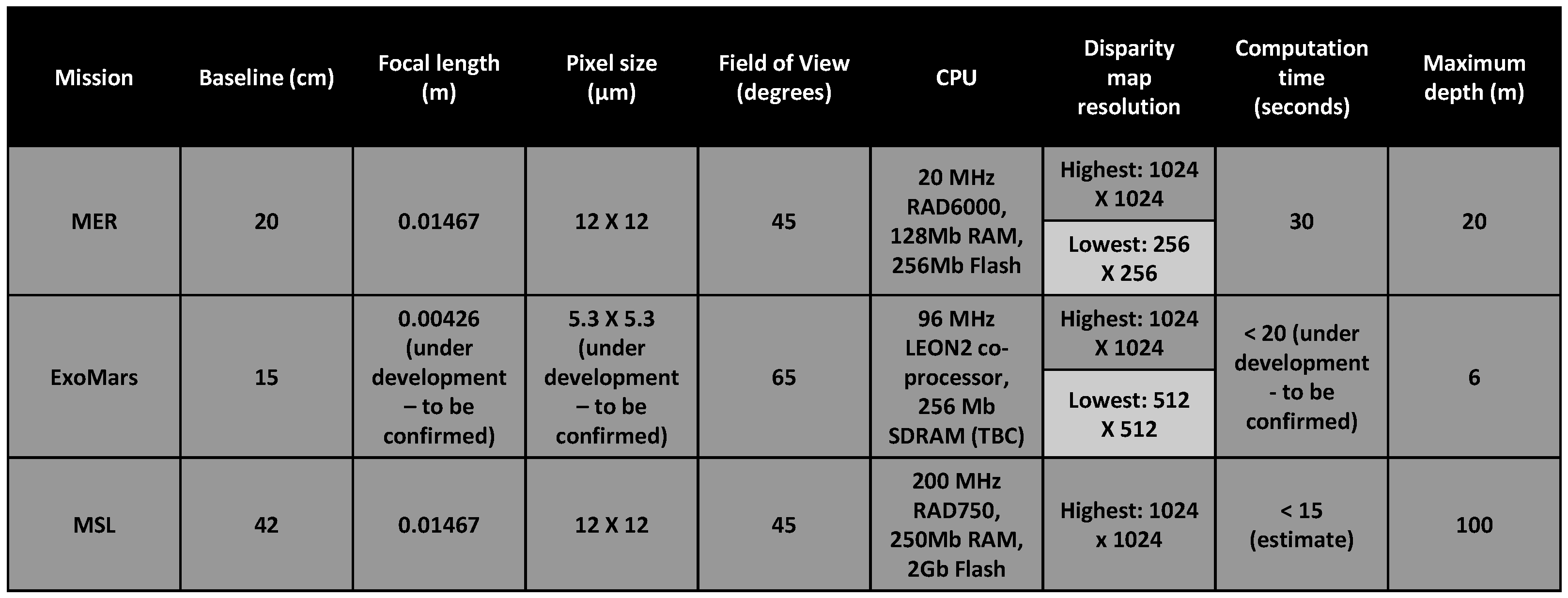
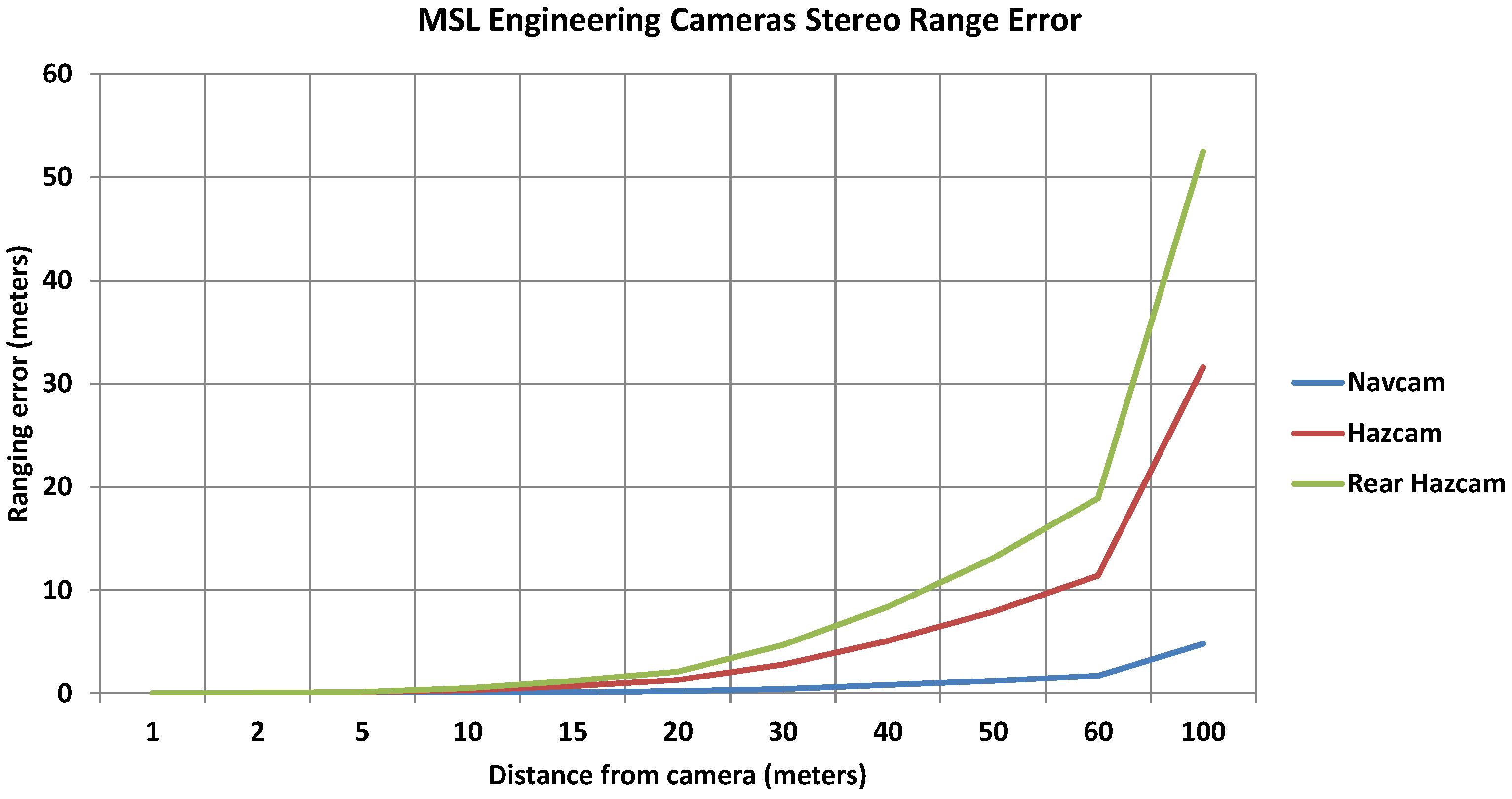
2.1. Cameras
2.2. Light Detection And Ranging (LIDAR)
3. Camera-LIDAR Fusion for Planetary Terrain Perception
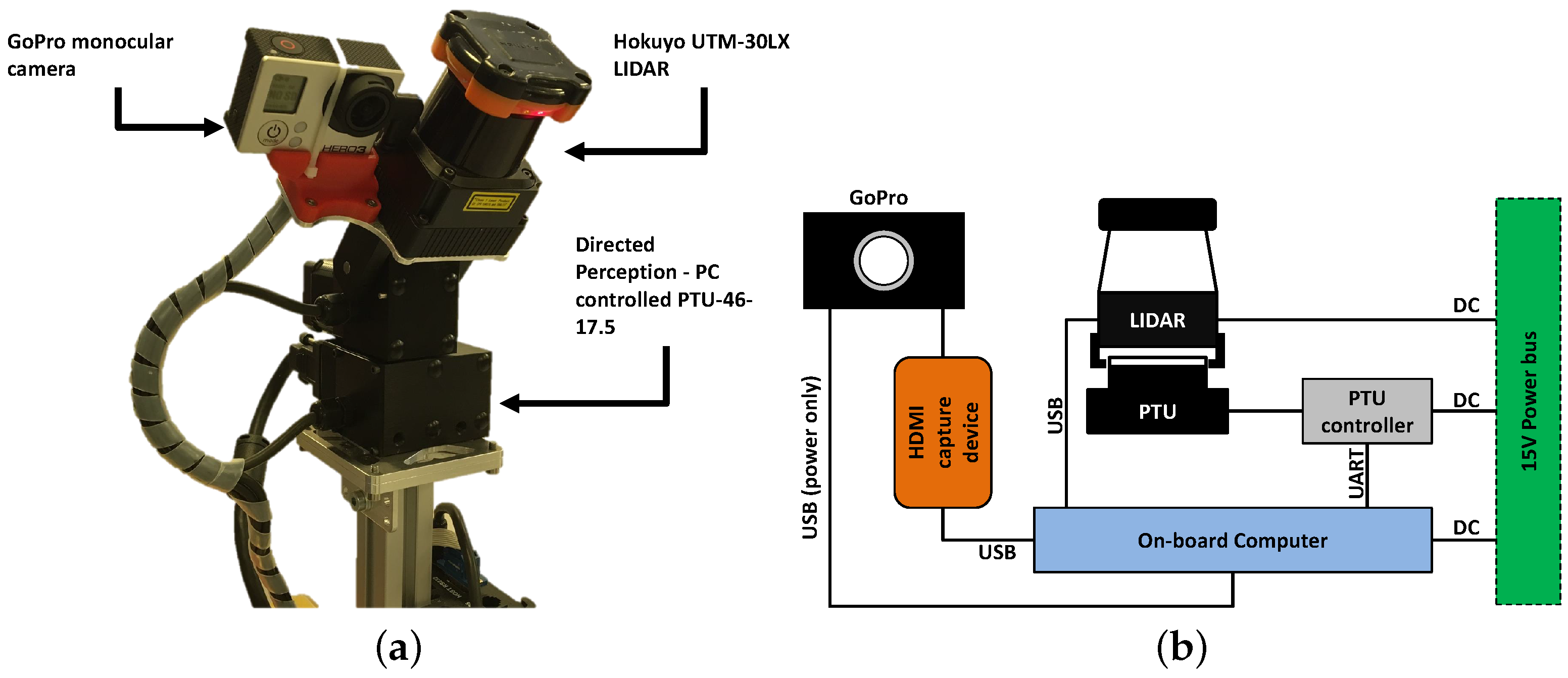
3.1. Hardware Setup
3.2. Sensor Data
3.3. Sensor Calibration
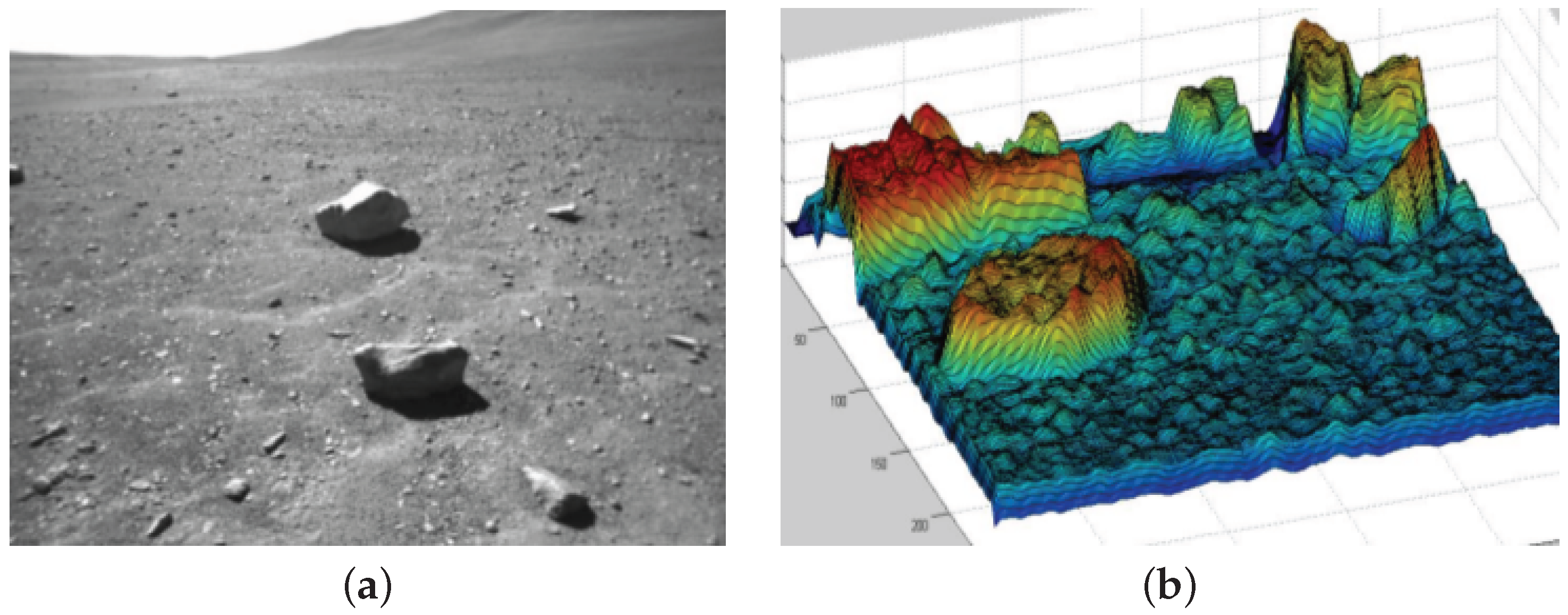
3.4. Sensor Fusion for Surface Reconstruction
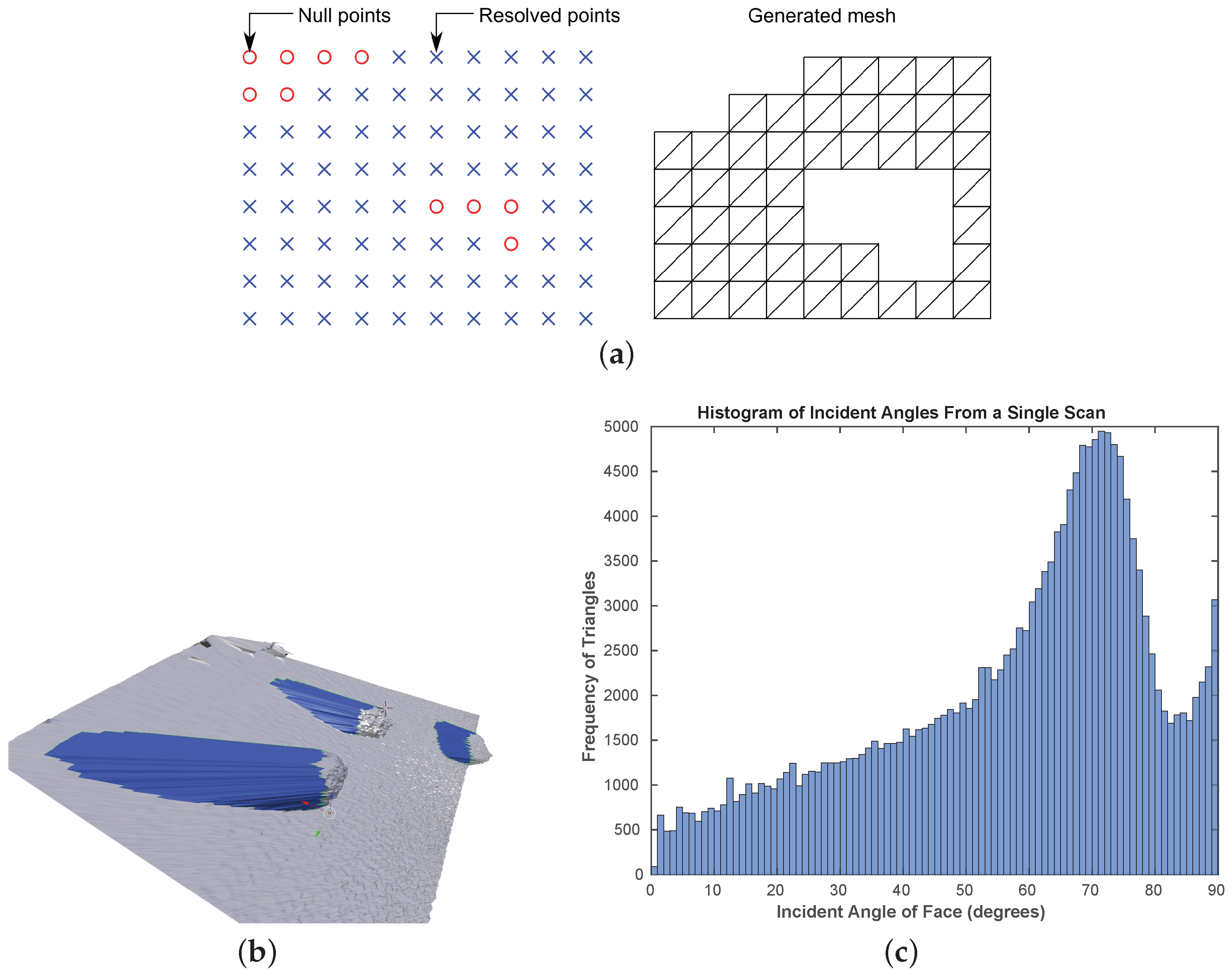
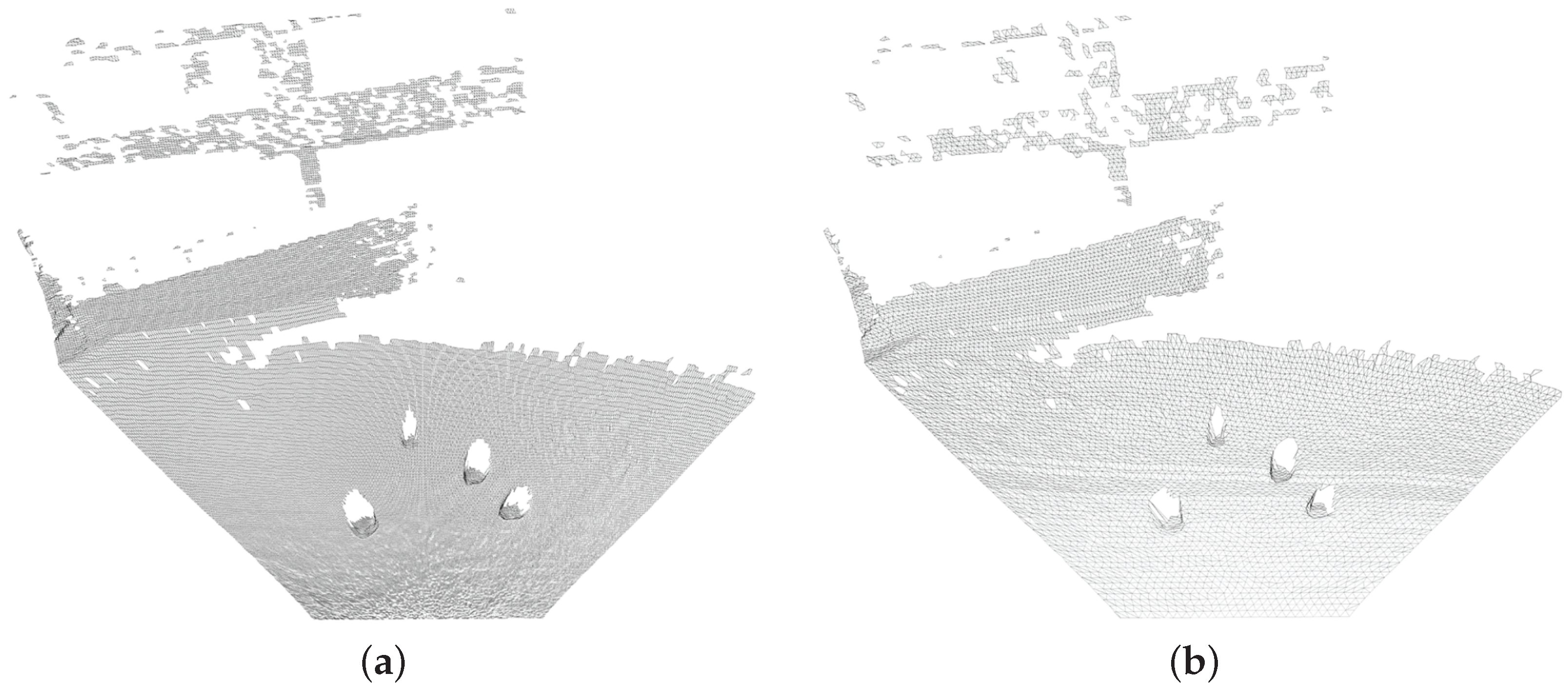
3.5. Point Cloud Triangulation and Surface Mesh Generation
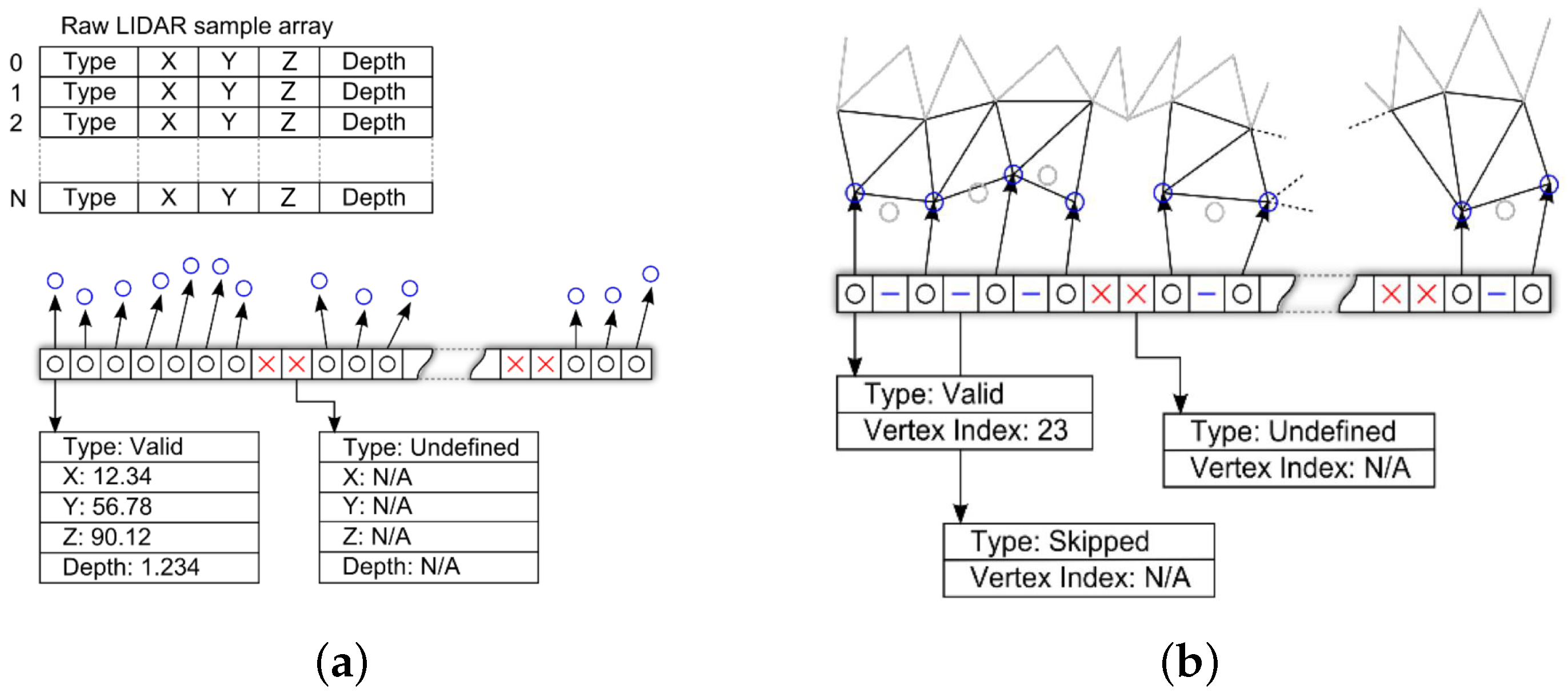
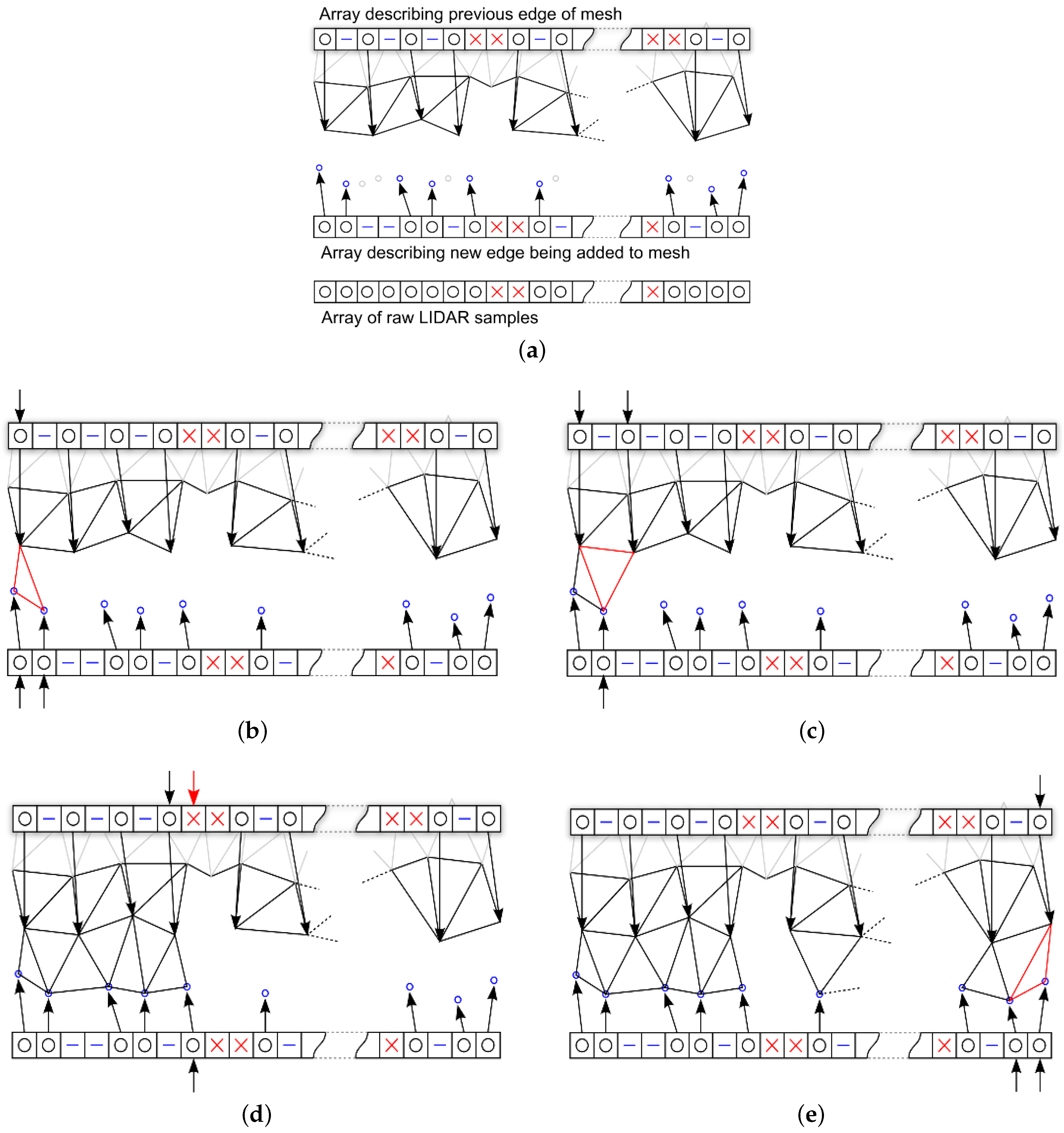
3.6. Proposed Pipelined Mesh Simplification Algorithm
- The first and last valid vertices in the raw data array are always added to the mesh and a reference added in the new edge array.
- A valid vertex is added to the mesh and the new edge if its Cartesian distance from the previous is greater than the required δ.
- If a vertex is less than δ from the previous added vertex then a skipped entry is added to the new edge array.
- Undefined vertices are always added to the new edge array.
- A valid vertex that follows an undefined vertex is always added to the new edge array.
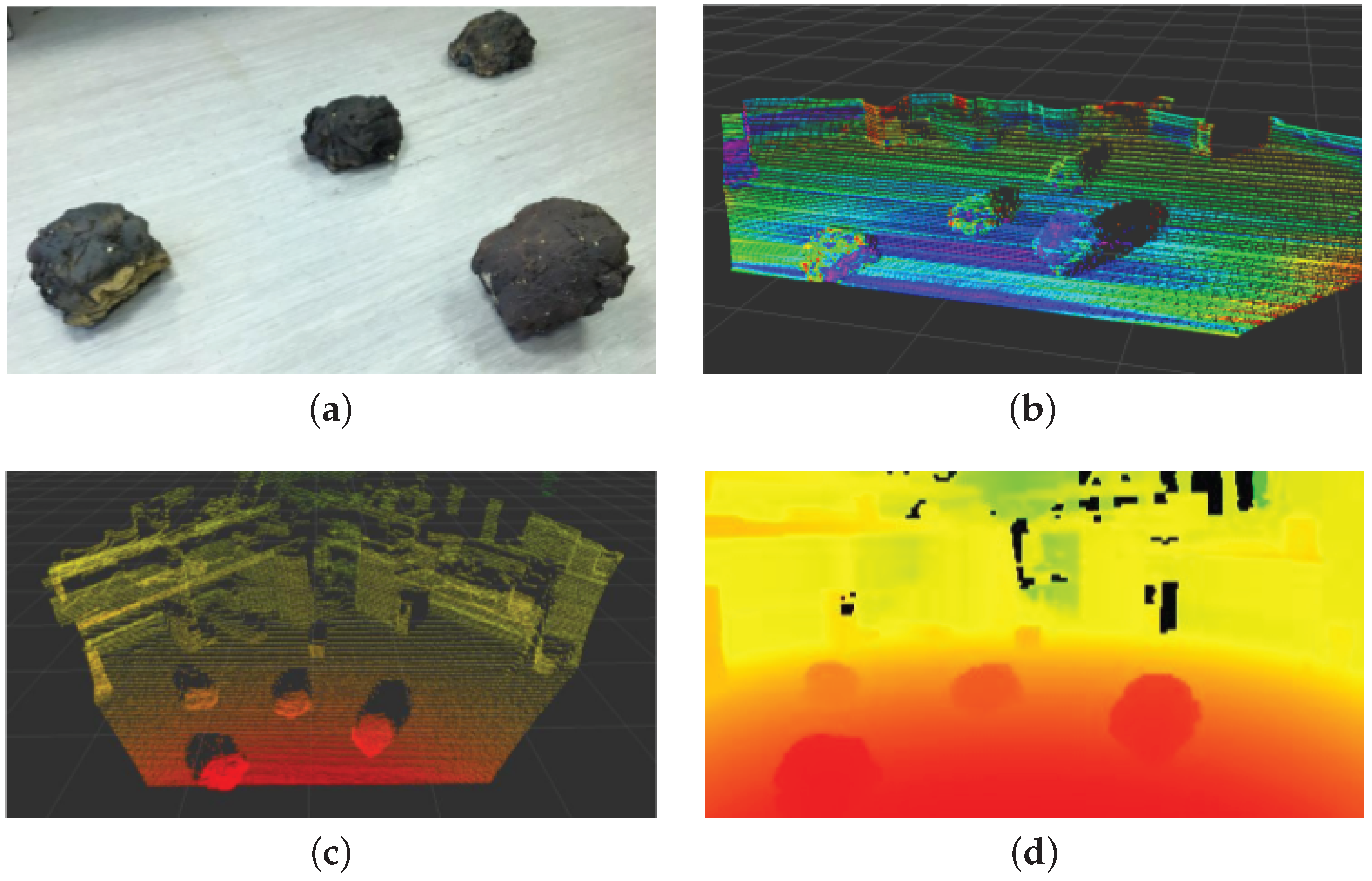
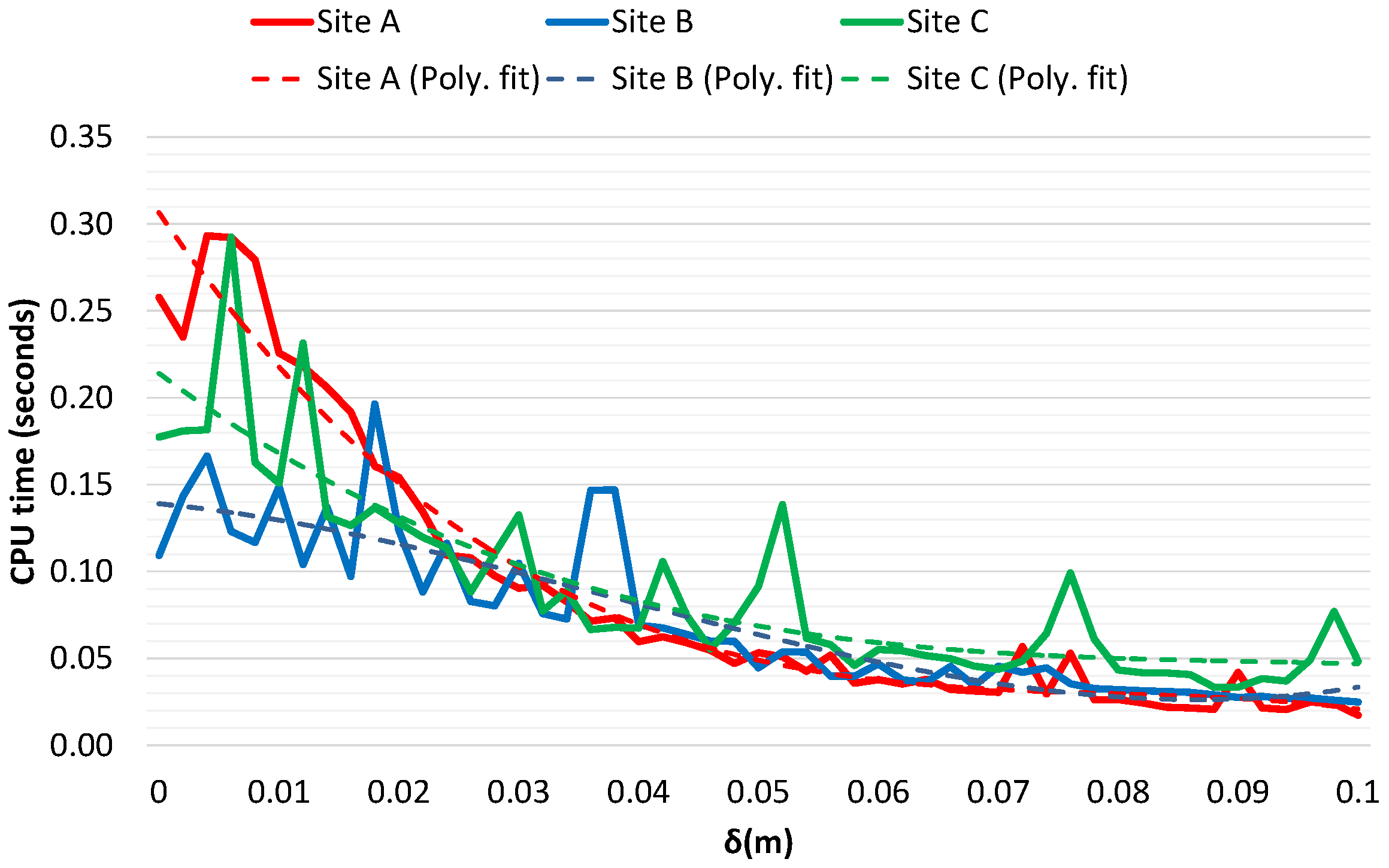
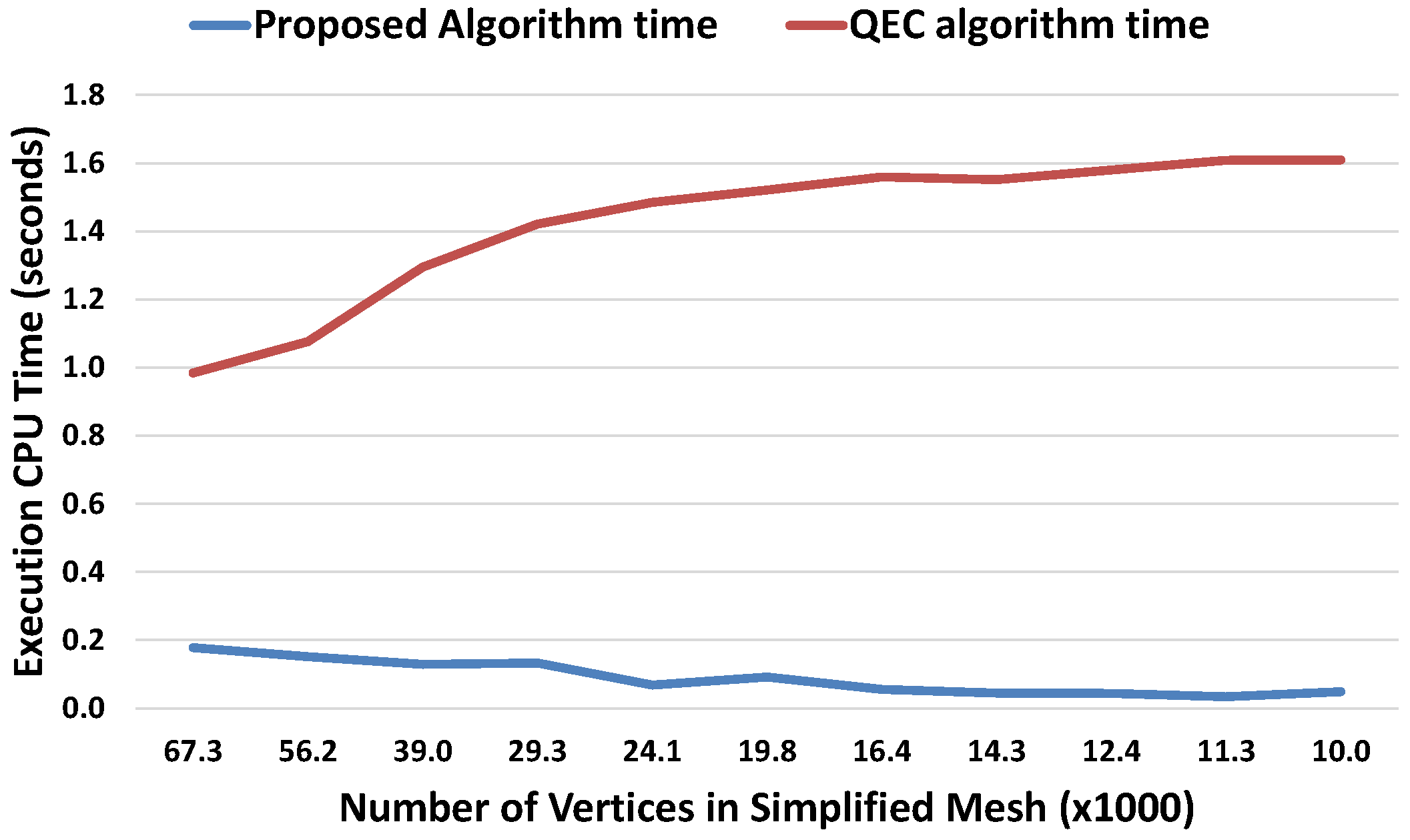
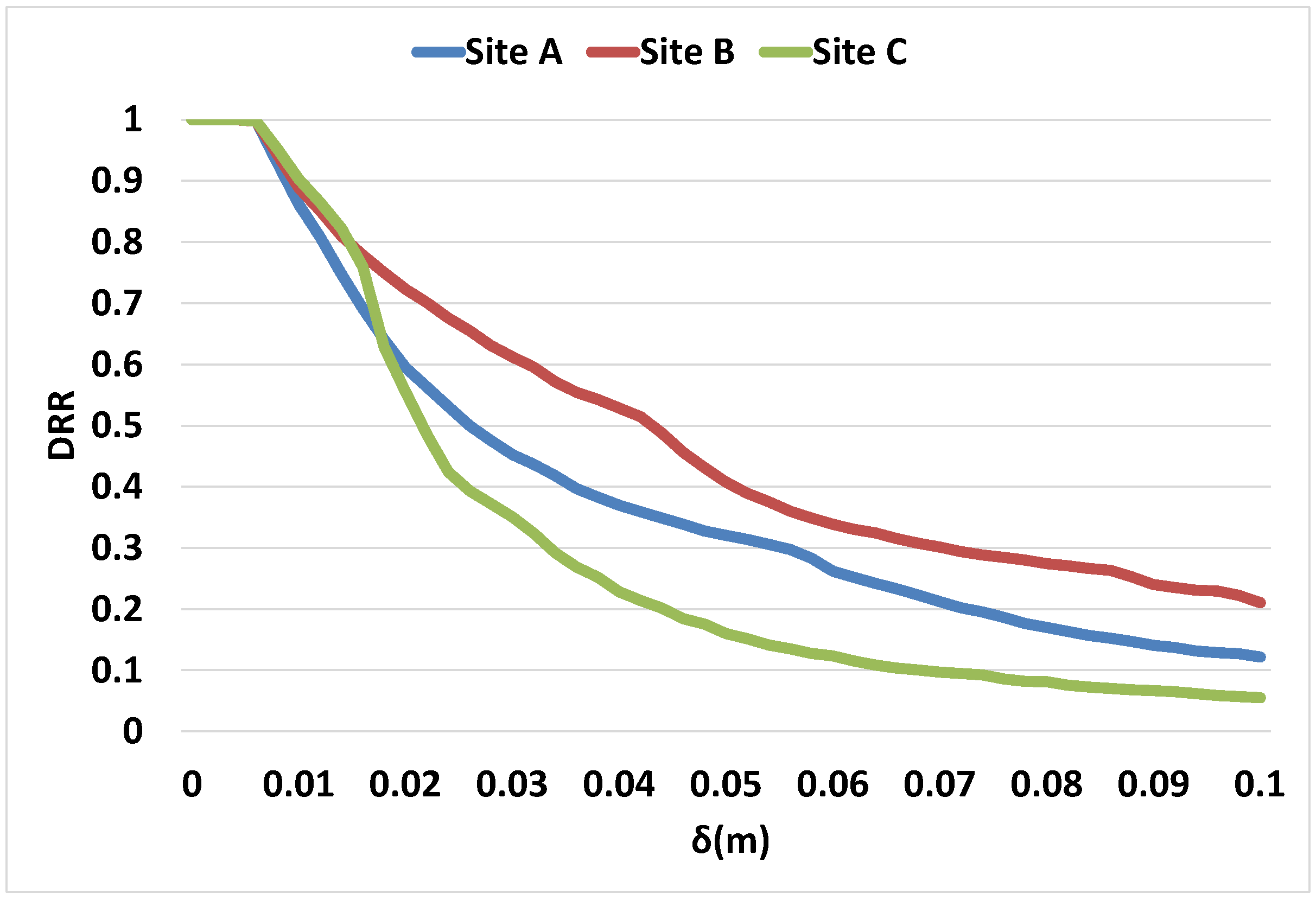
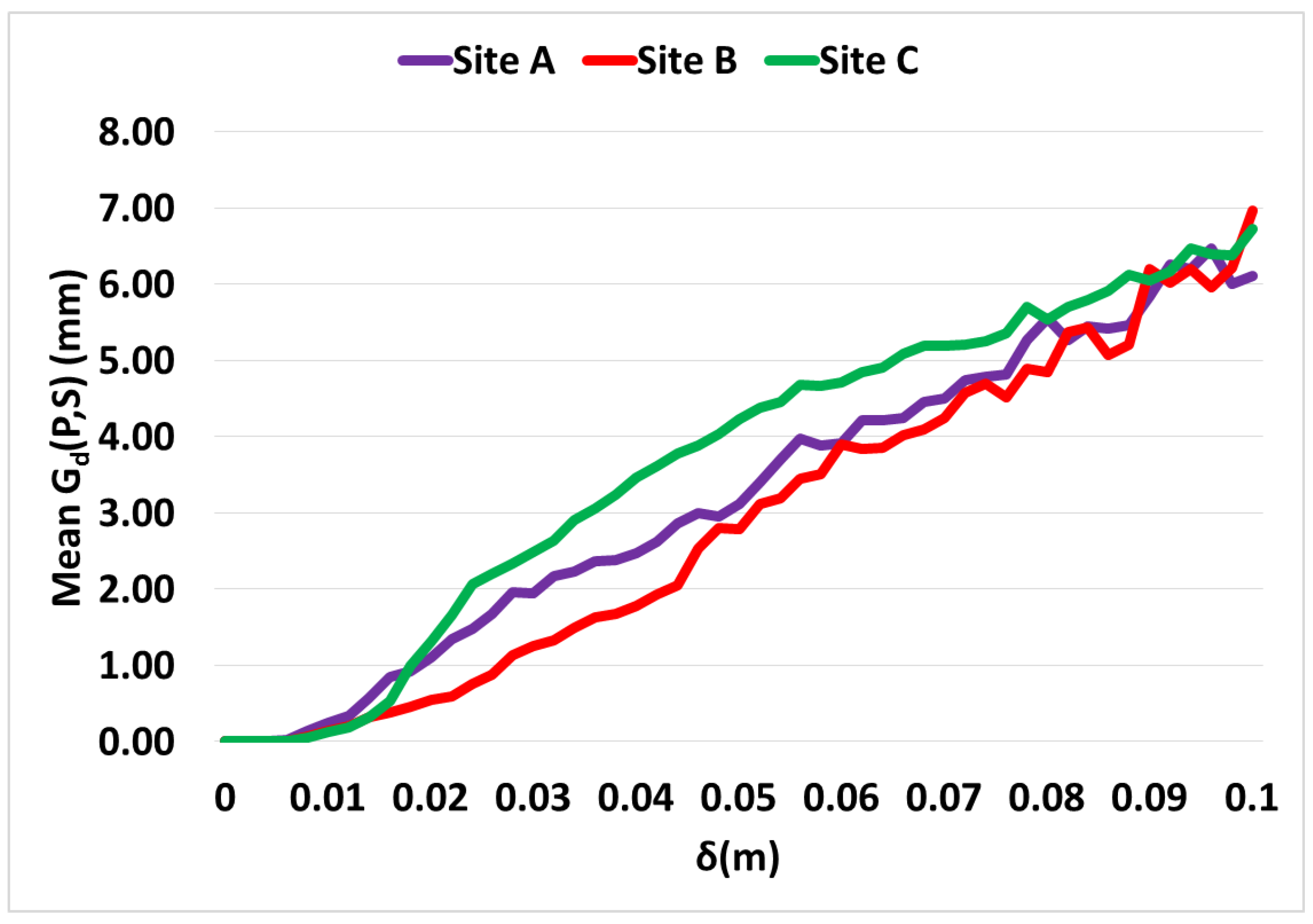
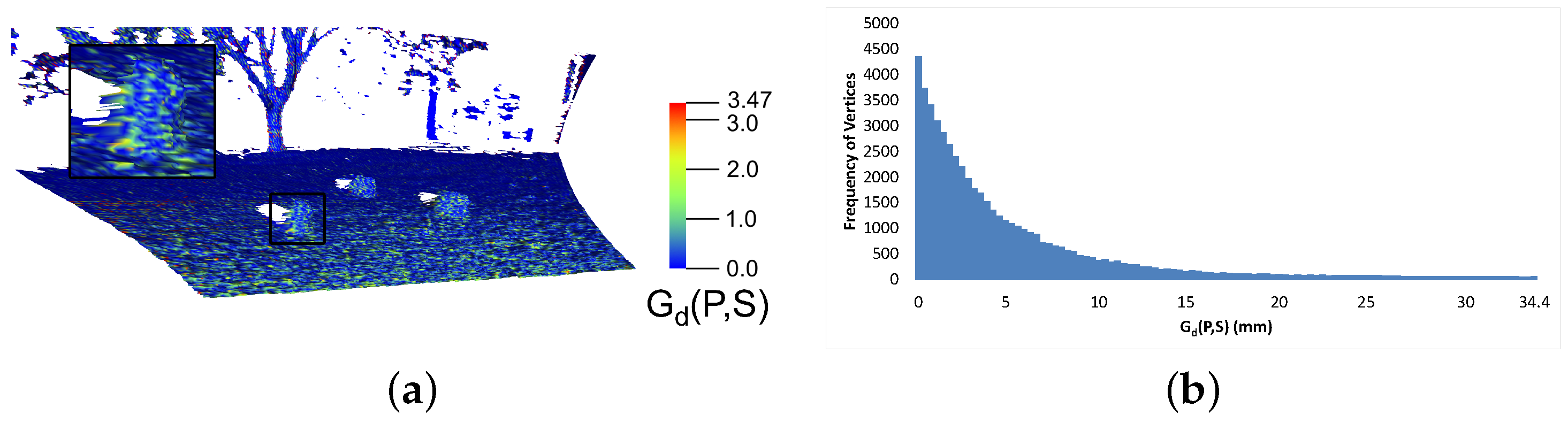
3.7. Performance Analysis
4. Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Kulkarni, J.; Campbell, M.; Dullerud, G. Stabilization of Spacecraft Flight in Halo Orbits: An H∞ Approach. IEEE Trans. Control Syst. Technol. 2006, 14, 572–578. [Google Scholar] [CrossRef]
- Koekemoer, A.M.; Aussel, H.; Calzetti, D.; Capak, P.; Giavalisco, M.; Kneib, J.P.; Leauthaud, A.; Le Fèvre, O.; McCracken, H.J.; Massey, R.; et al. The COSMOS Survey: Hubble Space Telescope Advanced Camera for Surveys Observations and Data Processing. Astrophys. J. Suppl. Ser. 2007, 172, 196. [Google Scholar] [CrossRef]
- Mutch, T.A.; Arvidson, R.E.; Binder, A.B.; Huck, F.O.; Levinthal, E.C.; Liebes, S.; Morris, E.C.; Nummedal, D.; Pollack, J.B.; Sagan, C. Fine particles on Mars: Observations with the viking 1 lander cameras. Science 1976, 194, 87–91. [Google Scholar] [CrossRef] [PubMed]
- Mutch, T.A.; Grenander, S.U.; Jones, K.L.; Patterson, W.; Arvidson, R.E.; Guinness, E.A.; Avrin, P.; Carlston, C.E.; Binder, A.B.; Sagan, C.; et al. The surface of Mars: The view from the viking 2 lander. Science 1976, 194, 1277–1283. [Google Scholar] [CrossRef] [PubMed]
- Matthies, L.; Maimone, M.; Johnson, A.; Cheng, Y.; Willson, R.; Villalpando, C.; Goldberg, S.; Huertas, A.; Stein, A.; Angelova, A. Computer Vision on Mars. Int. J. Comput. Vis. 2007, 75, 67–92. [Google Scholar] [CrossRef]
- Estlin, T.A.; Bornstein, B.J.; Gaines, D.M.; Anderson, R.C.; Thompson, D.R.; Burl, M.; Castaño, R.; Judd, M. AEGIS Automated Science Targeting for the MER Opportunity Rover. ACM Trans. Intell. Syst. Technol. 2012, 3, 50. [Google Scholar] [CrossRef]
- Gao, Y.; Spiteri, C.; Pham, M.T.; Al-Milli, S. A survey on recent object detection techniques useful for monocular vision-based planetary terrain classification. Robot. Auton. Syst. 2014, 62, 151–167. [Google Scholar] [CrossRef]
- Shaukat, A.; Al-Milli, S.; Bajpai, A.; Spiteri, C.; Burroughes, G.; Gao, Y. Next-Generation Rover GNC Architectures. In Proceedings of the 13th Symposium on Advanced Space Technologies in Robotics and Automation, Noordwijk, The Netherlands, 11–13 May 2015.
- Matthies, L.; Gat, E.; Harrison, R.; Wilcox, B.; Volpe, R.; Litwin, T. Mars microrover navigation: Performance evaluation and enhancement. Auton. Robots 1995, 2, 291–311. [Google Scholar] [CrossRef]
- Biesiadecki, J.; Maimone, M. The Mars Exploration Rover surface mobility flight software driving ambition. In Proceedings of the 2006 IEEE Aerospace Conference, Big Sky, MT, USA, 4–11 March 2006; p. 15.
- Moravec, H. Obstacle Avoidance and Navigation in the Real World by a Seeing Robot Rover. Ph.D. Thesis, Stanford University, Stanford, CA, USA, 1980. [Google Scholar]
- Matthies, L.H. Dynamic Stereo Vision. Ph.D. Thesis, Carnegie Mellon University, Pittsburgh, PA, USA, 1989. [Google Scholar]
- Olson, C.F.; Matthies, L.; Schoppers, M.; Maimone, M.W. Rover navigation using stereo ego-motion. Robot. Auton. Syst. 2003, 43, 215–229. [Google Scholar] [CrossRef]
- Helmick, D.; Cheng, Y.; Clouse, D.; Matthies, L.; Roumeliotis, S. Path following using visual odometry for a Mars rover in high-slip environments. In Proceedings of the 2004 IEEE Aerospace Conference, Big Sky, MT, USA, 6–13 March 2004; pp. 772–789.
- Cheng, Y.; Maimone, M.; Matthies, L. Visual odometry on the Mars exploration rovers—A tool to ensure accurate driving and science imaging. IEEE Robot. Autom. Mag. 2006, 13, 54–62. [Google Scholar] [CrossRef]
- Maki, J.N.; Bell, J.F., III; Herkenhoff, K.E.; Squyres, S.W.; Kiely, A.; Klimesh, M.; Schwochert, M.; Litwin, T.; Willson, R.; Johnson, A.; et al. Mars Exploration Rover engineering cameras. J. Geophys. Res. E Planets 2003, 108, E12. [Google Scholar] [CrossRef]
- Maki, J.; Thiessen, D.; Pourangi, A.; Kobzeff, P.; Litwin, T.; Scherr, L.; Elliott, S.; Dingizian, A.; Maimone, M. The Mars Science Laboratory Engineering Cameras. Space Sci. Rev. 2012, 170, 77–93. [Google Scholar] [CrossRef]
- McManamon, K.; Lancaster, R.; Silva, N. ExoMars Rover Vehicle Perception System Architecture and Test Results. In Proceedings of the 12th Symposium on Advanced Space Technologies in Robotics and Automation, Noordwijk, The Netherlands, 15–17 May 2013.
- Gao, Y.; Liu, J. China’s robotics successes abound. Science 2014, 345, 523–523. [Google Scholar] [CrossRef] [PubMed]
- Ellery, A. Planetary Rovers, 1st ed.; Springer: Berlin, Germany, 2016. [Google Scholar]
- Saxena, A.; Chung, S.H.; Ng, A.Y. Learning depth from single monocular images. In Advances in Neural Information Processing Systems; MIT Press: Cambridge, MA, USA, 2005; pp. 1161–1168. [Google Scholar]
- Saxena, A.; Chung, S.H.; Ng, A.Y. 3-D Depth Reconstruction from a Single Still Image. Int. J. Comput. Vis. 2008, 76, 53–69. [Google Scholar] [CrossRef]
- Zhuo, S.J.; Sim, T. On the Recovery of Depth from a Single Defocused Image. In Proceedings of the 13th International Conference on Computer Analysis of Images and Patterns (CAIP 2009), Münster, Germany, 2–4 September 2009; pp. 889–897.
- Genchi, S.A.; Vitale, A.J.; Perillo, G.M.E.; Delrieux, C.A. Structure-from-Motion Approach for Characterization of Bioerosion Patterns Using UAV Imagery. Sensors 2015, 15, 3593–3609. [Google Scholar] [CrossRef] [PubMed]
- Dani, A.P.; Fischer, N.R.; Dixon, W.E. Single Camera Structure and Motion. IEEE Trans. Autom. Control 2012, 57, 238–243. [Google Scholar] [CrossRef]
- Wu, C. Towards Linear-Time Incremental Structure from Motion. In Proceedings of the 2013 International Conference on 3D Vision (3DV ’13), Seattle, WA, USA, 29 June–1 July 2013; pp. 127–134.
- Van Diggelen, J. A photometric investigation of slopes and heights of the ranges in maria of the moon. Bull. Astron. Inst. Netherlands 1951, 11, 283. [Google Scholar]
- Spiteri, C.; Shaukat, A.; Gao, Y. Structure Augmented Monocular Saliency for Planetary Rovers. Robot. Auton. Syst. 2016, in press. [Google Scholar]
- Gao, Y.; Spiteri, C.; Li, C.L.; Zheng, Y.C. Lunar soil strength estimation based on Chang’E-3 images. Adv. Space Res. 2016, 58, 1893–1899. [Google Scholar] [CrossRef]
- Bajpai, A.; Burroughes, G.; Shaukat, A.; Gao, Y. Planetary Monocular Simultaneous Localization and Mapping. J. Field Robot. 2016, 33, 229–242. [Google Scholar] [CrossRef]
- Gao, Y.; Allouis, E.; Iles, P.; Paar, G.; de Gea Fernandez, J.; Deen, R.G.; Muller, J.P.; Silva, N.; Shaukat, A.; Iles, P.; et al. Contemporary Planetary Robotics: An Approach Toward Autonomous Systems; Wiley-VCH, John Wiley & Sons: Weinheim, Germany, 2016. [Google Scholar]
- Ahuja, S.; Iles, P.; Waslander, S.L. Three-dimensional Scan Registration Using Curvelet Features in Planetary Environments. J. Field Robot. 2016, 33, 243–259. [Google Scholar] [CrossRef]
- Jiang, X.; Sun, X.; Han, C.; Li, X.; Zhao, Y. LIDAR based terrain slope detection on fractal based lunar surface modeling. In Proceedings of the 2013 Fourth International Conference on Intelligent Control and Information Processing (ICICIP), Beijing, China, 9–11 June 2013; pp. 451–454.
- Schafer, H.; Hach, A.; Proetzsch, M.; Berns, K. 3D obstacle detection and avoidance in vegetated off-road terrain. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA 2008), Pasadena, CA, USA, 19–23 May 2008; pp. 923–928.
- Pedersen, L.; Allan, M.; Utz, H.; Deans, M.; Bouyssounouse, X.; Choi, Y.; Fluckiger, L.; Lee, S.Y.; To, V.; Loh, J.; et al. Tele-Operated Lunar Rover Navigation Using Lidar. In Proceedings of the International Symposium on Artificial Intelligence, Robotics and Automation in Space (I-SAIRAS), Turin, Italy, 4–6 September 2012.
- Loh, J.; Elkaim, G. Roughness Map for Autonomous Rovers. In Proceedings of the American Control Conference, ACC13, Washington, DC, USA, 17–19 June 2013.
- Langer, D.; Rosenblatt, J.K.; Hebert, M. A behavior-based system for off-road navigation. IEEE Trans. Robot. Autom. 1994, 10, 776–783. [Google Scholar] [CrossRef]
- Bakambu, A.J.; Nimelman, M.; Mukherji, R.; Tripp, J.W. Compact Fast Scanning LIDAR For Planetary Rover Navigation. In Proceedings of the International Symposium on Artificial Intelligence, Robotics and Automation in Space (I-SAIRAS), Turin, Italy, 4–6 September 2012.
- Dupuis, E.; Bakambu, J.N.; Rekleitis, I.; Bedwani, J.L.; Gemme, S.; Rivest-Caissy, J.P. Autonomous Long-Range Rover Navigation-Experimental Results. In Proceedings of the 9th ESA Workshop on Advanced Space Technologies for Robotics and Automation, Noordwijk, The Netherlands, 28–30 November 2006.
- Rekleitis, I.; Bedwani, J.L.; Dupuis, E.; Lamarche, T.; Allard, P. Autonomous over-the-horizon navigation using LIDAR data. Auton. Robots 2013, 34, 1–18. [Google Scholar] [CrossRef]
- Osinski, G.R.; Barfoot, T.D.; Ghafoor, N.; Izawa, M.; Banerjee, N.; Jasiobedzki, P.; Tripp, J.; Richards, R.; Auclair, S.; Sapers, H.; et al. Lidar and the mobile Scene Modeler (mSM) as scientific tools for planetary exploration. Planet. Space Sci. 2010, 58, 691–700. [Google Scholar] [CrossRef]
- Hähnel, D.; Burgard, W.; Thrun, S. Learning compact 3D models of indoor and outdoor environments with a mobile robot. Robot. Auton. Syst. 2003, 44, 15–27. [Google Scholar] [CrossRef]
- Weingarten, J.; Siegwart, R. 3D SLAM using planar segments. In Proceedings of the 2006 IEEE/RSJ International Conference on Intelligent Robots and Systems, Beijing, China, 9–15 October 2006; pp. 3062–3067.
- Lamon, P.; Stachniss, C.; Triebel, R.; Pfaff, P.; Plagemann, C.; Grisetti, G.; Siegwart, R. Mapping with an Autonomous Car. In Proceedings of the Workshop on Safe Navigation in Open and Dynamic Environments at the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Beijing, China, 9–15 October 2006.
- Sheshadri, A.; Peterson, K.M.; Jones, H.L.; Whittaker, W.L.R. Position estimation by registration to planetary terrain. In Proceedings of the 2012 IEEE Conference on Multisensor Fusion and Integration for Intelligent Systems (MFI), Hamburg, Germany, 13–15 September 2012; pp. 432–438.
- Martins, H.; Birk, J.; Kelley, R. Camera models based on data from two calibration planes. Comput. Graph. Image Process. 1981, 17, 173–180. [Google Scholar] [CrossRef]
- Fryer, J.G.; Brown, D.C. Lens Distortion for Close-Range Photogrammetry. Photogramm. Eng. Remote Sens. 1986, 52, 51–58. [Google Scholar]
- Kannala, J.; Brandt, S.S. A generic camera model and calibration method for conventional, wide-angle, and fish-eye lenses. IEEE Trans. Pattern Anal. Mach. Intell. 2006, 28, 1335–1340. [Google Scholar] [CrossRef] [PubMed]
- Davidon, W.C. New least-square algorithms. J. Optim. Theory Appl. 1976, 18, 187–197. [Google Scholar] [CrossRef]
- Zhang, Z. Camera Calibration. In Emerging Topics in Computer Vision; Medioni, G., Kang, S.B., Eds.; Prentice Hall PTR: Upper Saddle River, NJ, USA, 2004; pp. 4–43. [Google Scholar]
- Luebke, D.P. A Developer’s Survey of Polygonal Simplification Algorithms. IEEE Comput. Graph. Appl. 2001, 21, 24–35. [Google Scholar] [CrossRef]
- Garland, M.; Heckbert, P.S. Surface Simplification Using Quadric Error Metrics. In Proceedings of the 24th Annual Conference on Computer Graphics and Interactive Techniques (SIGGRAPH ’97), Los Angeles, CA, USA, 3–8 August 1997.











© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shaukat, A.; Blacker, P.C.; Spiteri, C.; Gao, Y. Towards Camera-LIDAR Fusion-Based Terrain Modelling for Planetary Surfaces: Review and Analysis. Sensors 2016, 16, 1952. https://doi.org/10.3390/s16111952
Shaukat A, Blacker PC, Spiteri C, Gao Y. Towards Camera-LIDAR Fusion-Based Terrain Modelling for Planetary Surfaces: Review and Analysis. Sensors. 2016; 16(11):1952. https://doi.org/10.3390/s16111952
Chicago/Turabian StyleShaukat, Affan, Peter C. Blacker, Conrad Spiteri, and Yang Gao. 2016. "Towards Camera-LIDAR Fusion-Based Terrain Modelling for Planetary Surfaces: Review and Analysis" Sensors 16, no. 11: 1952. https://doi.org/10.3390/s16111952
APA StyleShaukat, A., Blacker, P. C., Spiteri, C., & Gao, Y. (2016). Towards Camera-LIDAR Fusion-Based Terrain Modelling for Planetary Surfaces: Review and Analysis. Sensors, 16(11), 1952. https://doi.org/10.3390/s16111952




