Microelectromechanical Resonant Accelerometer Designed with a High Sensitivity
Abstract
:1. Introduction
2. Background
2.1. Operation Principle
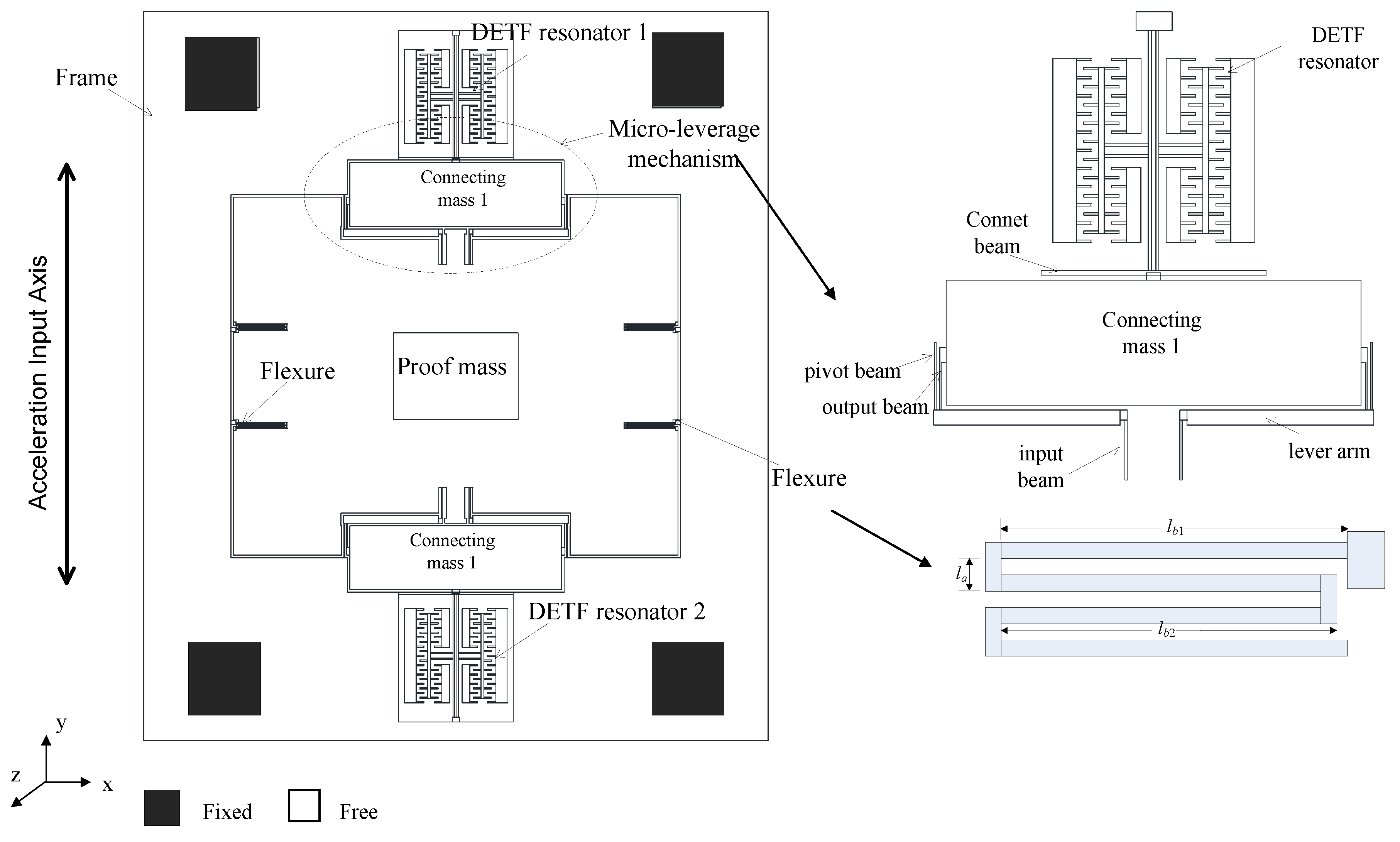
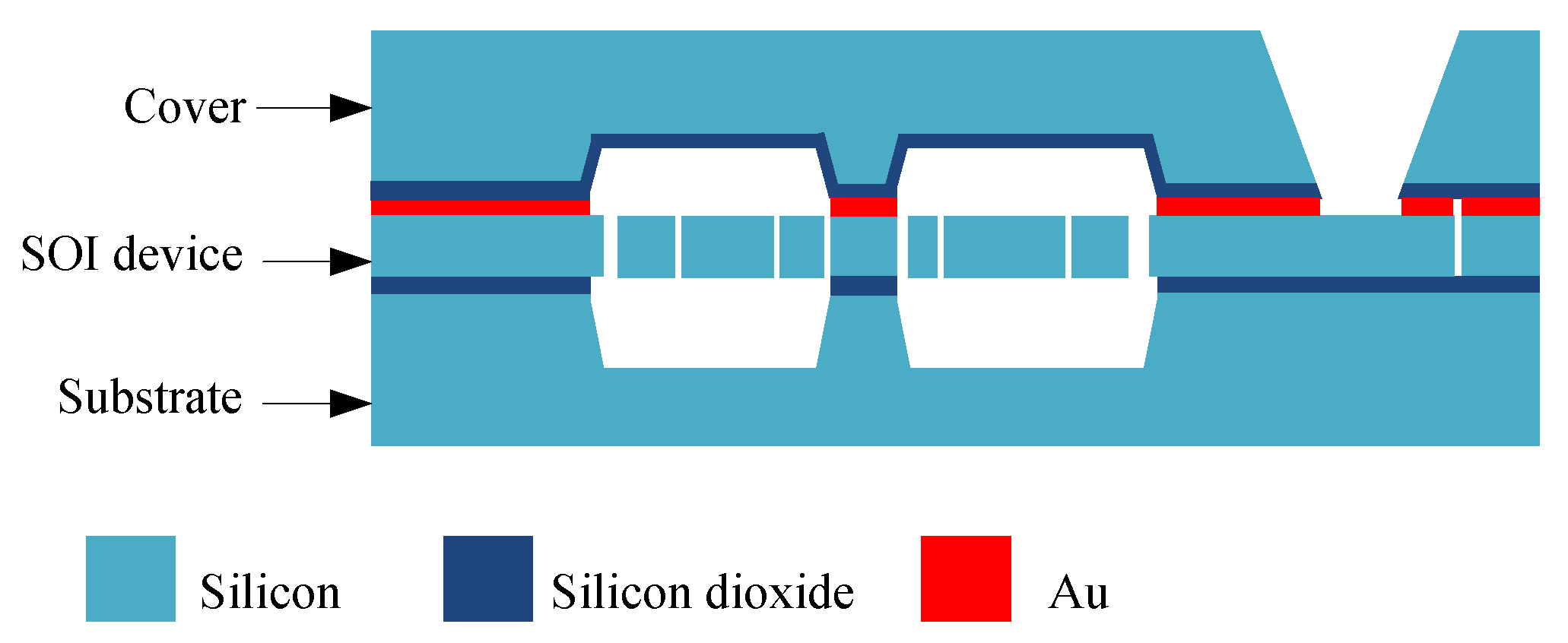
2.2. Dies Based on the SOI-MEMS Process

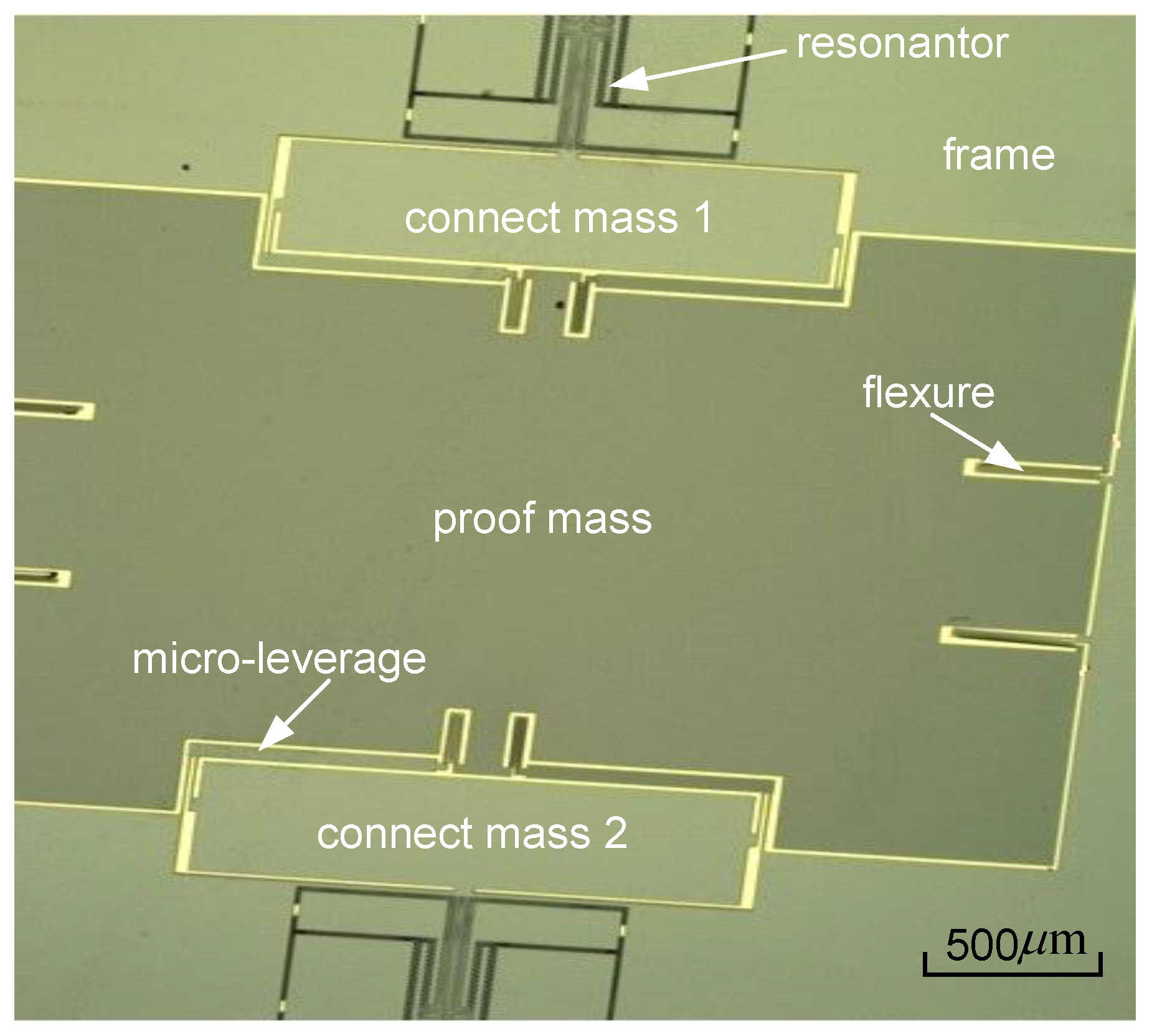
3. Device Design
3.1. Theoretical Analysis
3.2. Effective Amplification Factor A*
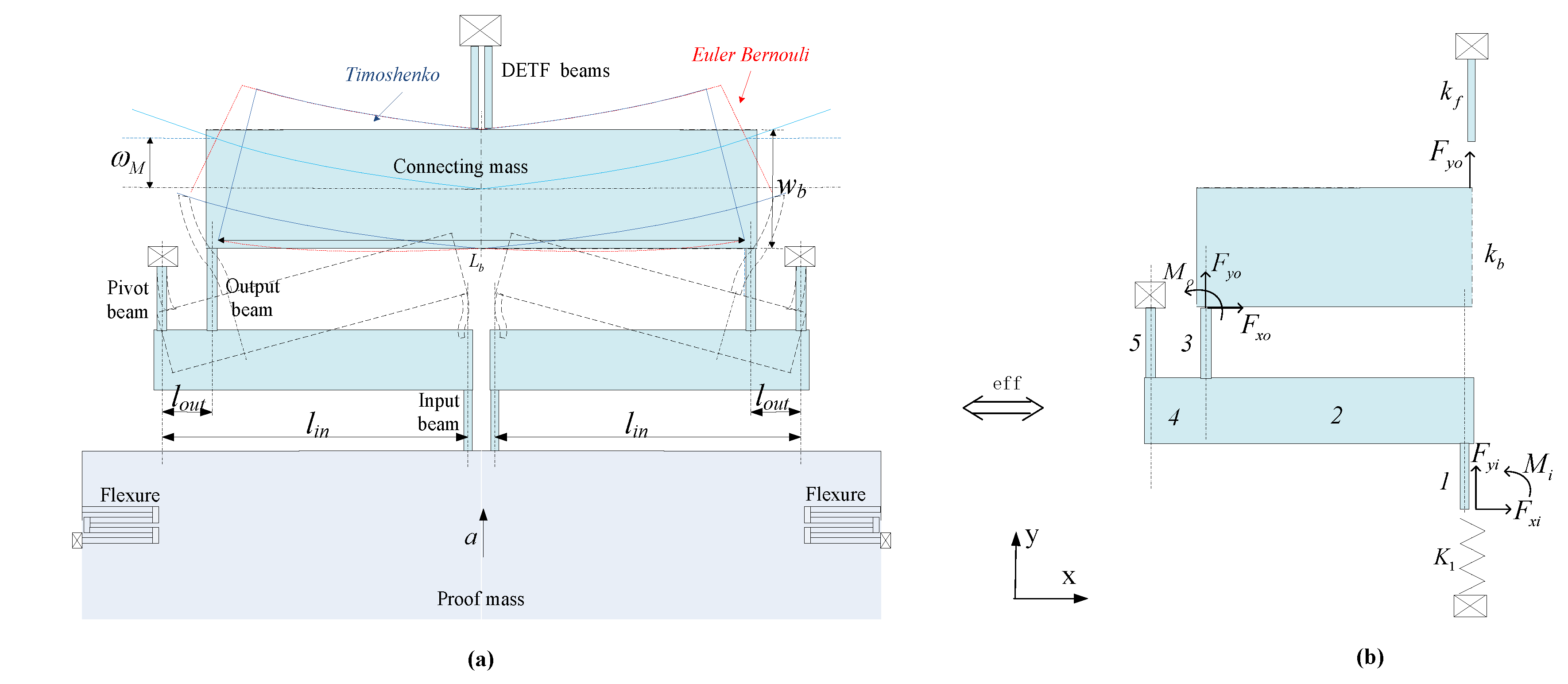
3.3. DETF Design Analysis

3.4. Reasonable Design of the Structure
| Variable | lr (μm) | wr (μm) | li (μm) | wi (μm) | lo (μm) | wo (μm) | lp (μm) | wp (μm) | lin (μm) | lout (μm) | wc (μm) | Lc (μm) | la (μm) | lb1 (μm) | lb2 (μm) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Size range | 100–1500 | 5.5–8 | 50–480 | 4.5–10 | 20–350 | 4.5–10 | 10–350 | 4.5–10 | 200–1650 | >(wo+ wp)/2 | lin/10 < wc < lin/2 | 2lin-10 | 9–20 | 200–1000 | Lb1–20 |
| Optimal value | 761.4 | 5.5 | 242.2 | 5.63 | 44.8 | 5.24 | 196.1 | 4.5 | 1641 | 54.9 | 1225 | 3272 | 10.7 | 390.3 | 370.3 |
| Corrected value | 761.5 | 5.5 | 242 | 5.5 | 45 | 5 | 196 | 4.5 | 900 | 29 | 525 | 1700 | 11 | 390 | 370 |
| Earlier structure | 1000 | 8 | 300 | 6 | 60 | 4 | 270 | 6 | 644 | 19 | -- | -- | 16 | 650 | 650 |
| Component | Energy Consume × 10−17a2 (J) | Ratio (%) | ||
|---|---|---|---|---|
| Earlier Structure | This Work | Earlier Structure | This work | |
| DETF | 7.96 × 10−4 | 24.56 | 6.58 × 10−4 | 59.6 |
| Flexure | 41.93 | 6.51 | 34.64 | 15.8 |
| Input beam | 51.69 | 2.19 | 42.71 | 5.3 |
| Output beam | 23.35 | 1.09 | 19.3 | 2.6 |
| Pivot beam | 3.825 | 1.04 | 3.16 | 2.5 |
| Lever arm(in) | 0.24 | 2.55 | 0.198 | 6.2 |
| Lever arm(out) | 9.47 × 10−5 | 0.07 | 7.82 × 10−7 | 0.2 |
| Connecting mass | 8.8 × 10−4 | 3.27 | 7.27 × 10−6 | 7.9 |
| SMRA | Sensitivity of DETF (Hz/N) | Effective Amplification Factor A* | The Proof Mass (kg) | Sg (Hz/g) |
|---|---|---|---|---|
| Previous design | 399,393 | 22.04 | 1.42 × 10−6 | 127.33 |
| This work | 490,303 | 26.67 | 1.7 × 10−6 | 211.5 |
| Ratio for the improvement | 22.8% | 21% | 19.72% | 66% |
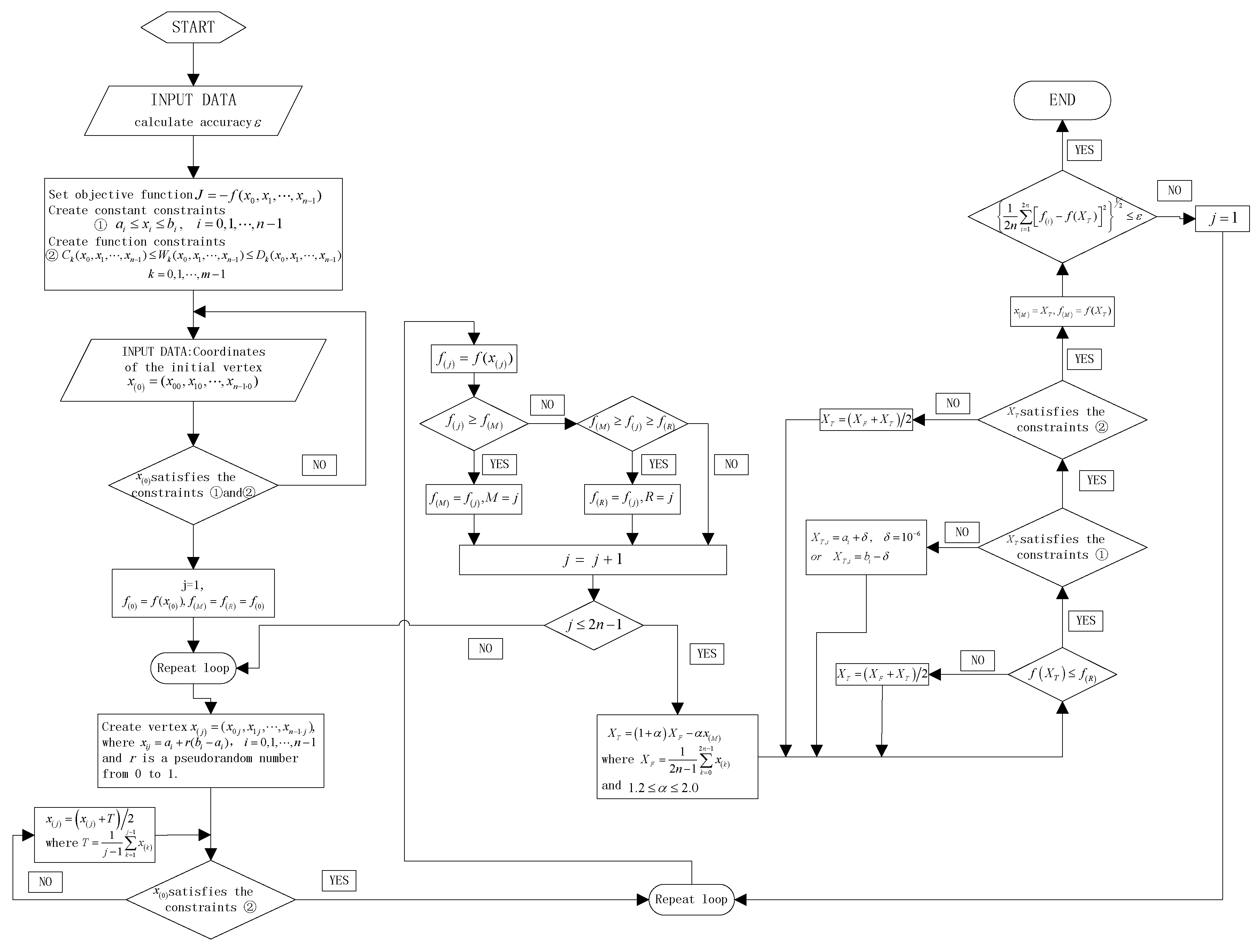
4. Simulation and Experiments for the SMRA
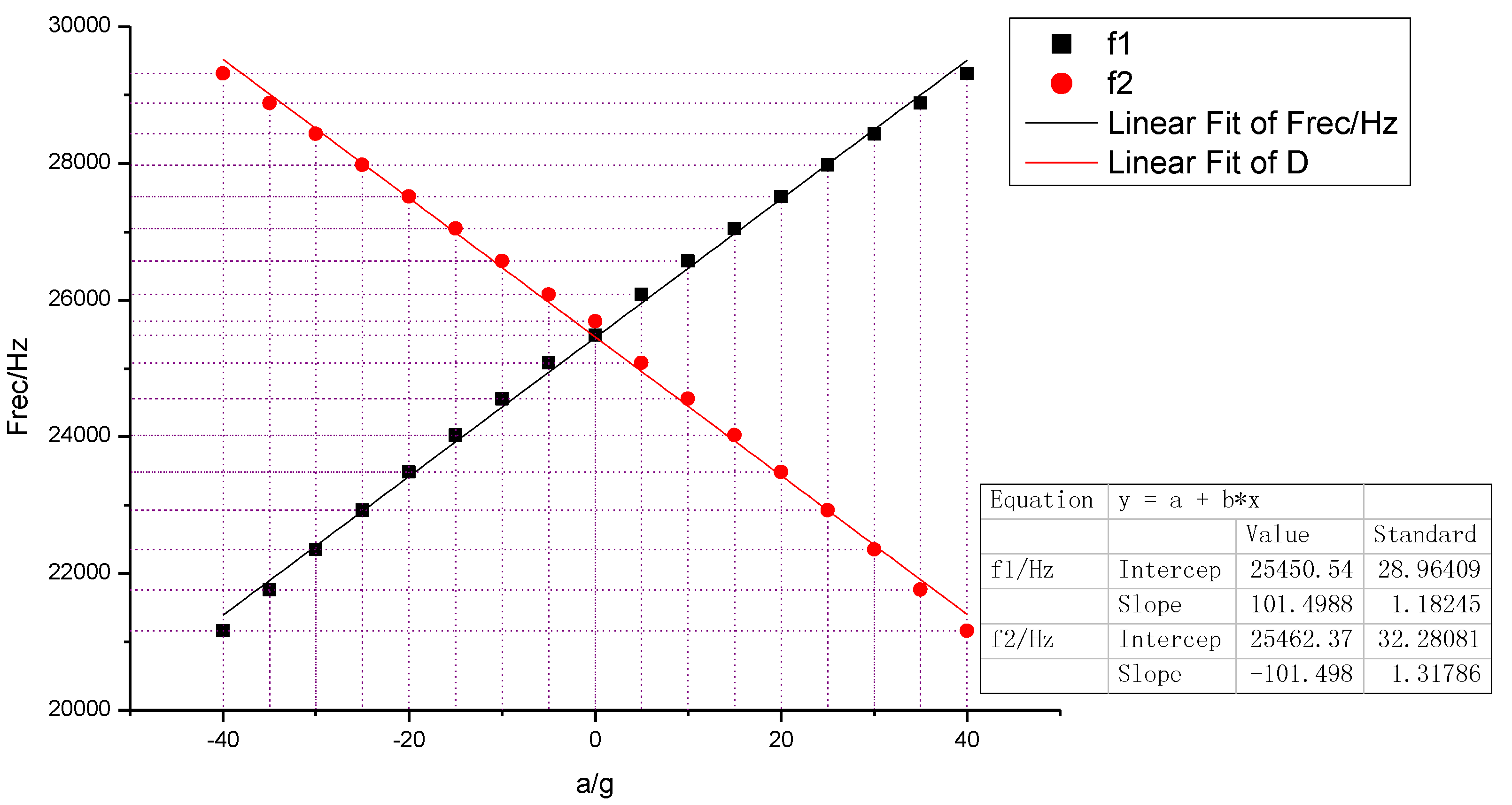
| Results and Errors | f0 (Hz) | Effective Amplification Factor A* | Sg (Hz/g) |
|---|---|---|---|
| Theory results | 26,053.5 | 26.2 | 211.5 |
| Simulated values | 25,585.4 | 26.67/25.33 | 203 |
| Relative shift | 1.8% | 1.88%/3.33% | 4.19% |
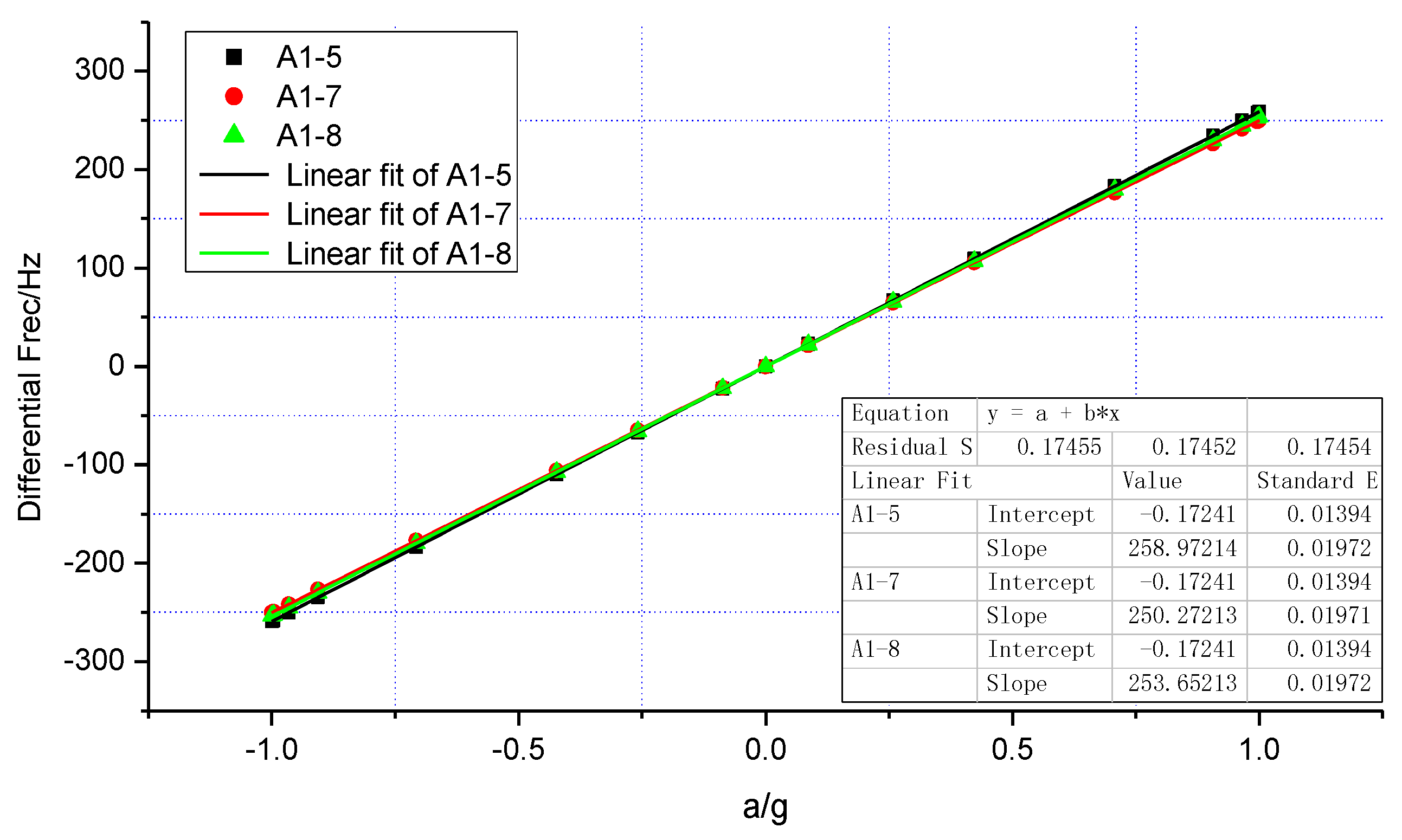
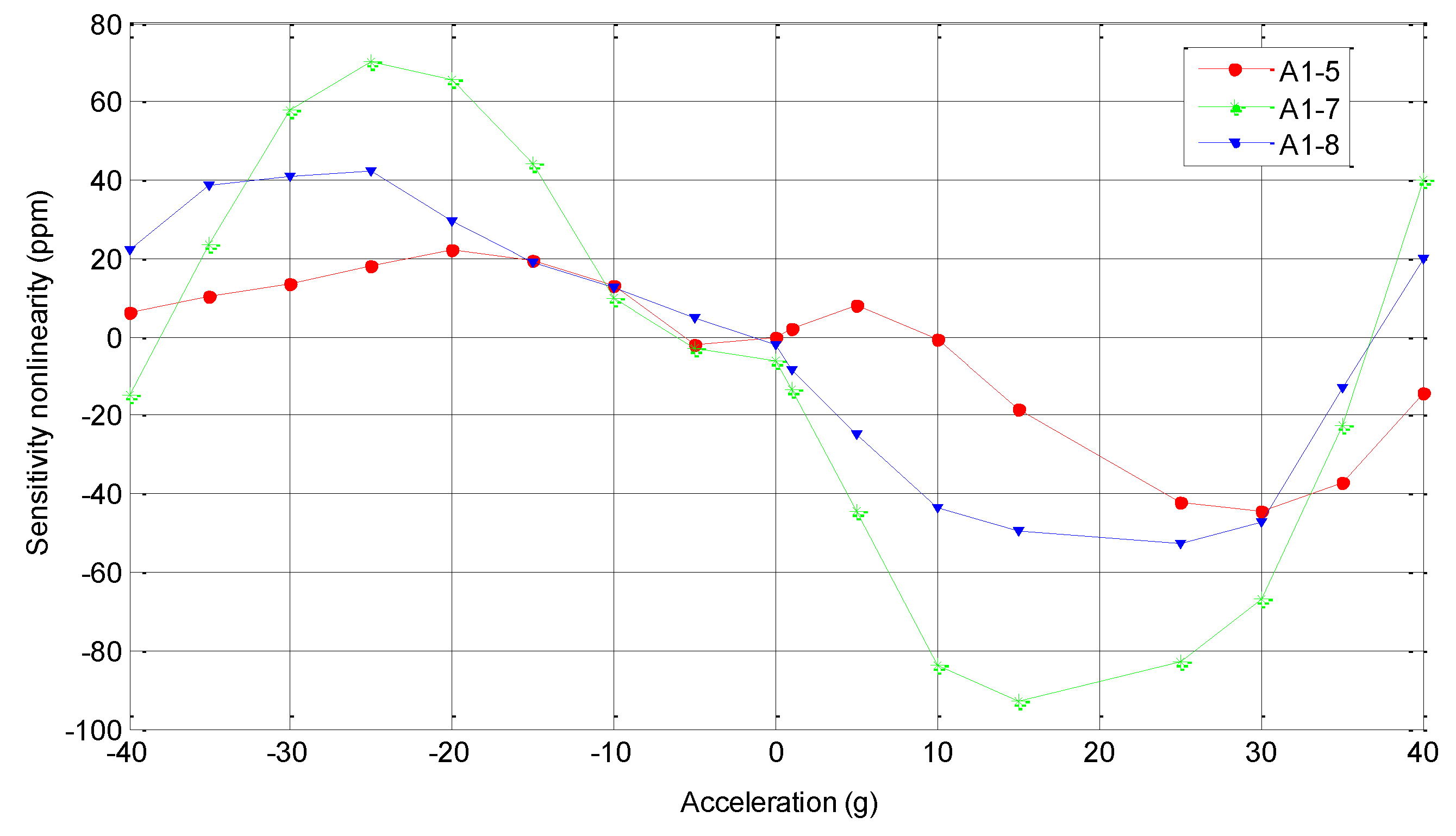

5. Conclusions/Outlook
Appendix A
| Beam Number | Axial Force Fj | Moment Mj (j = 1, 2, 3, 4, 5) |
|---|---|---|
| 1 | ||
| 2 | ||
| 3 | ||
| 4 | ||
| 5 |
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Marek, J.; Gómez, U.M. MEMS (micro-electro-mechanical systems) for automotive and consumer electronics. In Chips A Guide to the Future of Nanoelectronics the Frontiers Collection; Springer-Verlag: Berlin Heidelberg, Germany, 2012; p. 293. [Google Scholar]
- Seshia, A.A.; Palaniapan, M.; Roessig, T.A.; Howe, R.T.; Gooch, R.W.; Schimert, T.R.; Montague, S. A vacuum packaged surface micromachined resonant accelerometer. J. Microelectromech. Syst. 2002, 11, 784–793. [Google Scholar] [CrossRef]
- Comi, C.; Corigliano, A.; Langfelder, G.; Longoni, A.; Tocchio, A.; Simoni, B. A resonant microaccelerometer with high sensitivity operating in an oscillating circuit. J. Microelectromech. Syst. 2010, 19, 1140–1152. [Google Scholar] [CrossRef]
- Pinto, D.; Mercier, D.; Kharrat, C.; Colinet, E.; Nguyen, V.; Reig, B.; Hentz, S. A small and high sensitivity resonant accelerometer. Procedia Chem. 2009, 1, 536–539. [Google Scholar] [CrossRef]
- Shi, R.; Jia, F.-X.; Qiu, A.-P.; Su, Y. Phase noise analysis of micromechanical silicon resonant accelerometer. Sens. Actuators A Phys. 2013, 197, 15–24. [Google Scholar] [CrossRef]
- Chae, J.; Kulah, H.; Najafi, K. A cmos-compatible high aspect ratio silicon-on-glass in-plane micro-accelerometer. J. Micromech. Microeng. 2005, 15, 336–345. [Google Scholar] [CrossRef]
- Fan, K.; Che, L.; Xiong, B.; Wang, Y. A silicon micromachined high-shock accelerometer with a bonded hinge structure. J. Micromech. Microeng. 2007, 17, 1206–1210. [Google Scholar] [CrossRef]
- Krishnamoorthy, U.; Olsson, R., III; Bogart, G.R.; Baker, M.; Carr, D.; Swiler, T.; Clews, P. In-plane mems-based nano-g accelerometer with sub-wavelength optical resonant sensor. Sens. Actuators A Phys. 2008, 145, 283–290. [Google Scholar] [CrossRef]
- Zou, X.; Thiruvenkatanathan, P.; Seshia, A.A. A seismic-grade resonant mems accelerometer. J. Microelectromech. Syst. 2014, 23, 768–770. [Google Scholar] [CrossRef]
- Zou, X.; Thiruvenkatanathan, P.; Seshia, A.A. Micro-electro-mechanical resonant tilt sensor. In Proceedings of the 2012 IEEE International Frequency Control Symposium (FCS), Baltimore, MD, USA, 21–24 May 2012; pp. 1–4.
- Su, S.X.; Yang, H.S.; Agogino, A.M. A resonant accelerometer with two-stage microleverage mechanisms fabricated by soi-mems technology. IEEE Sens. J. 2005, 5, 1214–1223. [Google Scholar] [CrossRef]
- Xia, G.-M.; Qiu, A.-P.; Shi, Q.; Su, Y. Test and evaluation of a silicon resonant accelerometer implemented in soi technology. In Proceedings of the 2013 IEEE Sensors, Baltimore, MD, USA, 3–6 November 2013; pp. 1–4.
- Dong, J.-H.; Qiu, A.-P.; Shi, R. Temperature influence mechanism of micromechanical silicon oscillating accelerometer. In Proceedings of the 2011 IEEE Power Engineering And Automation Conference (PEAM), Wuhan, China, 8–9 September 2011; pp. 385–389.
- Shi, R.; Jiang, S.; Qiu, A.-P.; Su, Y. Application of microlever to micromechanical silicon resonant accelerometers. Opt. Precis. Eng. 2011, 19, 805–811. [Google Scholar]
- Lagarias, J.C.; Reeds, J.A.; Wright, M.H.; Wright, P.E. Convergence properties of the Nelder-Mead simplex method in low dimensions. SIAM J. Optim. 1998, 9, 112–147. [Google Scholar] [CrossRef]
- Nelder, J.A.; Mead, R. A simplex method for function minimization. Comput. J. 1965, 7, 308–313. [Google Scholar] [CrossRef]
- Brosnihan, T.J.; Bustillo, J.M.; Pisano, A.P.; Howe, R.T. Embedded interconnect and electrical isolation for high-aspect-ratio, soi inertial instruments. In Proceedings of the 1977 Internatonal Conference Solid State Sensors and Actuators, Transducers ’97, Chicago, IL, USA, 16–19 June 1997; Volume 631, pp. 637–640.
- Torunbalci, M.M.; Alper, S.E.; Akin, T. Wafer level hermetic encapsulation of mems inertial sensors using soi cap wafers with vertical feedthroughs. In Proceedings of the 2014 International Symposium on Inertial Sensors and Systems (ISISS), Laguna Beach, CA, USA, 25–26 Februar 2014; pp. 1–2.
- Renard, S. SOI micromachining technologies for MEMS. In Micromachining and Microfabrication; International Society for Optics and Photonics: Santa Clara, CA, USA, 25 August 2000; pp. 193–199. [Google Scholar]
- Lin, C.-W.; Hsu, C.-P.; Yang, H.-A.; Wang, W.C.; Fang, W. Implementation of silicon-on-glass mems devices with embedded through-wafer silicon vias using the glass reflow process for wafer-level packaging and 3D chip integration. J. Micromech. Microeng. 2008, 18. [Google Scholar] [CrossRef]
- Harris, C.M.; Piersol, A.G.; Paez, T.L. Harris’ Shock and Vibration Handbook; McGraw-Hill New York: New York, NY, USA, 2002; Volume 5. [Google Scholar]
- Roessig, T.-A.W. Integrated Mems Tuning Fork Oscillators for Sensor Applications; University of California: Berkeley, CA, USA, 1998. [Google Scholar]
- IEEE. 1293–1998—IEEE standard specification format guide and test procedure for linear, single-axis, non-gyroscopic accelerometers. IEEE Standards Association: New York, NY, USA, 1999; pp. 200–201. [Google Scholar]
- Allan, D.W. Time and frequency (time-domain) characterization, estimation, and prediction of precision clocks and oscillators. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 1987, 34, 647–654. [Google Scholar] [CrossRef] [PubMed]
- Lefort, O.; Jaud, S.; Quer, R.; Milesi, A. Inertial grade silicon vibrating beam accelerometer. In Proceedings of Inertial Sensors and Systems 2012, Karlsruhe, Germany, 18–19 September 2012.
- He, L.; Xu, Y.P.; Palaniapan, M. A cmos readout circuit for soi resonant accelerometer with 4-bias stability and 20-resolution. Solid-State Circuits, IEEE J. 2008, 43, 1480–1490. [Google Scholar] [CrossRef]
- Argyris, J.H.; Kelsey, S. Energy Theorems and Structural Analysis; Springer: Bradford, UK, 1960; Voluem 960. [Google Scholar]
- Iyer, S.V. Modeling and Simulation of Non-Idealities in a Z-Axis Cmos-Mems Gyroscope. Ph.D. Thesis, Carnegie Mellon University, Pittsburgh, PA, USA, 2003; pp. 24–28. [Google Scholar]
- Timoshenko, S.; Woinowsky-Krieger, S.; Woinowsky-Krieger, S. Theory of Plates and Shells; McGraw-hill New York: New York, NY, USA, 1959; Volume 2. [Google Scholar]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, J.; Su, Y.; Shi, Q.; Qiu, A.-P. Microelectromechanical Resonant Accelerometer Designed with a High Sensitivity. Sensors 2015, 15, 30293-30310. https://doi.org/10.3390/s151229803
Zhang J, Su Y, Shi Q, Qiu A-P. Microelectromechanical Resonant Accelerometer Designed with a High Sensitivity. Sensors. 2015; 15(12):30293-30310. https://doi.org/10.3390/s151229803
Chicago/Turabian StyleZhang, Jing, Yan Su, Qin Shi, and An-Ping Qiu. 2015. "Microelectromechanical Resonant Accelerometer Designed with a High Sensitivity" Sensors 15, no. 12: 30293-30310. https://doi.org/10.3390/s151229803
APA StyleZhang, J., Su, Y., Shi, Q., & Qiu, A.-P. (2015). Microelectromechanical Resonant Accelerometer Designed with a High Sensitivity. Sensors, 15(12), 30293-30310. https://doi.org/10.3390/s151229803





