Applying Population Viability Analysis to Inform Genetic Rescue That Preserves Locally Unique Genetic Variation in a Critically Endangered Mammal

Abstract

Genetic rescue can reduce the extinction risk of inbred populations, but it has the poorly understood risk of ‘genetic swamping’—the replacement of the distinctive variation of the target population. We applied population viability analysis (PVA) to identify translocation rates into the inbred lowland population of Leadbeater’s possum from an outbred highland population that would alleviate inbreeding depression and rapidly reach a target population size (N) while maximising the retention of locally unique neutral genetic variation. Using genomic kinship coefficients to model inbreeding in Vortex, we simulated genetic rescue scenarios that included gene pool mixing with genetically diverse highland possums and increased the N from 35 to 110 within ten years. The PVA predicted that the last remaining population of lowland Leadbeater’s possum will be extinct within 23 years without genetic rescue, and that the carrying capacity at its current range is insufficient to enable recovery, even with genetic rescue. Supplementation rates that rapidly increased population size resulted in higher retention (as opposed to complete loss) of local alleles through alleviation of genetic drift but reduced the frequency of locally unique alleles. Ongoing gene flow and a higher N will facilitate natural selection. Accordingly, we recommend founding a new population of lowland possums in a high-quality habitat, where population growth and natural gene exchange with highland populations are possible. We also recommend ensuring gene flow into the population through natural dispersal and/or frequent translocations of highland individuals. Genetic rescue should be implemented within an adaptive management framework, with post-translocation monitoring data incorporated into the models to make updated predictions.

1. Introduction

Many threatened species are restricted to small and isolated populations, which places them at elevated risk of inbred matings and loss of beneficial genetic variation by genetic drift [1,2]. Small and isolated populations of diploid species that usually outbreed nearly always exhibit reduced fitness as a consequence of inbreeding (i.e., inbreeding depression) [3]. Usually concurrent with inbreeding depression, the loss of beneficial variation and the accumulation of harmful variation further reduce the population mean fitness [4]. Together with the loss of genetic variation that would otherwise facilitate adaptation to future environmental conditions, these issues reduce population viability [1,5]. If inbred populations remain isolated, extinction becomes increasingly likely due to the ‘extinction vortex’ effect, wherein a shrinking population size is reinforced by increasing inbreeding depression and fitness loss [6,7].

Translocations of individuals from other populations can increase genetic diversity of isolated populations and elevate population fitness by reducing inbreeding depression and alleviating the harmful effects of beneficial variation being lost from the population (i.e., causing genetic rescue), thus increasing the persistence and adaptive capacity of populations [2,8,9]. Such genetic management is a highly effective conservation tool; when appropriate sources of genetic augmentation are used, outcrossing increases fitness in the vast majority of inbred populations that usually outbreed, and an enhanced ability to adapt can greatly increase population persistence in changing environments [10].

Despite its demonstrated effectiveness, genetic rescue has not been widely implemented, partly owing to concerns about ‘genetic swamping’ and a consequent loss of local adaptation and distinctiveness [11,12,13]. Genetic swamping can be defined as the replacement of a population’s locally adaptive genetic variation with that of immigrants [13]. This definition may be extended to include apparently neutral alleles within populations because distinguishing adaptive from non-adaptive variation can be extremely challenging, and such variation can contribute to future adaptive potential [14]. An extreme example of genetic swamping occurs in some hybridising species, in which hybrid vigour (heterosis) causes the extirpation of the original locally adapted population and their alleles [15]. A subtler form of genetic swamping occurs when locally unique genetic variation is replaced during the immigration of conspecifics [16]. Concerns about genetic swamping tend to promote conservation strategies that maintain genetic distinctiveness of isolated populations rather than evaluating alternative management options in a risk-benefit framework, but a different strategy might have a better outcome for the stated conservation goals [17]. On one hand, species-wide genetic variation could be lost if translocation strategies cause the replacement of locally unique alleles, potentially reducing the adaptive potential and increasing extinction risk [13,18,19,20]. Conversely, the genetic distinctiveness of small and isolated populations is often an artefact of genetic stochasticity rather than local adaptation, and if ‘uniqueness’ reflects harmful variation that would have been removed by selection in larger and/or more connected populations, maintaining the distinctiveness of small populations can even exacerbate extinction risk [21].

Effective population sizes (N_e) >100 are needed to limit the mean inbreeding coefficient (the probability that any two alleles are identical by descent) to F < 0.1 over five generations [10]. Smaller and more inbred populations need high supplementation rates to reverse inbreeding, which could elevate the risk of swamping [1]. Nevertheless, alleviating inbreeding depression while avoiding the replacement of the local gene pool may be achievable by appropriately managing gene flow during genetic rescue. Even under considerable gene flow during intensive genetic rescue, selection can maintain locally adaptive genetic variation in the face of potential swamping [22]. However, selection is generally weaker in small populations because genetic drift has a greater influence on allele frequencies [23]. Preserving genome-wide variation, including variation that is currently neutral, also enhances future adaptive potential [14,24,25]. Thus, it is of interest to estimate how much locally unique genome-wide variation will persist in a population under genetic rescue, especially if candidate populations for genetic rescue are small. Accordingly, poor understanding of swamping during genetic rescue is a significant knowledge gap [13].

Population demographic and genetic models that account for inbreeding depression and the genetic contribution of outbred immigrants could be useful for designing genetic rescue regimes that help retain locally unique alleles. Forward-based computer simulations can project the changes in the genetic profile of populations under different demographic and population genetic scenarios [26]. Such simulations have been used to estimate the impacts of inbreeding depression and predict changes in the viability of inbred populations after genetic rescue [14,27]. PVAs can be used to predict how much of the genetic variation from a source population can be retained when founding a new population or supplementing an existing population [28,29,30]. However, the preservation of alleles unique to a local population that is supplemented with unrelated individuals has been less scrutinised, and fitness disparities between outbred immigrants and inbred locals can cause the replacement of local variation [31]. Incorporating inbreeding and inbreeding depression into models accounts for the reduced contribution to the gene pool of inbred locals relative to immigrants. Models that consider locally unique variation and the lower fitness of inbred locals relative to immigrants could therefore be useful for designing genetic rescue programs that improve population viability without replacing the local gene pool.

Leadbeater’s possum (Gymnobelideus leadbeateri) is a critically endangered Australian marsupial and a strong candidate for genetic rescue. Genetic rescue of this species could be informed by population viability analysis (PVA) modelling the effect of various translocation scenarios on the retention of unique alleles when the recipient gene pool has reduced fitness due to severe inbreeding. The species has suffered extensive loss and deterioration of habitat caused by vegetation clearing, bushfires, and logging, and has a highly restricted distribution (Figure 1) within a 70 × 95 km area within the Central Highlands of Victoria, Australia, with a neighbouring lowland isolate [32,33]. The single population of Leadbeater’s possum outside of the Central Highlands is localised entirely within a narrow 6 km stretch of lowland swamp forest habitat in the Yellingbo Nature Conservation Reserve [34]. The Yellingbo population is genetically distinct from highland populations and is thought to represent the sole remnant of a previously widespread evolutionary lineage adapted to lowland swamp [32,35,36]. The geographic isolation of the Yellingbo population makes contemporary gene flow with other populations highly unlikely [36]. This population had greatly reduced genetic diversity compared to all conspecific populations and exhibited substantial inbreeding depression for survival to sexual maturity, longevity, probability of breeding during lifetime, and lifetime reproductive output [37]. Inbreeding depression likely contributed to the decline from ~120 individuals in 1997 to 35 individuals in 2017. Heterozygosity concurrently declined by 12%, putatively limiting the capacity of the population to adapt to environmental change and prevent the expression of deleterious variation [37]. Furthermore, suitable habitat for Leadbeater’s possum has declined in extent and quality, mainly because of habitat succession and altered hydrology [32]. Based on monotonic decline in population size, presence of inbreeding depression, and deteriorating habitat condition, the extinction of the Yellingbo population is highly likely without intervention [37,38]. Translocation of lowland Yellingbo individuals to high-quality habitat beyond Yellingbo and outcrossing with genetically diverse highland animals is planned to prevent the extinction of this population. Sourcing migrants for genetic rescue of the lowland population from highland populations is the only available option, which has been assessed to have a low risk of outbreeding depression [37]. Although genetic variation unique to the lowland population at Yellingbo has been characterised with microsatellite markers and short mitochondrial sequences [36], it was not assessed with genome-wide markers, which should better approximate functional and standing variation [24,25]. Doing so would be an important step in planning translocation strategies that do not replace the local gene pool.

We aimed to design a translocation regime of lowland and highland Leadbeater’s possums into new habitat that would rapidly increase population size, demographic stability, and genetic diversity, while providing for the retention of unique lowland alleles. We predicted the level of retention of alleles unique to the lowland population, incorporating inbreeding depression to reflect the potential fitness advantage of translocated outbred individuals and their descendants over inbred locals. We used genome-wide SNP markers to detect genomic variation unique to the lowland population, which was then monitored across simulated scenarios. We also used genome-wide SNPs to model inbreeding and genetic diversity within simulated populations. The following objectives were targeted:

(1)

Predict the trajectory of the lowland population at Yellingbo without genetic rescue;

(2)

Determine whether genetic rescue can retain genetic variation unique to the lowland population;

(3)

Assess whether more rapid genetic rescue presents a greater risk of uniquely lowland variation being replaced.

Our results will inform genetic rescue of the last extant population of the lowland lineage of this critically endangered species. More generally, our approach for designing genetic rescue regimes to retain locally unique variation should be useful for other conservation programs.

2. Materials and Methods

2.1. Study System and Sampling

The lowland population at Yellingbo was extensively surveyed from 1997–2019, with mark–recapture data available for >70% of the population in any given year [37,39]. These data provided estimates of key demographic parameters, such as mortality and reproduction rates (see below). Genetic samples (n = 304) were collected from Yellingbo during surveys from 1997 to 2001 and 2011 to 2019 [36,37]. A further 216 individuals were genetically sampled throughout the species’ range in the Central Highlands (Figure 1), against which to estimate the locally unique variation at Yellingbo. These included 113 individuals from Lake Mountain—the thoroughly sampled population used to represent allele frequencies of a donor highland population in simulations. For most samples, a small (~2 mm²) tissue biopsy of skin and cartilage was taken from the outer pinna of the ear and stored in ethanol prior to extraction. Skin samples were also taken from animals found dead or from the pelts of preserved museum specimens.

2.2. Defining Conservation Targets

Conservation programs guided by PVAs require clearly defined criteria of success [40]. We defined a strategy as successful if it resulted in a population of at least 110 individuals. This target was chosen to recreate apparent demographic stability observed at Yellingbo in the 1990s before the rapid deterioration of habitat conditions and concurrent population decline. The limited availability of lowland habitat also means that founded populations must necessarily be <120 individuals in size, with translocations maintaining population size and genetic diversity. This target represents a first (and urgent) milestone to prevent the extinction of the lowland population; however, further population expansion would be required thereafter. We assumed that genetic rescue would begin with 20 Yellingbo founders, which represents 57% of the population in 2019.

2.3. General Assumptions of the PVA Model

All PVAs were performed using the software package Vortex v.10.3.5.0 [41], an individual-based Monte Carlo simulation program that models the impact of deterministic and stochastic forces on animal populations. Demographic, environmental, and genetic processes were incorporated by inputting parameter estimates for mortality and fecundity, along with environmental variability. For a range of scenarios (

Table 1. Scenarios simulated in Vortex. Initial lowland population size (N), carrying capacity (K), whether or not the starting population was made inbred by providing a kinship matrix (Inbred), whether inbreeding depression was modelled, and whether estimated or adjusted values for juvenile (0–1 y) mortality were used is indicated. Supplementation rate is the number of individuals supplemented (by translocation) into the population per year. Supplementation duration is the number of years the population was supplemented. Simulation duration is the number of years simulations were run. Source is the population that animals were sourced from for supplementation.

Scenario	N	K	Inbred	Inbreeding Depression	Juvenile Mortality	Supplementation Rate	Supplementation Duration (Years)	Simulation Duration (Years)	Source
1990s Condition	110	120	No	Yes and no	Estimated	0	NA	50	NA
		1000	No	Yes and no	Estimated	0	NA	50	NA
2019 Trajectory	35	40	Yes	Yes	6%	0	NA	50	NA
		120	Yes	Yes	6%	0	NA	50	NA
Demographic Rescue	20	1000	Yes	Yes	6%	2; 4; 6; 8; 10	50	50	Lowland
Genetic Rescue	20	1000	Yes	Yes	6%	2; 4; 6; 8; 10	50	50	Highland
Genetic Swamping Test	20	1000	Yes	Yes	6%	2; 4; 6; 8; 10	50	10; 20; 30; 40; 50	Highland

), the program tracked individuals from birth to death, with reproduction and mortality occurring at pre-defined probabilities, derived from actual population data (below). Environmental catastrophes were not included in the model. Due to the uncertainty of environmental effects on fitness, environmental effects were minimised by setting the standard deviation for mortality and reproduction parameters to 10% of their mean value (

Table 2. Biological parameters used in Vortex simulations. The study that provided each parameter estimate is given.

Parameter	Value (SD)	Source
Diploid lethal equivalents	6.29	[42]
Percent inbreeding due to lethal recessives	50	[43]
Environmental variation correlation between reproduction and survival	0	Not used
Environmental variation correlation among populations	0	Not used
Age producing first offspring (years)	2	[39]
Maximum lifespan (years)	9	[37]
Maximum litters per year	2 *	[39]
Maximum progeny per litter	2	[39]
Maximum age of reproduction (years)	9	[37]
Sex ratio at birth	01:01	[39]
Percent adult females breeding	66.6 (6.7)	[39]
Distribution of litters per year
0 litter	0	[44]
1 litter	7	[44]
2 litter	93	[44]
Distribution of offspring per litter
1 offspring	45	[39]
2 offspring	55	[39]
Mortality
0–1 years (males)	42 (4.2) †	[44]
0–1 years (females)	41 (4.1) †	[44]
1–2 years (males)	17 (1.7)	[44]
1–2 years (females)	22 (2.2)	[44]
Annual >2 years (males)	29 (2.9)	[37]
Annual >2 years (females)	29 (2.9)	[37]
Percent males in breeding pool	100

* Up to three litters per year can be produced; however, this only occurs if a previous litter is lost. † 6% was added to early mortality estimates because these did not include partial litter loss, except for 1990s Condition and 2019 Trajectory (main text).

). This was possible only for the parameters modelled using mean and standard deviation values.

Genetic data were incorporated into all but one analysis (1990s Condition being the exception) as the input allele frequencies and pairwise kinships among individuals (detailed methods below). Alleles were assumed to be neutral and randomly assorting. Vortex uses pairwise kinships to calculate inbreeding coefficients for individuals and their offspring. Inbreeding depression was included in some models as a reduced survival probability in the first year of life (the default in Vortex). Inbreeding depression is caused by an increased expression of deleterious recessive alleles and a loss of heterozygote advantage with increasing autozygosity [45]. Lethal equivalents represent recessive alleles that compromise fitness when homozygous in an individual, with a single homozygous lethal equivalent imposing a fitness cost equivalent to the death of an individual [3]. Decreases in individual survival probability are determined by the number of lethal equivalents, the relative contribution of lethal recessive alleles and the heterozygote advantage to inbreeding depression, and the individual inbreeding coefficient. The default value of 6.29 diploid lethal equivalents for first year survival was used. This value was used in preference to estimates of lethal equivalents in the lowland Leadbeater’s possum population obtained in a previous study because these estimates were found to have wide confidence intervals and varied between different inbreeding coefficients [37]. Vortex randomly assigns lethal equivalents to each founder at the beginning of simulations. In Vortex, homozygosity for any lethal recessive always results in mortality in the first year of life. The relative contribution of lethal and sub-lethal recessive alleles to inbreeding depression is not well understood, and therefore, we specified 50% inbreeding depression due to lethal recessive alleles, a classic empirical estimate from fruit flies [43]. The reduction in first year survival caused by reduced heterozygote advantage is calculated by applying an exponential equation that includes the inbreeding coefficient of an individual.

2.4. Genotyping

DNA was extracted by salting-out [46] or using the DNeasy Blood and Tissue Kit following Qiagen’s (the manufacturer) instructions. The preparation of reduced-representation genome libraries, sequencing, and the discovery of genome-wide single nucleotide polymorphism loci (SNPs) was carried out using the DArTseq complexity reduction methodology of Diversity Arrays Technology [47] and described in a previous study [37]. This generated 13368 SNP loci that were then filtered for downstream analysis using the R package dartR [48], as explained below. The function gl.sexlinkage was used to detect putatively sex-linked loci, which were removed from the dataset. Loci containing more than one SNP were thinned to retain the SNP with the highest polymorphism information. Locus reproducibility was determined during marker discovery from technical replicates representing 25% of all data, and loci with average reproducibility <100% were removed from the dataset to minimise error rates.

Three genetic datasets were then created by sub-setting the data by sampling location and applying different quality-filtering criteria in dartR to meet the requirements of each downstream analysis. The first dataset of 4218 loci, created by retaining individuals from all sampling locations and removing loci with a call rate of <85%, was used to detect alleles unique to the lowland population at Yellingbo. The second dataset of 1066 loci, created by retaining only the Lake Mountain and Yellingbo populations and removing loci with a call rate of <100%, was used during simulations to represent genetic variation at Yellingbo and a thoroughly sampled representative highland population. The third dataset of 1076 loci, created by retaining only Yellingbo individuals and removing loci with a call rate of <99%, was used to calculate pairwise kinships at Yellingbo.

2.5. Detecting Alleles Unique to the Lowland Population

Alleles occurring only within the lowland population at Yellingbo (locally unique alleles) were detected by comparing the allele frequencies of all highland individuals pooled together with allele frequencies of lowland individuals sampled at Yellingbo from 1997–2019. The package poppr [49] was used to report unique alleles and counts of each locally unique allele in the population. Loci with locally unique alleles found as a single copy in only one Yellingbo individual were removed, as these could represent genotyping errors or rare deleterious mutations. Allele frequencies calculated for loci with locally unique alleles for Yellingbo individuals sampled in 2011–2019 were used in genetic rescue simulations.

2.6. Pairwise Kinship Estimation

Inbreeding among individuals in the population was estimated using pairwise kinships, which measure the proportion of the genome that is identical by shared ancestry between pairs of individuals [50]. Kinships calculated using genetic markers often better represent genomic similarity than do pedigree-derived estimates [51]. Pairwise kinships were calculated with the beta.dosage function in the R package hierfstat [52] using 1076 loci and all Yellingbo genotypes from 1997 to 2019. This kinship estimator has a mean of zero for the focal population, with negative values representing below-average kinship and positive values representing above-average kinship [53]. Vortex requires positive kinship values that represent the probability that any two homologous alleles drawn from a pair of individuals are identical by descent [41]. Therefore, we used the transformation described previously [54] to convert calculated kinships to proportions, with the resulting pairwise kinship value for the least-related pair equal to zero. Kinship values for the 2019 population were incorporated into simulations as a matrix. By default, Vortex regards non-genotyped individuals as completely outbred and unrelated, which is unrealistic. Accordingly, five non-genotyped individuals were represented in the kinship matrix with pairwise kinship values set to the mean calculated for the 2019 individuals.

2.7. Survival and Reproduction Parameters Used in Vortex Models

The Vortex models were populated with realistic parameter values (Table 2) using published estimates of reproduction and mortality at different life stages [39]. The age classes for which that study calculated mortality differed from those required by Vortex. As such, mortality from 0 to 1 years was calculated as the sum of total litter loss (9%) for both sexes, plus mortality for each sex from when juveniles first emerged from the pouch to 12 months old. The mean annual adult (>2 years old) mortality rate was estimated by averaging the annual estimates from 1996 to 1999.

Based on the observation of a relatively stable Yellingbo population at ~110 individuals in the 1990s, simulations using realistic demographic parameters were expected to yield a demographically stable population—that is, one that did not change in size by more than 10% over 50 years in the absence of inbreeding depression or environmental catastrophes (see scenario 1990s Condition below). However, simulations using published mortality estimates resulted in a rapidly growing population (Supplementary Figure S1). To achieve demographic stability, we increased the mortality rates for individuals aged 0 to 1 years by 6% for both sexes to 42% in males and 41% in females. Actual mortality at <3 months old was likely underestimated in the empirical studies because the initial number of young present in the pouch at birth (one or two) could not readily be established, preventing a reliable estimation of partial litter loss [39]. Accordingly, increasing mortality at age 0–1 years by 6% to achieve demographic stability was deemed a realistic adjustment.

2.8. Sensitivity Analysis

The sensitivity of PVAs to input parameter estimates was investigated using perturbation analysis—using simulations of scenario 1990s Condition (with no inbreeding depression) while increasing or decreasing a single input parameter by 10% relative to its baseline value (Table 2). The average growth rate (r) was calculated from 200 replicate runs. The growth rate was used to assess model sensitivity because other parameters, such as survival probability and population size, have theoretical limits of zero and/or one, which limits their usefulness for estimating effect size. The relative sensitivity of the model to each parameter was calculated with the following formula: (r₊ – r₋)/(0.2 × r₀), where r₊ is the mean r with the parameter increased by 10%, r₋ is the mean r with the parameter decreased by 10%, r₀ is the mean r using the baseline parameter value, and 0.2 is equal to the perturbation in the parameter value. These estimates indicated whether certain parameters had a disproportionate effect on models, which can make predictions less reliable if the parameter estimates are inaccurate.

2.9. Simulated Scenarios

Five general scenarios were tested, which are outlined in Table 1 and described in detail below. For all scenarios except 1990s Condition, the starting population was specified using a studbook file (a list of founder individuals and their characteristics in Vortex) that included the age and sex of each individual at Yellingbo in 2019. Relationships among individuals were not provided in the studbook file. Instead, a kinship matrix was also provided for all scenarios except 1990s Condition to estimate individual inbreeding. For scenarios in which the lowland population was supplemented with highland individuals, the population started with the same set of 20 (10 male and 10 female) Yellingbo founders that were randomly sampled from the studbook containing 35 Yellingbo individuals in 2019. Translocated animals had the same mortality and reproduction rates as the recipient population once added to the population (not including inbreeding depression effects), and all were assumed to survive translocation. For each simulated scenario, the extinction probability was estimated as the proportion of replicate runs that went extinct, with extinction defined as only individuals of one sex remaining; this definition was used in all subsequent simulations. Mean and standard deviation for output parameter estimates were generated using 200 replicate iterations for each scenario. Increasing the number of replicates above 200 did not decrease the standard error of estimates. Simulation outputs included observed heterozygosity, population size (N), growth rate across all years (r), and time to reach N = 110.

(i)

1990s Condition: The effect of limited carrying capacity and inbreeding on population size at Yellingbo

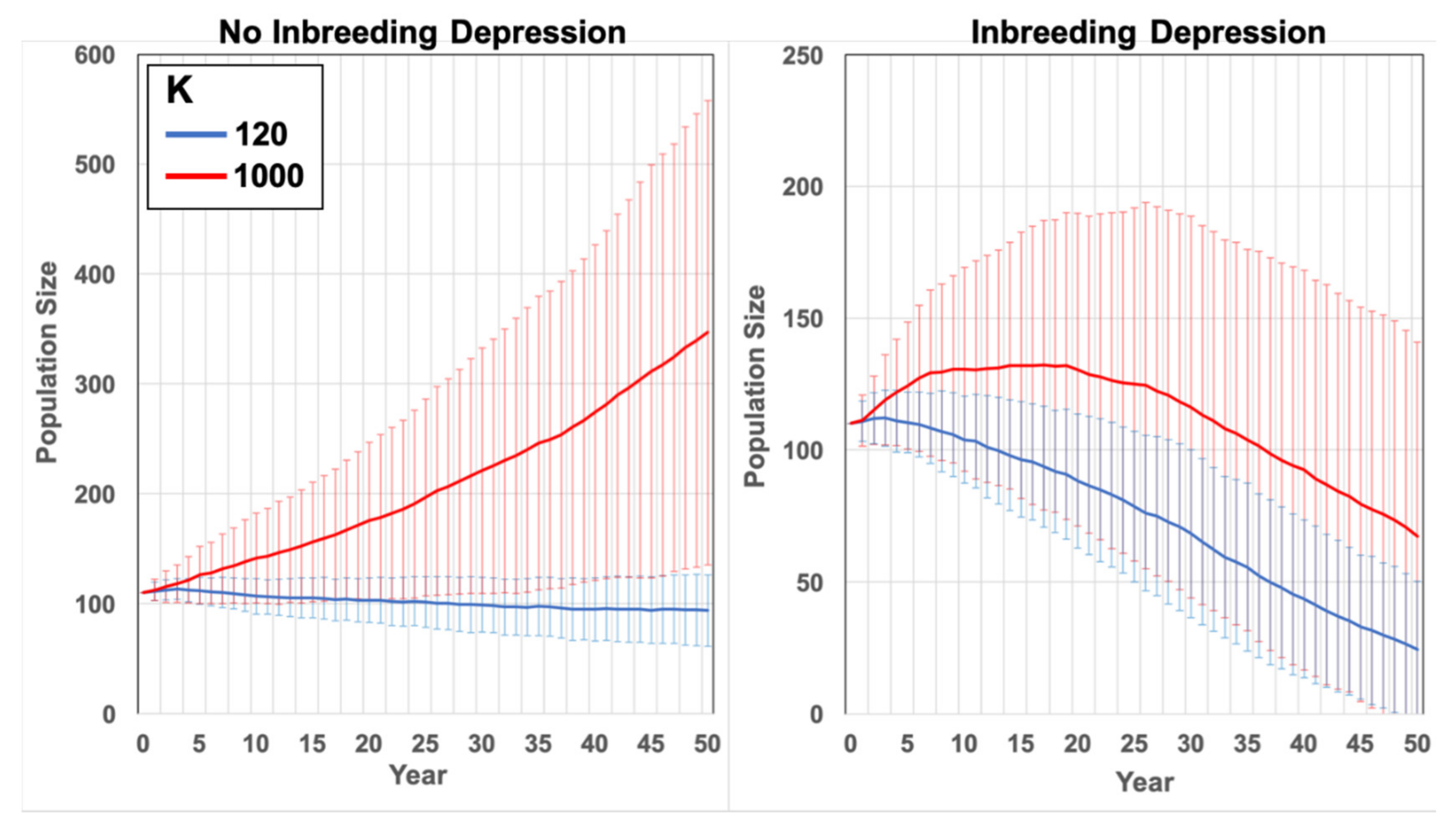
The influence of the limited carrying capacity and inbreeding on the lowland population size at Yellingbo since the 1990s was determined. A population of 110 individuals with all pairwise kinships equal to zero was simulated to represent the population in the 1990s, varying the carrying capacity to K = 120 and K = 1000. These scenarios were run using actual juvenile mortality estimates rather than those increased by 6% to achieve a demographically stable baseline in other scenarios. Simulations at these carrying capacities were run with and without inbreeding depression.

(ii)

2019 Trajectory: The forward projection of the population size of lowland possums at Yellingbo without genetic rescue

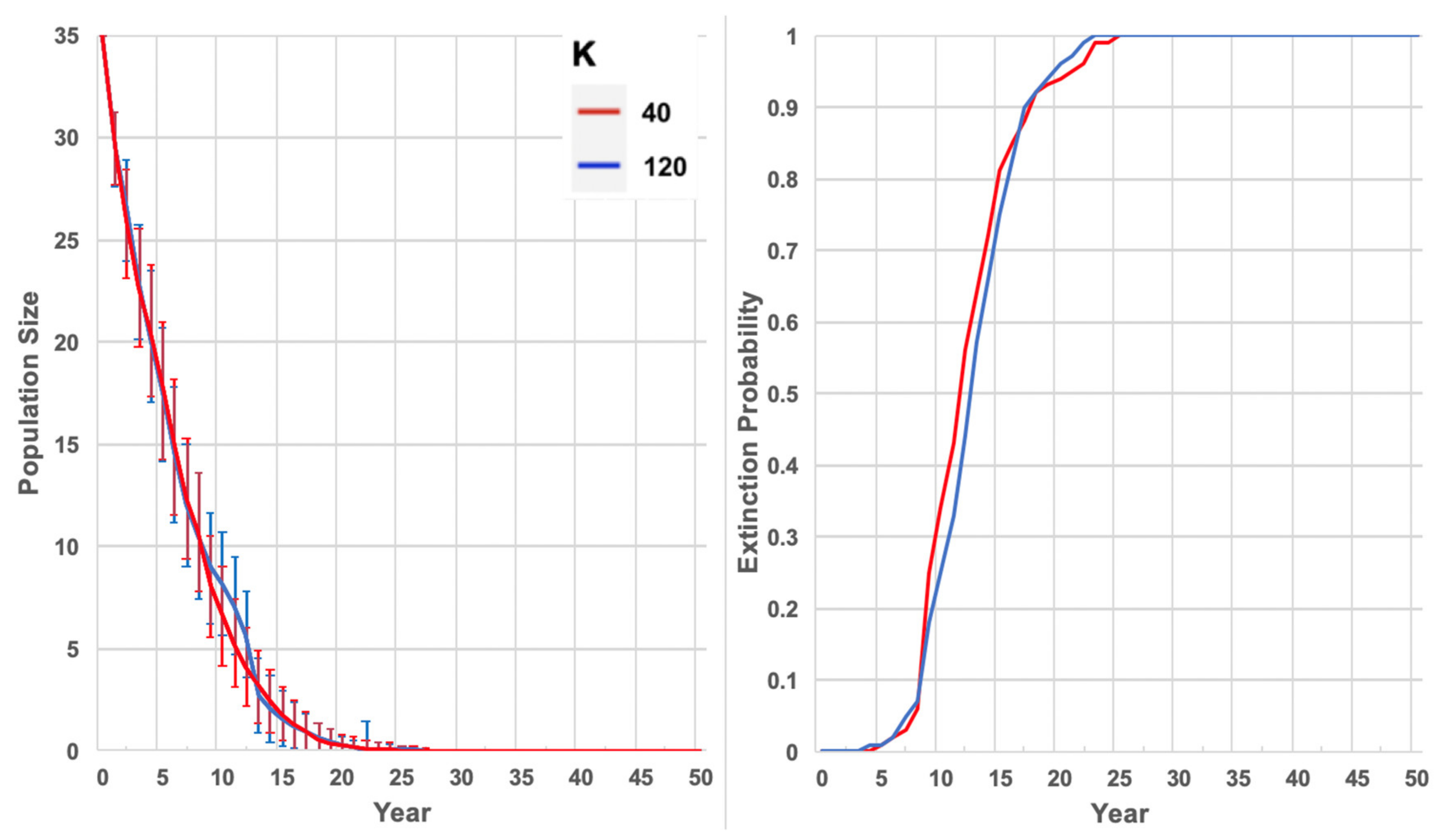
The time until extinction of the lowland population at Yellingbo without genetic rescue was estimated with simulations, starting with 35 lowland individuals alive in 2019 in the absence of supplementation and specifying pair-wise kinships, including inbreeding depression and as actual juvenile mortality rates (as for the 1990 Condition above). These simulations were carried out using two different carrying capacities; K = 40, representing the currently degraded habitat conditions, and K = 120, representing higher quality habitat present in the 1990s.

(iii)

Demographic Rescue: The effect of numerical population reinforcement on population growth

Scenarios were run to separate the effect of supplementation on population growth (i.e., demographic rescue) from the effect of genetic rescue. The effect of supplementation on population size was estimated by introducing migrants from a donor population genetically similar to the lowland population. The donor population was made genetically similar to that of Yellingbo by setting non-zero kinships between Yellingbo and donor individuals. Kinship values were set at the beginning of each run by randomly sampling from a Poisson distribution with a mean equal to the average pairwise kinship between individuals at Yellingbo (mean = 0.5, the kinship matrix is provided in the Supporting Data). This was also done for pairwise kinships between individuals within the donor population to make it similarly inbred to Yellingbo. Input allele frequencies for this donor population were identical to those of the lowland population.

(iv)

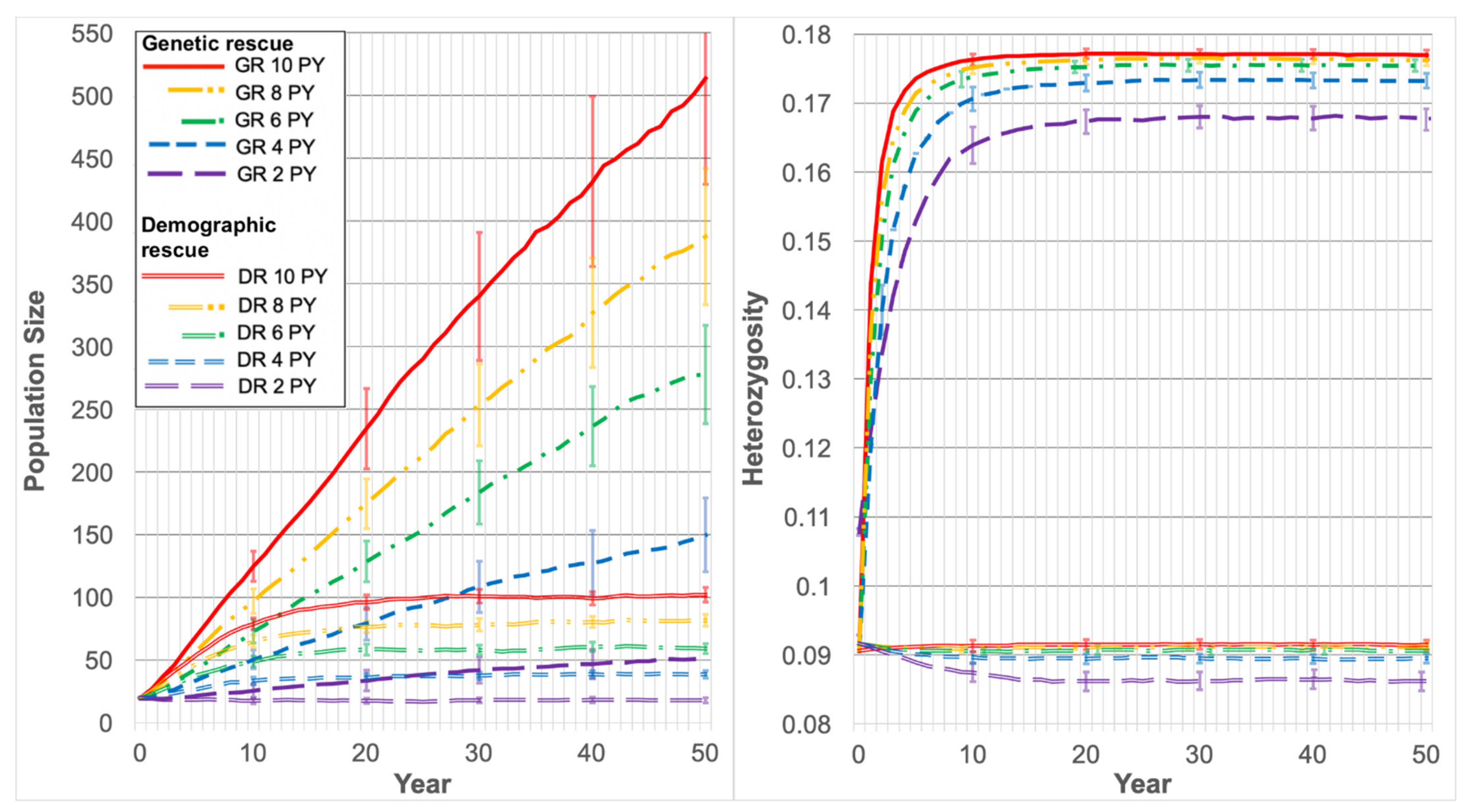
Genetic Rescue: The supplementation of a new lowland population with highland possums

All genetic rescue scenarios were carried out assuming that a new population would be founded using 20 lowland individuals relocated from Yellingbo. To represent the founding of a new population in high-quality habitat, a carrying capacity of 1000 was specified in genetic rescue scenarios. Scenarios were run to determine the minimum supplementation rate required to establish a demographically stable (N changing by <10% over 50 years) population of at least 110 individuals, starting with 20 lowland founders (Table 1). This target size was chosen to recreate the apparent demographic stability observed at Yellingbo in the 1990s and early 2000s [39]. The number of supplemented individuals increased by increments of two (one of each sex) to maintain equal sex ratios during simulations.

For genetic rescue scenarios, a highland population was created using allele frequencies calculated for the Lake Mountain population. These highland individuals were specified as unrelated to each other, and unrelated to lowland individuals, by setting pairwise kinships to zero. This enabled the simulation of genetic rescue by introducing outbred individuals. The size of the highland population was set to 1000 individuals with the mean and standard deviation set to 1 for survival at all life stages to ensure that the population remained sufficiently large for translocation and maintained genetic diversity for the duration of simulations. All other parameters were the same as those used for the lowland population at Yellingbo.

Genetic rescue effects were measured as changes in the mean observed heterozygosity and the mean population size from the first to the last year of simulation, the mean growth rate for all years (r), and the mean time to reach N=110. Changes in genetic diversity in the rescued population were modelled by specifying the observed allele frequencies for 1066 loci for the highland population and lowland individuals alive in 2019, and using these to calculate heterozygosity for each year of simulation.

(v)

Genetic Swamping Test: Determining whether a higher supplementation rate risks the replacement of locally unique alleles

Vortex outputs summary statistics for loci only at the end of simulations. Thus, allele frequencies and allele retention probabilities were estimated in a time series; genetic rescue scenarios were repeated with simulations that ran for 10, 20, 30, and 40 years. These values were compared between different supplementation rates to determine whether higher rates of gene flow reduced the retention of locally unique alleles. Whether unique lowland allele retention probabilities and frequencies differed significantly among supplementation rates was determined using aligned rank transformation analysis of variance (ART-ANOVA) in the R package ARTool v.0.10.7 [55]. This test is suitable for non-parametric data with paired observations with categorical predictors. Generalised linear models were fit with ARTool with the mean retention probability or frequency as the response, the translocation rate as a predictor, and with data paired by specifying a random intercept for each allele.

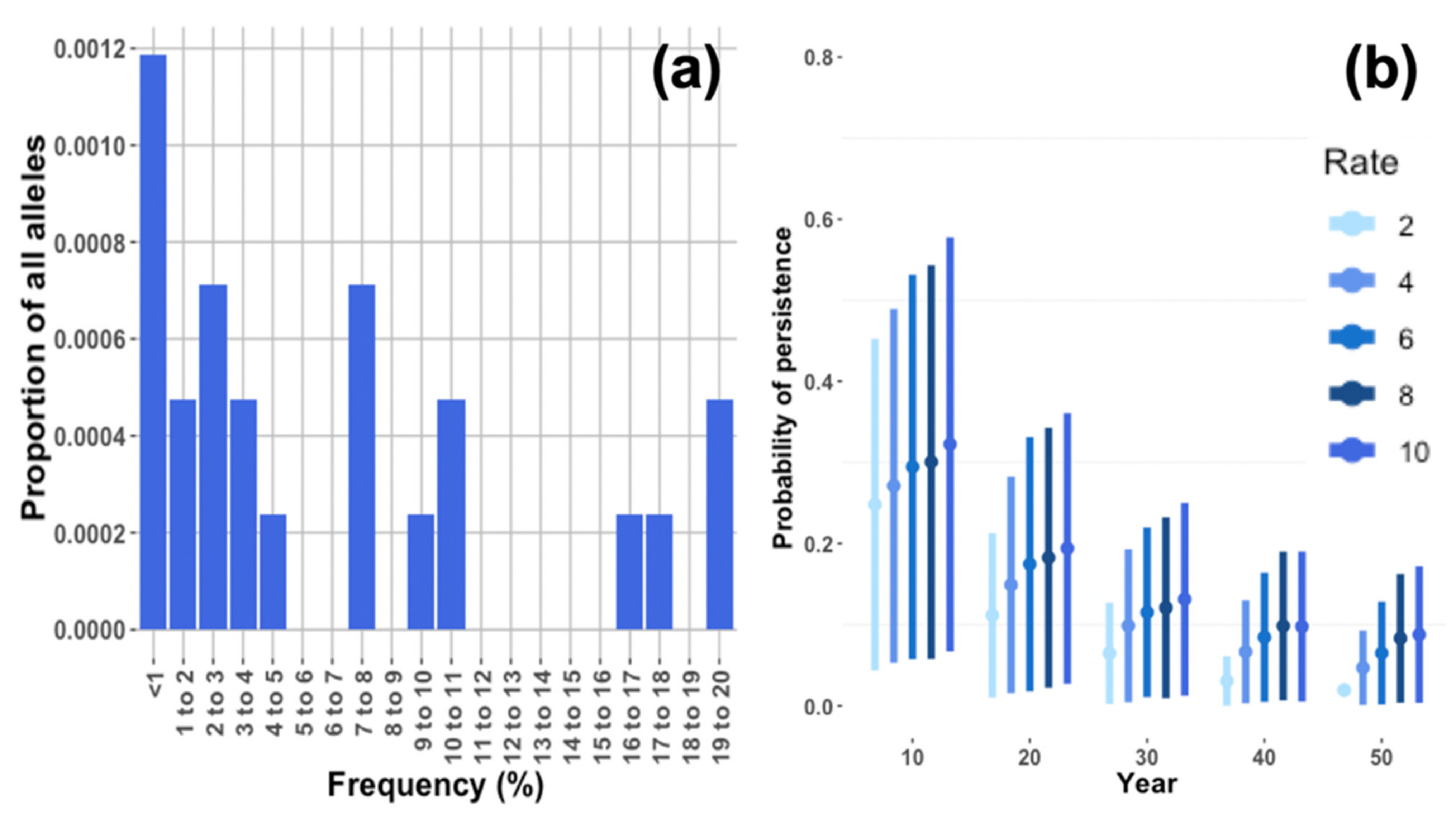
Only 23 loci with locally unique lowland alleles were detected (see Section 3.4). Because such a small number of locally unique alleles would make it difficult to predict the effect of the starting allele frequency on retention probability, we used 230 alleles with frequencies replicating those of the 23 observed unique alleles. Frequencies for these unique alleles were set to zero in the highland population. All alleles were assumed to be independently assorting and selectively neutral. The retention probability for each unique lowland allele was given by the proportion of replicate runs in which it did not go extinct.

3. Results

3.1. Sensitivity Analysis

Perturbation analysis indicated that no single input parameter had a greatly disproportionate effect on the population growth rate (

Table 3. Sensitivity analysis output. The relative sensitivity of PVAs to different input parameters based on perturbation analysis.

Input Parameter	Sensitivity Index
0–1 year annual mortality	−0.29
1–2 year annual mortality	−0.11
2+ year annual mortality	−0.44
Proportion of females breeding	0.35
Brood size	0.39

). Annual adult mortality (2+ years) had the greatest relative impact on the population growth rate, closely followed by the litter size (average number of individuals per litter). Point values for r at each parameter value are given in Supplementary Figure S4.

3.2. Trajectory of the Lowland Population without Genetic Management

In the absence of inbreeding depression, simulations using demographic rates estimated in the 1990s showed that population growth was limited by the carrying capacity (Figure 2). A large carrying capacity of 1000 resulted in positive growth (r = 0.02, SD = 0.08) for the 50-year simulated timeframe. Limiting the carrying capacity to a more realistic value of 120 resulted in population decline (r = −0.013, SD = 0.10) for the duration of the simulations. When inbreeding depression was incorporated into the models that assumed that individuals in the starting population are unrelated (MK = 0), the population declined regardless of whether the carrying capacity was 1000 (r= −0.028, SD = 0.12) or 120 (r = −0.039, SD = 0.15), although in the former case, it initially increased for half of the simulation period (Figure 2).

Simulations of the Yellingbo population from 2019 onwards without genetic rescue and with the level of inbreeding informed by genetic estimates (kinship matrix and 2019 allele frequencies) resulted in extinction probabilities of 50% within 11 years, and 100% within 23 years (Figure 3). The mean time to extinction was 11.7 years (SD = 3.4) with a growth rate (r) of −0.20 (SD = 0.24) regardless of the carrying capacity (K = 40 or K = 120). This suggests that the lowland population will likely be extinct within two decades without genetic rescue, even if habitat quality is improved.

3.3. Effect of Genetic and Demographic Rescue on Lowland Population Recovery

Mean population size at the end of simulations of genetic rescue scenarios increased with the supplementation rate (Figure 4). Supplementation with 10 highland individuals per year was the only scenario to reach the target size within 10 years, taking an average of 8.27 (SD = 2.0) years with a growth rate of r = 0.07 (SD = 0.1). This was closely followed by supplementation with 8 individuals per year, which took 11 years to reach the target size with a growth rate of r = 0.06 (SD = 0.09).

Alleviation of inbreeding had an effect distinguishable from merely increasing population size; demographic rescue scenarios (supplementation from the genetically Yellingbo-like population) failed to produce positive population growth in simulations regardless of the supplementation rate (Figure 4). The highest mean population size for the demographic rescue scenarios was 102 individuals and was reached after 49 years at a supplementation rate of 10 individuals per year. Varying the contribution of lethal recessive alleles from 0–75% did not substantially alter the simulation outcomes, although increasing the contribution of lethal alleles unrealistically to 100% resulted in much higher population viability and larger genetic rescue effects (Supplementary Figure S2).

Mean heterozygosity across replicate runs also increased with the supplementation rate for genetic rescue. The highest mean heterozygosity reached in simulations was 0.177 (SD = 0.001), at a supplementation rate of 10 individuals per year. This was the highest value possible, given the genetic diversity of the highland population (heterozygosity = 0.18). Maximum heterozygosity was reached sooner with higher rates of gene flow. For genetic rescue, all translocation rates reached at least 90% of the source population’s heterozygosity within ten years. As with the population size, the increase in genetic diversity from genetic rescue was distinguishable from that of demographic rescue. The highest heterozygosity for any demographic rescue scenario was 0.092, which was the highest possible, matching the genetic diversity at Yellingbo.

3.4. Locally Unique Alleles in the Lowland Population at Yellingbo

Out of 4218 loci examined, 23 loci (0.55%) were found to harbour alleles that occurred only in the lowland population. This excluded 70 alleles that occurred in the heterozygous state in a single individual and were removed; including these alleles would increase the proportion of loci with unique lowland alleles to 2.2%. A large proportion of the locally unique alleles were very rare; out of 23 locally unique alleles, 5 (22%), were found at frequencies below 1% in the lowland population (Figure 5a). When all Yellingbo samples from 2011–2019 were considered together, the highest recorded frequency for any unique allele was 57.7%. The highest frequency of any unique allele in 2019 was 19.9%. Of the 23 alleles detected from 2011–2019, 13 (57%) were not detected in 2019 (noting that 14% of individuals were not genotyped in this year).

3.5. Risk of Decreased Retention of Locally Unique Alleles from Genetic Rescue

The overall mean retention probability for locally unique alleles was 0.29 (SD = 0.01) at 10 years of genetic rescue, declining to 0.06 (SD = 0.07) at 50 years (Figure 5b). When considered separately, the retention probability for alleles with starting frequencies >10% (Figure 6a) during genetic rescue were somewhat higher, with the highest mean retention probability after 10 years of genetic rescue being 0.68 (SD = 0.11) and the lowest 0.54 (SD = 0.10). After 50 years of genetic rescue, the highest retention probability at any translocation rate was 0.21 (SD = 0.05). For locally unique alleles with starting frequencies <10% (Figure 6b), the highest mean retention probability at 10 years of genetic rescue was much lower at 0.20 (SD = 0.16), with the lowest at 0.15 (SD = 0.12). The highest retention probability at 50 years was 0.04 (SD = 0.04).

Higher supplementation rates did not produce lower retention probabilities of locally unique alleles during genetic rescue but instead yielded overall higher probabilities (Figure 5). After 20 years of genetic rescue, retention probabilities were substantially higher when the translocation rate was increased from 8 to 10 individuals per year. The difference in retention probability at different translocation rates was statistically significant for all years: 10 years (F = 169.02, df = 4, p < 0.0001), 20 years (F = 238.2, df = 4, p < 0.0001), 30 years (F = 221.8, df = 4, p < 0.0001), 40 years (F = 312.75, df = 4, p < 0.0001), and 50 years (F = 393.9, df = 4, p < 0.0001). Differences between the translocation rates were also statistically significant for alleles with starting frequencies of <10%: 10 years (F = 64.52, df = 4, p < 0.0001), 20 years (F = 212.76, df = 4, p < 0.0001), 30 years (F = 115.78, df = 4, p < 0.0001), 40 years (F = 157.18, df = 4, p < 0.0001), and 50 years (F = 179.6, df = 4, p < 0.0001).

Despite higher retention probabilities, locally unique alleles were lower in frequency at higher rates of gene flow (Figure 6). After 10 years of genetic rescue, the highest mean frequency for alleles with a >10% starting frequency was 4.0% (SD = 1.0), which was observed at the lowest supplementation rate of two individuals per year. Using a rate of 10 individuals per year yielded a substantially lower mean frequency of 1.6% (SD = 1.6). For alleles starting at <10% frequency, the highest mean frequency was 0.8% (SD = 0.7), which was also observed at the lowest supplementation rate of the individuals per year. Using a rate of 10 individuals per year yielded a somewhat lower mean frequency of 0.4% (SD = 0.3). The difference in allele frequency at different translocation rates was statistically significant for all years: 10 years (F = 551.21, df = 4, p < 0.001), 20 years (F = 268.1, df = 4, p < 0.0001), 30 years (F = 143.72, df = 4, p < 0.0001), 40 years, (F = 30.5, df = 4, p < 0.0001), and 50 years (F = 8.9, df = 4, p < 0.0001). Differences between the translocation rates were also statistically significant for the initially rare alleles (<10%): 10 years (F = 64.52, df = 4, p < 0.001), 20 years (F = 105.2, df = 4, p < 0.0001), 30 years (F = 35.35, df = 4, p < 0.0001), 40 years, (F = 8.43, df = 4, p < 0.0001), and 50 years (F = 12.31, df = 4, p < 0.0001).

4. Discussion

Many threatened wildlife species have highly disjunct distributions with little to no natural gene flow between populations, and translocations are critical for their long-term demographic and genetic stability [21]. Reintroducing populations within the historical range of a species or establishing populations beyond the historical range in low-threat areas (such as predator-free islands or reserves) are increasingly common [30,56,57]. Using predictive models to guide the founding of isolated populations with ongoing translocations is critical to maximising species-wide genetic variation [58]. We demonstrated how PVAs that incorporate inbreeding and inbreeding depression can predict how much locally unique variation can be retained while genetic rescue increases overall genetic variation.

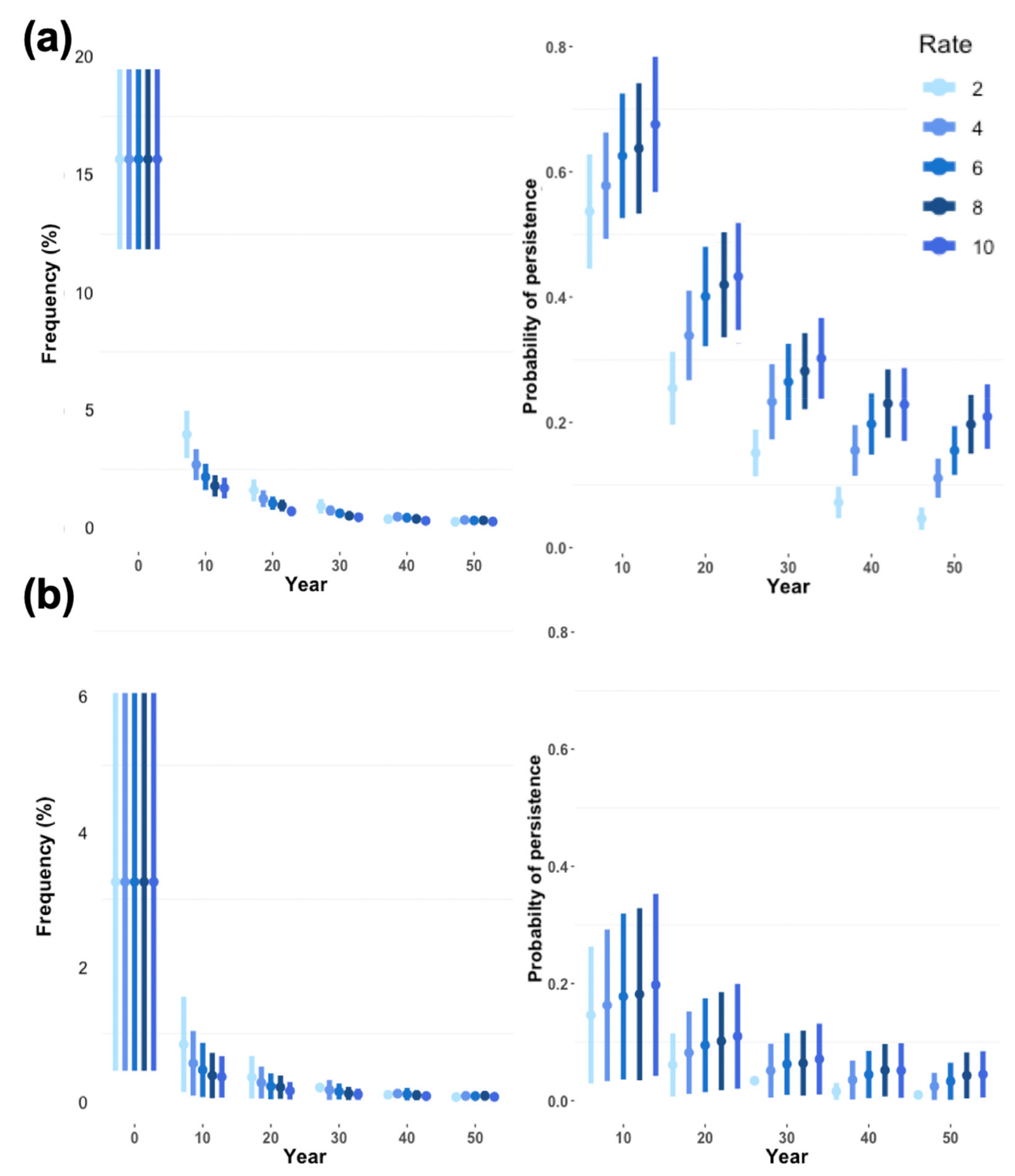
PVAs predicted a very high probability that the lowland population of Leadbeater’s possum will go extinct within two decades (100% in 23 years) without any intervention. As environmental impacts on mortality and reproduction were minimised in simulations to make inferences based primarily upon genetics, this is likely an overestimate of time to extinction. Inbreeding depression strongly increased population decline in simulations, although a low carrying capacity was shown to curtail population size, even in the absence of inbreeding depression. This highlights the importance of providing lowland individuals with high-quality habitat to achieve population growth under genetic rescue. Reinforcing the population with only Yellingbo individuals (demographic rescue) did not sufficiently support population growth to reach our target size of 110 individuals, even using the largest translocation rate of 10 individuals per year. We demonstrated that a modest portion of neutral locally unique variation detected in the lowland population can likely be preserved through a combination of population expansion and outcrossing. Approximately 26% of unique lowland alleles occurred at frequencies above 10%, which had a >50% probability of persistence after 10 years of rescue.

There were several key assumptions in our PVAs that could bias estimates of genetic rescue and allele retention. Random mating among highland and lowland individuals was assumed in all scenarios. Preferential mating among individuals originating from similar habitat or populations can impede outcrossing attempts [59]. For Leadbeater’s possum, this could cause translocated highland individuals to increase in abundance and supplant lowland individuals, increasing the risk of genetic swamping. This may be prevented by the careful choice of translocation sites, maximising the probability of highland-lowland pairings. Assortative mating among lowland individuals could also subvert genetic rescue efforts. However, females of some species become more selective in their mate choice if they are inbred, developing a preference for outbred males [60]. For lowland possums, this would result in a preference for highland mates, potentially increasing admixture rates and improving locally unique allele retention rates by increasing the fitness of individuals carrying such alleles, as well as increasing population growth and thus, reducing genetic drift. Our PVA models also assumed that the currently observed unique genetic variation is selectively neutral. If locally unique alleles are favourable, selection will increase their likelihood of persistence and frequency more so than if they are neutral. The effect of selection is expected to increase over time with increasing population size [22]. Alternatively, lowland-specific genetic variation may be maladapted if lowland individuals are relocated to a habitat that differs from Yellingbo, in which case, this variation would be selected against. All alleles were also assumed to be unlinked, whereas linkage can promote allele retention by genetic hitch-hiking of neutral alleles linked to loci under selection [31].

PVAs predicted that the supplementation rates of up to 10 individuals per year for 8 years will likely be necessary to meet population recovery targets. Although this supplementation rate is substantial, lower rates and less frequent supplements will likely be sufficient in reality to achieve the target population size. This is because the demographic rates modelled were estimated from data collected from the Yellingbo population during the 1990s, at which time the population was already inbred, having roughly half the genetic diversity of highland populations [36]. Therefore, the positive effects of genetic rescue and immigration will likely be greater than those estimated in this study, and fewer translocations might be necessary to provide the desired population benefits. Furthermore, Vortex does not account for a fixed genetic load in recipient populations [41], which means that fitness could be further improved by increasing heterozygosity at loci with fixed (100% homozygous) deleterious alleles. Using assumptions similarly optimistic as ours, such as completely unrelated migrants, population growth projections were still underestimated by Vortex relative to the real data for translocations in another marsupial species (Bettongia penicillata ogilbyi) [61]. Thus, it is conceivable that the required rate of translocation estimated in our study is an overestimate. Conversely, a higher rate of supplementation may be necessary given that all individuals in our simulations were assumed to have the same mortality rate as local individuals. This is unrealistic, given that elevated post-translocation mortality is common in wildlife [62]. Genetic rescue should be implemented within an adaptive management framework, with post-translocation monitoring data incorporated into the models to make updated predictions [63,64]. Ongoing monitoring of fitness will also enable incorporation into future models of unlikely but possible effects of outbreeding depression and maladaptation. The genetic diversity and viability of source populations must also be considered, and further PVAs can help predict and mitigate the negative impacts of harvest [58,65].

The sensitivity of our PVAs to different parameter estimates suggests that management interventions that improve survival and reproductive output could facilitate more rapid population growth during genetic rescue. In particular, the proportion of adult females that were breeding and adult mortality had somewhat larger effects on growth rates than other parameters. Establishing colonies with translocated individuals and unpaired local possums could increase the proportion of females breeding in any given year. Adult mortality could be decreased by feral predator elimination measures, given that predation by feral cats and foxes is a known cause of mortality in Leadbeater’s possum [66], and a common cause of translocation failure in Australian mammals [67]. Such measures could reduce the amount of supplementation required to reach a target population size.

Lower retention of locally unique lowland alleles at higher rates of supplementation with highland individuals was not observed in any of the simulated scenarios. However, locally unique alleles did decrease in frequency at higher supplementation rates, which is likely an effect of higher proportions of immigrants diluting neutral allele frequencies. A higher retention probability under more intensive gene flow was presumably caused by weaker genetic drift for scenarios where the population size increased more quickly. Thus, under the conditions used in simulations for the lowland population of Leadbeater’s possum, genetic drift poses a greater threat to the preservation of unique genetic variation than dilution at higher rates of translocation. The number of lowland and highland founders will be a strong determinant of the number of alleles retained. Based on allele retention models in another translocated marsupial, using 20 founders is expected to retain ~60% of rare (frequency = 0.05) alleles and using at least 60 founders is expected to retain ~90% of rare alleles [30]. Minimising genetic and demographic stochasticity in small populations by rapid supplementation has been recommended in other species to maximise the effectiveness of population reinforcement [68]. Our study suggests that this principle could also apply to genetic rescue and the preservation of locally unique variation. Although the frequency of these locally unique alleles may be reduced at higher supplementation rates, this would be offset by the benefits of a larger population size (such as reduced stochasticity), and selection will increase their frequency if they present a fitness advantage.

Previous experimental investigations into genetic swamping effects following genetic rescue have focused on locally adaptive alleles [22,69]. However, genetic variation that is not currently subject to selection (such as cryptic variation that only alters phenotype under atypical circumstances) can become useful if environments change; such enhancement of evolutionary potential would preserve apparently neutral variation in the face of uncertain futures [14,70]. Although only a small proportion of alleles (0.55–2.2% of loci) were unique to the lowland population at Yellingbo and none were fixed, it is possible that they could contribute to local adaptation or evolutionary potential. Much unique variation will have been lost from the lowland population owing to the small population size over decades, with an observable reduction in the number of locally unique alleles from 2011 to 2019 (Supplementary Figure S4). Nonetheless, locally adaptive genetic variation can persist in the presence of strong genetic drift [71]. The detection of locally unique variation is also dependent on marker type and density, with SNPs representing only one form of genetic variation. Other types of variation that contribute to local adaptation include structural and copy number variants [72]. Such variation is unlikely represented in SNP datasets, making the amount of unique variation among populations an underestimate when using SNPs alone. Deleterious alleles that are recent mutations tend to be prevalent at low frequencies [73], and many locally unique alleles detected were very rare (17% with <1% frequency). However, it is unclear whether the locally unique alleles detected could be deleterious, because intense genetic drift in the lowland population will have strongly influenced allele frequencies.

The contribution of ongoing post-rescue gene flow to demographic and genetic stability is another important management consideration. Although there is some potential that supplementing the lowland population with individuals from large populations will increase the genetic load, maintaining heterozygosity and minimising inbreeding via occasional gene flow will mask recessive genetic load. Some studies have cited pronounced population declines following the immigration of as few as a single individual as evidence that genetic rescue can further imperil small populations by introducing deleterious alleles that are more numerous in larger populations [74]. Fitness decline with insufficient genetic rescue is unsurprising because inbreeding (identity-by-descent) inevitably increases to pre-translocation levels in very small populations without ongoing gene flow [75]. Founding a new lowland population near existing Central Highlands populations could enable dispersal between populations, which would increase long-term population viability. Natural dispersal could also facilitate the spread of lowland genetic variation that is potentially adaptive to warmer conditions, improving the fitness of Central Highlands populations under climate change. The establishment of self-sustaining populations is a highly sought-after goal in conservation management [76]. However, populations that are genetically isolated with N_e < 1000 will inevitably require at least occasional assisted gene flow if natural gene flow is not possible [1,58]. Early interventions that prevent extreme reductions in N_e and mitigating the underlying causes of a small population size are the best means of reducing dependency on conservation management.

5. Conclusions

We estimate that without intervention, all unique lowland Leadbeater’s possum genetic variation will be lost due to extinction of the last population of the lineage within approximately two decades, whereas modest amounts of this unique variation can be preserved with genetic rescue. A higher proportion of locally unique variation is predicted to be retained by adding a greater number of highland animals each year with genetic rescue of the lowland population. Ongoing gene flow from highland populations will also be critical to maintaining long-term demographic and genetic stability within the lowland population. Although PVAs are based on many assumptions, they can form an integral component of adaptive genetic management and offer flexibility to incorporate post-translocation data to resolve uncertainties such as relative fitness among outbred and inbred individuals.